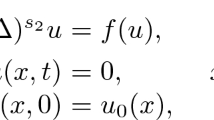Abstract
The Cauchy problem in \(\mathbb {R}^n\), \(n\ge 1\), for the degenerate parabolic equation
is considered for \(p\ge 1\). It is shown that given any positive \(f\in C^0([0,\infty ))\) and \(g\in C^0([0,\infty ))\) satisfying
one can find positive and radially symmetric continuous initial data with the property that the initial value problem for (\(\star \)) admits a positive classical solution such that
but that
and
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The nonlinear diffusion equation
has been understood quite thoroughly in regimes of solutions emanating from \(L^p\) initial data. Classical findings in this regard have asserted that the asymptotic behavior of finite-mass solutions to an associated Cauchy problem in \(\mathbb {R}^n\) essentially coincides with that of certain explicit self-similar solutions, the so-called Barenblatt solutions, both in the case \(m>1\) in which (1.1) becomes the porous medium equation, and in the case when \(m\in (\frac{n-2}{n},1)\) [13, 20, 21]. Further examples have revealed a substantially more colorful picture in the more singular range \(m\le \frac{n-2}{n}\), including more complex large time behavior of positive solutions [15, 16], phenomena of nonuniqueness, mass loss and finite-time extinction [8, 19, 21], and even instantaneous extinction in the flavor of results on nonexistence when \(m\le 0\) [6, 7]; especially subtleties of finite-time extinction mechanisms in dependence of spatial decay features of the initial data have been the object of study in a considerable part of the recent literature [2,3,4,5, 9, 10, 14].
In comparison to this, the knowledge about possibly nontrivial facets of solution behavior in the presence of initial data which grow near spatial infinity seems noticeably more restricted, mainly concentrating on the analysis of explicit examples [1], and of essentially one-dimensional wave-like transport mechanisms ([1]; see also [26, 27] for examples on propagation at non-constant speeds). In order to describe two exceptions in this direction recently achieved for \(m<0\), let us reformulate (1.1) in a way that appears convenient in this framework by involving bounded quantities rather than unbounded functions. Specifically, we shall subsequently be concerned with the full initial value problem
with \(p\ge 1\) and a prescribed positive function \(u_0\), recalling that when \(p>1\), via the substitution \(u=v^{-\frac{1}{p-1}}\) the PDE herein becomes equivalent to that in (1.2) with \(m=-\frac{1}{p-1}<0\).
In this setting, it is known that whenever \(u_0\in C^0(\mathbb {R}^n) \cap L^\infty (\mathbb {R}^n)\) is positive, the problem (1.2) possesses a minimal classical solution u ([6, 11]; cf. also Lemma 2.1 below for a precise statement), and that if in addition
then
[24]. On the other hand, in [11, Proposition 1.3] it has been found that any positive classical solution of (1.2) has the property that
so that, roughly speaking, any initial data satisfying (1.3) will lead to solution behavior somewhere between mere decay, as expressed in (1.4), and decrease at a rate near that of \(0<t\mapsto t^{-\frac{1}{p}}\), subject to the limitation in (1.5). That this latter restriction indeed is essentially sharp has recently been confirmed in [12, 28], where it has been seen that given any positive \(f\in C^0([0,\infty ))\) such that \(f(t)\rightarrow +\infty \) as \(t\rightarrow \infty \), one can find initial data such that the corresponding minimal solution of (1.2) satisfies
(see also Proposition 3.2 below).
Main results. The intention of the present note now is to provide an example which indicates that both the above two extremal types of decay behavior can actually be found approached by single trajectories. In fact, by means of a recursive design of initial data following the construction in the seminal work by Poláčik and Yanagida [18], we shall find a solution to (1.2), of quite simple basic structure by being radially symmetric and radially nonincreasing, which on the one hand exhibits arbitrarily slow decay along some unbounded sequence of times, and which on the other hand decreases at a close-to-maximum speed in the style of (1.6) along some further divergent time sequence. By fully acting within the realm of strictly positive smooth solutions, unlike previous discoveries of degeneracy-supported large-time oscillations in related problems [22, 25] this result does not rely on the presence of prescribed singular behavior at any point in space.
More precisely, our main result can be formulated as follows.
Theorem 1.1
Let \(n\ge 1\) and \(p\ge 1\), and let \(f\in C^0([0,\infty ))\) and \(g\in C^0([0,\infty ))\) be positive and such that
Then there exists a radially symmetric positive function \(u_0\in C^0(\mathbb {R}^n)\) such that
and that the corresponding minimal solution \(u\in C^0(\mathbb {R}^n\times [0,T)) \cap C^{2,1}(\mathbb {R}^n\times (0,T))\) of (1.2) has the properties that
that
but that with some \((t_j)_{j\in \mathbb {N}}\subset (0,\infty )\) fulfilling \(t_j\rightarrow \infty \) as \(j\rightarrow \infty \) we have
and
2 Minimal solutions: radial and radially nonincreasing data
To begin with, let us briefly recall from [11] a regularization-based construction of minimal solutions to (1.2) that will be appropriate for our purposes: Given an arbitrary family \((u_{0R})_{R>0}\) of functions satisfying
for \(R>0\) and \(\varepsilon \in (0,1)\) we consider the non-degenerate initial-boundary value problems
and the corresponding limit problems
On the basis thereof, the following statement on global existence of minimal solutions to (1.2) enjoying some convenient approximation features can be found proved in [11, Lemma 2.1, Proposition 1.1] (cf. also [6]).
Lemma 2.1
Let \(n\ge 1\), \(p\ge 1\) and \(u_0\in C^0(\mathbb {R}^n) \cap L^\infty (\mathbb {R}^n)\) be positive. Then given any family \((u_{0R})_{R>0}\) with the properties in (2.1), for each \(R>0\) and \(\varepsilon \in (0,1)\) one can find a positive classical solution \(u_{R\varepsilon } \in C^0(\bar{B}_R(0) \times [0,\infty )) \cap C^{2,1}(\bar{B}_R(0)\times (0,\infty ))\) of (2.2). These solutions satisfy \(u_{R\varepsilon }\searrow u_R\) in \(\bar{B}_R(0)\times [0,\infty )\) as \(\varepsilon \searrow 0\), where \(u_R\in C^0(\bar{B}_R(0) \times [0,\infty )) \cap C^{2,1}(B_R(0)\times (0,\infty ))\) is a positive classical solution of (2.3).
Moreover, there exists a positive function \(u\in C^0(\mathbb {R}^n \times [0,\infty )) \cap C^{2,1}(\mathbb {R}^n\times (0,\infty ))\) which is such that \(u_R\nearrow u\) in \(\mathbb {R}^n\times (0,\infty )\) as \(R\nearrow \infty \), and that u is a minimal solution of (1.2) in the sense that u solves (1.2) classically, and that whenever \(v\in C^0(\mathbb {R}^n\times [0,\infty )) \cap C^{2,1}(\mathbb {R}^n\times (0,\infty ))\) is positive and such that \(v_t=v^p\Delta v\) in \(\mathbb {R}^n\times (0,\infty )\) with \(v(x,0)=u_0(x)\) for all \(x\in \mathbb {R}^n\), we must have \(v\ge u\) in \(\mathbb {R}^n\times (0,\infty )\).
Having thus singled out a uniquely identifiable object to be dealt with subsequently, let us attach to this a convenient label that will facilitate notation in some places below.
Definition 2.1
Let \(n\ge 1\) and \(p\ge 1\). Then given any positive \(u_0\in C^0(\mathbb {R}^n) \cap L^\infty (\mathbb {R}^n)\), we let
where u denotes the minimal solution of (1.2) according to Lemma 2.1.
These minimal solutions satisfy a favorable comparison principle:
Lemma 2.2
Let \(n\ge 1\) and \(p\ge 1\), and suppose that \(u_0\) and \(v_0\) belong to \(C^0(\mathbb {R}^n) \cap L^\infty (\mathbb {R}^n)\) and satisfy \(0<u_0(x)\le v_0(x)\) for all \(x\in \mathbb {R}^n\). Then \(Su_0 \le Sv_0\) in \(\mathbb {R}^n\times (0,\infty )\).
Proof
Let \((u_{0R})_{R>0}\) be such that (2.1) holds. Then for each \(R>0\), the assumed positivity of v in \(\mathbb {R}^n\times [0,\infty )\) ensures that for the solutions of (2.3) from Lemma 2.1 we have the ordering \(0=u_R(x,t)<v(x,t)\) both for all \((x,t)\in \partial B_R(0) \times [0,\infty )\) and for any \((x,t)\in \bar{B}_R(0) \times \{0\}\). Since \(D^2 v\) is bounded in \(B_R(0) \times (0,T)\) for each \(T>0\), the comparison principle recorded in [23, Section 3.1] therefore applies and guarantees that \(u_R \le v\) in \(B_R(0)\times (0,\infty )\) for each \(R>0\), so that the claim results from the approximation part in Lemma 2.1, according to which, namely, we know that \(u_R(x,t)\rightarrow u(x,t)\) as \(R\rightarrow \infty \) for all \(x\in \mathbb {R}^n\) and \(t>0\). \(\square \)
The following observation will later on, in conjunction with Lemma 2.2, be used to make sure that minimal solutions cannot become unexpectedly small when initially bounded from below by positive constants.
Lemma 2.3
Let \(n\ge 1, p\ge 1\), \(a>0\) and \(u_0(x):=a\) for \(x\in \mathbb {R}^n\). Then \(Su_0 \equiv a\).
Proof
We let \(u:=Su_0\) and then first obtain that \(u\le a\) in \(\mathbb {R}^n\times (0,\infty )\) by Lemma 2.1, because \(\mathbb {R}^n\times [0,\infty ) \ni (x,t) \mapsto a\) solves (1.2) and u is minimal.
To see that for each \(x_0\in \mathbb {R}^n, t_0>0\) and \(\eta \in (0,a)\) we also have
given such \(x_0,t_0\) and \(\eta \) we pick \(R>0\) large enough such that
and introduce
with
and
Then using that \(\Delta \varphi \equiv \frac{-2n}{R^2}\), that \(\varphi ^{p-1} \le 1\) according to our assumption \(p\ge 1\), and that \(y'\equiv -\frac{2n}{R^2} \cdot y^{p+1}\), we see that
while \(\underline{u}\) lies below u on the corresponding parabolic boundary in that \(\underline{u}(x,t)=0<u(x,t)\) for all \(x\in \partial B_R(x_0)\) and \(t>0\) as well as \(\underline{u}(x,0)=y(0)\varphi (x)=(a-\frac{\eta }{2})\varphi (x) \le a-\frac{\eta }{2}<u(x,0)\) for all \(x\in B_R(x_0)\). As \(D^2 \underline{u}\) evidently is bounded, the comparison principle from [23, Section 3.1] therefore becomes applicable so as to ensure that \(\underline{u}\le u\) in \(\bar{B}_R(x_0)\times [0,\infty )\), and that thus (2.5) results upon an evaluation thereof at \((x,t)=(x_0,t_0)\), using (2.6) and recalling (2.7)–(2.9). \(\square \)
In what follows, for convenience in presentation we shall restrict most of our considerations to conveniently smooth radially symmetric and radially nonincreasing initial data by saying that a function \(\varphi :\mathbb {R}^n\rightarrow \mathbb {R}\) satisfies (H) if
By making use of the freedom to choose in (2.3) and (2.2) any family \((u_{0R})_{R>0}\) fulfilling (2.1), we can readily verify that when present initially, this property (H) is conserved throughout evolution:
Lemma 2.4
Let \(n\ge 1\) and \(p\ge 1\). If \(u_0\) complies with (H), then the minimal solution \(u=Su_0\) of (1.2) has the property that also \(u(\cdot ,t)\) satisfies (H) for all \(t>0\). In particular,
Proof
In the present situation, in (2.3) we can choose \((u_{0R})_{R>0}\) in such a way that, besides the requirements in (2.1), for each \(R>0\) the function \(u_{0R}=u_{0R}(r)\) is radially symmetric in \(B_R(0)\) and satisfies \(\partial _r u_{0R}(r) \le 0\) for all \(r\in (0,R)\). A standard argument applied to the non-degenerate problems (2.2) and their differentiated counterparts then shows that \(u_{R\varepsilon }(\cdot ,t)=u_{R\varepsilon }(r,t)\) is radially symmetric for all \(t>0, R>0\) and \(\varepsilon \in (0,1)\), and that \(\partial _r u_{R\varepsilon }(r,t) \le 0\) for all \(r\in (0,R), t>0, R>0\) and \(\varepsilon \in (0,1)\). In view of Lemma 2.1, taking \(\varepsilon \searrow 0\) and then \(R\nearrow \infty \) therefore yields the claim. \(\square \)
3 Preparing the inductive step: a result on continuous dependence
Besides the basic comparison property from Lemma 2.2, a second ingredient of crucial importance in our recurvive construction will be the following statement on monotone approximation that can be viewed as documenting a certain type of continuous dependence of solutions on the initial data.
Lemma 3.1
Let \(n\ge 1\) and \(p\ge 1\), let \(M>0\), and suppose that \((u_{0j})_{j\in \mathbb {N}} \subset C^0(\mathbb {R}^n)\) is such that
and that
with some positive \(u_0\in C^0(\mathbb {R}^n)\). Then the corresponding minimal solutions \(u_j:=Su_{0j}\) and \(u:=Su_0\) of (1.2) satisfy
Proof
We detail the proof only for the case when \(u_{0j}\searrow u_0\) as \(j\rightarrow \infty \), as the situation in which \(u_{0j} \nearrow u_0\) as \(j\rightarrow \infty \) can be covered by minor and obvious modification.
We fix any \(\alpha >\frac{n}{2}\) and observe that then
defines a positive function \(\varphi \in C^\infty (\mathbb {R}^n)\) which is such that
is finite, and which moreover satisfies
and
for all \(x\in \mathbb {R}^n\), because \(\frac{\xi }{\xi ^2+1}\le \frac{1}{2}\) and \(\frac{\xi }{(\xi +1)^2} \le \frac{1}{4}\) for all \(\xi \ge 0\).
Apart from that, taking any nonincreasing \(\zeta \in C^\infty ([0,\infty ))\) such that \(\zeta \equiv 1\) on \([0,\frac{1}{2}]\) and \(\mathrm{supp} \, \zeta \subset [0,1)\) we let
and note that then
with \(c_2:=\Vert \zeta '\Vert _{L^\infty ((0,1))}\) and \(c_3:=\Vert \zeta ''\Vert _{L^\infty ((0,1))} + 2(n-1)\Vert \zeta '\Vert _{L^\infty ((0,1))}\), because
and because \(|x|\ge \frac{R}{2}\) whenever \(R>0\) and \(\zeta '(\frac{|x|}{R})\ne 0\).
We now introduce
to rewrite the respective versions of (1.2) according to \(\partial _t H(u_j)=\Delta u_j\) and \(\partial _t H(u)=\Delta u\), and to thereby obtain that since \(\mathrm{supp} \, (\chi _R \varphi )\) is bounded for all \(R>0\),
for all \(t>0, R>0\) and \(j\in \mathbb {N}\). Here we may use that from Lemma 2.2 and the monotone approximation feature in (3.2) we already know that
to see that due to (3.6) and the inequalities \(0\le \chi _R \le 1\) for \(R>0\),
while combining (3.7) with (3.5) and (3.4) we obtain that
and that
because (3.1) together with Lemma 2.2 implies that
From (3.9)–(3.12) we thus infer that
and that hence
We now make full use of (3.2) to conclude, again by Lemma 2.2, that
with some limit function \(\widetilde{u}\) on \(\mathbb {R}^n\times [0,\infty )\) which satisfies
and hence particularly is strictly positive. We may therefore rely on Beppo Levi’s theorem, as well as on (3.2) explicitly once again, in turning (3.14) into the inequality
in which using the same token we may let \(R\nearrow \infty \) to obtain that
But since (3.8) in conjunction with the mean value theorem, (3.15) and (3.13) guarantees that for all \(x\in \mathbb {R}^n\) and \(T>0\) we can find \(\xi (x,T)\in (u(x,T),\widetilde{u}(x,T)) \subset [0,M]\) such that
this implies that
As thus
according to Grönwall’s lemma, thanks to the strict positivity of \(\varphi \) this shows that, again in view of (3.16), we must have \(\widetilde{u}=u\) a.e. in \(\mathbb {R}^n\times (0,\infty )\).
To conclude as intended, we only need to finally note that (3.15) and (3.13) together with (1.2) and standard parabolic regularity theory [17, Theorem V.1.1] warrant that for each compact subset K of \(\mathbb {R}^n\times (0,\infty )\), the sequence \((u_j)_{j\in \mathbb {N}}\) is bounded in \(C^{\theta ,\frac{\vartheta }{2}}(K)\) with some \(\theta \in (0,1)\), and hence relatively compact in \(C^0(K)\) by the Arzelà-Ascoli theorem. \(\square \)
In order to prepare an appropriate application of the previous lemma to particular classes of initial data, let us first recall a known feature of (1.2) with respect to the large time behavior of solutions corresponding to initial data that decay sufficiently fast in space. The following statement in this regard extracts from [12, Theorem 1.3] and [28, Lemma 2.6] what will be needed here.
Proposition 3.2
Let \(n\ge 1\) and \(p\ge 1\), and suppose that \(f\in C^0([0,\infty ))\) is positive and such that \(f(t)\rightarrow \infty \) as \(t\rightarrow \infty \). Then there exists \(\mathcal{L}\in C^0([0,1)) \cap C^2((0,1))\) with the properties that
and that whenever \(u_0\) satisfies (H) and is such that \(u_0<1\) in \(\mathbb {R}^n\) as well as
the minimal classical solution u of (1.2) satisfies
On the basis of this, we can design a template for infinitely many parts of the initial data to be finally used in the proof of Theorem 1.1.
Lemma 3.3
Let \(f\in C^0([0,\infty ))\) be positive and such that \(f(t)\rightarrow +\infty \) as \(t\rightarrow \infty \). Then for all \(a\in (0,1)\) there exists \(\phi _a\in C^1([0,\infty ))\) such that
and such that when \(u_0\) satisfies (H) with \(u_0<1\) in \(\mathbb {R}^n\) and
with some \(R\ge 0\), the corresponding minimal solution u of (1.2) has the property that (3.19) holds.
Proof
With \(\mathcal{L}\) taken from Proposition 3.2, for fixed \(a\in (0,1)\) we choose any \(\psi _a\in C^1([0,\infty ))\) such that \(\psi _a(0)=\mathcal{L}(a)\) and \(\psi _a'(\rho )<0\) for all \(\rho >0\) as well as
and define
noting that the existence of a strictly increasing inverse \(\mathcal{L}^{-1}\in C^0([0,\mathcal{L}(1)]) \cap C^1((0,\mathcal{L}(1))\) of \(\mathcal{L}\) is asserted by (3.17). While the properties in (3.20) thus immediately result from (3.23), to verify (3.19) for \(u=Su_0\) with arbitrary \(u_0\in C^0(\mathbb {R}^n)\) fulfilling \(0<u_0<1\) as well as (3.21) with some \(R>0\), we only need to observe that again by monotonicity of \(\mathcal{L}\), these asumptions ensure that according to (3.22),
and that hence (3.18) holds due to the evident fact that \(\int _{B_R(0)} \mathcal{L}(u_0) \le \mathcal{L}(1) \cdot |B_R(0)|\). \(\square \)
Having these preliminaries at hand, we can proceed to design the two basic nuclei of our construction, throughout the sequel making repeated use of the two different truncation and extension processes described in the following:
Lemma 3.4
Let \(n\ge 1\), and suppose that \(\varphi \) is such that (H) holds with \(\varphi (x)<1\) for all \(x\in \mathbb {R}^n\). Then with \((\phi _a)_{a\in (0,1)}\) taken from Lemma 3.3, for \(R>0\) letting
and
defines functions \(\mathcal{T}_R \varphi \) and \(\widehat{\mathcal{T}}_R \varphi \) on \(\mathbb {R}^n\) which satisfy (H).
Proof
This is an evident consequence of the fact that \(\phi _a\) is positive and nonincreasing for all \(a\in (0,1)\) by Lemma 3.3. \(\square \)
Thanks to the continuous dependence feature documented in Lemma 3.1, deviations encountered when performing the first of these operations can conveniently be estimated:
Lemma 3.5
Let \(n\ge 1\) and \(p\ge 1\), and let \(\widetilde{u}_0\) be such that (H) holds. Then given any \(R_\star >0\) and \(T>0\), one can find \(R>R_\star \) such that \(u_0:=\mathcal{T}_R \widetilde{u}_0\) has the property that \(\widetilde{u}:=S\widetilde{u}_0\) and \(u:=Su_0\) satisfy
Proof
Writing
and fixing \(R_1>0\) and \(R_2>R_1\), we see that
and that since \(0\le r\mapsto \widetilde{u}_0|_{\partial B_r(0)}\) is nonincreasing by (H),
as well as
Therefore, \(0<R\mapsto h(r,R)\) is nonincreasing for all \(r\ge 0\), so that
The claim hence results from Lemma 3.1 upon observing that \(\widetilde{u}(0,T)\) is positive. \(\square \)
The effects of the second manipulation type from Lemma 3.4 can be controlled in quite a similar fashion.
Lemma 3.6
Let \(n\ge 1\) and \(p\ge 1\), and suppose that beyond satisfying (H), the function \(\widetilde{u}_0\) is such that \(\widetilde{u}_0\equiv a\) in \(\mathbb {R}^n{\setminus }B_{R_0}(0)\) with some \(a\in (0,1)\) and \(R_0> 0\). Then for each \(R_\star >0\) and any \(T>0\) there exists \(R>R_\star \) such that writing \(u_0:=\widehat{\mathcal{T}}_R \widetilde{u}_0\), for the minimal solutions \(\widetilde{u}:=S\widetilde{u}_0\) and \(u:=Su_0\) of (1.2) we have
Proof
For \(R>R_0\), taking \(\phi _a\) from Lemma 3.3 we let
and note that then according to (3.25) we have
because \(\widetilde{u}_0|_{\partial B_r(0)}=a\) for \(r\ge R\). Moreover, given \(R_1>R_0\) and \(R_2>R_1\), we evidently have
while since \(\phi _a\le a\),
As furthermore, due to the inequality \(\phi _a' \le 0\),
it follows that \(h(\cdot ,R_2)\ge h(\cdot ,R_1)\) on \([0,\infty )\) for any such \(R_1\) and \(R_2\), meaning that \(\widehat{\mathcal{T}}_R \widetilde{u}_0 \nearrow \widetilde{u}_0\) in \(\mathbb {R}^n\) as \(R\nearrow \infty \). As a consequence of Lemma 3.1, the inequality in (3.27) can thus be achieved upon choosing \(R>R_\star \) suitably large. \(\square \)
4 Proof of the main results
Our concrete construction of initial data enforcing the claimed solution behavior now repeatedly combines Lemmas 3.5 and 3.6 in a style quite similar to that from [18] in its principal strategy:
Proof of Theorem 1.1
Replacing f(t) with \(\widetilde{f}(t):=\min \big \{ f(t) \, , \, (t+1)^\frac{1}{p}\big \}\) for \(t\ge 0\) if necessary, we may assume throughout that
Then picking any \(a\in (0,1)\) and taking \(\phi _a\) as accordingly provided by Lemma 3.3, from said lemma we infer that if we let
then \(u^{(0)}:=Su_0^{(0)}\) satisfies
so that we can pick \(t_1>0\) such that
Since evidently \(u_0^{(0)}\) satisfies (H), we may apply Lemma 3.5 to find \(R_1>0\) such that letting
for the corresponding solution \(u^{(1)}:=Su_0^{(1)}\) of (1.2) we have \(u^{(1)}(0,t_1) \le 2u^{(0)}(0,t_1)\), which entails that
due to (4.3) and the fact that \(\Vert u^{(0)}(\cdot ,t_1)\Vert _{L^\infty (\mathbb {R}^n)}=u^{(0)}(0,t_1)\), as implied by Lemma 2.4 in view of the downward monotonicity of \(0\le r \mapsto u_0^{(0)}|_{\partial B_r(0)}\).
Now since \(u_0^{(1)}(x) \ge a_1:=u_0^{(0)}|_{\partial B_{R_1}(0)}\) for all \(x\in \mathbb {R}^n\) according to the construction of \((\mathcal{T}_R)_{R>0}\) in (3.24), a combination of Lemma 2.3 with the comparison principle from Lemma 2.2 ensures that \(u^{(1)}(x,t)\ge a_1\) for all \(x\in \mathbb {R}^n\) and \(t>0\), whence in particular
thanks to our assumption on decay of g in (1.7). For some suitably large \(t_2>t_1+1\) we thus have
and keeping this number \(t_2\) fixed, we may now rely on the fact that, again by definition of \((\mathcal{T}_R)_{R>0}\), we actually have \(u_0^{(1)} \equiv a_1\) in \(\mathbb {R}^n{\setminus }B_{R_1}(0)\). Therefore, namely, we can employ Lemma 3.6 to find \(R_2>R_1+1\) with the property that
and \(u^{(2)}:=Su_0^{(2)}\) satisfy \(u^{(2)}(0,t_2) \ge \frac{1}{2} u^{(1)}(0,t_2)\) and thus
by (4.5), because once more in view of Lemma 2.4, the downward radial monotonicity of \(u_0^{(1)}\) guarantees that \(\Vert u^{(1)}(\cdot ,t_2)\Vert _{L^\infty (\mathbb {R}^n)}=u^{(1)}(0,t_2)\).
Repeating the above two-step argument, we recursively obtain a sequence \((u_0^{(j)})_{j\in \{0,1,2,...\}}\) of functions \(u_0^{(j)}\) fulfilling (H) for all \(j\in \mathbb {N}\), as well as \((t_j)_{j\in \{1,2,3,...\}}\subset (0,\infty )\) and \((R_j)_{j\in \{0,1,2,...\}} \subset (0,\infty )\) such that
that
and that if in addition to the above we define
then
and
Since (4.7) especially guarantees that \(R_j\rightarrow \infty \) as \(j\rightarrow \infty \), and since (4.8) and the definitions (3.24) and (3.25) of \((\mathcal{T}_R)_{R>0}\) and \((\widehat{\mathcal{T}}_R)_{R>0}\) imply that
it follows that letting
we obtain a well-defined function on \(\mathbb {R}^n\) which satisfies (H) as well as
according to (4.2), whence especially also (1.9) holds due to the conservation of radial symmetry and radial nonincrease asserted by Lemma 2.4. Apart from that, (4.8) in conjunction with the truncation features of \((\mathcal{T}_R)_{R>0}\) and \((\widehat{\mathcal{T}}_R)_{R>0}\) can readily be seen to ensure that
so that by (4.13),
Two applications of Lemma 3.1 therefore reveal that in line with (4.9) we have
where \(u:=Su_0\) satisfies
due to Lemma 2.2, and where
because of (4.14), Lemma 2.2 and Lemma 2.3. Once more drawing on Lemma 2.4, we can combine (4.10) and (4.11) with (4.17) to estimate
as well as
from which (1.11) and (1.12) follow.
Finally, knowing now that (1.11) holds, and that hence in line with (4.1) we must have
we may a posteriori conclude that \(u_0\) also satisfies (1.8), for if the radial and radially nonincreasing function \(u_0\) had a positive lower bound, then so would have u throughout \(\mathbb {R}^n\times (0,\infty )\) according to Lemma 2.2 and Lemma 2.3. The statements on asymptotics in (1.10) then only record what therefore directly results from [11, 24]. \(\square \)
References
Aronson, D.G.: The porous medium equation. Nonlinear diffusion problems. Lect. Notes Math. 1224, 1–46 (1986)
Blanchet, A., Bonforte, M., Dolbeault, J., Grillo, G., Vázquez, J.L.: Asymptotics of the fast diffusion equation via entropy estimates. Arch. Rat. Mech. Anal. 191, 347–385 (2009)
Bonforte, M., Dolbeault, J., Grillo, G., Vázquez, J.L.: Sharp rates of decay of solutions to the nonlinear fast diffusion equation via functional inequalities. Proc. Nat. Acad. Sci. 107, 16459–16464 (2010)
Bonforte, M., Grillo, G., Vázquez, J.L.: Special fast diffusion with slow asymptotics. Entropy method and flow on a Riemannian manifold. Arch. Rat. Mech. Anal. 196, 631–680 (2010)
Carrillo, J.A., Vázquez, J.L.: Fine asymptotics for fast diffusion equations. Commun. Partial Differ. Eqs. 28, 1023–1056 (2003)
Daskalopoulos, P., del Pino, M.: On nonlinear parabolic equations of very fast diffusion. Arch. Rat. Mech. Anal. 137, 363–380 (1997)
Daskalopoulos, P., del Pino, M.: On the Cauchy problem for \(u_t=\Delta \log u\) in higher dimensions. Math. Ann. 313, 189–206 (1999)
Esteban, J.R., Rodríguez, A., Vázquez, J.L.: A nonlinear heat equation with singular diffusivity. Commun. Partial Differ. Eqs. 13, 985–1039 (1988)
Fila, M., King, J., Winkler, M.: Rate of convergence to Barenblatt profiles for the fast diffusion equation with a critical exponent. J. Lond. Math. Soc. 90, 167–183 (2014)
Fila, M., Vázquez, J.L., Winkler, M., Yanagida, E.: Rate of convergence to Barenblatt profiles for the fast diffusion equation. Arch. Rat. Mech. Anal. 204, 599–625 (2012)
Fila, M., Winkler, M.: Slow growth of solutions of superfast diffusion equations with unbounded initial data. J. Lond. Math. Soc. 95, 659–683 (2017)
Fila, M., Winkler, M.: A Gagliardo–Nirenberg-type inequality and its applications to decay estimates for solutions of a degenerate parabolic equation. Adv. Math. 357, 106823 (2019)
Friedman, A., Kamin, S.: The asymptotic behaviour of a gas in an n-dimensional porous medium. Trans. Am. Math. Soc. 262, 551–563 (1980)
Galaktionov, V.A., Peletier, L.A.: Asymptotic behaviour near finite time extinction for the fast diffusion equation. Arch. Rational Mech. Anal. 139, 83–98 (1997)
Galaktionov, V.A., Peletier, L.A., Vazquez, J.L.: Asymptotics of the fast-diffusion equation with critical exponent. SIAM J. Math. Anal. 31, 1157–1174 (2000)
King, J.R.: Self-similar behaviour for the equation of fast nonlinear diffusion. Philos. Trans. Roy. Soc. Lond. Ser. A 343, 337–375 (1993)
Ladyženskaja, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasilinear Equations of Parabolic Type. AMS, Providence (1968)
Poláčik, P., Yanagida, E.: On bounded and unbounded global solutions of a supercritical semilinear heat equation. Math. Ann. 327, 745–771 (2003)
Rodriguez, A., Vazquez, J.L.: Non-uniqueness of solutions of nonlinear heat equations of fast diffusion type. Ann. Inst. H. Poincaré Analyse Non Linéaire 12, 173–200 (1995)
Vázquez, J.L.: Asymptotic behaviour for the porous medium equation posed in the whole space. J. Evol. Equ. 3, 67–118 (2003)
Vázquez, J.L.: Smoothing and Decay Estimates for Nonlinear Diffusion Equations. Oxford Lecture Notes in Maths. and its Applications, vol. 33. Oxford University Press, Oxford (2006)
Vázquez, J.L., Winkler, M.: Highly time-oscillating solutions for very fast diffusion equations. J. Evol. Equ. 11, 725–742 (2011)
Wiegner, M.: A degenerate diffusion equation with a nonlinear source term. Nonlinear Anal. 28, 1977–1995 (1997)
Winkler, M.: On the Cauchy problem for a degenerate parabolic equation. Z. Anal. Anw. 20(3), 677–690 (2001)
Winkler, M.: Oscillating solutions and large \(\omega \)-limit sets in a degenerate parabolic equation. J. Dyn. Differ. Equ. 20, 87–113 (2008)
Winkler, M.: Spatially monotone homoclinic orbits in nonlinear parabolic equations of super-fast diffusion type. Math. Ann. 355, 519–549 (2013)
Winkler, M.: One-dimensional super-fast diffusion: persistence vs. extinction revisited. Extinction at spatial infinity. J. Dyn. Differ. Equ. 30, 331–358 (2018)
Winkler, M.: Approaching critical decay in a strongly degenerate parabolic equation. J. Dyn. Differ. Equ. (2020). https://doi.org/10.1007/s10884-020-09892-x
Acknowledgements
The author thanks both reviewers for several helpful comments. He furthermore acknowledges support of the Deutsche Forschungsgemeinschaft (No. 444955436).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the section “Qualitative properties of solutions to nonlinear parabolic problems: In honor of Professor Eiji Yanagida on the occasion of his 65th birthday” edited by Senjo Shimizu, Tohru Ozawa, Kazuhiro Ishige, Marek Fila (Guest Editor)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Winkler, M. Oscillatory decay in a degenerate parabolic equation. Partial Differ. Equ. Appl. 3, 47 (2022). https://doi.org/10.1007/s42985-022-00186-z
Published:
DOI: https://doi.org/10.1007/s42985-022-00186-z