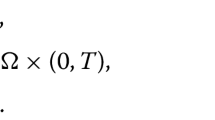Abstract
The paper deals with positive solutions of the initial-boundary value problem for \(u_t=f(u) (\Delta u+\lambda_1 u) \qquad (*)\) with zero Dirichlet data in a smoothly bounded domain \(\Omega \subset \mathbb{R}^{n}, n\ge 1\). Here \(f \in C^{0}([0,\infty)) \cap C^{1}((0,\infty))\) is positive on (0,∞) with f(0) = 0, and λ1 is exactly the first Dirichlet eigenvalue of −Δ in Ω. In this setting, (*) may possess oscillating solutions in presence of a sufficiently strong degeneracy. More precisely, writing \(H(s):=\int_{1}^{s} \frac{d\sigma}{f(\sigma)}\), it is shown that if \(\int_{0} sH(s)ds=-\infty\) then there exist global classical solutions of (*) satisfying \(\limsup_{t\to\infty} \|u(\cdot,t)\|_{L^\infty(\Omega)}=\infty\) and \(\liminf_{t\to\infty} \|u(\cdot,t)\|_{L^\infty(\Omega)}=0\). Under the additional structural assumption \(\frac{sf'(s)}{f(s)}\ge\kappa > 0\), s > 0, this result can be sharpened: If \(\int_0 sH(s)ds=-\infty\) then (*) has a global solution with its ω-limit set being the ordered arc that consists of all nonnegative multiples of the principal Laplacian eigenfunction. On the other hand, under the above additional assumption the opposite condition \(\int_0 sH(s)ds > -\infty\) ensures that all solutions of (*) will stabilize to a single equilibrium.
Similar content being viewed by others
References
Allen L.J.S. (1983). Persistence and extinction in single species reaction-diffusion models. Bull. Math. Biol. 45, 209–227
Angenent S. (1991). On the formation of singularities in the curve shortening flow. J. Differ. Geom. 33(3): 601–633
Aronson D.G.(1986). The porous medium equation. Nonlinear diffusion problems, Lect. 2nd 1985 Sess. C.I.M.E.. Montecatini Terme/Italy 1985, Lect. Notes Math. 1224, 1–46
Bertsch M., Dal Passo R., Ughi M. (1990). Discontinuous “viscosity” solutions of a degenerate parabolic equation. Trans. AMS 320(2): 779–798
Crandall M.G., Rabinowitz P.H., Tartar L. (1977). On a Dirichlet problem with a singular nonlinearity. Comm. Part. Differ. Equations 2, 193–222
Djie K.C.(2006). On the nonintegrability of expressions involving the distance to a nonsmooth boundary. Preprint, www.math1.rwth-aachen.de/Forschung-Research/ d_emath1.php
Friedman A., McLeod B. (1987). Blow-up of solutions of nonlinear degenerate parabolic equations. Arch. Rat. Mech. Anal. 96, 55–80
Gilbarg D., Trudinger N.S. (1977). Elliptic Partial Differential Equations of Second Order. Springer, Berlin/Heidelberg/New York.
Hamilton R.S. (1988). The Ricci flow on surfaces. Contemp. Math. 71, 237–262
Haraux A., Poláčik P. (1992). Convergence to positive equilibrium for some nonlinear evolution equations in a ball. Acta Math. Univ. Comenianae LXI, 129–141
Jendoubi M.A. (1998). A simple unified approach to some convergence theorems of L. Simon. J. Funct. Anal. 153, 187–202
Ladyzenskaja O.A., Solonnikov V.A., Ural’ceva N.N. (1968). Linear and Quasi- linear Equations of Parabolic Type. AMS, Providence
Lions P.L. (1984). Structure of the set of steady-state solutions and asymptotic behaviour of semilinear heat equations. J. Differ. Eq. 53, 362–386
Low B.C. (1973). Resistive diffusion of force-free magnetic fields in a passive medium. Astrophys. J. 181, 209–226
Luckhaus S., Dal Passo R. (1987). A degenerate diffusion problem not in divergence form. J. Differ. Eq. 69, 1–14
Matano H. (1978). Convergence of solutions of one-dimensional semilinear parabolic equations. J. Math. Kyoto Univ. 18, 221–227
Poláčik P. (2002). Some common asymptotic properties of semilinear parabolic, hyperbolic and elliptic equations. Math. Bohem. 127(2): 301–310
Poláčik P., Rybakowski K.P. (1996). Nonconvergent bounded trajectories in semilinear heat equations. J. Differ. Eq. 124, 472–494
Poláčik P., Simondon F. (2002). Nonconvergent bounded solutions of semilinear heat equations on arbitrary domains. J. Differ. Eq. 186, 586–610
Poláčik P., Yanagida E. (2003). On bounded and unbounded global solutions of a supercritical semilinear heat equation. Math. Annal. 327, 745–771
Wiegner M. (1997). A Degenerate Diffusion Equation with a Nonlinear Source Term. Nonlin. Anal. TMA 28, 1977–1995
Winkler M. (2001). Large time behavior of degenerate parabolic equations with absorption. Nonlinear Differ. Eq. Appl. 8(3): 343-361
Winkler M. (2003). Boundary behaviour in strongly degenerate parabolic equations. Acta Math. Univ. Comenianae 72(1): 129–139
Winkler M. (2004). A doubly critical degenerate parabolic problem. Math. Meth. Appl. Sci. 27(14): 1619–1627
Winkler M. (2004). Propagation vs. constancy of support in the degenerate parabolic equation u t = f(u) Δu. Rend. Univ. Di Trieste 36, 1–15
Winkler M. (2005). Large time behavior and stability of equilibria of degenerate parabolic equations. J. Dyn. Differ. Eq. 17(2): 331–351
Winkler M. Nontrivial ordered ω-limit sets in a linear degenerate parabolic equation. To appear in: Discr. Cont. Dyn. Syst.
Zelenyak T.I. (1968). Stabilization of solutions of boundary value problems for a second order parabolic equation with one space variable. Differ. Eq. (transl. from Differencialnye Uravnenia) 4, 17–22
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Winkler, M. Oscillating Solutions and Large ω-limit Sets in a Degenerate Parabolic Equation. J Dyn Diff Equat 20, 87–113 (2008). https://doi.org/10.1007/s10884-006-9061-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-006-9061-y