1 Introduction

Cartesian embedded boundary meshes for computing flow problems involving complex geometries have become very popular as mesh generation is fully automatic and fairly cheap: the geometry is simply cut out of Cartesian background cells. This results in cut cells where the object intersects the background mesh. Cut cells can have various shapes and can in particular be arbitrarily small. This causes various issues when standard methods are used to solve partial differential equations (PDEs) on these meshes. The specific issue depends on the kind of PDE to be solved.

In the context of time-dependent hyperbolic conservation laws the main issue is what is referred to as the small cell problem: typically, explicit time stepping schemes are used. By the CFL condition the time step size is coupled to the size of the cells. One wants to choose the time step based on the size of the larger background cells and use the same time step on the arbitrarily small cut cells. For standard schemes, this approach causes the values on the small cut cells to explode.

One approach to solve this issue is to use cell merging or cell agglomeration, see, e.g., [26, 38, 40]. In that approach cut cells that are too small are merged/combined with neighboring cells, which eliminates the problem. The downside is that the complexity is moved back into the mesh generation process. The alternative is to develop algorithmic solution approaches to overcome the small cell problem. Two very well-established approaches are the flux redistribution method [10, 12] and the h-box method [7, 8, 21]. More recent approaches include the dimensionally split approach [19, 25], the extension of the active flux method to cut cells [22], and the state redistribution scheme (SRD) [6]. All of these schemes are based on finite volume approaches (if one counts the active flux method as a finite volume scheme). A few years ago, the development of algorithmic solution approaches in the context of discontinuous Galerkin (DG) methods has started. Existing solution approaches here are the DoD stabilization [14, 35], the extension of the ghost penalty stabilization [9] to time-dependent first-order hyperbolic problems [16, 17], as well as the extension of the SRD scheme to a DG setting [18].

In this contribution we will consider the mixed explicit implicit scheme in more detail, which was introduced by May and Berger [30, 33, 34] in the context of a finite volume setting to overcome the small cell problem. The idea is quite simple: cut cells are treated implicitly for stability but cells away from the cut cells use a standard explicit time stepping scheme to keep the cost low. The switch happens by means of flux bounding. The authors combined a second-order explicit scheme with a second-order implicit scheme. Numerical experiments [34] have shown that the resulting mixed scheme converges with second order in the \(L^1\) norm. In the \(L^{\infty }\) norm, one numerically sees full second order in one dimension but in two and three dimensions orders between 1 and 2 were observed.

In this contribution we want to examine the error behavior of the mixed explicit-implicit scheme in more detail and also test possible cures. In one dimension, we will first analyze the one step error and then show that the mixed scheme indeed converges with second order. As numerical results indicate that we will not be able to prove the same result in higher dimensions, we will then introduce two new versions of the mixed explicit-implicit scheme with an improved transition error. These will be designed so that on a Cartesian mesh the transition between explicit and implicit time stepping has a third-order one step error. We will include results from a test involving cut cells to see whether this increases the overall accuracy of the scheme. Some of the material presented here has been part of the master thesis of Laakmann [27].

The idea of combining explicit and implicit time stepping to gain stability has been used by other authors as well and has in particular become more popular in recent years, see, e.g., [13, 15, 37, 39] and the references cited therein. Here, we will focus on the approach as introduced in [30, 34] in the context of cut cells. We note though that this approach can easily be extended to other problem settings as well. Recently, it has been applied in the context of two phase flow problems: if one uses a sharp interface method, then the creation of new phases (nucleation or cavitation) results in the creation of new tiny cells. In [36], the newly created tiny cells have successfully been treated with the first-order version of the mixed explicit-implicit scheme, extended to the isothermal Euler equations.

This contribution is structured as follows: in Sect. 2, we focus on the situation in one dimension. We introduce the mixed explicit-implicit MUSCL-Trap (monotonic upwind scheme for conservation laws and trapezoidal scheme) as used in [34] and examine its error. We then present two different variants of the mixed explicit-implicit scheme, which have a reduced transition error compared to the original scheme. In Sect. 3, we extend the considerations to two dimensions. We first formulate the new variants in two dimensions and then compare the three schemes numerically. We conclude with an outlook in Sect. 4.

2 Mixed Explicit-Implicit Schemes in One Dimension

We consider the linear advection equation

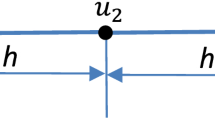
$$\begin{aligned} s(t,x)_t + u s(t,x)_x = 0, \quad u > 0 \,\, \text {constant} \end{aligned}$$
(1)

with initial data \(s(t_0,\cdot ) = s_0\). The standard model mesh for developing cut cell schemes in one dimension is shown in Fig. 1: an equidistant mesh with mesh width \(h\) contains one cell of length \(\alpha h\), labeled as cell 0, in the middle. Here, \(\alpha \in (0,1]\) denotes the volume fraction—the ratio of the small cell to full cell volume.

Fig. 1
figure 1

One-dimensional model problem: equidistant grid with one small cell of length \(\alpha h\) labeled as cell 0

Full size image

2.1 The MUSCL-Trap Scheme

The idea behind mixed explicit-implicit schemes for cut cell meshes as used in [30, 33, 34] is to employ an implicit scheme on the cut cell 0 for stability. Away from the cut cell an explicit scheme is used to keep the cost low. In [34], May and Berger developed what we will refer to as MUSCL-Trap, the combination of the explicit MUSCL and the implicit Trapezoidal scheme by means of flux bounding.

MUSCL [11, 28] is a common explicit finite volume scheme. The scheme is second-order accurate in space and time. In one dimension, the MUSCL for the linear advection (1) on an equidistant grid is given by

$$\begin{aligned} S_i^{n+1} = S_i^n - \frac{\Delta t}{h} \left( F_{i+1/2}^{n+1/2,M} -F_{i-1/2}^{n+1/2,M} \right) , \quad F_{i+1/2}^{n+1/2,M} = u \left( S_i^n + (1 - \lambda ) S_{i,x}^n \frac{h}{2} \right) \end{aligned}$$
(2)

with \(S_{i,x}^n \approx \partial _x s (t^n, x_i)\), computed using central difference gradients and a standard slope limiter [29], with CFL number \(\lambda = \tfrac{u \Delta t}{h}\). The scheme is stable for \(0 < \lambda \leqslant 1\) and would therefore become unstable on the cell 0 for \(\alpha < 1\).

The implicit Trapezoidal rule in time in combination with a suitable slope reconstruction in space is given by

$$\begin{aligned} S_i^{n+1}&= S_i^n - \frac{\Delta t}{h_i} \left( F_{i+1/2}^{n+1/2,T} -F_{i-1/2}^{n+1/2,T} \right) , \end{aligned}$$
(3a)
$$\begin{aligned} F_{i+1/2}^{n+1/2,T}&= \frac{u}{2} \left( S_i^n + S_{i,x}^n \frac{h_i}{2} + S_i^{n+1} + S_{i,x}^{n+1} \frac{h_i}{2}\right) \end{aligned}$$
(3b)

for a non-equidistant mesh with cells of length \(h_i\).

Fig. 2
figure 2

Flux bounding: first the cells away from the cut cell are updated using an explicit scheme (edges marked in green). Then the neighborhood of the cut cell is updated. The Cartesian neighbors of the cut cell are transition cells. The update on these cells employs both explicit fluxes (edges marked in green) and implicit fluxes (edges marked in light blue), see also [31] and [34, Fig. 6]

Full size image

In [30, 34], May and Berger examined various ways for combining an explicit scheme with an implicit scheme and found flux bounding to be the best way. The idea is illustrated in Fig. 2. One first updates all Cartesian cells that are not direct neighbors of the cut cell using the explicit scheme, see Fig. 2a. In a second step, one updates the value on cells \(-1\), 0, 1 comparing Fig. 2b. Here, cell 0 is treated fully implicitly to guarantee the stability on the small cut cell, indicated by the light blue edges. The cells \(-1\) and 1 are transition cells: when updating cell \(-2\) in Step (i) with the fully explicit scheme, one assumed that a certain amount of mass, represented by \(F_{-3/2}^{n+1/2,M}\), has left cell \(-2\). For the full scheme to be conservative, one needs to ensure that the mass arrives in cell \(-1\). This is achieved by reusing the explicit flux for the edge \(-3/2\) in Step (ii). Note that transition cells employ both explicit and implicit fluxes. Cut cells are treated fully implicitly, and Cartesian cells that are not neighbors of cut cells are treated fully explicitly. Flux bounding is set up in a symmetric manner, i.e., it does not distinguish between \(u > 0\) and \(u < 0\), allowing the extension to more general problems, such as Euler equations [36]. Flux bounding has the following properties.

  1. (i)

    It is conservative (by construction).

  2. (ii)

    It satisfies a TVD property in a suitable setting. May and Berger [34, Theorem 1] showed the TVD stability for a mixed scheme combining MUSCL (with the minmod limiter [29]) as an explicit scheme with implicit Euler and piecewise constant data as an implicit scheme for \(0 < \lambda \leqslant 1\), independent of the size of \(\alpha \in (0,1]\).

  3. (ii)

    It has a natural extension to two and three dimensions (see Sect. 3 as well as [34]).

This results in the following formulae for MUSCL-Trap in one dimension:

$$\left\{ \begin{aligned}S_{-2}^{n+1}&= S_{-2}^{n} - \frac{\Delta t}{h} \left[ F_{-3/2}^{n+1/2,M} - F_{-5/2}^{n+1/2,M}\right] \quad \text {(MUSCL)}, \nonumber \\ S_{-1}^{n+1}&= S_{-1}^n - \frac{\Delta t}{h} \left[ F_{-1/2}^{n+1/2,T} - F_{-3/2}^{n+1/2,M} \right] \quad \text {(transition)},\nonumber \\ S_0^{n+1}&= S_0^n - \frac{\Delta t}{\alpha h} \left[ F_{1/2}^{n+1/2,T} - F_{-1/2}^{n+1/2,T} \right] \quad \text {(Trapezoidal)},\nonumber \\ S_1^{n+1}&= S_1^n - \frac{\Delta t}{h} \left[ F_{3/2}^{n+1/2,M} - F_{1/2}^{n+1/2,T} \right] \quad \text {(transition)},\nonumber \\ S_{2}^{n+1}&= S_{2}^n - \frac{\Delta t}{h} \left[ F_{5/2}^{n+1/2,M} - F_{3/2}^{n+1/2,M} \right] \quad \text {(MUSCL)}. \end{aligned}\right.$$
(4)

For the slope reconstruction on cells \(i \leqslant -2\) and \(i \geqslant 2\) unlimited central differences are used. On the cut cell 0 and the transition cells \(-1\) and 1 a least squares approach is employed [5]. This extends in a straight-forward way to higher dimensions [3, 32]. Note that the least squares slope \(S_{1,x}\) enters the computation of the MUSCL flux \(F_{3/2}^{n+1/2}\). Except for this special case, only central difference slopes are used for the computation of MUSCL fluxes. Throughout this paper we will assume all slopes to be unlimited.

Remark 1

This contribution focuses on the accuracy of mixed schemes in general and the accuracy of MUSCL-Trap in particular. We will not discuss limiting here. For limiting on cut cells, see, e.g., [32].

2.1.1 The One Step Error of MUSCL-Trap

The one step error of scheme (4) has roughly been analyzed in [31, 34]. We will do this here more thoroughly. Let the MUSCL-Trap scheme be given by \(S_i^{n+1} = \Phi (S^n,S^{n+1})_i\) with

$$\begin{aligned} \Phi (S^n,S^{n+1})_i = S_i^n - \frac{\Delta t}{h_i} \left[ F_{i+1/2}^{n+1/2,X}(S^n,S^{n+1}) - F_{i-1/2}^{n+1/2,X} (S^n,S^{n+1}) \right] \end{aligned}$$
(5)

with \(F_{i+1/2}^{n+1/2,X}\) representing \(F_{i+1/2}^{n+1/2,M}\) or \(F_{i+1/2}^{n+1/2,T}\), depending on i. For the computation of the one step error, we replace the input arguments of \(\Phi _i\) with the true cell averages at time \(t^n\) and \(t^{n+1}\), given by \(\bar{s}_i^n\) and \(\bar{s}_i^{n+1}\), resulting in

$$\begin{aligned} L(\bar{s}^{n},\bar{s}^{n+1})_i = \Phi (\bar{s}^n,\bar{s}^{n+1})_i -\bar{s}_i^{n+1}. \end{aligned}$$
(6)

Remark 2

The one step error \(L(\bar{s}^{n},\bar{s}^{n+1})_i\) measures the error made in one time step \(t^n \rightarrow t^{n+1}\) on cell i. Typically, i.e., on uniform meshes, the order of convergence of the one step error is one order higher than the overall order of the scheme.

Fig. 3
figure 3

The one step error \(|{L(\bar{s}^{n}, \bar{s}^{n+1})_i} |\) for the MUSCL-Trap scheme for \(i=-3,\cdots ,3\)

Full size image

The numerically observed convergence order of the one step error for a smooth test problem is summarized in Fig. 3. We observe a third-order one step error on cells that are sufficiently far away from the cut cell. These cells use the full MUSCL scheme on a uniform mesh. In the neighborhood of the cut cell, we observe a second-order one step error. This is due to the following four error sources.

Error sources

  1. (i)

    The switch in the time stepping scheme between MUSCL and Trapezoidal rule results in an error term of size \({\mathcal {O}}(h^2)\). The examination of its propagation is one key aspect of this research.

  2. (ii)

    The irregularity of the cut cell causes several errors if \(\alpha < 1\):

    1. (a)

      the slope reconstruction, which uses a least squares approach, is only of first order, resulting in second-order error terms that we summarize in \(a_ih^2\) for cell i (this is the only reason for the error of size \({\mathcal {O}}(h^2)\) on cell 2);

    2. (b)

      in the computation of the fluxes, we use the variable \(S_i^n\) (which is supposed to be an approximation to the cell average \(\bar{s}_i^n\)) as the approximation to the point value \(s(t^n,x_i)\); this results in second-order error terms that we summarize in \(b_ih^2\);

    3. (c)

      for a third-order one step error, we would need to use a quadratic reconstruction in space instead of a linear one; we summarize the resulting error terms on cell i in \(c_ih^2\).

We note that on an equidistant mesh, i.e., \(\alpha =1\), all error terms listed under (ii) reduce to third-order errors, partly due to cancellation effects with neighboring cells. Using this notation, we observe on cells \(-1\), 0, and 1 the following errors:

$$\begin{aligned} L(\bar{s}^n,\bar{s}^{n+1})_{-1}&=\frac{1}{4}(1-\lambda )\lambda ^2h^2 s_{xx}(t^n,x_{-1}) +a_{-1}h^2 + b_{-1}h^2 + c_{-1}h^2 + {\mathcal {O}}(h^3), \end{aligned}$$
(7a)
$$\begin{aligned} L(\bar{s}^n,\bar{s}^{n+1})_{0}&=a_{0}h^2 + b_{0}h^2 + c_{0}h^2 + {\mathcal {O}}(h^3), \end{aligned}$$
(7b)
$$\begin{aligned} L(\bar{s}^n,\bar{s}^{n+1})_{1}&=- \frac{1}{4}(1-\lambda ) \lambda ^2h^2 s_{xx}(t^n,x_{1}) + a_{1}h^2 + b_{1}h^2 + c_{1}h^2 + {\mathcal {O}}(h^3). \end{aligned}$$
(7c)

Note that the error that we make when switching from MUSCL to Trapezoidal on cell \(-1\) is to lead order the negative of the error that we make when switching back from Trapezoidal to MUSCL on cell 1.

2.1.2 Numerical Results for MUSCL-Trap

In [34], the authors presented numerical results for the model problem shown in Fig. 1, which we will start with as well to keep the presentation mostly self-contained.

Test 1 Consider the model problem shown in Fig. 1. One cut cell is located in the interval \([0.5,0.5+\alpha h]\). The overall domain length is given by \([0,1+\alpha h]\). Periodic boundary conditions are used. The test function is \(\sin \left( \frac{2 \uppi (x+0.36)}{1 + \alpha h} \right)\), \(\alpha = 10^{-4}\), and the final time is \(T = 1+\alpha h\) so that the test function is back to its original position. The \(L^1\) error has been normalized to account for the changing domain length. We solve \(s_t + s_x = 0\) with \(\lambda = 0.8\), independent of \(\alpha\). The results for the one step error and the error at time T are shown in Table 1.

Table 1 Result of Test 1: MUSCL-Trap for the model problem in Fig. 1
Full size table

For the one step error in the \(L^{\infty }\) norm we observe second-order convergence, as expected. The third-order convergence in the \(L^{1}\) norm can be explained by a simple counting argument: let M denote the number of Cartesian cells. Then, there are \(M {-}3\) cells (out of \(M {+}1\) total cells) with an error of size \({\mathcal {O}}(h^3)\) and only four cells with an error of size \({\mathcal {O}}(h^2)\). This results in the third-order convergence in the \(L^{1}\) norm.

The results for the error at time T are more surprising: we observe full second-order convergence in the \(L^1\) and \(L^{\infty }\) norms despite the one step error only converging with second order in \(L^{\infty }\). However, there is a reasonable explanation for this behavior. Let us consider error accumulation from a Lagrangian view point: let us fix one cell, e.g., the cell that contains the peak of the sine curve, put a tracer there, and follow the tracer during the simulation. If we assume that our scheme is stable (and that error propagates with norm smaller/equal than 1), the error at time T essentially corresponds to the sum of all the one step errors of all the cells that our tracer has passed. Given that most cells have a one step error of third order and that there are only four isolated cells with a one step error of second order, this consideration actually implies to expect a second-order error on all cells at time T. This is consistent with the numerical results.

This consideration motivates the following new test, Test 2, which we expect to be more challenging: instead of using only one cut cell, we double the number of cut cells as we have the grid size \(h\). Then, the number of cells with one step error \({\mathcal {O}}(h^2)\) increases with \({\mathcal {O}}(\frac{1}{h})\) and should affect the convergence order at time T.

Fig. 4
figure 4

New one-dimensional model problem: the grid consists of L blocks with \(K+1\) cells that each contains K cells of length H (here \(H=h,\frac{h}{2}, \frac{h}{4}\)) and one cut cell of length \(\alpha H\) in the middle. When the mesh is refined by a factor of 2, we keep K (and \(\alpha\)) fixed but double L. Analogous to Fig. 1, we refer to cut cells as (cells of type) 0, to the left Cartesian neighbors of cut cells as (cells of type) \(-1\), and to the right Cartesian neighbor as (cells of type) 1

Full size image

Test 2 The test setup is shown in Fig. 4. We use \(K=40\) and \(L=4\) on the coarsest mesh. The overall domain length is given by \([0,1+4\alpha h_0]\) with \(h_0\) denoting the coarsest mesh (in our case \(h_0=\frac{1}{160}\)). Different to Test 1, the domain length stays constant. The test function is \(\sin \left( \frac{2 \uppi (x+0.36)}{1 + 4\alpha h_0} \right)\), \(\alpha = 10^{-4}\), and \(T = 1+4\alpha h_0\) so that the test function is back to its original position. The results for the one step error and the error at time T are shown in Table 2.

Table 2 Result of Test 2: error for MUSCL-Trap for the model problem shown in Fig. 4
Full size table

Despite the one step error being only of second order in both the \(L^1\) and \(L^{\infty }\) norms, the error after one period also converges with second order both in \(L^1\) and \(L^{\infty }\). This behavior of the error accumulation behaving differently on non-uniform meshes has been observed and analyzed before [41]. We will follow the proof from [41] to show the second order accuracy for MUSCL-Trap in Theorem 1. Similar ideas have also been used to show the second order accuracy of the h-box method [8].

Different to Test 1, we observe for the one step error measured in the \(L^1\) norm, a convergence order of 2 (compared to 3 before). This can be explained as follows: let \(e_i = S_i^n - \bar{s}_i^n\) denote the error on cell i, let \(K\text {+}1\) be the number of cells per block, and let there be L blocks. As before, M denotes the total number of Cartesian cells. This implies \(M+L = L \cdot (K+1)\). Then, the \(L^1\) error can be computed as (with c denoting a generic constant)

$$\begin{aligned} \sum _{\textrm{cells}} h_i \cdot |{e_i} |&= \mathop{\mathop{\sum}\limits_\text{normal}}\limits_\text{cells} h\cdot {\mathcal {O}}(h^3) + \mathop{\mathop{\sum}\limits_\text{cells}}\limits_{-1, \,1, \,2} h\cdot {\mathcal {O}}(h^2) + \sum _{\textrm{cell } 0} \alpha h\cdot {\mathcal {O}}(h^2) \\&= (M-3L) \cdot ch^4 + 3L \cdot ch^3 + L \cdot \alpha ch^3. \end{aligned}$$

Using \(L = \frac{M}{K}\) and \(M = {\mathcal {O}}(\frac{1}{h})\), we get

$$\begin{aligned} \sum _{\textrm{cells}} h_i \cdot |{e_i} | = \left( 1 - \frac{3}{K} \right) \cdot ch^3 + 3 \frac{1}{K} \cdot ch^2 + \frac{1}{K} \cdot \alpha ch^2. \end{aligned}$$

Therefore, for keeping K (the number of cells per block) fixed, we get an \(L^1\) error of \({\mathcal {O}}(h^2)\). This theoretical consideration coincides with our numerical observation. Note that in Test 1, K is increased with \({\mathcal {O}}(\frac{1}{h})\), explaining the better convergence rate of 3 in the \(L^1\) norm for the one step error.

2.1.3 Proof for MUSCL-Trap Being Second-Order Accurate

For the proof of second-order convergence, we require the stability of the method. Examining this stability mathematically is very challenging due to using a non-uniform mesh and a mixed scheme. Applying, for example, the von Neumann stability analysis is not feasible. We therefore formulate this as Assumption 1 in the proof below. In our numerical tests, we found that this was true for the \(L^1\) and \(L^{\infty }\) norms.

Theorem 1

Let Assumption 1 below hold true. Consider the MUSCL-Trap scheme given by (4), but assume that slopes are computed by means of an unlimited forward difference quotient. Let \(0 < \lambda \leqslant 1\) be independent of \(\alpha\). Then the scheme is second-order accurate with respect to the norm used in Assumption 1 for the linear advection equation for the model problem in Fig. 1d model problem for sufficiently smooth initial data \(s_0\).

Proof

For the proof, we use an idea that goes back to Wendroff and White [41], and which has also been used to show second-order accuracy of the h-box method [8]. Assume that we are able to construct a grid function with cell averages \(\bar{w}_i^n\) such that (i) the new grid function \(\bar{w}_i^n\) is sufficiently close to \(\bar{s}_i^n\) and (ii) the one step error is of third order for all cells. To be precise, \(\bar{w}_i^n\) is supposed to satisfy

$$\begin{aligned}&\text {(i)} \quad \bar{w}^n_i=\bar{s}^n_i + {\mathcal {O}}(h^2), \quad \forall \, i,n, \end{aligned}$$
(8a)
$$\begin{aligned}&\text {(ii)} \quad |{L(\bar{w}^{n},\bar{w}^{n+1})_i} | = {\mathcal {O}}(h^3), \quad \forall \, i,n. \end{aligned}$$
(8b)

Assumption 1

We assume that the MUSCL-Trap scheme is stable with respect to the norm \(\Vert \cdot \Vert\) in the following sense: there holds

$$\begin{aligned} \Vert \Phi (S^{n-1} - \bar{w}^{n-1},S^{n} - \bar{w}^n)\Vert \leqslant \Vert S^{n-1} - \bar{w}^{n-1}\Vert + {\mathcal {O}}(h^3), \quad \, \forall \, 1 \leqslant n \leqslant N \end{aligned}$$

for the error propagation.

For the error grid function \(E^n = S^n - \bar{w}^{n}\) there holds by linearity of \(\Phi,\)

$$\begin{aligned} S^n - \bar{w}^{n}&= \Phi (S^{n-1},S^{n}) - \bar{w}^{n} = \Phi (E^{n-1}+\bar{w}^{n-1},E^{n}+\bar{w}^{n}) - \bar{w}^{n}\\&= \Phi (E^{n-1},E^{n}) + \Phi (\bar{w}^{n-1},\bar{w}^{n}) - \bar{w}^{n} = \Phi (E^{n-1},E^{n}) + L(\bar{w}^{n-1},\bar{w}^{n}). \end{aligned}$$

From Assumption 1 and assumption (8b), we can conclude

$$\begin{aligned} \Vert S^N - \bar{w}^N\Vert&\leqslant \Vert \Phi (S^{N-1} -\bar{w}^{N-1},S^{N} - \bar{w}^N) \Vert + \Vert L (\bar{w}^{N-1},\bar{w}^{N}) \Vert \\& \leqslant \Vert S^{N-1} - \bar{w}^{N-1} \Vert + {\mathcal {O}}(h^3) \leqslant \Vert S^0 - \bar{w}^0\Vert + \frac{T}{\Delta t} {\mathcal {O}}(h^{3})={\mathcal {O}}(h^2) \end{aligned}$$

with \(N = \frac{T}{\Delta t}\) and \(\Delta t= {\mathcal {O}}(h)\). In other words, we have “normal” error accumulation with respect to the new solution \(\bar{w}^{n}\). Together with property (8a) we get by means of the triangle inequality

$$\begin{aligned} \Vert S^N-\bar{s}^N\Vert \leqslant \Vert S^N-\bar{w}^N\Vert +\Vert \bar{w}^N-\bar{s}^N\Vert = {\mathcal {O}}(h^2) + {\mathcal {O}}(h^2) = {\mathcal {O}}(h^2), \end{aligned}$$

which implies global, second-order convergence with respect to the true solution \(\bar{s}\).

It remains to find such a suitable grid function \(\bar{w}^{n}\). We note that this is the essence of this proof.

Case \(\alpha =1\). We first consider the case of a uniform mesh. The main error source that we like to examine is the switch in time stepping. Note though that different to (7), we now assume that forward differences are used. Therefore, the actual error terms look slightly different and are given by

$$\begin{aligned} L(\bar{s}^{n},\bar{s}^{n+1})_{-1}&= -\frac{1}{4}\lambda ^3h^2 s_{xx}(t^n,x_{-1}) + {\mathcal {O}}(h^3), \quad L(\bar{s}^{n},\bar{s}^{n+1})_{0} = {\mathcal {O}}(h^3), \\ L(\bar{s}^{n},\bar{s}^{n+1})_{1}&= \frac{1}{4}\lambda ^3h^2 s_{xx}(t^n,x_{1}) + {\mathcal {O}}(h^3). \end{aligned}$$

We define

$$\begin{aligned} \bar{w}^n_i = \bar{s}^n_i + \gamma ^n_i\quad \text { with } \quad \gamma ^n_i= {\left\{ \begin{array}{ll} - \frac{1}{2}\lambda ^2 h^2 s^n_{xx}(t^n,x_0) &{} \text { for } i=0,\\ 0 &{} \text { otherwise}.\\ \end{array}\right. } \end{aligned}$$
(9)

A direct computation then shows \(L(\gamma ^n,\gamma ^{n+1})_{0} ={\mathcal {O}}(h^3)\) as well as

$$\begin{aligned} L(\gamma ^n,\gamma ^{n+1})_{-1} = - \frac{\lambda }{2} \gamma ^n_0+ {\mathcal {O}}(h^3), \quad L(\gamma ^n,\gamma ^{n+1})_{1} = \frac{\lambda }{2} \gamma ^n_0+ {\mathcal {O}}(h^3). \end{aligned}$$

This implies by linearity

$$\begin{aligned} L(\bar{w}^n,\bar{w}^{n+1})_i = {\mathcal {O}}(h^3), \quad \forall \, i. \end{aligned}$$

Therefore, assumptions (8a) and (8b) are satisfied.

Case \(\alpha <1\). In this case we need to address all four error sources. First, a direct computation shows that for forward differences there holds with \(\beta = \frac{1+\alpha }{2}\)

$$\begin{aligned} L(\bar{s}^n,\bar{s}^{n+1})_{-1}&=\frac{\lambda }{4} \left( -\lambda ^2 + (1-\beta ) -\frac{1}{2\beta } \frac{1}{6}(\alpha ^2-1)\right) h^2s^n_{xx}(t^n,x_{-1}) + {\mathcal {O}}(h^3), \end{aligned}$$
(10a)
$$\begin{aligned} L(\bar{s}^n,\bar{s}^{n+1})_{0}&={\mathcal {O}}(h^3), \end{aligned}$$
(10b)
$$\begin{aligned} L(\bar{s}^n,\bar{s}^{n+1})_{1}&=\frac{\lambda }{4} \left( \lambda ^2 + (\beta -1) +\frac{1}{2\beta } \frac{1}{6}(\alpha ^2-1) \right) h^2s^n_{xx}(t^n,x_1) + {\mathcal {O}}(h^3). \end{aligned}$$
(10c)

Note in particular that for this setup, the one step error on the small cell is surprisingly of third order as errors cancel nicely. We define

$$\begin{aligned} \bar{w}^n_i = \bar{s}^n_i + \gamma ^n_i\quad \text { with } \quad \gamma ^n_i= {\left\{ \begin{array}{ll} \gamma ^n_0&{} \text { for } i=0,\\ 0 &{} \text { otherwise}\\ \end{array}\right. } \end{aligned}$$
(11)

with

$$\begin{aligned} \gamma ^n_0=\frac{\beta }{2}\left( -\lambda ^2+(1-\beta ) -\frac{1}{2\beta }\frac{1}{6}(\alpha ^2-1) \right) h^2 s^n_{xx}(t^n,x_0) . \end{aligned}$$
(12)

This results in \(L(\gamma ^n,\gamma ^{n+1})_{0} = {\mathcal {O}}(h^3)\) as well as in

$$\begin{aligned} L(\gamma ^n,\gamma ^{n+1})_{-1} = - \frac{\lambda }{2\beta } \gamma ^n_0+ {\mathcal {O}}(h^3), \quad L(\gamma ^n,\gamma ^{n+1})_{1} =\frac{\lambda }{2\beta } \gamma ^n_0+ {\mathcal {O}}(h^3), \end{aligned}$$

which implies the claim.

Remark 3

The advantage of forward differences compared to central differences lies in the reduced coupling of cells. For central differences, we have not been able to find suitable coefficients \(\gamma ^n\) when using periodic boundary conditions. But the numerical results in Sect. 2.1.2 imply that the same order of convergence holds true when one employs central differences instead of forward ones.

Remark 4

We note that we addressed two different error sources in this proof: the error caused by the switch in the time stepping scheme and the error caused by the irregular length of the cut cell. The reason that the former error does not accumulate is simply that we make an error of size \(-\frac{\lambda ^3}{4}h^2 s_{xx}(t^n,x_{-1})\) on cell \(-1\) and an error of size \(\frac{\lambda ^3}{4}h^2 s_{xx}(t^n,x_{1})\) on cell 1. In other words, the error that we made on cell \(-1\) cancels to leading order with the error that we make two cells later.

Finally, we verify our results numerically. We repeat Test 2 using forward difference quotients but this time we compare our discrete solution \(S_i^n\) to our new grid function \(\bar{w}\) given by (11) and (12). The result is given in Table 3 and shows the expected convergence rates.

Table 3 Result of Test 2: error for MUSCL-Trap using forward difference quotients for the model problem shown in Fig. 4
Full size table

2.2 New Variants of Mixed Explicit-Implicit Schemes

Our theoretical and numerical considerations above imply that the mixed scheme MUSCL-Trap is second-order accurate in one dimension, despite only having a second-order one step error. The numerical results in two dimensions though for MUSCL-Trap presented in [34] showed convergence rates between 1.3 and 1.6 measured in the \(L^{\infty }\) norm. This implies that in two dimensions the error does accumulate to some extent. Therefore, we cannot expect to be able to find a new grid function \(\bar{w}^n\) with properties (i) and (ii) in two dimensions.

In order to find a scheme with a third-order one step error, we would need to address all four error sources. As error sources (ii)(a)–(c) are very difficult to examine in two dimensions (due to varying sizes and shapes of cut cells) and are generally shared by most cut cell schemes, we focus here on the error caused by switching the time stepping scheme. Further, we expect the error for switching the time stepping scheme to have a very different effect in one dimension and two dimensions: in one dimension, characteristics are typically set up in a way that an error caused by switching from explicit to implicit is followed very briefly afterward by an error caused by switching from implicit back to explicit. In two dimensions, however, see the setup of the ramp test below in Fig. 6, this effect of switching back and forth might not be there. Instead there can be characteristics that mainly go through transition cells.

2.2.1 Developing Mixed Time Stepping Schemes with Better Transition Error

We will discuss the issue of reducing the error by switching the time stepping scheme in a sightly more general setting. For finite volume schemes, one typically uses the conservative update formula

$$\begin{aligned} S_i^{n+1} = S_i^n - \frac{\Delta t}{h} \left( F_{i+1/2} - F_{i-1/2} \right) \end{aligned}$$
(13)

with \(F_{i\pm 1/2}\) being an appropriate approximation to the flux at the edge \(x_{i\pm 1/2}\) during the time step. In the case of the linear advection (1) (with WLOG \(u=1\)), we try to approximate

$$\begin{aligned} F_{i+1/2}^{\textrm{true}} = \frac{1}{\Delta t} \int \nolimits _{t_n}^{t_{n+1}} s(t,x_{i+1/2}) \, \text {d}t. \end{aligned}$$
(14)

To only focus on the temporal error, we will reinterpret time stepping schemes as quadrature formulae for approximating the integral in (14), assuming that we know all values at the edges \(x=x_{i\pm 1/2}\) that we need. To give an example: using explicit Euler in time would correspond to approximating \(F_{i+1/2}^{\textrm{true}}\) by the point evaluation \(s(t^n,x_{i+1/2})\). For MUSCL and Trapezoidal time stepping we have the following results.

  • MUSCL: the corresponding time stepping scheme is the explicit midpoint rule, which corresponds to the following approximation of \(F_{i+1/2}^{\textrm{true}}\):

    $$\begin{aligned} F_{i+1/2}^{(M)} = s(t^n,x_{i+1/2}) + \frac{\Delta t}{2} \, s_t(t^n,x_{i+1/2}). \end{aligned}$$

    This results in

    $$\begin{aligned} F_{i+1/2}^{\textrm{true}} - F_{i+1/2}^{(M)} = \frac{\Delta t^2}{6} s_{tt} (t^n,x_{i+1/2}) + {\mathcal {O}}(\Delta t^3). \end{aligned}$$

  • Trapezoidal: the Trapezoidal time stepping scheme approximates \(F_{i+1/2}^{\textrm{true}}\) by

    $$\begin{aligned} F_{i+1/2}^{(T)} = \frac{1}{2} \left[ s(t^n,x_{i+1/2}) + s(t^{n+1}, x_{i+1/2}) \right] . \end{aligned}$$

    This results in the error

    $$\begin{aligned} F_{i+1/2}^{\textrm{true}} - F_{i+1/2}^{(T)} = - \frac{\Delta t^2}{12} s_{tt}(t^n,x_{i+1/2}) + {\mathcal {O}}(\Delta t^3). \end{aligned}$$

Therefore, assuming that the reconstruction in space is done sufficiently accurately, when using Trapezoidal rule time stepping, we approximate \(F_{i+1/2}^{\textrm{true}}\) with an error of \({\mathcal {O}}(\Delta t^2)\). However, when we use Trapezoidal on both edges, we make to leading order the same (systematic) error for the approximation of \(F_{i-1/2}^{\textrm{true}}\). When applying the update formula (13), the leading order error term cancels and there holds

$$\begin{aligned}&\left( F_{i+1/2}^{\textrm{true}} - F_{i-1/2}^{\textrm{true}} \right) - \left( F_{i+1/2}^{(T)} - F_{i-1/2}^{(T)} \right) \\& = -\frac{\Delta t^2}{12} s_{tt}(t^n,x_{i+1/2}) + \frac{\Delta t^2}{12} s_{tt}(t^n,x_{i-1/2}) + {\mathcal {O}}(\Delta t^3) = {\mathcal {O}}(\Delta t^2h) + {\mathcal {O}}(\Delta t^3). \end{aligned}$$

Therefore, for \(h= {\mathcal {O}}(\Delta t)\), we get an error of order \({\mathcal {O}}(\Delta t^3)\) (for the time approximation). However, if we use the explicit midpoint rule ( \(\hat{=}\) MUSCL) for \(F_{i-1/2}\) and Trapezoidal time stepping for \(F_{i+1/2}\), we get

$$\begin{aligned}&\left( F_{i+1/2}^{\textrm{true}} - F_{i-1/2}^{\textrm{true}} \right) - \left( F_{i+1/2}^{(T)} - F_{i-1/2}^{(M)} \right) \\& = -\frac{\Delta t^2}{12} s_{tt}(t^n,x_{i+1/2}) -\frac{\Delta t^2}{6} s_{tt}(t^n,x_{i-1/2}) + {\mathcal {O}}(\Delta t^3) = {\mathcal {O}}(\Delta t^2). \end{aligned}$$

This is the transition error that we saw before.

Note that these considerations have another important implication: the seemingly easiest way to improve the transition error that we observed for MUSCL-Trap would be to just keep MUSCL and use a third-order implicit scheme. Or to keep the Trapezoidal time stepping scheme and upgrade the explicit time stepping scheme to third order. However, both versions would not show the result one hoped for. The easiest way to see this is by combining, for example, the MUSCL flux \(F_{i-1/2}^{(M)}\) with the true flux \(F_{i+1/2}^{\textrm{true}}\). Then, when applying the conservative update formula (13), we would be left with an error of \({\mathcal {O}}(\Delta t^2)\) despite the scheme being apparently more accurate than when applying MUSCL fluxes on both edges.

Therefore, the two options to get a scheme with a third-order one step error (with respect to the time error) are to (a) either use both an explicit and an implicit time stepping scheme that approximate \(F_{i\pm 1/2}^{\textrm{true}}\) with third order or (b) to find a combination of a second-order explicit and a second-order implicit time stepping scheme such that the leading order error terms match.

Besides approach (a) being more expensive, third-order time stepping schemes also typically involve several stages, which makes the coupling very complicated. We therefore follow approach (b): we fix the implicit Trapezoidal rule and look for a new explicit time stepping scheme. We will consider two different modifications of the MUSCL scheme.

2.2.2 The MUSCLmod-Trap Scheme

The first approach is to change the MUSCL scheme given in (2) to use

$$\begin{aligned} F_{i+1/2}^{n+1/2,M\text {mod}} = u \left( S_i^n + (1 - \lambda ) S_{i,x}^n \frac{h}{2} - \frac{1}{4} \lambda (1-\lambda )h^2 S_{i,xx}^n \right) . \end{aligned}$$

The idea is to account for the error term \(\frac{\Delta t}{4}s_{tt}(t^n,x_{1+1/2})\) that we saw above when switching between Trapezoidal and explicit midpoint rule but the details slightly vary as we generally do not have the exact values on the edges. The precise formulation simply comes out of the error analysis for combining MUSCL with Trapezoidal. The truncation error analysis shows that

  • using MUSCLmod on an equidistant mesh as fully explicit scheme, there holds \(L(\overline{s}_i^{n+1}) = {\mathcal {O}}(h^3)\);

  • using MUSCLmod in a mixed MUSCLmod-Trap scheme (with \(\alpha =1\)), there holds \(L(\overline{s}_i^{n+1}) = {\mathcal {O}}(h^3)\).

A von Neumann stability analysis for the new MUSCL version shows a CFL condition of \(0 < \lambda \leqslant 1\).

In Table 4 we show the result for the new mixed MUSCLmod-Trap scheme for Test 2, but using \(\alpha =1\), i.e., we switch the time stepping between explicit and implicit at the corresponding cells but do that on an equidistant mesh to avoid error sources (ii)(a)–(c). As expected we observe third order for the one step error and second error for the error at time T. We use a standard second-order accurate difference quotient to evaluate the second derivatives.

Table 4 Result of Test 2: error for MUSCLmod-Trap for the model problem in Fig. 1d model problem \(\alpha =1\) (i.e., equidistant mesh but including change in time stepping scheme)
Full size table

2.2.3 The MPRKC-Trap Scheme

For the second variant, consider the explicit Trapezoidal rule, also known as the standard second-order SSP RK (strong stability preserving Runge-Kutta) scheme [20], and given by (for the ODE \(y_t = g(y(t))\))

$$\begin{aligned} y^{(1)} = y^n + \Delta tg(y^n), \quad y^{n+1} = y^n + \frac{\Delta t}{2} \left[ g(y^n) + g(y^{(1)}) \right] . \end{aligned}$$

If we compare that with the implicit Trapezoidal rule, we see that there is a \({\mathcal {O}}(\Delta t^2)\) difference due to using a second-order predictor step \(y^{(1)}\) instead of \(y^{n+1}\). Therefore, to get an explicit scheme that matches the leading order error term of \(F_{i+1/2}^{(T)}\) up to third order, we need to replace the predictor step (computation of \(y^{(1)}\)), which currently uses explicit Euler, by a more accurate predictor. We choose the explicit midpoint rule for this purpose. Together with a suitable space discretization (the new predictor step will correspond to the MUSCL scheme), this results in a new explicit finite volume scheme, which we will present now. Note that by construction this new scheme will show a third-order one step transition error when coupled to (implicit) Trapezoidal time stepping with slope reconstruction.

The new explicit scheme, which we call MPRKC (for MUSCL Predictor RK Corrector) scheme, is given by

$$\begin{aligned} S^{(1)}_i&=S^n_i-\frac{\Delta t}{h}\left( F^{n+1/2,M}_{i+1/2} - F^{n+1/2,M}_{i+1/2}\right) , \end{aligned}$$
(15a)
$$\begin{aligned} S^{n+1}_i&=S^n_i-\frac{\Delta t}{h} \left( F^{n+1/2,ET}_{i+1/2} -F^{n+1/2,ET}_{i-1/2}\right) \end{aligned}$$
(15b)

with

$$\begin{aligned} F^{n+1/2,ET}_{i+1/2}=\frac{u}{2} \left( S^n_i+S^n_{i,x} \frac{h}{2} + S^{(1)}_i+S^{(1)}_{i,x}\frac{h}{2}\right) . \end{aligned}$$
(16)

Remark 5

In terms of cost, the new scheme is roughly twice as expensive as MUSCL for taking one time step. Compared to using the standard second-order SSP RK scheme with slope reconstruction in space, the cost is roughly the same. We just exploit the information from the slope reconstruction in stage 1 more carefully.

Lemma 1

The scheme (15)–(16) is linearly stable for the linear advection equation (1) on an equidistant mesh under the CFL condition \(0 < \lambda \leqslant 1.\)

Proof

The claim follows by means of a von Neumann stability analysis. We analytically deduce a very lengthy and complicated expression for the amplification factor \(|{G} |\) (not given here). We then verify numerically that \(|{G} | \leqslant 1\) if and only if \(0 < \lambda \leqslant 1\).

We combine the explicit MPRKC scheme with the implicit Trapezoidal scheme (3) using flux bounding, resulting in MPRKC-Trap. This is sketched in Fig. 5. Due to MPRKC being a two-stage scheme, the implicit region has become bigger compared to MUSCL-Trap. The results for the mixed scheme on an equidistant mesh with \(\alpha =1\) but with switching the scheme as indicated in Test 2 are shown in Table 5. As expected, the one step error converges with the third order and the error at time T with the second order.

Table 5 Result of Test 2: error for MPRKC-Trap for the model problem in Fig. 1d model problem \(\alpha =1\) (i.e., equidistant mesh but including change in time stepping scheme)
Full size table
Fig. 5
figure 5

The new MPRKC-Trap scheme: we compute \(S_i^{(1)}\) using the MUSCL scheme for cells \(i \leqslant -2\) and \(i \geqslant 2\) as sketched in Fig. 2a. Then we compute the explicit flux \(F^{n+1/2,ET}\) given by (16) for all edges marked in green and update the fully explicitly treated cells \(i \leqslant -4\) and \(i \geqslant 4\). We combine this using flux bounding with an implicit treatment (edges marked in light blue) of cells \(-3,\cdots ,3\). Note that now cells \(-3\) and 3 correspond to the transition cells

Full size image

3 Mixed Explicit-Implicit Schemes in Two Dimensions

In the following we will discuss mixed explicit-implicit schemes in two dimensions: we will first briefly introduce the two dimensions version of the MUSCL-Trap scheme as presented in [34] and examine its error. Then, we will introduce variants of MUSCLmod-Trap and MPRKC-Trap in two dimensions. We will conclude with a comparison of the resulting schemes for both a fully Cartesian mesh and a cut cell mesh.

3.1 The MUSCL-Trap Scheme

In two dimensions, we solve the linear advection equation

$$\begin{aligned} s_t + u s_x + v s_y = 0. \end{aligned}$$
(17)

Here, s(t, x, y) denotes a scalar field. For simplicity, we will only consider a constant velocity field, i.e., u and v are assumed to be constant. This is sufficient to show our main findings.

As an explicit scheme, an unsplit, two-dimensional MUSCL scheme [2] is used. For brevity reasons, we will not present the details here. We note though that this MUSCL scheme uses corner-coupling to capture proper dependencies in two dimensions and is therefore stable under the CFL condition \(0 < \nu \leqslant 1\) in combination with the time step computation

$$\begin{aligned} \Delta t=\nu \min \left( \frac{\Delta x}{|{u} |},\frac{\Delta y}{|{v} |}\right) . \end{aligned}$$
(18)
Fig. 6
figure 6

Switching between schemes in two dimensions: cut cells are marked by pink color. Implicit fluxes are marked by a bold, red line, explicit fluxes by blue. Left: MUSCL-Trap: “Transition” cells (marked with “T”) are full Cartesian cells that share an edge with a cut cell. Right: MPRKC-Trap: the shaded cells corresponds to the layer of cells closest to the embedded object that can be updated using the MUSCL predictor step. Transition cells (marked with “T”) have been shifted by two cell layers compared to MUSCL-Trap

Full size image

Flux bounding is used to couple the explicit MUSCL scheme with an implicit scheme. The idea is sketched in the left graphic of Fig. 6. Full Cartesian cells that are edge neighbors of cut cells are marked as transition cells. Cut cells are treated fully implicit. Therefore, fluxes between cut cells and transition cells use an implicit scheme. All remaining fluxes, in particular fluxes between two transition cells, use an explicit scheme.

This results in the following two-step algorithm, which is analogous to the one dimension situation: given \(S_{ij}^n\),

  1. (i)

    compute all explicit fluxes using the MUSCL scheme and update all fully explicitly treated cells to \(S_{ij}^{n+1}\);

  2. (ii)

    compute all implicit fluxes and update cut cells and transition cells to \(S_{ij}^{n+1}\).

As an implicit scheme, Trapezoidal time stepping in combination with a least squares formulation for slope reconstruction in space [3, 32] is used. On Cartesian cells that are not transition cells standard central differences are used for slope reconstruction. No limiting is applied.

We note that on cut cells, one reconstructs to the midpoint of the cut cell edges, not to the midpoint of the Cartesian edges. To be more precise, the update on a cut cell is given by

$$\begin{aligned} S_{ij}^{n+1} = S_{ij}^n - \frac{\Delta t}{\alpha _{ij}\Delta x \Delta y} \left( F_{i+1/2,j}^{n+1/2,T} - F_{i-1/2,j}^{n+1/2,T} + G_{i,j+1/2}^{n+1/2,T} - G_{i,j-1/2}^{n+1/2,T} \right), \end{aligned}$$
(19)

where \(\alpha _{ij} \in (0,1)\) is the volume fraction and

$$\begin{aligned} F_{i+1/2,j}^{n+1/2,T}&= \frac{1}{2}u\beta _{i+1/2,j} \Delta y (S_{i+1/2,j}^{n} + S_{i+1/2,j}^{n+1}),\\ S_{i+1/2,j}^{n}&= {\left\{ \begin{array}{ll} S_{ij}^{n} + (x_{i+1/2,j}-x_{ij}) S_{ij,x}^n + (y_{i+1/2,j}-y_{ij}) S_{ij,y}^n &{} \text {if} \, u > 0,\\ S_{i+1,j}^{n} + (x_{i+1/2,j}-x_{i+1,j}) S_{i+1,j,x}^n + (y_{i+1/2,j}-y_{i+1,j}) S_{i+1,j,y}^n&{} \text {if} \, u < 0. \end{array}\right. } \end{aligned}$$

Here \((x_{i+1/2,j},y_{i+1/2,j})\) denotes the location of the edge midpoint of face \((i+1/2,j)\), \((x_{ij},y_{ij})\) denotes the centroid of cut cell (i, j), and \(S_{ij,x}\) and \(S_{ij,y}\) refer to the reconstructed unlimited x- and y-slopes respectively in cell (i, j). Further, \(\beta _{i+1/2,j} \in [0,1]\) represents the area fraction of cut cell edge \((i+1/2,j)\) compared to a full Cartesian edge. The fluxes \(G_{i,j+1/2}^{n+1/2,T}\) are defined analogously. This concludes the brief description of the MUSCL-Trap scheme. More details can be found in [34].

Remark 6

(Cost of MUSCL-Trap) In each time step, one needs to solve an implicit system that couples the cut cells and transitions cells. Since cut cells occur only at the boundary of the embedded object, the size of this system is one dimension lower than the overall number of cells. In two dimensions on a Cartesian grid with N cells in each direction, one expects \({\mathcal {O}}(N)\) unknowns in the implicit system. Therefore, using this mixed explicit-implicit approach is significantly cheaper than using an implicit scheme everywhere.

In [34], May and Berger presented numerical results for the (unlimited) MUSCL-Trap scheme in two dimensions. The \(L^1\) error converged with second order. The \(L^{\infty }\) error however showed convergence rates between 1.3 and 1.6. This is not in line with the second-order accuracy that we saw in one dimension. Newer results with DG codes on cut cell meshes for piecewise linear polynomials however have also showed reduced convergence rates in the \(L^{\infty }\) norm of 1.5–1.6 [14, 18]. This raises the general question of whether we can expect to see full second-order convergence in the \(L^{\infty }\) norm on two dimensional cut cell meshes at all but this is the goal.

In the following we want to examine the accuracy of the scheme in two dimensions more closely than done in [34]. Here, we will focus on the error caused by switching the time stepping scheme. Due to the complexity of cut cells in two dimensions, our examination will be mostly based on numerical experiments.

Remark 7

For our numerical tests in two dimensions, we use the code setup from [34] as the starting point: our implementation is based on BoxLib [4], a library for massively parallel AMR applications. For the generation of the cut cells, we use patchCubes, a variant of the cubes mesh generator that is part of the Cart3D package [1, 24]. The solution of the resulting implicit system is done using umfpack [23].

3.1.1 The Transition Error for MUSCL-Trap (in Absence of Cut Cells)

We would like to examine the time stepping transition error in the absence of error sources (ii)(a)–(c) caused by the irregularity of the cut cells. Therefore, we consider the test setup shown in Fig. 7: we create a setup where we switch between explicit and implicit time stepping but all cells are full Cartesian cells. As on a Cartesian mesh error sources (ii)(a)–(c) drop out, the remaining error should be dominated by the switch from MUSCL to Trapezoidal.

Fig. 7
figure 7

Setup for testing transition error in two dimensions: all cells are Cartesian cells but we simulate the switch in time stepping. To do so, we intersect a Cartesian grid with a line with angle \(\beta\). All cells cut by this line (marked in pink) are treated as “fake” (as Cartesian) cut cells. All “fake” cut cell edges as well as all edges of cells below the “fake” cut cells use the implicit scheme (marked in red). All remaining edges (marked in blue), i.e., all edges of cells above the “fake” cut cells use the explicit scheme. The switch takes place on the cells marked with a “T”

Full size image

For the theoretical considerations, we focus on the case of 45\(^\circ\) and choose \(u=v=1\) and \(\Delta x = \Delta y\). The update on a transition cell is given by

$$\begin{aligned} S_{ij}^{n+1} = S_{ij}^n - \frac{\Delta t}{\Delta x \Delta y} \left( F_{i+1/2,j}^{n+1/2,T} - F_{i-1/2,j}^{n+1/2,M} + G_{i,j+1/2}^{n+1/2,M} - G_{i,j-1/2}^{n+1/2,T} \right) . \end{aligned}$$

A lengthy computation, which involves the usage of the equation \(s_t + s_x+ s_y = 0\) to re-express derivatives, leads to the following formula for the one step error on transition cells:

$$\begin{aligned} L(\bar{s}^{n},\bar{s}^{n+1})_{ij} = \frac{1}{4} \left( \Delta t^2 - \tfrac{\Delta t^3}{h} \right) s_{xx}(t^n,x_i,y_j) - \frac{1}{4} \left( \Delta t^2 - \tfrac{\Delta t^3}{h}\right) s_{yy}(t^n,x_i,y_j) + {\mathcal {O}}(\Delta t^3). \end{aligned}$$

Therefore, we expect in general a one step error of second order. For the special case \(s_{xx} = s_{yy}\), we expect a third-order one step error (we confirmed this in numerical experiments not shown here).

In numerical tests, see e.g., Test 3 below, we often observed (for a variety of angles) that on a full Cartesian mesh, we have a second-order one step error in \(L^{\infty }\) due to this transition—but that this transition error accumulates “only” to a scheme of order \({\mathcal {O}}(h^{1.5})\) for the \(L^{\infty }\) error at time T.

3.2 New Mixed Explicit-Implicit Schemes

We now present the extensions of MUSCLmod-Trap and MPRKC-Trap to two dimensions.

3.2.1 The MUSCLmod-Trap Scheme

To derive the new explicit MUSCLmod scheme, we essentially do a truncation error analysis of the Trapezoidal rule and the MUSCL scheme on a mesh as shown in Fig. 7 and design MUSCLmod to contain the second-order transition error terms. One needs to be a bit careful in this computation as the original MUSCL scheme is based on an unsplit version, involving corner coupling and a more evolved evaluation of transverse derivatives. This then results in the following change of the reconstructed value \(S_{i+1/2,j}^{M,n+1/2}\) (the approximation to the solution at the midpoint of edge \((i+1/2,j)\) at time \(t^{n+1/2}\) used in the MUSCL scheme) for the case \(u,v>0\)

$$\begin{aligned} S_{i+1/2,j}^{M\text {mod},n+1/2} =S_{i+1/2,j}^{M,n+1/2} + \frac{\Delta t^2}{4} \left( u^2 S_{ij,xx}^n + 2uv S_{ij,xy}^n \right) - \frac{\Delta t \Delta x}{4} \left( u S_{ij,xx}^n + v S_{ij,xy}^n \right) . \end{aligned}$$

The second derivatives are computed using standard second-order difference quotients on Cartesian cells away from cut cells. On transition cells we fit a quadratic polynomial to compute them.

Numerical tests show for MUSCLmod as a fully explicit scheme on a Cartesian mesh a third-order one step error and standard second-order accuracy at time T. The numerical stability limit also seems to be very similar to the original unsplit MUSCL.

3.2.2 The MPRKC-Trap Scheme

We now extend the explicit MPRKC scheme, given by (15)–(16) in one dimension, to two dimensions. We use the unsplit MUSCL scheme described by Almgren et al. [2], which we also use for the MUSCL-Trap scheme, to compute the predictor \(S^{(1)}\). Afterwards, we use the two-dimensional analog of (16) for the computation of the fluxes \(F_{i\pm 1/2,j}^{n+1/2,ET}\) and \(G_{i,j \pm 1/2}^{n+1/2,ET}\).

The classic two-stage second-order SSP RK scheme in combination with central differences for \(\Delta x = \Delta y= h\) is stable with \(\nu \leqslant 1.0\) under the CFL condition [7]

$$\begin{aligned} \Delta t=\nu \frac{h}{|{u} |+|{v} |} \end{aligned}$$
(20)

due to using a split approach. The new MPRKC scheme uses the unsplit MUSCL as the predictor (instead of the split upwind scheme) but the split explicit Trapezoidal scheme as the corrector. We therefore expect MPRKC to be at least as stable as the classic two-stage second-order SSP RK scheme and to be in particular stable under the CFL condition (20). We confirmed this in numerical tests.

Next, we briefly sketch the extension of the mixed MPRKC-Trap to two dimensions. If we compare the one-dimensional sketches of MUSCL-Trap, see Fig. 2b, and MPRKC-Trap, see Fig. 5, we observe that the implicit zone has been extended by two cells. This holds also true in two dimensions: given \(S_{ij}^n\),

  1. (i)

    compute explicit fluxes using the MUSCL scheme and update all cells that have been treated fully explicitly by MUSCL-Trap to \({S}_{ij}^{(1)}\);

  2. (ii)

    use the predicted values \({S}_{ij}^{(1)}\) for taking the second step of the explicit MPRKC scheme; due to slope reconstruction, this will “cost” two layers of cells; therefore, the position of the transition cells has been shifted by two cell layers to the interior of the flow domain, comparing Fig. 6;

  3. (iii)

    compute all implicit fluxes for the extended implicit zone; update cut cells, fully implicitly treated implicit cells in the extended implicit zone, and transition cells to \(S_{ij}^{n+1}\).

Note that the MPRKC-Trap scheme has been constructed to have a third-order one step error on Cartesian meshes.

3.3 Numerical Results in Two Dimensions

We will consider two different tests in the following. We will first compare the various mixed schemes on a mesh that contains only Cartesian cells. This is to confirm our analytical considerations above. Afterwards we will compare the mixed schemes on a mesh that contains cut cells.

3.3.1 Test on Cartesian Mesh

Test 3 We consider the setup shown in Fig. 7. We set \(\beta =30^{\circ }\). The Cartesian mesh is chosen to cover \([0,1]^2\) with \(\Delta x = \Delta y\) and N denotes the number of Cartesian cells in one coordinate direction, i.e., \(N = \frac{1}{\Delta x}\). The ramp starts at approximately \(x_0=0.146\). We use as test function \(s_0 = 1 + \exp (-120*((x-0.49)^2+(y-0.20)^2))\) so that the peak of the Gaussian aligns with where we switch the scheme. We choose the velocity field parallel to the angle \(\beta\), i.e., \(\gamma =\beta\), and set \((u,v)^\text{T}=(2,2\tan (\beta ))\). We use \(T=0.15\). The initial data and the solution at the final time are shown in Fig. 8. We use \(\nu =0.8\). The time step \(\Delta t\) for the mixed schemes involving MUSCL and MUSCLmod is computed using (18), for the mixed scheme involving MPRKC we use (20). We compare MUSCL-Trap, MUSCLmod-Trap, and MPRKC-Trap. We also include results using the explicit versions of the scheme everywhere (i.e., in that case we do not switch to an implicit scheme).

In Fig. 9 we show the error after taking one time step, both in the \(L^1\) norm and in the \(L^{\infty }\) norm. As expected, all fully explicit versions show a third-order one step error. For the mixed schemes, both new versions (MUSCLmod-Trap and MPRKC-Trap) show third order in \(L^{\infty }\) whereas MUSCL-Trap only converges with second order.

In Fig. 10 we show the error at time T. We observe second-order convergence for the \(L^1\) norm for all six schemes. The error for MUSCL is smallest, followed by MUSCL-Trap. For the error in the \(L^\infty\) norm, all schemes except for MUSCL-Trap show second order. MUSCL-Trap converges on the finest meshes with order 1.5. So there is some error accumulation from the second-order one step error but we only seem to lose half an order. We have observed an order of 1.5 for MUSCL-Trap on Cartesian meshes in several tests. In terms of absolute error sizes, we observe the smallest errors for MUSCL, MUSCLmod, and MUSCLmod-Trap, with them being essentially identical on the finest mesh.

Fig. 8
figure 8

Setup Test 3. Initial data (left) and solution at \(T=0.15\) (right) for MUSCLmod-Trap on a 256\(\times\)256 mesh (only the zoom on the domain \([0,1]\times [0,0.6]\) is shown)

Full size image
Fig. 9
figure 9

Results for Test 3. Error after one time step. Left: \(L^1\) error. Right: \(L^\infty\) error

Full size image
Fig. 10
figure 10

Results for Test 3. Error at time T. Left: \(L^1\) error. Right: \(L^\infty\) error

Full size image

3.3.2 Test on Cut Cell Mesh

Our discussion of the schemes in two dimensions so far has focused on the transition error between the explicit and implicit schemes in the absence of cut cells. The goal was to examine and eliminate error source (i) separately from error sources (ii)(a)–(c). We now add cut cells again and conclude this contribution with a numerical comparison involving the following three schemes: MUSCL-Trap, MUSCLmod-Trap, and MPRKC-Trap. The goal is to examine whether the reduction of the transition error leads to more accurate results and better convergence orders for the cut cell situation as well.

Test 4 We consider the ramp setup shown in Fig. 6. We again choose \(\gamma =\beta\). We will consider 4 different angles for this test: 10\(^\circ\), 20\(^\circ\), 30\(^\circ\), and 40\(^\circ\). The setup is similar to Test 3 with the main difference being that we now have cut cells along the ramp. The Cartesian mesh is chosen to cover \([0,1]^2\) with \(\Delta x = \Delta y\). We use as test function again \(s_0 = 1 + \exp (-120*((x-x_0)^2+(y-y_0)^2))\). The starting point of the ramp and the centering of the test function \((x_0,y_0)\) vary for the different angles. They are chosen in such a way that at the initial time, the cut cells are located around the peak, see, e.g., Fig. 11 for the solution at the final time for ramp angle \(30^{\circ }\).

Besides the accuracy of the three different schemes, we also want to examine the effect of the inaccurate slope reconstruction on cut cells and transition cells. Typically, we use the least squares fit to construct gradients on cut cells and transition cells, see, e.g., [32], which is only first-order accurate. As an easy way of obtaining slopes with higher accuracy, we will also include results that use analytic slopes on cut cells and transition cells (together with standard second-order slope reconstruction on Cartesian cells that are updated fully explicitly). These will be marked with “ana” in the legend whereas “LS” implies that the least squares slope reconstruction has been used.

The tests will focus on comparing the accuracy of the different schemes. In terms of cost, for all schemes we need to solve implicit systems of size \({\mathcal {O}}(N)\). The costs for MUSCL-Trap and MUSCLmod-Trap are pretty comparable. MPRKC-Trap is somewhat more expensive due to applying the explicit scheme twice, the potentially reduced time step length caused by the different CFL conditions, and the extended implicit zone, which is also reflected in somewhat longer running times.

Fig. 11
figure 11

Results for Test 4 for \(30^{\circ }\) ramp. Left: zoom on the solution at time T using MUSCL-Trap for \(N=512\). Right: \(L^1\) error for various schemes

Full size image

In Fig. 11 we show the results for the error in the \(L^1\) norm for the \(30^{\circ }\) ramp. The results for the other angles are very comparable. We observe second order convergence for all schemes. Generally, using the original MUSCL scheme as an explicit scheme leads to slightly smaller \(L^1\) errors for this test. We have also included results for versions of MUSCL-Trap and MUSCLmod-Trap with an extended implicit zone, where the implicit zone has been extended by two cells. These are marked as “ext2”. As a result the set of implicitly treated cells is now the same as for MPRKC-Trap.

Fig. 12
figure 12

Results for Test 4. Error in \(L^{\infty }\) norm. Convergence orders are given in Table 6

Full size image
Table 6 Result of Test 4: convergence orders for errors in \(L^{\infty }\) norm, computed as a least squares fit for data shown in Fig. 12
Full size table

In Fig. 12 we present the results for the error in the \(L^{\infty }\) norm for all 4 angles. Recall that the test function was chosen such that we expect bigger errors on cut cells, which is actually the case. It is very common for errors on cut cells in the \(L^{\infty }\) norm to show a zig-zag behavior. In Table 6 we therefore also present slopes that we get from fitting straight lines through the data shown in Fig. 12 by means of a least squares approach. While the details vary a bit for the different ramp angles, we can generally observe that

  • when using the LS slopes, the three different schemes (MUSCL-Trap, MUSCLmod-Trap, and MPRKC-Trap) show similar absolute errors and also similar convergence orders (with the exception of the \(40^{\circ }\) ramp). Having improved the transition error does not result in smaller errors overall for this test;

  • using analytic slopes reduces the error (in terms of its size) significantly, with factors varying between 4 and 10;

  • for MPRKC-Trap, using analytic slopes instead of LS slopes improves the convergence orders, within a range of 0.15–0.42;

  • for MUSCL-Trap and MUSCLmod-Trap, we do not see significant improvement in convergence orders when using analytic slopes instead of LS slopes. For extending the implicit zone by two cell layers, we do see significant improvement for the angles \(10^{\circ }\) and \(20^{\circ }\) degrees but not for the higher ones;

  • we observe the highest convergence orders for MPRKC-Trap with analytic slopes. In terms of error sizes it is very comparable though with MUSCL-Trap and MUSCLmod-Trap when using analytic slopes and an extended implicit zone.

To sum it up, despite the improved transition error, we do not see a significantly improved convergence order or significantly smaller errors for the new versions MUSCLmod-Trap and MPRKC-Trap. Using analytic slopes leads to significantly smaller error sizes but not necessarily significantly improved convergence orders for this test.

4 Conclusions and Future Plans

In this contribution, we analyzed the accuracy of the mixed explicit implicit scheme consisting of MUSCL as an explicit scheme and the Trapezoidal rule with slope reconstruction as an implicit scheme. For the one step error, we identified several second-order error sources linked to the irregular size of the cut cells as well as a second-order transition error when switching from explicit to implicit schemes. For linear advection in one dimension, we can show that these errors do not accumulate in the usual way and that the resulting scheme is second-order accurate.

This is not the case in two dimensions. We therefore introduced two new mixed schemes, MUSCLmod-Trap and MPRKC-Trap, with improved transition errors that are based on exchanging the explicit scheme. Using the mixed scheme on a fully Cartesian mesh led to improved convergence orders in two dimensions. When using these new schemes on a test involving cut cells however there was no significant difference from using the original MUSCL-Trap. Using analytic slopes led to a slight improvement of convergence orders and a significant improvement in the actual error size. Note though that the improved convergence orders are not that different from the newer results with DG codes on cut cell meshes for piecewise linear polynomials, which show reduced convergence orders in the \(L^{\infty }\) norm of 1.5 to 1.6 [14, 18] as well. So maybe it is too much to aim for a full second order in \(L^{\infty }\) for the ramp test.

More intensive numerical tests are needed to make a definite statement. It currently seems that it might only pay off to reduce the transition error if also the other error sources (caused by the irregularity of the cut cells) are taken care of. The first step would be to upgrade the slope reconstruction on cut cells and neighbors of cut cells to second order. This can be achieved by fitting quadratic polynomials. Our initial attempts of implementing this have led to irritating results. It is currently not clear whether there is a bug in the implementation or whether there is some kind of weird interaction going on with the solutions necessary for the implicit time stepping. We currently use an approximate Newton scheme for that with the approximate Jacobian being based on a first-order discretization.