1 Introduction

In recent years, lunar missions are attracting a renewed interest, in the clear perspective of planning and completing robotic and human missions in the near future. Low-energy missions to the Moon were investigated for decades. Exterior and interior transfers to the Moon include transits through the regions located in the proximity of the collinear libration points. Former studies [1] established that the invariant manifolds associated with planar Lyapunov orbits play the role of separatrices. This means that in the phase space, the stable invariant manifold converging into the Lyapunov orbit separates the trajectories that transit from the Earth to the Moon from those that approach the interior collinear libration point and then return toward the Earth. Closely related to this, lunar capture dynamics represents a challenging and very significant problem of practical interest. In fact, a great deal of effort was dedicated to the identification and topological description of (non-periodic) lunar capture orbits, since the 60 s [2,3,4,5]. A fundamental conjecture on the topology of asymptotic and capture orbits dates back to the 60 s and is due to Conley [6]. A popular approach in low-energy Earth–Moon mission analysis, followed by a successful application in a real scenario, was proposed by Belbruno and Miller [7], and employs the concept of ballistic capture, leveraging the Sun gravitational influence. More recently, Giancotti et al. investigated lunar capture dynamics using isomorphic mapping [8], with the intent of relating capture orbits to asymptotic trajectories.

In the scientific literature, many studies employed the circular restricted three-body problem (CR3BP) to describe the spacecraft orbital dynamics in the Earth–Moon system [9]. This represents a suitable model for preliminary mission analysis. More recently, some studies focused on more sophisticated and accurate dynamical frameworks, such as the bicircular restricted four-body problem (BCR4BP) [10] and the elliptic restricted three-body problem (ER3BP) [11], and provided clear insights on the properties of the (ballistic) dynamical structures that preserve both in BCR4BP and in ER3BP.

In the last 2 decades, due to limited propellant consumption, the use of low-thrust propulsion has gained an increased interest, and already found application in several mission scenarios, e.g., the NASA Deep Space 1 and the ESA Smart-1 missions. Thanks to high values of the specific impulse, low-thrust propulsion allows substantial propellant savings, at the price of increasing—even considerably—the time of flight. In a very recent publication, Cox et al. [12] focus on transit and capture in the planar three-body problem, using low-thrust dynamical structures. In fact, under certain assumptions, periodic orbits and invariant manifolds can be proven to subsist even if low thrust is ignited. The study of low-thrust structures existing in the CR3BP offers many advantages over approaches that include only ballistic structures. In fact, the topological properties of low-thrust trajectories in the CR3BP can be properly shaped using low-thrust propulsion, making feasible some interesting mission scenarios that would be naturally infeasible otherwise. Similar considerations hold if solar sail propulsion is employed, with the advantage of not requiring any propellant expenditure [13]. In some mission scenarios, low-thrust can facilitate and reduce the time needed to complete orbit maneuvers aimed at reaching a specified operational condition [12]. Cox et al. [14] focused on obtaining a combined low-thrust multi-body dynamics model to guide the preliminary design process. The main challenge in the design of a low-thrust trajectory is in the identification of the thrust magnitude and direction. To address this issue, optimization techniques have been extensively employed in the context of low-thrust trajectory design. Betts [15], Conway [16], and Rao [17] offer excellent overviews on the available methods for spacecraft trajectory optimization. These approaches are extremely useful in preliminary mission analysis, and are implemented as offline algorithms. However, their convergence is strongly problem-dependent and usually requires availability of an approximate guess solution. Nonlinear orbit control [18, 19] represents an alternative, very interesting approach capable of identifying a feedback control law for the thrust direction and magnitude, in relation to the instantaneous spacecraft position and velocity.

This study employs the CR3BP as the dynamical framework, for the purpose of investigating low-thrust orbit dynamics in the Earth–Moon system. More specifically, this research investigates the effect of low thrust on some dynamical structures that exist in the CR3BP, i.e., zero velocity curves and surfaces, and periodic orbits. As a first step, low-thrust capture and escape dynamics in the proximity of the Moon is investigated, in relation to the geometry of zero velocity curves and surfaces, which can be suitably shaped with the use of low thrust. Second, low-thrust periodic orbits—with potential practical application—are detected. Previous research [20] identified a variety of periodic orbits, either in the proximity of libration points or about the two celestial bodies (Earth and Moon). Instead, this study focuses on the identification of periodic orbits that can be traveled using low-thrust propulsion, for relatively long durations. To do this, the theorem of mirror trajectories [21, 22], proven 6 decades ago, is extended to low-thrust trajectories. This represents the theoretical premise for the definition and use of a numerical search methodology based on modified Poincaré maps. This approach aims at identifying several low-thrust periodic orbits in the Earth–Moon system that are infeasible if only unpowered paths are considered. Two possible applications of low-thrust periodic orbits are suggested: (a) cycling transfer trajectories that connect Earth and Moon continuously, and (b) non-Keplerian periodic paths about the Moon, with potential use as operational orbits for satellite constellations.

The paper that follows first describes low-thrust orbit dynamics in the dynamical framework of the CR3BP, focusing on the low-thrust Jacobi integral and zero velocity curves and surfaces. Section 3 is devoted to lunar capture and evasion dynamics using low thrust. Section 4 addresses the problem of detecting low-thrust periodic orbits, and focuses on two applications of potential interest, i.e., (1) cycling orbits that connect continuously the Earth to the Moon and (2) satellite constellations about the Moon.

2 Low-Thrust Circular Restricted Three-Body Problem

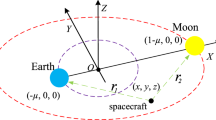
The CR3BP models the dynamics of a massless body, i.e., the spacecraft, subject to the simultaneous attraction of two massive bodies, called the primaries. The problem is conveniently described in the rotating synodic reference frame (cf. Fig. 1), parameterized by the mass ratio µ = m2/(m1 + m2), where m1 and m2 are the masses of the two primaries and m1 ≥ m2; for the Earth–Moon system, µ = 1/82.27. Origin of the synodic frame is the center of mass of the Earth–Moon system, the x-axis connects the two primaries at all times, and the z-axis points toward the angular momentum of the system. In the synodic frame, (x, y, z) denote the spacecraft position coordinates.

Fig. 1
figure 1

The primaries m1 and m2 in circular orbit, plus a third body m

Full size image

Low thrust can be introduced in the equations of motion as an acceleration vector, whose components are collected on the (3 × 1) vector \(\vec{a}_{lt}\)

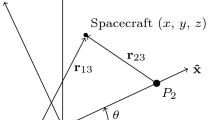
$$\vec{a}_{lt} = a_{lt} \left[ {\cos \alpha \cos \beta \,\,\,\, \sin \alpha \cos \beta \,\,\,\,\sin \beta } \right]^{T} ;$$
(1)

\(\vec{a}_{lt}\) has magnitude \(a_{lt}\), whereas α is the angle between the x-axis and the projection of \(\vec{a}_{lt}\) in the (x, y)-plane, and β is measured in counterclockwise sense in the (y, z)-plane, as shown in Fig. 2.

Fig. 2
figure 2

Thrust angles α and β

Full size image

This research assumes thrust acceleration with constant magnitude \(a_{lt}\). This means that the spacecraft mass reduction due to propellant consumption obeys the following equation:

$$\dot{m} = - \frac{T}{c} \Rightarrow \frac{{\dot{m}}}{m} = - \frac{{a_{lt} }}{c} \Rightarrow \frac{m}{{m_{0} }} = \exp \left[ { - \frac{{a_{lt} }}{c}t} \right],$$
(2)

where T and m denote the thrust and instantaneous spacecraft mass, \(a_{lt} : = \left( {{T \mathord{\left/ {\vphantom {T m}} \right. \kern-\nulldelimiterspace} m}} \right)\), t is the current time, and c is the constant effective exhaust velocity of the propulsion system. In this research, the following parameters of the propulsion system are assumed: \(a_{lt} = 2 \cdot 10^{ - 5} \, g_{0} \, \left( {g_{0} = 9.8 \, {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {{\text{s}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{s}}^{2} }}} \right)\) and \(c = 30 \, {{{\text{km}}} \mathord{\left/ {\vphantom {{{\text{km}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\).

2.1 Equations of Motion with Low-Thrust Propulsion

The equations of motion are obtained taking into account the gravitational attraction of the two primaries on the third body, and are written employing canonical units, which represent a set of conveniently normalized units. The distance unit (DU) is the constant distance between the two primaries, whereas the time unit 1/TU equals the angular velocity with which the two primaries rotate about their common barycenter. With the inclusion of the acceleration term due to low thrust, the equations of motion are

$$\left\{ {\begin{array}{*{20}c} {\ddot{x} = 2\dot{y} + \Omega_{x} + a_{{lt_{x} }} } \\ {\ddot{y} = - 2\dot{x} + \Omega_{y} + a_{{lt_{y} }} } \\ {\ddot{z} = \Omega_{z} + a_{{lt_{z} }} } \\ \end{array} ,} \right.$$
(3)

where Ω is the potential function, given by

$$\Omega = \frac{{x^{2} + y^{2} }}{2} + \frac{1 - \mu }{{\sqrt {\left( {x + \mu } \right)^{2} + y^{2} + z^{2} } }} + \frac{\mu }{{\sqrt {\left( {x + \mu - 1} \right)^{2} + y^{2} + z^{2} } }}.$$
(4)

2.2 Low-Thrust Jacobi Integral, Zero Velocity Curves and Surfaces

It is relatively straightforward to demonstrate that a Jacobi integral exists also for this dynamical system, under the assumption that the low-thrust components are constant. The equations of the system (3) are multiplied, respectively, by \(\dot{x}, \dot{y},\dot{z}\) and summed. Thus, one obtains [14]

$$\dot{x}\ddot{x} + \dot{y}\ddot{y} + \dot{z}\ddot{z} = \dot{x}\frac{{{\text{d}}\Omega }}{{{\text{d}}x}} + \dot{y}\frac{{{\text{d}}\Omega }}{{{\text{d}}y}} + \dot{z}\frac{{{\text{d}}\Omega }}{{{\text{d}}z}} + \frac{{d\left( {{ }a_{{lt_{x} }} x + a_{{lt_{y} }} y + a_{{lt_{z} }} z} \right)}}{{{\text{d}}t}},$$
(5)

leading to

$$\frac{1}{2}\frac{{{\text{d}}\left( {\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} } \right)}}{{{\text{d}}t}} = \frac{{{\text{d}}\Omega }}{{{\text{d}}t}} + \frac{{{\text{d}}\left( {{ }a_{{lt_{x} }} x + a_{{lt_{y} }} y + a_{{lt_{z} }} z} \right)}}{{{\text{d}}t}},$$
(6)
$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\Omega - \frac{1}{2}\left( {\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} } \right) + a_{{lt_{x} }} x + a_{{lt_{y} }} y + a_{{lt_{z} }} z} \right) = 0.$$
(7)

This means that a constant exists, referred to as the modified Jacobi integral and denoted with C

$$C = 2\Omega + 2\left( {a_{{lt_{x} }} x + a_{{lt_{y} }} y + a_{{lt_{z} }} z} \right) - \left( {\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} } \right).$$
(8)

The value of C remains unchanged during orbital motion and is associated with the energy of the system.

When low thrust is included in the CR3BP model, the natural dynamics of the system is perturbed. As shown by Cox and Howell [12], in this case, the equilibrium points move in the (x, y)-plane, depending upon α; in particular, the collinear points near the Moon remain close to the natural libration points. The Zero Velocity Curves and Surfaces (ZVCs and ZVSs) define the regions where the spacecraft motion is allowed. These curves change as α varies, due to low thrust. The gateways at the libration points can open in an order that is different from the ballistic one. For the planar case, a graphical study of the ZVC, based on selecting different values of α, equally spaced by 0.1 degree leads to finding that.

  • the ZVC that includes the libration point L1 is open at L2 if − 69.8° < α < 69.8°, unlike what occurs in the ballistic case. This makes feasible the transfers from the Moon to the outer space (cf. Fig. 3a). Moreover, transfers from the Earth realm to the outer space become feasible if − 180° < α < − 114.9° or 114.9° < α < 180°, as shown in Fig. 3b.

  • the ZVC that includes the libration point L2 is open at both L1 and L3 if − 180° < α < − 103.6° or 103.6° < α < 180°, as shown in Fig. 4a. Earth–Moon transfers remain feasible if − 180° < α < − 69.6° or 69.6° < α < 180.°, as shown in Fig. 4b, although the ZVC are no longer symmetric (except if α =  ± 180° or α = 0°)

Fig. 3
figure 3

ZVC when α = 0° (a) and when α = 180° (b)

Full size image
Fig. 4
figure 4

ZVC when α = 180° (a) and when α = 90° (b)

Full size image

It is worth remarking that symmetry of the ZVCs (with low thrust) with respect to the x-axis preserves only if the thrust direction is aligned with the latter, i.e., if α =  ± 180° or α = 0°. This is apparent by inspecting Figs. 3a, b and 4a. Moreover, the preceding bounds on α depend upon the specific value of the thrust acceleration magnitude.

The zero velocity surfaces can be regarded as the three-dimensional counterparts of the ZVCs. Two examples of ZVS at L1 using low thrust are shown in Figs. 5 and 6. In the first case, the gateway at L2 is open, while the gateway at L1 is closed. Instead, in the second case, the gateway at L3 is open, while both gateways at L1 and L2 are closed. Two examples of ZVS at L2 are shown in Figs. 7 and 8. In the first one, the peculiarity of the surface is that the L3 gateway is wider than that at L1. From inspection of Figs. 7 and 8, it is apparent that the corresponding ZVC is not symmetric with respect to the x-axis, unlike what occurs in the ballistic case. This feature is related to the specific value of α.

Fig. 5
figure 5

L1 ZVS, with α = 0° and β = 30°

Full size image
Fig. 6
figure 6

L1 ZVS, with α = 180° and β = 30°

Full size image
Fig. 7
figure 7

L2 ZVS, with α = 135° and β = 30°

Full size image
Fig. 8
figure 8

L2 ZVS, with α = 270° and β = 30°

Full size image

3 Lunar Capture Dynamics Using Low-Thrust

This section considers a two-dimensional trajectories lying in the plane of the two primaries, and addresses the problem of using low thrust for lunar capture, taking advantage of the geometrical properties of the zero velocity curves, illustrated in the previous section. Moreover, the use of low-thrust propulsion allows shaping the zero velocity curves in a way, such that escape becomes feasible, while return paths toward the Earth do not exist. This scenario cannot occur for ballistic trajectories.

3.1 Capture

At the end of a low-energy ballistic transfer from Earth to Moon, the spacecraft is assumed to reach the first periselenium, at altitude of 2255 km over the lunar surface. In this phase, the Jacobi integral equals 3.184 DU/TU2. The latter value is only slightly less than the limiting value that allows transits from the Earth to the Moon through the region where L1 is located. At the first periselenium, low thrust is ignited, with an angle α = 70°, and the gateways at L1 and L2 close as a result (cf. Fig. 9a). This means that the spacecraft is captured about the Moon, and cannot escape until the low-thrust propulsion remains ignited. In 25.4 days, which is the (planned) duration of the capture phase, the space vehicle travels at a distance of closest approach of 759 km from the lunar surface (cf. Fig. 9b).

Fig. 9
figure 9

Spacecraft trajectory in the capture phase (a), with zoom (b); ZVC is in blue

Full size image

3.2 Permanent Escape from the Earth–Moon System

At the end of the capture phase, a new thrust angle is selected, such that the L2 gateway opens while L1 remains closed. Among all the possible values of α, the one that minimizes the altitude over the Moon (before escape) is chosen. The value at hand is αout = − 21.6°, and the spacecraft remains in the proximity of the Moon for additional 16.5 days, with a distance of closest approach of 843 km over the lunar surface. When the thrust angle is set to αout = − 21.6° (at point (x2, y2)), the Jacobi integral becomes

$$C_{{{\text{ph3}}}} = 2\Omega \left( {x_{2} ,y_{2} } \right) + 2\left( {a_{{lt_{x} }} x_{2} + a_{{lt_{y} }} y_{2} } \right) - \left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right) = {3}.{3}0{\text{62DU}}/{\text{TU}}^{{2}} .$$
(9)

Then, the spacecraft passes through the gateway at L2 (cf. Fig. 10) and escapes the Earth–Moon system. After escaping the Earth–Moon system, permanent escape is pursued, to avoid that the spacecraft enters the system at future times. This is possible only if the zero velocity curve, obtained after switching off the thrust, exhibits no opening at L2. In the absence of thrust, the opening at L2 depends upon the Jacobi integral (evaluated for ballistic trajectories). Hence, the value of C after switching off low-thrust must be greater than the characteristic value of C at the libration point L2, denoted with C2 = 3.1721 DU2/TU2.

Fig. 10
figure 10

Escape phase (a), with zoom (b)

Full size image

Let (x3, y3) denote the point at which the thrust is switched off. As a result, the Jacobi integral changes to

$$C_{{{\text{ph4}}}} = C_{{{\text{ph3}}}} - 2a_{lt} x_{3} \cos \alpha_{{{\text{out}}}} - 2a_{lt} y_{3} \sin\alpha_{{{\text{out}}}} .$$
(10)

To obtain a permanent escape, \(C_{{{\text{ph4}}}} > C_{2}\). The line associated with the equality \(C_{{{\text{ph4}}}} = C_{2}\) is shown in Fig. 11, highlighted in blue, together with the point at which the thrust is switched off. This point corresponds to the intersection of the blue line with the outgoing path. The final mass ratio is obtained using Eq. (2) and equals 0.977.

Fig. 11
figure 11

Permanent escape: in a the low-thrust trajectory is shown in green, the final ballistic trajectory in red, and the line associated with the equality \(C_{{{\text{ph4}}}} = C_{2}\) in blue, with the corresponding ZVC (b)

Full size image

4 Low-Thrust Periodic Orbits

A wide variety of periodic orbits were proven to exist in the CR3BP, starting from the nineteenth century [23]. Different analytical and numerical approaches were adopted for detecting ballistic periodic orbits, for decades. Because the theorem of mirror trajectories holds also with low thrust, this section focuses on the detection of low-thrust periodic orbits in the Earth–Moon system. In this study, the problem is addressed by means of modified Poincaré maps [20], selecting values of α spaced by 15° and a maximum number of crossings of the x-axis equal to 6. Moreover, for all the orbits presented in this section, a mission duration of 5 years is considered, corresponding to a final mass ratio equal to 0.357 (using Eq. (2)).

4.1 Low-Thrust Mirror Trajectories

The theorem of mirror trajectories was proven in 1960 by Miele [21], and establishes the symmetry properties of ballistic trajectories in CR3BP. The theorem can be extended to low-thrust trajectories.

Proposition 1.

The initial conditions for the spacecraft position and velocity are specified, and the following equation describes a feasible path (with \(\xi , \, \eta {, }\zeta , \, \delta {\text{, and }}\chi\) denoting generic functions of time):

$${\text{T}}1{ }\left\{ {\begin{array}{*{20}c} {x = \xi \left( t \right)} \\ {y = \eta \left( t \right)} \\ {z = \zeta \left( t \right)} \\ \end{array} } \right.\quad \begin{array}{*{20}c} {\dot{x} = \dot{\xi }\left( t \right)} \\ {\dot{y} = \dot{\eta }\left( t \right)} \\ {\dot{z} = \dot{\zeta }\left( t \right)} \\ \end{array} \quad \begin{array}{*{20}c} {\alpha = \delta \left( t \right)} \\ {\beta = \chi \left( t \right)} \\ \end{array} \quad \begin{array}{*{20}c} {a_{{lt_{x} }} = a_{lt} c_{\alpha } c_{\beta } } \\ {a_{{lt_{y} }} = a_{lt} s_{\alpha } c_{\beta } } \\ {a_{{lt_{z} }} = a_{lt} s_{\beta } .} \\ \end{array}$$
(11)

The returning trajectory described by the following equation, is feasible, as well (τ is an arbitrary time constant):

$${\text{T}}2 \left\{ {\begin{array}{*{20}c} {x = \xi \left( {\tau - t} \right)} \\ {y = - \eta \left( {\tau - t} \right)} \\ {z = \zeta \left( {\tau - t} \right)} \\ \end{array} } \right.{ } \begin{array}{*{20}c} {\dot{x} = - \dot{\xi }\left( {\tau - t} \right)} \\ {\dot{y} = \dot{\eta }\left( {\tau - t} \right)} \\ {\dot{z} = - \dot{\zeta }\left( {\tau - t} \right)} \\ \end{array} \begin{array}{*{20}c} {\alpha = - \delta \left( {t - \tau } \right)} \\ {\beta = \chi \left( {t - \tau } \right)} \\ \end{array} \begin{array}{*{20}c} {a_{{lt_{x} }} = a_{lt} c_{\alpha } c_{\beta } } \\ {a_{{lt_{y} }} = - a_{lt} s_{\alpha } c_{\beta } } \\ {a_{{lt_{z} }} = a_{lt} s_{\beta .} } \\ \end{array}$$
(12)

Proof

The preceding statement can be demonstrated in a way similar to the proof of the theorem of mirror trajectories [21, 22] by substituting Eq. (11) in Eq. (3). This leads to

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {\ddot{\xi } - 2\omega \dot{\eta } - \omega^{2} \xi = - \frac{{\left( {1 - \mu } \right)\left( {\xi + \mu } \right)}}{{r_{1}^{3} }} - \frac{{\mu \left( {\xi + \mu - 1} \right)}}{{r_{2}^{3} }} + a_{lt} c_{\alpha } c_{\beta } } \\ { - \ddot{\eta } - 2\omega \dot{\xi } + \omega^{2} \eta = + \frac{{\left( {1 - \mu } \right)\eta }}{{r_{1}^{3} }} + \frac{\mu \eta }{{r_{2}^{3} }} - a_{lt} s_{\alpha } c_{\beta } } \\ \end{array} } \\ {\ddot{\zeta } = - \frac{{\left( {1 - \mu } \right)\zeta }}{{r_{1}^{3} }} - \frac{\mu \zeta }{{r_{2}^{3} }} + a_{lt} s_{\beta } .} \\ \end{array}$$
(13)

It is straightforward to recognize that the equation system of Eq. (13) is identical to the one that holds for T1, which is obtained by inserting Eq. (11) into Eq. (3). This proves that T2 is feasible, as well as T1. □

4.2 Modified Poincaré maps

As a preliminary step, the variable C0 is introduced as the value of the Jacobi integral in the absence of low-thrust propulsion. Modified Poincaré maps are obtained by considering α, C0, the interval along the x-axis, and the maximum number of crossings of the x-axis as the input parameters. For each point in the interval, the starting conditions correspond to an initial velocity, denoted with \(\dot{y}_{0} ,\) orthogonal to the x-axis and an initial position along the x-axis, denoted with x0. Starting from these conditions, Eq. (3) is integrated numerically. After processing all the initial values in the x-intervals [− 0.1,0.1] DU and [0.7,1.2] DU, the Poincaré map is built by representing the velocity vx = \(\dot{x},\) as a function of x, at each crossing point. If there exists a point at which \(\dot{x}\) is zero, then it corresponds to a vertical crossing, which is associated with a periodic trajectory. Visual inspection of the Poincaré maps leads to detecting a variety of periodic orbits. Figure 12 illustrates an example of Poincaré map. The arrow corresponds to an interesting periodic orbit, i.e., the orbit illustrated in Fig. 13c.

Fig. 12
figure 12

Poincarè map obtained with C = 3.00, n = 4 (4th crossing of the x-axis). The arrow points the crossing on the y-axis that corresponds to a periodic orbit

Full size image
Fig. 13
figure 13

Earth–Moon cycling orbits; primaries are denoted with a pink dot, while the collinear libration points are marked with an asterisk

Full size image

This study is specifically focused on the identification of periodic orbits that do not exist in the ballistic CR3BP, divided into two categories: (1) Earth–Moon cycling orbits and (2) lunar periodic orbits.

4.3 Earth–Moon Cycling Orbits

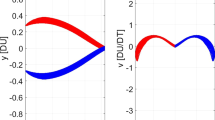
The study of periodic orbits that encircle both the Earth and the Moon leads to the identification of orbits that have long periods and show close approaches to the two primaries. These orbits could be particularly useful as transfer paths between the two bodies. Some examples of these orbits are shown in Fig. 13 and their features are reported in Table 1; the value of α refers to the trajectory arc before the (midway) orthogonal crossing, and the initial velocity has positive component along y, in all cases. The first orbit exhibits very close approaches to both primaries, while the second one includes many flybys, especially near the Earth.

Table 1 Parameters of orbits (a–f) of Fig. 13 in terms of C0, thrust angle α, initial point on the x-axis x0, minimum distance D☾ from the lunar surface, minimum distance D⊕ from the Earth surface, and repetition period T
Full size table

4.4 Lunar Periodic Orbits for Satellite Constellations

The study of low-thrust periodic orbits around the Moon leads to the identification of non-Keplerian orbits, with a short orbital period and with many passes near the Moon and the Lagrange points. It is worth remarking that these paths are infeasible in the absence of low-thrust propulsion. In mission scenarios of practical interest, these orbits could be traveled with modest propellant amounts. Some examples are shown in Fig. 14, while Table 2 reports some characteristic parameters of these trajectories.

Fig. 14
figure 14

Low-thrust lunar periodic orbits

Full size image
Table 2 Parameters of orbits (a), (b), (c), and (d) of Fig. 14 in terms of C0, thrust angle α, initial point on the x-axis x0, initial velocity component \(\dot{y}_{0}\), minimum distance D☾ from the Moon surface, and repetition period T
Full size table

To study the ground track of these orbits and the visibility properties, three reference frames are introduced:

  • the Earth Centered Inertial Frame (ECI) \(\left( {\hat{c}_{1} ,\hat{c}_{2} ,\hat{c}_{3} } \right)\) is a Cartesian inertial reference frame defined as follows. Its origin O is the center of the Earth. The unit vector \(\hat{c}_{3}\) is aligned with the Earth axis of rotation and is positive northward, whereas \(\hat{c}_{1}\) is aligned with the vernal axis, which corresponds to the intersection of the Earth equatorial plane and the ecliptic plane.

  • the Heliocentric Frame \(\left( {\hat{c}_{1}^{(S)} ,\hat{c}_{2}^{(S)} .\hat{c}_{3}^{(S)} } \right)\) is obtained from ECI by means of a rotation of ε = 23.4° (ecliptic obliquity) about axis \(\hat{c}_{1}\) [24]. In particular, the third axis is defined as \(\hat{c}_{3}^{(S)} = - \sin \varepsilon \hat{c}_{2} + \cos \varepsilon \hat{c}_{3}\). Under the approximating assumption that the lunar equatorial plane coincides with the ecliptic plane, then \(\hat{c}_{3}^{s}\) identifies both the ecliptic pole and the rotation axis of the Moon.

  • the Moon Frame \(\left( {\hat{i}_{1}^{(M)} ,\hat{i}_{2}^{(M)} ,\hat{i}_{3}^{(M)} } \right)\) is centered at the Moon center with axes defined in the following way: \(\hat{i}_{3}^{(M)}\) coincides with \(\hat{c}_{3}^{(S)} ; \hat{i}_{1}^{(M)}\) identifies the lunar prime meridian, and is aligned with the line that connects the center of the Earth to the center of the Moon; finally, \(\hat{i}_{2}^{(M)}\) completes the right-hand sequence.

From Table 2, it is evident that orbit (a) has an orbital period very close to the rotation period of the Moon, which approximately coincides with the orbital rate of the Moon about the Earth. For this reason, the related ground track is repeating. It is possible to study the visibility properties of this orbit, by considering that the inclination of the orbit of the Moon varies between 28.74° and 18.16°. Assuming that the inclination of the orbit of the Moon is 28.74°, the maximum visibility time of different locations over the lunar surface is shown in Fig. 15, from which the minimum number of satellites needed to guarantee continuous coverage over a certain site can be identified. In Fig. 16 the elevation of a constellation of three satellites is shown, over a single orbital period, with respect to a station located at -30° of longitude and 70° of latitude. This site corresponds to the maximum continuous visibility, equal to 9.149 days (single satellite). If the inclination of the Moon orbit equals 18.16°, a similar (mirrored) graph is obtained, with respect to a station located at 30° of longitude and 70° of latitude (cf. Fig. 17). If the inclination of the Moon orbit equals the intermediate value 23.4°, then the constellation performance slightly worsens. In this case, the most advantageous point has longitude equal to 0. From this discussion, it is apparent that the constellation at hand, composed of 3 satellites, is particularly effective to provide continuous coverage over a relatively large latitudinal region located in the dark side of the Moon.

Fig. 15
figure 15

Maximum visibility time from the lunar surface for a satellite deployed in orbit (a)

Full size image
Fig. 16
figure 16

Elevation graph of a 3-satellite constellation deployed in orbit (a) referred to a station located at − 30° of longitude and 70° of latitude (inclination of the lunar orbit equal to 28.74°)

Full size image
Fig. 17
figure 17

Elevation graph of a 3-satellite constellation deployed in orbit (a) referred to a station located at + 30° of longitude and 70° of latitude (inclination of the lunar orbit equal to 18.16°)

Full size image

4.5 Other Special Orbits

The study of low-thrust periodic orbits around the Moon leads to the identification of another particular orbit shown in Fig. 18, which has the remarkable property of traveling near three libration points: L2, L4, and L5. This orbit can be useful for missions directed toward the triangular libration points and its parameters are reported in Table 3.

Fig. 18
figure 18

Low-thrust special orbit in blue, Lagrangian points marked with an asterisk

Full size image
Table 3 Parameters of orbit in Fig. 16 in terms of C0, thrust angle α, initial point on the x-axis x0, sign of the initial velocity component \(\dot{y}_{0}\), minimum distance D☾ from the Moon surface, and repetition period T
Full size table

5 Concluding Remarks

This research investigates low-thrust orbit dynamics in the Earth–Moon system. Some dynamical structures that exist in the natural CR3BP are proven to persist, but with different—and rather interesting—topological properties. In fact, low-thrust zero velocity curves and surfaces exhibit a variety of configurations that are otherwise infeasible in the absence of low-thrust propulsion. As a first contribution of this research, these remarkable topological properties can be profitably leveraged in preliminary mission analysis. With this regard, this work investigates low-thrust lunar capture dynamics, and identifies a strategy that allows the temporary capture and the subsequent permanent escape of the spacecraft from the Earth–Moon system. A simple relation leads to identifying the region where low thrust must remain ignited to obtain subsequent permanent (ballistic) escape. Moreover, as further contributions, this study proves the existence of a variety of low-thrust periodic orbits, encircling either the two primaries or the Moon. Modified Poincaré maps are used to do this. Similar orbits may be useful for either (a) establishing a continuous Earth–Moon connection using spacecraft equipped with low-thrust propulsion and traveling cycling paths or (b) designing satellite constellations about the Moon with interesting coverage properties.