1 Introduction

Rolling bearings are very important components in rotating machinery. When the bearing system is running, the rolling balls exert the periodic contact force on the inner ring which is fixed to the rotor, and the time-varying force will excite different compliance vibrations, that is the varying compliance (VC) vibration. The source of this vibration is the periodic elastic force induced by the rolling balls. Vibration problems caused by geometric factors and kinematic factors in rolling bearing-rotor systems are widespread in engineering.

In recent decades, scholars have done a lot of research on the dynamics of rolling bearings and have achieved much progress. Sheng et al. [1] proposed a method to solve multiple degree of freedom stiffness matrix of the ball bearings under the variable speed conditions by solving the partial differential equations between the bearing load and the displacement. The method is used to study the influence of bearing variable speed stiffness on the dynamic characteristics of the rolling bearings [1]; Arslan and Akturk [2] developed a concentrated mass model to study the influence of the local defects on the vibration of the ball bearings. Compared with the quasi-static model of the bearing, the quasi-dynamic model has the ability to deal with the time-varying rotation of each component of the bearing [2]; Yang et al. [3] proposed a five DOF quasi dynamic model, using the quasi static model to get the initial value of the quasi-dynamic model.

With the development of modern industry, the working speed of the rolling bearings has gradually increased, and working conditions have become more and more severe. Rolling bearings based on the statics assumptions can no longer correctly predict the dynamic behavior of bearings, so the rolling bearing dynamic models that abandon all static constraints came into being. Gupta et al. [4] established a dynamic model of an imbalanced elastic rotor system supported by a ball bearing, and used FEM to study the influence of three parameters of the rotational unbalance, the bearing gap and the rotor flexibility on the instability and the chaotic behavior of the system. For simulating the vibration of the rotor system more accurately, Li et al. [5] improved Gupta's dynamic model of the rolling bearing and coupled it with the equivalent rotor model of the Timoshenko beam to establish a joint simulation dynamics of the rolling bearing-rotor system, the established dynamic model gathers the advantages of FE model and Gupta model. Based on this new model, the vibrational response of the rotor-bearing system under the different bearing gaps was simulated, and the experimental results were compared to the simulation results of the rolling bearing-rigid rotor dynamic model that does not consider the rotor elasticity. The results prove that the model is more accurate [5]; Niu et al. [6] considered the gyro torque, the centrifugal pull and the lubrication effect between the bearing components on the basis of the Gupta model, and developed a dynamic model to research the impact of ball bearing raceway defects on bearing vibration [6]; Patel et al. [7] proposed a new dynamic model for studying the vibration responses of the deep groove ball bearing with single and multiple faults on the inner and outer ring surfaces, and used the Runge–Kutta method to get the coupled solution of the motion control equation. The research found that compared with the vibration spectrum in the case of single defect, the velocity amplitude in the case of double defects is relatively higher [7]; Alireza et al. [8] proposed the improved nonlinear model under consideration of the limited size of the rolling ball. This improvement overcomes the rolling ball as a point caused by the modeling of the previous model; Wang and Zhu [9] proposed an advanced and effective dynamic model of a strongly nonlinear rotor-bearing system using the improved Runge–Kutta method.

Most of the research work mainly studies the nonlinear dynamic behavior caused by the fault and the imbalance of the rolling ball, the gap between the rolling ball and the seat ring, the Hertz contact nonlinearity, and the compliance or combination of some bearings [10,11,12]; Tiwari et al. [13, 14] studied the nonlinear dynamics of the balanced horizontal rigid rotor-bearing system and the unbalanced horizontal rigid rotor-bearing system, and observed that the instability of the large-gap high-speed bearing and the radial internal gap of the bearing will change the compliance of the system; Harsha proposed a variety of rotor bearing dynamic models to study the influence of the bearing gap, the Hertzian contact and the waviness on the dynamic characteristics of the rotor system [15,16,17]; Sopanen et al. [18] used the multiple body system software (MSC) to study the influence of bearing radial gap on the natural frequency and the vibrational response of the bearing-rotor system; Bai et al. [19] used Floquet theory to study the dynamic characteristics and the stability of the ball bearing-rotor system considering the different ball bearing gaps. The study found that the larger the ball bearing gap, the greater the instability range of VC-based vibration [19]; Gao et al. [20] proposed a six DOF model for studying the bearing system of a machine tool spindle supported by ball bearings, using numerical simulation to analyze the influence of bearing gap on the bifurcation and chaotic behaviors of the bearing system; Saeidy and Sticher [21] proposed a dynamic analysis formula of the rigid rotor under the foundation excitation and the mass imbalance, which is adopted for the nonlinear dynamic analysis of the rigid rotor bearing under the unbalance and the foundation excitation; Zhang et al. [22] studied the bifurcation and the resonance behavior of the variable compliance vibration of the rigid ball bearing-rotor system with the Hertz contact and the radial internal gap by using the arc extension algorithm, the harmonic balance method and the alternating frequency time algorithm(HB-AFT), it is found that the resonance of the system is essentially the Hertzian contact resonance, and the soft resonance hysteresis caused by the Hertzian contact is the main characteristic of the main resonance peak [22]; Jin Yulin et al. [23] considered the Hertzian contact deformation and the internal gap to study the nonlinear dynamics of the different compliance responses in a rotor-bearing system.

Some researchers have conducted much study on TRB and the ball bearing dynamics. Tong and Hong [24] proposed the running torque equations of the tapered rolling bearings with the angular misalignment (TRB), and studied the influence of the angular misalignment on the torque of TRB; Liu et al. [25] considered the influence of the continuous changes in the circumferential position of the rollers on the stiffness of the bearing, established the dynamical gear bearing model with the constant and the time-variant bearing rigidity through the analytical and the FE methods, and they used perturbation analysis and finite element contact mechanics to investigate the effect of the time-varying roller bearing stiffness on the vibration response of the bearing system [25]; Zhang et al. [26] considered the effect of the unbalanced force and the bearing load on the instability zone of the rotor-bearing system and proposed an improved Jones-Harris rigidity model, revealing the influence of the eccentric force on the stiffness of rolling ball bearings; Based on the Hertz theory, Gunduz and Singh [27] proposed a new formula for the rigidity matrix of double-column angular contact ball bearings, which provides help for the static and dynamic analysis of the double-column angular contact ball bearings; Zhao et al. [28] analyzed the high-speed load characteristics and the friction coefficient of the angular contact ball bearings. They studied the gyro torque of the rolling balls, and the results showed that the design of the axial force should focus on the combined influence of the gyro torque and the friction coefficient [28]; Kurvinen et al. [29] considered the effect of the centrifugal force and the gyro torque on the computational complexity of the ball bearing model, and established two types of the ball bearing models, one considering the high speed force and the other ignoring it. They simulated and compared the two models, studied the behavior of the bearing at different shaft speeds, and determined when to use a model with the gyroscopic force and the centrifugal force. Liu et al. [30] developed a comprehensive numerical dynamic model of a flexible-rotor bearing system based on the Hertzian and cubic polynomial nonlinear contact force methods, and discussed the displacements and spectrum of the flexible-rotor bearing system [30]. Kurvinen et al. [31] investigated carefully the effect of varying roundness profile and clearance on the sub-critical vibration excitation. Liu et al. [30] proposed an improved dynamic model of ACBB to consider the influences of elastic hysteresis, the differential sliding friction torques, and specially investigated effects of speed, load, and defect sizes on the acoustic characteristics for ACBB [32].

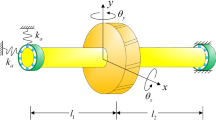
In this paper, an new improved model under the overall consideration of the unbalanced excitation, the asymmetric gap, the varying compliance vibration and the nonlinear Hertzian contact force will be developed and the improved model abandons the assumption of the traditional model, seen in Fig. 1. The model is more accurate and more general than the traditional model based on the hypothesis. The varying compliance vibration responses of the system are calculated and the influences of the gap, the mass eccentricity and the mass for the rotor on the nonlinear vibration are studied accurately in order to explore the internal physical mechanism. The authors investigated the nonlinear dynamics in the last paper about the rolling ball bearing based on the traditional model [33], and will carry out a in-depth study based on the new improved model in this article.

Fig. 1
figure 1

Comparison of traditional analytical model with improved model; a the traditional model based on hypothesis that the center of the outer ring O, the center of the inner ring I and the contact point between the inner ring and the rolling ball \({\text{R}}_{\text{t}}\) are collinear; b the improved analytical model which is not based on the hypothesis and is more general and accurate than (a); there is main difference: \({{\tilde{\theta}}}_{\text{i}}\) and \({\theta}_{i}\) between the improved model and the troditional model

Full size image

2 Modeling

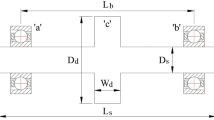
The rolling ball bearing is usually composed of the outer ring, the inner ring, the rolling balls, the retainer. The outer ring studied in this paper is fixed on a rigid support; and the inner ring is fixed on a rotational principle axis(rotor), as seen in Fig. 2. The lubrication conditions and materials are of great research significance and are very complicated, the nonlinear dynamic characteristic of the bearings based on the new model is focused on in this paper, therefore to simplify the study, the lubrication conditions is ignored. When the bearing system is operating, the rolling balls exert the elastic forces on the inner ring which will vibrate because of the time-variant contact force. The vibration is passed on the whole bearing system.This vibration originates from the periodic elastic restoring forces exerted by the rolling balls. Accordingly, the vibration is so called VC (varying compliance) vibration. The accurate model should be established firstly to study the dynamics of the system.

Fig. 2
figure 2

The more general analytical diagram for the rolling ball bearing without the hypothesis that the three center points of the inner ring, the outer ring and the rolling ball are collinear, i.e. the points O, I, \({\text{R}}_{\text{c}}\) are not collinear

Full size image

The two DOF of the inner ring center are \({\text{q}} = \left[ {u \, v} \right]^{T}\), where u and v are respectively the deflection of the rotor in x and y components (Plane XOY is the bearing plane).

Applying Lagrangian equation, the equations of motion for the bearing system are written as

$$\begin{gathered} m\ddot{u} + c_{x} \dot{u} + k_{x} u = F_{bix} \hfill \\ m\ddot{v} + c_{x} \dot{v} + k_{x} v = F_{biy} \hfill \\ \end{gathered}$$
(1)

They are denoted as follows in the matrix form

$$M\ddot{q} + C\dot{q} + Kq = F_{b} + F_{u}$$
(2)

\(M\), \(C\) and \(K\) are respectively the mass matrix, the damping matrix and the stiffness matrix, they are given by Eqs. (3)–(5)

$$M = \left[ \begin{gathered} m\quad \, \; \, 0 \hfill \\ 0\quad \, m \hfill \\ \end{gathered} \right]$$
(3)
$$C = \left[ \begin{gathered} c_{x}\quad \, 0 \hfill \\ 0\quad \, c_{y} \hfill \\ \end{gathered} \right]$$
(4)
$$K = \left[ \begin{gathered} k_{x}\quad \, 0 \hfill \\ 0\quad \, k_{y} \hfill \\ \end{gathered} \right]$$
(5)

\({\text{m}}\) is the mass of the the rotor at the bearing end; \({\text{c}}_{\text{x}}\) is the damping in x direction; \({\text{c}}_{\text{y}}\) is the damping in y direction; \({\text{k}}_{\text{x}}\) is the stiffness in x direction; \({\text{k}}_{\text{y}}\) is the stiffness in y direction.

The unbalanced force is dependent on the rotor eccentricity mass, the eccentricity radius and the rotational speed, the unbalance force is a vector including three elements, the size, the direction and the action point; the coordinate system can affect the direction and the coordinate value of the action point, and has no effect on the absolute value of the force size. Absolute value of the unbalance force is given by

$$F_{u} = me\omega^{2}$$
(6)

\({\text{e}}\) is the eccentric distance of the rotor. The force acting on the inner ring is given by

$$F_{b} = \sum\limits_{i = 1}^{N} {F_{bi} }$$
(7)

\({\text{F}}_{\text{b}}\) is the resultant force of the bearing induced by every rolling balls exerting on the rotor, which is the vector sum of the elastic restoring forces \({\text{F}}_{\text{bx}}\) and \({\text{F}}_{\text{by}}\), it is expressed as

$$F_{bi} = \left[ {F_{bix} \;\;F_{biy} } \right]^{T}$$
(8)

\({\text{F}}_{\text{bix}}\) and \({\text{F}}_{\text{biy}}\) are respectively the bearing forces for the ith rolling ball in the x and y directions. Adopting the Nonlinear Hertzian Contact Theory, the relational expression between the force and the deformation of the contact point is

$$F_{bi} = C_{b} H\left( {\delta_{I} } \right)\delta_{i}^{3/2}$$
(9)

\({\text{C}}_{\text{b}}\) is the Hertzian Contact Stiffness, which is associated with the property and the shape for the contact materials.

$$C_{b} = \left[ {\left( {\frac{1}{{K_{{{\text{inner}}}} }}} \right)^{2/3} + \left( {\frac{1}{{K_{{{\text{outer}}}} }}} \right)^{2/3} } \right]^{ - 1.5}$$
(10)
$$K_{{{\text{inner}}}} = \frac{2\sqrt 2 }{3}\left( {\frac{E}{{1 - \nu^{2} }}} \right)\left( {\sum {\rho_{i} } } \right)^{ - 0.5} \left( {\mu_{i}^{ * } } \right)^{ - 1.5}$$
(11)
$$K_{{{\text{outer}}}} = \frac{2\sqrt 2 }{3}\left( {\frac{E}{{1 - \nu^{2} }}} \right)\left( {\sum {\rho_{o} } } \right)^{ - 0.5} \left( {\mu_{o}^{ * } } \right)^{ - 1.5}$$
(12)

\({\text{E}}\) means the Elastic Modulus, v refers to the Poisson Ratio, \({\mu}_{\text{i}}^{*}\) means the Deformation Coefficient. It is easy to calculate the value of \({\text{K}}_{\text{inner}}\) and \({\text{K}}_{\text{outer}}\), if the dimension of the rolling ball bearing is known. \(\text{H}({\delta}_{\text{i}}{)}\) is the Heaviside function, it is equal to 1 when the function argument \({ \delta }_{\text{i}}\) is greater than 0; it is equal to 0 when the function argument \({ \delta }_{\text{i}}\) is less than 0. It is given by Eq. (13)

$$H\left( {\delta_{i} } \right) = \left\{ \begin{gathered} 1\;\;\;\;\;\;\;\;\;{\text{if}}\;\delta_{i} > 0\; \hfill \\ 0\;\;\;\;\;\;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.$$
(13)

As seen in Fig. 2, the angular displacement of the ith rolling ball is \({\theta}_{\text{i}}\)

$$\theta_{i} = \frac{2\pi }{N}i + \omega_{c} t$$
(14)

N is the number of the rolling balls and \({\omega}_{\text{c}}\) is the whirling speed of the inner ring.

$$\omega_{c} = \frac{1}{2}\omega \left( {1 - \frac{{D_{b} }}{{D_{p} }}} \right)$$
(15)

\({\text{D}}_{\text{b}}\) is the diameter of the rolling ball, \({\text{D}}_{\text{p}}\) is the pitch diameter of the rolling ball bearing and \({\omega}\) is the rotational speed of the rotor.

The deformation for the ith rolling ball \({\delta}_{\text{i}}\) is the function of the inner ring deflection relative to the outer ring displacement in the x and y components, the ball position and the gap (Kappaganthu and Nataraj [34]). The deformation of the rolling ball is strongly dependent on the gap and the displacement of the inner ring. Most researchers treated the gap as a dead band instead of the accurate real condition. In the traditional study of the rolling ball bearing, the potential hypothesis is that the three center points of the inner ring, the outer ring and the rolling ball are collinear, and the truth is the three points are not always on the same line because of the asymmetric gap or the defect of the rolling ball. An improved model in this paper abandons the hypothesis and a more accurate and more general model is developed. Hence, the angular displacement of the ith rolling ball has two values with respect to the centers of the outer ring and the inner ring, \({{ \tilde{\theta}}_{i}}\), \({\theta}_{i}\), as seen in Fig. 2. In the whole operation, the outer and inner rings are elastic. From the bearing geometry, the varying radius of the inner ring \({\text{r}}_{\text{inner}}\) is expressed as

$$r_{{{\text{inner}}}} = r_{{{\text{mean}}}} { - }r_{{{\text{bearing}}}}$$
(16)

\({\text{r}}_{\text{mean}}\) is the mean radius of the bearing; and \({\text{r}}_{\text{bearing}}\) is the radius of the rolling ball. The various radius of the outer ring is denoted as

$$r_{outer} \left( c \right) = r_{mean} + r_{bearing} + \frac{c}{2}$$
(17)

c is the gap; the outer ring center is fixed at origin O, and the inner ring center is at point \(\text{I(u, v)}\). The center of the ith rolling ball is at \({\text{R}}_{\text{c}}={(}{\text{R}}_{\text{cx}}, \, {\text{R}}_{\text{cy}}{)}\), it can be given by Eqs. (18), (19)

$$R_{cx} = u + \left( {r_{{{\text{inner}}}} + r_{{{\text{bearing}}}} } \right)\cos \theta_{i}$$
(18)
$$R_{cy} = v + \left( {r_{{{\text{inner}}}} + r_{{{\text{bearing}}}} } \right)\sin \theta_{i}$$
(19)

The angular displacement of the center with respect to the outer ring center \({{\tilde{\theta }}_{\text{i}}}\) is expressed by Eq. (20)

$$\tilde{\theta }_{i} = \tan^{- 1} \left( {\frac{{R_{y} }}{{R_{x} }}} \right)$$
(20)

Let \({\text{R}}_{\text{t}}\) be the circumferential point of the rolling ball on the line joining the outer ring center and the rolling ball center. The coordinate \({\text{R}}_{\text{t}}{(}{\text{R}}_{\text{ty}},{\text{R}}_{\text{tx}}{)}\) can be expressed as

$$R_{tx} = R_{cx} + r_{bearing} \cos \tilde{\theta }_{i}$$
(21)
$$R_{{t{\text{y}}}} = R_{cy} + r_{bearing} \sin \tilde{\theta }_{i}$$
(22)

Then, the deflection in the rolling ball is got

$${\updelta }_{{\text{i}}} = \sqrt {R_{tx}^{2} + R_{ty}^{2} } { - }r_{o}$$
(23)

\({\mathrm{r}}_{0}=({\mathrm{R}}_{\mathrm{c}}+{\mathrm{R}}_{\mathrm{t}})/2\) which is the average of the Rc and Rt. The dynamic analysis is investigated based on the new improved model.

3 Results and discussion based on new improved model

The dynamics of the varying compliance bearing system based on the improved model is digitally simulated in Matlab. The forth order Runge–Kutta method with adaptive step size is applied to solve the steady-state response of the governing equations.

In the improved model, more general motion characteristics are considered, i.e. the three center points(O, I, \({\text{R}}_{\text{c}}\)) are not always collinear. Dynamic responses between the improved model and traditional model are compared in Fig. 3, including (a) the time history and (b) the spectrum diagram. In Fig. 3a, the blue solid line is the response of the traditional model and the red dotted line is the response of the improved model. It can be shown from Fig. 3a that the new model is different from the traditional model in the phase position and amplitude; And the phase difference is more obvious. The fundamental reason for the phase difference in Fig. 3a is that the new model has different displacement angles compared with the traditional model. As shown in Fig. 2, the Angle of the new model (\({{\tilde{\theta }}_{\text{i}}}\)) is less than the displacement angle of the traditional model (\({\theta}_{i}\)), and this difference can cause changes in the vibration phase difference which can be quantitatively reflected in Fig. 3a. In Fig. 3b, It can be seen that the dominant frequency (49 Hz) is little difference from each other (improved and traditional model); and the amplitudes have somewhat difference, it is originated from the different phase angle which changes the phase state but does not change frequency. Based on the new modeling method, the dynamic characteristics are studied in the following sections.

Fig. 3
figure 3

Comparison of the new model with the traditional model a time history: the blue solid line is the response of the traditional model and the red dotted line is the response of the improved model; b spectrum diagram: the black figure is the improved model(new model) and the red figure is the traditional model (old model)

Full size image

3.1 Rotational speed

Rotational speed is a significant parameter for rotary machines. With the rotating speed increasing, the dynamic characteristics of the system is gradually changing, including the amplitude, the frequency, the steady state, the transient state, even much disorganized chaos. The research work only analyzes the relatively stable stages of the vibration time domain map which can obtain the conclusion of regularity. The authors pay more attention to the characteristics of stable time periods. Therefore, in the research work, only the signal of the stable time periods is extracted from the full time period signal, as seen in Fig. 5 where Fig. 5d–f are the steady state from the full time period Fig. 5a–c. Figure 4 is the bifurcation diagram of the vibrational response (the displacement Y in y component) versus the varying rotational speed n, where the rotational speed n is increasing in the range of 0 rpm to 6000 rpm, the step length is 50 rpm, and the gap is 10 \(\mu\text{m}\). It is seen only from Fig. 4 that when the rotational speed n is in the range of 0 rpm to 1368 rpm, the system shows the periodic motion (including a narrow amplitude fluctuation near 758 rpm), the typical time history, the spectrum, Poincare diagram for rotating speed n = 900 rpm confirm this point, as seen in Fig. 5d, g, j; from 1368 rpm to nearly 2972 rpm, the system shows a quasi-periodic vibration which is just like the transition condition from the periodical motion to chaotic motion, the corresponding time history, the spectrum, the Poincare diagrams for the rotating speed n = 1980 rpm verify this type of quasi-periodic, as seen in Fig. 5e, h, k; And the system shows a chaos state when the rotational speed is greater than 2972 rpm, the related time history, the spectrum, the Poincare diagrams for the rotating speed n = 4980 rpm confirm the chaos, as shown in Fig. 5f, i, l. How are these changes caused is associated with the changing excitation. The analysis will be given in the following sections.

Fig. 4
figure 4

Bifurcation diagram of the dynamic response: the displacement in y direction Y vs. rotational speed n

Full size image
Fig. 5
figure 5

a–f Time history; g–i Spectrum; j–l Poincare diagram

Full size image

The compound excitation forces of the rolling ball bearings mainly originate from the unbalanced rotating frequency and the internal parametric excitation which is related with the periodic varying compliance vibration. In order to analyze the different influence of the two excitation forces, the spectra of the different rotational speed are drawn. Figure 6a, b are respectively the history figure and the corresponding spectrum diagram under the rotating speed of 280 rpm. It is shown from Fig. 6b that the varying compliance vibration frequency and frequency multiplication of VC vibration can only be observed because the unbalance excitation is weak when the rotating speed is low (280 rpm). The VC vibration is 16.3 Hz (\({\text{f}}_{\text{vc}}\)) which is the Bn times(\(\text{Bn} = \frac{\text{r}}{\text{R+r }}{\text{N}}_{\text{b}}\)) of the rotating frequency; And the frequency multiplication of VC vibration includes 32.6 Hz (\({2}{\text{f}}_{\text{vc}}\)), 48.8 Hz (\({3}{\text{f}}_{\text{vc}}\)) and 65.2 Hz (\({\text{4f}}_{\text{vc}}\)). No rotating frequency arises. What phenomenon appears when the rotational speed increases? With the increase of the rotating speed, the unbalance force enhances. When the rotating speed increases up to 1200 rpm, the frequency of rotational speed appears (\({\text{f}}_{\text{r}}\text{=}\) 19.8 Hz), seen in Fig. 7. Meanwhile there exist the VC vibration and its multiplication frequencies, such as 70.1 Hz (\({\text{f}}_{\text{vc}}\)), 139.6 Hz (\({2}{\text{f}}_{\text{vc}}\)), 209.3 Hz (\({3}{\text{f}}_{\text{vc}}\)) and 279.2 Hz (\(4{\text{f}}_{\text{vc}}\)). However, the most intense vibration component is the VC vibration (\({\text{f}}_{\text{vc}}\text{=}\) 70.1 Hz), as seen in Fig. 7. With the increasing of the rotating speed up to 1600 and then to 1800 rpm, the rotating frequency and the combination frequency (\({\text{f}}_{\text{vc}}\) and \({\text{f}}_{\text{r}}\)) gradually strengthen; And the combination frequency (\({\text{f}}_{\text{vc}}{-3}{\text{f}}_{\text{r}}\)) becomes the maximum peak value, seen in Figs. 8 and 9. When the rotational speed increases up to 2000, the frequency peak value changes to the complicated combination frequency and the frequency division, seen in Fig. 10, where the VC frequency does not dominate the vibrations of the spectrum diagrams.

Fig. 6
figure 6

a Time history; b Spectrum diagram (n = 280 rpm)

Full size image
Fig. 7
figure 7

Spectrum diagram (n = 1200 rpm)

Full size image
Fig. 8
figure 8

Spectrum diagram (n = 1600 rpm)

Full size image
Fig. 9
figure 9

Spectrum diagram (n = 1800 rpm)

Full size image
Fig. 10
figure 10

Spectrum diagram (n = 2000 rpm)

Full size image

It can be inferred that with the increasing of the rotational speed, the VC frequency gradually loses the domination for the vibration. The rotational speed frequency (essential it is the unbalanced frequency, it is only one time of the frequency for the rotational speed) and its combination frequency with the VC frequency dominate the vibration. The peak exists in the lower frequency range. In order to design the parameter of the bearing system, the specific work rotational speed should be considered to analyze which factors is the domination of the vibrations, the VC vibration or the unbalanced vibration; and then quantitative calculation and optimization can be conducted for the perspective of the dynamic characteristics.

3.2 Gap, eccentricity and mass of the rotor

The bearing gap has vital impact on the fatigue life, the temperature rise, the noise and the vibration. Consequently, it is significant to study the influence of the gap on the dynamic behaviors. In this work, the gap varies in the range of 0–60 \({\mu m}\), the rotational speed is selected as 3000 rpm. Figure 11 is the bifurcation diagram of the vibration response versus the gap, which shows that when the gap is in the range of 0–40 \({\mu m}\), the system mostly shows the multiple periodic motion which is primary in certain span of the amplitude (only exist a small quantity of the jump span); and when gap is in the range of 40–50 \({\mu m}\), the figure presents the disorder shape of the response and there exists a larger response compared to that of the gap increasing from 0 to 40 \({\mu m}\). The gap can make the system vibration in a relatively stable, stable(“S” in Fig. 11) and unstable state(“U” in Fig. 11). This chaotic status is harmful to the bearing system. Therefore, the scientific designation of the gap is essential to the safety operation of the system. The similar parameter bifurcation diagrams (eccentric distance and mass of the rotor) are seen in Figs. 12 and  13. It can be shown from Figs. 12 and 13 that only in a few parameter sections, the system is stable; and in most parameter sections, the system is unstable. The detailed analysis for Figs. 12 and 13 is similar to the analysis above, therefore it will not be repeated.

Fig. 11
figure 11

Bifurcation diagram of response Y vs. gap; S means the relatively stable region; U means the relatively unstable region

Full size image
Fig. 12
figure 12

Bifurcation diagram of the dynamic response Y vs. eccentricity of the rotor ee; S means the relatively stable region; U means the relatively unstable region

Full size image
Fig. 13
figure 13

Bifurcation diagram of the dynamic response Y vs.mass of the rotor ms; S means the relatively stable region; U means the relatively unstable region

Full size image

4 Conclusion

Dynamic characteristics study of an imbalance rotor-bearing system with asymmetric gap is carried out in this article. An new improved dynamic model overall considering the asymmetric gap, the varying compliance vibration and the time-dependent unbalanced force is established; especially the new model abandons the traditional modeling assumption to get more universal and more accurate solution. The comparison between the improved mode and the traditional model is conducted. Results of the research show that the phase is difference between the proposed model and the traditional model; the dominant frequency is little difference between the two models; and the amplitudes have somewhat difference, it is originated from the different position angle which changes the phase but does not change vibration frequency. Based on the general model, the influences of the rotational speed, the asymmetric gap, the eccentric distance of the rotor and the mass of the rotor on the dynamic responses have been investigated to analyze the dynamical mechanism of the system. To design the parameters of the bearing system, the specific work rotational speed should be considered to analyze which factors is the domination of the vibration, the VC vibration or the unbalanced vibration; and then quantitative calculation and optimization are carried out for the perspective of the dynamic characteristics.

The rotational speed has important effect on the dynamic behaviors of the system. With the increasing of the rotating speed, the VC frequency gradually loses the domination for the vibration; the rotational speed frequency and its combination frequency with the VC frequency dominate the vibration. The peak exists in the lower frequency range. In order to design the parameter of the bearing system, the specific work rotational speed should be considered to analyze which factors is the domination of the vibrations, the VC vibration or the unbalanced vibration; and then quantitative calculation and optimization can be conducted for the perspective of the dynamic characteristics.

The bearing system shows the complex dynamic characteristics such as the periodical vibration, the quasi-periodic vibration, the chaotic motion and the jumping phenomenon, the bifurcation, sudden change; the bearing system is susceptible to the variations of the rotational speed, the gap, the eccentricity and the mass of the rotor in certain ranges. An improper parameter brings about a huge or a chaotic response, especially, when it makes the system into a chaotic state, the response is hard to forecast; and under this circumstances, a hidden occurrence of the fault may appear. Accordingly, the research work is essential in understanding of the internal dynamic mechanism of the rolling ball bearing; and the simulation results are practically meaningful for accurate fault diagnosis of rolling ball bearings, and the systematic design of the parameter for the safe and stable operation.