1 Introduction

The current technology trends in the world of electronics and communication are focused on wireless, portable, and wearable devices such as Internet-of-Things (IoT). The portable and wearable devices implicitly require battery power for operation. The present generation of electronics consumers have sophisticated personal communication because of the large number of portable and wearable communication devices available in the market. These portable and wearable devices are designed to create a wireless personal area network (WPAN). The backbone of these portable and wearable devices is the IEEE 802.15.4 standard for low-rate wireless personal area network (LR-WPAN) [1,2,3]. The specifications of the standard are listed in Table 1. The IEEE 802.15.4 standard applies stringent requirements on power consumption and silicon area consumption since the devices are required to be portable and wearable.

Table 1 Specifications of IEEE 802.15.4 receiver [1,2,3]
Full size table

The power consumption is prominent in the radio frequency (RF) front-end circuits such as LNA, Mixer, and VCO employed in the communication devices. Due to the movement of the communication devices, the signal strength varies and hence, more power is required by the RF circuits for proper signal reception. These devices are designed to be battery-operated, and hence, rapid battery discharge occurs due to the RF circuit operation. Therefore, the current necessity in the electronics and communication industry is to design energy-harvesting RF circuits for low-power operation of the wireless, portable, and wearable devices. This work intends to meet the necessity by proposing an ultra-low power LNA realised using UMC 180 nm process technology and its performance is validated using Cadence SpectreRF simulations.

There are low-power LNA topologies reported in the literature [4,5,6,7,8,9,10,11,12]. The sub-mW low-power LNA design techniques include current reuse and inductive \({g}_{m}\)-boosting [4], double \({g}_{m}\)-enhancement [5], inductive peaking feedback [6], inductive degeneration [7], forward body bias (FBB) [8], current reuse with negative feedback [9], active shunt-feedback [10], shunt feedback with dual capacitive cross-coupling (DCCC) [11], push–pull and current steering with shunt feedback [12]. From the analysis of the existing low-power LNA topologies, it is found that feedback techniques are more suitable for low-power design. Also, in sub-mW designs [4,5,6, 8, 10, 12], it can be noted that the noise figure (\(NF\)) less than 3 dB is difficult to achieve. In [9], low NF is achieved by sacrificing linearity and in [11], the extra transistors will lead to process and device mismatch deterioration. Hence, it is beneficial to develop techniques that will help in achieving sub-3 dB NF in sub-mW operation without deterioration in process and device mismatches.

One of the techniques for noise cancellation is using feedback. Some of the other LNA topologies employing feedback are reported in [6, 9,10,11,12,13,14,15,16,17,18,19,20,21] and they include active-feedback [13], resistive-feedback [14], dual negative feedback [15], local feedback [16], negative feedback [17], positive feedback [18], double feedback [19], dual capacitor cross-coupled feedback with negative impedance [20], and active-feedback using complementary source follower (CSF) [21]. It can be seen that by using feedback, the trade-off between input matching, gain, noise figure and transconductance (\({\mathrm{g}}_{\mathrm{m}}\)) of the input transistor is reduced. In CG based LNAs, input impedance, \({\mathrm{Z}}_{\mathrm{in}} \approx 1/{\mathrm{g}}_{\mathrm{m}}\). By employing current feedback, \({\mathrm{Z}}_{\mathrm{in}}\) can be reduced by a factor of (1 + \({\mathrm{A}}_{\mathrm{v},\mathrm{CG}}\)), such that \({\mathrm{Z}}_{\mathrm{in}} \approx 1/(1+{\mathrm{A}}_{\mathrm{v},\mathrm{CG}}){\mathrm{g}}_{\mathrm{m}}\). Hence, \({\mathrm{g}}_{\mathrm{m}}\) of the CG transistors can be lowered to achieve the required input impedance, thus leading to reduced power consumption. Also, it can be noted that the \({\mathrm{g}}_{\mathrm{m}}\) is now boosted by a factor of (1 + \({\mathrm{A}}_{\mathrm{v},\mathrm{CG}}\)) leading to improved gain and noise performance of the CG based LNAs employing feedback. In sub-mW LNA designs, it is difficult to simultaneously achiever proper NF and linearity performance. Since, NF and linearity performance is vital for portable electronic devices, in this paper, an ultra-low power LNA topology employing cross-coupled positive feedback and dual shunt peaking is proposed. It will be shown that the proposed LNA topology provides a scaling factor of (\(1+ {A}^{2}\)) thus achieving proper gain, NF and linearity performance required by the IEEE 802.15.4 standard for WPAN applications while operating at extremely low supply voltages.

The topology of the proposed LNA is discussed in the Sect. 2, where the expressions for gain, noise figure and linearity are derived. The proposed LNA’s post-layout performance is validated using UMC 180 nm CMOS process, and the results are discussed in the Sect. 3 and Sect. 4 concludes the work by highlighting the salient features.

2 Proposed low-noise amplifier topology

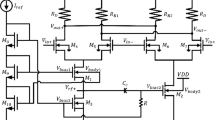
Before proceeding to the main theme of this work, a brief background on the use of positive feedback is illustrated in Fig. 1a. The feedforward network has a gain \(A\) and the feedback network has a gain \(\beta\). The difference between the input signal (\({V}_{in}\)) and the feedback signal is the error signal (\({V}_{e}\)). The characteristics of positive feedback in circuits and its subsequent effect on impedance and gain has been reported in [22,23,24,25,26]. In Fig. 1b, conceptual illustration of output voltage sensing and input current returning amplifier is shown. The gain of the feedforward network is a resistance (\({R}_{o}\)) and the gain of the feedback network is a transconductance (\({g}_{mF}\)). It can be seen that the input impedance of the amplifier is reduced by the current returning mechanism of the feedback network. The proposed LNA with positive feedback is shown in Fig. 1c. The input RF signal (\({v}_{rf}\)) is sensed at the source node of transistors \({M}_{1}\) and \({M}_{3}\) and the necessary bias for these transistors is given by \({V}_{bias}\). The transistors \({M}_{2}\) and \({M}_{4}\) are the cascode transistors whose bias (\({V}_{cas}\)) is used to control the current consumption in the circuit. The resistor \(R\) is the biasing resistor and \({C}_{c}\) is the coupling capacitor. The transistors \({M}_{f1}\) and \({M}_{f2}\) are connected to the source of the transistors \({M}_{1}\) and \({M}_{3}\) respectively, and their output resistances (\({r}_{o,Mf1}\) and \({r}_{o,Mf2}\)) provide degeneration to the transistors \({M}_{1}\) and \({M}_{3}\). \({M}_{f1}\) and \({M}_{f2}\) also provide the necessary phase shift for positive feedback operation of the circuit. The inductors \({L}_{1}\) and \({L}_{3}\) are present at the drain node of transistors \({M}_{1}\) and \({M}_{3}\) respectively to provide shunt peaking. The inductors \({L}_{2}\) and \({L}_{4}\) are connected to the drain of the cascode devices \({M}_{2}\) and \({M}_{4}\) to act as both the load and the shunt peaking impedance. The shunt peaking inductors \({L}_{\mathrm{1,3}}\) help in tuning out the parasitic capacitance at the drain node of transistors \({M}_{\mathrm{1,3}}\). The second pair of peaking inductors \({L}_{\mathrm{2,4}}\) tune with the capacitors at the drain node of \({M}_{\mathrm{2,4}}\). In wideband LNA with shunt peaking, the inductors are chosen to add a zero and not to tune with the capacitors. The same inductors when used to tune capacitances can yield good narrowband response and hence used in this work. The amplified differential output (\({v}_{out+}\) and \({v}_{out-}\)) is sensed at the drain node of the cascode devices \({M}_{2}\) and \({M}_{4}\), and the differential output is fed back through the feedback transistors \({M}_{f2}\) and \({M}_{f1}\) respectively by means of cross-coupling.

Fig. 1
figure 1

a Positive feedback network, b sensing and return mechanism of the proposed topology, c proposed LNA with cross-coupled positive feedback with dual shunt peaking

Full size image

The use of cross coupling provides the necessary phase shift without requirement of external circuitry. This method is more economical in terms of power and area and hence adopted in this work. The inductive load removes the voltage headroom difficulty and enable the circuit to operate at even 0.6 V. Ideally, the inductors remove the voltage headroom difficulty. However, the parasitic resistances cause few micro-volt drop and this drop in voltage is generally small and doesn’t affect the performance of the system substantially. Hence, the effect of parasitic resistances are ignored in the simulation. The inherent positive feedback to the output which effectively boosts the \({g}_{m}\) by a factor of (\(1+ {A}^{2}\)) helps in achieving the required performance of the LNA at low supply voltages. In [18], separate transconductance stage is used for generating positive feedback while in the proposed work the positive feedback is inherently generated by making use of the active source degenerators. As per the equation for closed loop gain in positive feedback from Fig. 1a, \(\frac{{v}_{out}}{{v}_{in}} = \frac{A}{1-A\beta }\), we have magnitude of closed-loop gain \(\left|{A}_{CL}\right| \approx \frac{1}{\beta }\), when \(A\beta \gg 1\). And if \(\beta \gg 1\), \(\left|{A}_{CL}\right|\) will always be less than 1 and the positive feedback will not be dominant. In this work, clearly feedback factor is >  > 1 and hence, the system is stable. Also, it is worth noting that the source and bulk of the input transistors are tied together to eliminate body effect. This is achieved by using triple well transistors offered by UMC. However, due to process and device mismatches, body effect may be prevalent and hence its effect is included in the analysis for completeness in this work. The effect of the cross-coupled positive feedback and dual shunt peaking on the circuit’s performance is analysed next.

2.1 Gain analysis

From the circuit schematic shown in Fig. 1c, the proposed circuit is analysed using the small-signal analysis to obtain the expression for mid-band gain. For calculating the dominant poles and zeros associated with the circuit, open-circuit time constant (OTC) analysis is carried out. From Fig. 1c, the mid-band gain without feedback (\(A_{v}\)) can be derived as

$$A_{v} \approx \frac{{\left( {g_{m,M1,3} + g_{mb,M1,3} } \right)}}{{1 + \left( {g_{m,M1,3} + g_{mb,M1,3} } \right)r_{o,Mf1} }}\cdot(Z_{L2,4} ||R_{down} )$$
(1a)

where \(g_{m,M1,3}\)—transconductance due to the gate to source voltage of the transistors \({M}_{\mathrm{1,3}}\), \({g}_{mb,M\mathrm{1,3}}\)—transconductance due to the bulk to source potential of the transistors \({M}_{\mathrm{1,3}}\), \({Z}_{L\mathrm{2,4}}\)—inductive impedance offered by the shunt peaking inductor, and \({R}_{down}\)—resistance looking down from the drain node of the cascode device.

Similarly, the gain with feedback can be derived by considering the gains offered by path due to transistors \({M}_{f1}\) and \({M}_{f2}\) respectively. By achieving proper symmetricity, the proposed circuit will have \({g}_{m,Mf1} = {g}_{m,Mf2}\), and \({Z}_{L1} = {Z}_{L2}\). Therefore, with feedback, the gain of the proposed LNA (\({A}_{v,fb}\)) is derived as

$$A_{v,fb} \approx A_{v} \cdot\left( {1 + g_{m,Mf1,2}^{2} (Z_{L2,4} ||R_{down} )^{2} } \right)$$
(1b)

By comparing (1a) and (1b), it can be noted that the gain with feedback \({A}_{v,fb}\) has a square dependence on the transconductance of the feedback transistors \({g}_{m,Mf\mathrm{1,2}}\). In existing feedback techniques, the gain is improved by a factor of (1 + A), whereas in this work, the gain is improved by (\(1+ {A}^{2}\)). Therefore, high gain can be achieved at low-power consumption.

The expression for \({R}_{down}\) is derived using small-signal analysis as

$${R}_{down} \approx \left({g}_{m,M\mathrm{2,4}}+ {g}_{mb,M\mathrm{2,4}}\right).{r}_{o\mathrm{2,4}}\cdot[{Z}_{L\mathrm{1,3}}+\left({g}_{m,M\mathrm{1,3}}+ {g}_{mb,M\mathrm{1,3}}\right)\cdot{r}_{o\mathrm{1,3}}\cdot{r}_{oMf1,Mf2}]$$
(2)

In (2), \({g}_{m,M\mathrm{2,4}}\)—transconductance due to the gate to source voltage of the transistors \({M}_{\mathrm{2,4}},\) \({g}_{mb,M\mathrm{2,4}}\)—transconductance due to the bulk to source potential of the transistors \({M}_{\mathrm{2,4}}\), \({r}_{o\mathrm{2,4}}\)—output resistance of the cascode transistors \({M}_{\mathrm{2,4}}\), \({Z}_{L\mathrm{1,3}}\)—inductive impedance offered by the shunt peaking inductors \({L}_{1}\) and \({L}_{3}\), \({r}_{o\mathrm{1,3}}\)—output resistance of the input transistors \({M}_{\mathrm{1,3}}\), and \({r}_{oMf1,Mf2}\)—output resistance of the feedback transistors \({M}_{f1}\) and \({M}_{f2}\) respectively.

Since \({R}_{down}\) is quantitatively very large as derived in (2), the expression for the mid-band gain of the circuit can be simplified as

$${A}_{v,fb} \approx \frac{\left({g}_{m,M\mathrm{1,3}}+ {g}_{mb,M\mathrm{1,3}}\right)}{1+ \left({g}_{m,M\mathrm{1,3}}+ {g}_{mb,M\mathrm{1,3}}\right){r}_{o,Mf1} }\cdot{Z}_{L\mathrm{2,4}}\cdot(1+{g}_{m,Mf1}^{2}{({Z}_{L\mathrm{2,4}})}^{2})$$
(3)

For high-frequency analysis, the expression for gain as a function of frequency in radians (ɷ) is given as

$${A}_{v,fb}\left(\omega \right)\approx {A}_{v,fb}\cdot H(\omega )$$
(4)

In (4), H \((\omega )\) is found using OTC analysis using the equivalent circuit in Fig. 2 and, the expression for the frequency response of the proposed LNA is derived as

Fig. 2
figure 2

Equivalent half-circuit of the proposed LNA. a TC with node-1, b TC with node-2, c TC with output node-3, d Noise sources in the LNA

Full size image
$${A}_{v,fb}(\omega ) \approx \frac{\frac{\left({g}_{m,M\mathrm{1,3}}+ {g}_{mb,M\mathrm{1,3}}\right)}{1+ \left({g}_{m,M\mathrm{1,3}}+ {g}_{mb,M\mathrm{1,3}}\right){r}_{o,Mf1} }\cdot{Z}_{L\mathrm{2,4}}.(1+{g}_{m,Mf1}^{2}{({Z}_{L\mathrm{2,4}})}^{2})}{\begin{array}{c} \left[{r}_{o,Mf1} ||\frac{{R}_{p,L1}}{{g}_{m,M1}+\frac{1}{{r}_{o,M1}}}\right].[ {c}_{gs,M1}+ {c}_{sb,M1}+ {c}_{gs,Mf1}+ {c}_{db,Mf1}+ {c}_{gd,Mf1}\left(2+\frac{1}{{g}_{m,Mf1.}{r}_{o,Mf1}}+ {g}_{m,Mf1.}{r}_{o,Mf1}\right)]+\\ ({c}_{gs.M2}+ {c}_{sb,M2}).(\frac{1}{{g}_{m,M2}+ {g}_{mb,M2}}||({R}_{p.L1}+({g}_{m,M1}{r}_{o,M1}{r}_{o,Mf1})))\\ + {(c}_{gd,M1}+ {c}_{db,M1}).({R}_{p,L1}|\left|\left({g}_{m,M1}{r}_{o,M1}{r}_{o,Mf1}\right)\right)+ \left({c}_{gd,M2}+ {c}_{db,M2}\right).{R}_{down}\end{array}}$$
(5)

Thus, (5) is the quantified expression for the frequency response of the proposed LNA. It can be noted that the shunt peaking inductor \({L}_{\mathrm{2,4}}\) contributes a zero while the parasitic resistance of the shunt inductor \({L}_{\mathrm{1,3}}\) contributes to the pole frequency. Since, the parasitic resistance, \({R}_{p,L1}\ll {Z}_{L\mathrm{2,4}}\), the effect of \({Z}_{L\mathrm{2,4}}\) is comparatively dominant and hence, results in a − 3 dB bandwidth (BW) extension up to 600 MHz as shown in the next section.

2.2 Noise figure analysis

The equivalent half-circuit with noise contributing sources is shown in Fig. 2d. For the analysis, flicker noise and thermal noise contributed by the MOS devices are considered. The equations for flicker noise and thermal noise is based on the models reported in [3]. Based on the equivalent circuit, the output noise (\(\widehat{{V}_{o,n}^{2}}\)) contribution by the proposed LNA can be given as

$$\widehat{{V}_{o,n}^{2}} = \widehat{{V}_{o,M1}^{2}}+ \frac{\widehat{{V}_{o,M2}^{2}}}{{a}_{v,M1}^{2}}+ \widehat{{V}_{o,Mf1}^{2}}$$
(6)

where

$${a}_{v,M1}\approx \left({g}_{m,M1}+ {g}_{mb,M1}\right)\cdot\left({r}_{0,M1}||\left({Z}_{L1}+ \frac{1}{{g}_{m,M2}+ {g}_{mb,M2}}\right)\right)$$
(7)
$$\widehat{{V}_{o,M1}^{2}}=\left(\frac{8kT}{3}{g}_{m,M1}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}$$
(8)
$$\widehat{{V}_{o,M2}^{2}}=\left(\frac{8kT}{3}{g}_{m,M2}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}$$
(9)
$$\widehat{{V}_{o,Mf1}^{2}}=\left(\frac{8kT}{3}{g}_{m,Mf1}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}$$
(10)

\(\widehat{{V}_{o,M1}^{2}}\) is the noise contributed by the input transistor \({M}_{1}\), \(\widehat{{V}_{o,M2}^{2}}\) is the noise contributed by the cascode transistor \({M}_{2}\), \(\widehat{{V}_{o,Mf1}^{2}}\) is the noise contributed by the current source \({M}_{f1}\), k is Boltzmann’s constant, T is the temperature in Kelvin, \({k}_{f}\) is flicker noise coefficient, \(\alpha f\) is technology parameter, \({I}_{D}\) is the current through the transistor, \({C}_{ox}\) is the gate-oxide capacitance, \(W\) is the width of the transistor, and \(L\) is the length of the transistor. From (6) and (7), it can be seen that the overall noise contribution is affected by the shunt inductor \({Z}_{L1}\). The presence of \({Z}_{L1}\) is also responsible for the frequency-dependent characteristic of the NF as discussed in the next section. By substituting (7)–(10) in (6), and dividing the output noise contribution (\(\widehat{{V}_{o,n}^{2}}\)) by \({A}_{v}^{2}\), the input-referred noise (\(\widehat{{V}_{i,n}^{2}}\)) can be derived as

$$\widehat{{V}_{i,n}^{2}} \approx \frac{\begin{array}{c}\left(\frac{8kT}{3}{g}_{m,M1}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}+\\ \frac{\left(\frac{8kT}{3}{g}_{m,M2}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}}{{[\left({g}_{m,M1}+ {g}_{mb,M1}\right)\cdot({r}_{0,M1}||({Z}_{L1}+ \frac{1}{{g}_{m,M2}+ {g}_{mb,M2}})) ]}^{2}}+\\ \left(\frac{8kT}{3}{g}_{m,Mf1}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right).{R}_{out}^{2}+\left(\frac{16KT}{{R}_{p,L1-4}}\right)\cdot{R}_{out}^{2}\end{array}}{{({A}_{v,fb})}^{2}}$$
(11)

Thus, from (11), for a source resistance \({R}_{s}\), the NF of the proposed LNA can be quantified as

$$NF \approx 1+ \frac{\begin{array}{c}\left(\frac{8kT}{3}{g}_{m,M1}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}+\\ \frac{\left(\frac{8kT}{3}{g}_{m,M2}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}}{{[\left({g}_{m,M1}+ {g}_{mb,M1}\right)\cdot({r}_{0,M1}||({Z}_{L1}+ \frac{1}{{g}_{m,M2}+ {g}_{mb,M2}})) ]}^{2}}+\\ \left(\frac{8kT}{3}{g}_{m,Mf1}+ \frac{{k}_{f}\cdot{I}_{D}^{\alpha f}}{{C}_{ox}^{2}WL}\right)\cdot{R}_{out}^{2}+ \left(\frac{16KT}{{R}_{p,L1-4}}\right)\cdot{R}_{out}^{2}\end{array}}{{({A}_{v,fb})}^{2}.(4KT{R}_{s})}$$
(12)

From the above expression, the effect of the inductors on NF performance can be observed. The inductors in the proposed LNA will have parasitic series resistances which contribute noise, and hence their noise contribution is also included in the analysis. The parasitic series resistance associated with the inductors is denoted as \({R}_{p,L}\), and each resistor will contribute a noise current of \((4KT/{R}_{p,L})\). Since we have four inductors in the circuit, the total noise current is equal to \((16KT/{R}_{p,L1-4})\). Also, the transconductance of transistors \({M}_{\mathrm{1,3}}\) also plays a significant role in reducing NF. It should be noted that the noise contribution is scaled down by a factor of (\(1+ {A}^{2}\)), thus enabling low NF even at reduced supply voltages. The proposed LNA is analysed for linearity performance using Volterra series expansion in the next sub-section.

2.3 Linearity analysis

The nonlinearity of RF circuits arises because of the nonlinear current–voltage relationship of the MOS (metal–oxide–semiconductor) devices. The nonlinearity behaviour of the RF CMOS circuits in deep sub-micron technologies is extensively studied and reported in [27,28,29,30,31,32,33,34,35]. For memoryless systems, the nonlinear output current (\({i}_{d}\)) as a function of the gate to source voltage (\({v}_{gs}\)) can be expanded using Taylor series as

$${i}_{d}= {g}_{m}^{1}{v}_{gs}+ {g}_{m}^{2}{v}_{gs}^{2}+ {g}_{m}^{3}{v}_{gs}^{3}+\dots + {g}_{m}^{n}{v}_{gs}^{n}$$
(13)

where \({g}_{m}^{n}\) is the nth-order transconductance and it is expressed as

$${g}_{m}^{n}= \frac{1}{n!}\cdot\frac{{\partial }^{n}}{\partial {v}_{gs}^{n}}({i}_{d})$$
(14)

The MOS devices have various capacitances associated with them, and the capacitive reactance is frequency-dependent. Hence, the nonlinear output expression must include the frequency-dependent components for accurate analysis and therefore, Volterra series expansion is used [27, 36,37,38]. The expression for Volterra series expansion of \({v}_{gs}\) due to an input signal \({v}_{in}\) restricted up to third-order can be given as

$${v}_{gs}= {A}_{1}\left({s}_{1}\right)^\circ {v}_{in}+ {A}_{2}\left({s}_{1},{s}_{2}\right)^\circ {v}_{in}^{2}+ {A}_{3}({s}_{1},{s}_{2},{s}_{3})^\circ {v}_{in}^{3}$$
(15)

where \({A}_{1}\left({s}_{1}\right)\), \({A}_{2}\left({s}_{1},{s}_{2}\right)\) and \({A}_{3}({s}_{1},{s}_{2},{s}_{3})\) are the Laplace transforms of the first-, second-, and third-order Volterra kernels. ‘°’ is the volteraa operator. Combining (13) and (15), the output drain current \({i}_{d}\) can be expressed as a function of the input signal \({v}_{in}\) as

$${i}_{d}({v}_{in})= {B}_{1}\left({s}_{1}\right)^\circ {v}_{in}+ {B}_{2}\left({s}_{1},{s}_{2}\right)^\circ {v}_{in}^{2}+ {B}_{3}({s}_{1},{s}_{2},{s}_{3})^\circ {v}_{in}^{3}$$
(16)

In (16), \({B}_{1}\left({s}_{1}\right)\), \({B}_{2}\left({s}_{1},{s}_{2}\right)\) and \({B}_{3}({s}_{1},{s}_{2},{s}_{3})\) are determined in terms of first-, second-, and third-order terms of (13) respectively. If \({Z}_{in}\) is the input impedance, then the input-referred third-order intercept point (\(IIP3\)) can be found by solving for the unknowns in (13)–(16). The expression for \(IIP3\) using Volterra kernels has been studied extensively [27, 36]. The dominant source of nonlinearity in the circuit is due to the transistors \({M}_{\mathrm{1,3}}\) and it is considered in this work. From [39], the expression for IIP3 in circuits having frequency-dependent components can be expressed as

$$IIP3= \frac{1}{6\mathfrak{R}({Z}_{in}(s))}\left|\frac{{{g}_{m}^{1}A}_{1}(s)}{{\left|{A}_{1}(s)\right|}^{2}[1- {g}_{m}^{1}{A}_{1}(s){Z}_{s}]\varepsilon }\right|$$
(17)

In (17), the expression for variables \({Z}_{in}(s)\), \({A}_{1}(s)\), \({Z}_{s}\) and ε are derived for the proposed LNA given in Fig. 1 and are as follows:

$${Z}_{in}\left(s\right) \approx \frac{(\frac{1}{{g}_{m,M1}}|\left|{r}_{o,M1} \right)||({r}_{o,Mf1}||{X}_{c})}{(1+ \frac{{R}_{T}}{{r}_{o,M1}})}$$
(18)
$${Z}_{s} \approx {r}_{o,Mf1}||{X}_{c}$$
(19)
$${A}_{1}\left(s\right) \approx \frac{\omega {c}_{gs}+ {r}_{o,Mf1}}{2{g}_{m}^{1}\omega {c}_{gs}{r}_{o,Mf1}}$$
(20)
$$\varepsilon \approx \frac{{g}_{m}^{3}- \frac{2}{3}{{(g}_{m}^{2})}^{2}}{\frac{1}{2{r}_{o,Mf1} }- 2\omega {c}_{gs}{r}_{o,Mf1}+ {g}_{m}^{1}}$$
(21)

In (18), \({R}_{T}\) is the resistance connected to the drain of transistor \({M}_{1}\) and derived as

$${R}_{T} \approx \frac{{Z}_{L2}}{{r}_{o,M2}(\frac{1}{{g}_{m,M2}}||{r}_{o,M2})}+{Z}_{L1}$$
(22)

In (19), \({Z}_{s}\) is the impedance connected to the source of the transistor \({M}_{1}\) and \({X}_{c}\) denotes the reactance of the gate to source capacitance \({c}_{gs}\). Therefore, by using the expressions derived in (18)–(22), the IIP3 of the proposed LNA including the frequency-dependent components is derived as

$$IIP3= \frac{{g}_{m}^{1}\frac{\omega {c}_{gs}+ {r}_{o,Mf1}}{2{g}_{m}^{1}\omega {c}_{gs}{r}_{o,Mf1}}\cdot(\frac{1}{2{r}_{o,Mf1} }- 2\omega {c}_{gs}{r}_{o,Mf1}+ {g}_{m}^{1})}{\begin{array}{c}6(\frac{1}{{g}_{m,M1}}|\left|{r}_{o,M1} \right)||({r}_{o,Mf1}|\left|{X}_{c}\right)\cdot\frac{{\omega }^{2}{c}_{gs}^{2}+ {r}_{o,Mf1}^{2}+2\omega {c}_{gs}{r}_{o,Mf1}}{4{\omega }^{2}{\left({g}_{m}^{1}\right)}^{2}{\left({r}_{o,Mf1}\right)}^{2}{c}_{gs}^{2}} \cdot\\ \left[1-{g}_{m}^{1}\frac{\omega {c}_{gs}+ {r}_{o,Mf1}}{2{g}_{m}^{1}\omega {c}_{gs}{r}_{o,Mf1}}\right]\cdot({g}_{m}^{3}- \frac{2}{3}{{(g}_{m}^{2})}^{2})\end{array}}$$
(23)

From (23), it can be seen that the IIP3 is dependent on the frequency, and IIP3 increases with an increase in spacing between the fundamental signal and the interferer.

3 Results

The proposed LNA is designed using UMC 180 nm mixed-mode radio frequency (MMRF) CMOS process technology. The performance of the LNA with extracted parasitic RC components is studied using Cadence SpectreRF circuit simulator. For analysis, the input signal power is set at − 85dBm because the minimum receiver sensitivity required for WPAN applications is − 85dBm [1,2,3]. The gain offered, and the noise contributed by the LNA are analysed using S-parameter analysis and the results are plotted in Figs. 3 and 4 respectively for the targeted frequency range of 2.4–2.485 GHz. It can be observed that the LNA offers a peak gain of 18.87 dB and 21.36 dB when operating in Mode-I and Mode-II respectively. In Mode-I, the LNA has − 3 dB bandwidth of 600 MHz from 2.3 to 2.9 GHz whereas in Mode-II, its bandwidth is 500 MHz from 2.3 to 2.8 GHz. Also, the input matching of the LNA is analysed using the S11 parameter and is shown in Fig. 3. It can be found that the LNA provides proper input matching and the proposed LNA has a flat S11 of − 11 dB in the required operating frequency range of 2.4–2.485 GHz. The small signal \({\mathrm{g}}_{\mathrm{m}}\) changes with change in small signal current. For DC conditions, it is possible to fix \({\mathrm{g}}_{\mathrm{m}}\) independent of the current given by the equation \([\mathrm{k}\frac{\mathrm{W}}{\mathrm{L}}\left({\mathrm{V}}_{\mathrm{GS}}- {\mathrm{V}}_{\mathrm{TH}}\right)]\). In the equation, \({\mathrm{g}}_{\mathrm{m}}\) is independent of the current. In this work, the source of the transistor is degenerated with an inductor and hence, Vs does not change and therefore, \({g}_{m}\) does not change. Although, the inductors will have parasitic series resistance, the voltage drop is very small and can negligible. Thus, with change in supply voltage, in this topology, the effect on change in \({g}_{m}\) is negligible and hence, S11 is almost the same as shown in Fig. 3.

Fig. 3
figure 3

Gain and input matching of the LNA

Full size image
Fig. 4
figure 4

NF of the LNA

Full size image

In Mode-I, the LNA has NF of 3.2–2.5 dB in the range of 2.3–3 GHz, and in Mode-II, the LNA has NF of 2.9–2.3 dB in the frequency range of 2.3–3 GHz. The NF of the proposed LNA is better than the other sub-mW designs reported in [4,5,6, 8,9,10,11,12, 18]. Also, it is worth noting that the LNA has a wide unity-gain bandwidth (UGB) ranging from 1.5–6 GHz in Mode-I, and 1.4–6.5 GHz in Mode-II respectively. In (3), (5), and (12), the parameters affecting the gain and NF is determined and to assist the design, the variation of the design parameters with bias voltage is plotted in Figs. 5 and 6. In Fig. 5, the effect of the gate voltage (\({V}_{bias}\)) of transistors \({M}_{\mathrm{1,3}}\) on the transistor’s first-order transconductance \({g}_{m}^{1}\) and the second-derivative of the transconductance \({g}_{m}^{3}\) is shown for both Mode-I and Mode-II respectively. Similarly, the effect of the gate bias voltage (\({V}_{cas}\)) of the transistors \({M}_{\mathrm{2,4}}\) on the transistor’s \({g}_{m}^{1}\) and \({g}_{m}^{3}\) is shown in Fig. 5. In Mode-I, the LNA operates at a supply voltage of 0.6 V whereas, in Mode-II, the LNA operates at 1 V supply. From (3), (5), and (12), it should be noted that the gain is enhanced by a factor of (\(1+ {A}^{2}\)) whereas the NF is scaled down by a factor of (\(1+ {A}^{2}\)). This is achieved by the positive shunt feedback topology of the proposed LNA.

Fig. 5
figure 5

Variation of \({g}_{m,M1}^{1}\) and \({g}_{m,M1}^{3}\) with \({V}_{bias}\)

Full size image
Fig. 6
figure 6

Variation of \({g}_{m,M2}^{1}\) and \({g}_{m,M2}^{3}\) with \({V}_{cas}\)

Full size image

IIP3 in dB calculated based on Taylor series approximation is given by \(\sqrt{\frac{4}{3}.\frac{{\mathrm{g}}_{\mathrm{m}}^{1}}{{\mathrm{g}}_{\mathrm{m}}^{3}}}\). By definition, making \({\mathrm{g}}_{\mathrm{m}}^{3} \approx 0\), increases IIP3. To assist in the design process, the variation of transconductance (\({\mathrm{g}}_{\mathrm{m}}^{1}\)) and the second derivative of transconductance \(({\mathrm{g}}_{\mathrm{m}}^{3})\) with respect to the gate bias voltage of the transistor \({\mathrm{M}}_{\mathrm{1,3}}\) is shown in Fig. 6. It can be seen from Fig. 5 that in Mode-I, \({\mathrm{g}}_{\mathrm{m}}^{3}\) is much closer to 0 than in Mode-II. Thus, it is expected that the IIP3 in Mode-I will be greater than the IIP3 in Mode-II. In Fig. 5, around 600 mV, \({g}_{m}^{3}\) of input transistor is near to zero and hence the IIP3 can be enhanced.

However, IIP3 depends on various other parameters such as \({Z}_{in}\), parasitic capacitors (17)–(23), and therefore, the IIP3 is swept as a function of the input transistor bias voltage in Fig. 8, where maximum IIP3 is obtained at 550 mV. It can be noted that the input transistor dominates the distortion more than the cascode as the cascode transistor can be viewed as a common-gate transistor where the signal path due to \({c}_{gs,M3}\) is grounded. The linearity of the RF circuits is a pivotal performance parameter in WPAN applications since the circuits are employed in the dense 2.4 GHz band where the interferer signal will be closely spaced to the fundamental signal, resulting in intermodulation components (IM) within the frequency band of operation. The linearity performance of the LNA is characterized using IIP3 by harmonic-balance (HB) analysis combined with harmonic-balance AC analysis (HBAC), and the results are shown in Fig. 7. The LNA achieves an IIP3 of − 8.4dBm in Mode-I and 14.5dBm in Mode-II for the fundamental signal at 2.4 GHz and an interferer spaced 100 MHz away. From (23), the IIP3 depends on \({g}_{m}^{1}\) and \({g}_{m}^{3}\) of the transistor \({M}_{\mathrm{1,3}}\) and since, the \({g}_{m}^{1}\) and \({g}_{m}^{3}\) depends on the gate bias (\({V}_{bias}\)), the IIP3 variation with (\({V}_{bias}\)) is plotted in Fig. 8.

Fig. 7
figure 7

IIP3 performance of the LNA

Full size image
Fig. 8
figure 8

IIP3 variation with \({V}_{bias}\)

Full size image

Thus, appropriate gate bias of the transistor \({M}_{\mathrm{1,3}}\) can be chosen for optimal linearity performance of the LNA. It can be seen that for a gate bias of \(\sim 550mV\), the LNA achieves 13.78dBm IIP3 in Mode-II and in Mode-I, the corresponding IIP3 is − 7.9dBm. The IIP3 achieved by the proposed LNA in Mode-II is better than the other sub-mW designs proposed in the literature [4, 8,9,10,11,12, 18].

The reliability of the LNA to operate under diverse operating conditions is studied by conducting corner, voltage, and temperature variation analysis. The LNA performance is characterized at different process corners (FF, FNSP, SNFP, SS) for both Mode-I and Mode-II and the results for gain and NF variation are shown in Figs. 9 and 10 respectively. For studying the effect of voltage variation on the performance of the LNA, the supply voltage is varied \(\pm 10\%\) from the nominal supply voltage of 0.6 V in Mode-I, and 1 V in Mode-II. The gain and NF performance of the LNA for supply voltage variation is plotted in Figs. 11 and 12 respectively and finally, the gain and NF performance of the LNA at different operating temperatures (-40ºC, 0ºC, 125ºC) is shown in Figs. 13 and 14 respectively. The corner, voltage, and temperature effects on IIP3 for Mode-I and Mode-II are listed in Tables 2 and 3 respectively. It can be noted from the analysis that the performance of the LNA is intact and within acceptable limits even under diverse operating conditions.

Fig. 9
figure 9

Variation of gain with process corners

Full size image
Fig. 10
figure 10

Variation of NF with process corners

Full size image
Fig. 11
figure 11

Variation of gain with supply voltage

Full size image
Fig. 12
figure 12

Variation of NF with supply voltage

Full size image
Fig. 13
figure 13

Variation of gain with temperature

Full size image
Fig. 14
figure 14

Variation of NF with temperature

Full size image
Table 2 CVT variation of IIP3 in Mode-I
Full size table
Table 3 CVT variation of IIP3 in Mode-II
Full size table

IIP3 is very sensitive to bias voltages, resistances and impedances present in the circuit. This can be seen from the transconductance variation shown in Figs. 5 and 6. In Mode-I, especially with reduced headroom and subthreshold region of operation at low-power mode, the sensitivities are enhanced. Nevertheless, the performance characterized by the PVT analysis shows that the LNA is robust to such variations in the operating environment.

To account for the process and device mismatches arising in the fabrication process, the performance parameters of the LNA is analysed using statistical models and Monte-Carlo (MC) simulations. Since the first-order transconductance \({g}_{m}^{1}\) of the transistors \({M}_{\mathrm{1,3}}\) and \({M}_{\mathrm{2,4}}\) affect the gain, NF and IIP3 of the LNA, the random variation of \({g}_{m,M1}\) and \({g}_{m,M2}\) with device parameters are analysed using MC simulations and plotted in Figs. 15, 16, 17 and 18. The MC simulations are carried out for 100 iterations of random variations of the process and device mismatch parameters. The MC simulation results show the mean (µ) and standard deviation (σ) of the parameters. Similarly, MC simulation results for NF and IIP3 in Mode-I and Mode-II are shown in Figs. 19, 20, 21 and 22. The process and device mismatch analysis using MC simulation is performed for both Mode-I and Mode-II respectively. Thus, from the results obtained from the corner, voltage, and temperature variation analyses and MC simulations, it can be concluded that the designed LNA is robust, dependable and reliable for battery-powered, portable and wearable devices. Since the proposed LNA concentrates on low-power consumption, the characteristics of transconductor efficiency \(({g}_{m}/{I}_{d})\), Power, current consumption (I), and Inversion coefficient (IC) of the transistors \({M}_{\mathrm{1,3}}\) and \({M}_{\mathrm{2,4}}\) is plotted with respect to their gate bias voltages \({V}_{bias}\) and \({V}_{cas}\) respectively and shown in Figs. 23, 24, 25 and 26. From Figs. 23, 24, 25 and 26, the weak inversion operation of the input transistors \({M}_{\mathrm{1,3}}\) can be seen and the required gate bias for the transistors can be chosen.

Fig. 15
figure 15

MC analysis of \({g}_{m,M1}^{1}\) in Mode-I

Full size image
Fig. 16
figure 16

MC analysis of \({g}_{m,M1}^{1}\) in Mode-II

Full size image
Fig. 17
figure 17

MC analysis of \({g}_{m,M2}^{1}\) in Mode-I

Full size image
Fig. 18
figure 18

MC analysis of \({g}_{m,M2}^{1}\) in Mode-II

Full size image
Fig. 19
figure 19

MC analysis for NF in Mode-I

Full size image
Fig. 20
figure 20

MC analysis for NF in Mode-II

Full size image
Fig. 21
figure 21

MC analysis for IIP3 in Mode-I

Full size image
Fig. 22
figure 22

MC analysis for IIP3 in Mode-II

Full size image
Fig. 23
figure 23

\({g}_{m}/{I}_{d}\) of \({M}_{\mathrm{1,3}}\) and Power consumption vs. \({V}_{bias}\)

Full size image
Fig. 24
figure 24

\({g}_{m}/{I}_{d}\) of \({M}_{\mathrm{2,4}}\) and Power consumption vs. \({V}_{cas}\)

Full size image
Fig. 25
figure 25

IC and Current consumption of \({M}_{\mathrm{1,3}}\) vs. \({V}_{bias}\)

Full size image
Fig. 26
figure 26

IC and Current consumption of \({M}_{\mathrm{2,4}}\) vs. \({V}_{cas}\)

Full size image

For a fair comparison of the proposed LNA with existing LNA topologies, the following figure-of-merit (FoM) is adopted [52].

$${FoM}_{1}=10.{\mathrm{log}}_{10}\frac{{10}^{Gain/20}\cdot{10}^{IIP3/20}}{{10}^{NF/10}.P}$$
(24)

In sub-mW designs, it is difficult to provide NF less than 4 dB and improve IIP3 simultaneously.

The comparison of the proposed LNA with recently reported low-power LNA topologies [9,10,11,12, 20, 21, 40,41,42,43] is shown in Table 4. In Table 4, [9, 11, 20, 21, 40,41,42,43] are post-layout simulation results. It can be seen that the proposed LNA offers a better alternative for ultra-low power applications. The proposed LNA has a core area of 0.45 \({mm}^{2}\) and the layout of the LNA is shown in Fig. 27 and the size of the devices and component values used in the circuit are listed in Table 5. The inductors used are from the process library provided by UMC and the required diameter, width, number of turns for achieving the inductance value is specified in Table 5. The input and output waveforms are shown in Figs. 28 and 29 for Mode-I and Mode-II respectively. The input signal \({v}_{in}\) has a peak-to-peak amplitude of \(35.14\mu V\) (\(\approx -85dBm\) for a 50Ω source impedance) at 2.4 GHz. The output signal \({v}_{out}\) has a peak-to-peak value of \(225\mu V\) for Mode-I and \(297.3\mu V\) for Mode-II respectively. For a 50Ω output impedance, the output power will be − 68.97dBm and − 66.55dBm for Mode-I and Mode-II respectively. The gain plotted in Fig. 3 correlates with the values calculated from the waveform.

Table 4 Comparison of the proposed LNA with literature
Full size table
Fig. 27
figure 27

The physical layout of the proposed LNA with a core area of 0.45mm2

Full size image
Table 5 Component values for design
Full size table
Fig. 28
figure 28

The input and output waveforms for VDD = 0.6 V

Full size image
Fig. 29
figure 29

The input and output waveforms for VDD = 1 V

Full size image

While the other feedback topologies rely on external circuits for feedback, the proposed LNA makes use of the active degeneration devices to provide positive feedback. Also, the topologies reported earlier scale up the gain by a factor of (\(1+A\)) while the proposed LNA scales up the gain by (\(1+ {A}^{2}\)). Thus, the proposed LNA can afford to operate at reduced voltages with reduced power consumption. Compared to the recently proposed LNA in [44], the proposed circuit operates at 55.5% reduced power consumption. Also, the proposed LNA has good performance at reduced supply voltage of 0.6 V making it viable for battery-powered, wireless applications that demand large data processing such as 5G.

Although positive feedback has been employed in [45], the proposed circuit reimagines the circuit for ultra-low-power operation with the use of series peaking inductors. Compared to [45], the proposed LNA design achieves 0.5 dB less NF, 0.96 dB higher gain in Mode-II while consuming only 0.5mW which is 5.3 times lesser in power. An LNA circuit without inductors and capacitors is reported in [46] with power consumption of 18mW. In contrast to the proposed work, the LNA in [46] trades power consumption for lower chip area. LNAs operating at sub-mW power consumption has been proposed in [47, 48]. Although the power is drastically reduced, the IIP3 of − 19dBm in the reported LNA [47] makes it susceptible to large signal interference and inadvertently causes signal blocking or erroneous signal detection. The LNA proposed in this work provides better noise performance over the ultra-low-power LNA reported in [48]. In comparison to the recent state-of-art LNA, the proposed LNA has better gain and NF performance compared to the LNAs in [52, 55]. The proposed LNA topology is more linear than the LNAs in [52,53,54,55]. Although the proposed ultra-low-power LNA consumes 50% more power than the LNA in [52], the IIP3 improvement is ~ 16 dB. Whereas the LNAs in [53,54,55] consume ~ 10 times, ~ 39 times and ~ 35 times more power than the proposed LNA in High-Power mode. Therefore, it is clear that the proposed LNA has improved the state-of-art substantially.

The input signal strength which causes the LNA to compress is characterized using 1 dB-compression point (1 dB-CP). It is found that the 1 dB-CP of the proposed LNA is − 18.58dBm for Mode-I and − 10.83dBm for Mode-II respectively and the graphs are plotted in Fig. 30. Since the desired signal power will be very low (-85dBm for IEEE 802.15.4 standard), LNA can work without compression. However, in the presence of an interferer, the proposed LNA can withstand an interferer power of − 18.58dBm in Mode-I and − 10.83dBm in Mode-II. Since the input signal power sensed by the LNA is in the order of − 85dBm (35.56 \(\upmu {\mathrm{V}}_{\mathrm{pp}}\)), the input signal will not affect the operation. The maximum input signal power that can be sensed without causing compression is characterized by the 1 dB-compression point. In the reported work, the 1 dB-CP is obtained at − 18.58dBm (~ 79mVpp) for Mode-I and − 10.83dBm (~ 200mVpp) for Mode-II respectively. Thus, it can be concluded that as long as the input signal level is below the 1 dB-CP, the output signal will not be compressed. The circuit has a common-mode gain (\({\mathrm{A}}_{\mathrm{CM}}\)) of − 231.86 dB and − 229.50 dB in Mode-I and Mode-II respectively as shown in Fig. 31. These \({\mathrm{A}}_{\mathrm{CM}}\) values combined with the differential voltage gain gives a common-mode rejection ratio (CMRR) of 250.73 dB and 250.86 dB for Mode-I and Mode-II respectively. Furthermore, to avoid latch-up in the proposed LNA at high-power mode, guard rings are placed in the layout. The causes and prevention of latch-up in CMOS circuits are studied in [49,50,51]. For completeness, the S22 characteristics is plotted in Fig. 32 along with S11. The input impedance seen by the signal source is, \(Z_{{in}} \approx {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {g_{{m{\text{1}},{\text{3}}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${g_{{m{\text{1}},{\text{3}}}} }$}}{\text{ }}\) since the values of \({C}_{gs\mathrm{1,3}}\) is very small, and hence the S11 is purely resistive in the required frequency range. The effect of small capacitances will come into effect at higher frequencies outside the band of interest. It is worth mentioning that this LNA is designed for on-chip radio receivers where the output of the LNA is given to the RF Mixer stage. Hence, simulations excluded the use of output buffers since the buffers only add to the NF and degrade the SNR of the receiver system. The presence of inductive load gives a tuned S22 as shown in Fig. 32.

Fig. 30
figure 30

The 1-dB Compression Point for Mode-I and Mode-II

Full size image
Fig. 31
figure 31

Common-Mode Gain of the LNA in Mode-I and Mode-II

Full size image
Fig. 32
figure 32

The input and output matching characteristics of the proposed LNA

Full size image

Finally, Table 6 compares the feedback LNA techniques active-feedback [13], resistive-feedback [14], dual negative feedback [15], local feedback [16], negative feedback [17], positive feedback [18], double feedback [19], dual capacitor cross-coupled feedback with negative impedance [20], and active-feedback using complementary source follower (CSF) [21] with the proposed LNA in terms of the achieved improvement in \({g}_{m}\) Table 6 clearly shows that the proposed LNA doubles the enhancement factor.

Table 6 Improvement in \({g}_{m}\) achieved by the state-of-the-Art LNAs
Full size table

4 Impact of technology scaling

Although the proposed topology can be used at lower technology nodes, the impact of technology scaling will be evident as similar performance may be hard to achieve. This is because of the short-channel effects (SCE) like Gate-induced-Drain-Lowering (GIDL), Drain-induced-Barrier-lowering (DIBL), velocity saturation, mobility degradation, gate tunnelling, hot carrier effects, threshold roll-off. However, with appropriate biasing and sizing of the devices along with other circuit techniques (if required), the proposed LNA topology can be implemented in lower nodes like 28 nm and beyond. Thus, making the LNA implementable in lower technology nodes for portable and wearable IoT applications. For example, the effect of velocity saturation, mobility degradation and DIBL can be modelled as follows:

$${\mathrm{g}}_{\mathrm{m}}={\mathrm{WC}}_{\mathrm{ox}}{\mathrm{v}}_{\mathrm{sat}}$$
(25)
$$\upmu = \frac{{\upmu }_{0}}{1+\uptheta ({\mathrm{V}}_{\mathrm{GS}}-{\mathrm{V}}_{\mathrm{TH}} -\mathrm{DIBL})}$$
(26)
$$\mathrm{DIBL}=0.80 \frac{{\upvarepsilon }_{\mathrm{si}}}{{\upvarepsilon }_{\mathrm{ox}}}.\left[1+ \frac{{\mathrm{x}}_{\mathrm{j}}^{2}}{{\mathrm{L}}_{\mathrm{el}}^{2}}\right].\frac{{\mathrm{t}}_{\mathrm{ox}}}{{\mathrm{L}}_{\mathrm{el}}}.\frac{{\mathrm{t}}_{\mathrm{dep}}}{{\mathrm{L}}_{\mathrm{el}}}\cdot{\mathrm{V}}_{\mathrm{bi}}$$
(27)

where \({\upvarepsilon }_{\mathrm{si}}\), \({\upvarepsilon }_{\mathrm{ox}}\) are the permittivity of Silicon and Oxide layers, \({\mathrm{t}}_{\mathrm{ox}}\) is the thickness of the oxide layer, \({\mathrm{t}}_{\mathrm{dep}}\) is the depletion thickness, \({\mathrm{L}}_{\mathrm{el}}\) is the effective length, \({\mathrm{x}}_{\mathrm{j}}\) is the source/drain junction width, \({\mathrm{V}}_{\mathrm{bi}}\) is the built-in potential. \(\uptheta\) is a proportionality factor and \({\mathrm{v}}_{\mathrm{sat}}\) is the saturation velocity. The parameters vary for every technology node and is generally specified by the foundry. Using the general equations and EDA tools, the circuits can be simulated and analysed. It is to be noted that with increasing complexity, the equations only give a general idea about the design. Therefore, the equations for voltage gain, NF and IIP3 derived in (5), (12) and (23) are now functions of SCE. Due to the complexity of the equations, analysis and design of the LNA can be carried out with EDA tools. In this work, Cadence SpectreRF is used for complex circuit simulations.

As an end note, with miniaturization of electronic devices especially for smart wearables in IoT and healthcare applications, the supply voltage is also reducing with technology scaling and for better battery life. For instance, with 5 nm process node, the supply voltage is 0.6 V. The intent of providing two modes of operation is to enable the customer to use the proposed topology in various end user applications as deemed beneficial by the product manufacturers. In the industry, it is a common practice to have two or more gain modes for the LNA. The gain of the LNA affects the NF and linearity of the RF front-end circuits. With having variable gain modes for the LNA, the use of variable gain amplifier can be reduced which will further improve the size of the receiver system. Also, by showing that the LNA can operate at two different modes, the LNA can cater to a wide customer base.

5 Conclusion

An ultra-low power LNA topology is proposed in this work for use in battery-powered, portable, wireless devices such as Internet-of-Things. The LNA with cross-coupled positive feedback and dual shunt peaking is implemented in UMC 180 nm CMOS process, and it can be operated in two modes namely, low power mode and high power mode. In low power mode, the LNA is operated at a reduced supply voltage of 0.6 V and offers 18.87 dB gain, whereas, in high power mode, the LNA is operated at 1 V supply and offers a gain of 21.36 dB and IIP3 of 13.78dBm. With the semiconductor industry approaching 5 nm technology node in the near future, the applications such as Internet-of-Things need to be powered by low-voltage, low-power RF circuits. With 219 µW of power consumption, the proposed LNA offers an alternative to be used in the next generation communication systems. The proposed LNA offers better FoM when compared to other recently reported low-power LNA topologies. Thus, it can be concluded that the proposed LNA is a suitable alternative for low power, low voltage applications.