1 Introduction

Large deformation and time-dependence are most significant mechanical behavior in rock rheology, which should be attached much importance to study. With the development of underground engineering, the creep properties of rock have attracted much interest for many researchers [1,2,3,4,5,6,7]. And much effort also has been devoted to exploring the various laws of creep. The most of explorations were directed toward the theoretical model of creep, which can be used to predict the creep properties of rock [8]. As a consequence, much advancements have been achieved in modeling creep under various boundary conditions for rock [9,10,11]. During the history of investigation in creep model of rock, there are so classical and representative element models (e.g., Kelvin, Maxwell and Nishihara), which can be introduced to characterize the creep mechanical behavior of rock.

However, due to the complex mechanical properties of rock under different stress status, many parameters of most models have no physical meaning and the nonlinear behavior of creep cannot be well described. Consequently, the fractional calculus has been put much effort for the sake of the long history dependence and memory effects. And the fractional calculus is considered as an effective tool to depict the creep behavior of rock and has obtained much progress [12,13,14,15,16,17]. Chen et al. [18] presented a fractional damage model for rock to predict the mechanical behavior. Kong et al. performed many experiments on coal and the fractional theory is used to imply the mechanical behavior of coal and the process of failure [19]. A series of creep tests were conducted on salt rock and then a damage creep model was proposed by the Zhou et al., which was based on the fractional operator and damage theory [20]. Qu et al. developed a fractional plastic flow model to characterize volumetric compression/dilation transition state [21]. And based on fractional theory, Lu et al. introduced 3-D fractional plastic flow rule into characteristic stress space and presented a new fractional elastoplastic model for soil [22, 23]. Sun et al. applied fractional-order dilatant equation to capture state-dependent stress-dilatant behavior of fine sand [24]. As it can be known, the fractional order has much influence on the viscoelastic proportion of materials and the above those studies all concentrated on the constant order of fractional theory. But in fact, the viscoelasticity of rock within creep under constant loading is not constant and it should have been varying. So the fractional order should be adjusted as a function related to time. Wu et al. proposed a variable-order fractional creep model of salt rock to describe its mechanical behavior [14]. Tang et al. conducted a series of experiments to verify the rationality of proposed model, which was based on the variable-order fractional theory [25]. Meng et al. proposed a variable-order fractional model to depict strain softening of polymer material and reveal mechanism of deformation [26, 27]. Di Paola et al. proposed a novel variable-order fractional model to describe elasticity, which is based on derived system response by applying Boltzmann principle on an equivalent system [28]. In view of those advancements in variable-order fractional theory, we can see that the varying-order can represent the evolution process of viscoelasticity of materials. So how to well describe the various process of order in details is a challenging topic and there is only a little research in this area.

As a consequence, in this paper, the aim of this work is to propose a nonlinear variable-order fractional damage creep model to well describe the creep mechanical behavior of rock materials. In Sect. 2, based on the variable-order fractional theory and continuous damage theory with sum function, a nonlinear variable-order fractional damage creep model will be proposed. And then the varying-order function is assumed as an exponential function. In Sect. 3, a series of creep experiments will be conducted on the sandstone and based on those experimental data, the applicability and rationality of this proposed model are verified in detail. During the analysis process, the ‘two-area-continuous-variable-order-analytical-method’ will be introduced to analyze the creep mechanical behavior. For better verifying the applicability of proposed model, except for sandstone, the creep experimental data of mudstone and salt rock are selected to prove the reasonability and validation of proposed model. In Sect. 4, the variation of order will be illustrated as a form of exponential function. The evolution of viscosity of materials will be analyzed by the variable-order fractional model and the order and parameters of the proposed model will be given. Finally, the conclusions of this study were given.

2 Theory of fractional calculus

2.1 Constant-order fractional calculus

In present, the fractional calculus has many definitions, and the most popular within the analyses of rheological model is the Riemann–Liouville (R–L) fractional integral operator, which is defined as follows [16, 29]:

$${}_{t_0}^{RL}{D}_t^{-\alpha }f(t)=\frac{1}{\varGamma \left(\alpha \right)}\int_{t_0}^t\frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{1-\alpha }} d\tau$$
(1)

where t > 0, Re(α) > 0, Γ is famous gamma function [30] and \({D}_t^{-\alpha }\) is R-L fractional integral operator of α order.

And the definition of fractional differential calculus can be expressed as follows:

$${}_{t_0}^{RL}{D}_t^{\alpha }f(t)=\frac{1}{\varGamma \left(n-\beta \right)}\frac{d^n}{d{t}^n}\int_{t_0}^t\frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{1-n+\beta }} d\tau$$
(2)

where n − 1 < β ≤ n.

And as we can know, the stress-strain relationship of pure solid body follows the Hooke’s law and its constitutive equation is:

$$\upsigma (t)= E\varepsilon (t)$$
(3)

where E is elastic modulus of materials, σ is stress and ε is strain.

When the material is considered as Newton fluid body, the constitutive model of pure viscous fluid body can be expressed as follows:

$$\upsigma (t)=\eta \dot{\varepsilon}=\eta \frac{d\varepsilon (t)}{d t}$$
(4)

where the η is viscosity coefficient of materials and \(\dot{\varepsilon}\) is strain rate.

But most of engineering materials are viscoelastic materials, which are called intermediate material between elasticity and viscosity. Based on the R-L fractional differential operator, a classical viscoelastic constitutive model (i.e., Scott-Blair model) is proposed as follows:

$$\sigma (t)=M\frac{d^{\alpha}\varepsilon (t)}{d{t}^{\alpha }}\ 0\le \alpha \le 1$$
(5)

where the M is material constant, α is fractional order and Dα is used by Eq. (2).

Then let the σ(t) be constant σ0, based on the Eqs. (1) and (2), the creep response of Eq. (5) can be deduced, which is shown as follows:

$$\varepsilon (t)=\frac{\sigma_0}{M}\frac{t^{\alpha }}{\varGamma \left(1+\alpha \right)}$$
(6)

where σ0 is constant stress in creep experiment.

As shown in Fig. 1, the strain increases with an increase in the fractional order. The nonlinear mechanical behavior can be well exhibited under various orders. Different order represents different proportion of viscosity and elasticity and it also demonstrates the evolution of viscoelasticity. But the constant order in fractional order creep model is regular, which will induce the transformation of viscoelasticity and time-dependence within creep behavior cannot be well characterized during the process of creep. And it is necessary to propose a varying-order function related to time in construction of fractional creep model.

Fig. 1
figure 1

The curves of ε(t) versus t by the Eq. (6) under various α

Full size image

2.2 Variable-order fractional calculus

It is well-known that the definition of fractional integral equation is:

$${I}_{a+}^{\upalpha}f(x)=\frac{1}{\varGamma \left(\alpha \right)}\int_a^x\frac{f(t)}{{\left(x-t\right)}^{1-\alpha }} dt, Re \left(\alpha \right)>0$$
(7)

where a denotes a time length scale, which is considered to be a constant value 0 in this work.

From the above expression, when a >  − ∞, we can achieve the Riemann equation. And when the a =  − ∞, the Liouville equation can be obtained. For corresponding to above the variation of fractional order, the constant-order fractional theory can be extended to one case, in which α is assumed as a function of x and it is shown as follows:

$${I}_{a+}^{\upalpha (x)}f(x)=\frac{1}{\varGamma \left(\alpha (x)\right)}\int_a^x\frac{f(t)}{{\left(x-t\right)}^{1-\alpha (x)}} dt,\quad {{Re}}\left(\alpha (x)\right)>0$$
(8)

Here when x > a, f(x) can be defined any function. And the presence of f(x) is for making sure that the convergence of integral.

The left Riemann-Liouville fractional derivation for differential operator of α(x) was introduced as follows (Almeida and Torres 2013):

$${D}_{a+}^{\upalpha (x)}f(x)=\frac{1}{\varGamma \left(1-\alpha (x)\right)}\frac{d}{dx}\int_a^x\frac{f(t)}{{\left(x-t\right)}^{\alpha (x)}} dt$$
(9)

So the application of variable-order fractional theory in Scott-Blair model is a direct way. And a variable-order fractional viscoelastic constitutive model can be expressed as follows:

$$\sigma (t)={M}_{\alpha (t)}\frac{d^{\alpha (t)}\varepsilon (t)}{d{t}^{\alpha (t)}}\ 0\le \alpha (t)\le 1$$
(10)

where α(t) is variable order function related to time and Mα(t) is material constant.

As it can be know, comparing to the constant-order fractional calculus, the variable-order fractional calculus has obvious superiority in memory of the effect of previous results [31]. So time can be segmented by the way of piece-wise and is defined as tn − 1 ≤ t ≤ tn and n ∈ N+. Corresponding to variation of time, the fractional order can be defined as 0 ≤ α(t) = αn ≤ 1.

Based on above calculus, the expression of variable-order fractional viscoelastic constitutive model is shown as follows:

$${D}_{a+}^{\upalpha (x)}\varepsilon (t)=\sum_{n=1}^{\infty}\varepsilon (t)\frac{{\left({t}_n-{t}_{n-1}\right)}^{-{\alpha}_n}}{\varGamma \left(1-{\alpha}_n\right)}$$
(11)

Then if stress is an constant value σ0, the creep response of Eq. (11) can be obtained as follows:

$$\varepsilon (t)=\sum_{n=1}^{\infty}\frac{\sigma_0}{M_{\alpha_n}}\frac{{\left({t}_n-{t}_{n-1}\right)}^{\alpha_n}}{\varGamma \left(1+{\alpha}_n\right)}$$
(12)

As shown in Fig. 2, the function of variable order is considered as a step-wise function, which corresponds to the each period of time. The each ∆t corresponds to αi. It can be demonstrated in this way that different function of fractional order is in each period of creep deformation.

Fig. 2
figure 2

The time period versus variable order

Full size image

3 A nonlinear damage creep constitutive model

As it is shown in Fig. 3, the process of creep can be divided into three stages: decaying, steady and accelerating stage. During the decaying stage (1–2), the strain rate decreases rapidly with time. And then the steady stage (2–3) exhibited the stable strain rate. When the actual stress exceeded long-term strength of sample, the accelerating stage (3–4) will appear with a rapid increase in strain rate. From the view of mechanics of material, the total process of creep can be considered as an evolution process of viscosity, elasticity and plasticity. And in the view of damage mechanic, with the accumulation of damage inside the material, the creep gradually advances towards the accelerating stage and eventually reaches at failure. To sum up, for better depicting and predicting the mechanical behavior of creep under various stress levels, a nonlinear damage creep constitutive model is necessary to construct in details.

Fig. 3
figure 3

Left strain versus time and right strain rate versus time within creep results

Full size image

Before the construction of damage creep model, an effective damage factor must be presented. As we can know that with the evolution of damage, the proportion of viscosity and plasticity decreases gradually and then the plasticity must be taken account into construction of damage creep model. For better presenting the time effect of damage and variation of viscoelastic plasticity, the loading time will be divided into infinite period, which corresponds to the infinite period of damage. Due to the continuity of damage in creep, the infinite series of function was adapted to describe the time effect of continuous damage. So according to the current research [17], based on the segment method, the damage factor can be expressed as follows:

$$D=1-\sum_{n=1}^{\infty }{e}^{-\gamma \left({t}_n-{t}_{n-1}\right)}$$
(13)

where D is damage factor and γ is damage parameter related to stress levels and property of material.

Under the constant loading on sample, with the development of damage, the viscosity coefficient can be modified as follows:

$$\eta ={\eta}_0\left(1-D\right)={\eta}_0\sum_{n=1}^{\infty }{e}^{-\gamma \left({t}_n-{t}_{n-1}\right)}$$
(14)

where η0 is initial viscosity coefficient.

Then based on the Norton power law [32], the constitutive model of material can be shown:

$${\varepsilon}^{\prime }(t)=\frac{\eta^{\ast }}{\eta }{\left(\frac{\sigma_1-{\sigma}_3}{\sigma^{\ast }}\right)}^m$$
(15)

where σ1 − σ3 represents additional vertical stress, σ∗ is unit stress, η∗ is unit viscosity of material and m is parameter related to stress level.

Following above expression of Norton power law, based on the modified viscosity coefficient, when we considered the actual stress in creep experiments, if m = 1 and σ1 − σ3 = σ0, the damage model can be expressed as follows:

$${\varepsilon}^{\prime }(t)=\frac{\sum_{n=1}^{\infty }{e}^{\gamma \left({t}_n-{t}_{n-1}\right)}}{\eta_0}{\sigma}_0$$
(16)

According to the Laplace transform and inverse transform, the Eq. (16) can be derived as follows:

$$\varepsilon (t)=\frac{\sum_{n=1}^{\infty }{e}^{\gamma \left({t}_n-{t}_{n-1}\right)}}{\gamma {\eta}_0}{\sigma}_0$$
(17)

In here, we can see that the damage always exists in process of creep with the development of time. And if the stress exceeds long-term strength of sample, the effect of damage becomes more and more obvious and it should be emphasized and put much effort. As a consequence, the nonlinear damage creep model should be constructed on the basis of damage effect. And whatever kinds of creep, the damage must be considered in construction of nonlinear damage creep model. For better describing the mechanical behavior of decaying creep and steady creep, the classical Maxwell model is modified. According to the variable-order fractional viscoelastic model proposed by this paper, based on constant stress, a modified Maxwell model can be expressed as follows:

$$\varepsilon (t)=\frac{\sigma_0}{E_0}+\sum_{n=1}^{\infty}\frac{\sigma_0}{M_{\alpha_n}}\frac{{\left({t}_n-{t}_{n-1}\right)}^{\alpha_n}}{\varGamma \left(1+{\alpha}_n\right)}$$
(18)

However, in Fig. 3, the accelerating stage is the main reason for failure of creep. When creep stress exceeds long-term strength of sample, the effect of damage will be considered in construction of nonlinear damage creep model. Then a new nonlinear damage creep model is given, which is based on the variable-order fractional theory and proposed damage function.

$$\varepsilon (t)=\left\{\begin{array}{ll}\frac{\sigma_0}{E_0}+\sum_{n=1}^{\infty}\frac{\sigma_0}{M_{\alpha_n}}\frac{{\left({t}_n-{t}_{n-1}\right)}^{\alpha_n}}{\varGamma \left(1+{\alpha}_n\right)},&\quad {\sigma}_0<{\sigma}_s\ \\ {}\frac{\sigma_0}{E_0}+\sum_{n=1}^{\infty}\frac{\sigma_0}{M_{\alpha_n}}\frac{{\left({t}_n-{t}_{n-1}\right)}^{\alpha_n}}{\varGamma \left(1+{\alpha}_n\right)}+\frac{\sum_{n=1}^{\infty }{e}^{\gamma \left({t}_n-{t}_{n-1}\right)}}{\gamma {\eta}_0}\left({\sigma}_0-{\sigma}_s\right),&\quad{\sigma}_0\ge {\sigma}_s\end{array}\right.$$
(19)
$$M=E{\tau}^{\alpha }={E}^{1-\alpha }{\eta}^{\alpha }$$
(20)

where E is elastic modulus, τ is relaxation time, η is viscous coefficient and σs is long-term strength. When α = 0, material is pure elastic body. When α = 1, material is pure fluid body.

Meanwhile, following the Eq. (12), the variable order has been defined as α(t) = f(t), which means that in each level of creep, the fractional order will exhibit a different trend with an increase in time. During the decaying and steady creep stage, in the view of property of material, the property of material mainly exhibit viscoelasticity and before creep deformation of material, the viscosity of material is regarded as 1. When material enters creep deformation, the viscosity of material will be consumed until material arrives at failure. During the process of deformation, the proportion of viscosity within property of material will reduce from 1 to 0. Based on above thinking, the special characteristic of exponential function is introduced and in conjunction with time-dependence of creep deformation, the variable-order function is assumed as exponential function. The aim of constructing variable-order function is to verify the applicability of proposed “Two-area-continuous-variable-order-analytical-method”. The proposed variable-order function can reflect the viscoelasticity of material within creep is flowing and the consumption of viscosity is also revealed by variable-order function. As it is shown in Eq. (21), the order varies from 1 to 0, which symbols the evolution of viscoelasticity of materials. So in this paper, the function of variable order will be assumed as follows:

$$\upalpha (t)={e}^{- at},0\le t\le {t}_1$$
(21)

where t1 is the time point of failure of material, a is the parameter related to relaxation time, strain rate and stress et al.

As a consequence, according to the each stage in creep and continuity of time, by substituting the Eq. (21) to Eq. (19), a nonlinear variable-order fractional damage creep model can be expressed as follows:

$$\varepsilon (t)=\left\{\begin{array}{ll}\frac{\sigma_0}{E_0}+\frac{\sigma_0}{M_0}\frac{t^{e^{- at}}}{\varGamma \left(1+{e}^{- at}\right)},&\quad 0\le t\le {t}_1,{\sigma}_0<{\sigma}_s\\ {}\frac{\sigma_0}{E_0}+\frac{\sigma_0}{M_0}\frac{t^{e^{- at}}}{\varGamma \left(1+{e}^{- at}\right)}+\frac{\left({\sigma}_0-{\sigma}_s\right){e}^{\gamma_0t}}{\gamma_0{\eta}_0},&\quad0\le t\le {t}_1,{\sigma}_0\ge {\sigma}_s\end{array}\right.$$
(22)

To sum up, the proposed nonlinear damage creep model has been given and the verification of proposed model by classical papers’ experimental creep data will be analyzed in next section.

4 Creep experiment of sandstone

4.1 Experimental apparatus

The five-connected rheological device in GeoMechanics and Deep Underground Engineering, China University of Mining and Technology (Beijing) was applied to conduct creep experiments on sandstone. This device is shown in Fig. 4 and it can apply vertical force with 0 to 600 kN. And five rock samples can be monitored simultaneously and the tested data can be recorded in real time by PC software.

Fig. 4
figure 4

Rheological apparatus in tests

Full size image

4.2 Experimental samples

In this section, the sandstone samples obtained from Ningtiaota coal mine in Shanxi, China were used to conduct creep experiments. The using right of sandstone sample obtained from Ningtiaota coal mine has been authorized by Ningtiaota Coal Mine. In Fig. 5, three samples named B-1, B-2 and B-3 were made as cylindrical samples with the height of 100 mm and the diameter of 50 mm, which were based on the criterion of “Test Standard for Engineering Rocks”. And all made sandstone samples must be checked out by the way of infrared non-destructive testing before conducting experiments. And in Table 1, basic mechanical parameters of sample and uniaxial compressive strength (UCS) of group B samples are shown.

Fig. 5
figure 5

Tested sandstone samples

Full size image
Table 1 Mechanical parameters of sample
Full size table

4.3 Experimental procedure

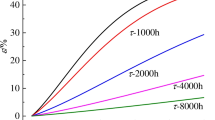
As shown in Fig. 6, the experimental program is introduced and this is divided into 8 stress levels. The each stress must be kept constant for more than 24 h. The experimental steps in this work will be segmented into the following three steps. (1) Uniaxial compressive strength of sandstone must be tested before conducting creep experiments, which decides the loading stress level of each experimental level; (2) It must be noted that the laboratory should be quiet and the platform of device should be clean. The plastic films must be applied on the surface of total sandstone samples. And the sensors of force and displacement must be stably installed in detail; (3) Following above procedures, each loading stress level should be confirmed, which can be adjusted that each stress increases with each 0.25 times of uniaxial compressive strength. And then keeping the constant stress level for more than 24 h is necessary. Finally, when the vertical displacement is lower than 0.001 mm during 4 h, we can judge this loading level is over.

Fig. 6
figure 6

Experimental program

Full size image

4.4 Creep experimental data of sandstone

In this section, we will select the B-1 sandstone sample as an example to discuss the various rule of creep with time and give particular mechanical mechanism of creep deformation. As we can see in Fig. 7, the curve of creep strain versus time was plotted and an upward trend was exhibited between creep strain and time. In Fig. 7a, the creep curves of first seven levels exhibit that creep increases with time, which only includes the decaying and steady creep. And the creep curve of the eighth level is representative, which includes three stages of creep. So this curve is selected to verify the applicability of proposed model. The curves ‘a-b’, ‘b-c’ and ‘c-d’ in Fig. 7b were known that decaying, steady and accelerating creep. During the decaying and steady creep, the creep rate rises up rapidly in initial time and then becomes constant gradually, which represents a shift from pure elasticity to viscoelasticity and the viscosity is consumed gradually with an increase in time. So the decaying and steady stages were named as ‘area 1’. For the accelerating creep, it is the main reason for the failure of sample, which can be accounted for that the effect of damage played a significant role in this stage. And the rate of damage accumulation increases fast in short time. All to all, in total process of creep, the nonlinear behavior is obvious and in next section, the proposed nonlinear fractional damage creep model will be applied to depict it and predict precise creep at various time.

Fig. 7
figure 7

The curve of total creep of sandstone

Full size image

5 Verification of proposed model

In this section, the reasonability and applicability of the proposed nonlinear damage creep model will be verified by various creep experimental data of sandstone, salt rock and mudstone, which is based on the least square method. It is necessary to note that those obtained experimental data all include accelerating creep stage, which means that those data contains the evolution of viscous-elastic-plasticity. And it is known that the fractional theory is a well way to describe the variation of viscoelasticity of materials [17]. However, most previous work have used the constant-order fractional theory to depict the viscoelasticity of materials [33], which symbols that during the total creep process, the fractional order is a constant value. But we can know that during the development of viscoelasticity, the proportion of viscosity and elasticity is not constant and it always varies with time.

Consequently, in this section, based on the variable-order function as expressed by Eq. (21) and mechanical property of creep, an analytical method named as ‘two-area-continuous-variable-order-analytical-method’ is firstly introduced, which means that the total process of creep is divided into two areas: area 1 and area 2. The area 1 includes decaying and steady creep and the area 2 represents accelerating creep. Comparing to conventional constant-order fractional creep model, the area 1 and 2 will all be depicted by the variable-order fractional damage creep model. And we can know that with the development of time, the variation of order represents the variation of proportion of viscosity. For better exhibiting this variation of order and proportion of viscosity, the proportion of variation of order or the variation of proportion of viscosity is defined as follows:

$$\left\{\begin{array}{c}{V}_{A1}=\frac{\alpha_a-{\alpha}_b}{\alpha_a-{\alpha}_c}\\ {}{V}_{A2}=\frac{\alpha_b-{\alpha}_c}{\alpha_a-{\alpha}_c}\end{array}\right.$$
(23)

where VA1 is variation of order of area 1 in total area, VA2 is variation of order of area 2 in total area. The αa, αb and αc is the value of order, which corresponds to starting time of decaying creep, starting time of accelerating creep and ending time of total creep, respectively.

As shown in Fig. 8a, the creep experimental data of sandstone under σ0 = 39.4 MPa included decaying, steady and accelerating stage, which will be used to verify the rationality of proposed model. The area 1 includes decaying creep and steady creep and the area 2 is accelerating creep. A well agreement can be seen in Fig. 8a between the experimental data of sandstone and fitting curve. Due to the variation of viscoelasticity in decaying, steady and accelerating stage, the variable-order fractional damage creep model is applied to depict the variation of creep data. The fitting curve is obtained by Eq. (22) with variable order. And what corresponds to this fitting curve is that the solid line in Fig. 8b has exhibited a various trend in the form of exponential function (i.e., α(t) = e−0.403t).

Fig. 8
figure 8

(a) Fitting curve in area 1 and other fitting curve in area 2 all obtained by the Eq. (22) versus experimental creep under σ0 = 39.4 MPa; (b) Variation of order versus time

Full size image

It is noted that the order always varies from 0 to 1 in area 1, which corresponds to the compatibility of viscoelasticity. It also can be seen in area 1 that the proportion of variation of order is 90.4%, which means that the consumption of viscosity mainly happens in area 1. And during the area 1, the variable-order falls down rapidly and then it accounts for most of change, which can be explained that with an increase in time, in area 1, the viscosity of material has been consumed gradually. And in area 2, including accelerating creep, the variable-order fractional function also can well describe the evolution of order and the proportion of variation of order is 10.6%. During the accelerating creep, the variation of order is small, which can be accounted for that the evolution of damage plays a major role in accelerating creep and the effect of viscosity is weak. Finally, the fitting parameters have been given in Table 2.

Table 2 Fitting parameters of proposed models for sandstone
Full size table

Except for the verification of experimental data of sandstone, for better demonstrating the applicability of the proposed model, the total creep experimental data of salt rock and mudstone also have been obtained to verify the proposed model by the way of ‘two-area-continuous-variable-order-analytical-method’.

As shown in Fig. 9a, the creep experimental data of salt rock was achieved from other researchers’ paper [34]. In area 1 and area 2, it can be seen that the fitting curves have a great match with the creep experimental data. And the fitting parameters of proposed models were also shown in Table 3. The function of order in area 1 and 2 is expressed as an exponential function (i.e., α(t) = e−0.0188t). It is clear that the variation of solid line in area 1 and 2 is mostly same as that in Fig. 8b, which can be interpreted that the proportion of viscosity decreases gradually in area 1 and the dissipation of viscosity occupy the main quantity in Fig. 9b. And the faster the viscosity of material dissipates, the greater the order varies. So the proportion of elasticity and viscosity varies uniformly. Then in area 2, the explanation and reason for the variable-order is same as that of sandstone in area 2.

Fig. 9
figure 9

(a) Fitting curve in area 1 and other fitting curve in area 2 all obtained by the Eq. (22) versus experimental creep under σ0 = 26.0MPa; (b) Variation of order versus time

Full size image
Table 3 Fitting parameters of proposed model for salt rock
Full size table

Meanwhile, as shown in Fig. 10a, the creep experimental data of mudstone was also selected to check the applicability and reliability of the proposed model in this paper [35]. The fitting curve can well correlate with the experimental data and the nonlinear behavior can be well described by the proposed model. And the fitting parameters of proposed model have been presented in Table 4. The fractional order corresponding to curves in area 1 and 2 are also presented as α(t) = e−0.0838t. Likewise, the various rule of order in Fig. 10b is same as that of sandstone and salt rock.

Fig. 10
figure 10

(a) Fitting curve in area 1 and other fitting curve in area 2 obtained by the Eqs. (22) and (23) versus experimental creep under σ0 = 30.0MPa, respectively; (b) Variation of order versus time

Full size image
Table 4 Fitting parameters of proposed models for salt rock
Full size table

From above analysis of proposed model for sandstone, salt rock and mudstone, we have identified that the proposed ‘two-area-continuous-variable-order-analytical-method’ have achieved great efficiency for analysis of nonlinear mechanical behavior of rock materials. The evolution of proportion of viscosity can be performed clearly by constructing an exponential function of variable-order. The mechanical property of accelerating creep stage also can be well described by the proposed variable-order fractional damage creep model. And then the different majority of viscoelasticity and plasticity also can be clearly exhibited by the proposed analytical method.

In summary, those analysis all reply that during the total process of creep, the decaying and steady creep include the majority of consumption of viscosity and the accelerating creep represents the evolution of viscoelasticity towards plasticity, which also verify the reasonability of proposed ‘two-area-continuous-variable-order-analytical-method’. And it is also concluded that the proposed ‘two-area-continuous-variable-order-analytical-method’ based on variable-order fractional theory have a great effect for describing the nonlinear mechanical behavior of creep of rock materials. Especially, based on the exponential function of variable-order, the evolution process of consumption of viscosity can be interrupted in details. And the accelerating creep also can be well depicted based on the presented variable-order fractional damage creep model.

6 Conclusions

  1. 1.

    Based on the variable-order fractional theory and damage theory, a new nonlinear variable-order fractional damage creep model is proposed to describe the creep mechanical behavior of rock materials. For the variable-order function, clear definition has been given and the order is assumed as exponential function. And then considering to the continuity of damage, we firstly proposed the damage of sum function, which can better describe the accelerating creep stage;

  2. 2.

    A series of creep experiments are performed on the sandstone by the five-connected rheological equipment. It is concluded that total creep included decaying, steady and accelerating creep. And according to mechanical property of materials, the decaying and steady creep stages are named as ‘area 1’ and the accelerating creep stage is named as ‘area 2’;

  3. 3.

    The applicability and reasonability of proposed nonlinear damage creep model have been verified by the creep experimental data of sandstone. Except for sandstone, for better highlighting the advantage of proposed model, the creep experimental data of salt rock and mudstone in classical papers also all are achieved to demonstrate it.

  4. 4.

    Based on the fitting results of sandstone, salt rock and mudstone, the ‘two-area-continuous-variable-order-analytical-method’ is firstly introduced in this work. The variation of consumption of viscosity in area 1 and 2 can be clearly expressed by this new method. Finally, all fitting parameters were given in Tables. And it is worth believing that the proposed nonlinear variable-order fractional damage creep model can well describe the creep mechanical behavior of most geotechnical materials.