Time-Dependent Behavior of Diabase and a Nonlinear Creep Model

Abstract

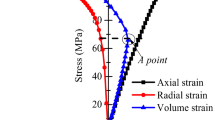
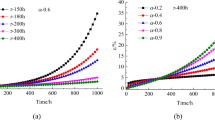
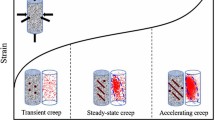
Triaxial creep tests were performed on diabase specimens from the dam foundation of the Dagangshan hydropower station, and the typical characteristics of creep curves were analyzed. Based on the test results under different stress levels, a new nonlinear visco-elasto-plastic creep model with creep threshold and long-term strength was proposed by connecting an instantaneous elastic Hooke body, a visco-elasto-plastic Schiffman body, and a nonlinear visco-plastic body in series mode. By introducing the nonlinear visco-plastic component, this creep model can describe the typical creep behavior, which includes the primary creep stage, the secondary creep stage, and the tertiary creep stage. Three-dimensional creep equations under constant stress conditions were deduced. The yield approach index (YAI) was used as the criterion for the piecewise creep function to resolve the difficulty in determining the creep threshold value and the long-term strength. The expression of the visco-plastic component was derived in detail and the three-dimensional central difference form was given. An example was used to verify the credibility of the model. The creep parameters were identified, and the calculated curves were in good agreement with the experimental curves, indicating that the model is capable of replicating the physical processes.

Appendix: Implementation of the Elasto-Visco-Plastic Model in FLAC3D

The three-dimensional finite difference model is developed and applied with FLAC^3D. In order to program the creep model, the three-dimensional finite difference constitutive equation is derived (Itasca Consulting Group, Inc. 2005).

Equation 18 is written in the incremental form:

$$\left\{ {\begin{array}{*{20}c} {\Updelta e_{ij} = \Updelta e_{ij}^{1} } \hfill & {{\text{YAI > YAI}}_{\text{ve}} } \hfill \\ {\Updelta e_{ij} = \Updelta e_{ij}^{1} + \Updelta e_{ij}^{2} } \hfill & {{\text{YAI}}_{\text{ve}} {\text{ > YAI > YAI}}_{\text{s}} } \hfill \\ {\Updelta e_{ij} = \Updelta e_{ij}^{1} + \Updelta e_{ij}^{2} + \Updelta e_{ij}^{3} (f(t))} \hfill & {{\text{YAI}} \le {\text{YAI}}_{\text{s}} ,t < t_{\text{s}} } \hfill \\ {\Updelta e_{ij} = \Updelta e_{ij}^{1} + \Updelta e_{ij}^{2} + \Updelta e_{ij}^{3} (f(t)) + \Updelta e_{ij}^{3} \left( {f(t - t_{\text{s}} )} \right)} \hfill & {{\text{YAI}} \le {\text{YAI}}_{\text{s}} ,t \ge t_{\text{s}} } \hfill \\ \end{array} } \right.$$

(I.1)

The second part of the model (Schiffman body) can be written in the central difference form as:

$$\bar{S}_{ij} \Updelta t = 2\eta_{1} \Updelta e_{ij}^{2} + 2G_{1} \bar{e}_{ij}^{2} \Updelta t$$

(I.2)

The first part of the model (Hook body) can also be written in the central difference form as:

$$\Updelta e_{ij}^{1} = \frac{{\Updelta S_{ij} }}{{2G_{0} }}$$

(I.3)

where the overbar indicates the mean value over the time step Δt:

$$\bar{S}_{ij} = \frac{{S_{ij}^{N} + S_{ij}^{O} }}{2}$$

(I.4)

$$\bar{e}_{ij} = \frac{{e_{ij}^{N} + e_{ij}^{O} }}{2}$$

(I.5)

The superscripts ^N and ^O denote new and old values, respectively. $S_{ij}^{N}$ and $S_{ij}^{O}$ are the new and old deviatoric stress tensors for a time step, respectively. $e_{ij}^{N}$ and $e_{ij}^{O}$ are the new and old deviatoric strain tensors for a time step, respectively.

After substituting Eqs. (I.4) and (I.5) into Eq. (I.2) and solving for $e_{ij}^{2,N} ,$ the Kelvin strain contribution may be expressed as:

$$e_{ij}^{2,N} = \frac{1}{A}\left[ {Be_{ij}^{2,O} + \frac{\Updelta t}{{4\eta_{1} }}\left( {S_{ij}^{N} + S_{ij}^{O} } \right)} \right]$$

(I.6)

where:

$$A = 1 + \frac{{G_{1} \Updelta t}}{{2\eta_{1} }},B = 1 - \frac{{G_{1} \Updelta t}}{{2\eta_{1} }}$$

(I.7)

After substituting Eqs. (I.3) and (I.6) into Eq. (I.1) and solving for the new deviatoric stress component, we find [using the mean value definitions Eqs. (I.4) and (I.5)]:

$$S_{ij}^{N} = \frac{1}{a}\left[ {\Updelta e_{ij} - \Updelta e_{ij}^{3} + bS_{ij}^{O} - \left(\frac{B}{A} - 1\right)e_{ij}^{2,O} } \right]$$

(I.8)

where:

$$a = \frac{1}{{2G_{0} }} + \frac{\Updelta t}{4} \cdot \frac{1}{{A\eta_{1} }}\;b = \frac{1}{{2G_{0} }} - \frac{\Updelta t}{4} \cdot \frac{1}{{A\eta_{1} }}$$

(I.9)

The volumetric deformation behavior is given by:

$$\sigma_{0}^{N} = \sigma_{0}^{O} + K(\Updelta e_{\text{vol}} - \Updelta e_{\text{vol}}^{3} )$$

(I.10)

The failure criterion used in the FLAC^3D model is a combination of the Mohr–Coulomb criterion with tension cutoff (Itasca 2005), which is also used in this study. However, the long-term parameters used in this study are different with FLAC^3D. A function h(σ ₁, σ ₃) = 0, which is represented by the diagonal between the representation of $f_{\infty }^{s} = 0$ and $f_{\infty }^{t} = 0$ in the (σ ₁, σ ₃)-plane, is defined. The positive and negative domains are indicated by this function, which is shown in Fig. 15, and the function has the form:

$$h = \sigma_{3} - \sigma_{{^{\infty } }}^{t} + a^{\text{P}} (\sigma_{1} - \sigma^{\text{P}} )$$

(I.11)

where a ^P and σ ^P are constants defined as:

$$\left. \begin{gathered} a^{\text{P}} = \sqrt {1 + N_{{\phi_{\infty } }}^{2} } + N_{{\phi_{\infty } }} \hfill \\ \sigma^{\text{P}} = \sigma_{{^{\infty } }}^{t} N_{{\phi_{\infty } }} - 2c_{\infty } \sqrt {N_{{\phi_{\infty } }} } \hfill \\ \end{gathered} \right\}$$

(I.12)

Fig. 15

Discrimination of plastic area by the modified Mohr–Coulomb criterion

If the stress state falls within domain 1, shear failure occurs, and the stress state is placed on the curve $f_{\infty }^{s} = 0$ using a flow rule derived using the potential function $g_{\infty }^{s} ,$ as shown in Eq. 24.

If the point falls within domain 2, tensile failure takes place, and the new stress state conforms to $f_{\infty }^{t} = 0$ using a flow rule derived using $g_{\infty }^{t} ,$ as shown in Eq. 25. The flow rule specifies that the direction of the plastic strain increment vector is normal to the plastic potential surface. Equation 19 can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {\Updelta \varepsilon_{ij}^{3} = \frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }} \cdot \Updelta t \cdot \frac{{\partial g_{\infty } }}{{\partial \sigma_{ij} }}} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\Updelta \varepsilon_{ij}^{3} = \frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right)\frac{{\partial g_{\infty } }}{{\partial \sigma_{ij} }}} & {J_{2}^{'} > J_{2}^{\text{vp}} } \\ \end{array} } \right.$$

(I.13)

In the principal stress space, Eq. (I.13) is:

$$\left\{ {\begin{array}{*{20}l} {\Updelta \varepsilon_{i}^{3} = \frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }} \cdot \Updelta t \cdot \frac{{\partial g_{\infty } }}{{\partial \sigma_{i} }}} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\Updelta \varepsilon_{i}^{3} = \frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right)\frac{{\partial g_{\infty } }}{{\partial \sigma_{i} }}} & {J_{2}^{'} > J_{2}^{\text{vp}} } \\ \end{array} } \right.$$

(I.14)

In the creep model implementation in FLAC^3D, the new trial stress components $\hat{S}_{i}^{N}$ and $\hat{\sigma }_{0}^{N}$ are computed from Eqs. (I.8) and (I.10), assuming visco-elastic increments. The trial principal stress components are calculated and sorted, and the yield function is computed. As long as $f \ge 0 ,$ the trial stresses are taken for new stresses. If $f < 0 ,$ plastic flow takes place and the trial stresses must be corrected by a component due to the incremental plastic strain before their value is assigned to the new stresses and the evolution law is updated (Itasca Consulting Group, Inc. 2005). Expressing Eqs. (I.8) and (I.10) in principal axes, the definition of trial stresses can be written as follows:

$$\begin{gathered} S_{i}^{N} = \hat{S}_{i}^{N} - \frac{1}{a}\Updelta e_{i}^{3} \hfill \\ \sigma_{0}^{N} = \hat{\sigma }_{0}^{N} - K\Updelta \varepsilon_{\text{vol}}^{3} \hfill \\ \end{gathered}$$

(I.15)

The stress tensor can be decomposed as the deviatoric stress and the spherical stress tensor. Combining the two equations in Eq. (I.15) yields:

$$\sigma_{i}^{N} = \hat{\sigma }_{i}^{N} - \frac{1}{a}\Updelta e_{i}^{3} - K\Updelta \varepsilon_{\text{vol}}^{3}$$

(I.16)

where:

$$\Updelta \varepsilon_{\text{vol}}^{3} = \Updelta \varepsilon_{\text{kk}}^{3} = \left\{ {\begin{array}{*{20}l} {\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\Updelta t \cdot \left( {\frac{{\partial g_{\infty } }}{{\partial \sigma_{1} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{2} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{3} }}} \right)} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right) \cdot \left( {\frac{{\partial g_{\infty } }}{{\partial \sigma_{1} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{2} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{3} }}} \right)} & {J_{2}^{'} > J_{2}^{\text{vp}} } \\ \end{array} } \right.$$

(I.17)

$$\begin{gathered} \Updelta e_{i}^{3} = \Updelta \varepsilon_{i}^{3} - \frac{1}{3}\Updelta \varepsilon_{\text{vol}}^{3} = \Updelta \varepsilon_{i}^{3} - \frac{1}{3}\left( {\Updelta \varepsilon_{1}^{3} + \Updelta \varepsilon_{2}^{3} + \Updelta \varepsilon_{3}^{3} } \right) \hfill \\ = \left\{ {\begin{array}{*{20}c} {\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\Updelta t\frac{{\partial g_{\infty } }}{{\partial \sigma_{i} }} - \frac{1}{3}\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\Updelta t\left( {\frac{{\partial g_{\infty } }}{{\partial \sigma_{1} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{2} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{3} }}} \right)} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right)\frac{{\partial g_{\infty } }}{{\partial \sigma_{i} }} - \frac{1}{3}\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right)\left( {\frac{{\partial g_{\infty } }}{{\partial \sigma_{1} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{2} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{3} }}} \right)} & {J_{2}^{'} > J_{2}^{\text{vp}} } \\ \end{array} } \right. \hfill \\ = \left\{ {\begin{array}{*{20}c} {\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\Updelta t \cdot \left\{ {\frac{{\partial g_{\infty } }}{{\partial \sigma_{i} }} - \frac{1}{3}\left( {\frac{{\partial g_{\infty } }}{{\partial \sigma_{1} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{2} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{3} }}} \right)} \right\}} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\frac{{\langle F_{\infty } \rangle }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right) \cdot \left\{ {\frac{{\partial g_{\infty } }}{{\partial \sigma_{i} }} - \frac{1}{3}\left( {\frac{{\partial g_{\infty } }}{{\partial \sigma_{1} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{2} }} + \frac{{\partial g_{\infty } }}{{\partial \sigma_{3} }}} \right)} \right\}} & {J_{2}^{'} > J_{2}^{vp} } \\ \end{array} } \right. \hfill \\ \end{gathered}$$

(I.18)

Using the definition for deviatoric components, Eq. (I.16) can also be expressed as:

$$\begin{gathered} \sigma_{1}^{N} = \hat{\sigma }_{1}^{N} - \left[ {\alpha_{1} \Updelta \varepsilon_{1}^{3} + \alpha_{2} \left( {\Updelta \varepsilon_{2}^{3} + \Updelta \varepsilon_{3}^{3} } \right)} \right] \hfill \\ \sigma_{2}^{N} = \hat{\sigma }_{2}^{N} - \left[ {\alpha_{1} \Updelta \varepsilon_{2}^{3} + \alpha_{2} \left( {\Updelta \varepsilon_{1}^{3} + \Updelta \varepsilon_{3}^{3} } \right)} \right] \hfill \\ \sigma_{3}^{N} = \hat{\sigma }_{3}^{N} - \left[ {\alpha_{1} \Updelta \varepsilon_{3}^{3} + \alpha_{2} \left( {\Updelta \varepsilon_{1}^{3} + \Updelta \varepsilon_{2}^{3} } \right)} \right] \hfill \\ \end{gathered}$$

(I.19)

where:

$$\begin{gathered} \alpha_{1} = K + \frac{2}{3a} \hfill \\ \alpha_{2} = K - \frac{1}{3a} \hfill \\ \end{gathered}$$

(I.20)

for shear yielding:

Partial differentiation of Eq. 24 yields:

$$\frac{{\partial g_{\infty }^{s} }}{{\partial \sigma_{1} }} = 1,\frac{{\partial g_{\infty }^{s} }}{{\partial \sigma_{2} }} = 0,\frac{{\partial g_{\infty }^{s} }}{{\partial \sigma_{3} }} = - N_{{\psi_{\infty } }}$$

(I.21)

Substituting Eqs. (I.14) and (I.21) into Eq. (I.19), shear yielding takes the following form:

$$\begin{gathered} \sigma_{1}^{N} = \hat{\sigma }_{1}^{N} - \lambda_{\infty } \left[ {\alpha_{1} - \alpha_{2} N_{{\psi_{\infty } }} } \right] \hfill \\ \sigma_{2}^{N} = \hat{\sigma }_{2}^{N} - \lambda_{\infty } \left[ {\alpha_{2} - \alpha_{2} N_{{\psi_{\infty } }} } \right] \hfill \\ \sigma_{3}^{N} = \hat{\sigma }_{3}^{N} - \lambda_{\infty } \left[ {\alpha_{2} - \alpha_{1} N_{{\psi_{\infty } }} } \right] \hfill \\ \end{gathered}$$

(I.22)

where:

$$\left\{ {\begin{array}{*{20}l} {\lambda_{\infty } = \frac{{\hat{\sigma }_{1}^{N} - \hat{\sigma }_{3}^{N} N_{{\phi_{\infty } }} + 2c_{\infty } \sqrt {N_{{\phi_{\infty } }} } }}{{2\eta_{2} }}\Updelta t} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\lambda_{\infty } = \frac{{\hat{\sigma }_{1}^{N} - \hat{\sigma }_{3}^{N} N_{{\phi_{\infty } }} + 2c_{\infty } \sqrt {N_{{\phi_{\infty } }} } }}{{2\eta_{2} }}\left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right)} & {J_{2}^{'} > J_{2}^{\text{vp}} } \\ \end{array} } \right.$$

(I.23)

and for tensile yielding:

Partial differentiation of Eq. 25 becomes:

$$\frac{{\partial g_{\infty }^{t} }}{{\partial \sigma_{1} }} = 0,\frac{{\partial g_{\infty }^{t} }}{{\partial \sigma_{2} }} = 0,\frac{{\partial g_{\infty }^{t} }}{{\partial \sigma_{3} }} = - 1$$

(I.24)

Substituting Eqs. (I.14) and (I.24) into Eq. (I.19) gives:

$$\begin{gathered} \sigma_{1}^{N} = \hat{\sigma }_{1}^{N} + \lambda_{\infty } \alpha_{2} \hfill \\ \sigma_{2}^{N} = \hat{\sigma }_{2}^{N} + \lambda_{\infty } \alpha_{2} \hfill \\ \sigma_{3}^{N} = \hat{\sigma }_{3}^{N} + \lambda_{\infty } \alpha_{1} \hfill \\ \end{gathered}$$

(I.25)

where:

$$\left\{ {\begin{array}{*{20}l} {\lambda_{\infty } = \frac{{\sigma_{\infty }^{t} - \hat{\sigma }_{3}^{N} }}{{2\eta_{2} }} \cdot \Updelta t} & {J_{2}^{'} \le J_{2}^{\text{vp}} } \\ {\lambda_{\infty } = \frac{{\sigma_{\infty }^{t} - \hat{\sigma }_{3}^{N} }}{{2\eta_{2} }} \cdot \left( {\Updelta t + t_{\text{un}} \left\langle {\frac{\Updelta t}{{t_{\text{un}} }}} \right\rangle^{n} } \right)} & {J_{2}^{'} > J_{2}^{\text{vp}} } \\ \end{array} } \right.$$

(I.26)

In summary, the stress–strain relationship of the complex nonlinear visco-elastic-plastic creep model can be expressed by using Eqs. (I.8) and (I.10). Visco-plastic correction is used by Eqs. (I.22) and (I.25), assuming that the principal directions have not been affected by the occurrence of plastic flow. The above equations are used to develop the model.