Skip to main content
SpringerLink
Log in

Vibration and Buckling Analysis of Elastically Supported Bi-directional FGM Mindlin Circular Plates Having Variable Thickness

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

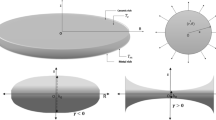
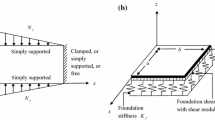
In the present study, the effect of non-linear thickness variation and that of Winkler’s foundation is investigated on radially symmetric vibrations of bi-directional FGM circular plates subjected to uniform in-plane peripheral loading. It is considered that the elastic modulus, as well as density of the FGM, varies in two mutually perpendicular directions (i.e., radial and transverse). This variation follows the power law. However, the variation in thickness of FGM plate varies along the radial direction and follows quadratic variation. Hamilton’s principle is used to obtain the coupled differential equations governing the motion. The approximate solutions of these equations for simply supported and clamped edge conditions are obtained by an elegant numerical technique: the Harmonic differential quadrature method. The effect of density parameter, gradient index, heterogeneity parameter, taper parameters, and thickness parameter of the plate is analyzed on the vibration characteristics for the first two modes of vibration for different values of foundation parameter together with in-plane peripheral loading parameter. Furthermore, critical buckling loads in compression by taking the frequencies zero are evaluated for both plates. The validity of the current approach is established by comparing the frequency parameter with true values and with the results of other authors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

References

  1. Miyamoto Y, Kaysser WA, Rabin BH, Kawasaki A, Ford RG (1999) Functionally graded materials: design, processing and applications. Kluwer Academic, Dordrecht

    Book  Google Scholar 

  2. Pompe W, Worch H, Epple M, Friess W, Gelinsky M, Greil P et al (2003) Functionally graded materials for biomedical applications. Mater Sci Eng A 362:40–60. https://doi.org/10.1016/S0921-5093(03)00580-X

    Article  CAS  Google Scholar 

  3. Asemi K, Babaei M, Kiarasi F (2022) Static, natural frequency and dynamic analyses of functionally graded porous annular sector plates reinforced by graphene platelets. Mech Based Des Struct Mach 50:3853–3881. https://doi.org/10.1080/15397734.2020.1822865

    Article  Google Scholar 

  4. Arshid E, Khorasani M, Soleimani-Javid Z, Amir S, Tounsi A (2021) Porosity-dependent vibration analysis of FG microplates embedded by polymeric nanocomposite patches considering hygrothermal effect via an innovative plate theory. Eng Comput. https://doi.org/10.1007/s00366-021-01382-y

    Article  Google Scholar 

  5. Yüksel YZ, Akbaş D (2021) Hygrothermal stress analysis of laminated composite porous plates. Struct Eng Mech 80:1–13. https://doi.org/10.12989/sem.2021.80.1.001

  6. Babaei M, Hajmohammad MH, Asemi K (2020) Natural frequency and dynamic analyses of functionally graded saturated porous annular sector plate and cylindrical panel based on 3D elasticity. Aerosp Sci Technol 96:105524. https://doi.org/10.1016/j.ast.2019.105524

  7. Thai H, Kim S (2015) A review of theories for the modeling and analysis of functionally graded plates and shells. Compos Struct 128:70–86. https://doi.org/10.1016/j.compstruct.2015.03.010

    Article  Google Scholar 

  8. Efraim E (2011) Accurate formula for determination of natural frequencies of FGM plates basing on frequencies of isotropic plates. Proc Eng 10:242–247. https://doi.org/10.1016/j.proeng.2011.04.043

    Article  Google Scholar 

  9. Irie T, Yamada G, Aomura S (1979) Free vibration of a Mindlin annular plate of varying thickness. J Sound Vib 66:187–197. https://doi.org/10.1016/0022-460X(79)90665-5

    Article  ADS  Google Scholar 

  10. Batra RC, Aimmanee S (2005) Vibrations of thick isotropic plates with higher order shear and normal deformable Plate theories. Comput Struct 83:934–955. https://doi.org/10.1016/j.compstruc.2004.11.023

    Article  Google Scholar 

  11. Mindlin RD (1951) Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J Appl Mech 18:31–38. https://doi.org/10.1115/1.4010217

    Article  Google Scholar 

  12. Xue K, Wang J, Li Q, Wang W, Wang P (2014) An exact series solution for the vibration of Mindlin rectangular plates with elastically restrained edges. Shock Vib. https://doi.org/10.1155/2014/286710

    Article  Google Scholar 

  13. Chen SS, Xu CJ, Tong GS, Wei X (2015) Free vibration of moderately thick functionally graded plates by a meshless local natural neighbor interpolation method. Eng Anal Bound Elem 61:114–126. https://doi.org/10.1016/j.enganabound.2015.07.008

    Article  MathSciNet  Google Scholar 

  14. Wang Q, Shi D, Liang Q, Shi X (2016) A unified solution for vibration analysis of functionally graded circular, annular and sector plates with general boundary conditions. Compos Part B Eng 88:264–294. https://doi.org/10.1016/j.compositesb.2015.10.043

    Article  Google Scholar 

  15. Ahlawat N, Lal R (2020) Effect of Winkler foundation on radially symmetric vibrations of bi-directional FGM non-uniform Mindlin’s circular plate subjected to in-plane peripheral loading. J Solid Mech 12:455–75. https://doi.org/10.22034/jsm.2019.1873720.1466

  16. Van VP, Dung NT, Tho NC, Van TD, Hoa LK (2021) Modified single variable shear deformation plate theory for free vibration analysis of rectangular FGM plates. Structures 29:1435–1444. https://doi.org/10.1016/j.istruc.2020.12.027

    Article  Google Scholar 

  17. Kumar V, Singh SJ, Saran VH, Harsha SP (2021) Vibration characteristics of porous FGM plate with variable thickness resting on Pasternak’s foundation. Eur J Mech A/Solids 85:104124. https://doi.org/10.1016/j.euromechsol.2020.104124

  18. Zaitoun MW, Chikh A, Tounsi A, Al-Osta MA, Sharif A, Al-Dulaijan SU, et al. (2022) Influence of the visco-Pasternak foundation parameters on the buckling behavior of a sandwich functional graded ceramic–metal plate in a hygrothermal environment. Thin-Walled Struct 170:108549. https://doi.org/10.1016/j.tws.2021.108549

  19. Daikh AA, Bachiri A, Houari MSA, Tounsi A (2022) Size dependent free vibration and buckling of multilayered carbon nanotubes reinforced composite nanoplates in thermal environment. Mech Based Des Struct Mach 50:1371–1399. https://doi.org/10.1080/15397734.2020.1752232

    Article  Google Scholar 

  20. Vinh P Van, Chinh N Van, Tounsi A (2022) Static bending and buckling analysis of bi-directional functionally graded porous plates using an improved first-order shear deformation theory and FEM. Eur J Mech/A Solids 96:104743. https://doi.org/10.1016/j.euromechsol.2022.104743

  21. Karami B, Janghorban M, Tounsi A (2019) Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Eng Comput 35:1297–1316. https://doi.org/10.1007/s00366-018-0664-9

    Article  Google Scholar 

  22. Fahsi B, Bouiadjra RB, Mahmoudi A, Benyoucef S, Tounsi A (2019) Assessing the effects of porosity on the bending, buckling, and vibrations of functionally graded beams resting on an elastic foundation by using a new refined quasi-3D theory. Mech Compos Mater 55:219–230. https://doi.org/10.1007/s11029-019-09805-0

    Article  ADS  Google Scholar 

  23. Xiang Y, Wei GW (2004) Exact solutions for buckling and vibration of stepped rectangular Mindlin plates. Int J Solids Struct 41:279–294. https://doi.org/10.1016/j.ijsolstr.2003.09.007

    Article  Google Scholar 

  24. Naderi A, Saidi AR (2011) An analytical solution for buckling of moderately thick functionally graded sector and annular sector plates. Arch Appl Mech 81:809–828. https://doi.org/10.1007/s00419-010-0451-6

    Article  Google Scholar 

  25. Ansari R, Gholami R, Faghih Shojaei M, Mohammadi V, Darabi MA (2013) Thermal buckling analysis of a Mindlin rectangular FGM microplate based on the strain gradient theory. J Therm Stress 36:446–465. https://doi.org/10.1080/01495739.2013.770657

    Article  Google Scholar 

  26. Zhang LW, Lei ZX, Liew KM (2015) Buckling analysis of FG-CNT reinforced composite thick skew plates using an element-free approach. Compos Part B Eng 75:36–46. https://doi.org/10.1016/j.compositesb.2015.01.033

    Article  CAS  Google Scholar 

  27. Hosseini-Hashemi S, Rokni Damavandi Taher H, Akhavan H (2010) Vibration analysis of radially FGM sectorial plates of variable thickness on elastic foundations. Compos Struct 92:1734–43. https://doi.org/10.1016/j.compstruct.2009.12.016

  28. Hosseini-Hashemi S, Derakhshani M, Fadaee M (2013) An accurate mathematical study on the free vibration of stepped thickness circular/annular Mindlin functionally graded plates. Appl Math Model 37:4147–4164. https://doi.org/10.1016/j.apm.2012.08.002

    Article  MathSciNet  Google Scholar 

  29. Zhang LW, Lei ZX, Liew KM (2015) Computation of vibration solution for functionally graded carbon nanotube-reinforced composite thick plates resting on elastic foundations using the element-free IMLS-Ritz method. Appl Math Comput 256:488–504. https://doi.org/10.1016/j.amc.2015.01.066

    Article  MathSciNet  Google Scholar 

  30. Saini R, Pradyumna S (2022) Effect of thermal environment on the asymmetric vibration of temperature-dependent two-dimensional functionally graded annular plate by Chebyshev polynomials. J Therm Stress 45:740–761. https://doi.org/10.1080/01495739.2022.2090472

    Article  Google Scholar 

  31. Saini R, Lal R (2022) Axisymmetric vibrations of temperature-dependent functionally graded moderately thick circular plates with two-dimensional material and temperature distribution. Eng Comput 38:437–452. https://doi.org/10.1007/s00366-020-01056-1

    Article  Google Scholar 

  32. Saini R, Lal R (2021) Effect of thermal environment and peripheral loading on axisymmetric vibrations of non-uniform FG circular plates via generalized differential quadrature method. J Vib Eng Technol 9:873–886. https://doi.org/10.1007/s42417-020-00270-x

    Article  Google Scholar 

  33. Allahyari E, Asgari M (2019) Effect of magnetic-thermal field on nonlinear wave propagation of circular nanoplates. J Electromagn Waves Appl 33:2296–2316. https://doi.org/10.1080/09205071.2019.1677271

    Article  Google Scholar 

  34. Allahyari E, Fadaee M (2015) Analytical investigation on free vibration of circular double-layer graphene sheets including geometrical defect and surface effects. Compos Part B Eng 85:259–267. https://doi.org/10.1016/j.compositesb.2015.09.036

    Article  CAS  Google Scholar 

  35. Allahyari E, Asgari M, Pellicano F (2019) Nonlinear strain gradient analysis of nanoplates embedded in an elastic medium incorporating surface stress effects. Eur Phys J Plus. https://doi.org/10.1140/epjp/i2019-12575-4

  36. Lal R, Saini R (2019) Thermal effect on radially symmetric vibrations of temperature-dependent FGM circular plates with nonlinear thickness variation. Mater Res Express. https://doi.org/10.1088/2053-1591/ab24ee

  37. Lal R, Saini R (2019) On the high-temperature free vibration analysis of elastically supported functionally graded material plates under mechanical in-plane force via GDQR. J Dyn Syst Meas Control 141:101003. https://doi.org/10.1115/1.4043489

  38. Saini R (2022) Thermoelastic vibrations of Functionally graded nonuniform nanobeams. In: Katiyar JK, Panwar V, Ahlawat N (eds). Nanomaterials Advanced Technology. Springer, Singapore, pp 141–71

  39. Saini R, Ahlawat N, Rai P, Khadimallah MA (2022) Thermal stability analysis of functionally graded non-uniform asymmetric circular and annular nano discs: size-dependent regularity and boundary conditions. Eur J Mech A/Solids 94:104607. https://doi.org/10.1016/j.euromechsol.2022.104607.

  40. Surappa MK (2003) Aluminium matrix composites: challenges and opportunities. Sadhana 28:319–334

    Article  CAS  Google Scholar 

  41. Kopeliovich D (2012) Tribological properties of alumina reinforced composites. SubsTech

  42. Striz AG, Wang X, Bert CW (1995) Harmonic differential quadrature method and applications to analysis of structural components. Acta Mech 111:85–94. https://doi.org/10.1007/BF01187729

    Article  Google Scholar 

  43. Irie T, Yamada G, Aomura S (1980) Natural frequencies of Mindlin circular plates. J Appl Mech 47:652–655

    Article  Google Scholar 

  44. Gupta US, Lal R, Sharma S (2007) Vibration of non-homogeneous circular Mindlin plates with variable thickness. J Sound Vib 302:1–17. https://doi.org/10.1016/j.jsv.2006.07.005

    Article  ADS  Google Scholar 

  45. Wang CM, Xiang Y, Kitipornchai S, Liew KM (1993) Axisymmetric buckling of circular Mindlin plates with ring supports. J Struct Eng 119:782–793. https://doi.org/10.1061/(asce)0733-9445(1993)119:3(782)

    Article  Google Scholar 

  46. Rao GV, Raju KK (1986) A study of various effects on the stability of circular plates. Comput Struct 24:39–45

    Article  Google Scholar 

  47. Hong GM, Wang CM, Tan TJ (1993) Analytical buckling solutions for circular Mindlin plates: inclusion of inplane prebuckling deformation. Arch Appl Mech 63:534–542. https://doi.org/10.1007/BF00804755

    Article  Google Scholar 

Download references

Acknowledgements

The authors are thankful for the constructive comments from the reviewers to improve the quality of the article.

Author information

Authors and Affiliations

  1. Department of Mathematics, Jaypee Institute of Information Technology, Noida, India

    Neha Ahlawat

  2. Department of Mathematics (Applied Sciences), School of Engineering and Technology, H N B Garhwal University (A Central University), Srinagar, Uttarakhand, India

    Rahul Saini

Authors
  1. Neha Ahlawat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rahul Saini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rahul Saini.

Ethics declarations

Conflict of interest

The authors declare that they do not have any conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$X = \left[ {\begin{array}{*{20}c} {W_1 } & {W_2 } & {W_3 } & \ldots & {W_m } & {\phi_1 } & {\phi_2 } & {\phi_3 } & \ldots & {\phi_m } \\ \end{array} } \right]^{\prime} , F^C = \left[ {\begin{array}{*{20}c} {A_{ij}^{\left( {11} \right)} } & {A_{ij}^{\left( {12} \right)} } \\ {A_{ij}^{\left( {21} \right)} } & {A_{ij}^{\left( {22} \right)} } \\ {A_{R1} } & {A_{R2} } \\ \end{array} } \right]_{\left( {2m - 2} \right) \times 2m} ,$$
$${\text{where }}A_{ij}^{\left( {11} \right)} = U_{5,i} C_{ij}^{\left( 1 \right)} ,{ }i = 2,{ }3,{ }4,{ } \ldots ,\left( {m - 1} \right),{ }j = 1,{ }2,{ }3, \ldots ,{ }m,$$
$$A_{ij}^{\left( {12} \right)} = \left\{ {\begin{array}{*{20}c} {U_{1,i} C_{ij}^{\left( 2 \right)} + U_{2,i} C_{ij}^{\left( 1 \right)} , if i \ne j,} \\ {U_{1,i} C_{ij}^{\left( 2 \right)} + U_{2,i} C_{ij}^{\left( 1 \right)} + U_{3,i} + k_1 U_{4,i} \lambda^2 , if i = j,} \\ \end{array} i = 2, 3, 4, \ldots ,\left( {m - 1} \right), j = 1, 2, 3, \ldots ,m} \right.,$$
$$A_{ij}^{\left( {21} \right)} = \left\{ {\begin{array}{*{20}c} {V_{1,i} C_{ij}^{\left( 2 \right)} + V_{2,i} C_{ij}^{\left( 1 \right)} , if i \ne j,} \\ {V_{1,i} C_{ij}^{\left( 2 \right)} + V_{2,i} C_{ij}^{\left( 1 \right)} + V_{3,i} \lambda^2 + V_{4,i} , if i = j,} \\ \end{array} i = 2, 3, 4, \ldots ,\left( {m - 1} \right), j = 1, 2, 3, \ldots ,m} \right.,$$
$$A_{ij}^{\left( {22} \right)} = \left\{ {\begin{array}{*{20}c} {V_{5,i} C_{ij}^{\left( 1 \right)} , if i \ne j,} \\ {V_{5,i} C_{ij}^{\left( 1 \right)} + V_{6,i} , if i = j,} \\ \end{array} i = 2, 3, 4, \ldots ,\left( {m - 1} \right), j = 1, 2, 3, \ldots ,m} \right.,$$
$${\text{Regularity conditions }}A_{R1} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & \ldots & 0 & 0 \\ {C_{n1}^{\left( 1 \right)} } & {C_{n2}^{\left( 1 \right)} } & {C_{n3}^{\left( 1 \right)} } & \ldots & {C_{nn}^{\left( 1 \right)} } & {C_{nn}^{\left( 1 \right)} } \\ \end{array} } \right]_{2 \times m} ,{ }A_{R2} = \left[ {\begin{array}{*{20}c} {{ }1} & 0 & 0 & \ldots & 0 \\ {{ }1} & 0 & 0 & \ldots & 0 \\ \end{array} } \right]_{2 \times m} ,$$
$$F^S = \left[ {\begin{array}{*{20}c} { 0} & 0 & 0 & \ldots & 1 & 0 & 0 & 0 & \ldots & 0 & 0 \\ { 0} & 0 & 0 & \ldots & 0 & {C_{n1}^{\left( 1 \right)} } & {C_{n2}^{\left( 1 \right)} } & {C_{n3}^{\left( 1 \right)} } & \ldots & {C_{nn}^{\left( 1 \right)} } & {C_{nn}^{\left( 1 \right)} + \nu } \\ \end{array} } \right]_{2 \times 2m} ,$$
$$F^C = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & \ldots & 1 & 0 & 0 & 0 & \ldots & 0 \\ 0 & 0 & 0 & \ldots & 0 & 0 & 0 & 0 & \ldots & 1 \\ \end{array} } \right]_{2 \times 2m} .$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahlawat, N., Saini, R. Vibration and Buckling Analysis of Elastically Supported Bi-directional FGM Mindlin Circular Plates Having Variable Thickness. J. Vib. Eng. Technol. 12, 513–532 (2024). https://doi.org/10.1007/s42417-023-00856-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-023-00856-1

Keywords

Search

Navigation