Skip to main content
SpringerLink
Log in

Dynamic Analysis of Micro-shock Absorbers

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Objective

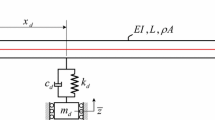
In this paper, the dynamic characteristics of a miniature shock absorber by electrostatic excitation are studied. The 3 degrees of freedom (DOF) nonlinear forced vibration equations were established by Hamiltonian variational principle. The approximate analytical solution of the nonlinear differential equation is calculated. The nonlinear vibration behavior of the shock absorber under primary resonance was investigated.

Methods

The amplitude-frequency response equation and the relational expression of the component system with two dampers (Tuned Mass Damper and Nonlinear Energy Sink passive vibration absorbers) were obtained using the multiscale method.

Results

It is found that the amplitudes of main component and dampers may be in the same or opposite direction by adjusting the parameter values. Furthermore, the energy absorbed by the dampers results in decrease of the main component amplitude magically. Meanwhile, it is also concluded that the increase of the damping ratio and/or mass ratio of the two dampers on the system caused a decrease in the amplitude of the main components.

Conclusions

TMD and/or NES play an important role in the shock absorption system which can kill the amplitude of the main component magically. The vibration amplitude of the main components can be largely decreased by increasing the mass ratio and damping ratio of TMD and NES. The association of external and internal resonances causes the energy of the external excitation moves to the TMD or NES, thus reducing the amplitude of main component. The amplitudes of main component and dampers may be in the same or opposite direction by adjusting the parameter values.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Santo DR, Balthazar JM, Tusset AM, Picciriol V, Brasil R, Silveira M (2018) On nonlinear horizontal dynamics and vibrations control for high-speed elevators. J Vib Control 24:825–838

    Article  MathSciNet  MATH  Google Scholar 

  2. Ezzat MA, El-Bary AA, Morsey MM (2010) Space approach to the hydro-magnetic flow of a dusty fluid through a porous medium. Comput Math Appl 59:2868–2879

    Article  MathSciNet  MATH  Google Scholar 

  3. Lisitano D, Jiffri S, Bonisoli E, Mottershead JE (2018) Experimental feedback linearisation of a vibrating system with a non-smooth nonlinearity. J Sound Vib 416:192–212

    Article  MATH  Google Scholar 

  4. Ezzat MA, El-Bary AA (2016) Effects of variable thermal conductivity on Stokes’ flow of a thermoelectric fluid with fractional order of heat transfer. Int J Therm Sci 100:305–315

    Article  Google Scholar 

  5. Chen J, Dong DW, Shi WZ (2016) Study on vibration isolation design of double layer vibration isolation system with dynamic package of beh system. J Vib Shock 35:211–218

    Google Scholar 

  6. Ezzat MA, El-Karamany AS, El-Bary AA (2017) On dual-phase-lag thermoelasticity theory with memory-dependent derivative. Mech Adv Mater Struct 24(11):908–916

    Article  Google Scholar 

  7. Yang F, Sedaghati R, Esmailzadeh E (2009) Vibration suppression of non-uniform curved beams under random loading using optimal tuned mass damper. J Vib Control 15:233–261

    Article  MathSciNet  Google Scholar 

  8. Yang F, Sedaghati R, Esmailzadeh E (2009) Optimal vibration suppression of Timoshenko beam with tuned mass damper using finite element method. J Vib Acoust 131:837–838

    Article  Google Scholar 

  9. Ezzat MA, El-Karamany AS, El-Bary AA, Fayik MA (2014) Fractional ultrafast laser-induced magneto thermoelastic behavior in perfect conducting metal films. J Electromagn Waves Appl 28(1):64–82

    Article  Google Scholar 

  10. Cheng Y, Li DY, Li C (2011) Dynamic vibration absorbers for vibration control within a frequency band. J Sound Vib 330:1582–1598

    Article  Google Scholar 

  11. Roberson RE (1952) Synthesis of a non-linear dynamic vibration absorber. J Franklin Inst 254:205–220

    Article  MathSciNet  Google Scholar 

  12. Srinivasa AV (1969) Analysis of parallel damped dynamic vibration absorbers. J Eng Ind Trans ASME 91:282–287

    Article  Google Scholar 

  13. Ture SA, Lamarque C-H, Dimitrijevic Z (2012) Vibratory energy exchange between a linear and a nonsmooth system in the presence of the gravity. Non-linear Dyn 70:1473–1483

    Article  MathSciNet  Google Scholar 

  14. Lamarque C-H, Ture SA, Dimitrijevic Z (2014) Dynamics of a linear system with time-dependent mass and a coupled light mass with non-smooth potential. Meccanica 49:135–145

    Article  MathSciNet  MATH  Google Scholar 

  15. Gendelman OV (2008) Targeted energy transfer in systems with non-polynomial non-linearity. J Sound Vib 315:732–745

    Article  Google Scholar 

  16. Vakakis AF, Gendelman O (2000) Energy pumping in nonlinear mechanical oscillators: Part II—resonance capture. J Appl Mech 68:42–48

    Article  MATH  Google Scholar 

  17. Nucera F, Vakakis AF, McFarland DM, Bergman LA, Kerschen G (2007) Targeted energy transfers in vibro-impact oscillators for seismic mitigation. Nonlinear Dyn 50:651–677

    Article  MATH  Google Scholar 

  18. Gourc E, Michon G, Seguy S, Berlioz A (2015) Targeted energy transfer under harmonic forcing with a vibro-impact nonlinear energy sink: analytical and experimental developments. J Vib Acoust 137:031008

    Article  Google Scholar 

  19. Gendelman OV, Alloni A (2015) Dynamics of forced system with vibro-impact energy sink. J Sound Vib 358:301–314

    Article  Google Scholar 

  20. Ohtori Y, Christenson RE, Spencer BF, Dyke SJ (2004) Benchmark control problems for seismically excited nonlinear buildings. J Eng Mech 130:366–385

    Article  Google Scholar 

  21. Nucera F, LoIacono F, McFarland DM, Bergman LA, Vakakis AF (2008) Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: experimental results. J Sound Vib 313:57–76

    Article  Google Scholar 

  22. Gendelman OV, Vakakis AF, Manevitch LI, McCloskey R (2000) Energy pumping in nonlinear mechanical oscillators I: dynamics of the underlying Hamiltonian system. J Appl Mech 68:34–41

    Article  MathSciNet  MATH  Google Scholar 

  23. Sapsis TP, Vakakis AF, Gendelman OV, Bergman LA, Kerschen G, Quinn DD (2009) Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: Part II, analytical study. J Sound Vib 325:297–320

    Article  Google Scholar 

  24. Kerschen G, Kowtko JJ, McFarland DM, Bergman LA, Vakakis AF (2007) Theoretical and experimental study of multimodal targeted energy transfer in a system of coupled oscillators. Nonlinear Dyn 47:285–309

    Article  MathSciNet  MATH  Google Scholar 

  25. Ezzat MA, El-Bary AA (2014) Two-temperature theory of magneto-thermo-viscoelasticity with fractional derivative and integral orders heat transfer. J Electromagn Waves Appl 28(16):1985–2004

    Article  Google Scholar 

  26. Vakakis AF, Manevitch L, Gendelman O, Bergman L (2003) Dynamics of linear discrete systems connected to local essentially non-linear attachments. J Sound Vib 264:559–577

    Article  Google Scholar 

  27. Vakakis AF, Gendelman O (2001) Energy pumping in nonlinear mechanical oscillators: Part II: resonance capture. J Appl Mech 68:42–48

    Article  MathSciNet  MATH  Google Scholar 

  28. Malhotra PK, Wenk T, Wieland M (2000) Simple procedure for seismic analysis of liquid-storage tanks. Struct Eng Int 10:197–201

    Article  Google Scholar 

  29. Nagurka M, Huang S (2004) A mass-spring-damper model of a bouncing ball. Am Control Conf 1:499–504

    Google Scholar 

  30. Hamamoto K, Fukuda T, Sugie T (2000) Iterative feedback tuning of controllers for a two-mass spring system with friction. Control Eng Pract 11:1061–1068

    Article  Google Scholar 

  31. Nayfeh AH, Mook DT (1979) Nonlinear oscillations. Wiley, New York, pp 365–431

    MATH  Google Scholar 

  32. Gao XM, Jin DP, Chen T (2018) Nonlinear analysis and experimental investigation of a rigid-flexible antenna system. Meccanica 53:33–48

    Article  MathSciNet  MATH  Google Scholar 

  33. Navazi HM, Hojjati M (2017) Nonlinear vibrations and stability analysis of a rotor on high-static-low-dynamic-stiffness supports using method of multiple scales. Aerosp Sci Technol 63:259–265

    Article  Google Scholar 

  34. Krylov S, Dick N (2016) Dynamic stability of electrostatically actuated initially curved shallow micro beams. Continuum Mech Thermodyn 7:445–468

    MathSciNet  MATH  Google Scholar 

  35. Li L, Zhang QC (2017) Nonlinear dynamic analysis of electrically actuated viscoelastic bistable micro-beam system. Nonlinear Dyn 87:587–604

    Article  MATH  Google Scholar 

  36. Ezzat MA, El-Bary AA (2012) MHD free convection flow with fractional heat conduction law. Magnetohydrodynamics 48(4):587–606

    Article  Google Scholar 

  37. Farid M, Levy N, Gendelman OV (2017) Vibration mitigation in partially liquid-filled vessel using passive energy absorbers. J Sound Vib 406:51–73

    Article  Google Scholar 

  38. Tong CH, Zhang XD (2007) Tuning mass damper parameter optimization and its application. J Vib Meas Diagn 2:146–149

    Google Scholar 

Download references

Acknowledgements

The work described in this paper is supported by the scientific research foundation of Yunnan Provincial Department of Education (Grant nos.: 2022J0477 and 2022J0066) and the natural science foundation of Yunnan Provincial Department of science and Technology (Grant no.: 202201AU070227). The authors are grateful for their financial support.

Author information

Authors and Affiliations

  1. School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, 650500, Yunnan, People’s Republic of China

    Chunxia Liu

  2. Yunnan Key Laboratory of Applied Mathematics, School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, 650221, People’s Republic of China

    Chunxia Liu

  3. Faculty of Public Security and Emergency Management, Kunming University of Science and Technology, Kunming, 650500, Yunnan, People’s Republic of China

    Daohang Wang

Authors
  1. Chunxia Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Daohang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daohang Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Wang, D. Dynamic Analysis of Micro-shock Absorbers. J. Vib. Eng. Technol. 11, 3029–3038 (2023). https://doi.org/10.1007/s42417-022-00728-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00728-0

Keywords

Search

Navigation