Skip to main content
SpringerLink
Log in

A Two-Part Analytical Solution for the Shock Response Spectrum with Coulomb Damping

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

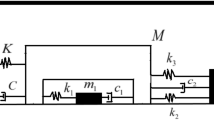
The present work primarily focuses on arriving at an analytical solution for the response of a Coulomb damped harmonic oscillator when subjected to aperiodic excitation.

Methods

The signum function used in modelling the Coulomb friction model is reduced to a first harmonic term. This is carried out by assuming that vibratory motion exists for at least one full cycle, by means of harmonic balance (HB) method. The equation of motion thus reduced is solved to obtain an analytical solution for half-sine, rectangular, and triangular shock inputs. The solution thus obtained is combined with another analytical solution derived by the phase space coordinate averaging method. The total solution is now expressed as a two-part analytical solution, which comprises the response during the action of the input pulse and after the pulse ends.

Results

The analytical results are compared with numerical ones to establish validity and accuracy. A comparison is also made with the experimental readings, and a reasonably good agreement is observed for the response of the oscillator with Coulomb damping. The study is extended further to plot the shock response spectrum (SRS) for the three shock inputs over a wide range of damping values (\(\alpha \)) and frequency ratios (\(\Omega \)). The \(1/2\Omega \) range over which the \(n^\textrm{th}\) peak of the system response is dispersed in the SRS increases with a corresponding increase in \(\alpha \).

Conclusion

The two-part analytical solution proposed here predicts the SRS for the first dominant peak in the vibratory response to a good degree of accuracy and is quantified by directly comparing it with experiment(s).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Den Hartog JP (1985) Mechanical vibrations. Courier Corporation

  2. Craig Jr, RR, Kurdila AJ (2006) Fundamentals of structural dynamics. Wiley

  3. Rao SS (2001) Mechanical vibrations

  4. Meirovitch L (2010) Fundamentals of vibrations. Waveland Press

  5. De Silva CW (2005) Vibration and shock handbook. CRC Press

  6. Parfitt G, Snowdon J (1962) Incidence and prevention of damage due to mechanical shock. J Acoust Soc Am 34(4):462–468

    Article  Google Scholar 

  7. Tsai TY, Yeh CL, Lai YS, Chen RS (2007) Response spectra analysis for undamped structural systems subjected to half-sine impact acceleration pulses. Microelectron Reliab 47(8):1239–1245

    Article  Google Scholar 

  8. Shu D, Shi B, Meng H, Yap F, Jiang D, Ng Q, Zambri R, Lau J (2006) The pulse width effect of single half-sine acceleration pulse on the peak response of an actuator arm of hard disk drive. Mater Sci Eng A 423(1–2):199–203

    Article  Google Scholar 

  9. Shu DW, Shi BJ, Meng H, Yap FF, Jiang DZ, Ng Q, Zambri R, Lau JH, Cheng CS (2007) Shock analysis of a head actuator assembly subjected to half-sine acceleration pulses. Int J Impact Eng 34(2):253–263

    Article  Google Scholar 

  10. Jayaraman S, Trikha M, Kamesh D, Ravindra M et al (2016) Response spectrum analysis of printed circuit boards subjected to shock loads. Procedia Eng 144:1469–1476

    Article  Google Scholar 

  11. Alexander JE (2009) Shock response spectrum—a primer. Sound Vib 43(6):6–15

    Google Scholar 

  12. Makris N, Chang SP (2000) Response of damped oscillators to cycloidal pulses. J Eng Mech 126(2):123–131

    Article  Google Scholar 

  13. Narkhede DI, Sinha R (2017) Influence of shock impulse characteristics on vibration control using nonlinear fluid viscous dampers. J Vib Control 23(9):1463–1479

    Article  MathSciNet  Google Scholar 

  14. Chopra AK (2007) Dynamics of structures. Pearson Education India

  15. Harris CM (2010) Shock and vibration handbook

  16. de Benedetti M, Garofalo G, Zumpano M, Barboni R (2007) On the damping effect due to bolted junctions in space structures subjected to pyro-shock. Acta Astronaut 60(12):947–956

    Article  Google Scholar 

  17. Hundal M (1982) Passive pneumatic shock isolator: analysis and design. J Sound Vib 84(1):1–9

    Article  Google Scholar 

  18. Johnson CD, Wilke PS, Pendleton SC (2006) In Proceedings of the 38th aerospace mechanisms symposium, Langley Research Center, pp 89–102

  19. Tapia-González PE, Ledezma-Ramírez DF (2017) Experimental characterisation of dry friction isolators for shock and vibration. J Low Freq Noise Vib Active Control 36(1):83–95

    Article  Google Scholar 

  20. Shekhar NC, Hatwal H, Mallik A (1999) Performance of non-linear isolators and absorbers to shock excitations. J Sound Vib 227(2):293–307

    Article  Google Scholar 

  21. Ledezma-Ramirez D, Ferguson N, Brennan M (2011) Shock isolation using an isolator with switchable stiffness. J Sound Vib 330(5):868–882

    Article  Google Scholar 

  22. Ismail MI, Ferguson NS et al (2017) Passive shock isolation utilising dry friction. Shock Vib

  23. Ismail MI, Ferguson N (2019) A friction control strategy for shock isolation. Int J Mech Eng Appl 7(3):78–90

    Google Scholar 

  24. Mercer C, Rees P (1971) An optimum shock isolator. J Sound Vib 18(4):511–520

    Article  Google Scholar 

  25. Hartog JD (1930) Lxxiii. forced vibrations with combined viscous and coulomb damping. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 9(59), 801–817

  26. Ferri A (1995) Friction damping and isolation systems

  27. Hundal M (1979) Response of a base excited system with coulomb and viscous friction. J Sound Vib 64(3):371–378

    Article  Google Scholar 

  28. Shaw S (1986) On the dynamic response of a system with dry friction. J Sound Vib 108(2):305–325

    Article  MathSciNet  Google Scholar 

  29. Anderson J, Ferri A (1990) Behavior of a single-degree-of-freedom system with a generalized friction law. J Sound Vib 140(2):287–304

    Article  Google Scholar 

  30. Lopez I, Busturia J, Nijmeijer H (2004) Energy dissipation of a friction damper. J Sound Vib 278(3):539–561

    Article  Google Scholar 

  31. Andersson S, Söderberg A, Björklund S (2007) Friction models for sliding dry, boundary and mixed lubricated contacts. Tribol Int 40(4):580–587

    Article  Google Scholar 

  32. Stein GJ, Zahoranskỳ R, Múčka P (2008) On dry friction modelling and simulation in kinematically excited oscillatory systems. J Sound Vib 311(1–2):74–96

    Article  Google Scholar 

  33. Berger E (2002) Friction modeling for dynamic system simulation. Appl Mech Rev 55(6):535–577

    Article  Google Scholar 

  34. Karthik B, Shreesha RB, Shrikanth, V, Gaonkar, AK, Naveen M (2023) Krylov–bogolyubov averaging method-based analytical solution of an unforced nonlinear coulomb damped oscillator. J Vib Eng Technol 1–12

  35. Sawant KR, Shrikanth V (2021) Energy dissipation and behavioral regimes in an autonomous double pendulum subjected to viscous and dry friction damping. Eur J Phys 42(5):055008

Download references

Acknowledgements

The authors would like to thank Prof. Amar K. Gaonkar, Department of Mechanical, Materials and Aerospace Engineering, Indian Institute of Technology Dharwad, for his valuable input. The authors would like to thank Science and Engineering Research Board (SERB) for partially funding this work.

Author information

Authors and Affiliations

  1. Department of Mechanical, Materials and Aerospace Engineering, Indian Institute of Technology Dharwad, Dharwad, Karnataka, 580011, India

    Pramod Kumar Verma & Venkoba Shrikanth

Authors
  1. Pramod Kumar Verma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Venkoba Shrikanth
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pramod Kumar Verma.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Verma, P.K., Shrikanth, V. A Two-Part Analytical Solution for the Shock Response Spectrum with Coulomb Damping. J. Vib. Eng. Technol. (2024). https://doi.org/10.1007/s42417-024-01307-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42417-024-01307-1

Keywords

Search

Navigation