Nonlinear dynamic analysis of electrically actuated viscoelastic bistable microbeam system

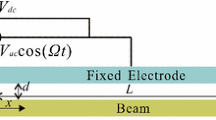
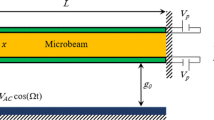
Abstract

Viscoelastic phenomena widely exist in MEMS materials, which may have certain effects on transition mechanism of nonlinear jumping phenomena and transient chaotic behaviors. This article aims to theoretically investigate the static and dynamic characteristics of electrically actuated viscoelastic bistable microbeam via a low-dimensional model. An improved single-degree-of-freedom model to describe microbeam-based resonators is obtained by using Fractional Kelvin constitutive model, Hamilton’s principle and Galerkin method. Through static bifurcation analysis, three kinds of parameter conditions of the bistable system are obtained, and potential energy function of the Hamiltonian system is theoretically derived. The influence of fractional viscoelasticity on dynamic pull-in phenomena is distinguished from the viewpoint of energy. Then, the method of multiple scales is applied to determine the response and stability of the system for small vibration amplitude and AC voltage. The influence of fractional viscoelasticity on amplitude, frequency and bifurcation behavior is investigated. Results show that compared with the elastic material, nonlinear phenomenon becomes weak, resonance frequency increases and amplitude decreases in the viscoelastic system. Besides, the numerical discretization method of fractional derivative is given to verify theoretical results. To study the influence of fractional viscoelasticity on complicated vibration, Melnikov method is applied to predict the existence of chaos, and numerical simulation is carried out to find the stable regions, chaotic regions and dynamic pull-in regions by using bifurcation diagrams with local maximum method. Rational increase in material modulus ratio parameter and fractional order is effective to reduce the possibility of chaos and dynamic pull-in. This analysis has the potential of developing parameter design in MEMS.

Appendix

$$\begin{aligned}&\chi = 1-2x_e^2 \int _0^1 {\phi ^{4}\hbox {d}x} +x_e^4 \int _0^1 {\phi ^{6}\hbox {d}x} \end{aligned}$$

(56)

$$\begin{aligned}&a_m = \frac{-4x_e \int _0^1 {\phi ^{4}\hbox {d}x} +4x_e^3 \int _0^1 {\phi ^{6}\hbox {d}x} }{\chi } \end{aligned}$$

(57)

$$\begin{aligned}&a_n =\frac{-2\int _0^1 {\phi ^{4}\hbox {d}x} +6x_e^2 \int _0^1 {\phi ^{6}\hbox {d}x} }{\chi } \end{aligned}$$

(58)

$$\begin{aligned}&\omega _n^2 =\frac{\omega ^{2}-4\alpha _2 V_\mathrm{dc}^2 -6\omega ^{2}x_e^2 \int _0^1 {\phi ^{4}\hbox {d}x} -3\alpha _1 x_e^2 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi \hbox {d}x} +5x_e^4 \omega ^{2}\int _0^1 {\phi ^{6}\hbox {d}x} }{\chi } \nonumber \\&\quad \qquad \frac{+10\alpha _1 x_e^4 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} -7\alpha _1 x_e^6 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} }{\chi } \end{aligned}$$

(59)

$$\begin{aligned}&a_q =\frac{-6\omega ^{2}x_e \int _0^1 {\phi ^{4}\hbox {d}x} -3\alpha _1 x_e \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi \hbox {d}x} +10x_e^3 \omega ^{2}\int _0^1 {\phi ^{6}\hbox {d}x} }{\chi } \nonumber \\&\qquad \quad \frac{+20\alpha _1 x_e^3 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} -21\alpha _1 x_e^5 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} }{\chi } \end{aligned}$$

(60)

$$\begin{aligned}&a_c =\frac{-2\omega ^{2}\int _0^1 {\phi ^{4}\hbox {d}x} -\alpha _1 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi \hbox {d}x} +10x_e^2 \omega ^{2}\int _0^1 {\phi ^{6}\hbox {d}x} }{\chi } \nonumber \\&\qquad \quad \frac{+20\alpha _1 x_e^2 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} -35\alpha _1 x_e^4 \Gamma (\phi ,\phi )\int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} }{\chi } \end{aligned}$$

(61)

$$\begin{aligned}&a_p =\frac{-\alpha _1 \Gamma (\phi ,\phi ){\bar{{\eta }}}(2x_e^2 \int _0^1 {{\phi }''\phi \hbox {d}x} -4x_e^4 \int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} +2x_e^6 \int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} )}{\chi } \nonumber \\&\qquad \quad \frac{+\omega ^{2}{\bar{{\eta }}}(1-2x_e^2 \int _0^1 {\phi ^{4}\hbox {d}x} +x_e^4 \int _0^1 {\phi ^{6}\hbox {d}x} )}{\chi } \end{aligned}$$

(62)

$$\begin{aligned}&a_r =\frac{-2x_e \alpha _1 \Gamma (\phi ,\phi ){\bar{{\eta }}}(\int _0^1 {{\phi }''\phi \hbox {d}x} -6x_e^2 \int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} +5x_e^4 \int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} )}{\chi } \nonumber \\&\qquad \quad \frac{-4x_e \omega ^{2}{\bar{{\eta }}}\int _0^1 {\phi ^{4}\hbox {d}x} +4x_e^3 \omega ^{2}{\bar{{\eta }}}\int _0^1 {\phi ^{6}\hbox {d}x} }{\chi } \end{aligned}$$

(63)

$$\begin{aligned}&a_e =\frac{\omega ^{2}{\bar{{\eta }}}(-2\int _0^1 {\phi ^{4}\hbox {d}x} +6x_e^2 \int _0^1 {\phi ^{6}\hbox {d}x} )-2x_e \alpha _1 \Gamma (\phi ,\phi ){\bar{{\eta }}}(-6x_e \int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} +10x_e^3 \int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} )}{\chi } \end{aligned}$$

(64)

$$\begin{aligned}&a_h =\frac{-\alpha _1 \Gamma (\phi ,\phi ){\bar{{\eta }}}(x_e \int _0^1 {{\phi }''\phi \hbox {d}x} -2x_e^3 \int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} +x_e^5 \int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} )}{\chi } \end{aligned}$$

(65)

$$\begin{aligned}&a_s =\frac{-\alpha _1 \Gamma (\phi ,\phi ){\bar{{\eta }}}(\int _0^1 {{\phi }''\phi \hbox {d}x} -6x_e^2 \int _0^1 {{\phi }''\phi ^{3}\hbox {d}x} +5x_e^4 \int _0^1 {{\phi }''\phi ^{5}\hbox {d}x} )}{\chi } \end{aligned}$$

(66)

$$\begin{aligned}&f=\frac{2\alpha _2 V_\mathrm{dc} V_\mathrm{ac} (\int _0^1 {\phi \hbox {d}x} +2x_e +x_e^2 \int _0^1 {\phi ^{3}\hbox {d}x} )}{\chi } \end{aligned}$$

(67)