Skip to main content
SpringerLink
Log in

Nonlinear Dynamic Response of a Thin Rectangular Plate Vibration System Excited by a Non-ideal Induction Motor

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

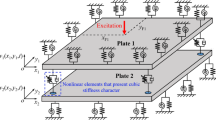
The Sommerfeld effect describes a non-linear jump phenomenon caused by non-ideal sources in a vibration system. The Sommerfeld effect and stability of a thin rectangular plate vibration system excited by a non-ideal induction motor are investigated in this study using an analytical method that combines the average perturbation method and the semi-inverse method.

Methods

The Hamilton principle is applied to construct a non-ideal electromechanical coupling dynamic model. The continuous system model is discretized using the assumed mode method and simplified without taking into account minor cross terms. The exact form of the mode shape function and the transcendental frequency equation of the thin rectangular plate are derived by the semi-inverse method. The system’s steady-state response is achieved by omitting the impact of the motor speed ripple. Meanwhile, the stability of the average speed solution is analyzed with the average perturbation method.

Results

The analytical results are compared to the MATLAB/Simulink simulation results to verify that the proposed method is feasible. Furthermore, the impacts of eccentric masses and motor powers on the dynamic characteristics and stability of the non-ideal vibration system are explored. The results indicate that the speed capture and release may occur around the resonance region. The eccentric masses and motor powers have an impact on the output torque and electromagnetic torque, respectively, which further affects the system’s nonlinear dynamic response.

Conclusion

This paper can serve as a resource for determining the motor power in a vibration system supported by an elastic plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Availability of Data and Materials

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Djanan AAN, Nbendjo BRN (2018) Effect of two moving non-ideal sources on the dynamic of a rectangular plate. Nonlinear Dyn 92:645–657. https://doi.org/10.1007/s11071-018-4080-x

    Article  Google Scholar 

  2. Jiang J, Kong XX, Chen CZ, Zhang ZG (2021) Dynamic and stability analysis of a cantilever beam system excited by a non-ideal induction motor. Meccanica 56:1675–1691. https://doi.org/10.1007/s11012-021-01333-3

    Article  MathSciNet  Google Scholar 

  3. Bharti SK, Bisoi A, Sinha A, Samantaray AK, Bhattacharyya R (2019) Sommerfeld effect at forward and backward critical speeds in a rigid rotor shaft system with anisotropic supports. J Sound Vib 442:330–349. https://doi.org/10.1016/j.jsv.2018.11.002

    Article  Google Scholar 

  4. Samantaray AK, Dasgupta SS, Bhattacharyya R (2010) Sommerfeld effect in rotationally symmetric planar dynamical systems. Int J Eng Sci 48:21–36. https://doi.org/10.1016/j.ijengsci.2009.06.005

    Article  Google Scholar 

  5. Felix JLP, Balthazar JM (2009) Comments on a nonlinear and nonideal electromechanical damping vibration absorber, Sommerfeld effect and energy transfer. Nonlinear Dyn 55:1–11. https://doi.org/10.1007/s11071-008-9340-8

    Article  MATH  Google Scholar 

  6. Kovriguine DA (2012) Synchronization and Sommerfeld effect as typical resonant patterns. Arch Appl Mech 82:591–604. https://doi.org/10.1007/s00419-011-0574-4

    Article  MATH  Google Scholar 

  7. Munteanu L, Brisan C, Chiroiu V, Dumitriu D, Ioan R (2014) Chaos-hyperchaos transition in a class of models governed by Sommerfeld effect. Nonlinear Dyn 78:1877–1889. https://doi.org/10.1007/s11071-014-1575-y

    Article  MathSciNet  Google Scholar 

  8. Goncalves PJP, Silvera M, Pontes BR (2014) Numerical and experimental investigation of a vibration system with non-ideal vibration source. In: 9th international conference on structural dynamics. Porto, Portugal, pp 2113–2117

  9. Bisoi A, Samantaray AK, Bhattacharyya R (2017) Sommerfeld effect in a gyroscopic overhung rotor-disk system. Nonlinear Dyn 88:1565–1585. https://doi.org/10.1007/s11071-017-3329-0

    Article  Google Scholar 

  10. Mahmoudi A, Hosseini S, Zamanian M (2018) Nonstationary analysis of nonlinear rotating shafts passing through critical speed excited by a nonideal energy source. P I Mech Eng C-J Mec 232:572–584. https://doi.org/10.1177/0954406216684364

    Article  Google Scholar 

  11. Balthazar JM, Tusset AM, Brasil RMLRF, Felix JLP, Rocha RT, Janzen FC, Nabarrete A, Oliveira C (2018) An overview on the appearance of the Sommerfeld effect and saturation phenomenon in non-ideal vibrating systems (NIS) in macro and MEMS scales. Nonlinear Dyn 93:19–40. https://doi.org/10.1007/s11071-018-4126-0

    Article  Google Scholar 

  12. Bisoi A, Samantaray AK, Bhattacharyya R (2018) Sommerfeld effect in a two-disk rotor dynamic system at various unbalance conditions. Meccanica 53:681–701. https://doi.org/10.1007/s11012-017-0757-3

    Article  MathSciNet  MATH  Google Scholar 

  13. Dantas MJH, Sampaio R, Lima R (2018) Sommerfeld effect in a constrained electromechanical system. Comput Appl Math 37:1894–1912. https://doi.org/10.1007/s40314-017-0428-y

    Article  MathSciNet  MATH  Google Scholar 

  14. Sinha A, Bharti SK, Samantaray AK, Chakraborty G, Bhattacharyya R (2018) Sommerfeld effect in an oscillator with a reciprocating mass. Nonlinear Dyn 93:1719–1739. https://doi.org/10.1007/s11071-018-4287-x

    Article  Google Scholar 

  15. Jha AK, Dasgupta SS (2019) Attenuation of Sommerfeld effect in an internally damped eccentric shaft-disk system via active magnetic bearings. Meccanica 54:311–320. https://doi.org/10.1007/s11012-018-00936-7

    Article  MathSciNet  Google Scholar 

  16. Varanis M, Balthazar JM, Silva A, Mereles AG, Pederiva R (2019) Remarks on the Sommerfeld effect characterization in the wavelet domain. J Vib Control 25:98–108. https://doi.org/10.1177/1077546318771804

    Article  MathSciNet  Google Scholar 

  17. Bharti SK, Sinha A, Samantaray AK, Bhattacharyya R (2020) The Sommerfeld effect of second kind: passage through parametric instability in a rotor with non-circular shaft and anisotropic flexible supports. Nonlinear Dyn 100:3171–3197. https://doi.org/10.1007/s11071-020-05681-9

    Article  Google Scholar 

  18. Kong XX, Jiang J, Zhou C, Xu Q, Chen CZ (2020) Sommerfeld effect and synchronization analysis in a simply supported beam system excited by two non-ideal induction motors. Nonlinear Dyn 100:2047–2070. https://doi.org/10.1007/s11071-020-05626-2

    Article  Google Scholar 

  19. Zhang XL, Li ZM, Li M, Wen BC (2021) Stability and sommerfeld effect of a vibrating system with two vibrators driven separately by induction motors. Ieee-Asme T Mech 26:807–817. https://doi.org/10.1109/TMECH.2020.3003029

    Article  Google Scholar 

  20. Bharti SK, Samantaray AK (2021) Resonant capture and Sommerfeld effect due to torsional vibrations in a double Cardan joint driveline. Commun Nonlinear Sci 97:105728. https://doi.org/10.1016/j.cnsns.2021.105728

    Article  MathSciNet  MATH  Google Scholar 

  21. Ling WW, Wu PX (2021) A fractal variational theory of the Broer-Kaup system in shallow water waves. Therm Sci 25:2051–2056. https://doi.org/10.2298/TSCI180510087L

    Article  Google Scholar 

  22. Wang KJ (2021) Generalized variational principle and periodic wave solution to the modified equal width-Burgers equation in nonlinear dispersion media. Phys Lett A 419:127723. https://doi.org/10.1016/j.physleta.2021.127723

    Article  MathSciNet  MATH  Google Scholar 

  23. Wang KJ, Wang GD (2021) Study on the nonlinear vibration of embedded carbon nanotube via the Hamiltonian-based method. J Low Freq Noise V A. https://doi.org/10.1177/14613484211032757

    Article  Google Scholar 

  24. Romakina OM (2010) On the steady transverse vibrations of a rectangular orthotropic plate. Izv Sarat Univ Math Mech Inf 10:71–77. https://doi.org/10.18500/1816-9791-2010-10-1-71-77

    Article  Google Scholar 

  25. Fitzgerald AE, Kingsley C, Umans SD (2003) Electric machinery. McGraw-Hill, New York

    Google Scholar 

  26. Han Q, Qin Z, Lu W, Chu F (2015) Dynamic stability analysis of periodic axial loaded cylindrical shell with time-dependent rotating speeds. Nonlinear Dyn 81:1649–1664. https://doi.org/10.1007/s11071-015-2097-y

    Article  MathSciNet  Google Scholar 

  27. Amabili M, Balasubramanian P, Ferrari G (2021) Nonlinear vibrations and damping of fractional viscoelastic rectangular plates. Nonlinear Dyn 103:3581–3609. https://doi.org/10.1007/s11071-020-05892-0

    Article  Google Scholar 

  28. Xing YF, Liu B (2015) Exact solutions of free vibrations of plates and shells. Science Press, Beijing

    Google Scholar 

Download references

Funding

This study was funded by National Natural Science Foundation of China (Grant No. 51705337), China Postdoctoral Science Foundation (Grant No. 2017M611258), and Natural Science Foundation of Liaoning Province (Grant No. 2019MS245 and LJGD2020011).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Shenyang University of Technology, Shenyang, 110870, China

    Wenjie Li, Xiangxi Kong, Qi Xu, Chong Zhou & Ziyu Hao

Authors
  1. Wenjie Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiangxi Kong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qi Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ziyu Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by WL, XK, QX, CZ and ZH. The first draft of the manuscript was written by WL, and all the authors commented on previous versions of the manuscript. All the authors read and approved the final manuscript.

Corresponding author

Correspondence to Xiangxi Kong.

Ethics declarations

Conflict of Interest

All the contributing authors have read and consented to the submission of the manuscript in its present form. The authors also declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary file1 (RAR 55640 KB)

Appendix A

Appendix A

The corresponding expressions of Eq. (21)

The differential equation for free vibration of thin plate:

$$D\nabla^{4} w + \rho h\ddot{w} = 0.$$
(A.1)

The form of any order principal vibration is

$$w = \left( {A_{1} \cos (\omega t) + A_{2} \sin (\omega t)} \right)\Phi (x,y).$$
(A.2)

Substituting Eq. (A.2) into Eq. (A.1) and eliminating the time function, we can obtain the eigenvalues equation as follows:

$$\nabla^{4} \Phi (x,y) - \frac{{\omega^{2} \rho h\Phi (x,y)}}{D} = 0$$
(A.3)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, W., Kong, X., Xu, Q. et al. Nonlinear Dynamic Response of a Thin Rectangular Plate Vibration System Excited by a Non-ideal Induction Motor. J. Vib. Eng. Technol. 11, 1211–1227 (2023). https://doi.org/10.1007/s42417-022-00637-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00637-2

Keywords

Search

Navigation