Skip to main content
SpringerLink
Log in

Stability Study of a Sandwich Beam with Asymmetric and Non-uniform Configuration Supported Viscoelastically Under Variable Temperature Grade

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Background

The end conditions, temperature gradient and geometric parameters affect the system stability.

Purpose

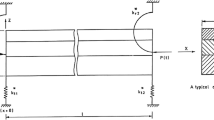
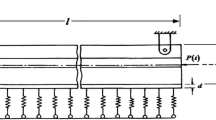
This research work concerns with the parametric instability study of a non-uniform asymmetric sandwich beam supported viscoelastically at the ends acted upon by a harmonic axial load and a variable temperature grade which is more appropriate along with a constant temperature grade.

Methods

Hamilton’s energy principle is used to develop the equations of motion and associated end conditions. Then the non-dimensional form of the equation of motion is obtained. Galerkin’s process is used to find a set of Hill’s equations. The parametric instability regions are acquired by means of Saito-Otomi conditions.

Results

The consequences of taper parameter, uniform as well as variable temperature grade, shear parameter, spring parameters and spring loss factors on the instability regions are examined and represented by a number of plots.

Conclusion

The results reveal that rise in the values of thermal gradient for bottom layer and shear parameter, make the beam more stable against harmonic load. Increase in the values of taper parameters and thermal gradient for top layer reduce the flexural rigidity of the system, hence worsen the system stability. The dynamic instability of the system reduces with increase in the values of spring loss factors and spring parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Abbreviations

B :

Beam width

\(l\) :

Beam length

\(E_{i} \;\;\left( {i = 1,2,3} \right)\) :

Young’s Module, i = 1 for upper layer

\(A_{i} \;\;\left( {i = 1,2,3} \right)\) :

i = 3 for bottom layer, cross sectional area

\({{G_{2} } \mathord{\left/ {\vphantom {{G_{2} } {E_{i} \;\;\left( {i = 1,3} \right)}}} \right. \kern-0pt} {E_{i} \;\;\left( {i = 1,3} \right)}}\) :

The ratio of shear modulus of the core to the modulus of elasticity of the elastic layer

\(\gamma_{2}\) :

Core shear strain

\(2h_{i} \;\;\left( {i = 1,2,3} \right)\) :

Depth of the \(i\text{th}\) layer

\(h_{31}\) :

\({{\left( {h_{3} } \right)_{0} } \mathord{\left/ {\vphantom {{\left( {h_{3} } \right)_{0} } {\left( {h_{1} } \right)}}} \right. \kern-0pt} {\left( {h_{1} } \right)}}_{0}\)

\(h_{21}\) :

\({{\left( {h_{2} } \right)_{0} } \mathord{\left/ {\vphantom {{\left( {h_{2} } \right)_{0} } {\left( {h_{1} } \right)}}} \right. \kern-0pt} {\left( {h_{1} } \right)}}_{0}\)

\(g^{*}\) :

\(g\left( { 1\, + \,j\eta } \right)\), shear parameter in complex form

\(g\) :

Shear parameter

\(I_{i} \;\;\left( {i = 1,2,3} \right)\) :

Area moment of inertia, \(i = 1\) for upper layer

\(lh_{10}\) :

\({l \mathord{\left/ {\vphantom {l {\left( {h_{1} } \right)_{0} }}} \right. \kern-0pt} {\left( {h_{1} } \right)_{0} }}\)

\(\overline{m}\) :

Mass/unit longitudinal dimension of beam

\(\overline{{P_{1} }}\) :

Dynamic load amplitude

\(w\,(x,t)\) :

Deflection of beam in transverse direction

\(Y\) :

Geometric parameter

\(\overline{t}\) :

Non-dimensional time

t :

Time

\(\overline{w}\) :

\(\frac{w}{l}\)

\(\overline{w}^{\prime \prime }\) :

\(\frac{{\partial^{2} \overline{w} }}{{\partial \overline{x}^{2} }}\)

\(\ddot{\overline{w}}\) :

\(\frac{{\partial^{2} \overline{w} }}{{\partial \overline{t}^{2} }}\)

\(\overline{x}\) :

\(\frac{x}{l}\)

\(U_{i,x}\) :

\(\frac{{\partial U_{i} }}{\partial x}\) (i = 1,3)

\(\omega\) :

Frequency of forcing function

\(\rho_{i}\) :

Density of ith layer

\(\lambda\) :

Thermal expansion coefficient of beam material

\(u^{\prime}_{1}\) :

\(\frac{{\partial u_{1} }}{\partial x}\)

\(\overline{{u_{1} }}^{\prime \prime }\) :

\(\frac{{\partial^{2} \overline{u}_{1} }}{{\partial \overline{x}^{2} }}\)

\(E\left( \xi \right)\) :

Modulus of elasticity at any section of beam

δ :

Temperature gradient parameter

\(E_{31}\) :

\({{E_{3} } \mathord{\left/ {\vphantom {{E_{3} } {E_{1} }}} \right. \kern-0pt} {E_{1} }}\)

\(T\left( \xi \right)\) :

Distribution of elasticity modulus

\(\overline{\omega }\) :

Non-dimensional forcing frequency

\(\alpha\) :

\(\frac{{E_{1} \,A_{1} }}{{E_{3} \,A_{3}^{{}} }}\)

\(\psi_{0}\) :

Reference temperature

\(\alpha_{1}\), \(\alpha_{3}\) :

Taper parameters for top and bottom layer respectively

\(\mu_{1}\) :

\({{\rho_{2} } \mathord{\left/ {\vphantom {{\rho_{2} } {\rho_{1} }}} \right. \kern-0pt} {\rho_{1} }}\)

\(\mu_{2}\) :

\({{\rho_{2} } \mathord{\left/ {\vphantom {{\rho_{2} } {\rho_{3} }}} \right. \kern-0pt} {\rho_{3} }}\)

\(\beta\) :

\({{\left( {h_{2} } \right)_{0} } \mathord{\left/ {\vphantom {{\left( {h_{2} } \right)_{0} } {\left( {h_{1} } \right)}}} \right. \kern-0pt} {\left( {h_{1} } \right)}}_{0}\)

\(\eta_{{t_{2} }} ,\eta_{{r_{2} }}\) :

The spring loss at factors \(\overline{x} = 1\)

\(\overline{k}_{{t_{1} }}^{*} ,\overline{k}_{{t_{2} }}^{*}\) :

Spring constants for the translational springs at \(\overline{x} = 0\) and \(\overline{x} = 1\)

\(\overline{k}_{{\text{r}_{1} }}^{*} ,\overline{k}_{{\text{r}_{2} }}^{*}\) :

Spring constants for the rotational springs at \(\overline{x} = 0\) and \(\overline{x} = 1\)

\(\eta_{{\text{t}_{1} }} ,\;\;\eta_{{\text{r}_{1} }}\) :

Spring loss factors at \(\overline{x} = 0\)

References

  1. Saito H, Otomi K (1979) Parametric response of viscoelastically supported beams. J Sound Vibr 63(2):169–178

    Article  MATH  Google Scholar 

  2. Abbas BAH (1984) Vibrations of Timoshenko beams with elastically restrained ends. J Sound Vibr 97(4):541–548

    Article  Google Scholar 

  3. Cortinez VH, Laura PAA (1985) Vibrations and buckling of a non-uniform beam elastically restrained against rotation at one end and with concentrated mass at the other. J Sound Vibr 99(1):144–148

    Article  Google Scholar 

  4. Maurizi MJ, Bambill De Rossit DV, Laura PAA (1988) Free and forced vibrations of beams elastically restrained against translation and rotation at the ends. J Sound Vibr 120(3):626–630

    Article  Google Scholar 

  5. Kar RC, Sujata T (1988) Parametric instability of a non-uniform beam with thermal gradient and elastic end support. J Sound Vibr 122(2):209–215

    Article  Google Scholar 

  6. Kar RC, Sujata T (1990) Parametric instability of an elastically restrained cantilever beam. Comput Struct 34(3):469–475

    Article  MATH  Google Scholar 

  7. Kar RC, Sujata T (1991) Dynamic stability of a tapered symmetric sandwich beam. Comput Struct 40(6):1441–1449

    Article  Google Scholar 

  8. Lin Chung-Yi, Chen Lien-Wen (2003) Dynamic stability of a rotating beam with a constrained damping layer. J Sound Vibr 267(2):209–225

    Article  Google Scholar 

  9. Pradhan M, Dash PR (2016) Stability of an asymmetric tapered sandwich beam resting on a variable Pasternak foundation subjected to a pulsating axial load with thermal gradient. Compos Struct 140:816–834

    Article  Google Scholar 

  10. Ghosh R, Dharmavaram S, Ray K, Dash P (2005) Dynamic stability of a viscoelastically supported sandwich beam. Struct Eng Mech 19(5):503–517

    Article  Google Scholar 

  11. Nayak B, Dwivedy SK, Murthy KSRK (2011) Dynamic analysis of magnetorheological elastomer-based sandwich beam with conductive skins under various boundary conditions. J Sound Vibr 330(9):1837–1859

    Article  Google Scholar 

  12. Nayak B, Dwivedy SK, Murthy KSRK (2012) Multi-frequency excitation of magnetorheological elastomer-based sandwich beam with conductive skins. Int J Non-Linear Mech 47(5):448–460

    Article  Google Scholar 

  13. Dwivedy SK, Mahendra N, Sahu KC (2009) Parametric instability regions of a soft and magnetorheological elastomer cored sandwich beam. J Sound Vibr 325(4):686–704

    Article  Google Scholar 

  14. Nayak S et al (2014) Static stability of a viscoelastically supported asymmetric sandwich beam with thermal gradient. Int J Adv Struct Eng (IJASE) 6(3):1–7

    Article  Google Scholar 

  15. Lenci Stefano, Clementi Francesco (2012) Effects of shear stiffness, rotatory and axial inertia, and interface stiffness on free vibrations of a two-layer beam. J Sound Vibr 331(24):5247–5267

    Article  Google Scholar 

  16. Lenci Stefano, Clementi Francesco, Warminski Jerzy (2015) Nonlinear free dynamics of a two-layer composite beam with different boundary conditions. Meccanica 50(3):675–688

    Article  MathSciNet  MATH  Google Scholar 

  17. Metrikine AV, Dieterman HA (1997) Instability of vibrations of a mass moving uniformly along an axially compressed beam on a viscoelastic foundation. J Sound Vibr 201(5):567–576

    Article  MATH  Google Scholar 

  18. Zheng DY, Au FTK, Cheung YK (2000) Vibration of vehicle on compressed rail on viscoelastic foundation. J Eng Mech 126(11):1141–1147

    Article  Google Scholar 

  19. Wang TM, Stephens JE (1977) Natural frequencies of Timoshenko beams on Pasternak foundations. J Sound Vibr 51(2):149–155

    Article  MATH  Google Scholar 

  20. Clementi F et al (2014) Nonlinear vibrations of non-uniform beams by the MTS asymptotic expansion method. Continuum Mech Thermodyn 2014:1–15

    MathSciNet  Google Scholar 

  21. Caruntu DI (2009) Simultaneous resonances of geometric nonlinear nonuniform beams. In: ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers

  22. Ray K, Kar RC (1995) Parametric instability of a sandwich beam under various boundary conditions. Comput Struct 55(5):857–870

    Article  MATH  Google Scholar 

  23. Dash PR, Maharathi BB, Ray K (2010) Dynamic stability of an asymmetric sandwich beam resting on a Paternak foundation. J Aerosp Sci Technol 62(1):66

    Google Scholar 

  24. Pradhan SC, Murmu T (2009) Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundations using differential quadrature method. J Sound Vibr 321(1):342–362

    Article  Google Scholar 

  25. Szekrényes A (2015) A special case of parametrically excited systems: free vibration of delaminated composite beams. Eur J Mech A/Solids 49:82–105

    Article  MathSciNet  MATH  Google Scholar 

  26. Celep Z, Güler K, Demir F (2011) Response of a completely free beam on a tensionless Pasternak foundation subjected to dynamic load. Struct Eng Mech 37(1):61

    Article  Google Scholar 

  27. Yokoyama T (1988) Parametric instability of Timoshenko beams resting on an elastic foundation. Comput Struct 28(2):207–216

    Article  MATH  Google Scholar 

  28. Leipholz H (1987) Stability theory 2nd Edition. Wiley, Chichestar

    Book  MATH  Google Scholar 

  29. Kerwin EM Jr (1959) Damping of flexural waves by a constrained viscoelastic layer. J Acoust Soc Am 31(7):952–962

    Article  Google Scholar 

  30. Ray K, Kar RC (1995) Parametric instability of a sandwich beam under various boundary conditions. Comput Struct 55(5):857–870

    Article  MATH  Google Scholar 

  31. Ghosh R, Dash P, Dharmavaram Y, Pavan Kumar VVS, Ray K (2008) Parametric instability of a tapered, asymmetric, sandwich beam under various boundary conditions. Adv Vibr Eng 7(1):71–89

    Google Scholar 

  32. Lim CW, Wu BS, Zeng Q (2003) Accurate approximate analytical solutions to nonlinear oscillating systems with a non-rational restoring force. Adv Vibr Eng 2:381–387

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty, Department of Mechanical Engineering, VSSUT, Sambalpur, Burla, Odisha, 768018, India

    M. Pradhan & P. R. Dash

Authors
  1. M. Pradhan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. R. Dash
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Pradhan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pradhan, M., Dash, P.R. Stability Study of a Sandwich Beam with Asymmetric and Non-uniform Configuration Supported Viscoelastically Under Variable Temperature Grade. J. Vib. Eng. Technol. 7, 149–157 (2019). https://doi.org/10.1007/s42417-019-00087-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-019-00087-3

Keywords

Search

Navigation