Skip to main content
SpringerLink
Log in

Static and dynamic stability analysis of an asymmetric sandwich beam resting on a variable pasternak foundation subjected to thermal gradient

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

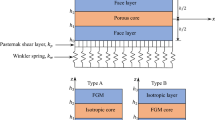
The purpose of the article is to analyze the static and dynamic stability of an asymmetric sandwich beam with viscoelastic core lying on a variable Pasternak foundation under the action of a pulsating axial load subjected to one-dimensional thermal gradient under three different boundary conditions by the computational method. A set of Hill’s equation has been obtained by the application of Hamilton’s principle along with the generalized Galerkin’s method. The effects of thermal gradient, elastic foundation variation parameter, thickness ratio of two elastic layers, the ratio of modulus of the shear layer of Pasternak foundation to the young’s modulus of elastic layer, the ratio of the length of the beam to the thickness of the elastic layer, the ratio of in phase shear modulus of the viscoelastic core to the young’s modulus of the elastic layer, the ratio of thickness of Pasternak foundation to the length of the beam, coreloss factor on the non-dimensional static buckling loads and on the regions of parametric instability are studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Abbreviations

A i (i = 1, 2, 3):

Areas of cross section of a 3 layered beam, i = 1 for top layer

B :

Width of beam

c :

h 1 + 2h 2 + h 3

E i (i = 1, 2, 3):

Young’s Module, i = 1 for top layer

G s :

Modulus of the shear layer of a Pasternak Foundation

G S /E i (i = 1, 3):

The ratio of modulus of the shear layer of Pasternak foundation to the young’s modulus of elastic layer

G *2 :

G 2 (1 + jη), complex shear modulus of core

G 2/E i (i = 1, 3):

The ratio of in phase shear modulus of the viscoelastic core to the young’s modulus of the elastic layer

g*:

g (1 + jη), complex shear parameter

g :

Shear parameter

2h i (i = 1, 2, 3):

Thickness of the ith layer, i = 1 for top layer

h 12 :

h 1/h 2

h 31 :

h 3/h 1

I i (i = 1, 2, 3):

Second moments of area of cross section about a relevant axis, i = 1 for top layer

l :

Beam length

\( l_{h1} \) :

l/h 1

m:

Mass/unit length of beam

\( \bar{P}_{1} \) :

Non dimensional amplitude for the dynamic loading

t:

Time

\( \overline{t} \) :

Non-dimensional time

u(x, t), U 1(x, t):

Axial displacement at the middle of the top layer of beam

w(x, t):

Transverse deflection of beam

\( w^{\prime} \) :

\( \frac{\partial w}{\partial x} \)

\( w^{\prime\prime} \) :

\( \frac{{\partial^{2} w}}{{\partial x^{2} }} \)

Y:

Geometric parameter

\( \bar{w} \) :

\( \frac{w}{l} \)

\( \ddot{\bar{w}} \) :

\( \frac{{\partial^{2} \bar{w}}}{{\partial \bar{t}^{2} }} \)

\( \bar{w}^{\prime \prime } \) :

\( \frac{{\partial^{2} \bar{w}}}{{\partial \bar{x}^{2} }} \)

U i,x :

\( \frac{{\partial U_{i} }}{\partial x} \) (here i = 1, 3)

\( \bar{x} \) :

\( \frac{x}{l} \)

d :

Thickness of the shear layer of a Pasternak foundation

ρ i :

Density of ith layer

[ϕ]:

A null matrix

to :

\( \sqrt {\frac{{ml^{4} }}{{E_{1} I_{1} + E_{3} I_{3} }}} \)

\( u^{\prime}_{1} \) :

\( \frac{{\partial u_{1} }}{\partial x} \)

\( \bar{u}_{1}^{\prime \prime } \) :

\( \frac{{\partial^{2} \bar{u}_{1} }}{{\partial \bar{x}^{2} }} \)

\( \bar{\omega } \) :

ωt 0

ω:

Frequency of forcing function

\( \bar{\omega } \) :

Non-dimensional forcing frequency

δ:

Thermal gradient parameter

ψ 0 :

Reference temperature

\( E_{31} \) :

E 3/E 3

γ :

Coefficient of thermal expansion of beam material

E(ξ):

Variation of modulus of elasticity of beam

T(ξ):

Distribution of elasticity modulus

α:

\( \frac{{E_{1} \,A_{1} }}{{E_{3} \,A_{3}^{{}} }} \)

References

  1. Hetenyi M (1946) Beams of elastic foundation. The University of Michigan Press, Michigan

    Google Scholar 

  2. Kerwin EM Jr (1959) Damping of flexural waves by a constrained viscoelastic layer. J Acoust Soc Am 31:952–962

    Article  ADS  Google Scholar 

  3. Wang TM, Stephens JE (1977) Natural frequencies of Timoshenko beams on pasternak foundations. J Sound Vib 51:149

    Article  ADS  MATH  Google Scholar 

  4. Clementi F, Demecio L, Mazzailli CEN, Lenci S (2014) Nonlinear vibrations of non-uniform beams by the MTS asymptotic expansion method. Continuum Mech Thermodyn. doi:10.1007/s00161-014-0368-3

    Google Scholar 

  5. Caruntu ID (2009) On nonlinear forced response of nonuniform beams. In: Proceedings of the ASME dynamic systems and control conference, DSCC 2008, Issue PART A, pp 53–58

  6. Basu D, Rao NSVK (2012) Analytical solutions for Euler–Bernoulli beam on visco-elastic foundations subjected to moving load. Int J Numer Anal Methods Geomech. doi:10.1002/nag.1135

    Google Scholar 

  7. Saito H, Otomi K (1979) Parametric response of viscoelastically supported beams. J Sound Vib 63:169–178

    Article  ADS  MATH  Google Scholar 

  8. Tomar JS, Jain R (1984) Effect of thermal gradient on frequencies of wedge shaped rotating beams. AIAA J 22:848–850

    Article  ADS  Google Scholar 

  9. Sato M, Kanie S, Mikami T (2008) Mathematical analogy of a beam on elastic supports as a beam on elastic foundation. Appl Math Model 32:688–699

    Article  MATH  Google Scholar 

  10. Wang L, Ma J, Peng J, Li L (2013) Large amplitude vibration and parametric instability of inextensional beams on the elastic foundation. Int J Mech Sci 67:1–9

    Article  Google Scholar 

  11. Wang L, Ma J, Peng J, Li L (2013) Three-to-one resonant responses of inextensional beams on the elastic foundation. J Vib Acoust 135. doi:10.1115/1.4007019

  12. Wang L, Ma J, Yang M, Li L, Zhao Y (2013) Multimode dynamics of inextensional beams on the elastic foundations with two-to-one internal resonances. J Appl Mech 80. doi:10.1115/1.4023694

  13. Yokoyama T (1988) Parametric instability of Timoshenko beams resting on an elastic foundation. Comput Struct 28:207

    Article  MATH  Google Scholar 

  14. Szekrenyes A (2015) A special case of parametrically excited systems: free vibration of delaminated composite beams. Eur J Mech A Solids 49:82–105

    Article  MathSciNet  Google Scholar 

  15. Wang L, Ma J, Zhao Y, Liu Q (2013) Refined modeling and free vibration of inextensional beams on the elastic foundations. ASME J Appl Mech 80(4):041026. doi:10.1115/1.4023032

    Article  Google Scholar 

  16. Babilio E (2013) Dynamics of an axially functionally graded beam under axial load. Eur Phys J Spec Topics 222(7):1519–1539

    Article  ADS  Google Scholar 

  17. Babilio E (2014) Dynamics of functionally graded beams on viscoelastic foundation. Int J Struct Stab Dyn 14(8):1440014-10

    Article  MathSciNet  Google Scholar 

  18. Kar RC, Sujata T (1988) Parametric instability of a non-uniform beam with thermal gradient resting on a Pasternak foundation. Comput Struct 29:591

    Article  MATH  Google Scholar 

  19. Kar RC, Sujata T (1990) Parametric instability of Timoshenko beam with thermal gradient resting on a variable Pasternak foundation. Comput Struct 36:659

    Article  Google Scholar 

  20. Ray K, Kar RC (1995) Parametric instability of a sandwich beam under various boundary conditions. Comput Struct 55:857–870

    Article  ADS  MATH  Google Scholar 

  21. Celep Z, Guler K, Demir F (2011) Response of a completely free beam on a tensionless Pasternak foundation subjected to dynamic load. Struct Eng Mech 37:61–77

    Article  Google Scholar 

  22. Cao CY, Zhong Y (2008) Dynamic response of a beam on a Pasternak foundation and under a moving load. J Chongqing Univ 7(4):311–316

    Google Scholar 

  23. Nayak S, Bisoi A, Dash PR, Pradhan PK (2014) Static stability of a viscoelastically supported asymmetric sandwich beam with thermal gradient. Int J Adv Struct Eng 65:1–7

    Google Scholar 

  24. Lenci S, Clementi F, Warminski J (2015) Nonlinear free dynamics of a two-layer composite beam with different boundary conditions. Meccanica 50:675–688

    Article  MathSciNet  Google Scholar 

  25. Pradhan SC, Murmu T (2009) Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundations using differential quadrature method. J Sound Vib 321:342–362

    Article  ADS  Google Scholar 

  26. Nayak B, Dwivedy SK, Murthy KSRK (2011) Dynamic analysis of magneto rheological elastomer-based sandwich beam with conductive skins under various boundary conditions. J Sound Vib 330:1837–1859

    Article  ADS  Google Scholar 

  27. Nayak B, Dwivedy SK, Murthy KSRK (2012) Multi-frequency excitation of magnetorheological elastomer-based sandwich beam withconductive skins. International Journal of Nonlinear Mechanics 47(5):448–460

    Article  ADS  Google Scholar 

  28. Dash PR, Maharathi BB, Ray K (2010) Dynamic stability of an asymmetric sandwich beam resting on a Pasternak foundation. J Aerosp Sci Technol 62(1):66–75

    Google Scholar 

  29. Lenci S, Clementi F (2012) Effect of shear stiffness, rotatory and axial inertia, and interface stiffness on free vibrations of a two-layer beam. J Sound Vib 331:5247–5267

    Article  ADS  Google Scholar 

  30. Ding H, Chen L, Yang S (2012) Convergence of Galerkin truncation for dynamic response of infinite beams on nonlinear foundations under a moving load. J Sound Vib 331:2426–2442

    Article  ADS  Google Scholar 

  31. Dwivedy SK, Mahendra N, Sahu KC (2009) Parametric instability regions of a soft and magnetorheological elastomer cored sandwich beam. J Sound Vib 325:686–704

    Article  ADS  Google Scholar 

  32. Lenci S, Clementi F, Mazzilli CEN (2013) Simple formulas for the natural frequencies of non-uniform cables and beams. Int J Mech Sci 77:155–163

    Article  Google Scholar 

  33. Leipholz H (1987) Stability theory, 2nd edn. Wiley, Chichestar

    Book  MATH  Google Scholar 

  34. Lenci S, Clementi F (2012) On flexural vibrations of shear deformable laminated beams. In: Proceedings of the ASME 2012 international mechanical engineering congress & exposition IMECE 2012 November 9–15, 2012, Houston, Texas, USA, vol 4, Issue Parts A and B, pp 581–590

  35. Caruntu DI (2010) Simultaneous resonances of geometric nonlinear nonuniform beams. In: Proceedings of the ASME international design engineering technical conferences and computers and information in engineering conference 2009, DETC2009, vol 1, Issue Part B, pp 1397–1402

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, VSSUT, Burla, 768018, India

    M. Pradhan, P. R. Dash & P. K. Pradhan

Authors
  1. M. Pradhan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. R. Dash
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. P. K. Pradhan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Pradhan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pradhan, M., Dash, P.R. & Pradhan, P.K. Static and dynamic stability analysis of an asymmetric sandwich beam resting on a variable pasternak foundation subjected to thermal gradient. Meccanica 51, 725–739 (2016). https://doi.org/10.1007/s11012-015-0229-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-015-0229-6

Keywords

Search

Navigation