Static stability of a viscoelastically supported asymmetric sandwich beam with thermal gradient

Abstract

The static stability of an asymmetric sandwich beam with viscoelastic core on viscoelastic supports at the ends and subjected to an axial pulsating load and a steady, one-dimensional temperature gradient is investigated by computational method. The equations of motion and associated boundary conditions are obtained using the Hamilton’s energy principle. Then, these equations of motion and the associated boundary conditions are non-dimensionalised. A set of Hill’s equations is obtained from the non-dimensional equations of motion by the application of the general Galerkin method. The static buckling loads are obtained from the Hill’s equations. The effects of shear parameter, geometric parameters, core loss factors, and thermal gradient on the non-dimensional static buckling loads zones have been investigated.

Introduction

Vibration control of machines and structures incorporating viscoelastic materials in suitable arrangement is an important aspect of investigation. The use of viscoelastic layers constrained between elastic layers is known to be effective for damping of flexural vibrations of structures over a wide range of frequencies. The energy dissipated in these arrangements is due to shear deformation in the viscoelastic layers, which occurs due to flexural vibration of the structures. The effect of temperature on the modulus of elasticity is far from negligible, especially in high-speed atmospheric flights and nuclear engineering applications in which certain parts have to operate under elevated temperatures. Most engineering materials have a linear relationship between Young’s modulus and temperature. Kerwin (1959) was the first to develop a theory for the damping of flexural waves by a viscoelastic damping layer. Evan-Iwanowski (1965), Ariarathnam (1986) and Simitses (1987) gave exhaustive account of literature on vibration and stability of parametrically excited systems. Review article of Habip (1965) gives an account of developments in the analysis of sandwich structures. Articles of Nakra (1976, 1981, 1984) have extensively treated the aspect of vibration control with viscoelastic materials. Saito and Otomi (1979) considered the response of viscoelastically supported ordinary beams. Bauld (1967) considered the dynamic stability of sandwich columns with pinned ends under pulsating axial loads. The effect of translational and rotational end-flexibilities on natural frequencies of free vibration of Timoshenko beams was investigated by Abbas (1984).

Tomar and Jain (1984, 1985) studied the effect of thermal gradient on the frequencies of rotating beams with and without pre-twist. Kar and Sujata (1988) studied the parametric instability of a non-uniform beam with thermal gradient resting on a pasternak foundation. Lin and Chen (2003) studied the dynamic stability of a rotating beam with a constrained damping layer. Ghosh et al. (2005) studied the dynamic stability of a viscoelastically supported sandwich beam. Dwivedy et al. (2009) studied the parametric instability regions of a soft and magneto rheological elastomeric cored sandwich beam. The dynamic analysis of magneto rheological elastomeric-based sandwich beam with conductive skins under various boundary conditions was studied by Nayak et al. (2011).

Although some studies have been carried out in the past on the static and parametric instability of a symmetric sandwich beam under various boundary conditions by Ray and Kar (1995), as well as effect of temperature gradient on the frequencies of vibration of beams, it appears to the author’s knowledge that no work exists concerning the effect of viscoelastic layer and thermal gradient on the static stability of a asymmetric sandwich beams under pulsating axial loads.

Thus, the purpose of this paper is to present the static stability of an asymmetric beam with viscoelastic core subjected to a steady, one-dimensional temperature gradient along its length. Finally, the effect of shear parameter, geometric parameters, core loss factors, and thermal gradient on the non-dimensional static buckling loads zones is investigated by computational method and the results are presented graphically.

Formulation of the problem

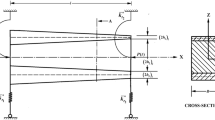
Figure 1 shows the system configuration. The top layer of the beam is made of an elastic material of thickness 2h₁ and Young’s modulus E₁ and bottom layer is made of an elastic material of thickness 2h₃ and Young’s modulus E₃. The core is made of a linearly viscoelastic material with shear modulus $G_2^{\ast }=G_2(1+j\mathit{\eta })$ where G ₂ is the in-phase shear modulus, η is the core loss factor and j = √−1. The core has a thickness of 2h₂. The beam is restrained by translational and rotational springs. The moduli of the springs are given as $k_{t1}^{\ast }=k_{t1}\left(1+j{\mathit{\eta }}_{t1}\right)$, $k_{t2}^{\ast }=k_{t2}\left(1+j{\mathit{\eta }}_{t2}\right)$, $k_{r1}^{\ast }=k_{r1}\left(1+j{\mathit{\eta }}_{r1}\right)$, $k_{r2}^{\ast }=k_{r2}\left(1+j{\mathit{\eta }}_{r2}\right)$, subscripts t and r refer to the translational and rotational springs, respectively, ${\mathit{\eta }}_{t1},{\mathit{\eta }}_{t2},$${\mathit{\eta }}_{r1}\dots$, etc. being the spring loss factors.

Fig. 1

System configuration

The beam is subjected to pulsating axial loads $P\left(t\right)=P_0+P_{1}cos(\mathit{\omega }t)$ acting along the undeformed axis as shown. Here ω is the frequency of the applied load, P₀ and P₁ are, respectively, the static and dynamic load amplitudes and t is the time. A steady one-dimensional temperature gradient is assumed to exist in the top and bottom layers.

The following assumptions are made for deriving the equations of motion:

• 1. The deflections of the beam are small and the transverse deflection w(x, t) is the same for all points of a cross-section.

• 2. The layers are perfectly bonded so that displacements are continuous across interfaces, that is, no slipping conditions prevail between the elastic and viscoelastic layers at their interfaces.

• 3. The elastic layers obey Euler–Bernoulli beam theory.

• 4. Damping in the viscoelastic core is predominantly due to shear.

• 5. A steady one-dimensional temperature gradient is assumed to exist along the length of the beam.

• 6. Bending and the extensional effects in the core are negligible.

• 7. Extension and rotary inertia effects are negligible.

The expressions for potential energy, kinetic energy and work done are as follows:

$$\begin{array}{cc}\hfill V& =\frac{1}{2}{E}_1{A}_1\underset{0}{\overset{L}{\int }}{u}_{1,x}^2\mathrm{d}x+\frac{1}{2}{E}_3{A}_3\underset{0}{\overset{L}{\int }}{u}_{3,x}^2\mathrm{d}x+\frac{1}{2}\left(E_1{I}_1+E_3{I}_3\right)\underset{0}{\overset{L}{\int }}{w}_{,x}^2\mathrm{d}x\hfill \\ \hfill & +\frac{1}{2}{G}_2^{\ast }{A}_2\underset{0}{\overset{L}{\int }}{\mathit{\gamma }}_2^2\mathrm{d}x+\frac{1}{2}{k}_{t_1}^{\ast }{w}^2\left(0,t\right)+\frac{1}{2}{k}_{t_2}^{\ast }{w}^2\left(L,t\right)+\frac{1}{2}{k}_{r_1}^{\ast }{\mathit{\gamma }}_2^2\left(0,t\right)\hfill \\ \hfill & +\frac{1}{2}{k}_{r_2}^{\ast }{\mathit{\gamma }}_2^2\left(L,t\right)\hfill \end{array}$$

(1)

$$T=\frac{1}{2}m\underset{0}{\overset{L}{\int }}{w}_{,t}^2\mathrm{d}x$$

(2)

$$W_p=\frac{1}{2}\underset{0}{\overset{L}{\int }}P(t)w_{,x}^2\mathrm{d}x$$

(3)

where, u₁ and u₃ are the axial displacements in the top and bottom layers and ${\mathit{\gamma }}_2$ is the shear in the layer given by ${\mathit{\gamma }}_2=\frac{u_1-u_3}{2h_2}-\frac{c{w}_{,x}}{2h_2}$ . u₃ is eliminated using the Kerwin assumption (Kerwin 1959).

The application of the extended Hamilton’s principle

$$\mathit{\delta }\underset{t_1}{\overset{t_2}{\int }}\left(T-V+W_p\right)dt=0$$

(4)

gives the following system of equations of motion

$$m{w}_{,tt}+\left(E_1{I}_1+E_3{I}_3\right)w_{,xxxx}-\left(\frac{G_2^{\ast }{A}_2{c}^2}{{\left(2h_2\right)}^2}-P\left(t\right)\right)w_{,xx}+\frac{G_2^{\ast }{A}_{2}c\left(1+\mathit{\alpha }\right)}{{\left(2h_2\right)}^2}{u}_{1,x}=0$$

(5)

$$\left(E_1{A}_1+{\mathit{\alpha }}^2{E}_3{A}_3\right)u_{1,xx}-\frac{G_2^{\ast }{A}_2{\left(1+\mathit{\alpha }\right)}^2}{{\left(2h_2\right)}^2}{u}_1+\frac{G_2^{\ast }{A}_{2}c(1+\mathit{\alpha })}{{\left(2h_2\right)}^2}{w}_{,x}=0$$

(6)

At x = 0, the associated boundary conditions are,

$$\left(E_1{I}_1+E_3{I}_3\right)w_{,xxx}-\left(\frac{G_2^{\ast }{A}_2{c}^2}{{\left(2h_2\right)}^2}-P\left(t\right)\right)w_{,x}-k_{t1}^{\ast }w+\frac{G_2^{\ast }{A}_{2}c\left(1+\mathit{\alpha }\right)}{{\left(2h_2\right)}^2}{u}_1=0$$

(7)

or

$$w=0$$

(8)

$$\left(E_1{I}_1+E_3{I}_3\right)w_{,xx}+\frac{k_{r1}^{\ast }\left(h_1+h_3\right)}{{\left(2h_2\right)}^2}\left\{\left(h_1+h_3\right)w_{,x}-\left(1+\mathit{\alpha }\right)u_1\right\}=0$$

(9)

or

$$w_{,x}=0$$

(10)

$$\left(E_1{A}_1+{\mathit{\alpha }}^2{E}_3{A}_3\right)u_{1,x}+\frac{k_{r1}^{\ast }\left(1+\mathit{\alpha }\right)}{{\left(2h_2\right)}^2}\left\{\left(1+\mathit{\alpha }\right)u_1-\left(h_1+h_3\right)w_{,x}\right\}=0$$

(11)

or

$$u=0$$

(12)

The boundary conditions at x = l are obtained from Eqs. (7) to (12) by replacing $k_{t1}^{\ast }$ and $k_{r1}^{\ast }$ by $k_{t2}^{\ast }$ and $k_{r2}^{\ast }$, respectively.

In the above, $w_{,tt}=\frac{{\mathit{\partial }}^{2}w}{\mathit{\partial }{t}^2},w_{,xx}=\frac{{\mathit{\partial }}^{2}w}{\mathit{\partial }{x}^2},$ etc. Also, $\mathit{\alpha }=\frac{E_1{A}_1}{E_3{A}_3}$ where A₁ and A₃ are cross-sectional areas of the top and bottom layer, respectively.

Moreover, $c=h_1+2h_2+h_3,$I₁ and I₃ are the moments of inertia of the top and bottom layer cross-sections about relevant axes. u₁ is the axial deflection of the middle of top layer and ${\overline{w}}_{,\overline{tt}}=\frac{{\mathit{\partial }}^2\overline{w}}{\mathit{\partial }{\overline{t}}^2}$, ${\overline{w}}_{,\overline{x}}=\frac{\mathit{\partial }\overline{w}}{\mathit{\partial }\overline{x}}$ are in above equations.

Introducing the dimensionless parameters $\overline{x}=x/l$, $\overline{w}=w/l$, ${\overline{u}}_1=u_1/l$,

$$\begin{array}{c}\overline{t}=t/t_0,\mathrm{where}{t}_0^2=m{l}^4/\left(E_1{I}_1+E_3{I}_3\right),\overline{\mathit{\omega }}=\mathit{\omega }{t}_0,{\overline{P}}_0=\left(P_0{l}^2\right)/\left(E_1{I}_1+E_3{I}_3\right),\\ {\overline{P}}_1=\left(P_1{l}^2\right)/\left(E_1{I}_1+E_3{I}_3\right),\overline{P}\left(\overline{t}\right)={\overline{P}}_0+{\overline{P}}_{1}cos\overline{\mathit{\omega }}\overline{t},\\ \end{array}$$

$\dot{g}=\frac{G_2^{\ast }{h}_{21}{l}_{h1}^2}{E_1\left(1+E_{31}{h}_{31}^3\right)}=\left(1+j{\mathit{\eta }}_r\right)$, g being the shear parameter and $\dot{g}$ being the complex shear parameter

$$h_{21}=1/h_{12}=h_2/h_1,h_{31}=h_3/h_1,h_{32}=h_3/h_2,l_{h1}=l/h_1,$$

$E_{31}=E_3/E_1$, Eq. (5)–(12) reduce to,

$$\begin{array}{cc}& {\overline{w}}_{,\overline{tt}}+{\overline{w}}_{,\overline{xxxx}}+\left\{\overline{P}\left(\overline{t}\right)-3g^{\ast }{\left(1+\frac{h_{12}+h_{32}}{2}\right)}^2\right\}{\overline{w}}_{,\overline{xx}}\hfill \\ \hfill & +\frac{3}{2}{g}^{\ast }{h}_{12}{l}_{h1}\left(1+\frac{h_{12}+h_{32}}{2}\right)\left(1+\mathit{\alpha }\right){\overline{u}}_{,\overline{x}}=0\hfill \end{array}$$

(13)

$${\overline{u}}_{1,\overline{xx}}-\frac{g^{\ast }}{4}{h}_{12}^2\left(1+\mathit{\alpha }\right)\left(1+E_{31}{h}_{31}^3\right){\overline{u}}_1+\frac{g^{\ast }}{2}\frac{h_{12}}{l_{h1}}\left(1+E_{31}{h}_{31}^3\right)\left(1+\frac{h_{12}+h_{32}}{2}\right){\overline{w}}_{,\overline{x}}=0.$$

(14)

The non-dimensional boundary conditions at $\overline{x}=0$ are as follows

$$\begin{array}{c}{\overline{w}}_{\overline{1,xxx}}+\left\{\overline{P}\left(\overline{t}\right)-3g^{\ast }{\left(1+\frac{h_{12}+h_{32}}{2}\right)}^2\right\}{\overline{w}}_{1,\overline{x}}-{\overline{k}}_{t1}^{\ast }\overline{w}\\ +\frac{3}{2}{g}^{\ast }{h}_{12}{l}_{h1}\left(1+\frac{h_{12}+h_{32}}{2}\right)\left(1+\mathit{\alpha }\right){\overline{u}}_1=0\\ \end{array}$$

(15)

or

$$\overline{w}=0$$

(16)

$${\overline{w}}_{,\overline{xx}}-{\overline{k}}_{r1}^{\ast }\frac{\left(1+h_{31}\right)}{l_{h1}}{\overline{w}}_{,\overline{x}}-{\overline{k}}_{r1}^{\ast }\left(1+\mathit{\alpha }\right){\overline{u}}_1=0$$

(17)

or

$${\overline{w}}_{,\overline{x}}=0$$

(18)

$${\overline{u}}_{1,\overline{x}}+\frac{1}{3}{\overline{k}}_{r1}^{\ast }\frac{\left(1+E_{31}{h}_{31}^3\right)}{l_{h1}\left(1+h_{31}\right)}\left(1+\mathit{\alpha }\right){\overline{u}}_1-\frac{2}{3}{\overline{k}}_{r1}^{\ast }\frac{\left(1+E_{31}{h}_{31}^3\right)}{l_{h1}^2}{\overline{w}}_{,\overline{x}}=0$$

(19)

or

$${\overline{u}}_1=0$$

(20)

In the above equations, ${\overline{k}}_{t1}^{\ast }={\overline{k}}_{t1}\left(1+j{\mathit{\eta }}_{t1}\right)=\frac{k_{t1}^{\ast }{l}^3}{\left(E_1{I}_1+E_3{I}_3\right)},{\overline{k}}_{r1}^{\ast }={\overline{k}}_{r1}\left(1+j{\mathit{\eta }}_{r2}\right)=\frac{k_{r1}^{\ast }\left(h_1+h_3\right)l^2}{4h_2^2\left(E_1{I}_1+E_3{I}_3\right)}$, ${\mathit{\eta }}_{t1}$ and ${\mathit{\eta }}_{r1}$ being the non-dimensional spring loss factors corresponding to the translational and rotational springs at the left end, and ${\overline{k}}_{t1}^{\ast }$ and ${\overline{k}}_{r1}^{\ast }$ are the non-dimensional spring parameters for the springs at x = 0.

The boundary conditions at x = 1 can be obtained from Eqs. (15)–(20) by replacing $k_{t1}^{\ast }$ and $k_{r1}^{\ast }$ by $k_{t2}^{\ast }$ and $k_{r2}^{\ast }$, respectively, where $k_{t2}^{\ast }$ and $k_{r2}^{\ast }$ are defined similar to ${\overline{k}}_{t1}^{\ast }$ and ${\overline{k}}_{r1}^{\ast }.$

Approximate solutions

Approximate solutions of Eq. (13) and (14) are assumed as

$$\overline{w}=\sum _{i=1}^{i=N}{w}_i\left(\overline{x}\right)f_i\left(\overline{t}\right)$$

(21)

$${\overline{u}}_1=\sum _{k=N+1}^{k=2N}{u}_{1k}\left(\overline{x}\right)f_k\left(\overline{t}\right)$$

(22)

where f _i (r = 1, 2,…, 2N) are the generalized coordinates and $w_i\left(\overline{x}\right)$ and $u_{1k}\left(\overline{x}\right)$ are the shape functions to be so chosen as to satisfy as many of the boundary conditions as possible (Leipholz 1987). For the above-mentioned boundary conditions, the shape functions chosen are of the following general form (Ray and Kar 1995),

$$w_i\left(\overline{x}\right)=a_0{\overline{x}}^{i+1}+a_1{\overline{x}}^{i+2}+a_2{\overline{x}}^{i+3}$$

(23)

$$u_{ik}\left(\overline{x}\right)=b_0{\overline{x}}^{\overline{k}}+b_1{\overline{x}}^{\overline{k}+1}\mathrm{where}\overline{k}=k-N$$

(24)

for i = 1, 2,…,N and k = N + 1, N + 2,…,2N. The specific values of coefficients a₀, a₁, a₂, b₀ and b₁ are obtained by substituting Eqs. (23) and (24) into Eqs. (15), (17) and (19) and arbitrarily setting a₀ and b₀ (here $a_0=b_0=1$).

Substitution of Eqs. (21) and (22) in the non-dimensional equations of motion and application of general Galerkin method (Leipholz 1987) leads to the following matrix equations of motion.

$$\left[m\right]\left\{{\ddot{f}}_j\}\right\}+\left[k_{11}\right]\left\{f_j\right\}+\left[k_{12}\right]\left\{f_l\right\}=\left\{0\right\}$$

(25)

$$\left[k_{22}\right]\left\{f_l\right\}+\left[k_{21}\right]\left\{f_j\right\}=\left\{0\right\}$$

(26)

For j = 1, 2…N and l = (N + 1)…2N, the various matrix elements are given by

$$m_{ij}=\underset{0}{\overset{1}{\int }}{w}_i{w}_{j}d\overline{x}$$

(27)

$$\begin{array}{c}{k}_{11ij}=\underset{0}{\overset{1}{\int }}{w}_i^{″}{w}_j^{″}d\overline{x}+\left[3g^{\ast }{\left(1+\frac{h_{12}+h_{32}}{2}\right)}^2-\overline{P}\left(\overline{t}\right)\right]\underset{0}{\overset{1}{\int }}{w}_i^{\prime }{w}_j^{\prime }d\overline{x}+{\overline{k}}_{t1}^{\ast }{w}_i\left(0\right)w_j\left(0\right)\\ +{\overline{k}}_{t2}^{\ast }{w}_i\left(1\right)w_j\left(1\right)+{\overline{k}}_{r1}^{\ast }{w}_i^{\prime }\left(0\right)w_j^{\prime }\left(0\right)+{\overline{k}}_{r2}^{\ast }{w}_i^{\prime }\left(1\right)w_j^{\prime }\left(1\right)\\ \end{array}$$

(28)

$$\begin{array}{c}{k}_{12ik}=-\frac{3}{2}{g}^{\ast }{h}_{12}{l}_{h1}\left(1+\mathit{\alpha }\right)\left(1+\frac{h_{12}+h_{32}}{2}\right)\underset{0}{\overset{1}{\int }}{w}_i^{\prime }{u}_{1k}d\overline{x}+{\overline{k}}_{r1}^{\ast }{u}_{1k}\left(0\right)w_i^{\prime }\left(0\right)\\ +{\overline{k}}_{r2}^{\ast }{u}_{1k}\left(1\right)w_i^{\prime }\left(1\right)\\ \end{array}$$

(29)

$$\begin{array}{c}{k}_{22kl}=3l_{h1}^2\frac{1+{\mathit{\alpha }}^2{E}_{31}{h}_{31}}{1+E_{31}{h}_{31}^3}\underset{0}{\overset{1}{\int }}{u}_{1k}^{\prime }{u}_{1l}^{\prime }d\overline{x}+\frac{3}{4}{g}^{\ast }{l}_{h1}^2{h}_{12}^2{\left(1+\mathit{\alpha }\right)}^2\underset{0}{\overset{1}{\int }}{u}_{1k}{u}_{1l}d\overline{x}\\ +{\overline{k}}_{r1}^{\ast }{u}_{1k}\left(0\right)u_{1l}\left(0\right)+{\overline{k}}_{r1}^{\ast }{u}_{1k}\left(1\right)u_{1l}\left(1\right)\\ \end{array}$$

(30)

Also, $\left[k_{21}\right]={\left[k_{21}\right]}^T$. From Eq. (26), $\left\{f_l\right\}=-{\left[k_{22}\right]}^{-1}\left[k_{21}\right]\left\{f_j\right\}$. Substitution of this in Eq. (25) leads to,

$$\left[m\right]\left\{\ddot{f}\}\right\}+\left[k\right]\left\{f\right\}-{\overline{P}}_{1}cos\left(\overline{\mathit{\omega }}\overline{t}\right)\left[H\right]\left\{f\right\}=\left\{0\right\}$$

(31)

where $\left\{f\right\}={\left\{f_{1,\dots ,}{f}_N\right\}}^T$, $H_{ij}={\int }_0^1{w}_i^{\prime }{w}_j^{\prime }d\overline{x}$ and $\left[k\right]=\left[T_{11}\right]-\left[k_{12}\right]{\left[k_{22}\right]}^{-1}{\left[k_{12}\right]}^T$ with,

$$\begin{array}{c}{T}_{11ij}=\underset{0}{\overset{1}{\int }}{w}_i^{″}{w}_j^{″}d\overline{x}+\left[3g^{\ast }{\left(1+\frac{h_{12}+h_{32}}{2}\right)}^2-{\overline{P}}_0\right]\underset{0}{\overset{1}{\int }}{w}_i^{\prime }{w}_j^{\prime }d\overline{x}+{\overline{k}}_{t1}^{\ast }{w}_i\left(0\right)w_j\left(0\right)\\ +{\overline{k}}_{t2}^{\ast }{w}_i\left(1\right)w_j\left(1\right)+{\overline{k}}_{r1}^{\ast }{w}_i^{\prime }\left(0\right)w_j^{\prime }\left(0\right)+{\overline{k}}_{r2}^{\ast }{w}_i^{\prime }\left(1\right)w_j^{\prime }\left(1\right)\\ \end{array}$$

(32)

Static buckling loads

Substitution of $\overline{P_1}=0$ and $\{\ddot{f}\}=\{0\}$ in Eq. (31) leads to the eigenvalue problem ${[k]}^{-1}\left[H\right]\left\{f\right\}=\frac{1}{P_o}\left\{f\right\}.$ The static buckling loads ${({\overline{P}}_o)}_{\mathrm{crit}}$ for the first few modes are obtained as the real parts of the reciprocals of the eigenvalues of ${[k]}^{-1}\left[H\right]$.

Numerical results and discussion

Numerical results were obtained for various values of the parameters such as shear parameter, geometric parameter, core loss factors and thermal gradient. The following parameter values have been taken, unless stated otherwise.

$$\begin{array}{c}\mathit{\eta }=0,{\mathit{\eta }}_{t1}={\mathit{\eta }}_{t2}=0.1,{\mathit{\eta }}_{r1}={\mathit{\eta }}_{r2}=0.01,k_{t1}=k_{t2}=1,000,k_{r1}=k_{r2}=750,l_{h1}=10,\\ g=0.05,E_{31}=1,\mathit{\alpha }=1,h_{31}=h_{12}=1,{\overline{P}}_0=0.1,{\mathit{\delta }}_1=1\mathrm{and}{\mathit{\delta }}_2=0.2.\\ \end{array}$$

The temperature above the reference temperature at any point ξ from the end of the beam is assumed to be $\mathit{\Psi }\mathit{\psi }=\mathit{\psi }{\mathit{\Psi }}_0(1-\mathit{\xi })$. Choosing $\mathit{\Psi }{\mathit{\psi }}_0=\mathit{\psi }{\mathit{\Psi }}_1$, the temperature at the end ξ = 1 as the reference temperature, the variation of modulus of elasticity of the beam (Kar and Sujata 1988) is denoted by

$$\begin{array}{c}E\left(\mathit{\xi }\right)=E_1[1-\mathit{\gamma }{\mathit{\Psi }}_1(1-\mathit{\xi })],0\le \mathit{\gamma }\mathit{\psi }{\mathit{\Psi }}_1<1\\ =E_{1}T(\mathit{\xi })\\ \end{array}$$

where, $\mathit{\gamma }$ is the coefficient of thermal expansion of the beam material, δ = $\mathit{\gamma }{\mathit{\Psi }}_1$ is the thermal gradient parameter and T($\mathit{\xi }$) = $[1-\mathit{\delta }(1-\mathit{\xi })$].

Here, we are considering $\mathit{\alpha }=\frac{E_1{A}_1}{E_3{A}_3}=\frac{E_{1}T(\mathit{\xi })}{E_{3}T(\mathit{\xi })}\ast \frac{A_1}{A_3}=\frac{E_1[1-{\mathit{\delta }}_1(1-\mathit{\xi })]}{E_3[1-{\mathit{\delta }}_2(1-\mathit{\xi })]}\ast \frac{A_1}{A_3}=\frac{E_1}{E_3}\ast \frac{\frac{1}{{\mathit{\delta }}_2}-\frac{{\mathit{\delta }}_1}{{\mathit{\delta }}_2}\ast (1-\mathit{\xi })}{\frac{1}{{\mathit{\delta }}_2}-(1-\mathit{\xi })}\ast \frac{A_1}{A_3}$ where δ₁ and δ₂ are thermal gradient in the top and bottom layer, respectively.

The static stability of the system has been analyzed as follows.

Figure 2 addresses the effect of the shear parameter (g) on the static buckling loads. The non-dimensional static buckling load almost remains constant for the first two modes. The static buckling load for the third mode increases appreciably for higher values of g and the rate of increase being higher for the higher modes. Hence to increase the buckling effect of the system, g value should be more for higher modes.

Fig. 2

Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$with g (shear parameter)

When h₃₁ (as shown in Fig. 3) is increased, static buckling load decreases slowly for mode 1 and rapidly for modes 2 and 3. The rate of decrease is maximum for the highest mode for moderate $h_{31}$ values. For higher buckling effect of the system, the value of h₃₁ should be small.

Fig. 3

Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$ with h₃₁

Figure 4 shows the variation of the static buckling load with l_h1. The variation (increment) is a non-linear nature. With increase in the value of l_h1, the static buckling load increases. Hence for more static stability of the system, the value of l_h1 should be large.

Fig. 4

Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$ with l_h1

As shown in Fig. 5, the static buckling loads are almost independent of the core loss factor. This means static stability does not change with the variation of η.

Fig. 5

Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$ with η (core loss factor)

The static buckling loads ${({\overline{P}}_o)}_{\mathrm{crit}}$ are almost independent of the rotational spring constant K_r1 (as shown in Fig. 6).

Fig. 6

Variation of${({\overline{P}}_o)}_{\mathrm{crit}}$ with K_r1

Variation of the static buckling load with rotational spring constant K_r2 for mode 1 and mode 2 almost remains constant but for mode 3 shows a slight increasing trend, the rate of increase being higher for the higher mode (as shown in Fig. 7). K_r2 has very marginal incremental effect for the static stability of the model for higher modes.

Fig. 7

Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$ with K_r2

Increase of thermal gradient δ (when δ₁$>{\mathit{\delta }}_2)$ reduces static buckling load for all the mode (as shown in Fig. 8a). Also similar effects have been observed when δ₂$>{\mathit{\delta }}_1$(shown in Fig. 8b). For more static stability of the structure, the values of δ₁ and δ₂ should be small. The variation of static buckling load with K_t1 and K_t2 is similar to those of K_r1 and η, respectively, and those are not shown.

Fig. 8

a Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$ with δ₁ (first layer at a higher temperature). b Variation of ${({\overline{P}}_o)}_{\mathrm{crit}}$ with δ₂ (third layer at a higher temperature)

Conclusion

In this paper, a computational analysis of the static stability of an asymmetric sandwich beam with viscoelastic core is considered. The programming has been developed using MATLAB. The following are the conclusions drawn from the study.

For small values, g has a detrimental effect and for large values, it improves the static stability for higher modes. An increase in h₃₁ is seen to have a detrimental effect on the non-dimensional static buckling loads. Hence a symmetric beam is seen to have better resistance against static buckling. A higher l_h1 improves the buckling loads, however for small values, it has a detrimental effect. Static buckling loads are almost independent of core loss factor (η), rotational spring constant K_r1, and translational spring constants K_t1 and K_t2. Increase in K_r2 shows slight increasing trend for mode 3 only. Increase in thermal gradient (δ) reduces static buckling loads for all the modes.