Computational analyses of tail fin configurations for a sounding rocket

Abstract

Missiles and sounding rockets usually deviate from the trajectory due to unstable roll. Fins with cant angles are generally used to provide a rolling moment in sounding rockets and missiles to minimize the instability. Inducing a rolling moment also leads to an increase in the rocket motor’s power consumption due to the rise in drag, so inducing an optimal rolling moment with a minimal increase in drag is a crucial design criterion. It is crucial to maintain the similarity parameters while testing a scaled-down model in a wind tunnel. Therefore, computational fluid dynamics (CFD) is more efficient than extensive wind tunnel tests. In this paper, three-dimensional, incompressible simulations were performed on different models of sounding rockets using commercial CFD package fluent. The simulations were performed with the help of $k-\epsilon$ standard turbulence model. The results obtained were tabulated and graphically represented, and the trends of aerodynamic coefficients like $C_{\text {d}}$ and $C_{\text {m}}$ were analyzed. The purpose of this study is to analyze the dependency of aerodynamic coefficients on different fin configurations with emphasis on the cant angle. This study will be helpful to researchers designing a sounding rocket and help in maximizing apogee. The experimental and computational results show a favourable comparison. The results will show a particular configuration of fin having greater $C_{\text {m}}/C_{\text {d}}$ which yields in a greater rolling moment and least amount of drag.

1 Introduction

Sounding rockets are primarily used to perform scientific experiments at a certain altitude. The design and optimization are done through computational fluid dynamics and wind tunnel experiments. The fins of a sounding rocket play a crucial part in maintaining stability. The fins make sure that the center of pressure is held behind the rocket’s center of mass. A stable rocket flies smoothly and in a uniform direction, while an unstable rocket follows a wrong path, often tumbling or even flipping. The fins can be fixed to provide passive control or can be movable to provide active control. Movable fins create an angle between the root chord of the fins and the rocket’s longitudinal axis, known as the cant angle. As the cant angle increases, the rolling moment of the rocket increases hence the increase in angular momentum.

Although wind tunnel tests and actual flight tests can accurately simulate actual flight conditions, they are both expensive and time-consuming. With advancements in computer technology, several computational numerical techniques have been developed, which are cheap and fast, and can produce results with reasonable accuracy. Computational fluid dynamics is used to study airflow around a given body and its effects on it by discretizing the fluid domain into small elements and solving the governing equations in each of those elements [1]. Rodi [2] compared different turbulence models for modeling of incompressible flow and led us to the fact that the standard $k-\epsilon$ model will be more feasible for us, since it has been tested for a wide variety of flows, its requirement of low computational costs, and the ability to model many complex three-dimensional flows including those involving separation. Poroseva et al. [3] presented methods to improve the quality of CFD results for external flow problems, including boundary layer under adverse pressure gradients, by accurately predicting the mean velocity and shear-stress profiles which can be done by tweaking the model constants. Smith et al. [4] conducted a study on how manufacturing defects in cant fins would lead to an increase in roll rates associated with increased drag which leads to the motor under-performing, resulting in reduced vehicle apogee. A fin cant correction model was created based on the data collected from the predictions to obtain optimum roll rate. Stamminger et al. [5] used a mobile rocket base to launch a two-stage rocket with an irregular-shaped nosecone at hypersonic speeds. The first-stage fins are canted to induce spin for stability. Calculations are found based on CFD and wind tunnel testing that helped broaden our understanding of CFD methods and the effects of a canted fin on a sounding rocket. Initial CFD simulations were performed on the Sonda-III, a sounding rocket developed by the Brazilian Institute of Aeronautics and Space (IAE). The simulation results obtained were validated with wind tunnel tests conducted by Reis et al. [6] on a 1:11 scaled model.

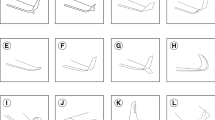
Simulation techniques used to simulate Sonda-III (elaborated in the Sect. 2) are used to simulate Phoenix, a sounding rocket developed by thrustMIT. Simulations have been performed on the two most commonly used types of fins: trapezoidal and elliptical, at three different aspect ratios, i.e., 0.5, 0.6, and 0.7 at cant angles of $0^{\circ }$, $2.5^{\circ }$, and $5^{\circ }$ at three different angles attack which are $0^{\circ }$, $3^{\circ }$ and $8^{\circ }$ to identify the most efficient type of fin that can be used on a sounding rocket. In the simulations performed, the clockwise rolling moment is considered to be positive.

A thorough and extensive review of previous literature was carried out and is summarized in the following paragraph. Fuller [7] studied the effects of different geometries of nose cone and fins on static stability by investigating the nonlinearities in pitching moments and found out that the changes in these did not have significant effects on improving the nonlinearities, although high aspect ratio fins improved directional stability and delayed the rolling moments at high angles of attack. Jones [8] investigated the aerodynamic properties of low aspect ratio wings and found out that the lift of such wings depends on the width. The span-wise loading does not depend on the plan form, and the lift distribution is not affected by the compressibility effects at subsonic and supersonic speeds. Hatalsky et al. [9] studied the effects of induced roll and roll lock for different fin designs, and brought out parameters such as taper ratio, aspect ratio, and sweep angles which helped to reduce roll lock and induced roll. Price et al. [10] conducted a study to investigate the effects of the flexibility of the body and fins and aerodynamic characteristics on roll resonance. Ma et al. [11] studied the effects of asymmetric transition on asymmetric vortices and found out their effects on side forces and also the effect of boundary layer transition on the vortices. DeSpirito et al. [12] conducted CFD simulations on canard guided-missile configuration to study its aerodynamic characteristics and flow field around it and found out an uneven distribution of pressure due to downwash and trailing vortices from canards which resulted in high side forces and induced rolling moments caused by interactions of these vortices with the planar tail fins. Both of these problems were solved by implementing grid fins instead of planar fins. Sigal [13] used a vortex lattice technique to study the roll characteristics of missiles for twelve configurations at different Mach numbers and found the results to be in good agreement with practical and CFD results. Stern et al. [14] have presented a comprehensive approach to procedures and methodology to verify and validate CFD simulations. The approach has applicability to a vast range of CFD codes. Pathan et al. [15] studied the variations of base pressure for internal and external flows at a wide range of Mach numbers and concluded that the base pressure variations for external flows for Mach numbers except those very close to unity could be analyzed by considering them as internal flow. Azlin et al. [16] performed CFD simulations, and found out aerodynamic characteristics of a wing fitted with winglets and their significance. Patel et al. [17] performed CFD simulations and found out aerodynamic characteristics of a symmetric airfoil at different angles of attack. Crippa et al. [18] studied the flow patterns over a delta wing with a blunt leading edge using the CFD technique. They studied the vortex formation at different angles of attack and surface flow patterns and found the location of origination of the vortices, and verified them with the experimental data. Menter et al. [19] performed CFD simulations on a variety of cases ranging from subsonic incompressible flow to high supersonic flows and the formulation of the method for different Mach regimes. All of the above-mentioned literature is focused on aerodynamic characteristics of fins of different geometries on sounding rockets and missiles in different flight regimes. These studies include roll characteristics, roll resonance, nonlinearities in aerodynamic coefficients, and wingtip vortices. Inducing a rolling moment also leads to an increase in drag due to the formation of wingtip vortices. Hence, a fin design that can induce roll with the slightest increase in drag is always desired. We have tried to contribute to this field by comparing $C_{\text {m}}/C_{\text {d}}$ ratio of different fin geometries, and the results can be used for designing aerodynamically efficient fins for roll control.

Murphy et al. [20] have presented methods for estimating mathematical models useful for stability and control analysis which can be applied to CFD simulations and wind tunnel experiments. Hossain et al. [21] has shown how to tabulate and analyze the CFD results. The importance of Reynolds averaged Navier-Stokes was understood from Jan Bartl et al. [22]. A good understanding of aerodynamic loads was found in Dongyang et al. [23] where they has used a movable canard surface. Based on these, the implementation and the numerical investigation of canted fins to improve the efficiency of the sounding rocket with lesser resources used for testing was the way forward.

2 Methodology

2.1 Geometric modelling

2.1.1 Sonda-III

The subscale model used by the Brazilian Institute of Aeronautics and Space (IAE) to perform wind tunnel experiments [6] is modeled on the commercial CAD software Autodesk Fusion 360 as seen in Fig. 1. The different models that were prepared are depicted in Table 1.

Fig. 1

CAD model of Sonda-III with a $5^{\circ }$ cant angle

Table 1 Model condition for Sonda-III

Fig. 2

CAD model for phoenix with trapezoidal fins (dimensions are in ‘mm’)

Fig. 3

CAD model for phoenix with elliptical fins (dimensions are in ‘mm’)

2.1.2 Phoenix

The sounding rocket Phoenix is modeled as a full-scale model on the CAD software Autodesk Fusion 360 with different fin configurations which are represented in Figs. 2 and 3. The different models that were prepared are depicted in Table 2.

2.2 Grid generation

2.2.1 Sonda-III

A tetrahedral mesh was used to discretize the domain. A face sizing was used on the rocket, to obtain a finer grid closer to the area of fins. An inflation was introduced near the surface of rocket to capture the boundary layer as seen in Fig. 4.

2.2.2 Phoenix

A similar meshing technique was used in Phoenix with the addition of a sphere of influence around the fins to capture the flow precisely, due to the fact that the simulations were performed on a full-scale model. This can be observed in Fig 5.

2.3 Boundary conditions

2.3.1 Sonda-III

The boundary conditions used for simulations depicted in Table 3, which were obtained from the wind tunnel experiments conducted by the Brazilian Institute of Aeronautics and Space (IAE) [1]. A cuboidal domain has been used to simulate Sonda-III, with the faces of the domain defined as follows:

• Inlet: velocity inlet

• Outlet: pressure outlet with gauge pressure = 0

• Operating pressure: 101,325 Pa

• Rocket wall: no-slip condition

• Turbulent viscosity ratio = 10

• Turbulent intensity = 5%.

For the coupling of pressure–velocity, “Simple Method” has been used. Pressure, momentum, turbulent kinetic energy, and turbulent dissipation rate were set to second-order upwind. The relaxation factors were kept as default.

2.3.2 Phoenix

A cuboidal domain has been used to simulate Sonda-III, with the faces of the domain defined as follows:

• Inlet: velocity inlet

• Outlet: pressure outlet with gauge pressure = 0

• Operating pressure : 101,325 Pa

• Rocket wall: no-slip condition

• Turbulent viscosity ratio = 10

• Turbulent intensity = 5%.

The boundary conditions defined are depicted by Table 4

For the coupling of pressure–velocity, “Simple method” has been used. Pressure, momentum, turbulent kinetic energy, and turbulent dissipation rate were set to second-order upwind. The relaxation factors were kept as default.

2.4 Forces and moments

The coefficients of forces and moments are calculated by Eqs. (1) and (2) [24, 25]. Considering reference values as defined in the previous section for each rocket.

Coefficient of drag:

$$\begin{aligned} c_{{\text {d}}} = \frac{ 2F_{{\text {d}}}}{ \rho u^2 A}. \end{aligned}$$

(1)

Coefficient of rolling moment:

$$\begin{aligned} c_{{\text {m}}} = \frac{2M}{ \rho u^2 {\text {Al}}}. \end{aligned}$$

(2)

2.5 Governing equations and turbulence modelling

The selection of an effective turbulence method to accurately predict the turbulent flow is an essential part of the successful simulation. The numerical simulation of the sounding rockets Sonda-III and Phoenix is performed on the FLUENT code. FLUENT uses the Finite Volume Method (FVM) to solve the incompressible form of the Reynolds Average Navier–Stokes (RANS) with turbulence models, as the flow being simulated is limited to 0.3 mach. In the description of the turbulence model, which is required to model the Reynolds stresses and the scalar transport terms, two extra transport equations are introduced in the form of the $k-\epsilon$ model.

The $k-\epsilon$ model has been used to perform simulations on both Sonda-III and Phoenix. $k-\epsilon$ has become one of the most commonly used turbulence modeling equations to solve many different engineering models. The $k-\epsilon$ model has been used to model with high accuracy relatively smaller pressure gradients, wall-bounded, and internal flows. The $k-\epsilon$ model cannot be extended to flows with gradients of detrimental pressure as the accuracy decreases.

Table 2 Model condition for phoenix

Fig. 4

Mesh for Sonda-III with a $5^{\circ }$ cant angle

Fig. 5

Mesh generated for Phoenix for a 0.6 aspect ratio trapezoidal fins with a $5^{\circ }$ cant angle

It involves two extra sets of transport equations, the equation for turbulent kinetic energy given by Eqs. (6) and (7) for turbulent dissipation rate along with continuity given by Eq. (3) and momentum by Eq. (4). The Reynolds Averaged Navier–Stokes equation is given by Eq. (5). The first transported variable is the turbulent kinetic energy K, which determines the energy in the turbulence. The second transported variable, in this case, is the turbulent dissipation rate $\epsilon$, which defines the scale of the turbulence. The governing equations therefore are as follows:

2.5.1 Continuity equation

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \frac{\partial }{\partial x_{j}} (\rho u_{j}) = 0. \end{aligned}$$

(3)

2.5.2 Momentum equation

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial t}\left( \rho u_i \right) + \frac{\partial }{\partial x_j} \left[ \rho u_i u_j + p \delta _{ij} - \tau _{ji} \right] = 0, \\&\quad i=1,2,3. \end{aligned} \end{aligned}$$

(4)

2.5.3 Reynolds averaged Navier–Stokes equations

$$\begin{aligned} \frac{ \partial \overline{u_{i}} }{\partial t} + \overline{u_{j}} \frac{ \partial \overline{u_{i}} }{ \partial x_{j} } = - \frac{1}{\rho } \frac{\partial \overline{p} }{ \partial x_{i} } + \frac{1}{\rho } \frac{\partial }{\partial x_{j}} \left( \mu \frac{\partial \overline{u_{i}}}{\partial x_{j}} - \rho \overline{u_i^\prime u_j^\prime } \right) . \end{aligned}$$

(5)

2.5.4 $k-\epsilon$ equations

• Turbulent kinetic energy:

  $$\begin{aligned} \frac{\partial k}{\partial t} + U_j \frac{\partial k}{\partial x_j}&= \tau _{ij} \frac{\partial U_i}{\partial x_j} - \epsilon \nonumber \\&\quad +\frac{\partial }{\partial x_{j}} \left[ ( \nu + \nu _{T} / \sigma _{k} ) \frac{\partial k}{\partial x_{j}} \right] . \end{aligned}$$

  (6)

• Turbulent dissipation rate:

  $$\begin{aligned} \frac{\partial \epsilon }{\partial t} + U_j \frac{\partial \epsilon }{\partial x_j}&= C_{\epsilon 1} \frac{\epsilon }{k} \tau _{ij} \frac{\partial U_i}{\partial x_j} - C_{\epsilon 2} \frac{\epsilon ^{2}}{k}\nonumber \\&\quad +\frac{\partial }{\partial x_j} \left[ ( \nu + \nu _{T}/\sigma _{\epsilon } ) \frac{\partial \epsilon }{\partial x_{j}} \right] . \end{aligned}$$

  (7)

  These equations contain dimensionless constants. The standard $k-\epsilon$ model employs values for the constants that are arrived at by comprehensive data fitting for a wide range of turbulent flows

  $$\begin{aligned}&\!\!\!C_{\epsilon 1} = 1.4, C_{\epsilon 2} = 1.92, C_{\mu } = 0.09, \sigma _{k} = 1.0\\&\!\!\!\sigma _{\epsilon } = 1.3,\omega = \epsilon / {C_{\mu } k}, l = C_{\mu } k^{3/2} / \epsilon . \end{aligned}$$

The below-mentioned constants allow for the correct proportionality between the terms in the k and $\epsilon$ equations [1]

$$\begin{aligned} C_{\epsilon 1},C_{\epsilon 2}. \end{aligned}$$

3 Grid test and validation

To ensure that CFD results are mesh independent, the mesh density in the Sonda-III CFD model was adjusted from 2,607,887 to 4685962. The drag coefficient is calculated for various mesh densities, as shown in the table. When the number of elements is increased from 4,211,112 to 4,685,962, the variance in coefficient of drag is just about $-0.07$%. For all subsequent investigations, the CFD model is meshed with at least 4,211,112 elements. To accommodate the cant in the fins, additional elements are provided. The simulations performed with different elements are shown in Table 5.

Table 3 Operating conditions and reference values for Sonda-III

Table 4 Operating conditions and reference values for Phoenix

Table 5 Grid dependence study

4 Results and discussion

A total of 63 simulations were performed, nine simulations were performed on Sonda-III to validate the wind tunnel data, and 54 simulations were performed on Phoenix on the various fins settings. On all the simulations that were completed, the scaled residuals were observed to stagnate. Surface monitors of drag and roll moment were introduced. Both pressure and viscous effects were considered during the calculation of drag and rolling moment coefficients.

It was observed that these surface monitors remained constant for the better part of the last 300 iterations. This was used to determine the solution as a converged solution.

4.1 Sonda-III

The coefficients of drag and the coefficients of rolling moment obtained through CFD simulations and wind tunnel tests are tabulated in Tables 6 and 7, respectively. Column three in both the tables show the values obtained from CFD simulations, and column four represents the values obtained from the wind tunnel test [6]. It can be seen that the results obtained from CFD simulations and the results obtained from the wind tunnel tests are very close and are within the permissible limit of error.

The possible reason for error between the results of CFD and wind tunnel data is the usage of the standard k $\epsilon$ turbulence model for modelling turbulence. The non-zero values of the rolling moment for zero fin cant angle in the wind tunnel data can be accounted for manufacturing irregularities of the test model.

Table 6 Comparison of coefficient of drag between CFD results and wind tunnel results

Table 7 Comparison of coefficient of moment between CFD results and wind tunnel results

The flow can be observed by the velocity contour shown in Fig. 6. This is the general trend for the flow properties that is observed in all the nine cases.

Fig. 6

Velocity contour of Sonda-III at $5^{\circ }$ cant and $0^{\circ }$ angle of attack

Fig. 7

Graph of $C_{\text {d}}$ versus angle of attack for 0.5 aspect ratio of trapezoidal fins

Fig. 8

Graph of $C_{\text {m}}$ versus angle of attack for 0.5 aspect ratio of trapezoidal fins

Fig. 9

Graph of $C_{\text {d}}$ versus angle of attack for 0.6 aspect ratio of trapezoidal fins

Fig. 10

Graph of $C_{\text {m}}$ versus angle of attack for 0.6 aspect ratio of trapezoidal fins

Fig. 11

Graph of $C_{\text {d}}$ versus angle of attack for 0.7 aspect ratio of trapezoidal fins

Fig. 12

Graph of $C_{\text {m}}$ versus angle of attack for 0.7 aspect ratio of trapezoidal fins

Fig. 13

Graph of $C_{\text {d}}$ versus angle of attack for 0.5 aspect ratio of elliptical fins

Fig. 14

Graph of $C_{\text {m}}$ versus angle of attack for 0.5 aspect ratio of elliptical fins

Fig. 15

Graph of $C_{\text {d}}$ versus angle of attack for 0.6 aspect ratio of elliptical fins

Fig. 16

Graph of $C_{\text {m}}$ versus angle of attack for 0.6 aspect ratio of elliptical fins

Fig. 17

Graph of $C_{\text {d}}$ versus angle of attack for 0.7 aspect ratio of elliptical fins

Fig. 18

Graph of $C_{\text {m}}$ versus angle of attack for 0.7 aspect ratio of elliptical fins

Fig. 19

Velocity contour of Phoenix with trapezoidal fins 0.5 aspect ratio at $5^{\circ }$ cant and $0^{\circ }$ angle of attack

Fig. 20

Velocity contour of Phoenix with elliptical fins 0.6 aspect ratio at $2.5^{\circ }$ cant and $0^{\circ }$ angle of attack

Table 8 Ratio of $C_{\text {m}}$ to $C_{\text {d}}$ to identify the optimal fin set and fin setting

4.2 Phoenix

Results obtained from the CFD simulations of Phoenix are graphically represented from Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, and 18. These graphs have the angle of attack in degrees on the X-axis and the coefficient of drag on the Y-axis for one case and the coefficient of rolling moment on the Y-axis for the other case.

The flow can be observed by the velocity contour shown in Figs. 19 and 20 for a trapezoidal fin set and an elliptical fin set, respectively. This is the general trend for the flow properties that is observed in all the 54 cases.

Table 8 gauges the ratio of coefficient of rolling moment to the coefficient of drag for all the cases simulations were performed on.

5 Conclusion

In accordance with the results obtained from CFD simulations, a significant increase in the coefficient of drag is observed in both trapezoidal as well as elliptical fin sets, with an increase in the angle of attack and the cant angle in all cases for a particular aspect ratio. It can be visualized with the help of a quadratic equation, which is obtained by curve fitting.

It is observed for the trapezoidal fin set and elliptical fin set for a particular aspect ratio that increasing the cant angle increases the coefficient of rolling moment. For all the cant angles, the increase in the angle of attack results in a very non-significant increase in the coefficient of rolling moment. Hence, $C_{\text {m}}/C_{\text {d}}$ ratio decreases with increase in angle of attack for a given fin.

It can be observed a higher $C_{\text {m}}/C_{\text {d}}$ ratio for a trapezoidal fin set when compared with the elliptical fin set, which gets predominant with an increase in the aspect ratio of the fins. This parameter will help in evaluating the most optimum fin configuration that will be required. In the elliptical fin set, we can observe lesser drag; hence, higher $C_{\text {m}}/C_{\text {d}}$ ratio is expected, but in contrast, the trapezoidal fin set shows higher $C_{\text {m}}/C_{\text {d}}$ which concludes that for a given aspect ratio, the trapezoidal fin set provides higher rolling moment.