1 Introduction

Optimization is a sort of decision-making and one of the essential quantitative techniques in decision-making machinery. Under specific predetermined conditions, decisions must be made to optimize one or more objectives. Most real-world problems may be stated in optimization models, including numerous criteria and goals [1]. Optimization techniques are based on biology, artificial intelligence, nature, and scientific areas such as physics, chemistry, etc. [2]. The scope of research with optimization is vast. Optimization methods can solve problems from linear programming, integer programming, quadratic programming, non-convex optimization, engineering, science, and economics, etc. Solving these problems becomes more complicated when the nature of the problem cannot be known in advance. Without knowing the nature of the problem, it is also tough to select a proper method for finding the solution [1].

Furthermore, an equilibrium between exploration and exploitation, also known as global and local search, is critical in any optimization approach. An algorithm must maintain a healthy balance between exploration and exploitation to be effective [3]. According to the theory of "No Free Lunch" (NFL) [4], theorems, no algorithm can solve problems of all types with equal efficiency. Even the same algorithm may give different solutions based on different parameter values. This has led to the development of new algorithms and their modified forms by researchers worldwide. The last few decades have seen a surge in developing algorithms classified as meta-heuristics.

Meta-heuristic methods being different from deterministic methods can search the global solution without gradient information of the optimization issue [5]. The Differential Evolution (DE) technique is a part of evolutionary programming. It is designed by R. Storn and K. Price [6] to optimize issues over the continuous field. In DE, the worth of every variable is a real number. DE utilizes mutation and selection during the search to guide the pursuit toward the potential zone. The standard DE method comprises four essential phases—initialization of population, calculation of donor vector, the crossover between donor vector and target vector to form a trial vector, selection of target vector for the next generation from trial vector, and target vector of the present generation. The last three stages of DE execute as a circle for ensuing DE generations until a termination criterion is triggered.

1.1 Advantages and Disadvantages of DE

DE is a powerful and valuable global optimizer. DE is a population-based method that belongs to the evolutionary algorithm’s category. In DE, siblings are formed by disrupting the arrangements with a scaled distinction between two randomly selected individuals from the population. It distinguishes DE from other evolutionary methods. DE employs a process of coordinated substitution. "On the off occasion that the trial vector is superior to the parent solution, it is chosen." In contrast to a few other evolutionary calculation methods, DE is a simple method that can be implemented with a few lines of code in any standard programming language. Also, DE requires not many control parameters (3 to be exact: the scale factor, the crossover rate, and the population size) a component that makes it simple to use for the experts", as per Das et al. [7]. The authors likewise referenced that "no other single search paradigm has been able to secure competitive ranking in nearly all the CEC competitions on a single objective, constrained, dynamic, large-scale, multi-objective, and multimodal optimization problems." DE is exceptionally adequate to researchers and specialists because of its reliability and high performance; Neri et al. [8]. The writers of the similar article likewise called attention to the explanation for the massive achievement of DE is a suggested self-variation delimited in the design of the actual DE technique. As solutions are spread inside the pursuit space, the algorithm should be explorative in its beginning phase. In the later stage of the optimization process, exploitation is fundamental. DE is profoundly explorative toward the start of the process, and bit by bit, it becomes exploitative.

Regardless of these benefits, DE has a couple of burdens. It tends to be composed that the search process is indeed negotiated if promising arrangements are not discovered in hardly any explorative moves. The proficient working of DE relies upon the three control parameters referenced previously. The population size is related to the possible moves. A small population can have a predetermined number of developments, and an enormous population has numerous exercises. If the population is small, that may lead to premature convergence, Eiben et al. [9]. The scaling factor and crossover rate value play a crucial role in the algorithm's well-functioning. Still, the selection of these values is a tedious task. The problem of parameter setting can be typical while solving real-life optimization problems with larger dimensions; the risk of stagnation increases in DE with increased dimensionality, Zamuda et al. [10]. Not only the dimensionality problem, but DE is also inefficient in noisy optimization problems. Standard DE can fail in handling the noisy fitness function, Krink et al. [11]. Based on the above facts, the scientific community is aware that although DE is a decent algorithm, there is extensive scope for updating the algorithmic structure.

1.2 Types of Modifications on DE

Several works on DE have been done over the previous 2 decades, and new modified forms of DE have been proposed using the methodologies which are mentioned in following subsections. Also, a pictorial representation of different DE variants using different strategies is shown in Fig. 1.

Fig. 1
figure 1

Percentage of different DE variants developed using various strategies

Full size image

1.2.1 Modification in Population Initialization

In population-based search methods, the initial population generated through the system produced arbitrary numbers that generally follow a uniform distribution. However, this is a straightforward strategy for instating the population; specialists saw that altering the introduction interaction may help in improving the effectiveness of the method. Therefore, an assortment of initialization techniques has been proposed in the literature. For the most part, these changes depend on one or the other contracting the search space before all else itself to empower quicker convergence or, again, depend on isolating the population into more modest subgroups of populations that can simultaneously tune the population adaptively.

1.2.2 Alteration in Mutation Strategy

The mutation phase of DE is the most important, since it introduces a new individual into the population. The nature of the problem determines the choice of mutation strategy. The amplification factor's strategy determines the population's diversity. The researchers put a lot more work into designing algorithms by changing current methods, merging many techniques in one algorithm, and adaptively determining the strategy.

1.2.3 Variation in Crossover Strategy

The trial vector is created from the donor and target vector using the crossover approach. Exponential crossover is used in the original DE. Later on, the binomial kind of crossover gained prominence. Since DE's debut, scholars have proposed several crossover approaches.

1.2.4 Change in the Selection Strategy

DE has a novel selection mechanism that isolates it from other methods. Even though alterations proposed in the selection mechanism are restricted to a couple of papers, analysts have shown that reasonable changes can also help improve the method's efficacy.

1.2.5 Variation in Choosing the Parameter

Parameters are the essential elements of an evolutionary process. Canonical DE uses three basic parameters, mutation factor, crossover rate, and population size. The selection of parameters can be deterministic, adaptive, or self-adaptive. In deterministic parameter selection, values are modified using some deterministic rule after a fixed number of generations is elapses. Adaptive parameter selection is when parameters are changed according to feedback from the search process. During self-adaptation, parameters encoded into the chromosomes, the better value of these parameters produces better offspring, propagating to the next generation.

1.2.6 Hybridization

Sometimes the effectiveness of an algorithm may be increased in terms of convergence speed, computational complexity, ability to get out from local optima, identifying the stagnation, etc., by utilizing the working procedure of one or more other algorithms. Therefore, hybridization is the technique of merging two or more algorithms to design a robust method.

1.3 Few Works on Verification of Performance and Real-World Problem Solving

A reasonable number of surveys using the basic meta-heuristic algorithms or their variants have been carried out. Nama et al. [12] studied the performance of Harmony Search Algorithm (HSA), Teaching–Learning Based Optimization (TLBO), and Particle Swarm Optimization (PSO) for finding the total active earth force on the back of a retaining wall. Yildiz et al. [5] solved six mechanical engineering problems utilizing ten meta-heuristics and presented a comparative study on their effectiveness. Kashani et al. [13] evaluated the uses of PSO on geo-specialized issues and finally offered a comparative study solving three geotechnical engineering problems using the PSO variants. Foroutan et al. [14] proposed the green hybrid traction power supply substation model and investigated the performance of a few recent optimization algorithms on the problem. The effect of various nature-inspired algorithms on intrusion detection problems is tested by Thakur & Kumar [15]. Effectiveness of some recently designed algorithms and few DE variants tested on economic optimization of cooling tower problem by Patel et al. [16]. Performance of 12 meta-heuristics on wind farm layout optimization problem studied by Kunakote et al. [17]. Nama et al. [18] modified the Backtracking Search algorithm (BSA), incorporating a new adaptive control parameter, and used the modified method to determine active earth pressure on retaining wall supporting c-Ф backfill using the pseudo-dynamic method. Demirci and Yıldız [19] designed a novel hybrid approach, referred to as Hybrid Gradient Analysis (HGA) which is introduced for the evaluation of both convex and concave constraint functions in Reliability-Based Design Optimization (RBDO). Yıldız et al. [20] developed Henry Gas Solubility Optimization (HGSO) algorithm and solved the shape optimization of a vehicle brake pedal. Champasak et al. [21] designed a new self-adaptive meta-heuristic based on decomposition and solved unmanned aerial vehicle (UAV) problem with six objective functions. Sharma et al. [22] integrated the mutualism phase of the SOS algorithm with BOA and optimized some engineering design problems. Yildiz et al. [23] used the Butterfly Optimization Algorithm (BOA) to optimize coupling with a bolted rim problem. They also used it to solve the shape optimization of a vehicle suspension arm. Nama et al. [24] introduced a new variant of Symbiotic Organisms Search (SOS) algorithm with self-adaptive benefit factors and modified the mutualism phase. The authors used the new algorithm to solve five real-world problems. Yıldız et al. [25] used Equilibrium Optimization Algorithm (EOA) to solve a structural design optimization problem for a vehicle seat bracket. Yıldız et al. [26] used the Sine Cosine Algorithm (SCA) to solve the shape optimization of a vehicle clutch lever. Panagant et al. [27] used Seagull Optimization Algorithm (SOA) to solve the shape optimization of a vehicle bracket. The design problem is to find structural shape while minimizing structural mass and meeting a stress constraint. Dhiman et al. [28] introduced the evolutionary multi-objective version of the Seagull Optimization Algorithm (SOA), entitled Evolutionary Multi-objective Seagull Optimization Algorithm (EMoSOA). Twenty-four benchmark functions and four real-world engineering design problems are validated using the proposed algorithm. Chakraborty et al. [29] designed a modified WOA and applied it to optimize real-world problems from civil and mechanical engineering disciplines. Yıldız et al. [30] developed a new approach based on the Grasshopper Optimization Algorithm and Nelder–Mead Algorithm to optimize robot gripper problem with a fast and accurate solution. Additionally, vehicle side crash design, multi‐clutch disk, and manufacturing optimization problems were also solved with the developed method. Sharma et al. [31] designed a balanced variant of BOA incorporating mutualism and parasitism phases of SOS with the basic BOA. Image segmentation problem with multilevel thresholding approach was solved using the new algorithm. Chakraborty et al. [32] modified the Whale Optimization Algorithm (WOA) and segmented the COVID-19 X-ray images to diagnose the disease easily.

Though all the CEC-winning algorithms are highly efficient in solving optimization problems, comparing performance among these efficient algorithms can be an attractive effort. With this motivation in this study, DE and its eight CEC-winning variants, SaDE, jDE, SHADE, LSHADE, LSHADE-EpSin LSHADE-cnEpSin, LSHADE-SPACMA, and ELSHADE-SPACMA, are selected for the experiment. Table 1 displays the rank of the algorithms and the year of holding the position. First, CEC 2019 and CEC 2020 bound-constrained suite is evaluated using the chosen methods, and then, a total of six real-world problems are solved. Among the problems selected, one is an unconstrained problem from CEC 2011 problem suite and five other constrained mechanical engineering design problems. Four mechanical engineering problems are taken from CEC 2020 non-convex constrained optimization suite. Statistically, the performance of the algorithms is analyzed using non-parametric tests like Friedman's test and Wilcoxon test.

Table 1 List of DE variants employed
Full size table

The rest of the paper is organized as follows: Sect. 2 summarizes the algorithms employed here for comparison. Evaluated IEEE CEC 2019 and CEC 2020 results are tabulated, and a discussion on the results is given in Sect. 3. Section 4 represents a brief discussion of the real-world problems employed and a discussion on the results evaluated by the algorithms. Statistical analysis of the evaluated numerical data is carried out in Sect. 5. Discussion on the evaluated run time of the real-world problems is given in Sect. 6. Section 7, finally, concludes the study with future extensions.

2 Brief Description of DE and Its Variants Employed

A brief description of DE and its CEC-winning variants preferred here for comparison is given in this section.

2.1 Differential Evolution (DE) [6]

Differential Evolution is a population-based, stochastic optimization algorithm. It is used for solving the nonlinear optimization problem. It is a parallel direct search technique that uses population size (\({N}_{p}\)) parameter vectors as a population for each generation. Here, weighted difference vector between two population members is added to a third member to produce a new parameter vector. The resultant vector, having a lower objective function value than a predetermined population member, is selected. This selected vector will replace the vector with which it has been compared in the next generation. The performance of DE depends on the proper selection of the trial vector generation technique and corresponding control parameter values. Finding of most suitable method and associated parameter settings in a trial-and-error approach involves more computational costs. Different approaches may need to couple with different parameter settings in various stages of evolution to get the best performance. DE has three steps in each generation: mutation, crossover, and selection. In the mutation phase, each individual in the population produces a respective mutation vector based on some strategy. The mutation vector and target vector exchange internal components during crossover to create a resultant vector. The selection step decides which vectors enter the next generation using greedy binary selection between the target and trial vectors. \(DE/rand/1\) is the mutation strategy used in basic DE. Later on, this strategy is altered using diverse concepts to modify the DE algorithm. The well-known mutation strategies used in DE algorithms are given below

$$rnd/1/bml:$$
$${{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}={{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}1}^{{\varvec{k}}}+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}2}^{{\varvec{k}}}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}3}^{{\varvec{k}}}\right);$$
(1)
$$rnd/2/ bml:$$
$${{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}={{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}1}^{{\varvec{k}}}+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}2}^{{\varvec{k}}}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}3}^{{\varvec{k}}}\right)+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}4}^{{\varvec{k}}}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}5}^{{\varvec{k}}}\right);$$
(2)
$$Best/1/ bml:$$
$${{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}={{\varvec{p}}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}^{k}+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}1}^{k}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}2}^{k}\right);$$
(3)
$$Best/2/ bml:$$
$${{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}={{\varvec{p}}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}^{k}+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}1}^{k}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}2}^{k}\right)+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}3}^{k}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}4}^{k}\right);$$
(4)
$$Current-to-best/1/ bml:$$
$${{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}={{\varvec{p}}}^{k}+F.\left( {{\varvec{p}}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}^{k}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}1}^{k}\right)+F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}2}^{k}-{{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}3}^{k}\right);$$
(5)
$$Current-to-pbest/1/ bml:$$
$${{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}={{\varvec{p}}}^{k}+F.\left( {{\varvec{p}}}_{\mathbf{b}\mathbf{e}\mathbf{s}\mathbf{t}}^{k}-{{\varvec{p}}}^{{\varvec{k}}}\right)+ F.\left( {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}1}^{k}- {{\varvec{p}}}_{\mathbf{r}\mathbf{n}\mathbf{d}2}^{k}\right).$$
(6)

In the above equations, \({p}^{k}\) is the kth solution of the population \((P)\) and \({{{\varvec{p}}}^{\boldsymbol{^{\prime}}}}^{\left(k\right)}\) is the donor vector. Crossover types used in DE can be binomial or exponential. Here, \(bml\) signifies the binomial crossover.

2.2 Differential Evolution Algorithm with Strategy Adaptation (SaDE) [33]

Trial vector generation methods and related control parameters are slowly self-adapted by learning from their past experiences in the Self-adaptive DE (SaDE) technique to produce the best solutions. It keeps a candidate pool of many powerful trial vector generation techniques. A particular method is selected from the candidate pool in the evolution process for each target vector in the present population. The collection contains four mutation strategies, namely, \("DE/rand/1/bin, DE/rand-to-best/2/bin, DE/rand/2/bin,\) and \(DE/current-to-rand/1".\) A technique is chosen based on past probability learned of producing favorable solutions, and this is applied to perform mutation operation. To generate a trial vector in the SaDE algorithm, control parameters are assigned probabilistically to each target vector in the present population. The probabilities are slowly learned from the experience to produce better solutions. Here, the parameter resembled a normal distribution with a mean value of 0.5 and a standard deviation of 0.3. A batch of values is sampled randomly and used in each target vector in the present population. In this way, for small values, ' exploitation' and large values' exploration' are maintained throughout the evolution process.

2.3 Self-adapting Control Parameters in Differential Evolution (jDE) [34]

It is one of the most efficient DE variants. jDE uses a self-adaptive control technique to change the control parameters. The control parameters are adjusted with the Evolution. Here, user needs not to assume the appropriate values, which are problem-dependent. This technique changes the control parameters \(F\) and \({c}^{r}\) during the run. The third control parameter \({N}_{p}\), the number of members in a population is not changed during the run. The control parameters \(F\) and \({c}^{r}\) are adjusted during the evolution process, and both are applied at each level. The upper and lower value of \(\mathrm{F}\) is 0.1 and 0.9, respectively. \({c}^{r}\) takes a value between (0,1). \(F\) and \({c}^{r}\) are evaluated using the following equations:

$${F}_{g+1}^{k}=\left\{\begin{array}{l}{F}_{l}+rnd* {F}_{u}\, if\, rnd<{\varnothing }^{1}\\ {F}_{g}^{k}\, Otherwise\end{array}\right.$$
(7)
$${C}_{g+1}^{r (k)}=\left\{\begin{array}{l}rnd\, if\, rnd<{\varnothing }^{2}\\ {C}_{g}^{r (k)}\, Otherwise\end{array}.\right.$$
(8)

Value of \({\varnothing }^{1}\) and \({\varnothing }^{2}\) remain fixed, and it is 0.1. Superior values of these control parameters generate better individuals. This individual produces offspring and propagates these better parameter values. In this approach, multiple runs are not needed to adjust control parameters. Self-adaptive DE is more independent than DE.

2.4 Success-History-Based Parameter Adaptation for Differential Evolution (SHADE) [35]

SHADE is a kind of adaptive DE. The origin of this algorithm is JADE and uses the \(current-to-pbest/1\) mutation strategy, an external archive, and adaptively controls the parameter values \(F\) and \({c}^{r}\). It uses a historical memory of successful control parameter settings to guide the selection of future control parameter values. It uses a historical memory \({M}_{c}r \& {M}_{F}\) that stores set of \({c}^{r}\) & \(F\) values which achieved a better result in the past. The SHADE approach maintains a historical memory with H entries for both DE control parameters. New \({c}^{r}\) & \(F\) pair is assessed directly by sampling the parameter space close to one of these stored pairs as per the following equations:

$${c}_{i}^{r}=\left\{\begin{array}{l}0 , if\, {M}_{{c}^{r},r{nd}_{i}}=\perp \\ rnd{n}_{i}\left({M}_{{c}^{r},r{nd}_{i}},0.1\right), other wise\end{array},\right.$$
(9)
$${F}_{i}=rnd{c}_{i}(\left({M}_{F,r{nd}_{i}},0.1\right).$$
(10)

In any case, if the value of \({\mathrm{c}}_{\mathrm{i}}^{\mathrm{r}}\) goes outside [0,1], replaced by the value 0 or 1, which is near the generated value. If the value of \({F}_{i}>1\), it is transformed to 1, and when \({F}_{i}\le 0\), eqn. \((x)\) is executed repeatedly to generate a legal value. The parameter \(p\), which is used to adjust the greediness of the current-to-best/1 mutation strategy, is set for each solution in the population using the equation

$${p}^{\mathrm{i}}=rnd\left[{p}^{\mathrm{min}},0.2\right].$$
(11)

2.5 Improving the Search Performance of SHADE Using Linear Population Size Reduction (LSHADE) [36]

L-SHADE is the extended version of SHADE with Linear Population Size Reduction (LPSR). It is a simple deterministic population resizing method that continuously reduces population size according to a linear function. LPSR method is a simplified, particular case of SVPS, which reduces the population linearly as a function of the number of fitness evaluations and requires only one parameter (initial population sizes). In LSHADE, minimum size of the population is defined in advance. Reduction of population increases the algorithm's convergence speed and decreases the computational complexity. Excluding the population reduction process, the search steps of LSHADE are precisely the same as SHADE. Population reduction is accomplished in the algorithm using the formula

$${N}_{p,g+1}=\left[\mathrm{round}\left(\frac{{N}_{p}^{\mathrm{min}}-{N}_{p}^{\mathrm{initl}}}{maxnfes}\right)*nfe+{N}_{p}^{\mathrm{initl}}\right].$$
(12)

Whenever \({N}_{p,g+1}<{N}_{p,g}\), then \({N}_{p,g}-{N}_{p,g+1}\); the number of population is deducted from the population.

2.6 An Ensemble Sinusoidal Parameter Adaptation Incorporated with L-SHADE (LSHADE-EpSin) [37]

In the LSHADE-EpSin approach, a different parameter adaptation technique is used to select control parameters to perform better than the L-SHADE algorithm. Like LSHADE, it also uses \(DE/current-to-pbest/1\) mutation strategy. The proposed algorithm uses a new ensemble sinusoidal approach to adapt the DE algorithm's scaling factor automatically. This ensemble technique combines two sinusoidal formulas: (i) a non-adaptive sinusoidal decreasing adjustment and (ii) an adaptive history-based sinusoidal increasing adjustment. These two strategies were used to generate scaling factor for each solution of the population during the first half of the iteration process using the following equations:

$${F}_{g}^{i}=\frac{1}{2}*\left(\mathrm{sin}\left(2\pi *\mathrm{freqn}*g+\pi \right)*\frac{{g}_{\mathrm{max}}-g}{{g}_{\mathrm{max}}}+1\right)$$
(13)
$${F}_{g}^{i}=\frac{1}{2}*\left(\mathrm{sin}\left(2\pi *{\mathrm{freqn}}_{i,g}*g+\pi \right)*\frac{g}{{g}_{\mathrm{max}}}+1\right);$$
(14)

\(\mathrm{freqn}\) in Eq. (13) represents the frequency of sinusoidal function and \({\mathrm{freqn}}_{\mathrm{i}}\) in Eq. (14) is an adaptive frequency estimated using an adaptive scheme. At every generation \({\mathrm{freqn}}_{i,g}\) is calculated using a Cauchy distribution. During the second half of the search process, \(F\) & \({c}^{r}\) is estimated using Cauchy and normal distributions, respectively. This sinusoidal ensemble approach aims to find an effective balance between exploiting the already found best solutions and exploring non-visited regions. The Gaussian walks-based local search method is used to increase the exploitation ability of the process. In this method, a self-adaptive system is used to adapt the control settings during the search. A new ensemble of adaptive version sinusoidal techniques is used to adjust the scaling factor values automatically.

2.7 Ensemble Sinusoidal Differential Covariance Matrix Adaptation with Euclidean Neighborhood (LSHADE-cnEpSin) [38]

This algorithm is an enhanced version of LSHADE-EpSin. The modification is based on two main changes, like an ensemble of sinusoidal approaches based on performance adaptation and covariance matrix learning for the crossover operator. Non-adaptive sinusoidal decreasing adjustment and an adaptive sinusoidal increasing adjustment are used to adapt the scaling factor. In this method, a performance adaptation mechanism based on previous success selects the sinusoidal waves. To set up a satisfactory coordinate system and improve LSHADE-EpSin, covariance matrix learning with the Euclidean neighborhood is used for the crossover operator. This will tackle issues with high correlation among the variables. In this technique, the individuals are first sorted according to their function values, and the best individual, P, is marked. After that, the Euclidean distance is calculated between P and every other individual in the population. Finally, the individuals are sorted based on their Euclidean distance.

2.8 LSHADE with Semi-parameter Adaptation Hybrid with CMA-ES (LSHADE-SPACMA) [39]

It is a hybrid variant of LSHADE-SPA and modified CMA-ES. LSHADE-SPA was proposed with a semi-parameter adaptation scheme to generate scaling factor. Two different strategies were adopted for estimation of \(F\) & \({c}^{r}.\) During the first half of the iteration process, \(\mathrm{F}\) & \({\mathrm{c}}^{\mathrm{r}}\) are evaluated using the formulas given below

$${F}^{i}=0.45+0.1*rnd$$
(15)
$${C}^{r\left(i\right)}=rndn\left({M}_{c}r\left(i\right),0.1\right);$$
(16)

\({M}_{c}r\left(i\right)\) is the position selected arbitrarily from the pool of successful mean values. \(rnd,\) here, is a random number between (0,1). During the second half of the search process, the estimation process of \({C}^{r}\) does not change, and scaling factor is selected using Cauchy distribution as per the following equation:

$${F}^{i}=rndc\left({M}_{{F}^{i}},\partial \right),$$
(17)

\(\partial\) here denotes the standard deviation. After every iteration, Lehmer mean is evaluated using successful \({F}^{i}\) values and one position of \({M}_{F}\) is updated. LSHADE-SPA and modified CMA-ES are hybridized and named LSHADE-SPACMA. The modified CMA-ES goes through the crossover operation to enhance the exploration capability. In this approach, both techniques work parallelly on the same population, and more solutions from the population will be allocated slowly to the algorithm with better performance.

2.9 Enhanced LSHADE-SPACMA Algorithm (ELSHADE-SPACMA) [40]

An Enhanced LSHADE-SPACMA technique is the improved variant of LSHADE-SPACMA. In this approach, the \(p\) value of the \(DE/current-to-pbest/1\) strategy responsible for the greediness of the mutation strategy is made dynamic. The larger value of \(p\) enhances the exploration, and smaller values will enhance the exploitation. \(p\) is calculated using the following equation:

$${p}_{{\varvec{g}}+1}=\left[\mathrm{round}\left(\frac{{p}_{\mathrm{min}}-{p}_{\mathrm{initl}}}{maxnfes}\right)*nfe+{p}_{\mathrm{initl}}\right];$$
(18)

\({p}_{\mathrm{initl}}\) and \({p}_{\mathrm{min}}\) symbolizes the initial and minimum value of the variable. Again, a directed mutation strategy has been added within the hybridization framework to improve the performance. Dual enhancement is done for better performance improvement of LSHADE-SPACMA. First, 50% of each LSHADE-SPACMA and AGDE algorithm is integrated into a hybridized framework. In this process, the population is shared alternatively among the algorithms. The second adjustment is the evaluation of \(p\) according to the behavior of ELSHADE-SPACMA. Value of \(p\) starts with a bigger value to increase exploration and reduces linearly later on. This technique improves the explorative capability at the end of the search.

3 Experimental Results and Discussion on IEEE CEC 2019 and CEC 2020 Functions

The selected algorithms are first tested with IEEE CEC 2019 [41] function suite. The suite contains ten complicated multimodal functions. Then, the IEEE CEC 2020 [42] bound-constrained functions are evaluated. This function set contains unimodal, basic, hybrid, and composite categories functions. In this paper, the function set is assessed using dimension 20. Appendix-I represents the function sets used for the comparison. The termination criteria are set as D*10,000 function evaluations for all the comparison algorithms during the IEEE function evaluation. The parameters of all the chosen algorithms were kept the same as advised in the respective original study. The results are collected as the average value of 30 independent runs. The experiment's device configuration consists of MATLAB version R2015a with an Intel i3 processor, 8 GB DDR-4 RAM, and operating system Windows10.

3.1 Comparison Using IEEE CEC 2019 Functions

DE and its variants were used to examine the results, as shown in Table 2. The table shows the average (avg), standard deviation (sd), and best (bst) values calculated by the algorithms for each of the functions. "NA" represents a function that an algorithm cannot evaluate. An equivalent value denoted by the symbol ≈. SHADE, LSHADE-SPACMA, LSHADE-cnEpSin, and ELSHADE-SPACMA outperform comparison algorithms on 3, 1, 1, and 3 functions, respectively, according to Table 2. SHADE calculates the minimal optimal value on F2, F3, and F5. LSHADE-SPACMA and LSHADE-cnEpSin determine the ideal value for functions F4 and F9. ELSHADE-SPACMA generates the minimum value for functions F7, F8, and F10. The function F1 cannot be evaluated using the LSHADE-cnEpSin algorithm. On functions F1 and F6, just a few algorithms produce identical optimal values. SHADE and ELSHADE-SPACMA were created as the best-performing algorithms. DE and jDE appeared as the worst algorithms, since they generated maximum value on four functions.

Table 2 Comparison of evaluated results on IEEE CEC 2019 function suite
Full size table

3.2 Comparison Using IEEE CEC 2020 Functions

DE and its variants were used to examine the results, as shown in Table 3. The same optimal value evaluated by many algorithms is an equivalent value denoted by the sign ≈. Table 3 show that DE, SHADE, LSHADE-EpSin, LSHADE-SPACMA, and LSHADE-cnEpSin outperform comparison algorithms on the 2, 3, 1, 1, and 1 function, respectively. DE determines the best value for the functions F15 and F20. SHADE calculates the minimal optimal value on F12, F14, and F19. LSHADE-EpSin, LSHADE-SPACMA, and LSHADE-cnEpSin, respectively, measure the best value for functions F13, F16, and F17. On functions F11 and F18, just a few algorithms produce identical optimal values. SHADE has been identified as the algorithm with the most significant results. On CEC 2020 functions, DE and LSHADE-EpSin appeared as the worst algorithms, since both of them generated maximum value on three functions.

Table 3 Comparison of evaluated results on IEEE CEC 2020 function suite
Full size table

4 Description of Real-World Problems Employed and Discussion on the Results

Total six engineering design problems are solved using the algorithms employed. Among the issues selected, one is unconstrained, and the rest are constrained. The termination criteria are set as D*10,000 function evaluations for all the comparison algorithms during the evaluation. The parameters of all the chosen algorithms were kept the same as advised in the respective original study. While solving constrained problems, the death penalty method [43] is used.

This simple and popular strategy simply rejects the population's unfeasible answers. There will never be any unfeasible solutions in the population in this circumstance. According to this process, if any constraint is violated, a penalty value is assigned, and later sum of all the penalty values is added or subtracted with the objective function. This strategy should perform well if a possible search space is convex or a reasonable portion of the entire search space. However, when the problem is extremely limited, the algorithm will waste a lot of time identifying a small number of viable solutions. Furthermore, just evaluating points in the viable portion of the search space precludes superior solutions from being found.

4.1 Parameter Estimation for Frequency-Modulated Sound Waves Problem

This problem is collected from CEC 2011 real-world optimization problem suit [44]. Description of the problem and analysis of the results assessed are given below:

4.1.1 Problem Definition

The frequency-modulated (FM) sound system is necessary for the present-day musical frameworks. The goal here is to produce a sound like the perfect sound naturally, and the highlights are extricated utilizing dissimilarity of highlights among integrated and goal sounds. This cycle of highlight extraction is followed, except if both integrated and target sounds become comparative. The issue is exceptionally convoluted and with multi-modular capacity having epistasis. The optimal value of objective function \(f\left({X}^{*}\right)=0\). A considerable number of researchers have already solved the problem. The mathematical expression for assessed sound \(y(t)\) and wanted sound \({y}_{0}(t)\) waves are given by

$$y\left(t\right)={a}_{1}.\mathrm{sin}({\omega }_{1}.t.\theta +{a}_{2}.\mathrm{sin}\left({\omega }_{2}.t.\theta +{a}_{3}.\mathrm{sin}\left({\omega }_{3}.t.\theta \right)\right))$$
(19)
$${y}_{0}\left(t\right)=\left(1.0\right).\mathrm{sin}\left(5.0.t.\theta -1.5.\mathrm{sin}\left(4.8.t.\theta +2.0.\mathrm{sin}\left(4.9.t.\theta \right)\right)\right).$$
(20)

In this problem, \(\theta =\frac{2\Pi }{100}\) and the parameters lie within the range [− 6.4, 6.35]. The fitness function is defined as the summation of square errors between the assessed sound and the wanted sound. The objective function of the problem is defined as

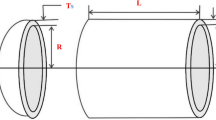
$$f\left(X\right)=\sum_{t=0}^{100}{\left(y\left(t\right)-{y}_{0}\left(t\right)\right)}^{2}.$$
(21)

A diagram of the problem is given in Fig. 2a.

Fig. 2
figure 2

Diagram of the real-world problems

Full size image

4.1.2 Analysis of Result

Table 4 shows the results of the algorithms used to calculate them. Table 4 reveals that most of the algorithms can determine the best ideal value. DE identifies the problem's minimal average, standard deviation, and best among all the comparison algorithms. The other two algorithms on the list, SaDE, and LSHADE, are ranked second and third. LSHADE-SPACMA calculates the problem's worst mean value.

Table 4 Comparison of results on the parameter estimation for frequency-modulated sound waves problem
Full size table

4.2 Car Side Impact Design Problem

This problem was initially proposed by Gu et al. [45]. A diagram of the problem is given in Fig. 2b. Description of the problem and discussion on the evaluated results are given below:

4.2.1 Problem Definition

The car is exposed to a side impact on the foundation of the European Enhanced Vehicle Safety Committee (EEVC) procedures. The objective is to minimize the car's total weight using eleven mixed variables while maintaining safety performance according to the standard. These variables represent the thickness and material of critical parts of the vehicle. The 8th and 9th variables are discrete, and these are material design variables, while the rest are continuous and represent thickness design variables.

The symbols \({a}_{1},\boldsymbol{ }{a}_{2},{a}_{3},\boldsymbol{ }{a}_{4},\boldsymbol{ }{a}_{5},\boldsymbol{ }{a}_{6},\boldsymbol{ }{a}_{7},{a}_{8},{a}_{9},\boldsymbol{ }{a}_{10},{a}_{11}\) are used here to represent the variables thickness of B-pillar inner, the thickness of B-pillar reinforcement, the thickness of floor side inner, the thickness of cross members, the thickness of door beam, the thickness of door beltline reinforcement, the thickness of roof rail, the material of B-pillar inner, the material of floor side inner, barrier height, and barrier hitting position, respectively. The problem is subjected to ten inequality constraints. The car side impact design is considered a confirmed case of a mechanical optimization problem with mixed discrete and continuous design variables. This problem can be mathematically described as

$${\varvec{a}}=\left\{{a}_{1},\boldsymbol{ }{a}_{2},{a}_{3},\boldsymbol{ }{a}_{4},\boldsymbol{ }{a}_{5},\boldsymbol{ }{a}_{6},\boldsymbol{ }{a}_{7},{a}_{8},{a}_{9},\boldsymbol{ }{a}_{10},{a}_{11}\right\}.$$
(22)

Objective function

$$Min f\left({\varvec{a}}\right)=1.98+4.90 {a}_{1}+6.67 {a}_{2}+6.98 {a}_{3}+4.01 {a}_{4}+1.78 {a}_{5}+2.73 {a}_{7},$$
(23)

subject to:

$${h}_{1}\left({\varvec{a}}\right)=1.16-0.3717 {a}_{2} {a}_{4}-0.00931 {a}_{2} {a}_{10}-0.484 {a}_{3} {a}_{9}+0.01343 {a}_{6} {a}_{10 }\le 1$$
(24)
$${h}_{2}\left({\varvec{a}}\right)=0.261-0.0159 {a}_{1} {a}_{2}-0.188 {a}_{1} {a}_{8}-0.019 {a}_{2} {a}_{7} +0.0144 {a}_{3} {a}_{5} + 0.0008757 {a}_{5} {a}_{10}+0.080405 {a}_{6} {a}_{9}+0.00139 {a}_{8} {a}_{11} + 0.00001575 {a}_{10} {a}_{11}\le 0.32,$$
(25)
$${h}_{3}\left({\varvec{a}}\right)=0.214+0.00817 {a}_{5}-0.131 {a}_{1}{a}_{8}-0.0704 {a}_{1}{a}_{9}+0.03099 {a}_{2}{ a}_{6}-$$
$$0.018 {a}_{2}{ a}_{7}+0.0208 {a}_{3}{ a}_{8}+0.121 {a}_{3}{ a}_{9} -0.00364 {a}_{5}{ a}_{6}+ 0.0007715 {a}_{5}{ a}_{10}-0.0005354 {a}_{6}{ a}_{10} +0.00121 {a}_{8}{ a}_{11}\le 0.32,$$
(26)
$${h}_{4}\left({\varvec{a}}\right)=0.074-0.061 {a}_{2}-0.163 {a}_{3} {a}_{8}+0.001232 {a}_{3} {a}_{10}-0.166 {a}_{7 }{a}_{9}$$
$$+0.227{ a}_{2}^{2}\le 0.32,$$
(27)
$${h}_{5}\left({\varvec{a}}\right)=28.98+3.818 {a}_{3}-4.2 {a}_{1} {a}_{2}+0.0207{ a}_{5} {a}_{10}+6.63 {a}_{6} {a}_{9}-7.7 {a}_{7} {a}_{8}+0.32 {a}_{9} {a}_{10}\le 32,$$
(28)
$${h}_{6}\left({\varvec{a}}\right)=33.86+2.95 {a}_{3}+0.1792 {a}_{10}-5.05 {a}_{1} {a}_{2}-11.0 {a}_{2} {a}_{8} - 0.0215 {a}_{5} {a}_{10}-9.98 {a}_{7} {a}_{8}+22.0 {a}_{8} {a}_{9}\le 32,$$
(29)
$${h}_{7}\left({\varvec{a}}\right)=46.36-9.9 {a}_{2}-12.9 {a}_{1} {a}_{8}+0.1107 {a}_{3} {a}_{10}\le 32,$$
(30)
$${h}_{8}\left({\varvec{a}}\right)=4.72-0.5 {a}_{4}-0.19 {a}_{2} {a}_{3}-0.0122 {a}_{4} {a}_{10}+0.009325 {a}_{6} {a}_{10} +0.000191 {a}_{11}^{2} \le 4,$$
(31)
$${h}_{9}\left({\varvec{a}}\right)=10.58-0.674 {a}_{1} {a}_{2}-1.95 {a}_{2} {a}_{8}+0.02054 {a}_{3} {a}_{10}-0.0198 {a}_{4} {a}_{10}+0.028 {a}_{6} {a}_{10}\le 9.9,$$
(32)
$${h}_{10}\left({\varvec{a}}\right)=16.45-0.489 {a}_{3} {a}_{7}-0.843 {a}_{5} {a}_{6}+0.0432 {a}_{9} {a}_{10}-0.0556 {a}_{9} {a}_{11} -0.000786 {a}_{11}^{2} \le 15.7,$$
(33)

where

$$0.5\le {a}_{i}\le 1.5, i=1, 2, 3, 4, 5, 6, 7 , {a}_{8},{a}_{9}\in \left(0.192, 0.345\right),$$
$$-30\le {a}_{10}, {a}_{11}\le 30.$$

4.2.2 Analysis of Results

Table 5 shows the results of the comparison algorithms' calculations. Table 5 reveals that LSHADE-EpSin is capable of finding the smallest best value. On the problem, LSHADE-cnEpSin determines the second minimum optimal value. LSHADE-EpSin determines the issue's minimal average value and the best value among all the comparison methods. Other algorithms, however, found a lower standard deviation value. Different algorithms rated 2nd and 3rd are DE and LSHADE and ELSHADE-SPACMA. SaDE calculates the problem's worst mean value.

Table 5 Comparison of results on the car side impact design problem
Full size table

4.3 Multiple Disk Clutch Brake Design Problem

It comes from the category of a mechanical engineering design problem. Figure 2c represents the diagram of the problem. The problem is described in [29]. Details of the problem and analysis of the results assessed by different algorithms are given below:

4.3.1 Problem Definition

The minimization of the mass of multiple disk clutch brake is the prime objective of the problem. This can be achieved by optimizing five decision variables, namely inner radius (\({x}_{1})\), outer radius (\({x}_{2})\), disk thickness (\({x}_{3})\), the force of actuators (\({x}_{4})\), and the number of frictional surfaces (\({x}_{5})\). It is a constrained problem and contains eight nonlinear constraints. The mathematical formulation of the problem is given below.

Objective function

$$\mathrm{Min} f\left(x\right)=\pi \left({x}_{2}^{2}-{x}_{1}^{2}\right){x}_{3}\left({x}_{5}+1\right)\rho .$$
(34)

Constraints

$${h}_{1}\left(x\right)=-{p}_{\mathrm{max}}+{p}_{rz}\le 0,$$
(35)
$${h}_{2}\left(x\right)={p}_{rz}{V}_{sr}-{V}_{sr,\mathrm{max}}{p}_{\mathrm{max}}\le 0,$$
(36)
$${h}_{3}\left(x\right)=\Delta R+{x}_{1}-{x}_{2}\le 0,$$
(37)
$${h}_{4}\left(x\right)={-L}_{\mathrm{max}}+{(x}_{5}+1)\left({x}_{3}+\partial \right)\le 0,$$
(38)
$${h}_{5}\left(x\right)=s{M}_{s}-{M}_{h}\le 0,$$
(39)
$${h}_{6}\left(x\right)=T\ge 0,$$
(40)
$${h}_{7}\left(x\right)=-{V}_{sr,\mathrm{max}}+{V}_{sr}\le 0,$$
(41)
$${h}_{8}\left(x\right)=T-{T}_{\mathrm{max}}\le 0,$$
(42)

where

$${M}_{h}=\frac{2}{3}\mu {x}_{4}{x}_{5}\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}^{2}-{x}_{1}^{2}} ,$$
$$\omega =\frac{\Pi n}{30}\frac{\mathrm{rad}}{s},$$

\( A= \pi ({x}_{2}^{2}-{x}_{1}^{2})\),

\( {p}_{rz}=\frac{{x}_{4}}{A}\),

$${V}_{sr}=\frac{\Pi {R}_{sr}n}{30},$$
$${R}_{sr}=\frac{2}{3}\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}^{2}{x}_{1}^{2}} ,$$
$$T=\frac{{I}_{z}\omega }{{M}_{h}+{M}_{f}} ,$$
$$\Delta R=20, { L}_{\mathrm{max}}=30,\boldsymbol{ }\mu =0.6\boldsymbol{ },$$
$${V}_{sr,\mathrm{max}}=10, \partial =0.5 ,\boldsymbol{ }s=1.5\boldsymbol{ },$$
$${T}_{\mathrm{max}}=15 , n=250 ,\boldsymbol{ }{I}_{z}=55$$
$${M}_{s}=40,{M}_{f}=3,\boldsymbol{ }\mathrm{and}\boldsymbol{ }{p}_{\mathrm{max}}=1.$$

Variable range

$$60\le {x}_{1}\le 80, 90\le {x}_{2}\le 110, 1\le {x}_{3}\le \mathrm{3,0}\le {x}_{4}\le \mathrm{1000,2}\le {x}_{5}\le 9.$$

4.3.2 Analysis of Result

Table 6 shows the results provided by the comparison algorithms. Table 6 shows that, except for LSHADE-SPACMA and LSHADE-cnEpSin, all algorithms discover the same value as average ideal value, standard deviation value, and best value. On this problem, LSHADE-cnEpSin is the worst performer of the compared algorithms.

Table 6 Comparison of results on the multiple disk clutch brake design problem
Full size table

4.4 Weight Minimization of a Speed Reducer Problem

The issue is related to the Mechanical Engineering discipline. A diagram of the problem is given in Fig. 2d.

4.4.1 Problem Definition

The notched is used as an independent element to reduce or increase the speed, and a firm covering is used to enclose them. When this unit is used to minimize any device's speed, it is called a speed reducer. Reducer is widely used in turbines, rolling mills to reduce speed. The parameters required to optimize this problem are the gear's \(b\)-face width, \(z\)-number of pinning teeth, m-teeth module, \({l}_{1}\)-length of the shaft-1 between bearing, \({l}_{2}\)-length of the shaft-2 between bearing, \({d}_{1}\)- diameter of shaft-1, and \({d}_{2}\)- diameter of shaft-2. Here, the problem's design variables are represented by the position vectors of the algorithm in the following manner:

Face width of the gear \((b)\) = \({x}_{1}\)

Teeth module \((m)\) = \({x}_{2}\)

Number of pinning teeth \((z)\) = \({x}_{3}\)

Length of shaft-1 between bearing \({(l}_{1})\)= \({x}_{4}\)

Length of shaft-2 between bearing \({(l}_{2})\)= \({x}_{5}\)

Diameter of shaft-1 \({(d}_{1})\)  = \({x}_{6}\)

Diameter of shaft-1 \({(d}_{2})\)  = \({x}_{7}\).

The problem is found in [29]. The mathematical representation of the problem is

Objective function

$$\mathrm{Min}. f\left(x\right)=0.7854 {x}_{2}^{2}{x}_{1}\left(14.9334{x}_{3}+3.3333{x}_{3}^{2}-43.0934\right)+0.7854\left({x}_{4}{x}_{6}^{2}+{x}_{5}{x}_{7}^{2}\right)+7.477\left({x}_{7}^{3}+{x}_{6}^{3}\right)-1.508\left({x}_{7}^{2}+{x}_{6}^{2}\right)$$
(43)
$${h}_{1}\left(x\right)={x}_{1}{x}_{2}^{2}{x}_{3}+27\le 0,$$
(44)
$${h}_{2}\left(x\right)=-\left(1\right){x}_{2}^{2}{x}_{3}^{2}+397.5\le 0,$$
(45)
$${h}_{3}\left(x\right)=-{x}_{2}{x}_{2}^{4}{x}_{3}{x}_{4}^{-3}+1.93\le 0,$$
(46)
$${h}_{4}\left(x\right)=-{x}_{2}{x}_{7}^{4}{x}_{3}{x}_{5}^{-3}+1.93\le 0,$$
(47)
$${h}_{5}\left(x\right)=10{x}_{6}^{-3}\sqrt{16\cdot 91\times {10}^{6}+{\left(745{x}_{4}{x}_{2}^{-1}{x}_{3}^{-1}\right)}^{2}}-1100\le 0,$$
(48)
$${h}_{6}\left(x\right)=10{x}_{7}^{-3}\sqrt{157.5\times {10}^{6}+{\left(745{x}_{5}{x}_{2}^{-1}{x}_{3}^{-1}\right)}^{2}}-850\le 0,$$
(49)
$${h}_{7}\left(x\right)={x}_{2}{x}_{3}-40\le 0,$$
(50)
$${h}_{8}\left(x\right)=-{x}_{1}{x}_{2}^{-1}+5\le 0,$$
(51)
$${h}_{9}\left(x\right)={x}_{1}{x}_{2}^{-1}-12\le 0,$$
(52)
$${h}_{10}\left(x\right)=1.5{x}_{6}-{x}_{4}+1.9\le 0,$$
(53)
$${h}_{11}\left(x\right)=1.1{x}_{7}-{x}_{5}+1.9\le 0.$$
(54)

Variable range

$$2.6\le {x}_{1}\le 3.6, 0.7\le {x}_{2}\le 0.8, 17\le {x}_{3}\le 28,$$
$$2.9\le {x}_{6}\le 3.9, 5\le {x}_{7}\le 5.5, 7.3\le {x}_{4},{x}_{5}\le 8.3.$$

4.4.2 Analysis of Result

Table 7 shows the estimated results from the comparison algorithms. Examining Table 7 shows that all algorithms, except LSHADE-cnEpSin and LSHADE-EPSin, find the same value as average ideal value, standard deviation value, and best value as average optimal value, standard deviation value, and best value. LSHADE-cnEpSin can determine the optimal value, which is lower than the value found in the literature. The average and best values determined by LSHADE-cnEpSin are lower than those determined by the other algorithms used in this study. LSHADE-EpSin is the worst contrast algorithms in terms of average and standard deviation values.

Table 7 Comparison of results on the weight minimization of a speed reducer problem
Full size table

4.5 Welded Beam Design Problem

This is a design problem from the mechanical engineering discipline. Figure 2e shows a diagram of the problem.

4.5.1 Problem Definition

The minimization of the fabrication cost of the welded beam is the main objective of the problem. The problem comprises five constraints and four variables. Limitations are shear stress \((\tau )\), bending stress within the beam (θ), buckling load \(({P}_{c})\), and end deflection of the beam \((\delta )\). The variables to be optimized here are the height of the bar \((t)\), the thickness of the weld \((h),\) the thickness of the bar \((b),\) and the length of the clamped bar \((l). h, l, t,\) and \(b\) in the problem are represented by \({x}_{1}\), \({x}_{2}\), \({x}_{3}\), and \({x}_{4}.\) The problem is described in the Mechanical engineering category of the literature [29]. The mathematical formulation of the problem is.

Objective function

$$\mathrm{Min}.\mathrm{f}\left(x\right)=0.04811{x}_{3}{x}_{4}\left\{{x}_{2}+14\right\}+1010471{x}_{1}^{2}{x}_{2}$$
(55)

subject to.

\({h}_{1}\left(x\right)={x}_{1}-{x}_{4}\le 0\), (56)

$${h}_{2}\left(x\right)=\delta \left(x\right)-{\delta }_{\mathrm{max}}\le 0,$$
(57)
$${h}_{3}\left(x\right)=P\le {P}_{c}\left(x\right),$$
(58)
$${h}_{4}\left(x\right)={\tau }_{\mathrm{max}}\ge \tau \left(x\right),$$
(59)
$${h}_{5}\left(x\right)= \sigma \left(x\right)-{\sigma }_{\mathrm{max}}\le 0,$$
(60)

where

$$\mathrm{R}=\sqrt{\frac{{x}_{2}^{2}}{4}+{\left(\frac{{x}_{1}+{x}_{3}}{2}\right)}^{2}} ,\mathrm{ J}=2 \frac{{x}_{2}^{2}}{4}+\left(\begin{array}{c}2\\ \left(\left(\frac{{x}_{1}+{x}_{3}}{2}\right)\right)\sqrt{2}{x}_{1}{x}_{2}\end{array}\right) ,$$
$$\upsigma \left(x\right)=\frac{6\mathrm{PL}}{{x}_{4}{x}_{3}^{2}} ,\updelta \left(x\right)= \frac{6{\mathrm{PL}}^{3}}{\mathrm{E}{x}_{3}^{2}{x}_{4}} , {\mathrm{P}}_{\mathrm{c}}\left(x\right)=\frac{4.013\mathrm{E}{x}_{3}{x}_{4}^{3}}{6{\mathrm{L}}^{2}}\left(1-\frac{{x}_{3}}{2\mathrm{L}}\sqrt{\frac{\mathrm{E}}{4\mathrm{G}}}\right),$$
$$L=14 , P=6000, E=30\times {1}^{6} , G=12\times {10}^{6}$$
$${\sigma }_{\mathrm{max}}=\mathrm{30,000}, {\delta }_{\mathrm{max}}=0.25 , {\tau }_{\mathrm{max}}=13600,$$

where

$$0.1\le {x}_{3},{x}_{2}\le \mathrm{10,0.125}\le {x}_{1}\le \mathrm{2,0.1}\le {x}_{4}\le 2.$$

4.5.2 Analysis of Result

Results calculated by the comparison algorithms are presented in Table 8. Table 8 reveals that the average value and the best value evaluated by most employed algorithms are the same. LSHADE-cnEpSin is not suitable for this problem. Though other algorithms except LSHADE-EpSin and LSHADE-cnEpSin generate the same average value and best value, their standard deviation value differs. The minimum standard deviation value designates the algorithm's robustness in finding the solution. SaDE, DE, and LSHADE-SPACMA are ranked as 1st, 2nd, and 3rd algorithms based on generated standard deviation values. The performance of LSHADE-EpSin is recorded as the worst on this problem.

Table 8 Comparison of results on the welded beam design problem
Full size table

4.6 Robot Gripper Problem

This problem was first modeled by Osyczka et al. [46]. It is a design problem from the discipline Mechanical Engineering. Diagram of the problem are given in Fig. 2f, g.

4.6.1 Problem Definition

This problem has seven decision variables denoted by \(x=\left[a, b, c, e, f, I, \delta \right]\) where, \(a, b, c, e, f, I,\) are dimensions of the gripper, and \(\delta\) is the angle between c and b shown in Fig. 2g. The objective function of the problem is the absolute value of the difference between the maximum and minimum force generated by the robot. The mathematical formulation of the robot gripper problem is shown below:

$$f\left(x\right)=\left|\mathrm{max}{F}_{K}\left(x,z\right)-\mathrm{min}{F}_{K}\left(x,z\right)\right|$$
(61)

subject to

$${g}_{1}\left(x\right)=y\left(x, {z}_{\mathrm{max}}\right)-{Y}_{\mathrm{min}}\le 0$$
(62)
$${g}_{2}\left(x\right)=y\left(x, {z}_{\mathrm{max}}\right)\le 0$$
(63)
$${g}_{3}\left(x\right)={Y}_{\mathrm{max}}-y\left(x, 0\right)\le 0$$
(64)
$${g}_{4}\left(x\right)=y\left(x, 0\right)-{Y}_{G}\le 0$$
(65)
$${g}_{5}\left(x\right)={I}^{2}+{e}^{2}-{\left(a+b\right)}^{2}\le 0$$
(66)
$${g}_{6}\left(x\right)={b}^{2}-{\left(a-e\right)}^{2}-{\left(I-{z}_{\mathrm{max}}\right)}^{2}\le 0$$
(67)
$${g}_{7}\left(x\right)={z}_{\mathrm{max}}-I\le 0,$$
(68)

where

$$\alpha =\mathrm{Arc} \mathrm{Cos}\left(\frac{{g}^{2}+{a}^{2}-{b}^{2}}{g\times 2b}\right)+\varphi ;\, {g}^{2}-{e}^{2}={\left(z-I\right)}^{2};\, \varphi =\mathrm{Arc} \mathrm{Tan}\left(\frac{e}{1-z}\right)$$
$$\beta =\mathrm{Arc} \mathrm{Cos}\left(\frac{{g}^{2}+{b}^{2}-{a}^{2}}{g\times 2b}\right)-\varphi ;\, y(x,z)=2(c+e+f\times \mathrm{sin}\left(\delta +\beta \right))$$
$${F}_{k}=\left(\frac{\mathrm{sin}\left(\alpha +\beta \right)\times b\times p}{2c\times \mathrm{cos}\alpha }\right); {Y}_{\mathrm{min}}=50 ; {Y}_{\mathrm{max}}=100 ; {Y}_{G}=150 ; {z}_{\mathrm{max}}=100; p=100$$
$$10\le f,a,b\le 150; 0\le e\le 50 ; 100\le l\le 300 ; 100\le c\le 200; 1\le \delta \le 3.14.$$

4.6.2 Analysis of Result

The optimal value of this problem is 2.5287918415. Numerical results evaluated by the algorithms are given in Table 9. LSHADE records the average value close to the optimal value found in the literature. The standard deviation value calculated by SHADE is minimum among the algorithms. LSHADE-EpSin algorithm evaluates the best optimal value. LSHADE-SPACMA is not suitable for this problem. SHADE and ELSHADE-SPACMA are ranked as 2nd and 3rd, respectively, on this problem. LSHADE-cnEpSin is the worst algorithms in terms of results among the compared algorithms.

Table 9 Comparison of results on the robot gripper problem
Full size table

5 Statistical Analysis

Statistical test of the evaluated results is performed using Friedman's rank test of results on IEEE CEC 2019 and IEEE 2020 functions. The Wilcoxon signed-rank test is executed based on the algorithms evaluating real-world problems employed. Friedman's test and Wilcoxon signed-rank test fall into the non-parametric statistical hypothesis test category and compare two related samples, matched samples, or repeated measurements on a single sample to assess whether their population mean ranks differ (i.e., it is a paired difference test). Tables 10 and 11 illustrate the outcomes of Friedman's test, and Table 12 demonstrates the results of the Wilcoxon signed-rank test. Analysis of the data in Table 10 exposes that SHADE, ELSHADE-SPACMA, and LSHADE-EpSin can be ranked as 1st, 2nd, and 3rd, respectively. Similarly, the analysis of Table 11 reveals that SHADE, LSHADE, and ELSHADE-SPACMA are the algorithms that can be ranked as 1st, 2nd, and 3rd, respectively. Therefore, the performance of SHADE and ELSHADE-SPACMA are consistent with the IEEE functions employed in this study.

Table 10 Result of Friedman's rank test on IEEE CEC 2019 functions
Full size table
Table 11 Result of Friedman's rank test on IEEE CEC 2020 functions
Full size table
Table 12 Result of Wilcoxon signed-rank test on real-world problems
Full size table

Table 12 displays the results of the Wilcoxon signed-rank test on real-world problems. It can be seen from the results that DE is the best algorithm in terms of the minimum rank obtained by the algorithm. ELSHADE-SPACMA and SaDE are the algorithms ranked as 2nd and 3rd. Evaluating the mean final rank, it can be concluded that SHADE is the best algorithm and ELSHADE-SPACMA is the 2nd best algorithm among the algorithms employed here for comparison.

6 Run-Time Analyses of the Algorithms in Real-World Problems

The total time taken by every algorithm to evaluate the mean, standard deviation, and best value within 30 independent runs on a particular problem is shown as the algorithm's run time. The run time of a problem depends on the algorithm's complexity, the number of dimensions, and the complexity of the problem. The six real-world issues evaluated in this study have 6, 11, 5, 7, 4, and 7 dimensions, respectively. Analyzing the runtimes being assessed in Tables 6, 7, 8 and 9 exposes that SHADE evaluates the first five out of six problems in less run time than other algorithms. ELSHADE-SPACMA optimizes the 6th problem in a minimum run time than the compared algorithms. The second problem (car side impact design) has the maximum dimension among the real-world problems employed. Thus, the evaluation time of this problem is more. Due to the problem complication evaluation time of the last problem (robot gripper) is greater than all the problems.

7 Conclusion

Numerous optimization algorithms are available in the literature. Among them, considering the efficacy of DE, the researchers have modified it extensively. Several variants of DE have won the CEC competitions. These CEC-winning variants are regarded as strong algorithms to solve complicated problems. Comparison of performance within the CEC competition-winning variants of DE has never been done as per our knowledge. In this study, performance of DE and its eight CEC competition-winning variants is studied, evaluating IEEE CEC 2019 function suite, IEEE CEC 2020 function suite, and one unconstrained and five constrained real-world engineering problems. The time taken by the algorithms for solving real-world problems is also assessed. Besides comparing the performance of the algorithms with numerical results, their performance is also analyzed statistically. Performance analysis exposes that SHADE is the best algorithm while solving CEC functions, and in five out of six real-world problems, it has been found the faster in calculating the result. On real-world problems, DE outperforms all its variants used here for comparison. ELSHADE-SPACMA emerged as a unique algorithm ranked 2nd or 3rd in every problem set. Evaluated optimal result in weight minimization of a speed reducer design problem is recorded minimum than the optimal value found in the literature. Finally, it can be concluded that among the compared algorithms, SHADE and ELSHADE-SPACMA can effectively solve complex problems and can be used to solve other problems from engineering and industry.