Leveraging Machine Learning to Automatically Derive Robust Decision Strategies from Imperfect Knowledge of the Real World

Abstract

Teaching people clever heuristics is a promising approach to improve decision-making under uncertainty. The theory of resource rationality makes it possible to leverage machine learning to discover optimal heuristics automatically. One bottleneck of this approach is that the resulting decision strategies are only as good as the model of the decision problem that the machine learning methods were applied to. This is problematic because even domain experts cannot give complete and fully accurate descriptions of the decisions they face. To address this problem, we develop strategy discovery methods that are robust to potential inaccuracies in the description of the scenarios in which people will use the discovered decision strategies. The basic idea is to derive the strategy that will perform best in expectation across all possible real-world problems that could have given rise to the likely erroneous description that a domain expert provided. To achieve this, our method uses a probabilistic model of how the description of a decision problem might be corrupted by biases in human judgment and memory. Our method uses this model to perform Bayesian inference on which real-world scenarios might have given rise to the provided descriptions. We applied our Bayesian approach to robust strategy discovery in two domains: planning and risky choice. In both applications, we find that our approach is more robust to errors in the description of the decision problem and that teaching the strategies it discovers significantly improves human decision-making in scenarios where approaches ignoring the risk that the description might be incorrect are ineffective or even harmful. The methods developed in this article are an important step towards leveraging machine learning to improve human decision-making in the real world because they tackle the problem that the real world is fundamentally uncertain.

Introduction

The decisions we have to make in the real world are too complex and too diverse for us to make them all with the same strategy. People therefore need different decision strategies for different types of decisions (Gigerenzer & Todd, 1999; Simon, 1956; Todd & Gigerenzer, 2012). While people often have good heuristics for certain types of decisions (Todd & Gigerenzer, 2012), they often lack good decision strategies for other situations. This negatively affects people’s decisions about their finances, health, and education (O’Donoghue and Rabin, 2015). The resulting mistakes can have devastating consequences for the individuals, families, organizations, and society at large. One way to address this problem is to increase people’s decision-making literacy. This idea is currently being advocated for as a public policy intervention under the name of boosting (Hertwig and Grüne-Yanoff, 2017). One approach to boosting is to discover clever heuristics for the types of decisions that people struggle with and teach them to people (Hafenbrädl et al., 2016; Gigerenzer & Todd, 1999). Recent work has built on the definition of optimal heuristics for human decision-making by (Lieder and Griffiths, 2020) to develop machine learning methods for discovering clever heuristics for human decision-making (Callaway et al., 2018a; Callaway, Gul et al., 2018; Lieder et al., 2017; Krueger et al., 2022; Callaway et al., 2022b; Skirzyński et al., 2021; Consul et al., 2022) as well as intelligent cognitive tutors that teach them to people (Callaway et al., 2022a; Consul et al., 2022) and AI-generated decision aids that guide people through the application of the discovered strategies (Becker et al., 2022). Here, we use the term “heuristic” in the broad sense of “any decision strategy that uses only a subset of all potentially relevant information and is not guaranteed to always yield the optimal solution.”

Automatic strategy discovery methods compute strategies that achieve the best possible trade-off between the quality of the resulting decisions and the amount of effort that people have to expend to reach them (Callaway et al., 2018a; Callaway, Gul et al., 2018; Lieder et al., 2017; Consul et al., 2022; Krueger et al., 2022). This optimization is performed on a model of the environment in which the decision strategies are to be used. This approach works well when the model of the decision environment is accurate. However, when there is a mismatch between the model and reality, the discovered strategy can perform arbitrarily poorly in the real world. To illustrate this problem, let us consider a hypothetical application of automatic strategy discovery to improving how credit officers decide which mortgage applications to approve. In this case, the decision strategy might take the form of a decision tree, such as “If the applicant’s credit score is at least 740, then approve the application. Else, if the applicant’s credit score is at least 580, then approve the application if the applicant’s disposable income is at least x% of the requested amount”.¹ The model of the decision environment would have to include which information is available to the credit officer (e.g., the price of the house the applicant is planning to buy, the mortgage’s interest rates, the applicant’s credit score, income, and savings), which outcomes of granting the mortgage would have in different scenarios (e.g., housing prices increase/decrease by x%), how probable those scenarios are, and how the outcomes the bank would experience in each of those scenarios (e.g., not getting their money back because the borrower goes bankrupt) depend on the available information. Building such a model requires estimates of the probabilities of various events (e.g., a collapse of the housing market) that have to be obtained from domain experts (e.g., credit officers). In the following, we will refer to such estimates as descriptions of the environment.

One important obstacle to applying automatic strategy discovery to improve human decision-making is that our models of the real-world scenarios in which people have to make decisions will usually be at least somewhat inaccurate (model-misspecification). For instance, prior to the subprime mortgage crisis, most credit officers’ descriptions of the housing market would have severely underestimated the risk that housing prices might drop as precipitously as they subsequently did (Demyanyk and Van Hemert, 2011). If extant automatic strategy discovery methods had been naively applied to the estimates of those domain experts, then they would most likely have recommended heuristics that pay too little attention to information about the applicant’s ability to pay back their mortgage if their house were to lose most of its value. Strategy discovery methods therefore have to be robust to the ways in which the description they are applied to might be wrong. Concretely, in this example, a robust strategy method should produce a heuristic for evaluating mortgage applications that works not only if the credit officers’ estimates were correct but also if those estimates were distorted by fallibility of human judgment that arises from limitations of human memory, systematic errors in people’s judgments (Tversky and Kahneman, 1974), limited information, and fundamental uncertainty about the future (Hertwig et al., 2019). Therefore, a robust strategy discovery method might have recommended a heuristic that pays more attention to the applicant’s income, savings, and credit score than would be necessary if the credit officers’ descriptions of the housing market were correct.

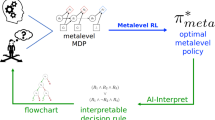
The main contribution of this article is to propose a general machine learning method for discovering clever heuristics that is robust to errors in the description of the decision problem (e.g., deciding which mortgage applications to approve and which to decline). Unlike previous methods, our new method yields good decision strategies even when the description of the decision problem is biased and incomplete (see Fig. 1). The basic idea is to find the heuristic that works best in expectation over all possible realities that could have given rise to the likely incomplete and partially incorrect description provided by a human expert. The resulting uncertainty about what the world might be like is handled using Bayesian inference. Our approach computes the heuristics that performs best in expectation over all possible worlds that might have given rise to the provided specification. In our example, this would include scenarios in which the risk that housing prices might drop is higher than the provided estimate, as well as scenarios in which it is lower. We thereby provide a first proof-of-concept for leveraging machine learning to discover heuristics that are robust to our uncertainty about the environment. We evaluate our new method in simulations and behavioral experiments across two domains: route planning and multi-alternative risky choice. In each case, we apply our machine learning method to derive adaptive decision strategies from incorrect descriptions of multiple decision problems and teach people to apply the automatically discovered strategies. In each case, people who were taught the strategies discovered by our new robust method made significantly better decisions than people who were either taught no strategies or strategies discovered by previous methods. Our findings suggest that our method is robust to common systematic and non-systematic errors in people’s descriptions of different decision problems. The discovered heuristics tend to work well in the true environment, even when the model was derived from a biased description of limited experience. This will be important for future efforts to derive clever heuristics from people’s descriptions of the decisions they face in the real world. Moreover, our definition of rational strategies for robust decision-making has implications for the debate about human rationality. Our theory and methods provide a starting point for understanding the robustness of human decision-making, modeling how people learn robust decision strategies, and recreating this robustness in machines.

Fig. 1

The general idea of robust strategy discovery. The goal is to discover heuristics that perform well in the real world when given only people’s biased descriptions. To achieve this, we explicitly model how cognitive biases distort domain expert’s descriptions of the scenarios in which people have to make decisions. Metaphorically speaking, the difference between those descriptions and the real-world scenarios they are meant to capture is akin to the difference between the maps that early explorers like Columbus used and the territory that those maps were meant to depict

The structure for this paper is as follows: We start by introducing the theoretical and technical background for automatic strategy discovery (Section 2). We then introduce our general new approach to making strategy discovery methods robust to uncertainty and model misspecification (Section 3). The following sections apply this general approach to the domains of planning (Section 4 and Section 5) and multi-alternative risky choice (Section 6 and Section 7), respectively. For each domain, we first apply our computational approach to discover robust decision strategies (Section 4 and Section 6) and then conduct experiments to test if teaching them to people is a viable approach to improve human decision-making (Section 5 and Section 7). In both cases, our approach succeeds to help people make better decisions when the true environment is partially unknown. We close with a discussion of directions for future work on understanding and improving human decision-making (Section 8).

Background

Our approach to improving human decision-making through robust strategy discovery builds on the theory of resource rationality, machine learning methods for automatic strategy discovery, empirical methods for assessing human decision-making, intelligent cognitive tutors, and previous findings about people’s cognitive biases. Here, we therefore briefly introduce each of these concepts in turn.

Resource Rationality

Lieder and Griffiths (2020) recently introduced a new theory of bounded rationality that provides a mathematical definition of optimal heuristics for human decision-making. Unlike previous normative theories, such as expected utility theory (von Neumann and Morgenstern, 1944), it takes into account that people’s time and cognitive resources are bounded. Its prescriptions for good decision-making (Lieder and Griffiths, 2020; Lieder et al., 2017; Krueger et al., 2022; Callaway et al., 2022b) thus, at least sometimes, resemble simple fast-and-frugal heuristics (Gigerenzer & Todd, 1999).

Building on the notion of bounded optimality from artificial intelligence (Russell and Subramanian, 1994), the theory of resource rationality states that people should make optimal use of their finite computational resources. These computational resources are modeled as a set of elementary information processing operations. Each of these operations has a cost that reflects how much computational resources it requires. Those operations are assumed to be the building blocks of people’s cognitive strategies. To be resource-rational, a planning strategy has to achieve the optimal tradeoff between the expected return of the resulting decision and the expected cost of the planning operation it will perform to reach that decision. Both depend on the structure of the environment. Concretely, Lieder and Griffiths (2020) define the extent to which using the cognitive strategy h in an environment E constitutes effective use of the limited computational resources of the agent’s brain B as the strategy’s resource rationality

$$\begin{aligned} \text {RR}(h,s,E,B)=\mathbb {E} \left[ u(\text {result} \; |\; h,s,E,B)\right] - \mathbb {E}\left[ \text {cost}(t_h,\rho )\; |\; h,s,B,E \right] , \end{aligned}$$

(1)

where $u(\text {result})$ is the agent’s subjective utility u of the outcomes ($\text {result}$) of the choices made by the heuristic h, and $\text {cost}(t_h,\rho )$ denotes the total opportunity cost of investing the cognitive resources $\rho$ used or blocked by the heuristic h for the duration $t_h$ of its execution. Both the result of applying the heuristic and its execution time depend on the situation in which it is applied. The expected value ($\mathbb {E}$) weighs the utility and cost for each possible situation by their posterior probability given the environment E, the situation s the decision-maker finds themselves in, and the cognitive capacities of the decision-maker (B).

The brain’s computational limitations and uncertainty about the environment limit how effective people’s decision strategies can be. That is, the brain can only execute some strategies ($H_B$) but not others, and the extent to which people can adapt to their environment is constrained by the limited data d that they have about the environment and which situations they will encounter (Lieder and Griffiths, 2020). Under these constraints, the resource-rational heuristic is

$$\begin{aligned} h^\star = \arg \max _{h \in H_B} \mathbb {E}_{E,s|d}\left[ \text {RR(h,s,E,B)} \right] . \end{aligned}$$

(2)

Automatic Strategy Discovery

Equation 2 specifies a criterion that optimal heuristics must meet. But it does not directly tell us what those optimal heuristics are. Finding out what those optimal heuristics are is known as strategy discovery.

Given a model of the environment, the resource-rational heuristic $h^\star$ for an agent with the computational resources B can be computed by reformulating the definition of the resource-rational heuristic as the solution to a metalevel Markov decision process (MDP) and applying methods from dynamic programming or reinforcement learning to compute its optimal policy (Callaway et al., 2018a; Callaway, Gul et al., 2018; Lieder et al., 2017; Krueger et al., 2022; Callaway et al., 2022b). This approach models the decision process as a series of computations that can be chosen one by one. Each computation updates the person’s beliefs about the returns of alternative courses of action. Rules for selecting computations correspond to alternative decision strategies.

As illustrated in Fig. 2a, the basic idea of this approach is to use a metalevel MDP to model the decision problems that people face and the cognitive architecture that they have available to solve them, and then apply a reinforcement learning method to approximate its optimal policy. Formally, a metalevel MDP (see Fig. 2b) is a four-tuple $M_{\text {meta}}=(\mathcal {B}, \mathcal {C}, T_{\text {meta}}, r_{\text {meta}})$ comprising the set of possible beliefs $\mathcal {B}$ that the agent can have, the set of computational primitives $\mathcal {C}$, a probabilistic model $T_{\text {meta}}(b,c,b')$ of how possible computations c might update the belief state (e.g., from b to $b'$), and the metalevel reward function $r_{\text {meta}}$ which encodes the cost of computations $c \in \mathcal {C}$ and the utility of the action chosen when deliberation is terminated. In this formal framework, cognitive strategies correspond to metalevel policies ($\pi _{\text {meta}}: \mathcal {B} \mapsto \mathcal {C}$) that specify which computation will be performed in a given belief state.

Fig. 2

Automatic strategy discovery. a Illustration of the general approach. We discover optimal decision strategies by modeling the decision problems people face as metalevel Markov decision processes (MDPs) and solving them using reinforcement learning methods. The discovered optimal strategies can then be taught to people using intelligent cognitive tutors. b Illustration of a metalevel MDP. A metalevel MDP is characterized by its set of belief states (B), the computations (C) which represent deliberation, and move an agent from one belief state to another belief state. Computations incur costs, and provide rewards (R) upon termination of deliberation

Methods for Assessing Human Decision-Making and Measuring People’s Decision Strategies

To find out which heuristics people use to make decisions, some decision scientists conduct experiments in which they measure which pieces of information participants acquire at which point in their decision-making process (Payne et al., 1993). These experiments initially conceal all information about the choices behind opaque boxes. To reveal the information underneath a box, the participant must click it. This requirement renders each click indicative of the elementary information processing operation that incorporates the revealed information into the decision. By reporting the sequence of clicks that a participant makes, these methods thereby yield insights into the underlying decision strategies.

We have recently extended this approach to sequential decision problems that require planning (Callaway et al., 2022b; Jain et al., in press). Our Mouselab-MDP paradigm (see Fig. 3) shows the participant a map of an environment where each location harbors an occluded positive or negative reward. To find out which path to take, the participant must click on the locations they consider visiting to uncover their rewards. Each of these clicks is recorded and interpreted as the reflection of one elementary planning operation. The cost of planning is externalized as a fee that people have to pay for each click. People can stop planning and start navigating through the environment at any time. However, once they have started to move through the environment, they cannot resume planning. The participant has to follow one of the paths along the arrows to one of the outermost nodes.

Fig. 3

Illustration of the Mouselab-MDP paradigm. Rewards are revealed by clicking with the mouse before selecting a path using the keyboard. This figure shows one concrete task you can create using this paradigm. Many other tasks can be created by varying the size and layout of the environment, the distributions the rewards are drawn from, and the cost of clicking

This experimental task allows us to measure the extent to which a person’s decision-making is resource-rational using the measure of resource rationality specified in Eq. 1. In this task, for a given trial, $u(\textit{result})$ is the sum of rewards along the chosen path. $\text {cost}(t_h,\rho )$ is the number of clicks the participant made because their opportunity cost is assumed to be $1 per click. The resource-rationality score $\text {RR}$ is then measured as the difference of the average result and the average cost of clicking across all the trials a participant goes through.

Intelligent Cognitive Tutors

Early work found that teaching people economic principles for arriving at the best possible decision had limited success at improving their decisions in the real world (Larrick, 2002). This is likely because economic principles ignore crucial constraints on human decision-making (i.e., limited time and bounded cognitive resources). The exhaustive planning that would be required to apply those principles to the real world would waste virtually all of a person’s time on the very first decision (e.g., “Should I get up or go back to sleep?”), thereby depriving them of the opportunities afforded by later decisions. In contrast, resource-rational heuristics allocate people’s limited time and bounded cognitive resources in such a way that they earn the highest possible sum of rewards across the very long series of decisions that constitute life. This is why teaching resource-rational heuristics might improve people’s decisions in large and complex real-world problems where exhaustive planning would either be impossible or take a disproportionately large amount of time that could be better spent on other things.

In some of our prior work, we have built on automatic strategy discovery methods to develop intelligent tutors that teach people the optimal planning strategies for a given environment (Lieder et al., 2019; Callaway et al., 2022a; Consul et al., 2022). Most of the tutors let people practice planning in the Mouselab-MDP paradigm and gave them immediate feedback on each planning operation that they chose to perform. Callaway et al. (2022a) found that participants learned to use the automatically discovered strategies, remembered them, and used them in larger and more complex environments with a similar structure. Furthermore, Callaway et al. (2022a) also found that participants were able to transfer the taught strategy to a naturalistic planning task. These findings suggest that automatic strategy discovery can be used to improve human decision-making if the discovered strategies are well-adapted to the real-world situations where people might use them. Finally, Consul et al. (2022) found that showing people video demonstrations of the click sequences made by the optimal strategy is also highly effective. Here, we build on this finding to develop cognitive tutors that teach automatically discovered strategies by demonstrating them to people.

Biases, Uncertainty, and Ignorance

Existing strategy discovery methods assume that the environment is completely known. But this is rarely the case for decision problems in the real world. On the contrary, decision-making in the real-world is characterized by fundamental uncertainty about the structure of the environment because the real world is very complex and even domain experts have only limited information about its structure (Hertwig et al., 2019). Research on judgment and decision-making has revealed a long list of systematic errors that people make when judging the probabilities of possible outcomes (Kahneman et al., 1982). For instance, people’s estimates of the probability that an event will occur are known to be biased by how easily it comes to mind (Tversky and Kahneman, 1973) and how easily an event comes to mind is affected by several biases in human memory. For example, when a person has experienced an event that was extremely bad or extremely good they remember it much more easily than an equally common event that is more neutral (Madan et al., 2014). Furthermore, recent events come to mind more easily than distant events (Deese and Kaufman, 1957) and people tend to underestimate the frequency of rare events in decisions from experience (Hertwig et al., 2004). As a consequence of these biases, people’s descriptions of real-world environments tend to be incomplete and biased. Modern methods for eliciting estimates from domain experts (Garthwaite et al., 2005) ask experts in such a way that the expert’s answers are not overly distorted by his or her biases, but even the best elicitation methods cannot eliminate the influence of cognitive biases entirely. Moreover, even if these methods succeeded at eliciting the expert’s true beliefs, those beliefs would still be distorted by the biases in how the expert formed those beliefs.

Robust Strategy Discovery

The definition of resource-rational heuristics in Eq. 2 integrates out our uncertainty about the true environment E and the situations that decision-makers might find themselves in. If we ignored this uncertainty and instead used an expert’s description $d=(d_s,d_E)$ of the environment ($d_E$) and the situation ($d_s$), then we could approximate the resource-rational heuristic by

$$\begin{aligned} h_{\text {nonrobust}}=\max _h \text {RR}(h,s,E,B). \end{aligned}$$

(3)

The danger of that approach is that the expert’s description of the environment (e.g., the stock market) could be wrong.

Even if we ask domain experts (e.g., investment bankers), their answers could be incomplete or biased in ways that suggest strategies that ignore critical information. For instance, the formal and informal models that led to the excessive risk taking that caused the global financial crisis did not consider that the housing market might collapse, and very few financial experts would have anticipated that a pandemic might cause a global recession in 2020. Overlooking the possibility of such significant extreme events is very dangerous (Taleb, 2007). It is therefore imperative to model and account for the ways in which people’s descriptions of a decision environment might be incorrect. We refer to these discrepancies as model-misspecification. The main contribution of this article is to propose a general method for discovering clever heuristics that are robust to model-misspecification. The basic idea is to find the heuristic that is most resource-rational in expectation over all possible true environments that could have given rise to the likely incomplete and partially incorrect description provided by a human expert. The following three subsections describe the three key steps of this process: (i) formulating a model of the ways in which people’s descriptions might be wrong (Section 3.1), (ii) using this model to infer which true environment might have given rise to this description (Section 3.2), and (iii) training strategy discovery methods (Section 3.3) on potential true environments.

Modeling Model Misspecification

People’s descriptions d of a given environment e vary depending on what they have experienced, which parts of their experience they remember, and how they interpret it. Each of these three aspects varies considerably across different people. We therefore model the process giving rise to a description d as a probabilistic generative model $P(d,e)=P(e)\cdot P(d|e)$. This model combines two parts: a broad prior distribution P(e) over which environments might be possible and the likelihood function P(d|e) that specifies how likely a given environment e is to give rise to a possible description d. This likelihood function expresses the probability with which different types of model misspecification might occur and what their consequences might be. One way to develop such a likelihood function is to model how likely different aspects of the environment will (not) be observed ($P(\mathbf {o}|e)$), what a person who has made those observations ($\mathbf {o}$) is likely to remember ($P(\mathbf {m}|\mathbf {o})$), and how a person might describe the environment based on their memories ($P(d | \mathbf {m})$). The first component will reflect the fact that rare events are unlikely to be experienced—a fact known to cause the underestimation of extreme events in decisions from experience (Hertwig et al., 2004). The latter two elements can be informed by the extension literature on biases in human memory, such as memory biases in favor of extreme events (Madan et al., 2014), and biases in human judgment (Kahneman et al., 1982). The three components can then be combined into a model of model misspecification, that is $P(d|e) = \sum _{\mathbf {o},\mathbf {m}} P(d|\mathbf {m}) \cdot P(m|\mathbf {o} \cdot P(o|e)) ;$ we will use a simple version of this approach in “4” and “5”. Alternatively, one can empirically estimate P(d|e) by having people interact with a known environment and modeling their descriptions as a function of the true environment; we will use this approach in “6” and “7” (see “6.2.1”).

Performing Bayesian Inference on the True Environment to Compute Resource-Rational Heuristics

According to Eq. 2, the optimal heuristic given a description d achieves the best possible cost-benefit trade-off in expectation across all possible environments. In this expectation, the heuristic’s resource rationality in each possible environment e is weighted by the posterior probability of that environment given the description d. This suggests that strategy discovery methods can be made robust by applying them to samples from the posterior distribution P(E|d) instead of applying them to the description d itself. Therefore, our solution proceeds in two steps:

• 1. Estimate $\mathbf {P(E|d)}$. We use Bayesian inference to get a probability distribution over the possible true environments. The posterior distribution over possible environments is

  $$\begin{aligned} P(E=e|d) = \frac{P(E=e)\cdot P(D=d|e)}{P(D=d)}, \end{aligned}$$

  (4)

  where $P(E=e)$ is the prior distribution over possible environments, and the likelihood function $P(D=d|e)$ is a probabilistic model of model misspecification.

• 2. Apply strategy discovery methods to samples from the posterior distribution. To generate a training set that encourages robust solutions, we independently sample training environments from the posterior distribution, that is $\{ e_{k} \}_{k=1}^{N} \sim P(E|d).$ Given sufficiently many samples from the posterior distribution, standard reinforcement learning methods can be used to approximate the resource-rational heuristic $h\star$ defined in Eq. 2 by the policy that maximizes the average return across the MDPs defined by the sampled environments $\{ e_{k} \}_{k=1}^{N}$.

Methods for (Robust) Strategy Discovery

In this work, we created a robust and a non-robust version of each of the three strategy discovery methods presented in the remainder of this section: deep recurrent Q-learning, deep meta-reinforcement learning, and Bayesian metalevel policy search. The robust versions are trained on the posterior distribution over the possible true environment given the description, whereas the non-robust versions are trained directly on the description or the decision problem. These two approaches approximate the resource-rational heuristic defined in Eq. 2 and the non-robust heuristic defined in Eq. 3, respectively. In the subsequent sections, we will evaluate the policies found by those six methods against each other and against a random policy, which always samples uniformly from the set of available computations.

The neural-network-based methods (i.e., deep recurrent Q-networks and meta reinforcement learning) were implemented using TensorFlow (version 1.12) (Abadi et al., 2015) in Python. For these methods, the Adam optimizer (Kingma & Ba, 2019) was used for training. Furthermore, for these approaches, we employed early stopping (Zhang and Yu, 2005) to prevent overfitting. Hyperparameter selection was carried out following the common principles and standard approaches (Smith, 2018), and the best model was stored for evaluation.

Bayesian Metalevel Policy Search (BMPS)

According to rational metareasoning, an optimal metalevel policy is one that chooses the action that maximizes the value of computation (VOC) at each step (Russell et al., 1991):

$$\begin{aligned} \pi ^\star _{\text {meta}} = \arg \max _c \text {VOC}(c,b) \quad \forall b \in \mathcal {B} \end{aligned}$$

(5)

where VOC(c,b) is the expected increase in utility on performing computation c in belief state b compared to taking a decision immediately.

The calculations of expected values of various possible computations can be arbitrarily hard. Therefore, the Bayesian metalevel policy search (BMPS) method (Callaway, Gul et al., 2018) attempts to approximate the VOC by a linear combination of information-theoretic features:

$$\begin{aligned} \widehat{\text {VOC}}(c,b;\mathbf{w} ) = w_1 \cdot \text {VOI}_{\text {1}}(c,b) + w_2 \cdot \text {VPI}(b) + w_3 \cdot \text {VPI}_{\text {sub}}(c,b) - w_4 \cdot \text {cost}(c) \end{aligned}$$

(6)

where the weights $\{ w_{i} \}_{i=1}^{3}$ are constrained to lie on the probabilistic simplex and $w_{4} \in [1, h]$, such that h is an upper bound on the number of performed computations. The weights are learned by using Bayesian Optimization (Mockus, 2012) with the expected return as an objective function.

Consequently, we obtain an approximately optimal policy that selects computations which maximize $\widehat{\text {VOC}}$:

$$\begin{aligned} \pi _{\text {meta}}(b;\mathbf{w} ) = \arg \max _c \widehat{\text {VOC}}(c,b;\mathbf{w} ) \end{aligned}$$

(7)

The following sections describe the methods we used as baselines for our new robust BMPS method; therefore, readers who are primarily interested in the results may wish to skip them.

Deep Recurrent Q-learning

Recent advances in deep reinforcement learning have led to great performance in planning tasks and sequential decision problems (Arulkumaran et al., 2017). The standard deep Q-network (DQN) (Mnih et al., 2013) architecture assumes that the state of the environment is fully observable. However, this is not the case for the robust strategy discovery problem, where the structure of the true environment is unknown. On such, so-called partially observable tasks, the performance of neural networks can be improved by adding recurrent layers to the neural network (Hausknecht & Stone, 2015; Narasimhan et al., 2015). We therefore use the resulting deep recurrent Q-network (DRQN) architecture as one of the models for comparison (Hausknecht & Stone, 2015).

Here, we represented the current state of the environment as a stack of two matrices. Each entry of the first matrix encoded whether the corresponding node had already been inspected or not. For the inspected nodes, the entries of the second matrix were the nodes’ rewards. For the uninspected nodes, the entries of the second matrix were zero. This representation allowed us to treat input as an array and pass it into a convolutional neural network(CNN) which formed the initial layers of our DRQN model. The model architecture consisted of four convolutional layers, which had 32, 64, 128, and 200 filters respectively. The outputs from convolutional layers were passed into a long short-term memory (LSTM) network layer with 200 units (Hochreiter & Schmidhuber, 1997). The activations of this layer were then passed on to a fully connected layer that outputs $Q_{\text {meta}}$ of the state predicted by the network for each possible computation. Action selection was performed in an epsilon-greedy fashion, that is, the action with the highest activation in the output layer was selected with probability $1-\varepsilon$ and otherwise the action was selected uniformly at random. The action output was either the number of the node to be clicked on next or the operation that terminates planning and selects the path with the highest expected value according to the current belief state ($\bot$).

We also used the additional training utilities like experience replay buffer as used in (Hausknecht & Stone, 2015). Experience buffers enable the learning algorithm to use the seen episodes multiple times while training, and Epsilon-Greedy action selection helps address the exploration-exploitation trade-off.

The pseudocode of our algorithm is provided in Algorithm 2 in Appendix 1. We selected hyperparameters following the standard practices for hyperparameter optimization (Smith, 2018); the resulting values are shown in Table 1 in Appendix 1 and were then used in the simulations reported below.

Deep Meta Reinforcement Learning

Even though the incorporation of a recurrent network makes the DRQN more flexible than the DQN, its architecture and training paradigm only make it suitable for discovering strategies in a single environment. Our aim, however, is to discover robust strategies that perform well across multiple potential true environments. We therefore need learning methods that can incorporate information from multiple training environments. One such method is the deep meta-reinforcement learning (Deep Meta-RL) (Wang et al., 2016). Deep Meta-RL learns to quickly adjust its strategy to the structure of the environment it is.

Our Deep Meta-RL method uses a neural network architecture that is similar to the DRQN architecture (see Fig. 4). The main difference is that the action taken and reward obtained in the previous time step serve as additional inputs to the state of the LSTM in the next time step (Wang et al., 2016). This enables the network to identify whether its current strategy is working or if it needs to be changed, hence increasing the adaptability of the method. The belief state that was an input to the CNN encoder was represented in that same manner as described in the DRQN section above. The CNN encoder had three convolutional layers with 32, 128, and 264 filters, respectively. The LSTM layer had 400 units.

Fig. 4

Deep Meta-RL network architecture. The DRQN architecture is identical, except that the LSTM does not receive the computation and cost of the previous time step as an input

Here, we trained this network architecture with the Asynchronous Actor-Critic Agent (A3C) Algorithm (Mnih et al., 2016). The hyperparameters we used are listed in Table 2 in Appendix 1.

Binz et al. (2022) have recently used a similar approach to discover heuristics for choosing between two alternatives based on multiple attributes.

Discovering Robust Planning Strategies by Modelling Biases in People’s Descriptions of the Environment

To evaluate our general approach to robust strategy discovery, we first apply it to the domain in which automatic strategy discovery has been studied most extensively so far: planning in the Mouselab-MDP paradigm. Concretely, we create two sets of benchmark problems based on two different tasks. For each set, we evaluate the robust versions of the three strategy discovery methods described in Section 3.3 against their non-robust counterparts and a metalevel policy that chooses planning operations randomly. We start by briefly describing how we applied our general approach to robust strategy discovery to the domain of planning, and then present benchmark problems and how well our methods performed on them. We found that Bayesian inference on the structure of the true environment significantly increases the robustness of all strategy discovery methods (Section 4.2). Moreover, we were able to replicate these findings on a second set of more complex benchmark problems (see Appendix 3).

Application of Robust Strategy Discovery to Planning Problems

To evaluate how good our approach is at discovering planning strategies, we applied it to a metalevel MDP model (Section 4.1.2) of the Mouselab-MDP planning paradigm (Section 4.1.1).

Modeling Planning Tasks and Planning Strategies

As it is not possible to observe human planning directly, the underlying cognitive processes must be inferred from their behavior. This makes it difficult to study what strategies they discover, learn, and use. Process-tracing paradigms, such as the Mouselab paradigm (Payne et al., 1988), present participants with tasks that make their behavior highly diagnostic of their unobservable cognitive strategies. The Mouselab-MDP paradigm (Callaway et al., 2017) is a process-tracing paradigm for measuring how people plan. An example Mouselab-MDP environment used in this study is shown in Fig. 5a. In these environments, participants are tasked to select one of several possible paths through a spatial environment, where each location harbors a reward. The participant’s goal is to maximize the sum of the rewards along the chosen path. All the rewards are initially concealed, but the participant can uncover them by clicking on the locations. Critically, each click has a cost of $\$1$. Thus, the participant has to trade the cost of collecting information off against the value of the collected information for making a better decision.

Fig. 5

a An example environment of the Mouselab-MDP paradigm as shown to participants. b Alternative representation of an example environment as a grid of three node types. The node values are independently sampled from a uniform distribution (U) with high (H; $U(\{-48,-24,24,48\})$), medium (M; $U(\{-8,-4,4,8\})$), and low (L; $U(\{-2,-1,1,2\}$) variance

Discovering (Robust) Planning Strategies by Solving Metalevel MDPs

Discovering Planning Strategies by Solving Metalevel MDPs

As described in Section 2.2, the problem of deciding how to plan in the Mouselab-MDP paradigm can be modelled as a metalevel MDP. The set of possible beliefs $\mathcal {B}$ consists of belief states b that represent the belief about the values underlying the all the nodes. The belief about the value of a node is represented by a probability distribution if the node is unobserved and the observed value if the node is observed. In our experiments, we use uniform distributions over a set of values. Thus, the belief state $b^{(t)}$ at a time t can be represented as ($R_1^{(t)}, ... R_K^{(t)}$) where $R_K^{(t)}$ represents the set of values $X_k$ the node K can take such that $b^{(t)}(X_k = x)) = U(x;R_K^{(t)})$ is the probability mass function of a discrete uniform distribution over the set $R_K^{(t)}$. The set of computations $\mathcal {C} = \{c_1, c_2, ... c_K, \perp \}$, where $c_k$ is the click reveals the value of the node k and $\perp$ terminates planning and selects the path with the highest expected sum of rewards according to the current belief state. The transition function $T_{\text {meta}}(b^{(t)},c,b^{(t+1)})$ of how the computation $c_k$ might update the belief state (e.g., from $b^{(t)}$ to $b^{(t+1)}$). Performing computation $c_k$ sets $R_k^{(t+1)}$ to {x} with probability $\frac{1}{|R_k^{(t+1)}|}$ and the metalevel reward function $r_{\text {meta}}$ which encodes the cost of computations $c \in \mathcal {C}$ and the utility of the action chosen when computation is terminated. $r_{meta}(b^{(t)}, c) = -\lambda$ for $c \in \{c_1, c_2, ... c_k\}$ and $r_{meta}((R_1, R_2, ..., R_k), \perp ) = \underset{t \in T}{\max } \sum _{k \in t} \frac{1}{|R_k|} \cdot \sum _{x \in R_k}x$ where T is the set of all paths $\varvec{t}$. In this formal framework, planning strategies correspond to metalevel policies ($\pi _{\text {meta}}: \mathcal {B} \mapsto \mathcal {C}$) that specify which computation will be performed in a given belief state. To find out the solution to the metalevel MDP, we use the strategy discovery methods described in Section 3.3.

Applying the Bayesian Approach to Discovering Robust Planning Strategies from Erroneous Descriptions

To discover robust planning strategies, we applied the general robust strategy discovery approach described in Section 3 to descriptions of planning tasks. That is, we perform Bayesian inference on the structure of the true environment given a description and then train our strategy discovery methods on samples from the posterior distribution over planning tasks (see Appendix 2).

In this case, the environment and its description are specified in terms of how variable the possible rewards are at the different locations along the possible routes one could plan (for more detail, see Section 4.2.1).

Strategy Discovery Methods

We discover (robust) planning strategies by solving the metalevel MDPs (Section 4.1.2) of deciding how to plan using the methods described in Section 3.3. In addition to the standard versions of these four learning methods, we also create the corresponding robust versions. To achieve robustness, we train each method on samples from the posterior distribution over possible true environments.

The BMPS policy is defined in terms of features that depend on assumptions about the structure of the environment. Therefore, the robust version of BMPS additionally performs online inference about the structure of the environment during the execution of the BMPS policy. We refer to the resulting version of BMPS as robust BMPS.

Robust Bayesian Metalevel Policy Search (BMPS)

In general, the robustness of the strategy discovery methods is achieved by the usage of the posterior distribution over the possible true environments. BMPS makes use of the posterior distribution by using it in its feature computation step.

The features of the BMPS method rely on a model of the environment. The standard version of the BMPS method would run on a model description d. We introduce a robust version of the BMPS method that performs online inference on the environment (E) based on the description (d) and the belief state (b) that the agent has formed by interacting with the environment, that is, $\mathrm {E}_{E|d,b}\left[ \widehat{\text {VOC}}_{E}(b,c;\mathbf{w} ) \right]$. Critically, this approximation becomes computationally expensive when there are many possible environments. Therefore, we approximate this expected value by the normalized weighted average across the smallest set of possible environments $\mathcal {E}_{\text {min}}$ whose combined posterior probability given the current belief state exceeds a threshold $p_{\text {thresh}}$.

$$\begin{aligned} p_{\text {total}|i,b}&= \left[ \sum _{e \in \mathcal {E}_{\text {min}}} P(E=e|d,b) \right] \ge p_{\text {thresh}} \\ \mathrm {E}_{E|d,b} \left[ \widehat{\text {VOC}}_{E}(b,c;\mathbf {w}) \right]&\approx \frac{1}{p_{\text {total}|d,b}} \cdot \sum _{e \in \mathcal {E}_{\text {min}}} P(E=e|d,b) \cdot \widehat{\text {VOC}}_{e}(b,c;\mathbf {w}) \end{aligned}$$

For the purpose of our experiments, we set $p_{\text {thresh}} = 0.99$.

Evaluation on the Flight Planning Task

The Flight Planning game is a three-step sequential decision-making task that we implemented using the Mouselab-MDP paradigm (see Fig. 5a). In this game, participants plan the route of an airplane across a network of airports. Figure 5b illustrates the statistical structure of one of the Mouselab-MDP task environments we used in this study. This environment is motivated to capture the sequential nature of decision-making in real life.

Benchmarks

To create the first set of benchmarks for robust strategy discovery, we build a dataset comprising 66 (e, d, p)-triplets where the environment e is a version of the task illustrated in Fig. 5, the description d is generated according to the model of model misspecification described below, and the probability $p=P(E=e)\cdot P(d|e)$ specifies the relative frequency of this pair in the set of benchmarks. The descriptions and the environments are $3~\times ~3$ matrices where each entry is either L, M, or H (see Fig. 5). Those entries specify whether the variance of the reward distribution at the corresponding location is low (L), medium (M), or high (H). There are 36 equally probable true environments ($P(E=e)=1/36$) and they all share the property that each row contains one high (H), one medium (M), and one low (L) variance node. Moreover, the arrangement of node types is the same in the bottom two rows.

For each true environment e, our model of model misspecification yields 2 possible descriptions d—one generated according to the recency effect (Deese and Kaufman, 1957) and the other from the underestimation of rare events (Hertwig et al., 2004). For six such environments, the resulting descriptions from the two biases turned out to be the same.

What makes these benchmark problems difficult is that many environments can give rise to the same specification. As a result, each description d could have plausibly been generated from 11 different true environments.

Model of Model Misspecification

As proof of concept, we worked with two admittedly simplistic models of how the recency effect and the underestimation of rare events affect the way a person would describe a 3-step Mouselab-MDP environment they experienced, represented by $P(d|e, m_{\text {recency}})$ and $P(d|e, m_{\text {underestimation}})$, respectively. Figure 6 illustrates these two models.

Fig. 6

Illustration of how cognitive biases might give rise to misspecified models of the environment shown on the left. Recency bias: the initial two rows are mistaken to be similar to the last row. Underestimation bias: the odd row (top row) is mistaken to be similar to the other two rows

In brief, the first model incorporates the recency effect in remembering experiences based on how far away in the past they occurred. This model always misremembers the rewards in the first two steps from the starting point as having been identical to the reward in the last step (top row). This is because of the order in which the nodes are walked upon after the participants stop clicking, making the first two steps the less recent ones, whereas the other incorporates the bias in representing rare events. This model underestimates the frequency of rare events by always remembering the rare event in each column as the most frequent one.

For simplicity, we assume that model misspecification arises half of the time from the recency bias and half of the time from the underestimation of the frequency of rare events. We therefore model the probability that a person with experience in an environment e will describe it by the description d as

$$\begin{aligned} P(d|e) = \frac{1}{2}\cdot P(d|e, m_{\text {recency}}) + \frac{1}{2}\cdot P(d|e, m_{\text {underestimation}}) \end{aligned}$$

(8)

These assumptions merely serve as a placeholder for a more realistic model of model misspecification to be developed in future work. The contribution of this article is the general approach that combines the Bayesian inversion of such a model with automatic strategy discovery methods.

Simulation Results

We found that robust and non-robust strategy discovery methods discovered qualitatively different types of planning strategies that achieved lower levels of resource rationality.

Figure 7 compares the behavior of two strategies that were discovered by the most-robust method versus the least-robust strategy discovery method, respectively. The strategies are compared in two different scenarios. In scenario A, where the true environment matches the model, both strategies make similar clicks. However, in scenario B, when the true environment differs from the model, the strategy discovered by the non-robust method fails to uncover the high-variance nodes because it inflexibly follows the approach that would have been optimal if the description were correct. In contrast, the robust strategy quickly adapts to the discrepancy between the model and the true environment and collects all the most valuable information. Intuitively, the click sequences generated by this robust strategy seem to illustrate the simple rule of thumb “Find and inspect the large positive or negative outcome of each row. Then choose a path that collects the large positive outcomes and avoids the large negative outcomes.” Critically, the planning strategy discovered with the robust method performs well in both environments, whereas the strategy discovered with the non-robust strategy fails when the true environment does not match the description.

Fig. 7

Comparison of the planning strategies discovered by a robust method (BMPS with Bayesian inference) versus a non-robust method (DRQN without Bayesian inference). Example A illustrates the strategies in the specified environment. Example B illustrates their behavior in a different environment that could have given rise to the same description

Fig. 8

Resource-rationality scores of the decision strategies discovered by different methods with versus without Bayesian robustness in the Flight Planning task

As shown in Fig. 8, we found that the BMPS method with Bayesian inference on the true environment achieved an almost perfect relative robustness score ($\rho _{\text {rel}}=0.99$, absolute score = 53.25) and outperformed all the other methods (all $p<.0001$). The second-best method was meta-RL with Bayesian inference on the true environment ($\rho _{\text {rel}}=0.91$, absolute score = 49.16). The addition of Bayesian inference on the true environment significantly improved the robustness of all methods: It improved the resource rationality of the decision strategies discovered by BMPS from $42.47 \pm 0.41$ to $53.25 \pm 0.42$ ($t(47914)=-34.78$, $p<.001$; effect size $d=.318$) and had similar effects for the meta-RL method ($35.54 \pm 0.43$ vs. $49.16\pm 0.41$; $t(47894)=-44.60$, $p<.001$, $d=.408$) and the DRQN method ($35.75 \pm 0.42$ vs. $46.26 \pm 0.40$; $t(47894)=-35.38$, $p<.001$, $d=.323$).

Discussion

We developed an approach for making automatic strategy discovery robust to model-misspecification and evaluated its performance on a set of benchmark problems. We found that Bayesian inference on the true environment that might have led to a given biased description significantly increases the robustness of automatic strategy discovery. Moreover, we were able to replicate this finding on a second set of more complex benchmark problems with a different model of model misspecification (see Appendix 11). This suggests that our approach to robust strategy discovery will likely be beneficial in other environments as well. Furthermore, both evaluations showed that BMPS is a more robust strategy discovery method than previous approaches based on neural networks. These findings suggest that combining BMPS with Bayesian inference is a promising approach to discovering planning strategies that are robust to all the ways in which the real world might differ from our descriptions. This approach might make it possible to improve human planning even when we cannot be sure which planning problems they might face in the real world. In the next section, we test this hypothesis by conducting a large online experiment.

Improving Human Planning

How people plan determines which choices they make. Previous research suggests that people sometimes fail to consider some of the most important potential consequences of their choices (O’Donoghue and Rabin, 1999; Jain et al., 2019; Taleb, 2007). The resulting choices can have devastating consequences for people’s physical, mental, and financial well-being and society at large. If people’s reliance on suboptimal planning strategies is partially responsible for this problem, then teaching near-optimal planning strategies might be a way to ameliorate such problems. To explore whether teaching the heuristics discovered by our robust strategy discovery methods might be a viable approach to improving human decision-making, we leveraged the robust strategy discovery methods introduced above to develop a robust version of the cognitive tutor introduced by (Lieder et al., 2019). This tutor uses our most-robust and best-performing strategy discovery method—the robust BMPS method—to discover a robust planning strategy from a given description of the environment and then teaches it to people by showing them video demonstrations of its planning behavior.

To evaluate how beneficial it is for people to be trained by the robust tutor, we conducted a behavioral experiment with the three-step sequential decision problem introduced in Section 4.2. That is, for each participant, we sampled one of the 66 benchmark problems according to their respective probabilities; for instance, the benchmark problem $(e_k,d_k,p_k)$ would be sampled with probability $p_k$. The participant was assigned the role of the novice who is being trained by the robust cognitive tutor and then tested on the true environment $e_k$. Critically, the cognitive tutor does not know the true environment $e_k$, but only the usually erroneous description $d_k$. The robust tutor infers what the true environment might be given the description ($P(E|d_k)$), derives the optimal strategy from this probabilistic knowledge, and then demonstrates it on environments sampled from its posterior distribution over possible environments ($P(E|d_k)$). To find out what aspects of the robust tutor contribute to the effective learning, we compared it to two conditions where no tutor was provided and a condition with a Non-Robust Tutor. The Non-Robust Tutor was based on the best-performing (non-robust) standard machine learning algorithm (non-robust DRQN, which assumes that $d_k$ is the true environment).²

Methods

Participants We recruited 357 participants on Amazon Mechanical Turk (average age 36.4 years, range: 18–77 years; 216 female). Participants were paid $1.20 plus a performance-dependent bonus (average bonus $1.54). The average duration of the experiment was 15.0 min. Participants were randomly assigned to the control condition without tutoring and without practice (89 participants), the control condition without tutoring but with practice (87 participants), the experimental condition with the non-robust cognitive tutor (94 participants), or the experimental condition with the robust cognitive tutor (87 participants).

Materials The experimental task was the Flight Planning game described in Section 4.2. As illustrated in Fig. 5, participants are tasked to select one of nine possible routes from the starting position at the bottom to one of the final destinations at the top. Each location harbors a reward. The participant’s goal is to maximize the sum of the rewards along the chosen path. All the rewards are initially concealed, but the participant can uncover them by clicking on the locations. Critically, each click has a cost of $\$1$. Thus, the participant has to trade the cost of collecting information off against the value of the collected information for making a better decision.

Procedure We conducted a between-subjects experiment with four groups. For each participant, we first randomly selected one of the 66 benchmark problems described in Section 4.2.1. The participant was not shown the description itself. Instead, the usually inaccurate description of the selected benchmark was used to generate the trials of the training blocks. In contrast, the trials of the subsequent test block were generated according to the benchmark’s true environment.

The experiment was structured into instructions, 5 rounds of playing the Flight Planning game in environments sampled from the prior distribution (see Section 4.2.1), a quiz that tested the participant’s understanding of the game, a training block (except in the control condition without tutoring and without practice) and a test block in which the participant played the Flight Planning game in the benchmark’s true environment. The instructions described the Flight Planning game in general and did not mention the description or potential differences between the practice trials and the training block versus the test block. In the two experimental conditions, the training block comprised 10 tutor demonstrations. Each tutor demonstrated the strategy that it had derived from the usually inaccurate description. In the control condition with practice and without demonstrations, the training block comprised 10 trials of playing the Flight Planning game in the environment specified by the benchmark’s inaccurate description. There was no training block in the control condition without tutoring and without practice.

To motivate participants to pay close attention to these demonstrations, they were told that their bonus would depend on correctly answering a quiz about the demonstrated strategy and were given the option to review the demonstrations before moving on to the quiz.

Each demonstration (see Fig. 7a-c in the training block of the two experimental conditions started from a different fully occluded instance of the task illustrated in Fig. 5a. In the non-robust tutor condition, the spatial layout of the rewards was generated according to the inaccurate description. In the robust tutor condition, the spatial layout of the rewards was sampled from the posterior distribution P(e|d) and each round used a different sample. The demonstration then showed the participant the first click that the automatically discovered strategy would make and the reward that it revealed. After a 1.1-s delay, the demonstration showed the second click that the strategy would make based on the outcome of the first click. This continued until the strategy decided to terminate planning. At this point, the participant was shown the sequence of moves that the strategy would choose, and the rewards collected along the way.

In the first experimental condition, the demonstrations showed the strategies that the DRQN method without Bayesian inference derived from the potentially misspecified models (Non-Robust Tutor). The strategy learned by the Non-Robust Tutor always clicks on the same three nodes that should have high variance according to the description of the environment in all demonstrations, regardless of what their values are (see Fig. 7b and d). In the second experimental condition, the demonstrations showed the strategies discovered by BMPS with Bayesian inference (Robust Tutor). When a high variance node is not in its expected location, then these robust strategies continue to search for it until they find it (see Fig. 7a and c). In the Non-Robust Tutor, all demonstrations were performed on the reward structure specified by the model, as illustrated in Fig. 7b. In contrast, the reward structures in the Robust Tutor were sampled from the posterior distribution over the true environment given the model specification; thus, some demonstrations were performed on environments that differed from the model as illustrated in Fig. 7c.

To ensure high data quality, we applied two pre-determined exclusion criteria. We excluded the 4% of participants who affirmed that they had not paid attention to the instructions or had not tried to achieve a high score in the task. We excluded 12% of the remaining participants who did not make a single click on more than half of the test trials because not clicking is highly indicative of speeding through the experiment without engaging with the task.

Results

Applying the Shapiro-Wilk test for normality, we find that the scores are normally distributed for all the conditions: control condition without tutor demonstrations and without practice ($W(68)=0.97$, $p=.086$), control condition without tutor demonstration but with practice ($W(77)=0.118$, $p=.002$), the non-robust tutor condition ($W(86)=0.98$, $p=.100$) and the robust tutor condition ($W(85)=0.99$, $p=.564$). ANOVA test showed that the three groups differed significantly in their resource-rationality score on the test trials ($F=4.5$, $p=.004$). Planned pair-wise comparisons confirmed that teaching people strategies discovered by the robust method significantly improved their resource-rationality score (41.6 points/trial) compared to the control condition without practice (33.5 points/trial, $t(153)=3.28$, $p<.001$, $d=.528$) and the control condition with practice (36.2 points/trial, $t(162)=2.08$, $p=.0193$, $d=.326$). In contrast, teaching strategies discovered by the non-robust method failed to improve people’s resource rationality (33.1 points/trial) when compared to the control condition without practice ($t(154)=0.0$, $p=.498$, $d=0.001$) and the control condition with practice ($t(154)=-1.03$, $p=.153$, $d=0.161$), and also led to significantly lower resource-rationality scores than teaching strategies discovered by the robust method ($t(171)=-3.49$, $p<.001$, $d=.533$). Each person’s resource-rationality score in the Mouselab-MDP task is the sum of the rewards they collected minus the cost of their clicks. We can therefore interpret it as a measure of how well their strategy trades off the quality of the resulting decisions with the cost of decision-making. To make the scores more interpretable, we compute each group’s resource-rationality quotient ($\frac{\text {RR}_{\text {people}}}{\text {RR}_{h^\star }}$ where $\text {RR}_{\text {people}}$ is the group’s average score). As shown in Fig. 9, teaching people strategies discovered by the robust method brought their resource rationality closer to that of the best possible heuristic for the true environment. Concretely, people’s resource-rationality quotient increased from 47.5% in the control condition without practice to 75.1% in the robust tutor condition and to only 56.7% in the control condition with practice and 56.8% in the non-robust tutor condition.

Fig. 9

Resource-rationality quotient by condition (average resource-rationality score of people divided by the resource-rationality score of the most resource-rational planning strategy)

These differences in resource rationality reflect differences in the underlying planning strategies. Inspecting the planning strategies that participants used in the test block showed that participants who had been taught by the robust tutor inspected the values of all the most informative high-variance nodes on 62.0% of the trials, whereas participants in the non-robust tutor condition or the control condition did so significantly less often (41.3% and $46.7\%$, respectively, $\chi ^2(2) = 117.3$, $p<.001$).

Discussion

The findings of our behavioral experiment showed that our new robust strategy discovery method (robust BMPS) can allow us to improve human decision-making in cases where two non-robust off-the-shelf machine learning methods failed. Because we compared BMPS with Bayesian inference against a non-robust machine learning method without Bayesian inference, we cannot be sure which proportion of this improvement was due to performing Bayesian inference on the structure of the environment versus using BMPS. The results shown in Fig. 8 suggest that more than half of the improvement was due to performing Bayesian inference. Future work could test this assumption by running an experiment with a factorial design that manipulates the use of Bayesian inference on the structure of the environment separately from the reinforcement learning algorithm trained on the samples from the posterior distribution (BMPS vs. DRQN).

Our experiment made the simplifying assumption that the utility participants derive from their decision is proportional to the number of points they earned in the task, even though the utility of money is nonlinear (Kahneman and Tversky, 1979). For a more detailed discussion of this issue, see Section 8. Another limitation of the present work is that it assumed a perfect model of the biases in the generation of model specifications. Furthermore, our assumptions about the cognitive biases were very simplistic. Another limitation is that the task used in the experiment is rather artificial. To address these shortcomings, the following two sections evaluate our approach on a more realistic problem, namely deriving investment strategies from erroneous descriptions provided by people. In that application, the cognitive biases are those of real people, and our method has to rely on a model of what those biases might be. Section 6 describes how we applied our robust strategy discovery approach to this problem. Section 7 reports a behavioral experiment in which we tested whether the risky choice strategies discovered in this way can improve people’s ability to make decisions under risk.

Discovering Robust Heuristics for Multi-alternative Risky Choice

In the previous sections, we introduced a robust machine learning method for deriving resource-rational decision strategies from potentially biased and incomplete descriptions of the decision problems to be solved. The robustness of strategy discovery methods is especially important for improving people’s decisions in scenarios where the stakes are high, and the environment is highly uncertain (Hertwig et al., 2019). A prime example of this kind of real-life decisions is investing in the stock market. Previous research has found that people make a number of systematic errors when deciding whether and how to invest in the stock market (Benartzi and Thaler, 1995; Hirshleifer, 2015). The stock market is highly unpredictable, and even experienced investors tend to overlook important eventualities. Therefore, the decision strategies that traders use have to be robust to our uncertainty about what the stock market is really like (Taleb, 2007). It has been argued that simple heuristics can help people make better financial decisions precisely because they are more robust to such uncertainties than more complex decision procedures (Neth et al., 2014; Lo, 2019). Previous work has developed machine learning methods for discovering resource-rational heuristics for risky choice (Lieder et al., 2017; Gul et al., 2018; Krueger et al., 2022). Here, we extend these approaches to a slightly more realistic formulation of risky choice and make them robust to model misspecification.

To capture some challenges of applying our approach to this real-world problem, we first collected people’s descriptions of how likely investments are to yield positive or negative returns of different magnitudes directly from people who had first-hand experience with those investments. We use these descriptions to create a naturalistic set of benchmark problems for discovering robust strategies for making decisions under risk (Section 6.1). We then extend and apply our Bayesian robust strategy discovery approach to this problem in Section 6.2 and evaluate it on the new benchmarks in Section 6.3.

Realistic Benchmarks for the Discovery of Robust Strategies for Risky Choice

To construct a challenging, yet tractable, set of benchmark problems for the robust discovery of risky choice strategies, we chose to work within the widely used Mouselab paradigm for studying risky choice (see Section 6.1.1). To make this paradigm more realistic, we base the distribution of its payoffs on stock market returns (Section 6.1.3). Critically, we base our benchmark problem’s on the generally erroneous descriptions of real people. To obtain those descriptions, we conducted an experiment in which participants first repeatedly chose between a number of investments and then described the distributions of their returns (Section 6.1.4). The resulting benchmark problems are publicly available.

Multi-alternative Risky Choice in the Mouselab Paradigm as a Model of Investment Decisions

Deciding which stock to invest in, like many other real-life decisions, entails choosing between several alternatives based on their multiple attributes. Although perusing the attributes is informative, one also cannot know exactly how well the investment will play out. The decision-maker can increase their chances of making a good decision by collecting more information, but collecting information takes time and effort. Therefore, the decision-maker has to find a good tradeoff between the quality of their decision and its costs. The experimental paradigm known as multi-alternative risky choice captures all of these important aspects of decision-making in the real world (Payne, 1976). In this paradigm, participants choose between multiple risky prospect based on what their payoffs would be in several possible scenarios (see Fig. 10). To make an informed decision, the participant can inspect what the payoffs of different gambles (columns) are in different scenarios (rows) by clicking on the corresponding cell of the payoff matrix for a certain fee. Participants can additionally inspect how likely each scenario is to occur.

Fig. 10

Screenshot of the Mouselab paradigm for studying multi-alternative risky choice. Each trial of the paradigm consists of a series of options to choose from, a set of outcomes which can occur for each option, and their corresponding probabilities of occurring. Participants can reveal the outcomes or their probabilities by clicking on the gray cells and paying a cost

Formally, each trial presents a choice among G gambles (see Fig. 10). After the participant has chosen a gamble, one of K event occurs. The payoff of gamble g in the case of the k^th event is given by the entry $v_{k,g}$ of the payoff matrix V. $\mathbf {p} = [p_{1},\ldots ,p_{k}]$ are the probabilities of the k possible events, where $p_k$ represents the probability of the $k^{\text {th}}$ outcome occurring. In our experiments, $\mathbf {p}$ is sampled from a symmetric Dirichlet distribution. We will vary the distribution parameter $\alpha$ to model two different situations. A small $\alpha$ leads to what we call the high dispersion case, wherein one outcome is much more likely than the others. A large $\alpha$ results in the low dispersion case, wherein the probabilities of the outcomes lie close to each other.

Initially, the values of V and $\mathbf{p}$ are unknown. To reveal them, the participant has to click on the corresponding cell on the screen. Each click is costly. The participant’s goal is to maximize the expected payoff minus the cost of clicking. Here, we focus on the special case where in each environment e all payoffs $V_{k,g}$ are independently drawn from the same distribution $\pi _e$. Moreover, we assume that this distribution is a piece-wise uniform distribution of the form $\pi _e(x)=\sum _{i=1}^{10} \pi _{e,1}\cdot \text {Uniform}(x; [-100; -80]) + \pi _{e,2}\cdot \text {Uniform}(x; [-80; -60]) + \cdots + \pi _{e,10}\cdot \text {Uniform}(x; [80; 100])$. We can therefore represent any given payoff distribution by a list of 10 numbers $\pi _{e,1},\cdots ,\pi _{e,10}$ where $\pi _{e,i}$ is the probability that a payoff falls into the i^th bin of that distribution. For instance, $\pi _{e,1}$ is the probability that the payoff is between $$-100$ and $$-80$.

We assume that different risky choice environments differ in the payoff distribution ($\pi _e$), the dispersion of the outcome probabilities ($\alpha _e$), and the cost of information ($\lambda _e$). We can therefore represent each multi-alternative risky choice environment e by a triplet $(\pi _e,\alpha _e,\lambda _e)$.

Problem Formulation

The problem we set out to solve was to develop a machine learning method that can derive resource-rational strategies for multi-alternative risky choice from inaccurate descriptions of payoff distribution. That is, we assume that the payoff distribution $\pi _e$ of the environment e is unknown and has to be estimated from expert testimony. Therefore, the strategy discovery method only has access to a usually inaccurate description of the true environment that we will refer to as $d=(\pi _d, \alpha _d, \lambda _d)$, where $\pi _d=(\pi _{d,1},\cdots ,\pi _{d,10})$ is a list of estimates of the corresponding probabilities of the true environment (i.e., $\pi _{e,1},\cdots ,\pi _{e,10}$) and $\alpha _d$ and $\lambda _d$ are estimates of the dispersion of the even probabilities ($\alpha _e$) and the cost of information ($\lambda _e$). For simplicity, we assume that only the description of the payoff distribution ($\pi _d$) can be inaccurate, whereas the other two components of the description are known to be accurate. To make this problem formulation more precise, we will now formulate a set of benchmark problems. Each benchmark problem will include a true payoff distribution and a human-generated description of that distribution. The following two sections specify the true payoff distributions and its descriptions, respectively.

Defining Realistic Payoff Distributions for the Risky Choice Problems

To investigate the importance of robustness for investment decisions in the real world, we chose to study decision problems whose payoff distributions mimic those of real-world investments in different kinds of stocks. Since the early 1900s, it was widely believed that stock returns followed the normal distribution. Mandelbrot (1963) pioneered the re-examination of the return distribution in terms of non-normal stable distributions³. Fama (1965) concluded that the distribution of monthly returns belonged to a non-normal member of the stable class of distributions. Various alternative classes of distributions have since been suggested. Examples include the Student’s t-distribution (Blattberg and Gonedes, 1974), the more general class of hyperbolic distributions (Eberlein and Keller, 1995) and the mixture of Gaussians (Kon, 1984). While there does not seem to be a fundamental theory that can suggest a distributional model of stock returns, it is now generally acknowledged that empirical return distributions are skewed and leptokurtic.

In this work, we mainly focus on heavy-tailed distributions because it is in these settings that people’s biases have the potential to be highly costly. We work with the class of stable distributions since they have been shown to be able to capture heavy tails and skewness. Additionally, they are supported by the generalized Central Limit Theorem, which states that stable laws are the only possible limit distributions for properly normalized and centered sums of independent, identically distributed random variables (Borak et al., 2005). One argument that has often been levelled against their usage is that they have infinite variance. However, real data would never have that property since it is bounded. To combat this as well as to make the task of eliciting biases easier, we truncate the distribution between fixed values, that is we assume that stock returns are bounded between -100% and +100%. Concretely, we created 9 stable distributions with varying riskiness and discretized them into 10 bins as shown in Fig. 11. The skewness parameter $\eta$ was kept negative to obtain thick left tails. The probability of each bin was set to be the difference in cumulative distribution functions of its upper and lower bounds except for the edge bins, which took the mass for the truncated tails as well. Therefore, each of these distributions can be represented by a list of 10 probabilities $\pi _{e,1},\cdots ,\pi _{e,10}$ that sum to 1. We will use the nine different distributions to define 9 different types of environments that differ in their payoff distributions.

Fig. 11

Distributions used to capture biases about stock returns

Eliciting Biased Descriptions of Payoff Distributions

To complete the specification of our benchmark problems, we complement the risky choice problems entailed by the 9 payoff distributions shown in Fig. 11 by people’s descriptions of those distributions. To obtain those descriptions, we conducted the online experiment described in the following paragraphs.

Participants We recruited 60 participants on Amazon Mechanical Turk (average age 38.0 years, range: 20–69 years; 36 male, 23 female, 1 other). Participants were paid $1.50 plus a performance-dependent bonus (average bonus $0.96). The average duration of the experiment was 21.1 min.

Procedure The experiment began with instructions about the task, followed by a quiz to test the participants’ understanding. They were then asked about how often they expected to see payoffs from each of the 10 bins for both the stocks before going through the 50 trials of the task (see Fig. 12a). In each trial, the participants had to choose one of the two stocks to invest in based on their name alone (see Fig. 12b). After choosing the stock, they were shown the payoffs from both stocks (that were sampled from their corresponding distributions) and were informed about their profit/loss in that trial ((see Fig. 12c). In all, they had to go through 50 such trials. On the conclusion of the task, we asked the participant to estimate how often each of the two stocks’ payoffs fell into each of the 10 equally spaced 20%-intervals between -100% and +100% (see Fig. 12d). Thus, from each participant, we obtained their prior and posterior expectations for two stocks. To ensure high data quality, we applied four predetermined exclusion criteria. We excluded 8.3% of participants who affirmed that they did not fill in their posterior expectations truthfully. Another 13.3% were excluded because they did not update their estimates after seeing the data. Another 5.0% were excluded because their posterior estimates for at least one stock were monotonically increasing or monotonically decreasing. Finally, 1.7% from the remaining participants were excluded because their posterior expectations for both stocks were identical.

Fig. 12

Screenshots from the online study used to collect people’s descriptions of investment decisions: a eliciting the prior, b choice, c feedback, and d eliciting the posterior

Results The exclusion criteria allowed for inclusion of 43 participants. After 50 trials of experiencing payoffs, each of them provided frequency estimates for two distributions. Converting those estimates from absolute frequencies into relative frequencies yielded $2 \times 43$ descriptions ($\pi _d$) of the payoff distributions ($\pi _e$) that were used to generate the trials a participant experienced.

Benchmarks

Building on the 86 descriptions of payoff distributions ($\pi _{d_1},\cdots , \pi _{d_{86}}$), we defined four sets of 86 benchmark problems each. Each benchmark is defined by a pair $(e_i,d_i)$ of a true environment $e_i=(\pi _{e_i},\alpha _{e_i}, \lambda _{e_i})$ and its description $d_i=(\pi _{d_i},\alpha _{d_i}, \lambda _{d_i})$. Concretely, we defined one set of 86 benchmark problems for each combination of a low versus high dispersion of the outcome probabilities ($\alpha _e=\alpha _d \in \lbrace 0.15, 10 \rbrace$) and a low versus high cost of information ($\lambda _e=\lambda _d \in \lbrace 1, 2 \rbrace$).⁴

Each ($e_i, d_i$)-pair specifies a multi-alternative risky choice benchmark were the true payoff distribution is $\pi _{e_i}(x)=\sum _{k=1}^{10} p_{e_i,k}\cdot \text {Uniform}(x; [-100+(k-1)\cdot 20; -100+k\cdot 20])$ and the described payoff distribution is $\pi _{d_i}(x)=\sum _{k=1}^{10} \pi _{d_i,k}\cdot \text {Uniform}(x; [-100+(k-1)\cdot 20; -100+k\cdot 20])$. By default, each benchmark problem is as assumed to be equally probable. We will use these benchmarks to assess the effectiveness of using robust strategy discovery to improve human decision-making in the experiment reported in Section 7.

Applying Bayesian Robust Strategy Discovery to Human-Generated Descriptions of Risky Choice Problems

To apply our Bayesian robust strategy discovery approach to the benchmark problems described in Section 6.1, we first model the relationship between the true distributions of stock returns and people’s descriptions of those distributions by a likelihood function (Section 6.2.1). We then develop an approximate Bayesian inference method for sampling from the resulting posterior distribution over possible true return distributions (Section 6.2.2). We combine this method with the strategy discovery methods presented in Section 3.3, formalize the problem of discovering heuristics for risky choice as a metalevel MDP (Section 6.2.3), and adapt the BMPS method for this problem (Section 6.2.4).

Modelling Model Misspecification

To perform Bayesian inference on the true payoff distributions given people’s fallible descriptions, we first have to model the likelihood function p(d|e). To achieve this, we collected an independent data set of descriptions (akin to the one described in Section 6.1) and used it to model the relationship between people’s descriptions and what they had observed. Our Bayesian method uses this information to probabilistically invert the distortion that led from the true payoff distribution to the description provided by a person who observed outcomes from that distribution. That in turn allows our method to derive strategies that work well in the true environment.

Obtaining People’s Descriptions To obtain biased descriptions, we reran the benchmark creation experiment described in Section 6.1.4. We recruited 58 participants on Amazon Mechanical Turk (average age 37.7 years, range: 21–71 years; 41 male, 17 female). Participants were paid $1.50 plus a performance-dependent bonus (average bonus $1.19). The average duration of the experiment was 21.0 min. Our four pre-defined exclusion criteria described in Section 6.1.4 led to the exclusion of 6.9%, 6.9%, 5.2%, and 0% participants respectively (19% in total).

Capturing People’s Biases We use the descriptions obtained from the above experiment to develop a model of people’s biases. We simultaneously observed overestimation of extreme outcomes and underestimation of rare events. To capture this, we model these phenomena as transformations of the true probabilities.

To model overestimation of extreme outcomes ($m_{uws}$), we use utility-weighted sampling (Lieder et al., 2015). For a discrete payoff distribution defined by its values ($\mathbf {x} = [x_{1},\ldots ,x_{10}]$) and their corresponding probabilities ($\pi = [\pi _{1},\ldots ,\pi _{10}]$), utility-weighted sampling involves first computing the expected value of the distribution ($\bar{x}$), and then weighting the values of the distribution in proportion to the product of the deviation of the value from the expected value. The procedure is described as follows:

$$\begin{aligned} \bar{x}&= \sum _{i=1}^{10} \pi _i \cdot x_i \\ m_{uws}(\pi _i)&= \dfrac{\mid x_i - \bar{x} \mid \cdot \pi _i}{\sum _{j = 1}^{10} \mid x_j - \bar{x} \mid \cdot \pi _j} \\ \text {therefore, } m_{uws}(\pi )&= \left[ m_{uws}(\pi _1),\ldots ,m_{uws}(\pi _{10}) \right] \end{aligned}$$

In our case, x represents the midpoints of the bins for which data was collected in the experiment and $\pi$ represents the true probability distribution according to which the values were sampled, where $\pi _{i}$ is the probability of bin i and $x_i$ is the midpoint of the i^th bin.

Similarly, for a discrete distribution, we model the underestimation of rare events ($m_{rare}$) using a weighted average exponentiated probabilities. The probabilities ($\pi _j$) are exponentiated by a scalar product of a constant (k) and the value (in our case, the midpoint of the bin) for which the probability corresponds to ($x_j$). The description is as follows:

$$\begin{aligned} m_{rare}(\pi _{i})&= \dfrac{\pi _{i}^{\mid k \cdot x_i \mid }}{\sum _{j = 1}^{10} \pi _{j}^{\mid k \cdot x_j \mid }} \\ \text {therefore, } m_{rare}(\pi )&= \left[ m_{rare}(\pi _1),\ldots ,m_{rare}(\pi _{10}) \right] \end{aligned}$$

We assume that people have a bias that is a weighted average of the usage of the two biases described above. This can be represented by a mixture model ($m_{\text {bias}}$) where the individual terms capture if one or both biases are present. In case of a participant having both the biases, it is assumed that underestimation of rare events happens first and then on these probabilities participants overestimate extreme outcomes. The final bias model is

$$\begin{aligned} m_{\text {bias}}(\pi ; w_1, w_2, k) = (1 - w_{1})\cdot (1 - w_{2})\cdot \pi + w_{1}\cdot (1 - w_2)\cdot m_{\text {rare}}(\pi ) +(1 - w_1)\cdot w_{2}\cdot m_{\text {uws}}(\pi ) + w_1\cdot w_2\cdot m_{\text {uws}}(m_{\text {rare}}(\pi )) \end{aligned}$$

(9)

Its free parameters $w_1, w_2 \in \left[ 0, 1\right]$ and $k \in \left[ 1, \infty \right)$ are fitted individually to each participant’s data using Bayesian optimization. By looking at the obtained distribution of these parameters across participants, we get information about how much people weight each bias.

Bayesian Inference on the True Payoff Distributions

To perform Bayesian inference and to get a posterior distribution over the true distributions requires formalizing the prior distribution and the likelihood function. We formalize the prior using samples from a stable distribution, and the likelihood function as a function of the bias model of the participants obtained above.

We formalize the prior as a Dirichlet distribution with 10 components (where each component represents one bin). We draw samples from a class of stable distributions with the stability parameter $\delta \in \left[ 1.2, 1.8\right]$ and the skewness parameter $\eta \in \left[ -0.8, -0.3\right]$. We then fit a 10-dimensional Dirichlet distribution on these samples using maximum likelihood estimation. Stable distributions have been discussed in detail in Section. 6.1.3.

The likelihood model is formalized as a multinomial distribution over the output from the bias model in Eq. 9 as the likelihood given the model parameters:

$$\begin{aligned} l(\pi ; w_1, w_2, k) = \frac{n!}{x_1!\ldots x_{10}!} \prod _{i=1}^{10} m_{\text {bias}}(\pi _i; w_1, w_2, k)^{x_i}, \end{aligned}$$

(10)

where n is the number of draws. Since the participants were asked about the number of times they observed payoffs from each bin, n can be set to the number of trials (50) and their observations naturally become $(x_1, x_2, \ldots , x_n)$. Since, we obtain a distribution over the model parameters from the participants, we take the final likelihood value as the average of the likelihood function of individual likelihood values.

Given the form of the likelihood function, it is intractable to compute the posterior distribution analytically. To overcome this, we make use of the Metropolis-Hastings algorithm (Hastings, 1970) to directly obtain samples from the product of the prior distribution and the likelihood function, instead of fitting a distribution. These parameter estimates are then used by strategy discovery methods to learn strategies that can be taught to participants using a tutor.

Modeling the Discovery of Risky Choice Strategies as a Metalevel MDP

We formalize this problem of choosing a gamble as a metalevel MDP. The metalevel MDP can be formally represented by the four-tuple $M_{\text {meta},e}=\left( \mathcal {B},\mathcal {C},T_{\text {meta},e},r_{\text {meta}}\right)$ that depends on the assumed environment e. Each belief state $b \in \mathcal {B}$ encodes information about the distribution over probabilities $\mathbf{p}$ and the distributions over payoffs $\{f_{k,g}\}$ for all the K outcomes and G gambles. For each element $v_{k,g}$ of the payoff matrix V, there is one computation $c_{k,g}$ that inspects the payoff $v_{k,g}$ and updates the belief about the expected value of the inspected gamble. Additionally, for each outcome k, there is one computation $c_{k}$ that inspects the probability $p_k$ that the k^th outcome will occur. All $f_{k,g}$ are initialized to continuous distributions as modeled in Section 6.1.3. All event probabilities $p_k$ are initially assumed to be equal, i.e., $\dfrac{1}{K}$.

The metalevel transition function $T_{\text {meta},\pi _e}$ describes how computations update beliefs. Executing computation $c_{k,g}$ sets $f_{k,g}$ to a discrete delta distribution that puts all probability mass on $x_i$ with probability $P(V_{k,g}=x_i)=\pi _{e,i}$. Executing the computation that inspects and processes the probability of the k^th outcome (i.e., $c_{k}$) updates $p_{k}$ and sets the remaining unobserved probabilities to $\dfrac{1 - \sum _{i \in \mathcal {K}_{observed}} p_i}{K - |\mathcal {K}_{observed}|}$ where $\mathcal {K}_{observed}$ is the set of outcomes whose probabilities have been observed. The terminal action $\perp$ always transitions to a unique terminal state, $b_{\perp }$.

Finally, the metalevel reward function $r_{\text {meta}}$ describes the cost and benefits of computation. The cost of computation (i.e., clicking) is captured by setting $r_{\text {meta}} (b, c) = - \lambda _e \forall c \in \mathcal {C} \setminus \{\perp \}$. The benefit of termination is given by the expected quality of the decision that is ultimately made,

$$\begin{aligned} r_{\text {meta}} (b, \perp ) = \max _{g \in \mathcal {G}} \sum _{k = 1}^{K} p_k \cdot \mathrm {E}\left[ f_{k,g} \right] \end{aligned}$$

(11)

where $\mathcal {G}$ is the set of gambles.

Adapting BMPS

The BMPS method described in Section 4.1.2 cannot be directly used for the risky choice task without adaptation because of the difference in the formulation of the metalevel MDP. For adapting BMPS to this paradigm, we need a posterior distribution over the environments. Here, each environment is defined by its payoff distribution. As described in Section 6.2.2, we sample potential payoff distributions $\tilde{\pi }=(\tilde{\pi }_1,\cdots ,\tilde{\pi }_n)$ from the posterior distribution $P(\pi _e|\pi _d)$ using the Metropolis-Hastings algorithm. To get an analytical form of the posterior distribution, we fit a Dirichlet distribution $\mathcal {D}(\beta _1, \beta _2, \ldots , \beta _{n})$ using maximum likelihood estimation, where n represents the number of bins the outcomes are drawn from. We then compute the posterior expectation of the value of a computation: $\mathrm {E}_{E|d,b}\left[ \widehat{\text {VOC}}_{E}(b,c;\mathbf{w} ) \right]$ for each computation. Since the posterior distribution is now continuous, computing it is not analytically tractable. We instead approximate it by calculating $\widehat{\text {VOC}}$ for the expected value of the distribution as follows:

$$\begin{aligned} \mathrm {E}_{E|d,b}\left[ \widehat{\text {VOC}}_{E}(b,c;\mathbf{w} ) \right] \approx \widehat{\text {VOC}}_{\mathrm {E}\left[ E |d,b \right] }(b,c;\mathbf{w} ) \end{aligned}$$

That is, given the posterior distribution $\mathcal {D}(\beta _1, \beta _2, \ldots , \beta _{n})$, we calculate the expected probability of each bin $(\hat{\pi }_{1}, \hat{\pi }_{2}, \ldots , \hat{\pi }_{n})$ where

$$\begin{aligned} \hat{\pi }_i = \dfrac{\beta _i}{\sum _{j=1}^{n} \beta _j} \end{aligned}$$

When a payoff x is observed the algorithm determines which of the n bins of the payoff distribution it falls into. The index of that bin (k(x)) is treated as a draw from a multinomial distribution:

$$\begin{aligned} k(x) \sim \mathcal {M}(\pi _{e,1}, \pi _{e,2}, \ldots , \pi _{e,n}) \end{aligned}$$

Payoffs are observed one-by-one and the belief about the true environment of the trial is updated according to the value of the observed payoff. Since the index k follows a multinomial distribution and the prior $\mathcal {D}$ is a Dirichlet distribution, which is one of its conjugate distributions, the posterior distribution is a Dirichlet distribution with the same parameters $\beta$ except that the the alpha corresponding to the bin k(x) has been incremented by 1:

$$\begin{aligned} P(\pi _{e,1}, \pi _{e,2}, \ldots , \pi _{e,n}) \mid k(x) ) = \mathcal {D}(\beta _1, \cdots , \beta _{k(x)}+1,\cdots ,\beta _n). \end{aligned}$$

The procedure for the BMPS method is summarized in Algorithm 1.

Resource Rationality of the Discovered Decision Strategies

We tested how robust the different strategy discovery methods are to the empirically measured inaccuracies of people’s descriptions of payoff distributions. As Fig. 13 shows, BMPS with Bayesian inference on the true environment discovered better heuristics than all the other strategy discovery methods in the scenarios of high dispersion and high cost, high dispersion and low cost, and low dispersion and low cost (all $p<.0001$). The DRQN method with Bayesian inference on the true environment outperformed all the other methods in the case of low dispersion and high cost. Combining all cases, the addition of Bayesian inference on the true environment significantly improved the robustness of BMPS from $13.67 \pm 0.02$ to $15.3 \pm 0.02$ ($t(2751998)=-68.35$, $p<.001$; effect size $d=.082$) and the DRQN method from $6.70 \pm 0.02$ to $7.70 \pm 0.02$ ($t(2719998)=-39.57$, $p<.001$; effect size $d=.048$), whereas it decreased the robustness of the Meta-RL method from $5.35 \pm 0.02$ to $5.17 \pm 0.02$ ($t(2743998)=6.77$, $p<.001$; effect size $d=.008$).

Fig. 13

Resource-rationality scores of the multi-alternative risky choice strategies discovered by different methods with versus without Bayesian inference across different scenarios of cost and dispersion

Figure 14 illustrates how the increased robustness of BMPS with Bayesian inference affects which kinds of decision strategies it discovers and how those strategies differ from those discovered by non-robust methods. In this example, different outcomes had vastly different probabilities. The non-robust method (DRQN without Bayesian inference) learned a strategy that ignores the outcome probabilities. In contrast, the robust method (BMPS with Bayesian inference) learned to inspect the outcome probabilities to find out which outcome is most likely and then applied Satisficing to that outcome. Intuitively, the click sequences of the strategy discovered by this robust method seem to illustrate the simple rule of thumb “First, find out which of the outcomes is most likely. Then, find an alternative that has a high payoff for that one outcome.”

Discussion

In this section, we have introduced a more realistic set of benchmark problems for robust strategy discovery. In these benchmarks, robust heuristics for risky choice have to be derived from people’s usually erroneous descriptions of how likely an investment is to yield different returns. Our formulation of the risky choice problems themselves is more realistic than in previous work (Lieder et al., 2017; Gul et al., 2018; Krueger et al., 2022) in that the probabilities are not known in advance but have to be inspected. Corroborating our findings in the domain of planning, we found that Bayesian inference on the structure of the true environment significantly improves the robustness of the discovered strategies. As in the two previous domains, our robust BMPS method outperformed all other strategy discovery methods. These findings were consistent across three different types of decision environments. The only exception was the environment where the cost of collecting information is high and none of the outcomes is particularly likely to occur. In that environment, the optimal strategy collects (almost) no information and robustness is not required to discover it. This illustrates a more general point: robustness to errors in the description of the environment is only required when the strategies that are optimal for the described environment perform poorly in the true environment. Some errors are inconsequential either because they have little implications for which strategy one should use or because the implied and the optimal strategy perform similarly well. Taken together, our results suggests that our key findings generalize across different types of decision-making and different types of environments. Having demonstrated that our Bayesian approach to robust strategy discovery succeeds on the risky choice benchmarks, we next evaluate its capacity to improve human decision-making in an online experiment.

One limitation of the way in which we constructed the benchmarks is that only about 72% of the MTurk workers providing the descriptions that were used to construct the benchmark met our stringent quality criteria. Therefore, our method’s performance on our benchmark is not representative of its performance on descriptions from randomly selected MTurk workers. We chose these quality criteria to make our benchmarks more similar to the kinds of descriptions that motivated domain experts would provide. In that sense, our stringent quality criteria made our findings more generalizable to potential real-world applications rather than less generalizable. Moreover, all of our quality criteria were objective, only aimed to exclude participants who did not perform the task, and were determined prior to applying our method to the resulting benchmarks.

Improving People’s Investment Decisions

The results presented in the preceding section suggest that it is possible to automatically discover clever heuristics that are robust to uncertainty and biased descriptions of the decisions to be made. Concretely, the previous section showed that our machine learning methods for discovering resource-rational heuristics for multi-alternative risky choice are robust to inaccuracies in the description of the payoff distribution. In this section, we evaluate whether seeing demonstrations of the heuristics discovered by the methods described in the previous section can help people make better decisions in the unknown true environment whose payoff distribution may differ from the description. We first describe the intelligent tutors we created to teach people the automatically discovered strategies (Section 7.1). We then describe the experiment we conducted to evaluate the potential benefits of basing those tutors on robust strategy discovery methods (Section 7.2) and its results (Section 7.3). We close by discussing the implications of our findings (Section 7.4).

Tutors for Multi-alternative Risky Choice

To teach people the multi-alternative risky-choice heuristics discovered in Section 6, we programmed tutors that demonstrate which probabilities and which payoffs a given strategy would inspect for a given risky choice problem. We created one tutor that demonstrates the strategies discovered by the most robust method (BMPS with Bayesian inference) and a second tutor that demonstrates the strategies discovered by the best-performing (non-robust) standard machine learning method (DRQN without Bayesian inference).⁵ In each demonstration, the participant is shown the series of clicks that the demonstrated strategy would make in a difference instance of the corresponding environment. The tutor demonstrates its strategy one click at a time. After each click, the payoff of the clicked cells is revealed, and the subsequent clicks were informed by the observed value. Figure 14 shows two screenshots comparing the strategies discovered by the robust versus the non-robust methods in the environment with high information costs and a high dispersion of the outcome probabilities. The strategy discovered by the robust method first identifies the most likely event before looking for a good outcome for that event. In contrast, the strategy discovered by the non-robust method fails to recognize the importance of the event probabilities and can therefore suffer from catastrophic failures (as illustrated in Fig. 14).

Fig. 14

Example demonstrations shown by the two tutors for the high-cost, high-dispersion environment. The numbers near the mouse pointers represent the order of clicks made by the demonstrated decision strategies. a Screenshot demonstrating the strategy discovered by the robust method. b Screenshot demonstrating the strategy discovered by the non-robust method

Experimental Methods

We ran an experiment with two types of investment decisions (environments): one with highly dispersed outcome probabilities and high cost of information, and the other with highly dispersed outcome probabilities and low cost of information. These two types of investment problems were selected because for these problems, the decision strategies discovered by the robust method behave substantially differently from those discovered by their non-robust equivalents (see Fig. 14).

Participants We recruited a total of 516 participants on Amazon Mechanical Turk (average age 39.3 years, range: 20–74 years, 206 female), out of which 266 participants were assigned to the environment with low cost, and 250 participants were assigned to the environment with high cost. Participants were paid $1.00 plus a performance-dependent bonus (average bonus $1.82). The average duration of the experiment was 10.3 min. For both environments, participants were randomly assigned to one of three groups: a control group that received no tutoring, an experimental group that was shown demonstrations of the strategy by the robust method, and a second experimental group that was shown demonstrations of the strategy discovered by the non-robust method. Thus, there were about 85 participants per condition for each environment. We will refer to the cognitive tutor demonstrating the strategy discovered by the (non)robust method as the (non)robust tutor. A total of $7.0\%$ of the participants were excluded because they failed the comprehension check.

Procedure

We conducted a between-subjects experiment with three groups. For each participant, we first randomly selected one of the 86 benchmark problems described in Section 6.1.4. The participant was not shown the description of the payoff distribution itself. Instead, the usually inaccurate description of the selected benchmark was used to generate the payoffs in the practice trials that introduced the participant to the task and the payoffs in their training block. In contrast, the payoffs in the trials of the subsequent test block were generated according to the benchmark’s true payoff distribution. Critically, the tutors teaching the experimental group demonstrated the strategies that the corresponding strategy discovery method had derived from the inaccurate description of the payoff distribution.

All participants first went through instructions that introduced them to the paradigm. Then, they went through 3 trials with uncovered rewards that were generated according to the description ($\pi _d$). All participants then answered a series of six quiz questions in which they had to demonstrate their comprehension of the task. Each quiz question was accompanied by an image of a fully revealed payoff matrix that had been generated according to the description. Participants who made more than 3 incorrect attempts at answering any of the questions were not allowed to continue further, and were paid the base pay. Next, participants went through 3 practice trials with fully uncovered rewards that were generated according to the description. This was followed by 3 additional practice trials in which all payoffs and outcome probabilities were initially occluded; those trials were also generated according to the description. The following training block comprised 5 additional practice trials in the control condition without the cognitive tutor and 5 trials with demonstrations by a cognitive tutor in the two experimental conditions, respectively. The practice trials of the control group were generated according to the description. The non-robust tutor showed its demonstrations on the environment specified by the (typically incorrect) description. The robust tutor showed its demonstrations on environments sampled from the posterior distribution over the true environment given the description. A different sample from this posterior distribution was used in each round. The strategies demonstrated by both tutors were derived from the inaccurate descriptions. After the training block, participants went through 10 test trials like the one shown in Fig. 10 where all cells were initially concealed. The payoffs in these test trials were sampled from the payoff distribution of the true environment ($\pi _e$). Participants had to pay a cost of $\$2$ for uncovering a reward in the environments with high information cost and $\$1$ in the environments with low information cost.

Results

As predicted by the comparison of the taught strategies shown in Fig. 14, the median number of clicks participants made to reveal the probabilities of outcomes was significantly higher in the condition with the robust tutor than in the condition with the non-robust tutor (3 clicks/trial vs. 2 clicks/trial, $U=1125672.5, p<.001$ according to a one-sided Mann-Whitney U-test). This shows that participants in the robust tutor condition paid more attention to aspects of the task that revealed the most information about which gamble to pick. Two-way ANOVAs confirmed that this difference in decision strategies affected participants’ scores (i.e., payoff minus information cost) in the predicted direction (see Fig. 15). We found that while participants taught by the robust tutor performed significantly better ($16.25 \pm 1.08$ points/trial) than the control group ($13.60 \pm 1.03$ points/trial, $F(1,4794)=8.85$, $p=.003$), participants in the non-robust tutor condition ($14.26 \pm 0.99$ points/trial) did not ($F(1,4794)=0.65$, $p=.419$). Moreover, the robust tutor group performed significantly better than the non-robust tutor group ($F(1,3186)=4.76$, $p=.029$). We found that there were no significant differences between the two environments with regard to the benefit of being taught by the robust tutor ($F(1,4794)=0.92$, $p=.337$) or the non-robust tutor ($F(1,4794)=0.23$, $p=.630$) over being in the control condition. The environment also had no significant effect on the benefit that the robust tutor condition experienced over the non-robust tutor condition ($F(1,3186)=0.24$, $p=.621$).

Fig. 15

Resource-rationality scores of participants in the risky choice experiment across conditions

Discussion

In this section, we applied our robust strategy discovery approach to a set of harder and more realistic benchmark problems in a new domain. Concretely, we tested if our approach can discover robust strategies for making investment decisions.

Paralleling our results in the domain of planning, we found that robust strategy discovery is a promising approach to helping people make better decisions under risk. Going beyond the work presented in Sections 4 and 5, we showed that our approach can be applied to human-generated descriptions even when the ground truth is unknown. Given that the Mouselab paradigm captures the essential elements of many real-life decisions, such as online shopping and investment, our method’s success in this domain suggests that it could be used to improve people’s decisions in such contexts. The results shown in Fig. 13 suggest that most of the benefit of the robust tutor over the non-robust tutor should be attributed to BMPS being a better and more robust strategy method than off-the-shelf reinforcement learning algorithms. However, those results also suggest that the addition of Bayesian inference on the structure of the environment significantly improved the quality of the strategy taught by the robust tutor. Accurately measuring the relative contributions of these two factors to the quality of human decision-making would require a very large follow-up experiment. Regardless thereof, our results clearly show that participants who were trained by the robust tutor made significantly better decisions than participants who received no tutoring.

The main limitation of this experiment is that we made the simplifying assumption that the utility participants derived from the outcomes of their decisions was proportional to the number of points they earned in our decision-making game. This assumption is in conflict with the well-known fact that the utility of money is a nonlinear function of the amount of money the participant gained or lost (Kahneman and Tversky, 1979). We discuss this limitation in more detail in the following section. Another limitation of this work is that the multi-alternative risky choice task we used to evaluate our robust strategy discovery method has a different structure from the investment task we used to estimate the biases in people’s descriptions. One important difference between these tasks is that investing is a dynamic decision-making problem, whereas multi-alternative risky choice is a one-shot decision. Another relevant difference between the two tasks is that the investment task reported the return as a percentage of the (presumably large) invested amount, whereas the multi-alternative risky choice task used small payoffs and reported them in absolute terms. It is conceivable that these differences enlarged the bias in the recorded descriptions; this seems plausible because losing 100% of a large investment is much worse than losing $100 on a gamble, and previous work suggested that people overestimate the frequency of more extreme events more strongly (Madan et al., 2014; Lieder et al., 2018).

Another limitation of our findings is that the effect of teaching people robust decision strategies was relatively small. Comparing the performance of the discovered strategies (Fig. 13) to the performance of the participants who were taught those strategies (Fig. 15) reveals that this was primarily because participants in the non-robust tutor condition and in the control condition performed substantially better than the strategies discovered by our non-robust methods. This suggests that in certain situations human learning and decision-making are already substantially more robust to errors in the descriptions of the decision-problem than standard machine learning methods. However, Experiment 1 suggested that this is not always the case. Future research should therefore investigate in which scenarios human decision-makers could benefit the most from robust strategy discovery, and what distinguishes those scenarios from scenarios in which human decision-making is already sufficiently robust. More generally, more research is needed to elucidate how the benefits of teaching robust decision strategies depends on the nature of the decision problem.

General Discussion

Boosting people’s decision-making competence in the real world is very important (Hertwig and Grüne-Yanoff, 2017). Although decision scientists can derive clever heuristics for specific types of decisions and teach them to dozens of people at a time, this solution does not scale well to improving the decisions of billions of people on thousands of different types of decisions. Recent work proposed that artificial intelligence can provide a more scalable solution. The basic idea is to combine machine learning and educational software to automatically derive useful decision strategies from descriptions of the decisions people have to make in the real world, and then teach them at scale (Callaway et al., 2022a; Consul et al., 2022; Skirzyński et al., 2021). The method introduced in this article addresses a crucial challenge for this approach, namely the standard methods’ sensitivity to the inevitable inaccuracies of our models of the real world.

Taken together, our findings suggest that the methods presented in this article are a step toward leveraging machine learning to discover robust heuristics that enable people to make better decisions in uncertain or ambiguous real-world settings. The robustness of the resulting heuristics is critical to their effectiveness because we generally cannot be certain about the structure of the decision problems people face in the real world. Therefore, it is critical that our strategy discovery methods are robust to our ignorance, our biases, and our uncertainties. The methods we developed in this article make this possible. The developed methods are very general and can be applied to discover robust heuristics for planning and risky choice. Importantly, we found that teaching these automatically discovered strategies to people significantly improved their decision-making skills in the environments that the imperfect descriptions were derived from. This indicates that combining robust strategy discovery with intelligent cognitive tutors is a promising approach to improving human decision-making in the real world. Our approach stands on a solid theoretical and technical foundation in that it combines state-of-the-art methods for metalevel reinforcement learning (Callaway, Gul et al., 2018) with Bayesian inference to compute the optimal heuristics defined by the theory of resource rationality (Lieder and Griffiths, 2020).

Relationship to Prior Work

The focus of this article was on making the best possible use of a given description of a decision problem. We did not address the question of how such descriptions should be obtained. Nor did we use the state-of-the-art methods for eliciting such descriptions from domain experts. Therefore, rather than simply asking domain experts to estimate the frequencies of different events directly, as we did in Section 6.1.4, future applications of our method should combine it with the best existing methods for reducing the amount of bias in domain experts’ estimates (Garthwaite et al., 2005). These so-called elicitation methods are complementary to our computational method for using the elicited descriptions to derive resource-rational decision strategies. If such a method led to significantly less bias, then it could be appropriate to reduce the amount of bias that our model assumed to occur in the generation of people’s descriptions (see Section 3.1). However, even if an elicitation method were able to elicit an expert’s true belief, that true belief would still be biased by the systematic errors that the expert made in forming his or her beliefs and the incompleteness and potential unrepresentativeness of his or her experience.

The method we introduced in this article can be seen as a computational tool for robust decision-making (Lempert, 2019). Robust decision-making is a family of methods for making decisions when one cannot have high confidence in any particular prediction about the future because the probability mass is spread out over many possible scenarios. The basic idea of robust decision-making is to identify decisions or policies that will fare reasonably well across a wide range of possible futures. One approach that is often used to aggregate across multiple possible scenarios is Wald’s maximin rule (Wald, 1945). This decision rule chooses the decision whose worst possible outcome is the least bad. This principle has also been applied to robust planning with a potentially inaccurate model of the environment (Nilim & Ghaoui, 2003). The resulting algorithms compute the plan that performs best in the worst-case scenario. Our method deviates from this approach in two ways. First, it generates a decision-making strategy rather than a decision. Second, while Wald’s maximin rule chooses exclusively based on the performance in the worst case scenario, our method averages the strategy’s performance across all possible scenarios, weighing each scenario according to its probability. As a consequence, the strategies identified by our method can be expected to perform better on average than the strategies that would have been selected by Wald’s method. On the other hand, contrary to Wald’s method, our method does not provide any guarantees on how well the selected strategy will perform in the worst case. Therefore, to ensure that our method has an appropriate level of risk sensitivity, it is important that its utility function puts an appropriate price tag on (large) negative outcomes. One advantage of Wald’s method is that it does not require estimates of how likely the different scenarios are. However, our method provides a principled way to obtain such estimates. In a real-world application, such as deciding who should receive a mortgage, obtaining experts’ estimates of the required probabilities could potentially cost thousands of dollars. However, the costs saved by averting even a few serious mistakes would be substantially higher.

Another related approach is risk-sensitive decision-making (Howard & Matheson, 1972; van der Ploeg, 1984; Kimball, 1993). Risk-sensitive decision-making puts a surcharge on risky actions whose outcomes are uncertain. This is implemented by maximizing a risk-averse utility function rather than the expected value of the outcomes. This approach has also been applied to planning (Howard & Matheson, 1972; Chow et al., 2015). Interestingly, there is a mathematical connection between robust planning and risk-sensitive decision-making that makes it possible to transform robust planning/decision problems into risk-sensitive planning/decision problems and vice versa (Osogami, 2012). The fact that people’s choices in decisions from description follow a highly risk-averse utility function (Kahneman and Tversky, 1979) could therefore be interpreted as a form of robust decision-making. Moreover, the fact that people appear to mentally correct very low/high probabilities towards a more moderate value (Kahneman and Tversky, 1979) could be interpreted as a form of Bayesian inference that serves to make their decisions more robust to potential inaccuracies of the experimenter’s description of how likely different outcomes are to occur. It is therefore possible that the robustness of human decision-making relies on computational principles that are similar to those of our robust strategy discovery methods (see Eq. 4).

In addition to strengthening the theoretical, methodological, and empirical foundations for improving human decision-making, the work presented in this article also contributes to the debate about human rationality. Concretely, we have mathematically formalized the idea that rational decision strategies have to be robust to misconstruals of the situation the decision-maker is in. That is, they have to work reasonably well across multiple different situations and environments. This robustness is necessary for rational decision-making in the real world for at least two reasons. First, real-life situations are often ambiguous and only partially observable. Therefore, even if the decision-maker knows a strategy that is optimal for the current situation, they might be unable to determine that or misconstrue the situation and select a different strategy instead. Second, the number of decision strategies in a bounded agent’s repertoire is limited not only by memory constraints but also by the cost of strategy selection (Milli et al., 2021). Our robust strategy discover method can be used to automatically derive resource-rational models of robust decision strategies (Lieder and Griffiths, 2020; Callaway et al., 2018b; Lewis et al., 2014). Such models could be an important step toward understanding why people use heuristics that appear to be sub-optimal for the specific environment in which they were tested. Concretely, these models might reveal that fast-and-frugal heuristics, such as Take-The-Best (Gigerenzer & Todd, 1999) and Satisficing (Simon, 1956), are resource-rational solutions to the problem of robust decision-making in partially unknown environments and ambiguous situations. More generally, we hope that the theory and methods developed in this article will help researchers understand the robustness of human decision-making and recreate it in machines. Moreover, our theory and methods could be used as a starting point for investigating and modeling how people discover robust heuristics for decision-making in the real world. This will be an important next step in our ongoing research on how people discover resource-rational heuristics (He et al., 2021b; He et al., 2021a; Jain et al., 2019; Krueger et al., 2017).

Limitations

One weakness of the reported work is its simplifying assumption that the utility of gaining or losing a given amount of money is equal to that amount. This does not take into account the well-known fact that the utility of money is highly nonlinear (Kahneman and Tversky, 1979). The rewards in our simulations and experiments should therefore be interpreted as utilities rather than money. While this slightly changes the interpretation of the environments, it does not affect our demonstration that our method is robust to errors in the description of those environments. Moreover, the range of rewards was relatively small, and the most significant non-linearities occur for larger amounts. Although assuming a linear utility function was sufficient for our proof-of-concept simulations, real-world applications involving financial decisions should use a more realistic utility function, such as the one proposed by prospect theory (Kahneman and Tversky, 1979). Importantly, our method can be applied with such more realistic utility functions just as easily. In fact, nothing about our method depends on the form of the utility function.

We have tested the effectiveness of discovering and teaching robust decision strategies in the context of two related process-tracing paradigms (i.e., the Mouselab paradigm and the Mouselab-MDP paradigm). In these paradigms, participants cannot immediately see all the information at once. This limits their capacity to rely on automatic processes that rapidly integrate all the available information in parallel (Glöckner and Betsch, 2008). This difference affects what kinds of strategies people are able to use and which strategies are resource-rational. Therefore, we cannot assume that the strategies our methods discovered for our process-tracing paradigms are also near-optimal for decision-making in the real-world. Efforts to apply our method to real-world decision-making should take these differences into account. Moreover, it is also possible that the availability of rapid automatic integration processes in the real-world reduces the potential improvements that can be achieved by teaching people slow and sequential deliberate decision strategies.

A limitation of our robust strategy discovery methods is that they cannot articulate the heuristic principles that the robust tutors demonstrate in natural language. In fact, the computational procedures that the robust tutors perform to generate the demonstrations are far more complex than the simple heuristics that their demonstrations seem to illustrate. This limitation could be overcome by combining our robust strategy discovery methods with our recently developed methods for generating human-interpretable descriptions of automatically discovered decision strategies (Skirzyński et al., 2021; Becker et al., 2022).

Future Directions

Regardless of the limitations, the progress reported in this article opens up several exciting avenues for future work. One line of future work is to apply robust strategy discovery methods to human-generated descriptions of decisions they face in the real world. To support this application, future work should develop probabilistic generative models of how people describe different types of decisions and the ways in which those descriptions tend to be incomplete or incorrect. The robust heuristics discovered by our method can then be conveyed to people by a cognitive tutor (Callaway et al., 2022a; Lieder et al., 2019; Consul et al., 2022), a flowchart (Skirzyński et al., 2021), or a procedural description of the decision procedure in natural language (Becker et al., 2022). The latter two could be used as decision aids, whereas the former approach relies on helping people internalize effective decision strategies through training. To decide which of these approaches is the most promising, future work should investigate how well people are able to apply the decision strategies they were taught by an intelligent tutor in the real world. To design decision aids and generate interpretable descriptions, our robust BMPS method can be combined with AI-Interpret (Skirzyński et al., 2021) to generate flowcharts that describe optimal decision procedures or procedural descriptions in natural language (Becker et al., 2022). This approach might enable decision scientists to rapidly discover a large number of clever heuristics and useful principles for good decision-making. These discoveries, the resulting decision aids, and the availability of intelligent tutors that can efficiently teach those strategies to large numbers of people could give a significant boost to ongoing efforts to boost people’s decision competencies (Hertwig and Grüne-Yanoff, 2017; Hertwig et al., 2019). Applications of this approach to problems such as purchasing, investment, business decisions, and admissions decisions may be feasible within a few years. But they are neither the only nor the most interesting applications that these methods might find. For instance, our method could also be extended to discover rational heuristics for strategic social interaction in economic games. The main difference would be that the available information would also include the behavior of the other player(s) and that the uncertain state of the environment would include the other player(s) strategy or strategies. In this way, the recent work by Spiliopoulos and Hertwig (2020) could be extended from evaluating the performance and robustness of known heuristics to potentially discovering new ones. Moreover, we foresee that this approach can also be applied to help people set better goals, plan their personal and professional projects, and make important life decisions, such as which career to pursue. These future applications will exploit scalable strategy discovery methods that are currently being developed (Consul et al., 2022).

So far, we have talked about robustness to inaccurate assumptions about the situation in which the decision is made. This is subtly different from robustness to known differences across different decision problems (Gigerenzer and Brighton, 2009; Spiliopoulos and Hertwig, 2020). Having a decision strategy that is robust to the many ways in which the decision problems within a given domain differ would allow a person to make good decisions without having to memorize many specialized decision strategies and being able to adaptively select between them. Strategies that possess this form of robustness could be derived by maximizing the strategy’s expected resource-rationality score with respect to the prior distribution over possible scenarios. This would require only minor modification of our method, namely sampling scenarios from the prior distribution instead of the posterior distribution. Evaluating how good the resulting strategies are depending on the size of the domain is an interesting direction for future research.

Appendices

Appendix 1: Details of the Neural-Network–Based Strategy Discovery Methods

We trained the DRQN architecture using the algorithm described by (Hausknecht & Stone, 2015). The pseudo-code of that algorithm is shown as Algorithm 2.

Table 1 shows the hyperparameters we used when we applied the DRQN method to discover strategies for planning and risky choice respectively.

Table 1 Hyperparameters of the DQRN method as it was used for discovering planning strategies and risky choice strategies, respectively

Table 2 shows the hyperparameters that we used with our meta-RL method to discover strategies for planning and risky choice respectively.

Table 2 Hyperparameters of the meta-RL method as it was used for discovering planning strategies and risky choice strategies, respectively

Appendix 2: Details of the Sampling Method Used for Discovering Planning Strategies

The standard way to sample from the posterior distribution over possible environment types e given a description d is to use a Monte Carlo algorithm, such as the Metropolis-Hastings algorithm (Hastings, 1970). In this particular application of our method, we used a different approach. Concretely, we first applied the standard approach for learning the posterior distribution of a label given an image (Martinek, 2020). Concretely, we approximated the posterior distribution P(e|d) by training a neural network to predict the type of the true environment from a provided description. The output layer of the neural network contained one unit per environment type. The network’s approximation of the posterior probability was obtained by normalizing the output units’ activations using the softmax function. The network was trained by minimizing the cross-entry loss between a one-hot vector representing the true environment type and the model’s prediction of the posterior probabilities using gradient descent.

The training examples were generated by sampling pairs of environment types and their descriptions. The environment types were sampled from the prior distribution. The descriptions were probabilistically generated according to the likelihood function. To approximate sampling from the posterior distribution, we computed the approximate posterior distribution using the trained neural network and then made the number of of training examples conforming to each potential environment type proportion to the outputted posterior probability.

Appendix 3: Evaluation on the Web of Cash Task

To test the generality of our findings, we next evaluated our approach on a different planning task called “Web of Cash.” (see Fig. 16). In this task, the player navigates a money-loving spider through a web of cash. Unlike, the network of airports used in the Flight Planning task, the web of cash has a tree structure and the first move determines which nodes can be reached later on. The values of the web’s nodes are independently drawn from a uniform distribution with diverse variances: low (L $\sim U(\{-4,-2,2,4\}$), medium (M $\sim U(\{-8,-4,4,8\})$), and high (H $\sim U(\{-48,-24,24,48\})$). The environment structure we chose has variances that increase with depth. This is intuitive because long-term benefits generally outweigh the short-term rewards in real life. Hence, it is advantageous to look at the long-term benefits of the alternatives before taking a decision. Concretely, all nodes at level 1 have low variance, all nodes at level 2 have medium variance, and nodes at level 3 can have both medium and high variance. For simplicity, we assume that sibling nodes (i.e., nodes that share an immediate parent node) at level 3 have the same variance and there is no preference of one variance type over the other. This leads to us having 8 equally likely true environments, a number that corresponds to the total number of branch-wise variance combinations at level 3.

Fig. 16

The Web of Cash Task is a three-step sequential decision-making task–based on the Mouselab-MDP paradigm. The participant’s task is to select one of the six paths leading from spider’s initial location in the center of the web to one of the six outermost nodes. The rewards of the nodes that can be reached in the first step (Level 1) are drawn from a distribution with low variance (L). The rewards of the nodes that can be reached in two steps (Level 2) are drawn from a distribution with moderate variance (M). The distribution of the rewards of nodes that can be reached in three steps (Level 3) can differ between the left branch, the upper branch, and the right branch. Depending on the location and the benchmark problem, the variance of rewards at any given location at level 3 is either moderate (M) or high (H)

Benchmarks

When the environment described above is combined with the model of model misspecification described below, then the set of possible descriptions d is identical to the set of possible true environments e which we call E. Each of the true environments in the Web of Cash task is equally likely to occur, that is $P(e) = \frac{1}{|E|} = \frac{1}{8}$, and each environment can give rise to any of the 8 possible descriptions. Therefore, there are 64 possible benchmarks in total. Thus, the set of possible benchmarks is $\lbrace (e,d,\frac{1}{8}\cdot P(d|e)) : e, d \in E \rbrace$. The probability with which each possible environment gives rise to each possible description as depicted in Fig. 17.

Model of Model Misspecification

The cognitive bias that we modelled for this environment structure is a combination of imperfect memory and exaggerated expectation. Exaggerated expectation (Hilbert , 2012) is defined as “the tendency to expect or predict more extreme outcomes than those outcomes that actually happen.” While imperfect memory introduces stochasticity to the bias model, exaggerated expectation makes it more likely that this uncertainty will be resolved in favor of remembering the more extreme events (H).

Since there is only one possible variance type on the first two levels in this environment, we model the cognitive bias to occur at the third level only. For the purpose of performing simulations, we chose the following values for the conditional probability distribution for each branch at level 3:

$$\begin{aligned} \mathrm {P}( d = \text {H} \, | \, e = \text {M})&= 0.55&\mathrm {P}( d = \text {M} \, | \, e = \text {M})&= 0.45 \\ \mathrm {P}( d = \text {H} \, | \, e = \text {H})&= 0.90&\mathrm {P}( d = \text {M} \, | \, e = \text {H})&= 0.10 \end{aligned}$$

For completeness, we define $\mathrm {P}( d = \text {L} \, | \, e = \text {M}) = \mathrm {P}( d = \text {L} \, | \, e = \text {H}) = 0$ since the person’s belief for variance L is a diminished expectation for the potential ground-truth variances M and H. Furthermore, we specify $\mathrm {P}( d = \text {X} \, | \, e = \text {L})$ as undefined for X $\in$ {L, M, H} since $\mathrm {P}(e = \text {L}) = 0$ at level 3 in the first place.

Fig. 17

Likelihood function $P(d \, | \, e)$ for the Web of Cash task. The three-letter abbreviations denote the node variance at the 3rd level for each branch, respectively

Fig. 18

Posterior distribution $P(E \, | \, d)$ for the Web of Cash task. The three-letter abbreviations denote the node variance at the 3rd level for each branch, respectively

Simulation Results

Given this likelihood function, the posterior distributions for the true environment given an environment specification are computed. These probabilities are depicted in Fig. 18. For the purposes of performing simulations, we applied the bias model to 10,000 true environments (1250 per environment type).

Robust and Non-robust Methods Discover Different Types of Strategies

Similar to the previous findings in Section 4.2.2, the behaviors of two strategies discovered by the most-robust method (BMPS) versus the least-robust strategy discovery method (Meta-RL) were qualitatively different. Figure 19 illustrates the learned planning strategies. In scenarios where the true environment matched the description, both strategies used similar information (Fig. 19A). But in scenarios where the true environment differed from the description, only the strategy discovered by the robust method was able to correct its approach upon discovering that the environment differed from the description (Fig. 19B). This robustness allowed it to always zoom in on the information that is most useful in the true environment. Concretely, in the example illustrated in Fig. 19B, the description of the environment incorrectly stated that all of the large gains and losses are on the right. But in the true environment, two of the locations on the right harbored low rewards and two of the high rewards were located in the center. The strategies discovered by the non-robust methods were unable to adapt for this discrepancy and inflexibly continued to focus exclusively on the nodes on the right.

Fig. 19

Comparison of the planning strategies discovered by a robust method (BMPS with Bayesian inference) versus a non-robust method (DRQN without Bayesian inference). “e” and “m” denote the true environment and model specifications of the sibling leaf nodes. The numbers near the mouse pointers represent the order of clicks made by the strategies. Row A illustrates the strategies in an environment that matches the description. Row B illustrates their behavior in a different environment that deviates from the description

The Robust Methods Performed Better

As shown in Fig. 20, we found that the BMPS method with Bayesian inference on the true environment achieved an almost perfect relative robustness score ($\rho _{\text {rel}} > 0.98$, absolute score = $29.59 \pm 0.50$) and outperformed all the other methods. The second-best method was BMPS without Bayesian inference on the true environment ($\rho _{\text {rel}} > 0.86$, absolute score = $27.95 \pm 0.51$). The addition of Bayesian inference on the true environment significantly improved the resource rationality of the decision strategies discovered by the meta-RL method ($22.77 \pm 0.52$ vs. $26.06\pm 0.49$, $t(15972)=-11.03$, $p<.0001$), BMPS ($27.95 \pm 0.51$ vs. $29.59 \pm 0.50$, $t(15994)=-5.66$, $p<.0001$), and the DRQN method ($26.44 \pm 0.52$ vs. $27.14 \pm 0.54$, $t(15,996)=-2.33$, $p=.0198$).

Fig. 20

Resource-rationality scores of the decision strategies discovered by different methods with versus without Bayesian inference in the 3-1-2 environment