Mixed-effects location-scale model based on generalized hyperbolic distribution

Abstract

Motivated by better modeling of intra-individual variability in longitudinal data, we propose a class of location-scale mixed-effects models, in which the data of each individual is modeled by a parameter-varying generalized hyperbolic distribution. We first study the local maximum-likelihood asymptotics and reveal the instability in the numerical optimization of the log-likelihood. Then, we construct an asymptotically efficient estimator based on the Newton–Raphson method based on the original log-likelihood function with the initial estimator being naive least-squares-type. Numerical experiments are conducted to show that the proposed one-step estimator is not only theoretically efficient but also numerically much more stable and much less time-consuming compared with the maximum-likelihood estimator.

1 Introduction

The key step in the population approach (Lavielle 2015) is modeling dynamics of many individuals to introduce a flexible probabilistic structure for the random vector $Y_i = (Y_i(t_{ij}))_{j=1}^{n_i} \in {\mathbb {R}}^{n_i}$ representing time series data (supposed to be univariate) from ith individual. Here, $t_{i1}<\dots <t_{in_i}$ denotes sampling times, which may vary across the individuals with possibly different $n_i$ for $i=1,\dots ,N$. The model is desired to be tractable from theoretical and computational points of view.

In the classical linear mixed-effects model (Laird and Ware 1982), the target variable $Y_i$ in ${\mathbb {R}}^{n_i}$ is described by

$$\begin{aligned} Y_i=X_i\beta +Z_ib_i+\epsilon _i, \end{aligned}$$

(1.1)

for $i=1,\dots ,N$, where the explanatory variables $X_i \in {\mathbb {R}}^{n_i}\otimes {\mathbb {R}}^{p}$ and $Z_i\in {\mathbb {R}}^{n_i}\otimes {\mathbb {R}}^{q}$ are known design matrices, where $\{b_i\}$ and $\{\epsilon _i\}$ are mutually independent centered i.i.d. sequences with covariance matrices $G\in {\mathbb {R}}^q\otimes {\mathbb {R}}^q$ and $H_i\in {\mathbb {R}}^{n_i}\otimes {\mathbb {R}}^{n_i}$, respectively; typical examples of $H_i=(H_{i,kl})$ include $H_i=\sigma ^2 I_{n_i}$ ($I_q$ denotes the q-dimensional identity matrix) and $H_{i,kl}=\sigma ^2 \rho ^{|k-l|}$ with $\rho$ denoting the correlation coefficient. Although the model (1.1) is quite popular in studying longitudinal data, it is not adequate for modeling intra-individual variability. Formally speaking, this means that for each i, conditionally on $b_i$ the objective variable $Y_i$ has the covariance which does not depend on $b_i$. Therefore, the model is not suitable if one wants to incorporate a random effect across the individuals into the covariance and higher order structures such as skewness and kurtosis.

1.1 Mixed-effects location-scale model

Let us briefly review the previous study which motivated our present study. The paper (Hedeker et al. 2008) introduced a variant of (1.1), called the mixed-effects location-scale (MELS) model, for analyzing ecological momentary assessment (EMA) data; the MELS model was further studied in Hedeker et al. (2009, 2012) and Hedeker and Nordgren (2013) from application and computational points of view. EMA is also known as the experience sampling method, which is not retrospective and the individuals are required to answer immediately after an event occurs. Modern EMA data in mental health research is longitudinal, typically consisting of possibly irregularly spaced sampling times from each patient. To avoid the so-called “recall bias” of retrospective self-reports from patients, the EMA method records many events in daily life at the moment of their occurrence. The primary interest is modeling both between- and within-subjects heterogeneities, hence one is naturally led to incorporate random effects into both trend and scale structures. We refer to Shiffman et al. (2008) for detailed information on EMA data.

In the MELS model, the jth sample $Y_{ij}$ from the ith individual is given by

$$\begin{aligned} Y_{ij} = x_{ij}^\top \beta + \exp \left( \frac{1}{2} z_{ij}^\top \alpha \right) \epsilon _{1,i} + \exp \left( \frac{1}{2} (w_{ij}^\top \tau + \sigma _w \epsilon _{2,i})\right) \epsilon _{3,ij} \end{aligned}$$

(1.2)

for $1\le j\le n_i$ and $1\le i\le N$. Here, $(x_{ij},z_{ij},w_{ij})$ are non-random explanatory variables, $(\epsilon _{1,i},\epsilon _{2,i})$ denote the i.i.d. random-effect, and $\epsilon _{3,ij}$ denote the driving noises for each $i\le N$ such that

$$\begin{aligned} (\epsilon _{1,i},\epsilon _{2,i},\epsilon _{3,ij}) \sim N_3\left( 0,~ \begin{pmatrix} 1 &{} \rho &{} 0 \\ \rho &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix} \right) \end{aligned}$$

and that $\epsilon _{3,i1}, \dots , \epsilon _{3,i n_i} \sim \text {i.i.d.}~N(0,1)$, with $(\epsilon _{1,i},\epsilon _{2,i})$ and $(\epsilon _{3,ij})_{j\le n_i}$ being mutually independent. Direct computations give the following expressions: $E[Y_{ij}]=x^{\top }_{ij}\beta$, $\textrm{Var}[Y_{ij}] =\exp (w^{\top }_{ij}\tau +\sigma _w^2/2) + \exp (z^{\top }_i\alpha )$, and also $\textrm{Cov}[Y_{ik},Y_{il}]=\exp (z^{\top }_i \alpha )$ for $k\ne l$; the covariance structure is to be compared with the one (2.2) of our model. Further, their conditional versions given the random-effect variable $R_i:= (\epsilon _{1,i},\epsilon _{2,i})$ are as follows: $E[Y_{ij}|R_i] = x_{ij}^{\top }\beta +\exp (z^{\top }_i \alpha /2)\epsilon _{1,i}$, $\textrm{Var}[Y_{ij}| R_i] = \exp (w^{\top }_{ij}\tau + \sigma _w \epsilon _{2,i})$, and $\textrm{Cov}[Y_{ik},Y_{il}| R_i] =0$ for $k\ne l$. We also note that the conditional distribution

$$\begin{aligned} {\mathcal {L}}(Y_{i1},\dots ,Y_{i n_i}| R_i) {=} N_{n_i}\left( X_i\beta {+} {\textbf{1}}_{n_i} e^{z_i^\top \alpha /2} \epsilon _{1,i}, ~\textrm{diag}\big ( e^{w_{i1}^\top \tau {+} \sigma _w \epsilon _{2,i}},\dots , e^{w_{i n_i}^\top \tau {+} \sigma _w \epsilon _{2,i}} \big ) \right) , \end{aligned}$$

where $X_i:=(x_{i1},\dots ,x_{i n_i})$ and ${\textbf{1}}_{n_i}\in {\mathbb {R}}^{n_i}$ has the entries all being 1. Importantly, the marginal distribution ${\mathcal {L}}(Y_{i1},\dots ,Y_{i n_i})$ is not Gaussian. See Hedeker et al. (2008) for details about the data-analysis aspects of the MELS model.

The third term on the right-hand side of (1.2) obeys a sort of normal-variance mixture with the variance mixing distribution being log-normal, introducing the so-called leptokurtosis (heavier tail than the normal distribution). Further, the last two terms on the right-hand side enable us to incorporate skewness into the marginal distribution ${\mathcal {L}}(Y_{ij})$; it is symmetric around $x_{ij}^\top \beta$ if $\rho =0$.

The optimization of the corresponding likelihood function is quite time-consuming since we need to integrate the latent variables $(\epsilon _{1,ij},\epsilon _{2,ij})$: the log-likelihood function of $\theta :=(\beta , \alpha , \tau , \sigma _w, \rho )$ is given by

$$\begin{aligned}{} & {} \theta \mapsto \sum _{i=1}^N \log \bigg \{ \int _{{\mathbb {R}}^2} \phi _{n_i}\Big (Y_{i};\, \mu _i(\beta ,\alpha ,X_i, z_{i};x_1),\, \Sigma _i(\tau ,\sigma _w,\rho ,w_{i};x_1,x_2)\Big )\nonumber \\{} & {} \quad \times \phi _{2}((x_1,x_2);0,I_2)dx_1 dx_2 \bigg \}, \end{aligned}$$

(1.3)

where $w_i:=(w_{ij})_{j\le n_i}$, $z_i:=(z_{ij})_{j\le n_i}$, $\phi _m(\cdot ; \mu ,\Sigma )$ denotes the m-dimensional $N(\mu ,\Sigma )$-density, and

$$\begin{aligned} \mu _i(\beta ,\alpha ,X_i,z_{i};x_1)&:{=} X_i\beta {+} {\textbf{1}}_{n_i}e^{z_i^\top \alpha /2} x_1,\\ \Sigma _i(\tau ,\sigma _w,\rho ,w_{i}; x_1,x_2)&:{=} \\&\textrm{diag}\Big ( e^{w_{i1}^\top \tau {+} \sigma _w (\rho x_1 {+} \sqrt{1{-}\rho ^2} x_2)},\dots , e^{w_{i n_i}^\top \tau {+} \sigma _w (\rho x_1 {+} \sqrt{1-\rho ^2} x_2)} \Big ). \end{aligned}$$

Just for reference, we present a numerical experiment by R Software for computing the maximum-likelihood estimator (MLE). We set $N=1000$ and $n_1=n_2=\cdots =n_{1000}=10$ and generated $x_{ij},z_{ij},w_{ij}\sim \text {i.i.d.}~N_2(0,I_2)$ independently; then, the target parameter is 8-dimensional. The true values were set as follows: $\beta =(0.6, -0.2)$, $\alpha =(-0.3,~0.5)$, $\tau =(-0.5,~0.3)$, $\sigma _w=\sqrt{0.8}\approx 0.894$, and $\rho = - 0.3$. The results based on a single set of data are given in Table 1. It took more than 20 h in our R code for obtaining one MLE (Apple M1 Max, memory 64GB; the R function adaptIntegrate was used for the numerical integration); we have also run the simulation code for $N=500$ and $n_1=n_2=\cdots =n_{500}=5$, and then it took about 8 h. The program should run much faster if other software such as Fortran and MATLAB is used instead of R, but we will not deal with that direction here. Though it is cheating, the numerical search started from the true values; it would be much more time-consuming and unstable if the initial values were far from the true ones.

Table 1 MLE results; the computation time for one pair was about 21 hours

The EM-algorithm type approach for handling latent variables would work at least numerically, while it is also expected to be time-consuming even if a specific numerical recipe is available. Some advanced tools for numerical integration would help to some extent, but we will not pursue it here.

1.2 Our objective

In this paper, we propose an alternative computationally much simpler way of the joint modeling of the mean and within-subject variance structures. Specifically, we construct a class of parameter-varying models based on the univariate generalized hyperbolic (GH) distribution and study its theoretical properties. The model can be seen as a special case of inhomogeneous normal-variance-mean mixtures and may serve as an alternative to the MELS model; see Sect. 1 for a summary of the GH distributions. Recently, the family has received attention for modeling non-Gaussian continuous repeated measurement data (Asar et al. 2020), but ours is constructed based on a different perspective directly by making some parameters of the GH distribution covariate dependent.

This paper is organized as follows. Section 2 introduces the proposed model and presents the local-likelihood analysis, followed by numerical experiments. Section 3 considers the construction of a specific asymptotically optimal estimator and presents its finite-sample performance with comparisons with the MLE. Section 4 gives a summary and potential directions for future issues.

2 Parameter-varying generalized hyperbolic model

2.1 Proposed model

We model the objective variable at jth-sampling time point from the ith-individual by

$$\begin{aligned} Y_{ij}=x_{ij}^{\top }\beta +s( z_{ij},\alpha )v_i+\sqrt{v_i}\, \sigma (w_{ij},\tau ) \epsilon _{ij} \end{aligned}$$

(2.1)

for $j=1,\dots ,n_i$ and $i=1,\dots ,N$, where

• $x_{ij}\in {\mathbb {R}}^{p_\beta }$, $z_{ij}\in {\mathbb {R}}^{p_\alpha '}$, and $w_{ij}\in {\mathbb {R}}^{p_\tau '}$ are given non-random explanatory variables;

• $\beta \in \Theta _\beta \subset {\mathbb {R}}^{p_{\beta }}$, $\alpha \in \Theta _\alpha \subset {\mathbb {R}}^{p_{\alpha }}$, and $\tau \in \Theta _\tau \subset {\mathbb {R}}^{p_{\tau }}$ are unknown parameters;

• The random-effect variables $v_1,v_2,\ldots \sim \text {i.i.d.}~GIG(\lambda ,\delta ,\gamma )$, where GIG refers to the generalized inverse Gaussian distribution (see Sect. 1);

• $\{\epsilon _{i}=(\epsilon _{i1},\ldots ,\epsilon _{in_i})^{\top }\}_{i\ge 1}\sim \text {i.i.d.}~N(0,I_{n_i})$, independent of $\{v_i\}_{i\ge 1}$;

• $s:{\mathbb {R}}^{p_{\alpha }'}\times \Theta _{\alpha }\mapsto {\mathbb {R}}$ and $\sigma :{\mathbb {R}}^{p_{\tau }'}\times \Theta _{\tau }\mapsto (0,\infty )$ are known measurable functions.

As mentioned in the introduction, for (2.1), one may think of the continuous-time model without system noise:

$$\begin{aligned} Y_{i}(t_{ij})=x_i(t_{ij})^{\top }\beta +s( z_{i}(t_{ij}),\alpha )v_i+\sqrt{v_i}\, \sigma (w_{i}(t_{ij}),\tau ) \epsilon _{i}(t_{ij}), \end{aligned}$$

where $t_{ij}$ denotes the jth sampling time for the ith individual.

We will write $Y_i=(Y_{i1},\ldots ,Y_{in_i})\in {\mathbb {R}}^{n_i}$, $x_i=(x_{i1},\ldots ,x_{in_i})\in {\mathbb {R}}^{n_i}\otimes {\mathbb {R}}^{p_\beta }$, and so on for $i=1,\ldots ,N$, and also

$$\begin{aligned} \theta :=(\beta ,\alpha ,\tau ,\lambda ,\delta ,\gamma ) \in \Theta _\beta \times \Theta _\alpha \times \Theta _\tau \times \Theta _{\lambda } \times \Theta _{\delta } \times \Theta _{\gamma } =:\Theta \subset {\mathbb {R}}^{p}, \end{aligned}$$

where $\Theta$ is supposed to be a convex domain and $p:=p_{\beta }+p_{\alpha }+p_{\tau }+3$. We will use the notation $(P_\theta )_{\theta \in \Theta }$ for the family of distributions of $\{(Y_i,v_i,\epsilon _i)\}_{i\ge 1}$, which is completely characterized by the finite-dimensional parameter $\theta$. The associated expectation and covariance operators will be denoted by $E_\theta$ and $\textrm{Cov}_\theta$, respectively.

Let us write $s_{ij}(\alpha )=s(z_{ij},\alpha )$ and $\sigma _{ij}(\tau )=\sigma (w_{ij},\tau )$. For each $i\le N$, the variable $Y_{i1},\ldots ,Y_{in_i}$ are $v_i$-conditionally independent and normally distributed under $P_\theta$:

$$\begin{aligned} {\mathcal {L}}(Y_{ij}|v_i) = N\left( x_{ij}^{\top }\beta +s_{ij}(\alpha )v_i,~\sigma ^2_{ij}(\tau )v_i\right) . \end{aligned}$$

For each i, we have the specific covariance structure

$$\begin{aligned} \textrm{Cov}_\theta [Y_{ij}, Y_{ik}] = {s_{ij}(\alpha )s_{ik}(\alpha )}\, \textrm{Var}_\theta [v_i]. \end{aligned}$$

(2.2)

The marginal distribution ${\mathcal {L}}(Y_{i1},\dots ,Y_{i n_i})$ is the multivariate GH distribution; a more flexible dependence structure could be incorporated by introducing the non-diagonal scale matrix (see Sect. 4 for a formal explanation). By the definition of the GH distribution, the variables $Y_{ij}$ and $Y_{ik}$ may be uncorrelated for some $(z_{ij},\alpha )$ while they cannot be mutually independent.

We can explicitly write down the log-likelihood function of $(Y_1,\dots ,Y_N)$ as follows:

$$\begin{aligned} \ell _N(\theta )&=-\frac{1}{2} \log (2\pi )\sum _{i=1}^N n_i +N\lambda \log \left( \frac{\gamma }{\delta }\right) - N\log K_\lambda (\delta \gamma ) - \frac{1}{2} \sum _{i,j} \log \sigma _{ij}^2(\tau ) \nonumber \\&\quad + \sum _{i=1}^N \left( \lambda -\frac{n_i}{2}\right) \log B_i(\beta ,\tau ,\delta ) - \sum _{i=1}^N \left( \lambda -\frac{n_i}{2}\right) \log A_i(\alpha ,\tau ,\gamma ) \nonumber \\&\quad + \sum _{i,j} \frac{ s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij}-x^{\top }_{ij}\beta ) + \sum _{i=1}^N \log K_{\lambda -\frac{n_i}{2}}\big (A_i(\alpha ,\tau ,\gamma ) B_i(\beta ,\tau ,\delta )\big ), \end{aligned}$$

(2.3)

where $\sum _{i,j}$ denotes a shorthand for $\sum _{i=1}^{N}\sum _{j=1}^{n_i}$ and

$$\begin{aligned} A_i(\alpha ,\tau ,\gamma )&:= \sqrt{\gamma ^2 + \sum _{j=1}^{n_i}\frac{s_{ij}^2(\alpha )}{\sigma _{ij}^2(\tau )}}~, \end{aligned}$$

(2.4)

$$\begin{aligned} B_i(\beta ,\tau ,\delta )&:= \sqrt{\delta ^2 + \sum _{j=1}^{n_i}\frac{1}{\sigma _{ij}^2(\tau )}(Y_{ij}-x_{ij}^{\top }\beta )^2}~. \end{aligned}$$

(2.5)

The detailed calculation is given in Sect. B.1.

To deduce the asymptotic property of the MLE, there are two typical ways: the global- and the local-consistency arguments. In the present inhomogeneous model where the variables $(x_{ij},z_{ij},w_{ij})$ are non-random, the two asymptotics have different features: on one hand, the global-consistency one generally entails rather messy descriptions of the regularity conditions as was detailed in the previous study (Fujinaga 2021), while entailing theoretically stronger global claims; on the other hand, the local one only guarantees the existence of good local maxima of $\ell _N(\theta )$ while only requiring much weaker local-around-$\theta _{0}$ regularity conditions.

2.2 Local asymptotics of MLE

In the sequel, we fix a true value $\theta _{0}=(\beta _0,\alpha _0,\tau _0,\lambda _0,\delta _0,\gamma _0) \in \Theta$, where $\Theta _\delta \times \Theta _\gamma \subset (0,\infty )^2$; note that we are excluding the boundary (gamma and inverse-gamma) cases for ${\mathcal {L}}(v_i)$.

For a domain A, let ${\mathcal {C}}^k({\overline{A}})$ denote a set of real-valued ${\mathcal {C}}^k$-class functions for which the lth-partial derivatives ($0\le l\le k$) admit continuous extensions to the boundary of A. The asymptotic symbols will be used for $N\rightarrow \infty$ unless otherwise mentioned.

Assumption 2.1

• (1) ${\sup _{i\ge 1}\left( n_i \vee \max _{1\le j\le n_i}\max \{|x_{ij}|, |z_{ij}|, |w_{ij}|\} \right) < \infty }$.

• (2) $\alpha \mapsto s(z,\alpha )\in {\mathcal {C}}^3(\overline{\Theta _\alpha })$ for each z.

• (3) $\tau \mapsto \sigma (w,\tau )\in {\mathcal {C}}^3(\overline{\Theta _\tau })$ for each w, and ${\inf _{(w,\tau )\in {\mathbb {R}}^{p_{\tau }'}\times \Theta _{\tau }} \sigma (w,\tau )>0}$.

We are going to prove the local asymptotics of the MLE by applying the general result (Sweeting 1980, Theorems 1 and 2).

Under Assumption 2.1 and using the basic facts about the Bessel function $K_\cdot (\cdot )$ (see Sect. 1), we can find a compact neighborhood $B_0\subset \Theta$ of $\theta _{0}$ such that

$$\begin{aligned} \forall K>0,\quad \sup _{i\ge 1}\max _{1\le j\le n_i}\sup _{\theta \in B_0} E_\theta \big [|Y_{ij}|^K\big ]<\infty . \end{aligned}$$

Note that $\min \{\delta , \gamma \} >0$ inside $B_0$.

Let $M^{\otimes 2}:= MM^\top$ for a matrix M, and denote by $\lambda _{\max }(M)$ and $\lambda _{\min }(M)$ the largest and smallest eigenvalues of a square matrix M, and by $\partial _\theta ^k$ the kth-order partial-differentiation operator with respect to $\theta$. Write

$$\begin{aligned} \ell _N(\theta )=\sum _{i=1}^{N}\zeta _i(\theta ) \end{aligned}$$

for the right-hand side of (2.3). Then, by the independence we have

$$\begin{aligned} E_\theta \left[ \left( \partial _\theta \ell _N(\theta )\right) ^{\otimes 2}\right] = \sum _{i=1}^{N}E_\theta \left[ \left( \partial _\theta \zeta _i(\theta )\right) ^{\otimes 2}\right] ; \end{aligned}$$

just for reference, the specific forms of $\partial _\theta \ell _N(\theta )$ and $\partial _\theta ^2\ell _N(\theta )$ are given in Sect. B.2. Further by differentiating $\theta \mapsto \partial _\theta ^2\ell _N(\theta )$ with recalling Assumption 2.1, it can be seen that

$$\begin{aligned} \forall K>0,\quad \sup _{i\ge 1}\sup _{\theta \in B_0} E_\theta \left[ \left| \partial _\theta ^m\zeta _i(\theta )\right| ^K \right] < \infty \end{aligned}$$

(2.6)

for $m=1,2$, and that

$$\begin{aligned} \limsup _N \sup _{\theta \in B_0} E_\theta \left[ \frac{1}{N} \sup _{\theta ' \in B_0} \left| \partial _\theta ^3\ell _N(\theta ')\right| \right] < \infty . \end{aligned}$$

(2.7)

These moment estimates will be used later on; unlike the global-asymptotic study (Fujinaga 2021), we do not need the explicit form of $\partial _\theta ^2\ell _N(\theta )$.

We additionally assume the diverging information condition, which is inevitable for consistent estimation:

Assumption 2.2

$$\begin{aligned} \liminf _N \inf _{\theta \in B_0} \lambda _{\min }\left( \frac{1}{N} \sum _{i=1}^{N}E_\theta \left[ \left( \partial _\theta \zeta _i(\theta )\right) ^{\otimes 2}\right] \right) > 0. \end{aligned}$$

Under Assumption 2.1, we may and do suppose that the matrix

$$\begin{aligned} A_N(\theta ):= \left( E_\theta \left[ \left( \partial _\theta \ell _N(\theta )\right) ^{\otimes 2}\right] \right) ^{1/2} = \left( \sum _{i=1}^{N}E_\theta \left[ \left( \partial _\theta \zeta _i(\theta )\right) ^{\otimes 2}\right] \right) ^{1/2} \end{aligned}$$

is well-defined, where $M^{1/2}$ denotes the symmetric positive-definite root of a positive definite M. We also have $\sup _{\theta \in B_0}|A_N(\theta )|^{-1} \lesssim N^{-1/2}\rightarrow 0$. This $A_N(\theta )$ will serve as the norming matrix of the MLE; see Remark 2.5 below for Studentization. Further, the standard argument through the Lebesgue dominated theorem ensures that $E_\theta \left[ \partial _\theta \ell _N(\theta )\right] = 0$ and $E_\theta \left[ \left( \partial _\theta \ell _N(\theta )\right) ^{\otimes 2}\right] = E_\theta \left[ - \partial _\theta ^2\ell _N(\theta )\right]$, followed by $A_N(\theta ) = \left( E_\theta \left[ -\partial ^2_\theta \ell _N(\theta )\right] \right) ^{1/2}$.

For $c>0$, Assumption 2.2 yields

$$\begin{aligned}&\sup _{\theta ':\, |\theta '-\theta |\le c/\sqrt{N}}\left| A_N(\theta )^{-1} A_N(\theta ') - I_p \right| \nonumber \\&\quad = \sup _{\theta ':\, |\theta '-\theta |\le c/\sqrt{N}} \left| \left( \frac{1}{\sqrt{N}}A_N(\theta )\right) ^{-1} \left( \frac{1}{\sqrt{N}}A_N(\theta ') - \frac{1}{\sqrt{N}}A_N(\theta )\right) \right| \nonumber \\&\quad \lesssim \sup _{\theta ':\, |\theta '-\theta |\le c/\sqrt{N}} \left| \frac{1}{\sqrt{N}}A_N(\theta ') - \frac{1}{\sqrt{N}}A_N(\theta )\right| \nonumber \\&\quad {\lesssim } \sup _{\theta ':\, |\theta '{-}\theta |\le c/\sqrt{N}} \left| \left( \frac{1}{N} \sum _{i=1}^{N}E_{\theta '}\left[ \left( \partial _\theta \zeta _i(\theta ')\right) ^{{\otimes } 2}\right] \right) ^{1/2} {-} \left( \frac{1}{N} \sum _{i=1}^{N}E_\theta \left[ \left( \partial _\theta \zeta _i(\theta )\right) ^{{\otimes } 2}\right] \right) ^{1/2} \right| \nonumber \\&\quad \rightarrow 0. \end{aligned}$$

(2.8)

Here, the last convergence holds since the function $\theta \mapsto N^{-1/2}A_N(\theta )$ is uniformly continuous over $B_0$.

Define the normalized observed information:

$$\begin{aligned} {\mathcal {I}}_N(\theta ):= - A_N(\theta )^{-1} \partial _\theta ^2\ell _N(\theta ) A_N(\theta )^{-1\,\top }. \end{aligned}$$

Then, it follows from Assumption 2.2 that

$$\begin{aligned} \left| {\mathcal {I}}_N(\theta )-I_p \right|&= \left| \left( \frac{1}{\sqrt{N}}A_N(\theta )\right) ^{-1} \left( {\mathcal {I}}_N(\theta ) - \left( \frac{1}{\sqrt{N}}A_N(\theta )\right) ^{\otimes 2} \right) \left( \frac{1}{\sqrt{N}}A_N(\theta )\right) ^{-1\,\top } \right| \\&\lesssim \left| {\mathcal {I}}_N(\theta ) - \left( \frac{1}{\sqrt{N}}A_N(\theta )\right) ^{\otimes 2} \right| \\&\lesssim \left| \frac{1}{N} \sum _{i=1}^{N}\left( \partial _\theta ^2 \zeta _i(\theta ) - E_\theta \left[ \partial _\theta ^2 \zeta _i(\theta )\right] \right) \right| . \end{aligned}$$

Then, (2.6) ensures that

$$\begin{aligned} \sup _{\theta \in B_0} E_\theta \left[ \left| {\mathcal {I}}_N(\theta )-I_p \right| ^2\right] \lesssim \frac{1}{N} \left( \frac{1}{N} \sum _{i=1}^{N}\sup _{\theta \in B_0} E_\theta \left[ \left| \partial _\theta ^2 \zeta _i(\theta )\right| ^2\right] \right) \lesssim \frac{1}{N}\rightarrow 0, \end{aligned}$$

followed by the property

$$\begin{aligned} \forall \epsilon>0,\quad \sup _{\theta \in B_0}P_\theta \left[ |{\mathcal {I}}_N(\theta )-I_p|>\epsilon \right] \rightarrow 0. \end{aligned}$$

(2.9)

Let $\xrightarrow {{\mathcal {L}}}$ denote the convergence in distribution. Having obtained (2.7), (2.8), and (2.9), we can conclude the following theorem by applying (Sweeting 1980, Theorems 1 and 2).

Theorem 2.3

Under Assumptions 2.1 and 2.2, we have the following statements under $P_{\theta _{0}}$.

• (1) For any bounded sequence $(u_N)\subset {\mathbb {R}}^p$,

  $$\begin{aligned} \ell _{N}\left( \theta _{0}+A_N(\theta _{0})^{\top \,-1}u_N\right) - \ell _{N}\left( \theta _{0}\right) = u_N^{\top } \Delta _N(\theta _{0}) - \frac{1}{2} |u_N|^2 + o_{p}(1), \end{aligned}$$

  with

  $$\begin{aligned} \Delta _N(\theta _{0}):= A_N(\theta _{0})^{-1} \partial _{\theta }\ell _{N}(\theta _{0}) \xrightarrow {{\mathcal {L}}}N(0, I_p). \end{aligned}$$

• (2) There exists a local maximum point ${\hat{\theta }}_{N}$ of $\ell _N(\theta )$ with $P_{\theta _{0}}$-probability tending to 1, for which

  $$\begin{aligned} A_N(\theta _{0})^{\top }({\hat{\theta }}_{N}-\theta _{0}) = \Delta _N(\theta _{0}) + o_{p}(1) \xrightarrow {{\mathcal {L}}}N(0, I_p). \end{aligned}$$

  (2.10)

Remark 2.4

(Asymptotically efficient estimator) By the standard argument about the local asymptotic normality (LAN) of the family $\{P_\theta \}_{\theta \in \Theta }$, any estimators ${\hat{\theta }}_{N}^*$ satisfying that

$$\begin{aligned} A_N(\theta _{0})^{\top }({\hat{\theta }}_{N}^*-\theta _{0}) = \Delta _N(\theta _{0}) + o_{p}(1) \end{aligned}$$

(2.11)

are regular and asymptotically efficient in the sense of Hajék–Le Cam. See Basawa and Scott (1983) and Jeganathan (1982) for details.

Remark 2.5

(Studentization of 2.10) Here is a remark on the construction of approximate confidence sets. Define the statistics

$$\begin{aligned} {\hat{A}}_N:= \left( \sum _{i=1}^{N}(\partial _\theta \zeta _i({\hat{\theta }}_{N}))^{\otimes 2}\right) ^{1/2}. \end{aligned}$$

(2.12)

Then, to make inferences for $\theta _{0}$, we can use the distributional approximations ${\hat{A}}_N({\hat{\theta }}_{N}-\theta _{0}) = \Delta _N(\theta _{0}) + o_{p}(1) \xrightarrow {{\mathcal {L}}}N_{p}(0, I_p)$ and

$$\begin{aligned} ({\hat{\theta }}_{N}-\theta _{0})^\top {\hat{A}}_N^2 ({\hat{\theta }}_{N}-\theta _{0}) \xrightarrow {{\mathcal {L}}}\chi ^2(p). \end{aligned}$$

(2.13)

To see this, it is enough to show that under $P_{\theta _{0}}$,

$$\begin{aligned} A_N(\theta _{0})^{-1}{\hat{A}}_N = I_p + o_p(1). \end{aligned}$$

(2.14)

We have $\sqrt{N}({\hat{\theta }}_{N}-\theta _{0})=O_p(1)$ by Theorem 2.3 and Assumption 2.2. This together with the Burkholder inequality and (2.6) yield that

$$\begin{aligned} N^{-1/2}{\hat{A}}_N&= \Bigg ( \frac{1}{N} \sum _{i=1}^{N}\left( (\partial _\theta \zeta _i({\hat{\theta }}_{N}))^{\otimes 2} - (\partial _\theta \zeta _i(\theta _{0}))^{\otimes 2} \right) \\&{}\qquad {+} \frac{1}{N} \sum _{i=1}^{N}\left( (\partial _\theta \zeta _i(\theta _{0}))^{{\otimes } 2} {-} E_{\theta _{0}}\left[ (\partial _\theta \zeta _i(\theta _{0}))^{{\otimes } 2} \right] \right) {+} \left( N^{{-}1/2}A_N(\theta _{0}) \right) ^{2} \Bigg )^{1/2} \\&= \left( O_p(N^{-1/2}) + \left( N^{-1/2}A_N(\theta _{0}) \right) ^{2} \right) ^{1/2} \end{aligned}$$

and hence

$$\begin{aligned} A_N(\theta _{0})^{-1} {\hat{A}}_N = \left( N^{-1/2}A_N(\theta _{0}) \right) ^{-1} \left\{ o_p(1) + \left( N^{-1/2}A_N(\theta _{0}) \right) ^{2} \right\} ^{1/2} =I_p + o_p(1), \end{aligned}$$

concluding (2.14). Note that, instead of (2.12), we may also use the square root of the observed information matrix

$$\begin{aligned} {\widetilde{A}}_N:= \left( -\sum _{i=1}^{N}\partial _\theta ^2\zeta _i({\hat{\theta }}_{N})\right) ^{1/2} \end{aligned}$$

(2.15)

for concluding the same weak convergence as in (2.13). In our numerical experiments, we made use of this ${\widetilde{A}}_N^2$ for computing the confidence interval and the empirical coverage probability. The elements of ${\widetilde{A}}_N^2$ are explicit while rather lengthy: see Sect. B.2.

Remark 2.6

(Misspecifications) In addition to the linear form $x_{ij}^\top \beta$ in (2.1), misspecification of a parametric form of the function $(s(z_i,\alpha ),\sigma (w_{ij},\tau ))$ is always concerned. Using the M-estimation theory (for example, see White (1982) and (Fahrmeir 1990, Section 5)), under appropriate identifiability conditions, it is possible to handle their misspecified parametric forms. In that case, however, the maximum-likelihood-estimation target, say $\theta _*$, is the optimal parameter (to be uniquely determined) in terms of the Kullback–Leibler divergence, and we do not have the LAN property in Theorem 2.3 in the usual sense while an asymptotic normality result of the form $\sqrt{N}({\hat{\theta }}_{N}-\theta _*) \xrightarrow {{\mathcal {L}}}N(0,\Gamma _0^{-1}\Sigma _0\Gamma _0^{-1})$ could be given, where (non-random) $\Sigma _0$ and $\Gamma _0$ are specified by $N^{-1/2}\partial _\theta \ell _N(\theta _*) \xrightarrow {{\mathcal {L}}}N(0,\Sigma _0)$ and $-N^{-1}\partial _\theta ^2\ell _N(\theta _*) \xrightarrow {p}\Gamma _0$.

Finally, we note that the statistical problem will become non-standard if we allow that the true value of $(\delta ,\gamma )$ for the GIG distribution ${\mathcal {L}}(v_i)$ satisfies that $\delta _0=0$ or $\gamma _0=0$. We have excluded these boundary cases at the beginning of Sect. 2.2.

2.3 Numerical experiments

For simulation purposes, we consider the following model:

$$\begin{aligned} Y_{ij}=x_{ij}^{\top }\beta +\tanh ( z_{ij}^{\top }\alpha )v_i+\sqrt{v_i\exp (w_{ij}^{\top }\tau )}\,\epsilon _{ij}, \end{aligned}$$

(2.16)

where the ingredients are specified as follows.

• $N=1000$ and $n_1=n_2=\cdots =n_{1000}=10$.

• The two different cases for the covariates $x_{ij},z_{ij},w_{ij} \in {\mathbb {R}}^2$:

• (i) $x_{ij}, z_{ij}, w_{ij} \sim \text {i.i.d.}~N(0,I_2)$;

• (ii) The first components of $x_{ij}, z_{ij}, w_{ij}$ are sampled from independent N(0, 1), and all the second ones are set to be $j-1$.

The setting (ii) incorporates similarities across the individuals; see Fig. 1.

• $v_1,v_2,\dots \sim \text {i.i.d.}~GIG(\lambda ,\delta ,\gamma )$.

• $\epsilon _{i}=(\epsilon _{i1},\ldots ,\epsilon _{in_i})\sim N(0,I_{n_i})$, independent of $\{v_i\}$.

• $\theta =(\beta ,\alpha ,\tau ,\lambda ,\delta ,\gamma ) = (\beta _0,\beta _1,\alpha _0,\alpha _1,\tau _0,\tau _1,\lambda ,\delta ,\gamma ) \in {\mathbb {R}}^9$.

• True values of $\theta$:

• (i) $\beta =(0.3,~0.5),~\alpha =(-0.04,~0.05),~\tau =(0.05,~0.07)$, $\lambda =1.2,~\delta =1.5,~\gamma =2$;

• (ii) $\beta =(0.3,~1.2),~\alpha =(-0.4,~0.8),~\tau =(0.05,~0.007)$, $\lambda =0.9,~\delta =1.2,~\gamma =0.9$.

Fig. 1

Longitudinal-data plots of 10 individuals in case (1) (left) and case (2) (right)

We numerically computed the MLE ${\hat{\theta }}_{N}$ by optimizing the log-likelihood; the modified Bessel function $K_\cdot (\cdot )$ can be efficiently computed by the existing numerical libraries such as besselK in R Software. We repeated the Monte Carlo trials 1000 times, computed the Studentized estimates ${\widetilde{A}}_N({\hat{\theta }}_{N}-\theta _{0})$ with (2.15) in each trial, and then drew histograms in Figs. 2 and 3, where the red lines correspond to the standard normal densities. Also given in Figs. 2 and 3 are the histograms of the chi-square approximations based on (2.13).

The computation time for one MLE was about 8 min for case (i) and about 6 min for case (ii). Estimation performance for $(\lambda ,\delta ,\gamma )$ were less efficient than those for $(\beta ,\alpha ,\tau )$. It is expected that the unobserved nature of the GIG variables make the standard-normal approximations relatively worse.

It is worth mentioning that case (ii) shows better normal approximations, in particular for $(\lambda ,\delta ,\gamma )$; case (ii) would be simpler in the sense that the data from each individual have similarities in their trend (mean) structures.

Table 2 shows the empirical $95\%$-coverage probability for each parameter in both (i) and (ii), based on the confidence intervals ${\hat{\theta }}_{N}^{(k)} \pm z_{\alpha /2}[(-\partial _{\theta }^2\ell _N({\hat{\theta }}_{N}))^{-1}]_{kk}^{1/2}$ for $k=1,\dots ,9$ with ${\hat{\theta }}_{N}=:({\hat{\theta }}_{N}^{(k)})_{k\le 9}$ and $\alpha =0.05$. We had 365 and 65 numerically unstable cases among 1000 trials, respectively (mostly cased by a degenerate $\det (-\partial _{\theta }^2\ell _N({\hat{\theta }}_{N}))$). Therefore, the coverage probabilities were computed based on the remaining cases.

Fig. 2

Standardized distributions of the MLE in case (i). The lower rightmost panel shows the chi-square approximation based on (2.13)

Fig. 3

Standardized distributions of the MLE in case (ii). The lower rightmost panel shows the chi-square approximation based on (2.13)

Let us note the crucial problem in the above Monte Carlo trials: the objective log-likelihood is highly non-concave, hence as usual the numerical optimization suffers from the initial-value and local-maxima problems. Here is a numerical example based on only a single set of data with $N=1000$ and $n_1=n_2=\cdots =n_{1000}=10$ as before. The same model as in (2.16) together with the subsequent settings was used, except that we set $\lambda =-1/2$ known from the beginning so that the latent variables $v_1,\dots ,v_N$ have the inverse-Gaussian population $IG(\delta ,\gamma )=GIG(-1/2,\delta ,\gamma )$. For the true parameter values specified in Table 3, we run the following two cases for the initial values of the numerical optimization:

• (i’) The true value;

• (ii’) $(\underbrace{1.0\times 10^{-8},\ldots ,~1.0\times 10^{-8}}_{\text {6 times}},~1.0\times 10^{-4},~1.0\times 10^{-3})$.

The results in Table 3 clearly show that the inverse-Gaussian parameter $(\delta ,\gamma )$ can be quite sensitive to a bad starting point for the numerical search. In the next section, to bypass the numerical instability we will construct easier-to-compute initial estimators and their improved versions asymptotically equivalent to the MLE.

3 Asymptotically efficient estimator

Building on Theorem 2.3, we now turn to global asymptotics through the classical Newton–Raphson type procedure. A systematic account for the theory of the one-step estimator can be found in many textbooks, such as (van der Vaart 1998, Section 5.7). Let us briefly overview the derivation with the current matrix-norming setting.

Suppose that we are given an initial estimator ${\hat{\theta }}_{N}^0=({\hat{\alpha }}_{N}^0,{\hat{\beta }}_{N}^0,{\hat{\tau }}_{N}^0,{\hat{\lambda }}_{N}^0,{\hat{\delta }}_{N}^0,{\hat{\gamma }}_{N}^0)$ of $\theta _{0}$ satisfying that

$$\begin{aligned} {\hat{u}}_N^0:= A_{N}(\theta _{0})^{\top }({\hat{\theta }}_{N}^0 -\theta _{0}) = O_p(1). \end{aligned}$$

By Theorem 2.3 and Assumption 2.2, this amounts to

$$\begin{aligned} \sqrt{N}({\hat{\theta }}_{N}^0 -\theta _{0}) = O_p(1). \end{aligned}$$

(3.1)

We define the one-step estimator ${\hat{\theta }}_{N}^1$ by

$$\begin{aligned} {\hat{\theta }}^1_N:= {\hat{\theta }}_N^0 - \left( \partial ^2_\theta \ell _N({\hat{\theta }}_N^0)\right) ^{-1}\partial _{\theta }\ell _N({\hat{\theta }}_N^0) \end{aligned}$$

(3.2)

on the event $\{{\hat{\theta }}_{N}^1\in \Theta ,~\det (\partial ^2_\theta \ell _N({\hat{\theta }}_N^0))\ne 0\}$, the $P_{\theta _{0}}$-probability of which tends to 1. Write ${\hat{u}}_N^1 = A_{N}(\theta _{0})^{\top }({\hat{\theta }}_{N}^1 -\theta _{0})$ and ${\hat{{\mathcal {I}}}}_N^0 = -A_N(\theta _{0})^{-1} \partial ^2_\theta \ell _N({\hat{\theta }}_N^0) A_N(\theta _{0})^{-1\,\top }$. Using Taylor expansion, we have

$$\begin{aligned} {\hat{{\mathcal {I}}}}_N^0 {\hat{u}}_N^1 = {\hat{{\mathcal {I}}}}_N^0 {\hat{u}}_N^0 + A_N(\theta _{0})^{-1} \partial _\theta \ell _N({\hat{\theta }}_N^0). \end{aligned}$$

(3.3)

By the arguments in Sect. 2.2, it holds that $|{\hat{{\mathcal {I}}}}_N^0| \vee |{\hat{{\mathcal {I}}}}_N^{0\,-1}|=O_p(1)$. From (3.1),

$$\begin{aligned} A_N(\theta _{0})^{-1} \partial _\theta \ell _N({\hat{\theta }}_N^0) = \Delta _N(\theta _{0}) - {\hat{{\mathcal {I}}}}_N^0 {\hat{u}}_N^0 + O_p\big (N^{-1/2}\big ). \end{aligned}$$

(3.4)

Combining (3.3) and (3.4) and recalling Remarks 2.4 and 2.5, we obtain the asymptotic representation (2.11) for ${\hat{\theta }}_{N}^1$, followed by the asymptotic standard normality

$$\begin{aligned} {\hat{u}}_N^1 = \Delta _N(\theta _{0}) + o_{p}(1) \xrightarrow {{\mathcal {L}}}N_{p}(0, I_p) \end{aligned}$$

and its asymptotic optimality.

Table 2 The empirical $95\%$-coverage probabilities of the MLE in cases (i) and (ii) based on 1000 trials

Table 3 MLE based on single data set; the running time was about 2 min for case (i’) and 8 min for case (ii’); the performance of estimating $(\delta ,\gamma )$ in case (ii’) shows instability

3.1 Construction of initial estimator

This section aims to construct a $\sqrt{N}$-consistent estimator ${\hat{\theta }}_{N}^0$ satisfying (3.1) through the stepwise least-squares type estimators for the first three moments of $Y_{ij}$. We note that the model (2.1) does not have a conventional location-scale structure because of the presence of $v_i$ in the two different terms.

We assume that the parameter space $\Theta _\beta \times \Theta _\alpha \times \Theta _\tau \times \Theta _\lambda \times \Theta _\delta \times \Theta _\gamma$ is a bounded convex domain in ${\mathbb {R}}^{p_\beta }\times {\mathbb {R}}^{p_\alpha }\times {\mathbb {R}}^{p_\tau }\times {\mathbb {R}}\times (0,\infty )^2$ with the compact closure. Write $\theta '=(\lambda ,\delta ,\gamma )$ for the parameters contained in ${\mathcal {L}}(v_1)$, the true value being denoted by $\theta '_0=(\lambda _0,\delta _0,\gamma _0)$. Let $\mu =\mu (\theta ')=E_\theta [v_1]$, $c=c(\theta '):=\textrm{Var}_{\theta }[v_1]$, and $\rho =\rho (\theta '):=E_\theta [(v_i -E_\theta [v_i])^3]$; write $\mu _0=\mu (\theta '_0)$, $c_0=c(\theta '_0)$, and $\rho _0=\rho (\theta '_0)$ correspondingly. Further, we introduce the sequences of the symmetric random matrices:

$$\begin{aligned} Q_{1,N}(\alpha )&:= \frac{1}{N} \sum _{i,j} \big ( \mu _0\,\partial _\alpha s_{ij}(\alpha ),\, x_{ij},\, s_{ij}(\alpha _0) \big )^{\otimes 2},\\ Q_{2,N}(\tau )&:= \frac{1}{N} \sum _{i,j} \left( \mu _0\,\partial _\tau (\sigma ^2_{ij})(\tau ),\, s_{ij}^2(\alpha _0) \right) ^{\otimes 2}. \end{aligned}$$

To state our global consistency result, we need additional assumptions.

Assumption 3.1

  In addition to Assumption 2.1, the following conditions hold.

• (1) Global identifiability of $(\alpha ,\beta ,\mu )$:

  • (a) $\displaystyle {\sup _\alpha |Q_{1,N}(\alpha ) - Q_1(\alpha ) | \rightarrow 0}$ for some non-random function $Q_{1}(\alpha )$;

  • (b) $\displaystyle {\liminf _N \inf _{\alpha } \lambda _{\min }(Q_{1,N}(\alpha ))>0}$.

• (2) Global identifiability of $(\tau ,c)$:

  • (a) $\displaystyle {\sup _\tau |Q_{2,N}(\tau ) - Q_2(\tau ) | \rightarrow 0}$ for some non-random function $Q_{2}(\tau )$;

  • (b) $\displaystyle {\liminf _N \inf _{\tau }\lambda _{\min }(Q_{2,N}(\tau ))>0}$.

• (3) Global identifiability of $\rho$: $\displaystyle {\liminf _N \frac{1}{N}\sum _{i,j} s_{ij}^6(\alpha _0)>0}$.

• (4) There exists a neighborhood of $\theta '_0$ on which the mapping $\psi :\,\Theta _\lambda \times \Theta _\delta \times \Theta _\gamma \rightarrow (0,\infty )^2\times {\mathbb {R}}$ defined by $\psi (\theta ')=(\mu (\theta '),c(\theta '),\rho (\theta '))$ is bijective, and $\psi$ is continuously differentiable at $\theta _{0}$ with nonsingular derivative.

To construct ${\hat{\theta }}_{N}^0$, we will proceed as follows.

• Step 1 Noting that $E_\theta [Y_{ij}]=x_{ij}^{\top }\beta +s_{ij}(\alpha ) \mu$, we estimate $(\beta ,\alpha ,\mu )$ by minimizing

  $$\begin{aligned} M_{1,N}(\alpha ,\beta ,\mu ):= \sum _{i,j}\left( Y_{ij} - x_{ij}^{\top }\beta - s_{ij}(\alpha ) \mu \right) ^2. \end{aligned}$$

  (3.5)

  Let $({\hat{\alpha }}_{N}^0,{\hat{\beta }}_{N}^0,{\hat{\mu }}_{N}^0)\in \mathop {\textrm{argmin}}\limits \nolimits _{(\alpha ,\beta ,\mu )\in \overline{\Theta _\beta \times \Theta _\alpha \times \Theta _\mu } } M_{1,N}(\alpha ,\beta ,\mu )$.

  For estimating the remaining parameters, we introduce the (heteroscedastic) residual

  $$\begin{aligned} {\hat{e}}_{ij}:=Y_{ij}-x_{ij}^{\top }{\hat{\beta }}_{N}^0 - s_{ij}({\hat{\alpha }}_{N}^0) {\hat{\mu }}_{N}^0, \end{aligned}$$

  (3.6)

  which is to be regarded as an estimator of the unobserved quantity $\sqrt{v_i}\,\sigma _{ij}(\tau _0)\epsilon _{ij}$.

• Step 2 Noting that $\textrm{Var}_\theta [Y_{ij}]=\sigma _{ij}^2(\tau )\mu + s_{ij}^2(\alpha )c$, we estimate the variance-component parameter $(\tau ,\alpha )$ by minimizing

  $$\begin{aligned} M_{2,N}(\tau ,c):= \sum _{i,j}\left( {\hat{e}}_{ij}^2 - \sigma _{ij}^2(\tau ){\hat{\mu }}_{N}^0 - s_{ij}^2({\hat{\alpha }}_{N}^0)c\right) ^2. \end{aligned}$$

  (3.7)

  Let $({\hat{\tau }}_{N}^0,{\hat{c}}_N^0) \in \mathop {\textrm{argmin}}\limits \nolimits _{(\tau ,c)\in \overline{\Theta _\tau } \times (0,\infty ) } M_{2,N}(\tau ,c)$.

• Step 3 Noting that $E_\theta [(Y_{ij}-E_\theta [Y_{ij}])^3] = 3 s_{ij}(\alpha ) \sigma _{ij}^2(\tau ) c + s_{ij}^3(\alpha ) \rho$, we estimate $\rho$ by the minimizer ${\hat{\rho }}_{N}^0$ of

  $$\begin{aligned} M_{3,N}(\rho ):= \sum _{i,j}\left( {\hat{e}}_{ij}^3 - 3 s_{ij}({\hat{\alpha }}_{N}^0) \sigma _{ij}^2({\hat{\tau }}_{N}^0) {\hat{c}}_N^0 - s_{ij}^3({\hat{\alpha }}_{N}^0) \rho \right) ^2, \end{aligned}$$

  that is,

  $$\begin{aligned} {\hat{\rho }}_{N}^0:= \left( \sum _{i,j} s_{ij}^6({\hat{\alpha }}_{N}^0)\right) ^{-1} \sum _{i,j} \left\{ {\hat{e}}_{ij}^3 - 3 s_{ij}({\hat{\alpha }}_{N}^0) \sigma _{ij}^2({\hat{\tau }}_{N}^0) {\hat{c}}_N^0\right\} s_{ij}^3({\hat{\alpha }}_{N}^0). \end{aligned}$$

  (3.8)

• Step 4 Finally, under Assumption 3.1(4), we construct ${\hat{\theta }}_{N}^{\prime 0} = ({\hat{\lambda }}_{N}^0,{\hat{\delta }}_{N}^0,{\hat{\gamma }}_{N}^0)$ through the delta method by inverting $({\hat{\mu }}_{N}^0,{\hat{c}}_N^0,{\hat{\rho }}_{N}^0)$:

  $$\begin{aligned} \sqrt{N}\big ({\hat{\theta }}_{N}^{\prime 0} - \theta _{0}'\big )&= \sqrt{N}\left( \psi ^{-1}({\hat{\mu }}_{N}^0,{\hat{c}}_N^0,{\hat{\rho }}_{N}^0) - \psi ^{-1}(\mu _0,c_0,\rho _0)\right) \\&= \big (\partial _{\theta '}\psi (\theta _{0}')\big )^{-1} \sqrt{N}\left( ({\hat{\mu }}_{N}^0,{\hat{c}}_N^0,{\hat{\rho }}_{N}^0) - (\mu _0,c_0,\rho _0)\right) =O_p(1). \end{aligned}$$

In the rest of this section, we will go into detail about Steps 1 to 3 mentioned above and show that the estimator ${\hat{\theta }}_{N}^0$ thus constructed satisfies (3.1); Step 4 is the standard method of moments (van der Vaart 1998, Chapter 4).

For convenience, let us introduce some notation. The multilinear-form notation

$$\begin{aligned} M[u] = \sum _{i_1,\dots ,i_k}M_{i_1,\dots ,i_k}u_{i_1}\dots u_{i_k} \in {\mathbb {R}}\end{aligned}$$

is used for $M=\{M_{i_1,\dots ,i_k}\}$ and $u=\{u_{i_1},\dots u_{i_k}\}$. For any sequence random functions $\{F_N(\theta )\}_N$ and a non-random sequence $(a_N)_N \subset (0,\infty )$, we will write $F_N(\theta )=O_p^*(a_n)$ and $F_N(\theta )=o_p^*(a_n)$ when $\sup _\theta |F_N(\theta )|=O_p(a_N)$ and $\sup _\theta |F_N(\theta )|=o_p(a_N)$ under $P_{\theta _{0}}$, respectively. Further, we will denote by $m_i=(m_{i1},\dots ,m_{i n_i})\in {\mathbb {R}}^{n_i}$ any zero-mean (under $P_{\theta _{0}}$) random variables such that $m_1,\dots ,m_N$ are mutually independent and $\sup _{i\ge 1}\max _{1\le j\le n_i}E_{\theta _{0}}[|m_{ij}|^K]<\infty$ for any $K>0$; its specific form will be of no importance.

3.1.1 Step 1

Put $a=(\alpha ,\beta ,\mu )$ and $a_0=(\alpha _0,\beta _0,\mu _0)$. By (2.1) and (3.5), we have

$$\begin{aligned} {\mathbb {Y}}_{1,N}(a)&:= \frac{1}{N} \left( M_{1,N}(a) - M_{1,N}(a_0) \right) \\&= -\frac{2}{N} \sum _{i,j} \left( x_{ij},s_{ij}(\alpha _0),\mu _0\right) \cdot \left( \beta -\beta _0, \mu -\mu _0, s_{ij}(\alpha ) - s_{ij}(\alpha _0)\right) m_{ij} \\&{}\qquad + \left( \frac{1}{N} \sum _{i,j} \left( \mu _0\, \partial _\alpha s_{ij}({\tilde{\alpha }}),\, x_{ij},\, s_{ij}(\alpha _0) \right) ^{\otimes 2}\right) \left[ (a-a_0)^{\otimes 2}\right] \\&= -\frac{2}{N} \sum _{i,j} \left( x_{ij},s_{ij}(\alpha _0),\mu _0\right) \cdot \left( \beta -\beta _0, \mu -\mu _0, s_{ij}(\alpha ) - s_{ij}(\alpha _0)\right) m_{ij} \\&{}\qquad + 2\left( Q_{1,N}({\tilde{\alpha }}) - Q_{1}({\tilde{\alpha }})\right) \left[ (a-a_0)^{\otimes 2}\right] + 2Q_{1}({\tilde{\alpha }}) \left[ (a-a_0)^{\otimes 2}\right] , \end{aligned}$$

where ${\tilde{\alpha }}={\tilde{\alpha }}(\alpha ,\alpha _0)$ is a point lying on the segment joining $\alpha$ and $\alpha _0$. The first term on the rightmost side equals $O_p^*(N^{-1/2})$. The second term equals $o_p^*(1)$ by Assumption 3.1(1), hence we conclude that $|{\mathbb {Y}}_{1,N}(a) - {\mathbb {Y}}_1(a)| = o_p^*(1)$ for ${\mathbb {Y}}_1(a):=2Q_{1}({\tilde{\alpha }}) \left[ (a-a_0)^{\otimes 2}\right]$. Moreover, we have $\inf _{\alpha } \lambda _{\min }(Q_{1}(\alpha ))>0$ hence $\mathop {\textrm{argmin}}\limits {\mathbb {Y}}_1=\{a_0\}$, followed by the consistency ${\hat{a}}_N \xrightarrow {p}a_0$.

To deduce $\sqrt{N}({\hat{a}}_N - a_0)=O_p(1)$, we may and do focus on the event $\{\partial _a M_{1,N}({\hat{a}}_N)=0\}$, on which

$$\begin{aligned} N^{-1}\partial _a^2 M_{1,N}({\tilde{a}}_N) \sqrt{N}({\hat{a}}_N - a_0) = -N^{-1/2}\partial _a M_{1,N}(a_0), \end{aligned}$$

(3.9)

where ${\tilde{a}}_N$ is a random point lying on the segment joining ${\hat{a}}_N$ and $\alpha _0$. Observe that

$$\begin{aligned} {-}\frac{1}{\sqrt{N}}\partial _a M_{1,N}(a_0) {=} \frac{2}{\sqrt{N}} \sum _{i,j} \textrm{diag}\left( \partial _\alpha s_{ij}(\alpha _0),\, I_{p_\beta },\, 1\right) \left[ (\mu _0, x_{ij}, s_{ij}(\alpha _0)) \right] m_{ij} {=}O_p(1). \end{aligned}$$

Similarly,

$$\begin{aligned} \frac{1}{N} \partial _a^2 M_{1,N}({\tilde{a}}_N)&= -\frac{2\mu _0}{N} \sum _{i,j} \left\{ m_{ij} - \left( x_{ij},s_{ij}(\alpha _0),\mu _0\right) \cdot \right. \\&\quad \times \left. \left( {\tilde{\beta }}_N-\beta _0, {\tilde{\mu }}_N-\mu _0, s_{ij}({\tilde{\alpha }}_N) - s_{ij}(\alpha _0)\right) \right\} \\&\quad + \frac{2}{N} \sum _{i,j} \left( \mu _0 \partial _\alpha s_{ij}({\tilde{\alpha }}_N),\, x_{ij},\, s_{ij}(\alpha _0)\right) ^{\otimes 2}. \end{aligned}$$

Concerning the right-hand side, the first term equals $o_p(1)$, and the inverse of the second term does $Q_{1,N}({\tilde{\alpha }}_N)^{-1} = \{2Q_{1,N}(\alpha _0) + o_p(1)\}^{-1}=O_p(1)$. The last two displays combined with Assumption 3.1(1) and (3.9) conclude that $\sqrt{N}({\hat{a}}_N - a_0)=O_p(1)$; it could be shown under additional conditions that $\sqrt{N}({\hat{a}}_N - a_0)$ is asymptotically centered normal, while it is not necessary here.

3.1.2 Step 2

Write ${\hat{u}}_{\beta ,N}=\sqrt{N}({\hat{\beta }}_{N}^0 -\beta _0)$, ${\hat{u}}_{\mu ,N}=\sqrt{N}({\hat{\mu }}_{N}^0 -\mu _0)$, and ${\hat{u}}'_{\alpha ,ij}=\sqrt{N}(s_{ij}({\hat{\alpha }}_{N}^0) -s_{ij}(\alpha _0))$. Let $b:=(\tau ,c)$ and $b_0:=(\tau _0,c_0)$, and moreover

$$\begin{aligned} e_{ij}&:= \sqrt{v_i} \sigma _{ij}(\tau _0) \epsilon _{ij}, \\ {\overline{e}}_{ij}&:= Y_{ij}-E_{\theta _{0}}[Y_{ij}] =e_{ij} + s_{ij}(\alpha _0) (v_i-\mu _0). \end{aligned}$$

We have ${\hat{e}}_{ij} = e_{ij} - N^{-1/2}{\hat{H}}_{ij}$ with ${\hat{H}}_{ij}:= x_{ij}^\top {\hat{u}}_{\beta ,N} + s_{ij}({\hat{\alpha }}_{N}^0) {\hat{u}}_{\mu ,N} + \mu _0 {\hat{u}}'_{\alpha ,ij}$. Introduce the zero-mean random variables $\eta _{ij}:={\overline{e}}_{ij}^2 - \left( \sigma _{ij}^2(\tau _0)+c_0 s_{ij}^2(\alpha _0)\right)$. Then, we can rewrite $M_{2,N}(b)$ of (3.7) as

$$\begin{aligned} M_{2,N}(b) = \sum _{i,j} \left( {\overline{\eta }}_{ij}(b) + \frac{1}{\sqrt{N}} {\hat{B}}_{ij}\right) ^2, \end{aligned}$$

where

$$\begin{aligned} {\overline{\eta }}_{ij}(b)&:= \eta _{ij} - \left( (\sigma _{ij}^2(\tau ) - \sigma _{ij}^2(\tau _0)) {\hat{\mu }}_{N}^0 + (c-c_0) s_{ij}^2({\hat{\alpha }}_{N}^0) \right) ,\\ {\hat{B}}_{ij}&:= -2{\hat{H}}_{ij} + \frac{1}{\sqrt{N}}{\hat{H}}_{ij}^2 -\sigma _{ij}^2(\tau _0) {\hat{u}}_{\mu ,N} - c_0 {\hat{u}}'_{\alpha ,ij}. \end{aligned}$$

As in Sect. 3.1.1, we observe that

$$\begin{aligned} {\mathbb {Y}}_{2,N}(b)&:= \frac{1}{N} \left( M_{2,N}(b) - M_{2,N}(b_0) \right) \\&= O_p^*\left( \frac{1}{\sqrt{N}}\right) + \frac{1}{N} \sum _{i,j} \left( {\overline{\eta }}_{ij}^2(b) - \eta _{ij}^2 \right) \\&= O_p^*\left( \frac{1}{\sqrt{N}}\right) + \frac{1}{N} \sum _{i,j} \left( (\sigma _{ij}^2(\tau ) - \sigma _{ij}^2(\tau _0)) {\hat{\mu }}_{N}^0 + (c-c_0)s_{ij}^2({\hat{\alpha }}_{N}^0) \right) ^2 \\&= o_p^*(1) + \frac{1}{N} \sum _{i,j} \left( (\sigma _{ij}^2(\tau ) - \sigma _{ij}^2(\tau _0)) \mu _0 + (c-c_0)s_{ij}^2(\alpha _0) \right) ^2 \\&= o_p^*(1) + 2Q_{2,N}({\tilde{\tau }}) \left[ (b-b_0)^{\otimes 2}\right] \end{aligned}$$

for some point ${\tilde{\tau }}={\tilde{\tau }}(\tau ,\tau _0)$ lying on the segment joining $\tau$ and $\tau _0$. Thus Assumption 3.1(2) concludes the consistency ${\hat{b}}_N \xrightarrow {p}b_0$: we have $|{\mathbb {Y}}_{2,N}(b) - {\mathbb {Y}}_2(b)| = o_p^*(1)$ with ${\mathbb {Y}}_2(b):=2Q_{2}({\tilde{\tau }}) \left[ (b-b_0)^{\otimes 2}\right]$ satisfying that $\inf _{\tau } \lambda _{\min }(Q_{2}(\tau ))>0$, hence $\mathop {\textrm{argmin}}\limits {\mathbb {Y}}_2=\{b_0\}$.

The tightness $\sqrt{N}({\hat{b}}_N - b_0) = O_p(1)$ can be also deduced as in Sect. 3.1.1: it suffices to note that

$$\begin{aligned} \frac{1}{\sqrt{N}}\partial _b M_{2,N}(b_0)&= \frac{2}{\sqrt{N}} \sum _{i,j} \left( \eta _{ij} + \frac{1}{\sqrt{N}}{\hat{B}}_{ij}\right) \partial _b {\overline{\eta }}_{ij}^2(b_0) \\&= -\frac{2}{\sqrt{N}} \sum _{i,j} \left( \mu _0\,\partial _\tau (\sigma ^2_{ij})(\tau ),\, s_{ij}(\alpha _0) \right) \eta _{ij} + O_p(1) = O_p(1), \end{aligned}$$

and that

$$\begin{aligned} \frac{1}{N}\partial _b^2 M_{2,N}({\tilde{b}}_N) = o_p(1) + 2Q_{2,N}(\tau _0) \end{aligned}$$

for every random sequence $({\tilde{b}}_N)$ such that ${\tilde{b}}_N \xrightarrow {p}b_0$.

3.1.3 Step 3

By the explicit expression (3.8) and the $\sqrt{N}$-consistency of $({\hat{\alpha }}_{N}^0,{\hat{\beta }}_{N}^0,{\hat{\mu }}_{N}^0,{\hat{c}}_N^0)$, we obtain

$$\begin{aligned}&\Bigg ( \frac{1}{N} \sum _{i,j} s_{ij}^6({\hat{\alpha }}_{N}^0)\Bigg ) \sqrt{N}({\hat{\rho }}_{N}^0 - \rho _0) \\&\quad = \frac{1}{\sqrt{N}} \sum _{i,j} s_{ij}^3({\hat{\alpha }}_{N}^0)\left( {\hat{e}}_{ij}^3 - 3 s_{ij}({\hat{\alpha }}_{N}^0) \sigma _{ij}^2({\hat{\tau }}_{N}^0) {\hat{c}}_N^0 - s_{ij}^3({\hat{\alpha }}_{N}^0) \rho _0 \right) \\&\quad {=} O_p(1) {+} \frac{1}{\sqrt{N}} \sum _{i,j} s_{ij}^3({\hat{\alpha }}_{N}^0)\left\{ \left( {\overline{e}}_{ij} {-} \frac{1}{\sqrt{N}}{\hat{H}}_{ij}\right) ^3 {-} 3 s_{ij}(\alpha _0) \sigma _{ij}^2(\tau _0)c_0 {-} s_{ij}^3(\alpha _0) \rho _0 \right\} \\&\quad = O_p(1) + \frac{1}{\sqrt{N}} \sum _{i,j} s_{ij}^3(\alpha _0)\left( {\overline{e}}_{ij}^3 - 3 s_{ij}(\alpha _0) \sigma _{ij}^2(\tau _0)c_0 - s_{ij}^3(\alpha _0) \rho _0 \right) = O_p(1). \end{aligned}$$

Hence $\sqrt{N}({\hat{\rho }}_{N}^0-\rho _0)=O_p(1)$ under Assumption 3.1(3).

We end this section with a few remarks.

Remark 3.2

As an alternative to (3.5), one could also use the profile least-squares estimator (Richards 1961): first, we construct the explicit least-squares estimator of $(\beta ,\mu )$ knowing $\alpha$, and then optimize $\alpha \mapsto M_{1,N}(\alpha ,{\hat{\beta }}_{N}(\alpha ),{\hat{\mu }}_{N}(\alpha ))$ to get an estimator of $\alpha$.

Remark 3.3

If one component of $\theta '=(\lambda ,\delta ,\gamma )$ is known from the very beginning, then it is enough to look at the estimation of $(\mu , c)$ and we can remove Assumption 3.1(3) with modifying Assumption 3.1(4).

Remark 3.4

Because of the asymptotic nature, the same flow of estimation procedures (the MLE, the initial estimator, and the one-step estimator) remain valid even if we replace the trend term $x_{ij}^\top \beta$ in (1.2) by some nonlinear one, say $\mu (x_{ij},\beta )$, with associated identifiability conditions.

Remark 3.5

We can construct a one-step estimator for the MELS model (1.2) in a similar manner to Steps 1 to 3 described in Sect. 3.1. To construct an initial estimator ${\hat{\theta }}_{N}^0=({\hat{\beta }}_{N}^0, {\hat{\alpha }}_{N}^0, {\hat{\tau }}_{N}^0, {\hat{\sigma }}^{2,0}_w, {\hat{\rho }}_{N}^0)$, we use the identities $E_\theta [Y_{ij}]=x_{ij}^{\top }\beta$, $\textrm{Var}_\theta [Y_{ij}]=\exp (w^{\top }_{ij}\tau +\sigma _w^2/2) + \exp (z^{\top }_i\alpha )$, and $E_\theta [(Y_{ij} - E_\theta [Y_{ij}])^3]=3\sigma _w \exp (z_{ij}^{\top }\alpha /2 + \sigma _w^2/2)\rho$. Then, we can obtain ${\hat{\beta }}_{N}^0$ in Step 1, $({\hat{\alpha }}_{N}^0,{\hat{\tau }}_{N}^0, {\hat{\sigma }}^{2,0}_{w,N})$ in Step 2, and then ${\hat{\rho }}_{N}^0$ in Step 3 in this order through the contrast functions to be minimized: denoting ${\hat{e}}'_{ij}:= Y_{ij}-x_{ij}^{\top }{\hat{\beta }}_{N}^0$, we have

$$\begin{aligned} \beta&\mapsto \sum _{i,j}\left( Y_{ij} - x_{ij}^{\top }\beta \right) ^2, \\ (\alpha ,\tau ,\sigma _w^2)&\mapsto \sum _{i,j}\left( {\hat{e}}_{ij}^{\prime \,2} - \exp (w^{\top }_{ij}\tau +\sigma _w^2/2) - \exp (z^{\top }_i\alpha ) \right) ^2, \\ \rho&\mapsto \sum _{i,j}\left( {\hat{e}}_{ij}^{\prime \, 3} - 3 \sqrt{{\hat{\sigma }}_{w,N}^{2,0}} \, \exp (z_{ij}^{\top }{\hat{\alpha }}_{N}^0 /2 + {\hat{\sigma }}_{w,N}^{2,0} /2)\rho \right) ^2. \end{aligned}$$

As in the case of (3.8), ${\hat{\rho }}_{N}^0$ is explicitly given while the meaning of the parameter $\rho$ is different in the present context. It is also possible to develop an asymptotic theory for the MLE of the MELS and the related one-step estimator in similar ways to the present study. However, the one-step estimator toward the log-likelihood function (1.3) still necessitates the numerical integration over ${\mathbb {R}}^2$ with respect to the two-dimensional standard normal random variables; the numerical integration would need to be performed for every $i=1,\dots ,N$ and $j=1,\dots , n_i$, hence the computational load would still be significant.

3.2 Numerical experiments

Let us observe the finite-sample performance of the initial estimator ${\hat{\theta }}_{N}^0$, the one-step estimator ${\hat{\theta }}_{N}^1$, and the MLE ${\hat{\theta }}_{N}$. The setting is as follows:

$$\begin{aligned} Y_{ij}=x_{ij}^{\top }\beta +\tanh ( z_{ij}^{\top }\alpha )v_i+\sqrt{v_i\exp (w_{ij}^{\top }\tau )}\,\epsilon _{ij}, \end{aligned}$$

(3.10)

where

• $N=1000$,    $n_1=n_2=\cdots =n_{N}=10$.

• $x_{ij},~z_{ij},~w_{ij} \in {\mathbb {R}}^2 \sim \text {i.i.d.}~N_2(0,I_2)$.

• $v_1,v_2,\ldots \sim \text {i.i.d.}~IG(\delta ,\gamma )=GIG(-1/2,\delta ,\gamma )$, the inverse-Gaussian random-effect distribution.

• $\epsilon _{i}=(\epsilon _{i1},\ldots ,\epsilon _{in_i}) \sim \text {i.i.d.}~N(0,I_{n_i})$, independent of $\{v_i\}$.

• $\theta =(\beta ,\alpha ,\tau ,\delta ,\gamma ) = (\beta _0,\beta _1,\alpha _0,\alpha _1,\tau _0,\tau _1,\delta ,\gamma ) \in {\mathbb {R}}^8$.

• True values are $\beta =(3,5),~\alpha =(-4,5)$, $\tau =(0.05, 0.07),~\delta =1.5,~\gamma =0.7$.

In this case $\theta '=(\delta ,\gamma )\in (0,\infty )^2$ and we need only $({\hat{\mu }}_{N}^0,{\hat{c}}_N^0)$: we have $\mu =E_{\theta '}[v_i]=\delta /\gamma$ and $c=\textrm{Var}_{\theta '}[v_i]=\delta /\gamma ^3$, namely

$$\begin{aligned} \gamma =\sqrt{\frac{\mu }{c}},\qquad \delta =\mu \gamma =\sqrt{\frac{\mu ^3}{c}}. \end{aligned}$$

As initial values for numerical optimization, we set the following two different cases:

• (i’) The true value;

• (ii’) $(1.0\times 10^{-8},\ldots ,~1.0\times 10^{-8},~1.0\times 10^{-4},~1.0\times 10^{-3})$.

In each case, we computed $\sqrt{N}({\hat{\xi }}_N-\theta _0)$ for ${\hat{\xi }}_N = {\hat{\theta }}_{N}^0$, ${\hat{\theta }}_{N}^1$, and ${\hat{\theta }}_{N}$, all being conducted 1000-times Monte Carlo trials. To estimate $95\%$-coverage probabilities empirically as in Sect. 2.3, we computed the quantities $-\partial _\theta ^2\ell _N({\hat{\theta }}_{N})$ and $-\partial _\theta ^2\ell _N({\hat{\theta }}_{N}^1)$ through the function $\theta \mapsto -\partial _\theta ^2\ell _N(\theta )$ for the approximately $95\%$-confidence intervals for each parameter. The results are shown in Table 4; therein, we obtained numerically unstable 4 MLEs and 5 one-step estimators for case (i’) and 299 MLEs and 6 one-step estimators for case (ii’), and then computed the coverage probabilities based on the remaining cases. In Figs. 4 and 5 (for cases (i’) and (ii’), respectively), we drew histograms of ${\hat{\theta }}_{N}^1$ and ${\hat{\theta }}_{N}$ together with those of the initial estimator ${\hat{\theta }}_{N}^0$ for comparison. In each figure, the histograms in the first and fourth columns are those for ${\hat{\theta }}_{N}^0$, those in the second and fifth columns for ${\hat{\theta }}_{N}^1$, and those in the third and sixth columns for ${\hat{\theta }}_{N}$, respectively; the red solid line shows the zero-mean normal densities with the consistently estimated Fisher information for the variances.

Table 4 The empirical $95\%$-coverage probabilities of the MLE and the one-step estimators in cases (i’) and (ii’) based on 1000 trials; MLE of $(\delta ,\gamma )$ in case (ii’) showed instability in numerical optimizations, while the one-step estimator is stable as in case (i’)

Fig. 4

Case (i’): Histograms of the initial estimator ${\hat{\theta }}_{N}^0$ (first and fourth columns), the one-step estimator ${\hat{\theta }}_{N}^1$ (second and fifth columns), and the MLE ${\hat{\theta }}_{N}$ (third and sixth columns). In each histogram panel, the solid red line shows the estimated asymptotically best possible normal distribution

Fig. 5

Case (ii’): Histograms of the initial estimator ${\hat{\theta }}_{N}^0$ (first and fourth columns), the one-step estimator ${\hat{\theta }}_{N}^1$ (second and fifth columns), and the MLE ${\hat{\theta }}_{N}$ (third and sixth columns). In each histogram panel, the solid red line shows the estimated asymptotically best possible normal distribution

Here is a summary of the important findings.

• Approximate computation times for obtaining one set of estimates are as follows:

• (i’) 0.2 s for ${\hat{\theta }}_{N}^0$; 10 s for ${\hat{\theta }}_{N}^1$; 2 min for ${\hat{\theta }}_{N}$;

• (ii’) 0.2 s for ${\hat{\theta }}_{N}^0$; 10 s for ${\hat{\theta }}_{N}^1$; 9 min for ${\hat{\theta }}_{N}$.

A considerable amount of reduction can be seen for ${\hat{\theta }}_{N}^1$ compared with ${\hat{\theta }}_{N}$.

• About Figs. 4 and 5:

• In both cases (i’) and (ii’), the inferior performance of ${\hat{\theta }}_{N}^0$ is drastically improved by ${\hat{\theta }}_{N}^1$, which in turn shows asymptotically equivalent behaviors to the MLE ${\hat{\theta }}_{N}$.

• On one hand, as in Sect. 2.3, the MLE ${\hat{\theta }}_{N}$ is much affected by the initial value for the numerical optimization, partly because of the non-convexity of the likelihood function $\ell _N(\theta )$; in Case (ii’), we observed the instability in computing the MLE of $(\delta ,\gamma )$ (in the bottom panels in Fig. 5), showing the local maxima problem. On the other hand, we did not observe the local maxima problem in computing ${\hat{\theta }}_{N}^0$ and the one-step estimator ${\hat{\theta }}_{N}^1$ does not require an initial value for numerical optimization.

In sum, ${\hat{\theta }}_{N}^1$ is asymptotically equivalent to the efficient MLE and much more robust in numerical optimization than the MLE. It is recommended to use the one-step estimator ${\hat{\theta }}_{N}^1$ against the MLE ${\hat{\theta }}_{N}$ from both theoretical and computational points of view.

We end this section with applications of the proposed one-step estimator ${\hat{\theta }}_{N}^1$ for (3.10) to the two real data sets riesby_example.dat and posmood_example.dat borrowed from the supplemental material of Hedeker and Nordgren (2013). Here are brief descriptions.

• riesby_example.dat contains the Hamiltonian depression rating scale as $Y_{ij}$. The covariates are given by $x_{ij}=(\texttt {intercept},\texttt {week},\texttt {edog})\in {\mathbb {R}}\times \{0,1,2,\dots ,5\}\times \{0,1\}$, $z_{ij}=(\texttt {intercept},\texttt {edog})$, and $w_{ij}=(\texttt {intercept},\texttt {week})$. Here, $N=66$ and the numbers of sampling times are 6 with a few missing slots, and edog denotes the dummy variable for indicating whether the depression of the patient is endogenous ($=1$) or not ($=0$).

• posmood_example.dat contains the individual mood items as $Y_{ij}$; the items are pre-processed using factor analysis and take values 1 to 10 with higher ones indicating a higher level of positive mood. The covariates are given by $x_{ij}=(\texttt {intercept},\texttt {alone},\texttt {genderf})\in {\mathbb {R}}\times \{0,1\}\times \{0,1\}$, $z_{ij}=(\texttt {intercept},\texttt {alone})$, and $w_{ij}=(\texttt {intercept},\texttt {alone})$. Here, $N=515$ with no missing value, with approximately 34 sampling times on average (ranging from 3 to 58). The variable alone and genderf respectively denote the dummy variables for indicating whether the person is alone ($=0$) or not ($=1$), which is time-varying, and whether the person is male ($=0$) or female ($=1$).

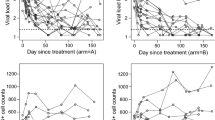
Figures 6 and 7 show some data plots and histograms, respectively; the former is positively skewed while the latter is negatively skewed. We could apply our one-step estimation methods for these data sets, although they can be seen as categorical data (with a moderately large number of categories). The results are given in Table 5; the parameters $\beta _0$, $\alpha _0$, and $\tau _0$ denote the intercept. The skewness mentioned above is reflected in the estimates of $\alpha _0$ and $\alpha _1$.

Fig. 6

Data plots of riesby_example.dat (left) and posmood_example.dat (right) borrowed from the supplemental material of Hedeker and Nordgren (2013); the former shows data of 10 patients over 6 time points with a few missing values, and the latter does those of 3 people over 26 time points with no missing value

Fig. 7

Histograms of data $(Y_{i1})_{i\le N},\dots ,(Y_{i6})_{i\le N}$ for riesby_example.dat (left) and posmood_example.dat (right) borrowed from the supplemental material of Hedeker and Nordgren (2013)

Table 5 One-step estimates for the two data sets riesby_example.dat and posmood_example.dat. It took 0.9 and 6.7 s, respectively

4 Concluding remarks

We proposed a class of mixed-effects models with non-Gaussian marginal distributions which can incorporate random effects into the skewness and the scale simply and transparently through the normal variance-mean mixture. The associated log-likelihood function is explicit and the MLE is asymptotically efficient (Remark 2.4) while computationally demanding and unstable. To bypass the numerical issue, we proposed the easy-to-use one-step estimator ${\hat{\theta }}_{N}^1$, which turned out to not only attain a significant reduction of computation time compared with the MLE but also guarantee the asymptotic efficiency property.

Here are some remarks on important related issues.

• (1) Inter-individual dependence structure. A drawback of the model (2.1) is that its inter-individual dependence structure is not flexible enough. Specifically, let us again note the following covariance structure for $j,k\le n_i$:

  $$\begin{aligned} \textrm{Cov}_{\theta }[Y_{ij}, Y_{ik}] = s_{ij}(\alpha ) s_{ik}(\alpha ) \textrm{Var}_{\theta }[v_i] = c(\theta ') s_{ij}(\alpha ) s_{ik}(\alpha ). \end{aligned}$$

  This in particular implies that $Y_{i1},\dots ,Y_{i n_i}$ cannot be correlated as long as $s(z,\alpha )\equiv 0$. Nevertheless, it is formally straightforward to extend the model (2.1) so that the distributional structure of $Y_i \in {\mathbb {R}}^{n_i}$ obeys the multivariate GH distribution for each ${\mathcal {L}}(Y_i)$ with a non-diagonal scale matrix. To mention it briefly, suppose that the vector of a sample $Y_i=(Y_{i1},\dots ,Y_{i n_i})\in {\mathbb {R}}^{n_i}$ from ith individual is given by the form

  $$\begin{aligned} Y_i = x_i\beta + s(z_i,\alpha )v_i + \Lambda (w_i,\tau )^{1/2} \sqrt{v_i}\,\epsilon _{i}. \end{aligned}$$

  Here, $v_1,\ldots ,~v_N\sim \text {i.i.d.}~GIG(\lambda ,\delta ,\gamma )$ as before, while we now incorporated the scale matrix $\Lambda (w_i,\tau )$ which should be positive definite and symmetric, but may be non-diagonal. Then, the dependence structure of $Y_{i1},\dots ,Y_{i n_i}$ can be much more flexible than (2.1).

• (2) Forecasting random-effect parameters. In the familiar Gaussian linear mixed-effects model of the form $Y_i=X_i\beta +Z_i b_i + \epsilon _i$, the empirical Bayes predictor of $v_i$ is given by ${\hat{b}}_i:= E_\theta [b_i|Y_i]|_{\theta ={\hat{\theta }}_{N}}$. One of the analytical merits of our NVMM framework is that the conditional distribution ${\mathcal {L}}(v_i|Y_i=y_i)$ of $v_i$ is given by $GIG(\nu _i,\eta _i,\psi _i)$, where

  $$\begin{aligned} \nu _i = \nu _i(\theta )&:= \lambda -\frac{n_i}{2}, \\ \eta _i = \eta _i(\theta )&:= \sqrt{\delta ^2+(y_i - x_i\beta )^{\top }\Lambda (w_,\tau )^{-1}(y_i-x_i\beta )}, \\ \psi _i = \psi _i(\theta )&:= \sqrt{\gamma ^2 + s_i(\alpha )^\top \Lambda (w_i,\tau )^{-1}s_i(\alpha )}. \end{aligned}$$

  This is a direct consequence of the general results about the multivariate GH distribution; see Eberlein and Hammerstein (2004) and the references therein for details. As in the Gaussian case mentioned above, we can make use of

  $$\begin{aligned} {\hat{v}}_i:= E_\theta [v_i|Y_i=y_i]|_{\theta ={\hat{\theta }}_{N}} =\frac{K_{{\hat{\nu }}_i+1}({\hat{\eta }}_i{\hat{\psi }}_i)}{K_{{\hat{\nu }}_i}({\hat{\eta }}_i{\hat{\psi }}_i)} \frac{{\hat{\eta }}_i}{{\hat{\psi }}_i}, \end{aligned}$$

  where ${\hat{\nu }}_i:= \nu _i({\hat{\theta }}_{N})$, ${\hat{\eta }}_i:= \eta _i({\hat{\theta }}_{N})$, and ${\hat{\psi }}_i:= \psi _i({\hat{\theta }}_{N})$; formally ${\hat{\theta }}_{N}$ could be replaced by the one-step estimator ${\hat{\theta }}_{N}^1$. Then, it would be natural to regard

  $$\begin{aligned} {\hat{Y}}_{ij}:= x_{ij}'{\hat{\beta }}_{N}+ s(z_{ij}',{\hat{\alpha }}_{N}) {\hat{v}}_i \end{aligned}$$

  as a prediction value of $Y_{ij}$ at $(x_{ij}',z_{ij}')$. This includes forecasting the value of ith individual at a future time point.

• (3) Lack of fit and model selection. In relation to Remark 2.6, based on the obtained asymptotic-normality results, we can proceed with lack-of-fit tests, such as the likelihood-ratio test, the score test, and the Wald test; typical forms are $s(z,\alpha )=\sum _{l=1}^{p_\alpha }\alpha _l s_l(z)$ and $\sigma (w,\tau )=\exp \{\sum _{m=1}^{p_\tau }\tau _m \sigma _m(w)\}$, with given basis functions $s_l(z)$ and $\sigma _m(w)$. In that case, we can estimate p-value for each component of $\theta$, say, by $2\Phi (-|{\hat{B}}_{k,N} {\hat{\theta }}_{k,N}|)$ for $\theta _k$ where ${\hat{B}}_{k,N}:=[(-\partial _{\theta }^2\ell _N({\hat{\theta }}_{N}))^{-1}]_{kk}^{-1/2}$. Alternatively, one may consider information criteria such as the conditional AIC (Vaida and Blanchard 2005) and the BIC-type one (Delattre et al. 2014). To develop these devices in rigorous ways, we will need to derive several further analytical results: the uniform integrability of $(\Vert \sqrt{N}({\hat{\theta }}_{N}-\theta _{0})\Vert ^2)_n$ for the AIC, the stochastic expansion for the marginal likelihood function for the BIC, and so on.

Appendices

Appendix A: GIG and GH distributions

Let $K_\lambda (t)$ denote the modified Bessel function of the second kind ($\nu \in {\mathbb {R}}$, $t>0$):

$$\begin{aligned} K_{\nu }(t)=\frac{1}{2}\int _0^{\infty }s^{\nu -1}\exp \left\{ -\frac{t}{2}\left( s+\frac{1}{s}\right) \right\} ds. \end{aligned}$$

We have the following recurrence formulae (Abramowitz and Stegun 1992): $K_{\nu +1}(t)=\frac{2\nu }{t}K_{\nu }(t)+K_{\nu -1}(t)$ and $K_{\nu -1}(t)+K_{\nu +1}(t)=-2\partial _t K_{\nu }(t)$. It follows that $K_{\nu }(t)$ is monotonically decreasing and that $\partial _t K_{\nu }(t)=-K_{\nu -1}(t)-\frac{\nu }{t}K_{\nu }(t)$. Further, we have

$$\begin{aligned} \partial _t \log K_{\nu }(t)&= - \frac{K_{\nu -1}(t)}{K_{\nu }(t)} -\frac{\nu }{t} =: -R_\nu (t) -\frac{\nu }{t}, \end{aligned}$$

(A.1)

$$\begin{aligned} \partial ^2_t \log K_{\nu }(t)&= - \frac{1}{K^2_{\nu }(t)}\left( K^2_{\nu -1}(t)-K_{\nu -2}(t)K_{\nu }(t)\right) -\frac{1}{t}\frac{K_{\nu -1}(t)}{K_{\nu }(t)}+\frac{\nu }{t^2} \nonumber \\&=: -S_\nu (t) - \frac{1}{t}R_\nu (t) + \frac{\nu }{t^2}. \end{aligned}$$

(A.2)

The following asymptotic behavior holds:

$$\begin{aligned} K_{\nu }(t)=\sqrt{\frac{\pi }{2t}}\exp (-t)\{1+(4\nu ^2-1)O(t^{-1})\},\qquad t\rightarrow \infty . \end{aligned}$$

The generalized inverse Gaussian (GIG) distribution $GIG(\lambda ,\delta ,\gamma )$ on ${\mathbb {R}}_{+}$ is defined by the density:

$$\begin{aligned} p_{GIG}(z;\lambda ,\delta ,\gamma )=\frac{(\gamma /\delta )^{\lambda }}{2K_{\lambda }(\gamma \delta )} z^{\lambda -1} \exp \left\{ -\frac{1}{2}\left( \frac{\delta ^{2}}{z}+\gamma ^{2}z\right) \right\} ,\qquad z>0. \end{aligned}$$

The region of admissible parameters is given by the union of $\{(\lambda ,\delta ,\gamma ):\,\lambda>0,\,\delta \ge 0,\, \gamma >0\}$, $\{(\lambda ,\delta ,\gamma ):\,\lambda =0,\,\delta> 0,\, \gamma >0\}$, and $\{(\lambda ,\delta ,\gamma ):\,\lambda <0,\,\delta>0,\, \gamma >0\}$, according to the integrability of $p_{GIG}$ at the origin and $+\infty$.

The generalized hyperbolic (GH) distribution denoted by $GH(\lambda ,\alpha ,\beta ,\delta ,\mu )$ is defined as the distribution of the normal variance-mean mixture Y with respect to $Z \sim GIG(\lambda ,\delta ,\gamma )$:

$$\begin{aligned} Y=\mu +\beta Z+\sqrt{Z}\eta , \end{aligned}$$

where $\alpha :=\sqrt{\beta ^2+\gamma ^2}$ and $\eta \sim N(0,1)$ independent of Z. By the conditional Gaussianity ${\mathcal {L}}(Y|Z=z)=N(\mu +\beta z, z)$, the density is calculated as follows:

$$\begin{aligned}&p_{GH}(y;\lambda ,\alpha ,\beta ,\delta ,\mu ) \\&\quad = \int _{0}^{\infty } \frac{1}{\sqrt{2\pi z}} \exp \left( -\frac{1}{2z}(y-\mu -\beta z)^2\right) p_{GIG}(z;\lambda ,\delta ,\gamma )dz\\&\quad =\frac{\left( \alpha ^2-\beta ^2\right) ^{\lambda /2}\sqrt{\delta ^2+(y-\mu )^2}^{\lambda -1/2}}{\sqrt{2\pi }\alpha ^{\lambda -1/2}\delta ^\lambda K_\lambda \left( \delta \sqrt{\alpha ^2-\beta ^2}\right) }K_{\lambda -\frac{1}{2}}\left( \alpha \sqrt{\delta ^2+(y-\mu )^2}\right) \exp [\beta (y-\mu )]. \end{aligned}$$

The region of admissible parameters is given by the union of $\{(\lambda ,\alpha ,\beta ,\delta ,\mu ):\,\lambda>0,\,\delta \ge 0,\, \alpha >|\beta |\}$, $\{(\lambda ,\alpha ,\beta ,\delta ,\mu ):\,\lambda =0,\,\delta> 0,\, \alpha >|\beta |\}$, and $\{(\lambda ,\alpha ,\beta ,\delta ,\mu ):\,\lambda <0,\,\delta >0,\, \alpha \ge |\beta |\}$. The mean and variance of $Y\sim GH(\lambda ,\alpha ,\beta ,\delta ,\mu )$ are given by

$$\begin{aligned} E[Y]&= \mu +\frac{\delta \beta K_{\lambda +1}(\delta \gamma )}{\gamma K_\lambda (\delta \gamma )}, \\ \textrm{Var}[Y]&= \frac{\delta K_{\lambda +1}(\delta \gamma )}{\gamma K_\lambda (\delta \gamma )}+\frac{\beta ^2\delta ^2}{\gamma ^2}\left[ \frac{ K_{\lambda +2}(\delta \gamma )}{ K_\lambda (\delta \gamma )} -\left( \frac{ K_{\lambda +1}(\delta \gamma )}{K_\lambda (\delta \gamma )}\right) ^2 \right] . \end{aligned}$$

See Eberlein and Hammerstein (2004) for further details of the GIG and GH distributions.

The normal inverse Gaussian (NIG) distribution is one of the popular subclasses of the GH-distribution family: $NIG(\alpha ,\beta ,\delta ,\mu ):=GH(-1/2,\alpha ,\beta ,\delta ,\mu )$, where $GIG(-1/2,\delta ,\gamma )$ corresponds to the inverse Gaussian distribution. The $NIG(\alpha ,\beta ,\delta ,\mu )$-density is given by

$$\begin{aligned} p_{NIG}(x;\alpha ,\beta ,\delta ,\mu )=\frac{\alpha \delta }{\pi }\exp \left( \delta \sqrt{\alpha ^2-\beta ^2}+\beta (x-\mu )\right) \frac{K_1\left( \alpha \sqrt{\delta ^2+(x-\mu )^2}\right) }{\sqrt{\delta ^2+(x-\mu )^2}}. \end{aligned}$$

All of the mean M, variance V, skewness S, and kurtosis K of $NIG(\alpha ,\beta ,\delta ,\mu )$ are explicitly given:

$$\begin{aligned}{} & {} M=\mu +\frac{\beta \delta }{(\alpha ^2-\beta ^2)^{\frac{1}{2}}}, \quad V=\frac{\delta \alpha ^2}{(\alpha ^2-\beta ^2)^{\frac{3}{2}}}, \quad S=\frac{3\beta }{\alpha \sqrt{\delta }(\alpha ^2-\beta ^2)^{\frac{1}{4}}}, \quad \\{} & {} K=\frac{3\alpha ^2+4\beta ^2}{\alpha ^2\delta (\alpha ^2-\beta ^2)^{\frac{1}{2}}}. \end{aligned}$$

Inverting these expressions gives

$$\begin{aligned}{} & {} \gamma =\frac{3}{\sqrt{V}\sqrt{3K-5S^2}}, \quad \beta =\frac{S\sqrt{V}\gamma ^2}{3}, \quad \alpha =\sqrt{\gamma ^2+\beta ^2}, \quad \delta =\frac{V\gamma ^3}{\gamma ^2+\beta ^2}, \quad \\{} & {} \mu =M-\frac{\beta \delta }{\gamma }, \end{aligned}$$

from which one can consider the method-of-moments estimation of $(\alpha ,\beta ,\delta ,\mu )$ based on the empirical counterparts of M, V, S, and K. One should note that the empirical quantity $3{\hat{K}}_n-5{\hat{S}}_n^2$ has to be positive, which may fail in a finite sample and for such a data set the MLE would be also non-computable or unstable. In Yoon et al. (2020), the estimation problem for the i.i.d. NIG model was studied from the computational point of view; the paper also introduced the change of variables for the parameters to sidestep the positivity restriction, resulting in stabilized results in numerical experiments.

Appendix B: Likelihood function

1.1 Derivation

Writing $\theta _1=(\beta ,\alpha ,\tau )$ and $\theta _2=(\lambda ,\delta ,\gamma )$, and using the obvious notation, we obtain

$$\begin{aligned} \ell _n(\theta )&=\log p_{\theta }(Y_1,\ldots ,Y_n)\\&=\log \int \cdots \int p_{\theta _1}(Y_1,Y_2,\ldots ,Y_n|v_1,\ldots ,v_n)\prod _{i=1}^N p_{\theta _2} (v_i)dv_i\\&=\log \left( \int \dots \int \prod _{i=1}^N p_{\theta _1} (Y_i|v_i)\prod _{i=1}^N p_{\theta _2} (v_i)dv_i\right) \\&=\sum _{i=1}^N \log \left[ \int \Bigg (\prod _{j=1}^{n_i} p_{\theta _1} (Y_{ij}|v_i)\Bigg )p_{\theta _2} (v_i)dv_i\right] \\&= \sum _{i=1}^N \log \left[ \int \left( \prod _{j=1}^{n_i} \frac{1}{\sqrt{2\pi \sigma ^2_{ij}(\tau )}}v_i^{-\frac{1}{2}}\exp \left[ -\frac{1}{2\sigma ^2_{ij}(\tau )}(Y_{ij}-x^{\top }_{ij}\beta - s_{ij}(\alpha )v_i)^2\right] \right) p_{\theta _2}(v_i) dv_i\right] \\&= \sum _{i=1}^N \log \Biggl [ (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-\frac{1}{2}}\int _0^{\infty } v_i^{-\frac{n_i}{2}}\\&\quad \times \prod _{j=1}^{n_i}\exp \left[ -\frac{1}{2v_i\sigma ^2_{ij}(\tau )}\left\{ (Y_{ij}-x^{\top }_{ij}\beta )^2+s^2_{ij}(\alpha )v^2_i-2 s_{ij}(\alpha )v_i(Y_{ij}-x^{\top }_{ij}\beta )\right\} \right] p_{\theta _2}(v_i) dv_i\Biggr ]\\&= \sum _{i=1}^N \log \Biggl [ (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-\frac{1}{2}}\int _0^{\infty } v_i^{-\frac{n_i}{2}}\\&\quad \times \prod _{j=1}^{n_i}\exp \left[ -\frac{1}{2v_i\sigma ^2_{ij}(\tau )}\left\{ (Y_{ij}-x^{\top }_{ij}\beta )^2+s^2_{ij}(\alpha )v^2_i\right\} + \frac{ s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij}-x^{\top }_{ij}\beta )\right] p_{\theta _2}(v_i) dv_i\Biggr ]\\&= \sum _{i=1}^N \log \Biggl [ (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-\frac{1}{2}}\prod _{j=1}^{n_i}\exp \left( \frac{ s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij}-x^{\top }_{ij}\beta )\right) \\&\quad \times \int _0^{\infty } v_i^{-\frac{n_i}{2}}\prod _{j=1}^{n_i}\exp \left\{ -\frac{1}{2\sigma ^2_{ij}(\tau )}\left( \frac{(Y_{ij}-x^{\top }_{ij}\beta )^2}{v_i}+s^2_{ij}(\alpha )v_i\right) \right\} p_{\theta _2}(v_i) dv_i\Biggr ]\\&= \sum _{i=1}^N \log \Biggl [ (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-\frac{1}{2}}\exp \left( \sum _{j=1}^{n_i}\frac{ s_{ij}(\alpha )(Y_{ij}-x^{\top }_{ij}\beta )}{\sigma ^2_{ij}(\tau )}\right) \\&\quad \times \int _0^{\infty } v_i^{-\frac{n_i}{2}} \exp \left\{ -\frac{1}{2}\left( \sum _{j=1}^{n_i}\frac{(Y_{ij}-x^{\top }_{ij}\beta )^2}{v_i\sigma ^2_{ij}(\tau )}+\sum _{j=1}^{n_i}\frac{s^2_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}v_i\right) \right\} p_{\theta _2}(v_i) dv_i\Biggr ]\\&= \sum _{i=1}^N \log \Bigg [ C_i(\alpha ,\beta ,\tau ) \int _0^{\infty } v_i^{-\frac{n_i}{2}}\exp \Bigg \{-\frac{1}{2}\Bigg (\sum _{j=1}^{n_i}\frac{(Y_{ij}-x^{\top }_{ij}\beta )^2}{v_i\sigma ^2_{ij}(\tau )}+\sum _{j=1}^{n_i}\frac{s^2_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}v_i \Bigg )\Bigg \} \\&\quad \times \frac{( \frac{\gamma }{\delta })^{\lambda }}{2K_\lambda (\delta \gamma )} v_i^{\lambda -1}\exp \left\{ -\frac{1}{2}\left( \frac{\delta ^2}{v_i}+\gamma ^2v_i \right) \right\} dv_i\Bigg ] \\&= \sum _{i=1}^N \log \Bigg [ C_i(\alpha ,\beta ,\tau ) \frac{( \gamma /\delta )^{\lambda }}{2K_\lambda (\delta \gamma )} \int _0^{\infty } \exp \Bigg [-\frac{1}{2}\Bigg \{\frac{1}{v_i}\Bigg (\sum _{j=1}^{n_i}\frac{(Y_{ij}-x^{\top }_{ij}\beta )^2}{\sigma ^2_{ij}(\tau )}+\delta ^2\Bigg ) \\&\quad +\Bigg (\sum _{j=1}^{n_i}\frac{s^2_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}+\gamma ^2\Bigg )v_i\Bigg \}\Bigg ] v_i^{\lambda -1-\frac{n_i}{2}}dv_i\Bigg ], \end{aligned}$$

where

$$\begin{aligned} C_i(\alpha ,\beta ,\tau ):= (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-\frac{1}{2}}\exp \Bigg ( \sum _{j=1}^{n_i}\frac{ s_{ij}(\alpha )(Y_{ij}-x^{\top }_{ij}\beta )}{\sigma ^2_{ij}(\tau )}\Bigg ). \end{aligned}$$

Making the change of variables $S_i^2 v_i/T_i = u_i$ with

$$\begin{aligned} S_i=S_i(\alpha ,\tau ,\gamma )&:= \sqrt{\gamma ^2 + \sum _{j=1}^{n_i}\frac{s^2_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}},\\ T_i=T_i(\beta ,\alpha ,\tau ,\delta ,\gamma )&:= S_i \, \sqrt{\delta ^2 + \sum _{j=1}^{n_i}\frac{1}{\sigma ^2_{ij}(\tau )} (Y_{ij}-x^{\top }_{ij}\beta )^2}, \end{aligned}$$

we can continue as

$$\begin{aligned} \ell _n(\theta )&= \sum _{i=1}^N \log \left[ C_i(\alpha ,\beta ,\tau ) \frac{( \frac{\gamma }{\delta })^{\lambda }}{2K_\lambda (\delta \gamma )} \int _0^{\infty } \exp \left\{ \right. \right. \\&\quad \left. \left. -\frac{1}{2}\left( \frac{S_i^2}{T_i u_i}\frac{T_i^2}{S_i^2}+\frac{T_i}{S_i^2}u_i S_i^2\right) \right\} \frac{T_i^{\lambda -1-\frac{n_i}{2}}}{S_i^{2\left( \lambda -1-\frac{n_i}{2}\right) }}u_i^{\lambda -1-\frac{n_i}{2}}\frac{T_i}{S_i^2}du_i\right] \\&= \sum _{i=1}^N \log \left[ C_i(\alpha ,\beta ,\tau ) \frac{( \frac{\gamma }{\delta })^{\lambda }}{2K_\lambda (\delta \gamma )} \int _0^{\infty } \exp \left\{ -\frac{T_i}{2}\left( \frac{1}{u_i}+u_i\right) \right\} \right. \\&\left. \frac{T_i^{\lambda -\frac{n_i}{2}}}{S_i^{2\left( \lambda -\frac{n_i}{2}\right) }}u_i^{\lambda -1-\frac{n_i}{2}}du_{i}\right] \\&= \sum _{i=1}^N \log \Biggl [ (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-1/2}\frac{(\gamma /\delta )^{\lambda }}{K_\lambda (\delta \gamma )}\exp \Bigg ( \sum _{j=1}^{n_i}\frac{ s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij}-x^{\top }_{ij}\beta ) \Bigg ) \\&\quad \times \frac{T_i^{\lambda -\frac{n_i}{2}}}{S_i^{2(\lambda -\frac{n_i}{2})}}\frac{1}{2} \int _0^{\infty } \exp \left\{ -\frac{T_i}{2}\left( \frac{1}{u_i}+u_i\right) \right\} u_i^{\lambda -1-\frac{n_i}{2}}du_{i}\Biggr ] \\&= \sum _{i=1}^N \log \Biggl [ (2\pi )^{-\frac{n_i}{2}}\Bigg (\prod _{j=1}^{n_i} \sigma ^2_{ij}(\tau )\Bigg )^{-1/2}\frac{(\gamma /\delta )^{\lambda }}{K_\lambda (\delta \gamma )}\exp \Bigg ( \sum _{j=1}^{n_i}\frac{ s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij} \\&\quad -x^{\top }_{ij}\beta )\Bigg ) \left( \frac{T_i}{S_i^2}\right) ^{\lambda -\frac{n_i}{2}} K_{\lambda -\frac{n_i}{2}}(T_i)\Biggr ]. \end{aligned}$$

This leads to the expression (2.3).

1.2 Partial derivatives

Recall the notation: $\ell _N(\theta )=\sum _{i=1}^{N}\zeta _i(\theta )$, $A_i=A_i(\alpha ,\tau ,\gamma )$ of (2.4), and $B_i=B_i(\beta ,\tau ,\delta )$ of (2.5). Let

$$\begin{aligned} T_i' = T_i'(\theta ):= R_{\lambda -\frac{n_i}{2}}(A_i B_i) + \frac{\lambda -\frac{n_i}{2}}{A_i B_i} \end{aligned}$$

for $R_\nu (t)$ defined by (A.1). Then, we have the following expressions for the components of $\partial _\theta \ell _N(\theta )$:

$$\begin{aligned} {\partial _\beta } \zeta _i(\theta )&= -\sum _{j=1}^{n_i}\frac{s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}x_{ij} +\left( \lambda -\frac{n_i}{2}\right) \frac{1}{B_i}\partial _{\beta }B_i-T_i' A_i\partial _{\beta }B_i \\&= -\sum _{j=1}^{n_i}\frac{s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}x_{ij} - \frac{1}{B_i} \left\{ \frac{1}{B_i}\left( \lambda -\frac{n_i}{2}\right) + T'_i A_i \right\} \sum _{j=1}^{n_i}\frac{(Y_{ij}-x_{ij}^{\top }\beta )}{\sigma ^2_{ij}(\tau )}x_{ij}, \\ {\partial _\alpha } \zeta _i(\theta )&= \sum _{j=1}^{n_i}\frac{\partial _\alpha s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij}-x_{ij}^{\top }\beta )-\left( \lambda -\frac{n_i}{2}\right) \frac{1}{A_i}\partial _\alpha A_i - T_i' B_i\partial _\alpha A_i \\&=\sum _{j=1}^{n_i}\frac{\partial _\alpha s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}(Y_{ij}-x_{ij}^{\top }\beta ) - \frac{1}{A_i} \left\{ \frac{1}{A_i}\left( \lambda -\frac{n_i}{2}\right) + T'_i B_i \right\} \sum _{j=1}^{n_i}\frac{s_{ij}(\alpha )}{\sigma ^2_{ij}(\tau )}\partial _\alpha s_{ij}(\alpha ), \\ {\partial _\tau }\zeta _i(\theta )&= -\frac{1}{2}\sum _{j=1}^{n_i}\frac{\partial _\tau (\sigma ^2_{ij}(\tau ))}{\sigma ^2_{ij}(\tau )} -\sum _{j=1}^{n_i}\frac{s_{ij}(\alpha )}{(\sigma ^2_{ij}(\tau ))^2}(Y_{ij}-x_{ij}^{\top }\beta )\partial _\tau (\sigma ^2_{ij}(\tau )) \\&\quad +\left( \lambda -\frac{n_i}{2}\right) \left( \frac{\partial _\tau B_i}{B_i}-\frac{\partial _\tau A_i}{A_i}\right) - T_i'\partial _\tau (A_iB_i) \\&= -\frac{1}{2}\sum _{j=1}^{n_i}\frac{\partial _\tau (\sigma ^2_{ij}(\tau ))}{\sigma ^2_{ij}(\tau )} -\sum _{j=1}^{n_i}\frac{s_{ij}(\alpha )}{(\sigma ^2_{ij}(\tau ))^2}(Y_{ij}-x_{ij}^{\top }\beta )\partial _\tau (\sigma ^2_{ij}(\tau )) \\&\quad -\frac{1}{2} \left( \lambda -\frac{n_i}{2}\right) \Bigg (\frac{1}{B_i^2}\sum _{j=1}^{n_i}\frac{(Y_{ij}-x_{ij}^{\top }\beta )^2}{(\sigma ^2_{ij}(\tau ))^2} \partial _\tau (\sigma ^2_{ij}(\tau ))\\&-\frac{1}{A_i^2}\sum _{j=1}^{n_i}\frac{s^2_{ij}(\alpha )}{(\sigma ^2_{ij}(\tau ))^2}\partial _\tau (\sigma ^2_{ij}(\tau ))\Bigg ) \\&\quad + \frac{1}{2} T_i' \Bigg (\frac{B_i}{A_i}\sum _{j=1}^{n_i}\frac{s^2_{ij}(\alpha )}{(\sigma ^2_{ij}(\tau ))^2}\partial _\tau (\sigma ^2_{ij}(\tau )) +\frac{A_i}{B_i}\sum _{j=1}^{n_i}\frac{(Y_{ij}-x_{ij}^{\top }\beta )^2}{(\sigma ^2_{ij}(\tau ))^2}\partial _\tau (\sigma ^2_{ij}(\tau ))\Bigg ), \\ {\partial _\lambda } \zeta _i(\theta )&= \log \left( \frac{\gamma }{\delta }\right) - \frac{ \partial _\lambda K_{\lambda }(\delta \gamma )}{ K_{\lambda }(\delta \gamma )}+\log B_i-\log A_i+\frac{ \partial _\lambda K_{\lambda -\frac{n_i}{2}}(A_iB_i)}{ K_{\lambda -\frac{n_i}{2}}(A_iB_i)}, \\ {\partial _\delta } \zeta _i(\theta )&= \gamma R_{\lambda }(\delta \gamma )+\left( \lambda -\frac{n_i}{2}\right) \frac{\delta }{B_i^2} - T_i' \frac{A_i}{B_i}\delta , \\ {\partial _\gamma } \zeta _i(\theta )&= \frac{2\lambda }{\gamma }+\delta R_{\lambda }(\delta \gamma )-\left( \lambda -\frac{n_i}{2}\right) \frac{\gamma }{A_i^2} - T_i' \frac{B_i}{A_i}\gamma . \end{aligned}$$

As for the second-order derivatives, for brevity, we write

$$\begin{aligned} U_i = S_{\lambda -\frac{n_i}{2}}(A_iB_i)+\frac{1}{A_iB_i}R_{\lambda -\frac{n_i}{2}}(A_iB_i)-\frac{\lambda - \frac{n_i}{2}}{A^2_iB_i^2}, \end{aligned}$$

for $R_\nu (t)$ and $S_\nu (t)$ defined by (A.1) and (A.2). Further, let

$$\begin{aligned} L_\nu (z):= \frac{1}{K^2_{\nu }(z)}\left( \partial _{\lambda }K_{\nu -1}(z)K_{\nu }(z)-\partial _{\lambda }K_{\nu }(z)K_{\nu -1}(z)\right) . \end{aligned}$$

Below we list the 21 components of $\partial _\theta ^2\zeta _i(\theta )$, which were used to compute the confidence intervals and the one-step estimator; the sizes of the matrices are not confusing, hence we are not taking care of them in notation and use the standard multilinear-form notation such as $(\partial _\beta B_i) \otimes (\partial _\alpha A_i):= \partial _\beta B_i\partial _\alpha ^{\top } A_i \in {\mathbb {R}}^{p_\beta }\otimes {\mathbb {R}}^{p_\alpha }$.

$$\begin{aligned} \partial _\beta ^2 \zeta _i(\theta )&= \frac{\left( \lambda - \frac{n_i}{2}\right) }{B_i^2}\left( B_i \partial _\beta ^2 B_i -(\partial _\beta B_i)^{\otimes 2}\right) - T_i' A_i \partial _\beta ^2 B_i -U_i A^2_i (\partial _\beta B_i)^{\otimes 2}, \\ \partial _\beta \partial _\alpha \zeta _i(\theta )&= -\sum _{j=1}^{n_i} \frac{1}{\sigma ^2_{ij}(\tau )}(x_{ij} \otimes \partial _\alpha s_{ij}(\alpha )) -(T_i' + U_i A_i B_i) \{(\partial _\beta B_i) \otimes (\partial _\alpha A_i)\}, \\ \partial _\beta \partial _\tau \zeta _i(\theta )&= \sum _{j=1}^{n_i} \frac{s_{ij}(\alpha )}{\left( \sigma ^2_{ij}(\tau )\right) ^2} \left( x_{ij} \otimes \partial _\tau (\sigma ^2_{ij}(\tau ))\right) +\frac{\left( \lambda -\frac{n_i}{2}\right) }{B_i^2}\left( B_i (\partial _\tau \partial _\beta B_i) -(\partial _\beta B_i)\otimes (\partial _\tau B_i) \right) \\&\quad - U_i A_i (\partial _\beta B_i) \otimes (\partial _\tau (A_i B_i)) - T_i' (\partial _\beta B_i)\otimes (\partial _\tau A_i) -T_i' A_i (\partial _\beta \partial _\tau B_i), \\ \partial _\beta \partial _\lambda \zeta _i(\theta )&= A_i (\partial _\beta B_i) L_{\lambda -\frac{n_i}{2} }(A_iB_i), \\ \partial _\beta \partial _\delta \zeta _i(\theta )&= -2\left( \lambda -\frac{n_i}{2}\right) \frac{\delta }{ B_i^{3}}\partial _\beta B_i -U_iA_i^2\frac{\delta }{B_i}\partial _{\beta }B_i+T_i'A_i\frac{\delta }{B_i^2}\partial _\beta B_i, \\ \partial _\beta \partial _\gamma \zeta _i(\theta )&= - \gamma U_i B_i \partial _{\beta }B_i - T_i'\frac{\gamma }{A_i}\partial _\beta B_i, \\ \partial _\alpha ^2 \zeta _i(\theta )&= \sum _{j=1}^{n_i}\frac{(y_{ij}-x_{ij}^{\top }\beta )}{\sigma ^2_{ij}(\tau )} \partial _\alpha ^2 s_{ij}(\alpha ) -\frac{\left( \lambda -\frac{n_i}{2}\right) }{A_i^2}\left\{ A_i \partial _\alpha ^2 A_i - (\partial _\alpha A_i)^{\otimes 2}\right\} \\&\quad -U_iB^2_i (\partial _{\alpha }A_i)^{\otimes 2} - T_i' B_i \partial _{\alpha }^2 A_i, \\ \partial _\alpha \partial _\tau \zeta _i(\theta )&= -\sum _{j=1}^{n_i}\frac{(y_{ij}-x_{ij}^{\top }\beta )}{\sigma _{ij}^4(\tau )} \left\{ (\partial _\alpha s_{ij}(\alpha )) \otimes \partial _\tau (\sigma ^2_{ij}(\tau ))\right\} \\&\quad - \frac{\left( \lambda -\frac{n_i}{2}\right) }{A_i^2}\left( A_i (\partial _\alpha \partial _\tau A_i) - (\partial _\alpha A_i)\otimes (\partial _\tau A_i)\right) \\&\quad -U_i B_i (\partial _\alpha A_i) \otimes (\partial _{\tau }(A_i B_i)) - T_i' \left( (\partial _\alpha A_i)\otimes (\partial _\tau B_i) + B_i \partial _\alpha \partial _\tau A_i)\right) , \\ \partial _\alpha \partial _\lambda \zeta _i(\theta )&= -2\frac{\partial _\alpha A_i}{A_i} - B_i (\partial _\alpha A_i) L_{\lambda -\frac{n_i}{2}}(A_iB_i), \\ \partial _\alpha \partial _\delta \ell _i(\theta )&= -\delta U_i A_i \partial _{\alpha }A_i - T_i'\frac{\delta }{B_i}\partial _\alpha A_i, \\ \partial _\alpha \partial _\gamma \zeta _i(\theta )&= 2\left( \lambda -\frac{n_i}{2}\right) \frac{\gamma }{ A_i^{3}}\partial _\alpha A_i - U_iB^2_i\frac{\gamma }{A_i}\partial _{\alpha }A_i+T_i'B_i\frac{\gamma }{A_i^2}\partial _\alpha A_i, \\ \partial _\tau ^2\zeta _i(\theta )&= \sum _{j=1}^{n_i} \frac{s_{ij}(\alpha )(y_{ij}-x_{ij}^{\top }\beta )}{\sigma ^8_{ij}(\tau )} \left( 2 \sigma ^4_{ij(\tau )} \left( \partial _\tau (\sigma ^2_{ij}(\tau )) \right) ^{\otimes 2} - \sigma ^4_{ij}(\tau ) \partial _\tau ^2 (\sigma ^2_{ij}(\tau )) \right) \\&\quad -\frac{1}{2} \sum _{j=1}^{n_i}\frac{\partial _\tau ^2 (\sigma ^2_{ij}(\tau ))\sigma ^2_{ij}(\tau ) - (\partial _\tau (\sigma ^2_{ij}(\tau )))^{\otimes 2}}{\sigma ^4_{ij}(\tau )} \\&\quad +\left( \lambda -\frac{n_i}{2}\right) \left[ \frac{1}{B_i^2}\left( B_i (\partial _\tau ^2 B_i) - (\partial _\tau B_i)^{\otimes 2}\right) -\frac{1}{A_i^2}\left( A_i(\partial _\tau ^2 A_i) - (\partial _\tau A_i)^{\otimes 2}\right) \right] \\&\quad - U_i\partial _{\tau }(A_iB_i) \otimes \partial _\tau (A_iB_i) - T_i' \partial _\tau ^2(A_iB_i), \\ \partial _\tau \partial _\lambda \zeta _i(\theta )&= -\frac{2\partial _\tau A_i}{A_i}-\partial _\tau (A_iB_i)L_{\lambda -\frac{n_i}{2}}(A_iB_i), \\ \partial _\tau \partial _\delta \zeta _i(\theta )&= -2\left( \lambda -\frac{n_i}{2}\right) \frac{\delta }{ B_i^{3}}\partial _\tau B_i-U_iA_i\frac{\delta }{B_i}\partial _{\tau }(A_iB_i)+\frac{\delta T_i'}{B_i}\left( \frac{A_i}{B_i}\partial _\tau B_i-\partial _\tau A_i\right) , \\ \partial _\tau \partial _\gamma \zeta _i(\theta )&= 2\left( \lambda -\frac{n_i}{2}\right) \frac{\gamma }{ A_i^{3}}\partial _\tau A_i-U_iB_i\frac{\gamma }{A_i}\partial _{\tau }(A_iB_i)+\frac{\gamma T_i'}{A_i}\left( \frac{B_i}{A_i}\partial _\tau A_i-\partial _\tau B_i\right) , \\ \partial ^2_\lambda \zeta _i(\theta )&= \frac{\partial ^2_{\lambda }K_{\lambda -\frac{n_i}{2}}(A_iB_i)}{K_{\lambda -\frac{n_i}{2}}(A_iB_i)}-\left( \frac{\partial _{\lambda }K_{\lambda -\frac{n_i}{2}}(A_iB_i)}{K_{\lambda -\frac{n_i}{2}}(A_iB_i)}\right) ^2-\frac{\partial ^2_{\lambda }K_{\lambda -1}(\delta \gamma )}{K_{\lambda }(\delta \gamma )}+\left( \frac{\partial _{\lambda }K_{\lambda }(\delta \gamma )}{K_{\lambda }(\delta \gamma )}\right) ^2, \\ \partial _\lambda \partial _\delta \zeta _i(\theta )&= -A_i\frac{\delta }{B_i}L_{\lambda -\frac{n_i}{2}}(A_iB_i)+\gamma L_{\lambda }(\delta \gamma ), \\ \partial _\lambda \partial _\gamma \zeta _i(\theta )&= \frac{2}{\gamma } -\frac{2\gamma }{A_i^2}+\delta L_{\lambda }(\delta \gamma )-B_i\frac{\gamma }{A_i}L_{\lambda -\frac{n_i}{2}}(A_iB_i), \\ \partial _\delta ^2\zeta _i(\theta )&= \left( S_{\lambda }(\delta \gamma )+\frac{1}{\delta \gamma }R_{\lambda }(\delta \gamma )\right) \gamma ^2+\left( \lambda -\frac{n_i}{2}\right) \left( \frac{1}{B_i^{2}}-\frac{2\delta ^2}{B_i^{4}}\right) \\&\quad -U_iA^2_i\frac{\delta ^2}{B^2_i}-T_i'A_i\left( \frac{1}{B_i}-\frac{2\delta ^2}{B_i^{3}}\right) , \\ \partial _\delta \partial _\gamma \zeta _i(\theta )&= 2R_{\lambda }(\delta \gamma )+\delta \gamma S_{\lambda }(\delta \gamma )-U_i\delta \gamma -T_i'\frac{\delta \gamma }{ A_iB_i}, \\ \partial _\gamma ^2\zeta _i(\theta )&= -\frac{2\lambda }{\gamma ^2}+\left( S_{\lambda }(\delta \gamma )+\frac{1}{\delta \gamma }R_{\lambda }(\delta \gamma )\right) \delta ^2-\left( \lambda -\frac{n_i}{2}\right) \left( \frac{1}{A_i^{2}}-\frac{2\gamma ^2}{A_i^{4}}\right) \\&\quad -U_iB^2_i\frac{\gamma ^2}{A^2_i}-T_i'B_i\left( \frac{1}{A_i}-\frac{\gamma ^2}{A_i^3}\right) . \end{aligned}$$