Free Vibration and Stability Study of an Axially Rotating Circular Cylindrical Shell Made of Shape Memory Alloy

Abstract

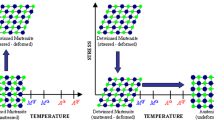
The free vibrations and stability of a simply supported thin-wall circular cylindrical shell made of shape memory alloy (SMA) with axially rotational motion are analyzed in this article. In this regard, the material damping and the structural damping effects of the shell on its vibration and stability are studied. A set of constitutive equations including convenient variables is utilized to consider the material properties. Hamilton’s principle is employed to extract a set of three equations governing the vibrations of the thin SMA circular cylindrical shell in radial direction for super-elastic state of the material, i.e., SMA. The governing equations of the shell are discriminated using Galerkin method and solved by the multiple scale method and the differential quadrature method to find its natural frequencies and its instability that may occur by external excitation. Critical rotational speeds, which predict the resonance of the shell and consequently its stable interval, are calculated as well. In this analysis, the influence of super-elasticity characteristic, phase transformation phenomenon of the material on the frequency response of the shell are investigated. The study presents phase transformation hysteresis property of SMA for rotating thin-walled circular cylindrical shell when speeding up and speeding down.

Appendices

Appendix 1

In this portion, the relation of SMA that is mentioned in Sect. 2 is given.

$${b}^{A}=-\Delta {s}_{0}\left({A}_{f}-{A}_{s}\right), { b}^{M}=-\Delta {s}_{0}\left({M}_{s}-{M}_{f}\right),{\mu }_{1}=\frac{1}{2}\rho \Delta {s}_{0}\left({M}_{s}+{A}_{f}\right)-\rho \Delta {u}_{0}$$

(87)

$${\mu }_{2}=\frac{1}{4}\rho \Delta {s}_{0}\left({A}_{s}-{A}_{f}+{M}_{s}-{M}_{f}\right)-\rho \Delta {u}_{0}$$

(88)

$$\Lambda =\left\{\begin{array}{c}\frac{3}{2}H\frac{{\sigma }^{{\prime}}}{{\tilde{\sigma }}^{{\prime}}}, \dot{\eta }>0\\ H\frac{{\varepsilon }^{t}}{\overline{{\varepsilon }_{t}}}, \dot{\eta }<0\end{array}\right.$$

(89)

$$\tilde{\sigma }={\left(\frac{3}{2}{\sigma }^{{\prime}}:{\sigma }^{{\prime}}\right)}^\frac{1}{2}={\left(\frac{3}{2}{\parallel {\sigma }^{{\prime}}\parallel }^{2}\right)}^\frac{1}{2}$$

(90)

$$\overline{{\varepsilon }^{t}}={\left(\frac{2}{3}{\varepsilon }^{t}:{\varepsilon }^{t}\right)}^\frac{1}{2}={\left(\frac{3}{2}{\parallel {\varepsilon }^{t}\parallel }^{2}\right)}^\frac{1}{2}$$

(91)

$$Y=\frac{1}{4}\rho \Delta {s}_{0}\left({M}_{s}+{M}_{f}-{A}_{s}-{A}_{f}\right)$$

(92)

$$\Delta {\varepsilon }_{q+1}^{t k}=\Delta {\eta }_{q+1}^{k}{\Lambda }_{q+1}^{k}$$

(93)

$$\Delta {\sigma }_{q+1}^{t k}=-\Delta {\eta }_{q+1}^{k}{S}_{q+1}^{k -1}:\left(\left\{\begin{array}{c}{\partial }_{\sigma }{\phi }_{q+1}^{k}, \dot{\eta }>0\\ -{\partial }_{\sigma }{\phi }_{q+1}^{k}, \dot{\eta }<0\end{array}\right)\right.$$

(94)

$${\phi }_{q+1}^{k}+{\partial }_{\upsigma }{\phi }_{q+1}^{k}:\Delta {\sigma }_{q+1}^{k}+{\partial }_{\upeta }{\phi }_{q+1}^{k}\Delta {\eta }_{q+1}^{k}=0$$

$$\Delta {\eta }_{q+1}^{k}=\left\{\begin{array}{c}\frac{{\upphi }_{q+1}^{k}}{{\partial }_{\upsigma }{\upphi }_{q+1}^{k}:{\mathrm{D}}_{q+1}^{k}:{\partial }_{\upsigma }{\upphi }_{q+1}^{k}-{\partial }_{\upeta }{\upphi }_{q+1}^{k}}, \dot{\upeta }>0\\ \frac{-{\upphi }_{q+1}^{k}}{{-\partial }_{\upsigma }{\upphi }_{q+1}^{k}:{\mathrm{D}}_{q+1}^{k}:{\partial }_{\upsigma }{\upphi }_{q+1}^{k}-{\partial }_{\upeta }{\upphi }_{q+1}^{k}}, \dot{\upeta }<0\end{array}\right.$$

(95)

$${\varepsilon }_{q+1}^{t(k+1) }={\varepsilon }_{q+1}^{t k}+\Delta {\varepsilon }_{q+1}^{t k}$$

(96)

$${\eta }_{q+1}^{t(k+1) }={\eta }_{q+1}^{t k}+\Delta {\eta }_{q+1}^{t k}$$

(97)

$${\sigma }_{q+1}^{t(k+1) }={\sigma }_{q+1}^{t k}+\Delta {\sigma }_{q+1}^{t k}$$

(98)

Appendix 2

In this portion, the parameters mentioned in Sect. 4 are explored:

$$S_{1} = \frac{{2L^{2} \left( {n^{2} L^{2} + R^{2} \pi^{2} \left( {\mu + 2} \right)} \right)n}}{{\left( {n^{2} L^{2} + R^{2} \pi^{2} } \right)^{2} }}$$

(99)

$$S_{2} = 0$$

(100)

$$S_{3} = \frac{{12\rho L^{2} R^{4} \pi^{2} \left( {L^{2} n^{2} + R^{2} \pi^{2} } \right)^{2} \left( {\upsilon - 1} \right)\left( {1 + \upsilon } \right){\hat{\Omega }}\left( t \right)^{2} - E(h^{2} n^{8} L^{8} + 4L^{6} R^{2} n^{6} \pi^{2} - 12\pi^{4} (R^{2} \left( {\upsilon^{2} - 1} \right).. + 4L^{2} h^{2} R^{6} \pi^{6} n^{2} + h^{2} R^{8} \pi^{8} }}{{12\left( {L^{2} n^{2} + R^{2} \pi^{2} } \right)^{2} }}$$

(101)

$$S_{4} = \frac{{ - 8\rho h\frac{{d{\Omega }\left( t \right)}}{dt} - 8C{\hat{\Omega }}\left( t \right)}}{3\rho hL}$$

(102)

$${a}_{1}=\frac{2{L}^{2}\left({n}^{2}{L}^{2}+{R}^{2}{\pi }^{2}\left(\mu +2\right)\right)n}{{({n}^{2}{L}^{2}+{R}^{2}{\pi }^{2})}^{2}\epsilon {\omega }_{n}}={a}_{11}+\varepsilon {a}_{12}\mathrm{cos}\left(\Omega t\right), {a}_{2}=0$$

(103)

$${b}_{1}={b}_{11}{\left(\widehat{\Omega }\left(t\right)\right)}^{2}+{b}_{12}==\frac{\begin{array}{c}12\rho {L}^{2}{R}^{4}{\pi }^{2}{\left({L}^{2}{n}^{2}+{R}^{2}{\pi }^{2}\right)}^{2}\left(\upsilon -1\right)\left(1+\upsilon \right){\widehat{\Omega }\left(t\right)}^{2}-E({h}^{2}{n}^{8}{L}^{8}+4{L}^{6}{R}^{2}{n}^{6}{\pi }^{2}-12{\pi }^{4}({R}^{2}\left({\upsilon }^{2}-1\right)..\\ +4{L}^{2}{h}^{2}{R}^{6}{\pi }^{6}{n}^{2}+{h}^{2}{R}^{8}{\pi }^{8}\end{array}}{12{\left({L}^{2}{n}^{2}+{R}^{2}{\pi }^{2}\right)}^{2}\epsilon }$$

(104)

$${b}_{2}={b}_{21}{\left(\widehat{\Omega }\left(t\right)\right)}^{2}+{b}_{22}=\frac{\begin{array}{c}-48\rho {L}^{2}{R}^{4}{\pi }^{2}{\left({L}^{2}{n}^{2}+{R}^{2}{\pi }^{2}\right)}^{2}\left(\upsilon -1\right)\left(1+\upsilon \right){\widehat{\Omega }\left(t\right)}^{2}-192E({h}^{2}{n}^{8}{L}^{8}+4{L}^{6}{R}^{2}{n}^{6}{\pi }^{2}..\\ -12{\pi }^{4}({R}^{2}\left({\upsilon }^{2}-1\right)+256{L}^{2}{h}^{2}{R}^{6}{\pi }^{6}{n}^{2}+256{h}^{2}{R}^{8}{\pi }^{8}\end{array}}{12{\left({L}^{2}{n}^{2}+{R}^{2}{\pi }^{2}\right)}^{2}\epsilon }={b}_{21}\left({{\Omega }_{0}}^{2}+\varepsilon \left({\Omega }_{1}{\mathrm{cos}\left({\omega }_{\widehat{\Omega }}t\right)}^{2}\right)\right)+{b}_{22}$$

(105)

$$M =\left(\genfrac{}{}{0pt}{}{1 0}{0 1}\right),C=\left(\begin{array}{cc}0& {a}_{11}\\ {-a}_{11}& 0\end{array}\right),K=(\begin{array}{cc}{\beta }_{1}& 0\\ 0& {\beta }_{2}\end{array})$$

(106)

$${\beta }_{1}={b}_{11}{{\Omega }_{0}}^{2}+{b}_{12},{\beta }_{2}={b}_{21}{{\Omega }_{0}}^{2}+{b}_{22}$$

(107)

$${P}_{i}=\frac{({{\omega }_{i}}^{2}-{\beta }_{1})}{i{a}_{11}{\omega }_{i}}, i=\mathrm{1,2}$$

(108)

$${f}_{11}=\frac{[i\alpha {\omega }_{1}+{a}_{21}{P}_{1}]}{(2i{\omega }_{1}+{a}_{11}{P}_{1})},{f}_{12}=\frac{[i\alpha {\omega }_{2}{P}_{2}+{a}_{21}]}{(2i{\omega }_{1}-{a}_{11})},{f}_{2n}={K}_{1n}+{K}_{3n}\mathrm{cos}\left(\sigma {T}_{1}\right)+i{K}_{3n}\mathrm{sin}\left(\sigma {T}_{1}\right)$$

(109)

$${\mu }_{1n}=\frac{(i{\alpha }_{n}{\omega }_{n}+{a}_{21n}{P}_{n}]}{(2i{\omega }_{n}+{a}_{11n}{P}_{n})},{\mu }_{1m}=\frac{(i{\alpha }_{m}{\omega }_{m}+{a}_{21m}{P}_{m}]}{(2i{\omega }_{m}+{a}_{11m}{P}_{m})},{\mu }_{2n}=\frac{[\frac{{a}_{12+}2{a}_{22}}{2}{p}_{n}{\omega }_{n}-i{b}_{11}{\Omega }_{0}{\Omega }_{1}]}{(2i{\omega }_{n}+{a}_{11}{P}_{n})}$$

(110)

$${\gamma }_{1}=\frac{[i\alpha {\omega }_{2}{P}_{1}-{a}_{21}]}{(2i{\omega }_{2}-{a}_{11})},{\gamma }_{2}=\frac{[i\alpha {\omega }_{1}{P}_{2}-{a}_{21}]}{(2i{\omega }_{2}-{a}_{11})}$$

(111)

$$H_{1} = \frac{{16\hat{\Omega }\left( t \right)}}{3L}{ },{ }H_{2} = \frac{C}{h\rho },{ }H_{3} = \frac{{8\rho h\frac{{d\hat{\Omega }\left( t \right)}}{dt} + 8C\hat{\Omega }\left( t \right)}}{3\rho hL}$$

(112)

$${H}_{4}=\left(\left(-48{\pi }^{2}\left(\nu -1\right)\rho \left(1+\nu \right){R}^{4}{L}^{2}{\left({4R}^{2}{\pi }^{2}+{{n}^{2}L}^{2}\right)}^{2}{\widehat{\Omega }\left(t\right)}^{2}-\left({h}^{2}{{n}^{8}L}^{8}+{16L}^{6}{R}^{2}{h}^{2}{n}^{6}{\pi }^{2}-{192R}^{4}{\pi }^{4}\left({R}^{2}\left({\nu }^{2}-1\right)-\frac{{n}^{4}{h}^{2}}{2}\right){L}^{4}+{256L}^{2}{R}^{6}{h}^{2}{{n}^{2}\pi }^{6}+{256\pi }^{8}{R}^{8}{h}^{2}\right)E\right)/\left(12{L}^{4}{R}^{4}{\left({4R}^{2}{\pi }^{2}+{n}^{2}{L}^{2}\right)}^{2}\rho {\omega }_{n}^{2}\left({\nu }^{2}-1\right)\right)\right)$$

(113)

Appendix 3: Differential quadrature method (DQM)

The first sentences of page 8 was amended and replaced with “in the given domain, the function values be known or desired on a grid of sampling points, where the grid is obtained by taking Nx and Ny points in the x and y directions, respectively.”

$$\frac{{\partial }^{n}f({x}_{i})}{\partial {x}^{n}}=\sum {A}_{ij}^{n}f\left({x}_{i}\right) \quad i=1,\dots ,N, n=1,\dots ,N$$

(114)

$$\frac{{\partial }^{n}f({x}_{i})}{\partial {y}^{n}}=\sum {B}_{ij}^{n}f\left({x}_{i}\right)\quad i=1,\dots ,N, n=1,\dots ,N$$

(115)

$${A}_{IJ}^{(1)}=\frac{\prod ({X}_{I})}{({X}_{I}-{X}_{J})},\quad{ i,j=1,\ldots ,N , i}\neq{{j}}$$

(116)

$${A}_{IJ}^{(k)}=k[{A}_{IJ}^{\left(k-1\right)}.{A}_{IJ}^{\left(1\right)}-\frac{{A}_{IJ}^{\left(k-1\right)}}{\left({x}_{i}-{x}_{j}\right)} ,\quad 2\le k\le N-1$$

(117)

$${A}_{IJ}^{(k)}=-\sum_{j=1,j\ne i}^{N}{A}_{IJ}^{(m)}$$

(118)

$$\prod \left({X}_{I}\right)=\prod_{j=1,j\ne i}^{N}\left({x}_{i}-{x}_{j}\right)$$

(119)

After computing the coefficients, the rth order differential equations can be found.

Then by imposing DQM rule, the governing equations are achieved as

$${[K-}{\Omega }_{n}^{2}{M]}\overrightarrow{\Delta } \, =0$$

(120)

Appendix 4: Nomenclature

${A}_{f}$/${A}_{s}$: Austenite finish/Austenite start

${C}_{A},{C}_{M}$: relation between temperature and critical stress.

${E}^{SMA}\left(E,\gamma ,T\right)$: the modulus of the shape memory alloy.

${E}^{A}$: amount of memory alloy in state of complete austenite.

${E}^{M}$: amount of memory alloy in state of complete martensite.

${M}_{f}$/${M}_{s}$: Martensite finish/Martensite start.

$\eta$: Fraction of the martensite.

${\Omega }_{T}:$ is associated with thermoelastic tensor.

Ω: Dimensionless fluctuation frequency.

$\widehat{\Omega }$: Rotational speed.

${\sigma }_{\theta },{\sigma }_{r}$: Stress in $\theta ,r$ direction

${\varepsilon }^{t}$: transformation strain