Skip to main content
SpringerLink
Log in

Free vibration of functionally graded truncated conical shells under internal pressure

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

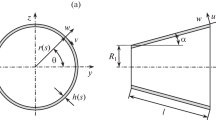
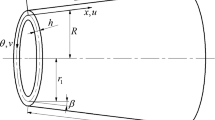
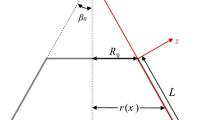
The influence of internal pressure on the free vibration behavior of functionally graded (FG) truncated conical shells are investigated based on the first-order shear deformation theory (FSDT) of shells. The initial mechanical stresses are obtained by solving the static equilibrium equations. Using Hamilton’s principle and by including the influences of initial stresses, the free vibration equations of motion around this equilibrium state together with the related boundary conditions are derived. The material properties are assumed to be graded in the thickness direction. The differential quadrature method (DQM) as an efficient and accurate numerical tool is adopted to discretize the governing equations and the related boundary conditions. The convergence behavior of the method is numerically investigated and its accuracy is demonstrated by comparing the results in the limit cases with existing solutions in literature. Finally, the effects of internal pressure together with the material property graded index, the semi-vertex angle and the other geometrical parameters on the frequency parameters of the FG truncated conical shells subjected to different boundary conditions are studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Abbreviations

R 1 and R 2 :

Small and large end mean radius

h :

Thickness of the truncated conical shell

L :

Length of the truncated conical shell

P i :

Internal pressure

p :

Power law index

P M :

Material property of the metal

P C :

Material property of the ceramic

N s :

Total number of nodes along the s-direction

G :

Shear rigidity

E :

Young’s modulus

k s :

Shear correction factor

t :

Time

m :

Circumferential wave number

s,θ,z :

Cylindrical coordinate variable

u 0,v 0,w 0 :

Initial displacement components

u,v,w :

Displacement components

r :

Mean radius of the truncated conical shell

K and U :

Kinetic and the potential energy of the shell

ω m :

Natural frequency

δK and δU :

Kinetic and the potential energy

λ mi :

Non-dimensional natural frequency parameters

β :

Semi-vertex angle

ν :

Poisson’s ratio

ρ :

Density

\(\varphi_{0}^{s}\), \(\varphi_{0}^{\theta}\) :

Initial bending rotation of the unit normal to the mid-surface of the shell about the θ- and s-axis, respectively

φ s and φ θ :

Bending rotation of the unit normal to the mid-surface of the shell about the θ- and s-axis, respectively

ε 0ss , ε 0θθ , γ 0sz :

Initial normal and the shear components of the strain tensor

σ 0ss , σ 0θθ , σ 0sz :

Initial normal and the shear components of the stress tensor

ε ss , ε θθ , γ sz , γ sθ , γ θz :

Normal and the shear components of the strain tensor

σ ss , σ θθ , σ sz , σ sθ , σ θz :

Normal and the shear components of the stress tensor

References

  1. Miyamoto Y, Kaysser WA, Rabin BH, Kawasaki A, Ford RG (1999) Functionally graded materials: design, processing and applications. Kluwer Academic, Boston

    Book  Google Scholar 

  2. Birman V, Byrd LW (2007) Modeling and analysis of functionally graded materials and structures. Appl Mech Rev 60:195–216

    Article  ADS  Google Scholar 

  3. Şimşek M, Kocatürk T (2009) Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Compos Struct 90:465–473

    Article  Google Scholar 

  4. Kitipornchai S, Ke LL, Yang J, Xiang Y (2009) Nonlinear vibration of edge cracked functionally graded Timoshenko beams. J Sound Vib 324:962–982

    Article  ADS  Google Scholar 

  5. Xia XK, Shen HS (2009) Nonlinear vibration and dynamic response of FGM plates with piezoelectric fiber reinforced composite actuators. Compos Struct 90:254–262

    Article  Google Scholar 

  6. Zhao X, Lee YY, Liew KM (2009) Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. J Sound Vib 319:918–939

    Article  ADS  Google Scholar 

  7. Malekzadeh P (2009) Three-dimensional free vibration analysis of thick functionally graded plates on elastic foundations. Compos Struct 89:367–373

    Article  Google Scholar 

  8. Hosseini-Hashemi S, Rokni Damavandi Taher H, Akhavan H, Omidi M (2010) Free vibration of functionally graded rectangular plates using first-order shear deformation plate theory. Appl Math Model 34:1276–1291

    Article  MATH  MathSciNet  Google Scholar 

  9. Malekzadeh P, Golbahar Haghighi MR, Atashi MM (2011) Free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment. Meccanica 46:893–913

    Article  MATH  MathSciNet  Google Scholar 

  10. Hosseini-Hashemi S, Fadaee M, Atashipour SR (2011) Study on the free vibration of thick functionally graded rectangular plates according to a new exact closed-form procedure. Compos Struct 93:722–735

    Article  Google Scholar 

  11. Yas MH, Jodaei A, Irandoust S, Nasiri Aghdam M (2012) Three-dimensional free vibration analysis of functionally graded piezoelectric annular plates on elastic foundations. Meccanica 47:1401–1423

    Article  MathSciNet  Google Scholar 

  12. Jodaei A, Jalal M, Yas MH (2012) Free vibration analysis of functionally graded annular plates by state-space based differential quadrature method and comparative modeling by ANN. Composites, Part B, Eng 43:340–353

    Article  Google Scholar 

  13. Malekzadeh P, Heydarpour Y (2012) Response of functionally graded cylindrical shells under moving thermo-mechanical loads. Thin-Walled Struct 58:51–66

    Article  Google Scholar 

  14. Malekzadeh P, Heydarpour Y (2012) Free vibration analysis of rotating functionally graded cylindrical shells in thermal environment. Compos Struct 94:2971–2981

    Article  Google Scholar 

  15. Sobhani Aragh B, Hedayati H (2012) Static response and free vibration of two-dimensional functionally graded metal/ceramic open cylindrical shells under various boundary conditions. Acta Mech 223:309–330

    Article  MATH  MathSciNet  Google Scholar 

  16. Bhangale RK, Ganesan N, Padmanabhan C (2006) Linear thermoelastic buckling and free vibration behavior of functionally graded truncated conical shells. J Sound Vib 292:341–371

    Article  ADS  Google Scholar 

  17. Tornabene F, Viola E, Inman DJ (2009) 2-D differential quadrature solution for vibration analysis of functionally graded conical, cylindrical shell and annular plate structures. J Sound Vib 328:259–290

    Article  ADS  Google Scholar 

  18. Tornabene F (2009) Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Comput Methods Appl Mech Eng 198:2911–2935

    Article  ADS  MATH  Google Scholar 

  19. Setoodeh AR, Tahani M, Selahi E (2012) Transient dynamic and free vibration analysis of functionally graded truncated conical shells with non-uniform thickness subjected to mechanical shock loading. Composites, Part B, Eng 43:2161–2171

    Article  Google Scholar 

  20. Malekzadeh P, Fiouz AR, Sobhrouyan M (2012) Three-dimensional free vibration of functionally graded truncated conical shells subjected to thermal environment. Int J Press Vessels Piping 89:210–221

    Article  Google Scholar 

  21. Malekzadeh P, Heydarpour Y (2013) Free vibration analysis of rotating functionally graded truncated conical shells. Compos Struct 97:176–188

    Article  Google Scholar 

  22. Maleki S, Andakhshideh A, Aghdam MM (2011) Bending analysis of moderately thick laminated conical panels with various boundary conditions. J Mech Eng Sci 225:1291–1300

    Article  Google Scholar 

  23. Heydarpour Y, Malekzadeh P, Golbahar Haghighi MR, Vaghefi M (2012) Thermoelastic analysis of rotating laminated functionally graded cylindrical shells using layerwise differential quadrature method. Acta Mech 223:81–93

    Article  MATH  Google Scholar 

  24. Malekzadeh P, Golbahar Haghighi MR, Alibeygi Beni A (2012) Buckling analysis of functionally graded arbitrary straight-sided quadrilateral plates on elastic foundations. Meccanica 47:321–333

    Article  MathSciNet  Google Scholar 

  25. Zamani M, Fallah A, Aghdam MM (2012) Free vibration analysis of moderately thick trapezoidal symmetrically laminated plates with various combinations of boundary conditions. Eur J Mech A, Solids 36:204–212

    Article  MathSciNet  Google Scholar 

  26. Efraim E, Eisenberger M (2007) Exact vibration analysis of variable thickness thick annular isotropic and FGM plates. J Sound Vib 299:720–738

    Article  ADS  Google Scholar 

  27. Liew KM, Ng TY, Zhao X (2005) Free vibration analysis of conical shells via the element-free kp-Ritz method. J Sound Vib 281:627–645

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Amirkabir University of Technology, Hafez Ave., Tehran, 15875-4413, Iran

    Y. Heydarpour & M. M. Aghdam

  2. Department of Mechanical Engineering, School of Engineering, Persian Gulf University, Bushehr, 75168, Iran

    P. Malekzadeh

Authors
  1. Y. Heydarpour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. Malekzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. M. Aghdam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. Heydarpour.

Appendix

Appendix

Based on the three-dimensional elasticity theory, the nonlinear strain displacement relations in the conical coordinate system can be presented as,

$$\begin{aligned} &{\hat{\varepsilon}_{ss} = \frac{\partial \hat{u}}{\partial s} + \frac{1}{2} \biggl[ \biggl( \frac{\partial \hat{u}}{\partial s} \biggr)^{2} + \biggl( \frac{\partial \hat{v}}{\partial s} \biggr)^{2} + \biggl( \frac{\partial \hat{w}}{\partial s} \biggr)^{2} \biggr],} \end{aligned}$$
(33a)
$$\begin{aligned} &{ \begin{aligned}[b] \hat{\varepsilon}_{\theta \theta}& = \frac{1}{r} \biggl( \frac{\partial \hat{v}}{\partial \theta} + \hat{u}\sin \beta + \hat{w}\cos \beta \biggr) \\ &\quad{} + \frac{1}{2r^{2}} \biggl[ \biggl( \frac{\partial \hat{w}}{\partial \theta} - \hat{v}\cos \beta \biggr)^{2}\end{aligned} } \\ &{ \begin{aligned}[b]&\quad{} + \biggl( \frac{\partial \hat{v}}{\partial \theta} + \hat{u}\sin \beta + \hat{w}\cos \beta \biggr)^{2} \\ &\quad{} + \biggl( \frac{\partial \hat{u}}{\partial \theta} - \hat{v}\sin \beta \biggr)^{2} \biggr],\end{aligned}} \end{aligned}$$
(33b)
$$\begin{aligned} &{\hat{\varepsilon}_{zz} = \frac{\partial \hat{w}}{\partial z} + \frac{1}{2} \biggl[ \biggl( \frac{\partial \hat{u}}{\partial z} \biggr)^{2} + \biggl( \frac{\partial \hat{v}}{\partial z} \biggr)^{2} + \biggl( \frac{\partial \hat{w}}{\partial z} \biggr)^{2} \biggr],} \end{aligned}$$
(33c)
$$\begin{aligned} &{\hat{\gamma}_{z\theta} = \frac{\partial \hat{v}}{\partial z} + \frac{1}{r} \biggl( \frac{\partial \hat{w}}{\partial \theta} - \hat{v} \cos \beta \biggr) } \\ &{\phantom{\hat{\gamma}_{z\theta} =}{} + \frac{1}{r} \biggl[ \frac{\partial \hat{w}}{\partial z} \biggl( \frac{\partial \hat{w}}{\partial \theta} - \hat{v}\cos \beta \biggr) + \frac{\partial \hat{v}}{\partial z} \biggl( \frac{\partial \hat{v}}{\partial \theta} } \\ &{\phantom{\hat{\gamma}_{z\theta} =}{} + \hat{u}\sin \beta + \hat{w}\cos \beta \biggr) }\\ &{\phantom{\hat{\gamma}_{z\theta} =}{} + \frac{\partial \hat{u}}{\partial z} \biggl( \frac{\partial \hat{u}}{\partial \theta} - \hat{v}\sin \beta \biggr) \biggr]} \end{aligned}$$
(33d)
$$\begin{aligned} &{ \begin{aligned}[b]\hat{\gamma}_{\theta s} &= \frac{\partial \hat{v}}{\partial s} + \frac{1}{r} \biggl( \frac{\partial \hat{u}}{\partial \theta} - \hat{v} \sin \beta \biggr) \\ &\quad{} + \frac{1}{r} \biggl[ \frac{\partial \hat{w}}{\partial s} \biggl( \frac{\partial \hat{w}}{\partial \theta} - \hat{v}\cos \beta \biggr) \\ &\quad {} + \frac{\partial \hat{v}}{\partial s} \biggl( \frac{\partial \hat{v}}{\partial \theta} + \hat{u}\sin \beta + \hat{w}\cos \beta \biggr) \\ &\quad + \frac{\partial \hat{u}}{\partial s} \biggl( \frac{\partial \hat{u}}{\partial \theta} - \hat{v}\sin \beta \biggr) \biggr]\end{aligned}} \end{aligned}$$
(33e)
$$\begin{aligned} &{\hat{\gamma}_{zs} = \frac{\partial \hat{w}}{\partial s} + \frac{\partial \hat{u}}{\partial z} + \frac{\partial \hat{u}}{\partial s}\frac{\partial \hat{u}}{\partial z} + \frac{\partial \hat{v}}{\partial s} \frac{\partial \hat{v}}{\partial z} + \frac{\partial \hat{w}}{\partial s}\frac{\partial \hat{w}}{\partial z} } \end{aligned}$$
(33f)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Heydarpour, Y., Malekzadeh, P. & Aghdam, M.M. Free vibration of functionally graded truncated conical shells under internal pressure. Meccanica 49, 267–282 (2014). https://doi.org/10.1007/s11012-013-9791-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-013-9791-y

Keywords

Search

Navigation