1 Introduction

Let \({\mathcal {H}}\) denote the class of analytic functions in the open unit disc \(\Delta = \{z\in {\mathbb {C}} : |z| < 1\}\) on the complex plane \({\mathbb {C}}\). Also let \({\mathcal {A}}\) denote the subclass of \({\mathcal {H}}\) including of functions normalized by \(f(0)=f'(0)-1=0\). The subclass of \({\mathcal {A}}\) that consists of all univalent functions f(z) in \(\Delta\) is denoted by \({\mathcal {S}}\). We denote by \({\mathfrak {B}}\) the class of functions w(z) analytic in \(\Delta\) with \(w(0) = 0\) and \(|w(z)| < 1\), \((z \in \Delta )\). For two analytic and normalized functions f and g, we say that f is subordinate to g, written \(f \prec g\) in \(\Delta\), if there exists a function \(w\in {\mathfrak {B}}\) such that \(f (z) = g(w(z))\) for all \(z\in \Delta\). In special case, if the function g is univalent in \(\Delta\), then

$$\begin{aligned} f (z)\prec g(z) \Leftrightarrow \left( f (0) = g(0)\quad \mathrm{and}\quad f (\Delta )\subset g(\Delta ) \right) . \end{aligned}$$

It is easy to see that for any complex numbers \(\lambda \ne 0\) and \(\mu\), we have:

$$\begin{aligned} f (z)\prec g(z) \Rightarrow \lambda f(z)+\mu \prec \lambda g(z)+\mu . \end{aligned}$$
(1.1)

The set of all functions \(f\in {\mathcal {A}}\) that are starlike univalent in \(\Delta\) will be denoted by \({\mathcal {S}}^*\) and the set of all functions \(f\in {\mathcal {A}}\) that are convex univalent in \(\Delta\) will be denoted by \({\mathcal {K}}\). Robertson (see Robertson 1985) introduced and studied the class \({\mathcal {S}}^*(\gamma )\) of starlike functions of order \(\gamma \le 1\) as follows

$$\begin{aligned} {\mathcal {S}}^*(\gamma ):=\left\{ f\in {\mathcal {A}}:\ \ \mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\} > \gamma , \ z\in \Delta \right\} . \end{aligned}$$

We note that if \(\gamma \in [0,1)\), then a function in \({\mathcal {S}}^*(\gamma )\) is univalent. Also we say that \(f\in {\mathcal {K}}(\gamma )\) (the class of convex functions of order \(\gamma\)) if and only if \(zf'(z)\in {\mathcal {S}}^*(\gamma )\). In particular we put \({\mathcal {S}}^*(0)\equiv {\mathcal {S}}^*\) and \({\mathcal {K}}(0)\equiv {\mathcal {K}}\).

Recently, Kargar et al. (2017) introduced and studied a class functions related to the Booth lemniscate as follows.

Definition 1.1

(see Kargar et al. 2017) The function \(f\in {\mathcal {A}}\) belongs to the class \(\mathcal {BS}(\alpha )\), \(0\le \alpha <1\), if it satisfies the condition

$$\begin{aligned} \left( \frac{zf'(z)}{f(z)}-1\right) \prec \frac{z}{1-\alpha z^2}\quad (z\in \Delta ). \end{aligned}$$
(1.2)

Recall that (Piejko and Sokół 2013), a one-parameter family of functions given by

$$\begin{aligned} F_{\alpha }(z):=\frac{z}{1-\alpha z^2}=\sum _{n=1}^{\infty }\alpha ^{n-1}z^{2n-1}\quad (z\in \Delta ,~0\le \alpha \le 1). \end{aligned}$$
(1.3)

are starlike univalent when \(0\le \alpha \le 1\) and are convex for \(0 \le \alpha \le 3-2\sqrt{2}\approx 0.1715\). We have also \(F_{\alpha }(\Delta )=D(\alpha )\), where

$$\begin{aligned} D(\alpha )=\left\{ x+iy\in {\mathbb {C}}: ~ \left( x^2+y^2\right) ^2-\frac{x^2}{(1-\alpha )^2}-\frac{y^2}{(1+\alpha )^2}<0, (0\le \alpha <1)\right\} \end{aligned}$$
(1.4)

and

$$\begin{aligned} D(1)=\left\{ x+iy\in {\mathbb {C}}: ~ \left( \forall t\in (-\infty ,-i/2]\cup [i/2,\infty )\right) [x+iy\ne it]\right\} . \end{aligned}$$
(1.5)

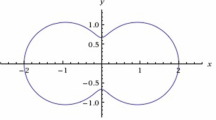
It is clear that the curve

$$\begin{aligned} \left( x^2+y^2\right) ^2-\frac{x^2}{(1-\alpha )^2}-\frac{y^2}{(1+\alpha )^2}=0\quad (x, y)\ne (0, 0), \end{aligned}$$

is the Booth lemniscate of elliptic type (see Fig. 1, for \(\alpha =1/3\)). For more details, see Kargar et al. (2017).

Fig. 1
figure 1

\(\left( x^2+y^2\right) ^2-9x^2/4-9 y^2/16=0\)

Full size image

Lemma 1.1

(see Kargar et al. 2017) Let\(F_{\alpha }(z)\)be given by (1.3). Then for\(0\le \alpha <1\), we have

$$\begin{aligned} \frac{1}{\alpha -1}< \mathrm{Re}\left\{ F_{\alpha }(z)\right\} <\frac{1}{1-\alpha }\quad (z\in \Delta ). \end{aligned}$$
(1.6)

Therefore by definition of subordination and by Lemma 1.1, \(f\in {\mathcal {A}}\) belongs to the class \(\mathcal {BS}(\alpha )\), if it satisfies the condition

$$\begin{aligned} \frac{\alpha }{\alpha -1}< \mathrm{Re}\left\{ \frac{zf'(z)}{f(z)}\right\} <\frac{2-\alpha }{1-\alpha }\quad (z\in \Delta ). \end{aligned}$$
(1.7)

The following lemma will be useful.

Lemma 1.2

(see Ruscheweyh and Stankiewicz 1985) Let\(F,G\in {\mathcal {H}}\)be any convex univalent functions in\(\Delta\). If\(f\prec F\)and\(g\prec G\), then

$$\begin{aligned} f*g\prec F*G\quad {in\ \ \Delta }. \end{aligned}$$

In this work, some geometric properties of the class \(\mathcal {BS}(\alpha )\) are investigated.

2 Main Results

We start with the following lemma that gives the structural formula for the function of the considered class.

Lemma 2.1

The function\(f\in {\mathcal {A}}\)belongs to the class\(\mathcal {BS}(\alpha )\), \(0\le \alpha <1\), if and only if there exists an analytic functionq,  \(q(0)=0\)and\(q\prec {F_{\alpha }}\)such that

$$\begin{aligned} f(z) = z \exp \left( \int _0^z \frac{q(t)}{t}\mathrm{d}t \right) . \end{aligned}$$
(2.1)

The proof is easy. Putting \(q={F_{\alpha }}\) in Lemma 2.1 we obtain the function

$$\begin{aligned} {\tilde{f}}(z) = z\left( \frac{1+z\sqrt{\alpha }}{1-z\sqrt{\alpha }} \right) ^{\frac{1}{2\sqrt{\alpha }}}, \end{aligned}$$
(2.2)

which is extremal function for several problems in the class \(\mathcal {BS}(\alpha )\). Moreover, we consider

$$\begin{aligned} F(z):=\frac{{\tilde{f}}(z)}{z} =\left( \frac{1+z\sqrt{\alpha }}{1-z\sqrt{\alpha }} \right) ^{\frac{1}{2\sqrt{\alpha }}} =1+z+\frac{1}{2}z^2+\frac{1}{3}\left( \alpha +\frac{1}{2}\right) z^3\cdots . \end{aligned}$$
(2.3)

From (1.7) we conclude that \(f \in \mathcal {BS}(\alpha )\) is starlike of order \(\frac{\alpha }{\alpha -1} < 0,\) hence f may not be univalent in \(\Delta\). It may therefore be interesting to consider a problem to find the radius of starlikeness of order \(\gamma\), \(\gamma \in [0,1)\) (hence univalence) of the class \(\mathcal {BS}(\alpha )\), i.e. the largest radius \(r_s(\alpha ,\gamma )\) such that each function \(f \in \mathcal {BS}(\alpha )\) is starlike of order \(\gamma\) in the disc \(|z|< r_s(\alpha ,\gamma )\). For this purpose we recall the following property of the class \({\mathfrak {B}}.\)

Lemma 2.2

(Schwarz lemma) (see Duren 1983) Letwbe analytic in the unit disc\(\Delta\), with\(w(0)=0\)and\(|w(z)|<1\)in\(\Delta .\)Then\(|w'(0)|\le 1\)and\(|w(z)|\le |z|\)in\(\Delta .\)Strict inequality holds in both estimates unlesswis a rotation of the disc:\(w(z)=e^{i\theta }z.\)

Theorem 2.1

Let\(\alpha \in (0,1)\)and\(\gamma \in [0,1)\)be given numbers. If\(f\in \mathcal {BS}(\alpha )\), thenfis starlike of order\(\gamma\)in the disc\(|z|< r_s(\alpha ,\gamma )=\frac{\sqrt{1+4\alpha (1-\gamma )}-1}{2\alpha (1-\gamma )}.\)The result is sharp.

Proof

Let \(f\in \mathcal {BS}(\alpha ),\)\(\alpha \in (0,1).\) Then through (1.2) we have \(\left( \frac{zf'(z)}{f(z)}-1\right) \prec \frac{z}{1-\alpha z^2}\) so there exists \(w\in {\mathfrak {B}}\) such that

$$\begin{aligned} \mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\} =\mathrm{Re}\left\{ \frac{1+w(z)-\alpha w^2(z)}{1-\alpha w^2(z)}\right\} \end{aligned}$$

for all \(z\in \Delta\). Applying the Schwarz lemma we obtain

$$\begin{aligned} \mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\}&=\mathrm{Re}\left\{ 1+\frac{w(z)}{1-\alpha w^2(z)}\right\} =1+\mathrm{Re}\left\{ \frac{w(z)}{1-\alpha w^2(z)}\right\} \\&\ge 1-\frac{|w(z)|}{1-\alpha |w(z)|^2}\ge 1-\frac{|z|}{1-\alpha |z|^2}=1-\frac{r}{1-\alpha r^2}, \end{aligned}$$

where \(r=|z|<1\). Let us consider a function \(h(r)=1-\frac{r}{1-\alpha r^2},\)\(r \in (0,1).\) Note that \(h'(r)=-\frac{1+\alpha r^2}{(1-\alpha r^2)^2}<0\) for all \(r \in [0,1)\) hence h is a strictly decreasing function and it decreases from 1 to \(\frac{\alpha }{\alpha -1}<0.\) Therefore the equation \(h(r)=\gamma\) has for given \(\alpha\) and \(\gamma\) the smallest positive root \(r_s(\alpha ,\gamma )\) in (0, 1). Therefore f is starlike of order \(\gamma\) in \(|z|<r\le r_s(\alpha ,\gamma )\). Note that for the function \({\tilde{f}}\) given in (2.2) we obtain

$$\begin{aligned} \mathrm{Re} \frac{z{\tilde{f}}'(z)}{{\tilde{f}}(z)}=\mathrm{Re}\left\{ 1+\frac{z}{1-\alpha z^2}\right\} =:A(z) \end{aligned}$$

and \(A(-r_s(\alpha ,\gamma ))=\gamma\). \(\square\)

Putting \(\gamma =0\) in Theorem 2.1, we obtain.

Corollary 2.1

Let\(\alpha \in (0,1)\). If\(f\in \mathcal {BS}(\alpha )\)thenfis starlike univalent in the disc\(|z|< r_s(\alpha )=\frac{\sqrt{1+4\alpha }-1}{2\alpha }\). The result is sharp.

Remark 2.1

Note that \(\lim _{\alpha \longrightarrow 0^+} r_s(\alpha )= \lim _{\alpha \longrightarrow 0^+} \frac{2}{\sqrt{1+4\alpha }+1}=1.\) Moreover, it is worth mentioning that \(\lim _{\alpha \longrightarrow 1^-} r_s(\alpha )=\frac{\sqrt{5}-1}{2}= 0,618\dots\), i.e. this limit is a reciprocal of the golden ratio \(\frac{\sqrt{5}+1}{2}.\)

Now we consider the following question:

For a given number \(r \in (0,1]\) find \(\alpha (r)\) such that for each function \(f\in \mathcal {BS}(\alpha (r))\) the image \(f(\{z:|z|<r\})\) is a starlike domain.

Theorem 2.2

Let\(r \in (0,1]\)be the given number. If \(0\le \alpha < \frac{1-r}{r^2}\), then each function\(f\in \mathcal {BS}(\alpha )\)maps a disc\(|z|<r\)onto a starlike domain.

Proof

After using the same argument as in the proof of Theorem 2.1 we conclude that \(f \in \mathcal {BS}(\alpha )\) satisfies the equality

$$\begin{aligned} \mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\} =\mathrm{Re}\left\{ \frac{1+w(z)-\alpha w^2(z)}{1-\alpha w^2(z)}\right\} \end{aligned}$$

for all \(z \in \Delta\) with some \(w\in {\mathfrak {B}}\). Then we have by Schwarz’s lemma that

$$\begin{aligned} \mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\} \ge 1-\frac{|w(z)|}{1-\alpha |w(z)|^2}\ge 1-\frac{|z|}{1-\alpha |z|^2}. \end{aligned}$$

Consequently, for \(|z|<r\), we obtain \(\mathrm{Re} \left\{ \frac{zf'(z)}{f(z)}\right\} >1-\frac{r}{1-\alpha r^2}.\) Let us note that a function \(g(\alpha )=1-\frac{r}{1-\alpha r^2},\)\(\alpha \in [0,1),\) has positive values for \(0\le \alpha < \frac{1-r}{r^2}\). Therefore the image of the disc \(|z|<r\) is a starlike domain. \(\square\)

Theorem 2.3

Let\(n\ge 2\)be integer. If one of the following conditions holds

(i):

\(\frac{1}{\alpha +n(1-\alpha )}< |c|<1,\)

(ii):

\(n > \frac{3-\alpha }{1-\alpha }\)   and    \(\frac{1}{\alpha -2+n(1-\alpha )}< |c|<1,\)

(iii):

\(n\ge \frac{2-\alpha }{1-\alpha }\)   and    \(|c|>1,\)

(iv):

\(n<\frac{2-\alpha }{1-\alpha }\)   and    \(1<|c|<\frac{1}{2-\alpha +n(\alpha -1)},\)

then the function\(g_n(z)=z+cz^n\)does not belong to the class\(\mathcal {BS}(\alpha )\).

Proof

Let us put \(G(z)=\frac{zg'_n(z)}{g_n(z)}-1=\frac{1+cnz^{n-1}}{1+cz^{n-1}}-1.\) To prove our assertion it suffices to show that the function G is not subordinate to \(F_{\alpha }\) or equivalently, because of the univalence of the dominant function \(F_{\alpha }\), that the set \(G(\Delta )\) is not included in \(F_{\alpha }(\Delta )=D(\alpha ).\) Upon performing simple calculation we find that the set \(G(\Delta )\) is the disc with the diameter from the point \(x_1=\frac{|c|(n-1)}{|c|-1}\) to the point \(x_2=\frac{|c|(n-1)}{|c|+1}.\) The set \(D(\alpha )\) is bounded by the curve

$$\begin{aligned} \left( x^2+y^2 \right) ^2-\frac{x^2}{(1-\alpha )^2}-\frac{y^2}{(1+\alpha )^2}=0,\quad (x,y)\ne (0,0). \end{aligned}$$

We have \(\min _{|z|=1}\mathrm{Re}\{F_{\alpha }(z)\}=F_{\alpha }(-1)=\frac{1}{\alpha -1}\) and \(\max _{|z|=1}\mathrm{Re}\{F_{\alpha }(z)\}=F_{\alpha }(1)=\frac{1}{1-\alpha }.\) If one of the conditions \((i)-(iv)\) is satisfied then \(\min \{x_1,x_2\}<\frac{1}{\alpha -1}\) or \(\max \{x_1,x_2\}>\frac{1}{1-\alpha },\) and then \(G(\Delta )\) is not included in \(D(\alpha ).\) The proof of theorem is completed. \(\square\)

Recently, one of the interesting problems for mathematician is to find bounds for \(\mathrm{Re}\{f(z)/z\}\) (see Kargar et al. 2016; Sim and Kwon 2013). In the sequel, we obtain lower and upper bounds for \(\mathrm{Re}\{f(z)/z\}\). We first get the following result for the function F(z) given by (2.3).

Theorem 2.4

The functionF(z) of the form (2.3) is convex univalent in\(\Delta\).

Proof

A simple calculation gives us

$$\begin{aligned} 1+\frac{zF''(z)}{F'(z)}=1+\left( \frac{1}{2\sqrt{\alpha }}-1\right) \left( \frac{2\sqrt{\alpha }z}{1-\alpha z^2}\right) +\frac{2\sqrt{\alpha }z}{1-\sqrt{\alpha }z}. \end{aligned}$$
(2.4)

It is sufficient to show that (2.4) has positive real part in the unit disc. From Lemma 1.1 we obtain

$$\begin{aligned} \mathrm{Re}\left\{ 1+\frac{zF''(z)}{F'(z)}\right\}= & {} \mathrm{Re}\left\{ 1+\left( \frac{1}{2\sqrt{\alpha }}-1\right) \left( \frac{2\sqrt{\alpha }z}{1-\alpha z^2}\right) +\frac{2\sqrt{\alpha }z}{1-\sqrt{\alpha }z}\right\} \\= & {} 1+2\sqrt{\alpha }\left( \frac{1}{2\sqrt{\alpha }}-1\right) \mathrm{Re}\left\{ \frac{z}{1-\alpha z^2}\right\} +2\sqrt{\alpha }\mathrm{Re}\left\{ \frac{z}{1-\sqrt{\alpha }z}\right\} \\> & {} 1+\left( 1-2\sqrt{\alpha }\right) \left( \frac{1}{\alpha -1}\right) -\frac{2\sqrt{\alpha }}{1+\sqrt{\alpha }}=:K(\alpha )\quad (0\le \alpha <1). \end{aligned}$$

It is easily seen that \(K'(\alpha )=\frac{1}{(\alpha -1)^2}>0\). Thus \(K(\alpha )\ge K(0)=0\), and hence F(z) is convex univalent function. \(\square\)

In the proof of the next theorem we will use the following result concerning the convexity of the boundary of \(D(\alpha )\).

Lemma 2.3

(see Piejko and Sokół 2013) Suppose that\(F_\alpha\)is given by (1.3). If \(0 \le \alpha \le 3-2\sqrt{2}\approx 0.1715\), then the curve\(F_\alpha (e^{i\varphi })\), \(\varphi \in [0,2\pi )\), is convex. If \(\alpha \in (3-2\sqrt{2},1)\), then the curve\(F_\alpha (e^{i\varphi })\), \(\varphi \in [0,2\pi )\), is concave.Moreover, in both cases this curve is symmetric with respect to both axes.

Theorem 2.5

If a functionfbelongs to the class\(\mathcal {BS}(\alpha )\), \(0 \le \alpha \le 3-2\sqrt{2}\), then

$$\begin{aligned} \frac{f(z)}{z}\prec F(z)\quad (z\in \Delta ), \end{aligned}$$
(2.5)

whereF(z) is given by (2.3).

Proof

Let \(0 \le \alpha \le 3-2\sqrt{2}\) and let f be in the class \(\mathcal {BS}(\alpha )\). Then we have

$$\begin{aligned} \phi (z):=\frac{zf'(z)}{f(z)}-1\prec F_\alpha (z)\quad (z\in \Delta ), \end{aligned}$$
(2.6)

where \(F_\alpha\) is given by (1.3). It is well known that the normalized function

$$\begin{aligned} l(z)=\log \frac{1}{1-z}=\sum _{n=1}^{\infty }\frac{z^n}{n}\quad (z\in \Delta ), \end{aligned}$$

belongs to the class \({\mathcal {K}}\) and for \(f\in {\mathcal {A}}\) we get

$$\begin{aligned} \phi (z)*l(z)=\int _{0}^{z}\frac{\phi (t)}{t}\mathrm{d}t\quad \mathrm{and}\quad F_\alpha (z)*l(z)=\int _{0}^{z}\frac{F_\alpha (t)}{t}\mathrm{d}t. \end{aligned}$$
(2.7)

By Lemma 2.3 we deduce that the function \(F_\alpha\) is convex. Thus applying Lemma 1.2 in (2.6) we obtain

$$\begin{aligned} \phi (z)*l(z)\prec F_\alpha (z)*l(z)\quad (z\in \Delta ). \end{aligned}$$
(2.8)

Now from (2.7) and (2.8), we can obtain

$$\begin{aligned} \int _{0}^{z}\frac{\phi (t)}{t}\mathrm{d}t\prec \int _{0}^{z}\frac{F_\alpha (t)}{t}\mathrm{d}t\quad (z\in \Delta ). \end{aligned}$$

Thus

$$\begin{aligned} \frac{f(z)}{z}= \exp \int _{0}^{z}\frac{\phi (t)}{t}\mathrm{d}t\prec \int _{0}^{z}\frac{F_\alpha (t)}{t}\mathrm{d}t=\frac{{\tilde{f}}(z)}{z}. \end{aligned}$$

This completes the proof of theorem. \(\square\)

Here by combining Theorem 2.4, Theorem 2.5 and (1.1), we get:

Theorem 2.6

Let \(f\in \mathcal {BS}(\alpha )\), \(0 \le \alpha \le 3-2\sqrt{2}\)and\(|z|=r<1\). Then

$$\begin{aligned} \left( \frac{1-r\sqrt{\alpha }}{1+\sqrt{\alpha }} \right) ^{\frac{1}{2\sqrt{\alpha }}}\le \mathrm{Re}\left( \frac{f(z)}{z}\right) \le \left( \frac{1+r\sqrt{\alpha }}{1-r\sqrt{\alpha }} \right) ^{\frac{1}{2\sqrt{\alpha }}}\quad (z\in \Delta ). \end{aligned}$$
(2.9)

The result is sharp.

Proof

By the subordination principle, we have:

$$\begin{aligned} f(z)\prec g(z)\Rightarrow f(|z|<r)\subset g(|z|<r)\quad (0\le r<1). \end{aligned}$$

From Theorem 2.4, since F(z) is convex univalent in \(\Delta\), and it is real for real z, thus it maps the disc \(|z|=r<1\) onto a convex set symmetric which respect to the real axis laying between \(F(-r)-1\) and \(F(r)-1\). Now the assertion is obtained from Theorem 2.5. \(\square\)