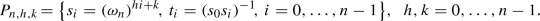Abstract
We find monodromy formulas for line arrangements that are fibered with respect to the projection from one point. We use them to find 0-dimensional translated components in the first characteristic variety of the arrangement  determined by a regular n-polygon and its diagonals. We also find new 1-dimensional translated components which generalize the well-known case of the \(B_3\)-deleted arrangement.
determined by a regular n-polygon and its diagonals. We also find new 1-dimensional translated components which generalize the well-known case of the \(B_3\)-deleted arrangement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An abelian local system  on the complement
on the complement  of a hyperplane arrangement
of a hyperplane arrangement  in \({\mathbb {C}}^N\) is defined by choosing one non-zero complex number \(\rho _{\ell }\) for each hyperplane
in \({\mathbb {C}}^N\) is defined by choosing one non-zero complex number \(\rho _{\ell }\) for each hyperplane  . For a generic choice of parameters \(\rho _{\ell }\), it is well known that homology concentrates in the top dimension N (see e.g. [14]). The i-th characteristic variety of
. For a generic choice of parameters \(\rho _{\ell }\), it is well known that homology concentrates in the top dimension N (see e.g. [14]). The i-th characteristic variety of  is the subvariety
is the subvariety

where  . Broad literature on this subject is known, also in connection with the theory of resonance varieties and the study of the cohomology of the associated Milnor fiber (see e.g. [1, 3,4,5,6, 8,9,10,11,12, 15, 17,18,19, 21, 24, 25, 27, 28]).
. Broad literature on this subject is known, also in connection with the theory of resonance varieties and the study of the cohomology of the associated Milnor fiber (see e.g. [1, 3,4,5,6, 8,9,10,11,12, 15, 17,18,19, 21, 24, 25, 27, 28]).
Probably the main problem is understanding if the characteristic varieties are combinatorially determined (see e.g. [16]). This is known to be true for their “homogeneous part”, which corresponds to the resonance variety by the tangent cone theorem (see e.g. [7] for general references). Meanwhile the translated components of the characteristic variety are still not well understood; in particular, the geometric description which is known for the translated components of dimension at least 1 does not work in the same way for the 0-dimensional translated components (see also [2]).
For these reasons we think that it can be useful to produce more examples (interesting in themselves) such that the characteristic variety has some translated 0-dimensional essential component.
In this paper we outline a different approach, based on an (apparently new) elementary description of the characteristic variety. We consider here the case \(N=2\). We find that the arrangement  determined by a regular n-polygon and its diagonals produces the above mentioned phenomenon for \(n\hbox {\,\,\char 062\,\,}5\), namely we find \(\phi (n)\) translated 0-dimensional components in its characteristic variety (here \(\phi \) is the Euler function). This fact was experimentally observed in [20] by using computer methods, up to \(n=7\).
determined by a regular n-polygon and its diagonals produces the above mentioned phenomenon for \(n\hbox {\,\,\char 062\,\,}5\), namely we find \(\phi (n)\) translated 0-dimensional components in its characteristic variety (here \(\phi \) is the Euler function). This fact was experimentally observed in [20] by using computer methods, up to \(n=7\).
The arrangement  belongs to the class of fibered arrangements: the projection through its “center” gives a fibration of the complement
belongs to the class of fibered arrangements: the projection through its “center” gives a fibration of the complement  over
over  with fiber
with fiber  .
.
We obtain the above result by using algebraic complexes which compute the parallel transport and the monodromy of the first homology group of the fiber, which we think are interesting in themselves. For example, we deduce a restriction on essential components of the characteristic variety (Theorem 2.9) and a description of 
 as the set of points such that the transpose of the monodromy operators have a common eigenvector (Theorem 2.10).
as the set of points such that the transpose of the monodromy operators have a common eigenvector (Theorem 2.10).
For the arrangement  , we use the algebraic complexes constructed in Sect. 2 to make explicit computations. If \(\omega _n\) is an n-th primitive root of 1, we find that assigning to the edges of the polygon the parameter \((\omega _n)^k\) and to the diagonals the parameter \((\omega _n)^{k(n-2)}\), for \(k=1,\dots ,n-1\), lowers the rank of the boundary operator in the algebraic complex computing
, we use the algebraic complexes constructed in Sect. 2 to make explicit computations. If \(\omega _n\) is an n-th primitive root of 1, we find that assigning to the edges of the polygon the parameter \((\omega _n)^k\) and to the diagonals the parameter \((\omega _n)^{k(n-2)}\), for \(k=1,\dots ,n-1\), lowers the rank of the boundary operator in the algebraic complex computing  , therefore the corresponding point \(P_{n,k}\) belongs to
, therefore the corresponding point \(P_{n,k}\) belongs to  . In case k and n are coprime, we deduce that \(P_{n,k}\) is an isolated point in the characteristic variety. Our argument works for \(n\hbox {\,\,\char 062\,\,}5\) and uses the description (Theorem 2.10) of the characteristic variety and the remark that triple points give simple eigenvalues for the corresponding monodromy operators. We find that the shape of the common eigenvector imposes equalities among the eigenvalues of the monodromy operators that define a 0-dimensional locus.
. In case k and n are coprime, we deduce that \(P_{n,k}\) is an isolated point in the characteristic variety. Our argument works for \(n\hbox {\,\,\char 062\,\,}5\) and uses the description (Theorem 2.10) of the characteristic variety and the remark that triple points give simple eigenvalues for the corresponding monodromy operators. We find that the shape of the common eigenvector imposes equalities among the eigenvalues of the monodromy operators that define a 0-dimensional locus.
When n and k are not coprime, our argument can also be used. In this case the shape of the common eigenvector imposes less equalities (so, a higher dimensional locus in general). For \(n=8\), we find (Theorem 3.7) a translated 1-dimensional component which contains the two points \(P_{8,2}\) and \(P_{8,6}\) (in contrast with [26, pp. 45–46]; see Remark 3.6). One can easily see that such translated component cannot be obtained by using the method of [6, Section 5.5]; therefore our method seems indeed novel. This last construction generalizes to the case \(n=4m\): we find an explicit 1-dimensional translated component containing \(P_{n,m}\) and \(P_{n,3m}\) (Theorem 3.12). When \(n=4\), this gives another description of the 1-dimensional translated component found in [24]. The examples in Theorems 3.7 and 3.12 are the first examples of translated 1-dimensional components to be found after [24], not obtained by the method in [6] (see Remark 3.9).
We also remark that our approach can be generalized (with some modifications) to not necessarily fibered arrangements (we will return to this in future work).
2 Algebraic complexes
In this section we produce an algebraic complex computing local homology for a line arrangement. This complex seems particularly convenient in case of a fibered arrangement, in which case it is smaller than the one in [12, 22].
Let  be an affine line arrangement; we assume that
be an affine line arrangement; we assume that  is defined over \({\mathbb {R}}\) because formulas are easier to write, but all we say can be generalized to general complex arrangements. Let
is defined over \({\mathbb {R}}\) because formulas are easier to write, but all we say can be generalized to general complex arrangements. Let  be its complement in
be its complement in  ; let \(\pi :{\mathbb {C}}^2\!\rightarrow {\mathbb {C}}\) be the projection \(\pi (x,y)=x\) onto the x-axis, and
; let \(\pi :{\mathbb {C}}^2\!\rightarrow {\mathbb {C}}\) be the projection \(\pi (x,y)=x\) onto the x-axis, and  its restriction. Let
its restriction. Let  be the set of singular points of the arrangement,
be the set of singular points of the arrangement,  its projection, and
its projection, and  . Then
. Then

is a fiber bundle with fibers  , \(x\in B\). We divide the arrangement
, \(x\in B\). We divide the arrangement

into horizontal and vertical lines, meaning that  for some
for some  , while \(\pi (\ell _i)={\mathbb {C}}\). Notice that if for all
, while \(\pi (\ell _i)={\mathbb {C}}\). Notice that if for all  the vertical line \(\pi ^{-1}(\xi )\) is in
the vertical line \(\pi ^{-1}(\xi )\) is in  , then
, then  , so the whole complement
, so the whole complement  is a fiber bundle over B. Let
is a fiber bundle over B. Let  , \(x\in B\); then
, \(x\in B\); then  , where
, where  for \(i=1,\dots ,n\).
for \(i=1,\dots ,n\).
We fix a fiber  , \(x_0\in B\), \(x_0\in {\mathbb {R}}\); take a basepoint \(P_0\equiv (x_0,y_0)\in F_0\) with
, \(x_0\in B\), \(x_0\in {\mathbb {R}}\); take a basepoint \(P_0\equiv (x_0,y_0)\in F_0\) with  , and elementary well-ordered generators \(\alpha _1,\dotsc ,\alpha _n\) of \(\pi _1(F_0)\), where \(\alpha _i\) is constructed by using a path connecting \(P_0\) to a small circle around \(\ell _i\cap F_0\). The indices of the lines are taken according to the growing intersections with the real axis
, and elementary well-ordered generators \(\alpha _1,\dotsc ,\alpha _n\) of \(\pi _1(F_0)\), where \(\alpha _i\) is constructed by using a path connecting \(P_0\) to a small circle around \(\ell _i\cap F_0\). The indices of the lines are taken according to the growing intersections with the real axis  .
.
We can make the same construction for any fiber \(F_x\), \(x\in B\), \(x\in {\mathbb {R}}\), by using the basepoint  and generators \(\alpha ^{(x)}_i\); the indices here are locally computed according to the growing intersections of the lines with
and generators \(\alpha ^{(x)}_i\); the indices here are locally computed according to the growing intersections of the lines with  .
.
We are interested in the local homology of  , where we consider the abelian local system defined by taking \({\mathbb {C}}\) as an
, where we consider the abelian local system defined by taking \({\mathbb {C}}\) as an  -module: the action is given by taking standard generators (small circles around the hyperplanes) into multiplication by non-zero numbers. So, such local systems correspond to
-module: the action is given by taking standard generators (small circles around the hyperplanes) into multiplication by non-zero numbers. So, such local systems correspond to  -tuples of parameters in \(({\mathbb {C}}^*)^{n+m}\).
-tuples of parameters in \(({\mathbb {C}}^*)^{n+m}\).
We call \(s_1,\dots ,s_n\) and \(t_1,\dots ,t_m\) the parameters corresponding to the lines \(\ell _1,\dots ,\ell _n\) and \(\ell '_1,\dots ,\ell '_m\), respectively. Denote by  the corresponding local system. We also set
the corresponding local system. We also set  .
.
In this paper we will assume that  fibers over B; it corresponds, as said before, to the case where the singular set
fibers over B; it corresponds, as said before, to the case where the singular set  is contained in the union of vertical lines.
is contained in the union of vertical lines.
Lemma 2.1
We have

where the second factor on the right vanishes if  is non-trivial (i.e., some \(s_i\ne 1\)).
is non-trivial (i.e., some \(s_i\ne 1\)).
Proof
By standard constructions (see e.g. [13, Section 4.17]),

This is (1) when we consider the homology groups  as \(\pi _1(B,x_0)\)-modules and the well-known correspondence between local systems and representations of the fundamental group on one fixed fiber (see [23]). The 0-th local homology group is well known to vanish for non-trivial coefficients. \(\square \)
as \(\pi _1(B,x_0)\)-modules and the well-known correspondence between local systems and representations of the fundamental group on one fixed fiber (see [23]). The 0-th local homology group is well known to vanish for non-trivial coefficients. \(\square \)
So we have to compute the term  , where
, where  is seen as a \(\pi _1(B)\)-module (actually, an \(H_1(B;{\mathbb {Z}})\)-module); the precise form of the action will be included in Theorem 2.8.
is seen as a \(\pi _1(B)\)-module (actually, an \(H_1(B;{\mathbb {Z}})\)-module); the precise form of the action will be included in Theorem 2.8.
Lemma 2.2
If  is non-trivial, then
is non-trivial, then  . As generators we can take the classes of
. As generators we can take the classes of

if no \(s_i\) equals 1.
Proof
The fiber \(F_0\) deformation retracts onto a wedge of n 1-spheres, given by \(\bigcup _{i=1}^n\ \alpha _i\). Therefore by standard methods to compute the homology we are done.\(\square \)
To compute the monodromy on \(H_1\), we need to understand the parallel transport

where \(\gamma (x,x')\) is a path in B connecting x with \(x'\) and  . We compute the parallel transport for any points
. We compute the parallel transport for any points  , where \({\mathbb {R}}\) is the real axis of the first coordinate (recall that we are assuming
, where \({\mathbb {R}}\) is the real axis of the first coordinate (recall that we are assuming  ). We denote by \({\widetilde{\alpha }}{}^{\,(x)}_{i,\,i+1}\), \(i=1,\dots ,n-1\), the generators of
). We denote by \({\widetilde{\alpha }}{}^{\,(x)}_{i,\,i+1}\), \(i=1,\dots ,n-1\), the generators of  , constructed as those in (2), by using the \(\alpha ^{(x)}_i\)’s. Formulas look better if we take as generators
, constructed as those in (2), by using the \(\alpha ^{(x)}_i\)’s. Formulas look better if we take as generators

Of course, this requires each \(s_i\ne 1\), but since we are interested in essential components of the characteristic variety (i.e., not contained in any coordinate tori \(s_i=1\)), this is not a serious restriction.
Given  , we consider a path
, we consider a path  , \(t\in [0,1]\), in B, connecting x and \(x'\), and such that \(\gamma \cap {\mathbb {R}}=\{x,x'\}\) and
, \(t\in [0,1]\), in B, connecting x and \(x'\), and such that \(\gamma \cap {\mathbb {R}}=\{x,x'\}\) and  for all \(t\in [0,1]\) (i.e., \(\gamma \) leaves the real axis on the left while traveling from x to \(x'\)). We denote by \(\tau (x,x')\) the corresponding transport isomorphism (3).
for all \(t\in [0,1]\) (i.e., \(\gamma \) leaves the real axis on the left while traveling from x to \(x'\)). We denote by \(\tau (x,x')\) the corresponding transport isomorphism (3).
Let \(\sigma =\sigma (x,x')\) be the permutation of the indices \(1,\dots ,n\) which is obtained as follows: the i-th line in the x-ordering (considering the growing intersections with  ) is the
) is the  -th line in the \(x'\)-ordering. For each \(i=1,\dots ,n-1\) we set
-th line in the \(x'\)-ordering. For each \(i=1,\dots ,n-1\) we set  or \(-1\) depending on whether
or \(-1\) depending on whether  or
or  .
.
Theorem 2.3
(Parallel transport) We have

Here  and
and  .
.
Proof
The proof is a standard computation and it is obtained by the following steps. First, remark that any generator in (2) is obtained from Fox calculus from the commutator \([\alpha _i,\alpha _{i+1}]\) as

where  is the valuation homomorphism taking \(\alpha _i\) to \(s_i\).
is the valuation homomorphism taking \(\alpha _i\) to \(s_i\).
Next, we remark that while the path \(\gamma \) turns around the projection of some singularity of a half-circle, the corresponding points in the vertical line make a half-twist, giving rise to a “local permutation” which takes a sequence of consecutive numbers to the opposite sequence (i.e., \(k,\dotsc ,k+h\) goes to \(k+h,\dotsc ,k\)).
By induction on the number of points in  separating x from \(x'\), we easily see that a generator \(\alpha ^{(x)}_i\) is taken by \(\gamma \) to
separating x from \(x'\), we easily see that a generator \(\alpha ^{(x)}_i\) is taken by \(\gamma \) to  , where P is the product (in increasing order) of the
, where P is the product (in increasing order) of the  such that
such that  and \(\sigma ^{-1}(j)>i\). Then we apply Fox calculus as in (5) to the transform
and \(\sigma ^{-1}(j)>i\). Then we apply Fox calculus as in (5) to the transform  and we conclude. \(\square \)
and we conclude. \(\square \)
The local monodromy around one point  is obtained by taking a point \(x\in {\mathbb {R}}\) very close to p and transporting the fiber of \(\pi ''\) starting from x around a circle centered at p. If
is obtained by taking a point \(x\in {\mathbb {R}}\) very close to p and transporting the fiber of \(\pi ''\) starting from x around a circle centered at p. If  is a point symmetric to x with respect to p, the local monodromy \(\mu _x\) is the automorphism of
is a point symmetric to x with respect to p, the local monodromy \(\mu _x\) is the automorphism of  which is obtained by composing
which is obtained by composing  . The “local permutation” \(\sigma (x,x')\) is determined by a partition \(\Delta _1,\Delta _2,\dotsc ,\Delta _h\) of the set \(\{1,\dotsc ,n\}\), where each \(\Delta \) is composed of consecutive numbers \(a,a+1,\dotsc ,a+r\) which are the indices (in the x-ordering) of the lines which intersect in a singular point P on the vertical line \({\mathbb {C}}_p\) (so the multiplicity of P as a singular point of
. The “local permutation” \(\sigma (x,x')\) is determined by a partition \(\Delta _1,\Delta _2,\dotsc ,\Delta _h\) of the set \(\{1,\dotsc ,n\}\), where each \(\Delta \) is composed of consecutive numbers \(a,a+1,\dotsc ,a+r\) which are the indices (in the x-ordering) of the lines which intersect in a singular point P on the vertical line \({\mathbb {C}}_p\) (so the multiplicity of P as a singular point of  equals \(\#\,\Delta +1\)).
equals \(\#\,\Delta +1\)).
Theorem 2.4
(Local monodromy) With the previous notations, the local monodromy around p is given by

where (a) occurs if i and \(i+1\) belong to the same block \(\Delta \) of \(\sigma (x,x')\) and (b) occurs if i is the last element of the block  and \(i+1\) is the first element of the next block
and \(i+1\) is the first element of the next block  .
.
Proof
The proof directly follows from (4) and  . \(\square \)
. \(\square \)
As an immediate consequence of (6) we have
Corollary 2.5
Let  and let \(P_1,\dotsc ,P_h\) be the singular points of
and let \(P_1,\dotsc ,P_h\) be the singular points of  in the vertical line \({\mathbb {C}}_p\), having multiplicities \(m_1,\dotsc ,m_h\), respectively (\(m_1+\cdots +m_h=n+h\)). Then the local monodromy \(\mu _x\) has characteristic polynomial
in the vertical line \({\mathbb {C}}_p\), having multiplicities \(m_1,\dotsc ,m_h\), respectively (\(m_1+\cdots +m_h=n+h\)). Then the local monodromy \(\mu _x\) has characteristic polynomial

and it is diagonalizable if all eigenvalues of the form \(\prod s_{\ell }\) are different from 1. Here we use \(s_{\ell }\) to denote the parameter corresponding to the horizontal line \(\ell \).
Now we consider the global monodromy  . For each point
. For each point  we denote by
we denote by  two points close to p and lying on opposite sides of p in \({\mathbb {R}}\); assume that \(x_p\) is the point lying in the segment \([p,x_0]\subset {\mathbb {R}}\).
two points close to p and lying on opposite sides of p in \({\mathbb {R}}\); assume that \(x_p\) is the point lying in the segment \([p,x_0]\subset {\mathbb {R}}\).
The easiest way to compute monodromy is to take generators  for \(\pi _1(B,x_0)\); such generator circles around all the projections of the singular points
for \(\pi _1(B,x_0)\); such generator circles around all the projections of the singular points  counterclockwise. By using the parallel transport (4) we get
counterclockwise. By using the parallel transport (4) we get
Theorem 2.6
(Global monodromy I) The global monodromy \(\mu \) is determined by

Here [a, b] stands for the segment connecting the two points a and b in the real axis (of \({\mathbb {C}}_{x'_p}\) and \({\mathbb {C}}_{x_0}\)).
It is convenient to take elementary generators of \(\pi _1(B,x_0)\) associated with p: the path \(\gamma _p\) is composed with the sequence

Clearly such paths give a well-ordered set of elementary generators of \(\pi _1(B,x_0)\), so the global monodromy is determined by their images.
Theorem 2.7
(Global monodromy II) The global monodromy \(\mu \) is determined by the maps
where \(\tau (x_0,x_p)\) is the parallel transport in (4) and \(\mu _{x_p}\) is the local monodromy in (6).
It is also possible to write explicit formulas for (9): formulas (4) and (6) make possible to compute the images of the generators \(\alpha _{i,\,i+1}\); we do not report such formulas here because we do not need their explicit form now. Notice also that (9) and (8) are related by
where the \(p_i\) are ordered according to increasing distance from \(x_0\). We now come back to the computation of  in (1). The space B deformation retracts onto a wedge of 1-spheres, actually onto the union \(\bigcup _{p\in \pi ({\mathcal {S}})} \gamma _p\), where the unique 0-cell is \(x_0\). By standard methods which compute local system homology we obtain
in (1). The space B deformation retracts onto a wedge of 1-spheres, actually onto the union \(\bigcup _{p\in \pi ({\mathcal {S}})} \gamma _p\), where the unique 0-cell is \(x_0\). By standard methods which compute local system homology we obtain
Theorem 2.8
The vector space  is the cokernel of the map
is the cokernel of the map

defined as

where we set here \(t_p\) for the parameter associated with the vertical line  .
.
Let \(M_p\) be the matrix of \(\mu ([\gamma _p])\) in the given basis. Then the matrix B of \(\partial _1\) consists of m square blocks \(B_p=t_pM_p-\mathrm {Id}\), one for each  , of order \(n-1\), so \(B=[B_1,\dotsc ,B_m]\). It follows that the block \(B_p\) has rank lower than \(n-1\) iff \(t_p\) coincides with the inverse of an eigenvalue of \(\mu ([\gamma _p])\). Therefore either \(t_p=1\) or \(t_p\prod _{P_i\in \ell } s_{\ell }=1\) for some singular point \(P_i\in {\mathbb {C}}_p\) of order at least 3 (see (7)). We obtain the following corollary.
, of order \(n-1\), so \(B=[B_1,\dotsc ,B_m]\). It follows that the block \(B_p\) has rank lower than \(n-1\) iff \(t_p\) coincides with the inverse of an eigenvalue of \(\mu ([\gamma _p])\). Therefore either \(t_p=1\) or \(t_p\prod _{P_i\in \ell } s_{\ell }=1\) for some singular point \(P_i\in {\mathbb {C}}_p\) of order at least 3 (see (7)). We obtain the following corollary.
Theorem 2.9
The essential components of the characteristic variety of  are contained in
are contained in

where we write \(\rho _{\ell }\) for the parameter associated with the line \(\ell \) (in our previous notations it is of the shape \(s_i\) for horizontal lines and  for vertical lines).
for vertical lines).
As another immediate consequence we get the following description of the characteristic variety of  .
.
Theorem 2.10
The essential part of the characteristic variety  coincides with the set of values \((s,t)\in ({\mathbb {C}}^*)^{n+m}\) such that the transpose of the monodromy operators \(\mu ([\gamma _p])(s)\),
coincides with the set of values \((s,t)\in ({\mathbb {C}}^*)^{n+m}\) such that the transpose of the monodromy operators \(\mu ([\gamma _p])(s)\),  , have a common eigenvector relative to eigenvalues \(t_p^{-1}\),
, have a common eigenvector relative to eigenvalues \(t_p^{-1}\),  .
.
Proof
Indeed, a linear relation among the rows of the boundary matrix B is given by a vector v such that \({}^{\mathrm{t}}v B_p = {}^\mathrm{t}v(t_p M_p-\mathrm {Id})=0\),  . \(\square \)
. \(\square \)
3 Some computations
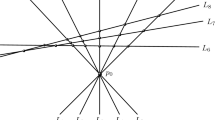
We consider here the arrangement  which is projectively given by taking the lines spanned by the edges of a regular n-polygon, together with all its n diagonals (see Figs. 1 and 3 for the case \(n=6\) and 7, respectively). Notice that there is an n-tuple point P which is the intersection of the diagonals. For odd n, on each diagonal we have, besides P, one double point at the intersection with the middle point of an edge, and \((n-1)/2\) triple points. For even n, \(n=2k\), we have k diagonals passing through two opposite vertices of the n-polygon, each of them containing k triple points; and other k diagonals passing through the middle points of two opposite sides of the n-polygon, each of them containing two double points and \(k-1\) triple points. Of course, the projection from P makes the complement
which is projectively given by taking the lines spanned by the edges of a regular n-polygon, together with all its n diagonals (see Figs. 1 and 3 for the case \(n=6\) and 7, respectively). Notice that there is an n-tuple point P which is the intersection of the diagonals. For odd n, on each diagonal we have, besides P, one double point at the intersection with the middle point of an edge, and \((n-1)/2\) triple points. For even n, \(n=2k\), we have k diagonals passing through two opposite vertices of the n-polygon, each of them containing k triple points; and other k diagonals passing through the middle points of two opposite sides of the n-polygon, each of them containing two double points and \(k-1\) triple points. Of course, the projection from P makes the complement  a fiber bundle. We take one of the diagonals to infinity, so the projection
a fiber bundle. We take one of the diagonals to infinity, so the projection  describes
describes  as a fiber bundle over
as a fiber bundle over  with fiber
with fiber  (see Figs. 2 and 4).
(see Figs. 2 and 4).
Let  , \(p_i\in {\mathbb {R}}\), be the vertical lines, ordered according to \(p_1>\cdots >p_{n-1}\). In the notations of the previous section, let \(x_0\in {\mathbb {R}}\) be a basepoint in the x-coordinate: we choose \(x_0\gg p_1\). Let also \(\ell _1,\dotsc ,\ell _n\) be the horizontal lines, ordered according to increasing intersections with the real axis of \({\mathbb {C}}_0\). Fix also points \(x_i=p_i+\epsilon \), \(x'_i= p_i-\epsilon \), with \(i=1,\dotsc , n-1\) and \(0<\epsilon \ll 1\). We trivially have (see Figs. 2 and 4)
, \(p_i\in {\mathbb {R}}\), be the vertical lines, ordered according to \(p_1>\cdots >p_{n-1}\). In the notations of the previous section, let \(x_0\in {\mathbb {R}}\) be a basepoint in the x-coordinate: we choose \(x_0\gg p_1\). Let also \(\ell _1,\dotsc ,\ell _n\) be the horizontal lines, ordered according to increasing intersections with the real axis of \({\mathbb {C}}_0\). Fix also points \(x_i=p_i+\epsilon \), \(x'_i= p_i-\epsilon \), with \(i=1,\dotsc , n-1\) and \(0<\epsilon \ll 1\). We trivially have (see Figs. 2 and 4)
Lemma 3.1
- (i):
-
For odd n the local permutation \(\sigma _i=\sigma (x_i,x'_i)\) is given by
-
\(\sigma _i=(1,2)(3,4)\cdots (n-2,n-1)(n)\) if i is odd;
-
\(\sigma _i=(1)(2,3)(4,5)\cdots (n-1,n)\) if i is even.
- (ii):
-
For even n the local permutation \(\sigma _i=\sigma (x_i,x'_i)\) is given by
-
\(\sigma _i=(1)(2,3)\cdots (n-2,n-1)(n)\) if i is odd;
-
\(\sigma _i=(1,2)(3,4)\cdots (n-1,n)\) if i is even.
Let \(\omega _n\) be a primitive n-th root of the unity. We use results from the previous section to find explicit points in the characteristic variety.
Theorem 3.2
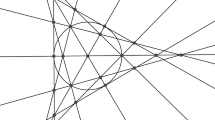
The n points \(P_{n,k}\in ({\mathbb {C}}^*)^{2n-1}\), \(k=0,\dotsc ,n-1\), whose coordinates are given by the (s, t) with  for \(j=1,\dotsc ,n\) and
for \(j=1,\dotsc ,n\) and  for \(j=1,\dotsc ,n-1\), belong to the characteristic variety.
for \(j=1,\dotsc ,n-1\), belong to the characteristic variety.
Proof
The case \(k=0\) is trivial since \(P_{n,0}=(1,\dotsc ,1)\) (\(2n-1\) entries). So assume \(k>0\). Let us consider the row vector

where we set for brevity \(\omega =\omega _n^k\). We prove that \(v_n\) is an eigenvector for the transpose operator \({}^\mathrm{t}\partial _1([\gamma _p])\) in (11) for all \(\gamma _p\) when the parameters take the above values. This shows that such parameters lower the rank of \(\partial _1\) in (10), so the corresponding point belongs to the characteristic variety.
Notice that by Lemma 3.1 the local monodromy around \(p_i\) coincides with the local monodromy \(M_1\) around \(p_1\) for odd i or with the local monodromy \(M_2\) around \(p_2\) for even i. Therefore by the expression (9) for the monodromy it is sufficient to prove that \(v_n\) is an eigenvector for \({}^{\mathrm{t}} M_1\) and \({}^{\mathrm{t}} M_2\) with parameters \(s_i=\omega \), with respect to the eigenvalue \(\omega ^{n-2}\), and that both \(\tau (x_1,x_2)^{-1}\) and \(\tau (x_2,x_3)^{-1}\) take \(v_n\) into an eigenvector of \({}^{\mathrm{t}}M_2\), \({}^{\mathrm{t}}M_1\) respectively.
The first assertion is easily proven by looking at formulas (6). With the given parameters, there are as many zero columns in \(t_iM_i-\mathrm {Id}\) as triple points. So, for odd n there are \((n-1)/2\) non-zero columns, at even position for \(t_1M_1-\mathrm {Id}\), at odd position for \(t_2M_2-\mathrm {Id}\); for even n, there are n/2 non-zero columns at odd position for \(t_1M_1-\mathrm {Id}\) and \((n-2)/2\) non-zero columns at even position for \(t_2M_2-\mathrm {Id}\). The non-zero j-th column has entries \(\omega ^{n-2}-1\) in position (j, j), preceded (if it is not the first entry of the column) by \(\omega ^{n-2}(1-\omega )\), and followed (if it is not the last entry of the column) by \(\omega ^{n-1}-1\); all other entries of the column vanish. Then it is easy to check that multiplying on the left by \(v_n\) gives zero.
The form of \(T=\tau (x_1,x_2)^{-1}\) and  (with the given parameters) is derived from formula (4) and from Lemma 3.1. In case n is odd one obtains:
(with the given parameters) is derived from formula (4) and from Lemma 3.1. In case n is odd one obtains:
-
for odd j,
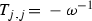 and \(T_{i,j}=0\) for \(i\ne j\);
and \(T_{i,j}=0\) for \(i\ne j\); -
for even j,
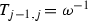 , \(T_{j,j}=T_{j+1,j}=1\), and \(T_{i,j}=0\) for all other i’s.
, \(T_{j,j}=T_{j+1,j}=1\), and \(T_{i,j}=0\) for all other i’s.
The shape of \(T'\) is completely analogous; it is enough to exchange the roles of even and odd j. For n even, the shape is the same exchanging T and \(T'\). Then it is easy to check directly that

and we conclude. \(\square \)
Remark 3.3
By symmetry, there is an obvious action of the cyclic group \(C_n\) generated by \(\sigma _n=(0,1,\dotsc ,n-1)\) onto the characteristic variety. Consider the edges of the n-polygon (in the projective picture) cyclically ordered as \(\ell _0,\dotsc ,\ell _{n-1}\). Let us cyclically order also the diagonals \(\ell '_0,\dotsc \ell '_{n-1}\), starting from the diagonal \(\ell '_0\) which is orthogonal to \(\ell _0\). Take a new parameter \(t_{n-1}\) for the line at infinity, with the condition that  . Then the action of \(\sigma _n\) on some point
. Then the action of \(\sigma _n\) on some point  in V is the point \((s_{\sigma _n(0)},\dotsc ,s_{\sigma _n(n-1)},t_{\sigma _n^2(0)},\dotsc ,t_{\sigma _n^2(n-1)})\) which also belongs to V. Notice that the points \(P_{n,k}\) are fixed by this action.
in V is the point \((s_{\sigma _n(0)},\dotsc ,s_{\sigma _n(n-1)},t_{\sigma _n^2(0)},\dotsc ,t_{\sigma _n^2(n-1)})\) which also belongs to V. Notice that the points \(P_{n,k}\) are fixed by this action.
With this labeling the double points are given by the intersection of the lines with indices  and the triple points are given by the intersections of the lines with indices
and the triple points are given by the intersections of the lines with indices  (taking indices mod n).
(taking indices mod n).
The next theorem needs a lemma.
Lemma 3.4
Let \(n\hbox {\,\,\char 062\,\,}5\) and let \(\omega _n\) be a primitive n-th root of 1.
- (i):
-
Let
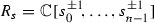 be the ring of Laurent polynomials in the variables \(s_0,\dotsc s_{n-1}\). The ideal
be the ring of Laurent polynomials in the variables \(s_0,\dotsc s_{n-1}\). The ideal 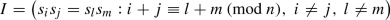
is 1-dimensional with n irreducible components

- (ii):
-
Let
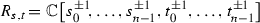 be the ring of Laurent polynomials in
be the ring of Laurent polynomials in 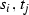 , \(i,j=0,\dots ,n-1\). Let J be the ideal
, \(i,j=0,\dots ,n-1\). Let J be the ideal 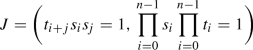
where we take all possible pairs
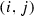 with \(i\ne j\), and the indices are mod n. Then J is 0-dimensional and defines the \(n^2\) points
with \(i\ne j\), and the indices are mod n. Then J is 0-dimensional and defines the \(n^2\) points 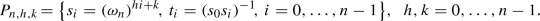
Proof
(i) At first we prove the relations
By multiplying the two relations (\(n>3\))
we deduce \(s_0^2=s_2s_{n-2}\). Therefore (13) follows for \(n>4\). So now we have all the relations of the form

Then one easily deduces for recurrence the relations

each time  . In particular, we have \(s_0^n=s_i^n\) for all \(i=1,\dotsc ,n-1\). Then \(s_1=(\omega _n)^h s_0\) for some h. From \(s_is_0=s_1s_{i-1}\) it follows by induction that \(s_i=(\omega _n)^{hi}s_0\) which proves (i).
. In particular, we have \(s_0^n=s_i^n\) for all \(i=1,\dotsc ,n-1\). Then \(s_1=(\omega _n)^h s_0\) for some h. From \(s_is_0=s_1s_{i-1}\) it follows by induction that \(s_i=(\omega _n)^{hi}s_0\) which proves (i).
For (ii), notice that the relations defining I follow from those which define J, so we have again \(s_i=(\omega _n)^{hi} s_0\), \(i=0,\dotsc ,n-1\), for some h in \(0,\dotsc ,n-1\). Now using \(t_i=(s_0s_i)^{-1}\) the last relation gives \(\prod s_i \prod \,(s_0s_i)^{-1}=(s_0)^{-n}=1\). Therefore \(s_0=\omega _n^k\) for some k in \(0,\dotsc ,n-1\). \(\square \)
In conclusion, we show
Theorem 3.5
The \(\phi (n)\) points \(P_{n,k}\) with \((n,k)=1\) of Theorem 3.2 are isolated points of the characteristic variety  .
.
Proof
We divide the proof into several steps.
I. We already know from Theorem 3.2 that  , \(k=0,\dotsc , n-1\). We directly check that
, \(k=0,\dotsc , n-1\). We directly check that  if \((n,k)=1\).
if \((n,k)=1\).
Indeed, the  -submatrix of \(\partial _1\) which corresponds to the local monodromy around the first two points \(p_1,p_2\) is already of rank \(n-2\). This follows from the explicit description of the matrices
-submatrix of \(\partial _1\) which corresponds to the local monodromy around the first two points \(p_1,p_2\) is already of rank \(n-2\). This follows from the explicit description of the matrices  , \(i=1,2\), given in Theorem 3.2. By taking a basepoint between the two points \(p_1\) and \(p_2\) (which amounts to simultaneously conjugate the blocks of the boundary matrix), the two blocks \(B_1\) and \(B_2\) are submatrices of the corresponding boundary \(\partial _1\). Reordering the \(n-1\) non-zero columns of \(B_1\) and \(B_2\) gives a tridiagonal matrix of order \(n-1\) which has clearly rank \(n-2\).
, \(i=1,2\), given in Theorem 3.2. By taking a basepoint between the two points \(p_1\) and \(p_2\) (which amounts to simultaneously conjugate the blocks of the boundary matrix), the two blocks \(B_1\) and \(B_2\) are submatrices of the corresponding boundary \(\partial _1\). Reordering the \(n-1\) non-zero columns of \(B_1\) and \(B_2\) gives a tridiagonal matrix of order \(n-1\) which has clearly rank \(n-2\).
Therefore,  if \(P'\) is a point close to \(P_{n,k}\). We have to show that
if \(P'\) is a point close to \(P_{n,k}\). We have to show that  if
if  and \(P'\) is close to \(P_{n,k}\).
and \(P'\) is close to \(P_{n,k}\).
II. It follows from the previous point that the left kernel of \(\partial _1\) is of dimension 1 in the given points, so it is spanned by the vector \(v_n\) of Theorem 3.2. Notice that, under the hypothesis \((n,k)=1\), all the coordinates of \(v_n\) are different from 0. It implies that any \(n-2\) rows of \(\partial _1\) are linearly independent, and this must remain true in a neighborhood of \(P_{n,k}\).
III. Recall from Theorem 2.10 that the vector \(v_n\) is a common eigenvector for the transposed monodromy operators. Let us write the explicit form of the first block \(t_1{}^{\mathrm{t}}M_1-\mathrm {Id}\) of the boundary operator for \(n=6\) and 7:
-
for \(n=6\),
$$\begin{aligned} t_1{}^{\mathrm{t}}M_1-\mathrm {Id}=\begin{bmatrix} t_1-1 &{}\quad t_1s_2(1-s_3) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad t_1s_2s_3-1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad t_1(1-s_2) &{}\quad t_1-1 &{}\quad t_1s_4(1-s_5) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad t_1s_4s_5-1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad t_1(1-s_4) &{}\quad t_1-1 \end{bmatrix}; \end{aligned}$$ -
for \(n=7\),
$$\begin{aligned} t_1{}^{\mathrm{t}}M_1-\mathrm {Id}=\begin{bmatrix} t_1s_1s_2-1 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ t_1(1-s_1) &{}\quad t_1-1&{}\quad t_1s_3(1-s_4) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad t_1s_3s_4-1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad t_1(1-s_3) &{}\quad t_1-1 &{}\quad t_1s_5(1-s_6) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad t_1s_5s_6-1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad t_1(1-s_5) &{}\quad t_1-1 \end{bmatrix}. \end{aligned}$$
Having  and all components of \(v_n\) different from 0 clearly gives
and all components of \(v_n\) different from 0 clearly gives
These conditions are equivalent to  each time
each time  form a triple point. Of course, we have the same conditions for all n.
form a triple point. Of course, we have the same conditions for all n.
IV. By symmetry, or changing coordinates by taking a point x close to the vertical line \(\ell '_i\) as basepoint, we obtain similar conditions for any vertical line.
Remark also that we can take to infinity any other line passing through the center of the n-polygon, obtaining similar conditions for the line \(\ell '_n\) with given parameter \(t_n\). Recall that in the projective situation, the product of all s and t equals 1.
V. It follows that \(P_{n,k}\) is contained in the zero locus of the ideal (with obvious notation)

Now notice that any point \(P'\) very close to \(P_{n,k}\) either does not belong to the characteristic variety or it corresponds to a common eigenvector \(v'_n\) still having non-vanishing components, so defining the same conditions. Therefore in a neighborhood of \(P_{n,k}\) the characteristic variety is contained in the zero locus of (14).
By Lemma 3.4 the ideal I is zero-dimensional (for \(n\hbox {\,\,\char 062\,\,}5\)), so we are done. \(\square \)
Remark 3.6
In [26, pp. 45–46] the case \(n=8\) is considered and the authors claim that the six points \(P_{8,k}\) for \(k=1,\dotsc ,7\), \(k\ne 4\), are isolated points in the characteristic variety. The argument used in Theorem 3.5 works for \((n,k)=1\); nevertheless, it can be refined in the following way. For \(n=8\) and \(k=2,6\), the eigenvector \(v_8\) in (12) has a unique zero component in the fourth coordinate:

(where \(\omega \) is a primitive 8-th root of the unity), and those are eigenvectors for both local monodromies \({}^{\mathrm{t}}M_1\) and \({}^{\mathrm{t}}M_2\). As in the proof of Theorem 3.5 we look at the explicit form of the local monodromy around the first two lines, which gives the two blocks in the boundary \(\partial _1\):
The non-zero positions of \(v_8\) give the equalities
from the first block, and
from the second block, which must hold in a neighborhood of \(P_{8,2}\).
Notice that the first vertical line corresponds in the projective picture to a line \(\ell '_0\) (notations of Remark 3.3) passing through the center and cutting two opposite edges of the octagon in the middle point. The second vertical line corresponds to a diagonal \(\ell '_1\) passing through two opposite vertices of the octagon. Among all triple points contained in these lines, the unique triple point which we are not considering in the equations (15) and (16) corresponds (in the projective picture) to that formed by \(\ell '_0\) and the two edges of the octagon which are “parallel” to \(\ell '_0\) (and parallel themselves).
By symmetry (or changing the coordinate system) we obtain analogous equations for all diagonals. That is, in a neighborhood of \(P_{8,2}\) (and of \(P_{8,6}\)), the characteristic variety is contained in the zero locus of the ideal \(I'\) which is obtained from the ideal I in (14) by deleting the four equations which correspond to the triple points determined by the four pairs of opposite edges of the octagon.
By making explicit computations we obtain that the ideal \(I'\) is 1-dimensional, and we finally get
Theorem 3.7
The characteristic variety of the arrangement  contains a 1-dimensional translated component with the following parametrization:
contains a 1-dimensional translated component with the following parametrization:

where x is a parameter in \({\mathbb {C}}^*\). Such component contains the two points \(P_{8,2}\) and \(P_{8,6}\) (which are therefore not isolated).
Proof
Once we have the explicit form (17) it is just a direct computation to see that it defines a component which is contained in the characteristic variety: we used both the expression of the matrix boundary \(\partial _1\) of Theorem 2.8 and also the description of the boundary in [12] (of course both of them give that (17) is contained in the characteristic variety).
It is also possible to give a proof which parallels the one in Theorem 3.2. In particular, we find an explicit common eigenvector for the transposed monodromy operators (Theorem 2.10), which is given (in terms of the parameter x) by
It is immediate to see that \(P_{8,2}\) and \(P_{8,6}\) are contained in (17) (with parameters \(x=\omega ^2\), \(x=\omega ^6\), respectively); in fact, notice that vectors \(v_{8,2}\) and \(v_{8,6}\) above are obtained as  and
and  .
.
As we have already remarked, in a neighborhood of these points the characteristic variety is 1-dimensional; therefore the component (17) is isolated. \(\square \)
Remark 3.8
Case \(n=4\), which corresponds to the \(B_3\)-deleted arrangement considered in [24], can also be included in our method. If we consider any of the points \(P_{n,k}\), \(k=1,2,3\), and we repeat the same construction as in Theorem 3.5, we obtain the same ideal I in (14), which is in this case 1-dimensional. In fact, the zero locus of I has four irreducible 1-dimensional components: one of these has the same shape as (17), being parametrized as

and it is the translated component appearing in [24]. It contains the two points \(P_{4,1}\) and \(P_{4,3}\). The other three components of the zero locus of I do not belong to the characteristic variety. (\(P_{4,2}\) belongs to a different component of the zero locus of I, and that component is not fully contained in the characteristic variety.)
Remark 3.9
In [6, Proposition 5.6] the authors explain a method to find translated, 1-dimensional components in terms of pointed multinets, which are a special case of multinets. The \(B_3\)-deleted arrangement is an example of an arrangement whose 1-dimensional translated component is obtained with this method.
One more example is given in [20, Chapter 5], where the arrangement  is given by ten projective lines with the following (affine) equation:
is given by ten projective lines with the following (affine) equation:
If we give all the ten lines weight 1 and add the infinity line \(\ell _{\infty }\) with weight 2, we obtain an arrangement of eleven lines which supports a pointed multinet, with special line \(\ell _{\infty }\). So  verifies the criterion in [6].
verifies the criterion in [6].
In case of the arrangement  of Theorem 3.7, such method would apply if one could find a bigger arrangement
of Theorem 3.7, such method would apply if one could find a bigger arrangement  with 17 lines, containing
with 17 lines, containing  , which supports a pointed multinet. It is just an exercise to prove the following
, which supports a pointed multinet. It is just an exercise to prove the following
Proposition 3.10
No arrangement  of 17 lines containing
of 17 lines containing  supports a multinet.
supports a multinet.
It follows that our example in Theorem 3.7 cannot be obtained by the method in [6].
Remark 3.11
Some other cases where \((n,k)\ne 1\) are known. For example, in case \(n=9\), \(k=3\), the point \(P_{9,3}\) is contained in a 2-dimensional component coming from a multinet (see [11]).
The argument outlined in Remark 3.6 can be extended to any case \(n=4m\) to produce a 1-dimensional translated component, generalizing (19), (17).
Theorem 3.12
When \(n=4m\), the characteristic variety  contains a 1-dimensional translated component parametrized as (the labelings are as in Remark 3.3)
contains a 1-dimensional translated component parametrized as (the labelings are as in Remark 3.3)

Proof
We outline the proof of the theorem, which parallels that of Theorem 3.7.
As in Theorem 3.2, by using the explicit form of the boundary one verifies that the points in (20) lower the rank of the boundary matrix, so the component is contained in  . We find a common eigenvector of the transposed monodromy operators, which generalizes (18),
. We find a common eigenvector of the transposed monodromy operators, which generalizes (18),

(the triple \([1,x-1,{}-x]\) repeats m times, separated by a 0).
Now consider the point \(P_{n,m}\), which is contained in (20) (with \(x=\omega ^m\)); a similar argument holds by using \(P_{n,3m}\) instead. As in the proof of Theorem 3.7, for this point the vector \(v_{n}\) in (12) is given by \(v_{n}={}-\omega ^mw_{n}(\omega ^m)\), where \(\omega \) is a primitive n-th root of the unity. Therefore \(v_{n}\) has \(4m-1\) entries which vanish exactly in the positions multiple of 4. The argument of Theorem 3.5 (or of Theorem 3.7) produces an ideal \(I'\) which is obtained from I by deleting, for each even i among \(0,\dotsc ,4m-1\), the \(m-1\) equations \(t_{i}s_{(i/2)+2j}s_{(i/2)-2j}=1\), for \(j=1,\dotsc ,m-1\) (indices are as in Remark 3.3 and are taken mod n). One sees that the zero locus \(Z(I')\) is of dimension 1 and (20) is contained in \(Z(I')\) as an irreducible component which contains \(P_{n,m}\) and \(P_{n,3m}\).
Then we conclude that such component is not contained in a higher dimensional one by the same argument as used in Theorem 3.5 (and Theorem 3.7): points of the characteristic variety which are close to \(P_{n,m}\) impose the same conditions, so they are contained in \(Z(I')\). \(\square \)
Remark 3.13
Analogous computations can be done for other points \(P_{n,k}\) where the number and the positions of the zero entries of the common eigenvector tell us what ideal to take. For example, we made some computations finding further isolated points in  for \(n=12\). Details and further applications will be provided later.
for \(n=12\). Details and further applications will be provided later.
References
Arapura, D.: Geometry of cohomology support loci for local systems I. J. Algebraic Geom. 6(3), 563–597 (1997)
Artal Bartolo, E., Cogolludo-Agustín, J.I., Matei, D.: Characteristic varieties of quasi-projective manifolds and orbifolds. Geom. Topol. 17(1), 273–309 (2013)
Callegaro, F.: The homology of the Milnor fiber for classical braid groups. Algebr. Geom. Topol. 6, 1903–1923 (2006)
Cohen, D.C., Orlik, P.: Arrangements and local systems. Math. Res. Lett. 7(2–3), 299–316 (2000)
Cohen, D.C., Suciu, A.I.: Characteristic varieties of arrangements. Math. Proc. Cambridge Philos. Soc. 127(1), 33–53 (1999)
Denham, G., Suciu, A.I.: Multinets, parallel connections, and Milnor fibrations of arrangements. Proc. London Math. Soc. 108(6), 1435–1470 (2014)
Dimca, A.: Hyperplane Arrangements. Universitext. Springer, Cham (2017)
Dimca, A., Papadima, Ş.: Finite Galois covers, cohomology jump loci, formality properties, and multinets. Ann. Sc. Norm. Super. Pisa Cl. Sci. 10(2), 253–268 (2011)
Dimca, A., Papadima, Ş., Suciu, A.I.: Topology and geometry of cohomology jump loci. Duke Math. J. 148(3), 405–457 (2009)
Falk, M.J.: Arrangements and cohomology. Ann. Combin. 1(2), 135–157 (1997)
Falk, M.J., Yuzvinsky, S.: Multinets, resonance varieties, and pencils of plane curves. Compositio Math. 143(4), 1069–1088 (2007)
Gaiffi, G., Salvetti, M.: The Morse complex of a line arrangement. J. Algebra 321(1), 316–337 (2007)
Godement, R.: Topologie algébrique et théorie des faisceaux. Actualités Sci. Ind. No. 1252. Publ. Math. Univ. Strasbourg. No. 13. Hermann, Paris (1958)
Kohno, T.: Homology of a local system on the complement of hyperplanes. Proc. Japan Acad. Ser. A Math. Sci. 62(4), 144–147 (1986)
Libgober, A.: Characteristic varieties of algebraic curves. In: Ciliberto, C., et al. (eds.) Applications of Algebraic Geometry to Coding Theory, Physics and NATO Science Series II: Mathematics, Physics and Chemistry Computation, vol. 36, pp. 215–254. Kluwer, Dordrecht (2001)
Libgober, A.: On combinatorial invariance of the cohomology of the Milnor fiber of arrangements and the Catalan equation over function fields. In: Terao, H., Yuzvinsky, S. (eds.) Arrangements of Hyperplanes - Sapporo 2009. Advanced Studies in Pure Mathematics, vol. 62, pp. 175–187. Mathematical Society of Japan, Tokyo (2012)
Libgober, A., Yuzvinsky, S.: Cohomology of the Orlik–Solomon algebras and local systems. Compositio Math. 121(3), 337–361 (2000)
Măcinic, A.D., Papadima, Ş.: On the monodromy action on Milnor fibers of graphic arrangements. Topology Appl. 156(4), 761–774 (2009)
Papadima, Ş., Suciu, A.I.: The Milnor fibration of a hyperplane arrangement: from modular resonance to algebraic monodromy. Proc. London Math. Soc. 114(6), 961–1004 (2017)
Papini, O.: Computational Aspects of Line and Toric Arrangements. PhD thesis, Università di Pisa (2018). https://etd.adm.unipi.it/t/etd-09262018-113931/
Salvetti, M., Serventi, M.: Twisted cohomology of arrangements of lines and Milnor fibers. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 17(4), 1461–1489 (2017)
Salvetti, M., Settepanella, S.: Combinatorial Morse theory and minimality of hyperplane arrangements. Geom. Topol. 11, 1733–1766 (2007)
Steenrod, N.E.: Homology with local coefficients. Ann. Math. 44(4), 610–627 (1943)
Suciu, A.I.: Translated Tori in the characteristic varieties of complex hyperplane arrangements. Topology Appl. 118(1–2), 209–223 (2002)
Suciu, A.I.: Hyperplane arrangements and Milnor fibrations. Ann. Fac. Sci. Toulouse Math. 23(2), 417–481 (2014)
Torielli, M., Yoshinaga, M.: Resonant bands, Aomoto complex, and real 4-nets. J. Singul. 11, 33–51 (2015)
Yoshinaga, M.: Milnor fibers of real line arrangements. J. Singul. 7, 220–237 (2013)
Yoshinaga, M.: Resonant bands and local system cohomology groups for real line arrangements. Vietnam J. Math. 42(3), 377–392 (2014)
Acknowledgements
Open access funding provided by Università di Pisa within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Ştefan Papadima
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Partially supported by: progetto PRA “Geometria e Topologia delle Varietà” (2018), Università di Pisa; INdAM; MIUR.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Papini, O., Salvetti, M. Some computations on the characteristic variety of a line arrangement. European Journal of Mathematics 6, 1020–1038 (2020). https://doi.org/10.1007/s40879-020-00422-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-020-00422-z



 (projective picture)
(projective picture)
 (affine picture) projected onto the x-axis
(affine picture) projected onto the x-axis
 (projective picture)
(projective picture)
 (affine picture) projected onto the x-axis
(affine picture) projected onto the x-axis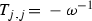 and
and 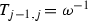 ,
, 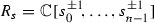 be the ring of Laurent polynomials in the variables
be the ring of Laurent polynomials in the variables 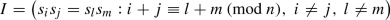

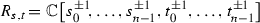 be the ring of Laurent polynomials in
be the ring of Laurent polynomials in 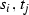 ,
, 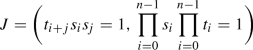
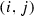 with
with