Objective Bayesian Estimation for the Differential Entropy Measure Under Generalized Half-Normal Distribution

Abstract

The evaluation of the information entropy content in the data analysis is an effective role in the assessment of fatigue damage. Due to the connection between the generalized half-normal distribution and fatigue extension, the objective inference for the differential entropy of the generalized half-normal distribution is considered in this paper. The Bayesian estimates and associated credible intervals are discussed based on different non-informative priors including Jeffery, reference, probability matching, and maximal data information priors for the differential entropy measure. The Metropolis–Hastings samplers data sets are used to estimate the posterior densities and then compute the Bayesian estimates. For comparison purposes, the maximum likelihood estimators and asymptotic confidence intervals of the differential entropy are derived. An intensive simulation study is conducted to evaluate the performance of the proposed statistical inference methods. Two real data sets are analyzed by the proposed methodology for illustrative purposes as well. Finally, non-informative priors for the original parameters of generalized half-normal distribution based on the direct and transformation of the entropy measure are also proposed and compared.

1 Introduction

The differential entropy $H_X(f)$ of a continuous random variable X with the probability density function (PDF) f(x) is defined (see, Shannon [1]) by

$$\begin{aligned} H_X(f)=\textrm{E}[-\ln f(x)]=-\int _{-\infty }^\infty f(x) \ln f(x) \,\hbox {d}x. \end{aligned}$$

(1)

In fact, it measures the uniformity of a distribution such that it increases when f(x) approaches uniform distribution that means the prediction of an outcome from f(x) gets more difficult. Additionally, for sharply picked distributions, the differential entropy $H_X(f)$ is low. In this sense $H_X(f)$ can be interpreted as a measure of uncertainty relative to f(x). For this, the parametric estimation of differential entropy under various statistical models was brought to the attention of a significant number of researchers [2,3,4,5,6,7,8]. Generally, most researchers have focused their attention on either classical or Bayesian estimation of entropy by adopting prior distributions for parameters involved in the underlying model. In contrast, adopting the prior distribution for the entropy itself has not received much attention and we, therefore, focus on this problem. In this context, Shakhatreh et al. [9] and Ramos et al. [10] presented some Bayesian estimates (BEs) of differential entropy under Weibull and gamma distributions, respectively. They considered the issue of estimation based on some non-informative prior distributions of differential entropy. Their results show satisfactory performance of recommended BEs relative to maximum likelihood estimate (MLE) of differential entropy.

The generalized half-normal (GHN) distribution, proposed by Cooray and Ananda [11], is one of the most popular models used to describe the lifetime process under fatigue. Let X be a random variable from a GHN distribution with shape parameter $\alpha >0$ and scale parameter $\theta >0$, the associated PDF and the cumulative distribution function (CDF) can be expressed as

$$\begin{aligned} f(x; \alpha , \theta )&=\sqrt{\frac{2}{\pi }}\left( \frac{\alpha }{x}\right) \left( \frac{x}{\theta }\right) ^{\alpha }\exp \left\{ -\frac{1}{2}\left( \frac{x}{\theta }\right) ^{2\alpha }\right\} ,\quad x\ge 0,\\ F(x; \alpha , \theta )&=1-2\Phi \left( -\left( \frac{x}{\theta }\right) ^{\alpha }\right) ,\quad x\ge 0, \end{aligned}$$

respectively, where $\Phi (\cdot )$ is the CDF of the standard normal distribution. Hereafter, we denote the GHN model with parameters $\alpha$ and $\theta$ as $GHN(\alpha , \theta )$. It is widely used in many practical applications because of its flexibility to fit various data sets. It is observed that the two-parameter GHN distribution can be monotonically increasing or decreasing and bathtub hazard rate shape depending upon the value of its parameters. It can be both positively and negatively skewed. Because of these properties, it is shown that the GHN distribution can be an alternative to the exponential, Weibull and gamma distributions, among others. It is shown in Cooray and Ananda [11] that the GHN model is followed from considerations of the relationship between static fatigue crack extension and the failure time of a certain specimen. Fatigue is a structural damage which occurs when a material is exposed to stress and tension fluctuations. Recently the GHN distribution has attracted the attention of many authors working on theory and methods as well as in various fields of applied statistics. For example, Kang et al.[12] discussed some non-informative priors for the GHN distribution when shape and scale parameters are of interest, respectively. They developed the first and second-order probability matching priors for the shape and scale parameters of GHN distribution when one of two parameters is the parameter of interest. They also discussed the reference priors for the shape and scale parameters of GHN distribution. Ahmadi et al. [13] derived estimation of parameters and reliability function under GHN distribution based on progressive type-II censoring. They considered both classical and Bayesian methods for estimation while the expectation-maximization (EM) algorithm and Lindley’s approximation were proposed to approximate suggested estimators. Wang and Shi [14] discussed the estimation issues in the constant-stress accelerated life test for GHN distribution. They just used classical methods and bootstrap technique for constructing confidence intervals. Ahmadi and Ghafouri [15] presented classical and Bayesian estimation of multi-component stress-strength reliability for GHN distribution in terms of progressive type-II censoring.

From (1), the differential entropy of a random variable $X\sim GHN(\alpha ,\theta )$ can be easily obtained by

$$\begin{aligned} H=H_{X}(f)=\frac{1}{2}-\ln \sqrt{\frac{2}{\pi }}-\left( 1-\frac{1}{\alpha }\right) \frac{\psi (\frac{1}{2})}{2\sqrt{2}}-\ln \left( \frac{\alpha }{\theta } \right) , \end{aligned}$$

where $\psi (\cdot )$ is the digamma function. So, the joint differential entropy based on independent and identically distributed (iid) random variables $X_1, X_2, \ldots , X_n$ from GHN distribution is $H_{X_1, X_2, \ldots , X_n}(f)=nH.$

To this end, it well known that entropic-based measures like differential entropy can be examined and demonstrated for application to fatigue failures. They have been used to predict damage and failure [16]. So, the differential entropy can play an efficient role in the assessment of fatigue damage. Due to the connection between the GHN distribution and fatigue crack extension explored by Cooray and Ananda [11], it is quite natural to quantify the entropy measure under the GHN lifetime data as no attempt has been made previously. The main aim of this paper is to develop some point and interval estimates for the differential entropy measure of GHN from a Bayesian perspective. In some practical situations, it is difficult to specify appropriate subjective prior information and selecting priors is like the other modeling in science that is always facing criticism. For this reason, we develop the Bayesian set-up by considering different objective priors to reflect prior knowledge on the parameters. There are some literature on objective Bayesian perspective, see for example [17,18,19]. Obviously, the differential entropy H is a function of the model parameters $\alpha$ and $\theta$. Although Kang et al.[12], based on some non-informative priors, have obtained different posterior distributions for the parameters of interest, the obtained posterior means cannot be directly plugging into H. Moreover, the BE of H using non-informative prior distributions of the original model parameters may lead to inappropriate results unless these prior distributions are invariant under one-to-one transformations, see [9]. Therefore, this paper focuses on the BEs of H based on different non-informative priors.

This paper is organized as follows. In Sect. 2, we first present some useful results on the objective priors which will be used in the next sections. In Sect. 3, we describe the Metropolis–Hastings (M–H) sampler approach used for computing the BEs of H. In Sect. 4, we discuss frequentist estimation methods including the MLE and asymptotic confidence interval of H. An extensive Monte Carlo simulation study is performed to assess how the proposed methods of estimation behave and two real data sets taken from practical fields are analyzed to illustrate the results developed here. Finally, some objective priors for the original parameters of GHN distribution are briefly discussed and some conclusions are made in Sect. 5.

2 Objective Bayesian Estimation Procedures

Let $X_1, X_2, \ldots , X_n$ be a complete sample from $GHN(\alpha ,\theta ).$ The likelihood function (LF) of this sample is

$$\begin{aligned} L(\alpha , \theta ; {\textbf {x}})=\left( \sqrt{\frac{2}{\pi }}\right) ^n \left( \frac{\alpha }{\theta ^\alpha } \right) ^n \left( \prod _{i=1}^{n}x_i \right) ^{\alpha -1} \exp \left\{ -\frac{1}{2}\sum _{i=1}^{n}\left( \frac{x_i}{\theta }\right) ^{2\alpha }\right\} . \end{aligned}$$

Under the reparameterization $\alpha =\frac{1}{W}$ and

$$\begin{aligned} \theta =\frac{1}{W} \exp \left\{ H-\frac{1}{2}+\ln \sqrt{\frac{2}{\pi }} +(1-W)\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right\} , \end{aligned}$$

the LF of H and W can be given by

$$\begin{aligned} L(H, W; {\textbf {x}})=&\left( \sqrt{\frac{2}{\pi }}\right) ^n W^{\frac{n}{W}-n}\delta _{H, W}^n \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}-1} \exp \left\{ -\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} , \end{aligned}$$

(2)

where

$$\begin{aligned} \delta _{H, W}=\exp \left\{ -\frac{1}{W}\left( H-\frac{1}{2}+\ln \sqrt{\frac{2}{\pi }} +(1-W)\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) \right\} . \end{aligned}$$

From Wang and Shi [14], the expected Fisher information (FI) matrix of $\alpha$ and $\theta$ is given by

$$\begin{aligned} \mathcal {I}(\alpha , \theta )=\begin{bmatrix} \mathcal {I}_{11} &{}\mathcal {I}_{12}\\ \mathcal {I}_{21} &{}\mathcal {I}_{22} \end{bmatrix}= \begin{bmatrix} \frac{1}{2\alpha ^2}\left[ \frac{\pi ^2}{2}-2+(2-\ln 2-\gamma )^2 \right] &{}-\frac{1}{\theta }(2-\ln 2-\gamma )\\ -\frac{1}{\theta }(2-\ln 2-\gamma ) &{}2\left( \frac{\alpha }{\theta }\right) ^2 \end{bmatrix}, \end{aligned}$$

(3)

where $\gamma$ is Euler’s constant. The FI matrix of H and W can be obtained easily by $\mathcal {I}(\alpha , \theta )$ and the Jacobian transformation $\mathcal {J}$, where

$$\begin{aligned} \mathcal {J}= \begin{bmatrix} 0 &{}-\frac{1}{W^2} \\ \frac{1}{W \delta _{H,W}^W} &{}-\left( 1+\frac{\psi (\frac{1}{2})}{2\sqrt{2}}W\right) \frac{1}{W^2 \delta _{H,W}^W} \end{bmatrix}. \end{aligned}$$

Therefore, the FI matrix of H and W is readily derived as

$$\begin{aligned} \varvec{\Sigma }(H,W)=\mathcal {J}^T \mathcal {I} \mathcal {J}= \begin{bmatrix} \Sigma _{HH} &{} \Sigma _{HW}\\ \Sigma _{WH} &{} \Sigma _{WW}\\ \end{bmatrix}, \end{aligned}$$

(4)

where

$$\begin{aligned} \Sigma _{HH}&=\frac{2}{W^2},\\ \Sigma _{HW}&=\Sigma _{WH}=\frac{2}{W^2}\left( \frac{\eta }{2}-\frac{1}{W}\right) ,\\ \Sigma _{WW}&=\frac{1}{W^2}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] , \end{aligned}$$

and

$$\begin{aligned} \eta =2-\ln 2-\gamma -\frac{\psi (\frac{1}{2})}{\sqrt{2}}. \end{aligned}$$

(5)

In this section, four types of non-informative Bayesian estimation of H, are discussed in further detail. For this purpose, posterior distributions of H and its Bayesian estimation under squared error loss (SEL) function under Jeffreys, reference, matching probability and maximal data information priors are investigated below.

2.1 Jeffreys Prior

The following non-informative prior, known as Jeffreys prior [20] is defined in terms of the FI, $\pi ^J(H, W)\propto \sqrt{\det \left( \Sigma (H, W)\right) }$ where

$$\begin{aligned} \det \left( \Sigma (H, W)\right) =\frac{1}{W^4}\left( \frac{\pi ^2}{2}-2 \right) , \end{aligned}$$

(6)

is the determinant of $\Sigma (H, W)$. From (6), we have

$$\begin{aligned} \pi ^J(H, W)\propto \frac{1}{W^2},~~ H\in (-\infty ,\infty ), W>0. \end{aligned}$$

(7)

Generally, this type of prior can be useful for three reasons. First, it is reparameterization-invariant; see [20]. Second, Jeffreys prior is a uniform density on the space of probability distributions in the sense that it assigns equal mass to each different distribution; see [21]. Third, Jeffreys prior maximizes the amount of information about the parameter of interest, in the Kullback–Leibler sense, see for example [22]. From (2) and (7), the Jeffreys posterior is concluded by

$$\begin{aligned} \pi ^{J}(H, W \vert {\textbf {x}})&\propto W^{\frac{n}{W}-n-2}\delta _{H, W}^n \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}}\nonumber \\&\times \exp \left\{ -\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} , \qquad H\in (-\infty ,\infty ), W>0. \end{aligned}$$

(8)

Since $\pi ^{J}(H, W)$ is not proper, we cannot be able to say that $\pi ^{J}(H, W \vert {\textbf {x}})$ is definitely a density. In the following theorem, the conditions that $\pi ^{J}(H, W \vert {\textbf {x}})$ can be a density are verified.

Theorem 1

For all $n\ge 2,$ the posterior density $\pi ^{J}(H, W \vert {\textbf {x}})$ is proper.

Proof

Using the change of variable $u=\delta _{H,W}^2$, we have

$$\begin{aligned} A({\textbf {x}})&= \int _{0}^{+\infty }\int _{-\infty }^{+\infty }\pi ^{J}(H, W\vert {\textbf {x}})\,\hbox {d}H \,\hbox {d}W \nonumber \\&= \frac{1}{2}\int _{0}^{+\infty }\int _{0}^{+\infty }W^{\frac{n}{W}-n-1}\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \,\hbox {d}u\,\hbox {d}W\nonumber \\&=\frac{1}{2^{1-\frac{n}{2}}}\Gamma \left( \frac{n}{2}\right) \int _{0}^{+\infty }\left( \frac{1}{W}\right) ^{n+1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\,\hbox {d}W. \end{aligned}$$

(9)

If $n=1,$ then we have $A({\textbf {x}})\propto \int _{0}^{+\infty } \frac{1}{W^2}\ \hbox {d}W=\infty .$ For $n\ge 2$, let $x_{(1)}, x_{(2)}, \ldots , x_{(n)}$ be the order observations such that $x_{(1)}\le x_{(2)}\le \ldots \le x_{(n)}$. From Cauchy–Schwarz inequality, it follows that

$$\begin{aligned} \frac{1}{n} \left( \sum _{i=1}^n x_{(i)}^{\frac{1}{W}}\right) ^2\le \sum _{i=1}^n x_{(i)}^{\frac{2}{W}}. \end{aligned}$$

(10)

There exists $\ell \in \{1, 2, \ldots , n\}$, such that $x_\ell <x_{(n)}$. Since $\frac{x_i^{\frac{1}{W}}}{\sum _{i=1}^{n}x_i^{\frac{1}{W}}}<1$, we have

$$\begin{aligned} \frac{\prod _{i=1}^{n}x_i^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{1}{W}} \right) ^{n}}<\left( \frac{x_\ell }{x_{(n)}}\right) ^{\frac{1}{W}}<1. \end{aligned}$$

(11)

From (10) and (11), it follows that

$$\begin{aligned} A({\textbf {x}})&<\frac{n^{\frac{n}{2}}}{2^{1-\frac{n}{2}}}\Gamma \left( \frac{n}{2}\right) \int _{0}^{+\infty }\left( \frac{1}{W}\right) ^{n+1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{1}{W}} \right) ^{n}}\,\hbox {d}W\nonumber \\&<\frac{n^{\frac{n}{2}}}{2^{1-\frac{n}{2}}}\Gamma \left( \frac{n}{2}\right) \int _{0}^{+\infty }\left( \frac{1}{W}\right) ^{n+1}\exp \left\{ -\frac{1}{W}\ln \left( \frac{x_{(n)}}{x_\ell } \right) \right\} \,\hbox {d}W <\infty . \end{aligned}$$

$\square$

Theorem 2

The posterior mean of H relative to $\pi ^{J}(H, W \vert {\textbf {x}})$ is finite for any $n\ge 2$.

Proof

Using the change of variable $u=\delta _{H,W}^2,$ we can write

$$\begin{aligned} \big \vert E(H\vert {\textbf {x}})\big \vert&=\Bigg \vert \int _{0}^{\infty }\int _{-\infty }^{\infty }H\pi ^{J}(H,W \vert {\textbf {x}})\,\hbox {d}H\,\hbox {d}W\Bigg \vert \nonumber \\&= \Bigg \vert \left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) A({\textbf {x}})+\frac{\psi (\frac{1}{2})}{4\sqrt{2}}B({\textbf {x}})-\frac{1}{4}C({\textbf {x}})\Bigg \vert \nonumber \\&\le \left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) A({\textbf {x}})+\Big \vert \frac{\psi (\frac{1}{2})}{4\sqrt{2}}\Big \vert B({\textbf {x}})+\frac{1}{4}\Big \vert C({\textbf {x}}) \Big \vert , \end{aligned}$$

where $A({\textbf {x}})$ is given in (9) and

$$\begin{aligned} B({\textbf {x}})&= \int _{0}^{\infty }\int _{0}^{\infty }W^{\frac{n}{W}-n}\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \,\hbox {d}u\,\hbox {d}W, \end{aligned}$$

(12)

$$\begin{aligned} C({\textbf {x}})&=\int _{0}^{\infty }\int _{0}^{\infty }W^{\frac{n}{W}-n}\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} (\ln u)\exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \,\hbox {d}u\,\hbox {d}W. \end{aligned}$$

(13)

From Theorem 1, $A({\textbf {x}})$ is finite for all $n\ge 2.$ Moreover, $B({\textbf {x}})$ is finite for all $n\ge 2$ (The proof is very similar to the proof of Theorem 1 and is therefore omitted for the sake of brevity). We shall show that $\vert C({\textbf {x}})\vert$ is finite for all $n\ge 2$. Using the fact that

$$\begin{aligned} \int _{0}^{\infty } t^{z-1}e^{-a t}\left( \ln t\right) \,\hbox {d}t=\frac{\Gamma (z)}{a^z}\left( \psi (z)-\ln (a) \right) , \end{aligned}$$

(14)

we can write $C({\textbf {x}})$ in the following form

$$\begin{aligned} C({\textbf {x}})=2^{\frac{n}{2}}\Gamma \left( \frac{n}{2} \right) \left[ \left( \psi \left( \frac{n}{2}\right) +\ln 2\right) C_1({\textbf {x}})-2C_{2}({\textbf {x}})-C_3({\textbf {x}})\right] , \end{aligned}$$

where

$$\begin{aligned} C_1({\textbf {x}})&=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\,\hbox {d}W, \nonumber \\ C_2({\textbf {x}})&=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n+1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\ln W\,\hbox {d}W, \nonumber \\ C_3({\textbf {x}})&=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\ln \left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) \,\hbox {d}W. \end{aligned}$$

(15)

Clearly, $C_1({\textbf {x}})$ is finite for all $n \ge 2.$ Let

$$\begin{aligned} C_4({\textbf {x}})=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n+2}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\,\hbox {d}W. \end{aligned}$$

(16)

Since for $W >0$, $\vert \ln W \vert \le \frac{1}{2}\left( W+\frac{1}{W}\right)$, then

$$\begin{aligned} \vert C_2({\textbf {x}})\vert \le \frac{1}{2} C_1({\textbf {x}})+\frac{1}{2}C_4({\textbf {x}})<\infty , \end{aligned}$$

(17)

for all $n \ge 2$. It remains to prove that $\vert C_3({\textbf {x}})\vert$ is finite for all $n \ge 2$. Note that for $\sum _{i=1}^{n}x_i^{\frac{2}{W}}<1,$ we have $\Big \vert \ln \sum _{i=1}^{n}x_i^{\frac{2}{W}}\Big \vert < \frac{2}{W}\Big \vert \ln x_{(n)} \Big \vert$ and also for $\sum _{i=1}^{n}x_i^{\frac{2}{W}}>1,$ we have $\Big \vert \ln \sum _{i=1}^{n}x_i^{\frac{2}{W}} \Big \vert <\ln n +\frac{2}{W}\Big \vert \ln x_{(n)} \Big \vert$. Therefore for $W>0,$ we immediately have

$$\begin{aligned} \left| \ln \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right| <\ln n +\frac{2}{W}\left| \ln x_{(n)} \right| . \end{aligned}$$

(18)

Let

$$\begin{aligned} C_5({\textbf {x}})&= \int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n+1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\,\hbox {d}W. \end{aligned}$$

(19)

From (18), it follows that

$$\begin{aligned} \vert C_3({\textbf {x}})\vert< (\ln n) C_1({\textbf {x}}) +2\vert \ln x_{(n)}\vert C_5({\textbf {x}})<\infty . \end{aligned}$$

The proof of Theorem 2 is readily complete. $\square$

The marginal posterior distribution of W is given by

$$\begin{aligned} \pi ^J(W \vert {\textbf {x}})\propto \left( \frac{1}{W}\right) ^{n+1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}},~~W>0. \end{aligned}$$

(20)

Moreover, the conditional posterior distribution of H is given by

$$\begin{aligned} \pi ^J(H \vert W, {\textbf {x}})\propto \exp \left\{ -\frac{nH}{W}-\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}} \right\} ,~~H\in (-\infty ,\infty ). \end{aligned}$$

(21)

2.2 Reference Prior

Despite of useful features and simple calculations of Jeffreys prior, it does not have good performance in multi-parameter problems. Hence, other non-informative priors like reference prior were introduced in the literature. Reference prior was originally defined by Bernardo [22], but its further results were found by Bernardo [23] and Berger and Bernardo [24,25,26,27]. Suppose a model described by density $f({\textbf {x}}\vert \phi ,\lambda )$, where $\phi$ is the parameter of interest and $\lambda$ is a nuisance parameter. Bernardo and Smith [28] obtained an effective formula for finding a reference prior based on Berger and Bernardo’s algorithm that is given below. Define

$$\begin{aligned} D_\phi (\phi ,\lambda )=\frac{\det ({\textbf {I}}( \phi ,\lambda ))}{{\textbf {I}}_{\lambda \lambda }( \phi ,\lambda )}, \end{aligned}$$

where ${\textbf {I}}_{\lambda \lambda }( \phi ,\lambda )$ is the $(\lambda ,\lambda )$-entry of that matrix. If $\phi$ and $\lambda$ are independent and if

$$\begin{aligned} D_\phi ^{\frac{1}{2}}(\phi ,\lambda )=f_1(\phi )g_1(\lambda )~~\text{ and }~~{\textbf {I}}_{\lambda \lambda }^{\frac{1}{2}}( \phi ,\lambda )=f_2(\phi )g_2(\lambda ), \end{aligned}$$

then the reference prior is equal to

$$\begin{aligned} \pi ^R( \phi ,\lambda )=f_1(\phi )g_2(\lambda ). \end{aligned}$$

(22)

In our study, H is the parameter of interest and W is a nuisance parameter. In the following theorem the reference prior of (H, W) is obtained.

Theorem 3

The improper reference prior of the parameter (H, W) is given by

$$\begin{aligned} \pi ^{R}(H, W) \propto \frac{1}{W}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}},~~H\in (-\infty ,\infty ), W>0. \end{aligned}$$

(23)

Proof

It can be easily shown that

$$\begin{aligned} D_{H}^{\frac{1}{2}}(H, W)=f_1(H)g_1(W), \end{aligned}$$

where

$$\begin{aligned} f_1(H)&=\sqrt{\frac{\pi ^2}{2}-2},\\ g_1(W)&=\frac{1}{W}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W}\right) ^2 \right] ^{-\frac{1}{2}}. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \Sigma _{WW}^{\frac{1}{2}}=f_2(H)g_2(W), \end{aligned}$$

where

$$\begin{aligned} f_2(H)&=1,\\ g_2(W)&=\frac{1}{W}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}. \end{aligned}$$

Therefore from (22), the reference prior $\pi ^{R}(H, W)=f_1(H)g_2(W)$. This completes the proof. $\square$

From (2) and (23), the reference posterior of (H, W) can be expressed as follows:

$$\begin{aligned} \pi ^{R}(H, W\vert {\textbf {x}})&\propto W^{\frac{n}{W}-n-1}\delta _{H, W}^n \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} \exp \left\{ -\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \nonumber \\&\times \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}},~~H\in (-\infty ,\infty ),~W>0. \end{aligned}$$

Theorem 4

For all $n\ge 2,$ the posterior density $\pi ^{R}(H, W\vert {\textbf {x}})$ is proper.

Proof

$$\begin{aligned} D({\textbf {x}})&= \int _{0}^{\infty }\int _{-\infty }^{\infty }\pi ^{R}(H, W\vert {\textbf {x}})\,\hbox {d}H \,\hbox {d}W \nonumber \\&=\frac{1}{2}\int _{0}^{\infty }\int _{0}^{\infty }W^{\frac{n}{W}-n}\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}\nonumber \\&\qquad \qquad \times u^{\frac{n}{2}-1}\exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \,\hbox {d}u\,\hbox {d}W\nonumber \\&=\frac{1}{2^{1-\frac{n}{2}}}\Gamma \left( \frac{n}{2}\right) \int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} \,\hbox {d}W . \end{aligned}$$

(24)

Since $\frac{\pi ^2}{4}-1>1$, for $n=1$, we have

$$\begin{aligned} D({\textbf {x}})> \frac{1}{\sqrt{2}} \Gamma (\frac{1}{2})\int _0^\infty \frac{\hbox {d}W}{W}=\infty . \end{aligned}$$

For $n\ge 2$, we have

$$\begin{aligned} D({\textbf {x}})< \frac{1}{2^{1-\frac{n}{2}}}\Gamma \left( \frac{n}{2}\right) \left[ \left( \frac{\pi ^2}{4}-1+\frac{\eta ^2}{2}\right) C_1({\textbf {x}})+2 C_4({\textbf {x}})-2\eta C_5({\textbf {x}})\right] , \end{aligned}$$

(25)

where $C_1({\textbf {x}}), C_4({\textbf {x}})$ and $C_5({\textbf {x}})$ are given in (15), (16) and (19), respectively. Using the fact that $C_1({\textbf {x}}), C_4({\textbf {x}})$ and $C_5({\textbf {x}})$ are finite for all $n \ge 2$, the proof of Theorem 4 is thus complete. $\square$

In what follows, we show the posterior mean of H under reference prior is finite for any $n \ge 3$.

Theorem 5

The posterior mean of H relative to $\pi ^{R}(H, W \vert {\textbf {x}})$ is finite for any $n\ge 3$.

Proof

$$\begin{aligned} E(H \vert {\textbf {x}})&=\int _{0}^{\infty }\int _{-\infty }^{\infty }H\pi ^{R}(H,W \vert {\textbf {x}})\,\hbox {d}H\,\hbox {d}W\nonumber \\&=\frac{1}{4}\int _{0}^{\infty }\int _{0}^{\infty } W^{\frac{n}{W}-n+1} \left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} u^{\frac{n}{2}-1} \nonumber \\&\qquad \times \left( \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\ln u\right) \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \,\hbox {d}u\,\hbox {d}W\nonumber \\&\qquad +\left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) D({\textbf {x}}), \end{aligned}$$

where $D({\textbf {x}})$ is defined in (24). Using (14), we get

$$\begin{aligned} E(H\vert {\textbf {x}})&=2^{\frac{n}{2}-2}\Gamma \left( \frac{n}{2} \right) \left[ \left( \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\psi (\frac{n}{2})-\ln 2 \right) G_1({\textbf {x}})+2G_2({\textbf {x}})+G_3({\textbf {x}}) \right] \nonumber \\&\qquad +\left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) D({\textbf {x}}), \end{aligned}$$

where

$$\begin{aligned} G_1({\textbf {x}})&=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n-1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}\,\hbox {d}W, \\ G_2({\textbf {x}})&=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}(\ln W) \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}\,\hbox {d}W, \\ G_3({\textbf {x}})&=\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n-1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\ln \left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}\,\hbox {d}W. \end{aligned}$$

Now, it is shown that $G_1({\textbf {x}})$ is finite for $n\ge 3$.

$$\begin{aligned} G_1({\textbf {x}})&\le \left( \frac{\pi ^2}{4}-1+\frac{\eta ^2}{2}\right) K({\textbf {x}})+\frac{2^{2-\frac{n}{2}}}{\Gamma (\frac{n}{2})} A({\textbf {x}})-2\eta C_1({\textbf {x}}), \end{aligned}$$

(26)

where $A({\textbf {x}})$ and $C_1({\textbf {x}})$ are defined in (9) and (15) respectively, and

$$\begin{aligned} K({\textbf {x}})=\int _0^\infty \left( \frac{1}{W}\right) ^{n-1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \hbox {d}W. \end{aligned}$$

By similar arguments to the proof of Theorem 1, $K({\textbf {x}})$ is finite for $n\ge 3$. Moreover, $A({\textbf {x}})$ and $C_1({\textbf {x}})$ are finite for $n\ge 2$. Therefore, $G_1({\textbf {x}})$ is finite for $n \ge 3$. We have

$$\begin{aligned} \vert G_2({\textbf {x}})\vert&\le \frac{1}{2}\int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n+1}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} \,\hbox {d}W\nonumber \\&\quad +\frac{1}{2}G_1({\textbf {x}}), \end{aligned}$$

(27)

and using (18)

$$\begin{aligned} \vert G_3({\textbf {x}})\vert&\le 2 \vert \ln x_{(n)} \vert \int _{0}^{\infty }\left( \frac{1}{W}\right) ^{n}\frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} \,\hbox {d}W\nonumber \\&\quad + (\ln n)G_1({\textbf {x}}). \end{aligned}$$

(28)

Using arguments similar to the ones applied in the proof of Theorem 4, it follows that integrals given in (27) and (28) are finite for $n\ge 3$. Since $G_1({\textbf {x}}), \vert G_2({\textbf {x}})\vert , \vert G_3({\textbf {x}})\vert$ and $D({\textbf {x}})$ are finite for $n\ge 3$, we conclude that

$$\begin{aligned} \Big \vert E(H \vert {\textbf {x}})\Big \vert&\le 2^{\frac{n}{2}-2}\Gamma \left( \frac{n}{2} \right) \left[ \bigg \vert \left( \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\psi (\frac{n}{2})-\ln 2 \right) \bigg \vert G_1({\textbf {x}})+2\Big \vert G_2({\textbf {x}})\Big \vert +\Big \vert G_3({\textbf {x}})\Big \vert \right] \nonumber \\&\qquad +\Bigg \vert \left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) \Bigg \vert D({\textbf {x}})<\infty . \end{aligned}$$

For $n=2,$ the expected value of $\vert H\vert$ relative to posterior $\pi ^{R}(H,W \vert {\textbf {x}})$ is given by $E(\vert H\vert \vert {\textbf {x}})=G_{11}({\textbf {x}})+G_{12}({\textbf {x}}),$

where

$$\begin{aligned} G_{11}({\textbf {x}})&=-\int _0^\infty \int _{-\infty }^0 H\, W^{\frac{2}{W}-3}\, \delta _{H,W}^2\, \left( \prod _{i=1}^2 x_i \right) ^{\frac{1}{W}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} \\&~~~~~\times \exp \left\{ -\frac{1}{2} \delta _{H,W}^2 \sum _{i=1}^2(Wx_i)^{\frac{2}{W}}\right\} \hbox {d}H\, \hbox {d}W, \\ G_{12}({\textbf {x}})&=\int _0^\infty \int _{0}^\infty H\, W^{\frac{2}{W}-3}\, \delta _{H,W}^2\, \left( \prod _{i=1}^2 x_i \right) ^{\frac{1}{W}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} \\&~~~~~\times \exp \left\{ -\frac{1}{2} \delta _{H,W}^2 \sum _{i=1}^2(Wx_i)^{\frac{2}{W}}\right\} \hbox {d}H\, \hbox {d}W. \end{aligned}$$

On the other hand, by Definition A.4 of Ramos et al. [10], we have $\delta _{H,W}\propto \exp \left\{ \frac{\psi (\frac{1}{2})}{2\sqrt{2}}-\frac{H}{W}\right\} ,$ $W^{\frac{1}{W}} \propto 1$ and $x_i^{\frac{1}{W}} \propto 1, ~~ i=1, 2$, as W tends to infinity. Therefore, from Proposition A.5 of Ramos et al. [10], we deduce the following assertion:

$$\begin{aligned} G_{11}({\textbf {x}})&>-\int _1^\infty \int _{-\infty }^0 H\, W^{\frac{2}{W}-3}\, \delta _{H,W}^2\, \left( \prod _{i=1}^2 x_i \right) ^{\frac{1}{W}}\exp \left\{ -\frac{1}{2} \delta _{H,W}^2 \sum _{i=1}^2(Wx_i)^{\frac{2}{W}}\right\} \hbox {d}H\,\hbox {d}W\nonumber \\&\propto -\exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} \int _1^\infty \int _{-\infty }^0 \frac{H}{W^{3}} \exp \left\{ -\frac{2H}{W} -\exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\frac{2H}{W}\right\} \right\} \hbox {d}H\,\hbox {d}W\nonumber \\&=\frac{1}{4} \exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} \int _1^\infty \int _{1}^{\infty }\frac{\ln u}{W} \exp \left\{ -\exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} u\right\} \hbox {d}u\, \hbox {d}W\nonumber \\&>\frac{1}{4} \exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} \bigg (\int _1^\infty \frac{\hbox {d}W}{W} \bigg )\bigg (\int _{\exp \{1\}}^{\infty } \exp \left\{ -\exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} u\right\} \hbox {d}u \bigg ) \nonumber \\&=\infty . \end{aligned}$$

(29)

Similarly, we also conclude

$$\begin{aligned} G_{12}({\textbf {x}})&>-\frac{1}{4} \exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} \bigg (\int _1^\infty \frac{\hbox {d}W}{W} \bigg )\bigg (\int _{0}^{\exp \{-1\}} \exp \left\{ -\exp \left\{ \frac{\psi (\frac{1}{2})}{\sqrt{2}}\right\} u\right\} \hbox {d}u \bigg )\nonumber \\&=\infty . \end{aligned}$$

(30)

From (29) and (30), the posterior mean of H relative to $\pi ^{R}(H, W \vert {\textbf {x}})$ does not exist for $n=2$. $\square$

The marginal reference posterior of W and conditional reference posterior of H can be derived, respectively, as follows:

$$\begin{aligned} \pi ^{R}(W \vert {\textbf {x}})\propto \left( \frac{1}{W}\right) ^n \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}, ~~W>0, \end{aligned}$$

and

$$\begin{aligned} \pi ^R(H \vert W, {\textbf {x}})\propto \exp \left\{ -\frac{nH}{W}-\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}} \right\} ,~~H\in (-\infty ,\infty ). \end{aligned}$$

2.3 Probability Matching Prior

Another type of non-informative prior is called probability matching prior which was introduced by Welch and Peers [29]. It is mainly based on a possible agreement between frequentist and Bayesian inferences. Based on methods presented in Welch and Peers [29], the probability matching prior of (H, W) is derived in the following theorem:

Theorem 6

The probability matching prior of (H, W) is proportional to

$$\begin{aligned} \pi ^{PM}(H, W)\propto {\left\{ \begin{array}{ll} \frac{1}{2-\eta W}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}} &{} 0<W< \frac{2}{\eta }\\ \frac{1}{\eta W-2}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}} &{} W>\frac{2}{\eta }, \end{array}\right. } \end{aligned}$$

(31)

where $H\in (-\infty ,\infty )$ and $\eta$ defined in (5).

Proof

The second-order probability matching prior of (H, W) when H is the parameter of interest and W is a nuisance parameter can be obtained by solving following partial differential equation in terms of $\pi ^{PM}(H,W)$.

$$\begin{aligned} \frac{\partial }{\partial W} \Big (\frac{{\varvec{\Sigma }}_{HW}\pi ^{PM}(H,W) }{{\varvec{\Sigma }}_{WW}\sqrt{K}}\Big )-\frac{\partial }{\partial H}\Big (\frac{\pi ^{PM}(H,W)}{\sqrt{K}} \Big )=0, \end{aligned}$$

(32)

where $K={\varvec{\Sigma }}_{WW}^{-1} \det \left( {\varvec{\Sigma }}_{HW}\right)$. From (4), it is obvious that the FI matrix of (H, W) does not depend on H. So, (32) can be reduced to

$$\begin{aligned} \frac{\partial }{\partial W} \Big (\frac{{\varvec{\Sigma }}_{HW}\pi ^{PM}(H,W) }{{\varvec{\Sigma }}_{WW}\sqrt{K}}\Big )=0. \end{aligned}$$

(33)

Utilizing (4), and after some simplifications, (33) is equivalent to

$$\begin{aligned} \frac{\partial }{\partial W} \left[ \frac{\left( \eta W-2\right) \pi ^{PM}(H, W) }{\sqrt{\frac{\pi ^2}{2}-2} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}}}\right] =0, \end{aligned}$$

and thus (31) is readily obtained by solving the above equation in terms of $\pi ^{PM}(H, W)$. This completes the proof. $\square$

Therefore, the probability matching posterior is as follows

$$\begin{aligned} \pi ^{PM}(H, W\vert {\textbf {x}})&\propto \frac{ W^{\frac{n}{W}-n}}{\vert \eta W-2\vert }\delta _{H, W}^n \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\nonumber \\&\times \exp \left\{ -\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} , \end{aligned}$$

(34)

where $H\in (-\infty ,\infty )$ and $W>0$.

Theorem 7

For all $n\ge 2,$ the posterior density $\pi ^{PM}(H, W \vert {\varvec{x}})$ is proper.

Proof

Let’s take

$$\begin{aligned} R({\textbf {x}})&=\int _0^\infty \int _{-\infty }^\infty \pi ^{PM}(H,W\vert {\textbf {x}}) \hbox {d}H \hbox {d}W\nonumber \\&=\frac{1}{2^{1-\frac{n}{2}}} \Gamma (\frac{n}{2})\int _0^\infty \frac{\left( \frac{1}{W}\right) ^{n-1}}{|\eta W -2|} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W, \end{aligned}$$

(35)

where $\eta$ defined in (5). For $n=1,$

$$\begin{aligned} R({\textbf {x}})>\frac{1}{\sqrt{2}}\Gamma (\frac{1}{2})\int _{0}^{\infty }\frac{\hbox {d}W}{|\eta W-2 |}=\infty . \end{aligned}$$

For $n \ge 2,$ $R({\textbf {x}})$ can be rewritten as

$$\begin{aligned} R({\textbf {x}})&=\frac{1}{2^{1-\frac{n}{2}}}\Gamma (\frac{n}{2})\left( R_1({\textbf {x}})+R_2({\textbf {x}})\right) , \end{aligned}$$

where

$$\begin{aligned} R_1({\textbf {x}})=\int _0^{\frac{2}{\eta }} \frac{\left( \frac{1}{W}\right) ^{n-1}}{2- \eta W} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W, \end{aligned}$$

and

$$\begin{aligned} R_2({\textbf {x}})= \int _{\frac{2}{\eta }}^\infty \frac{\left( \frac{1}{W}\right) ^{n-1}}{ \eta W -2} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W. \end{aligned}$$

From Definition A.4 of Ramos et al. [10], we get

$$\begin{aligned} {2-\eta W} \underset{W\rightarrow 0}{\propto }2, \text{ and } \quad \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\underset{W\rightarrow 0}{\propto }\frac{1}{W}. \end{aligned}$$

(36)

According to Proposition A.5 of Ramos et al. [10] and the results in (36), we conclude

$$\begin{aligned} R_1({\textbf {x}}) \propto \frac{1}{2} \int _0 ^{\frac{2}{\eta }} \left( \frac{1}{W}\right) ^{n} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \hbox {d}W <~~\frac{1}{2} C_1({\textbf {x}}), \end{aligned}$$

where $C_1({\textbf {x}})$ defined in (15) and it is finite for $n\ge 2$. So, $R_1({\textbf {x}})$ is finite for each $n\ge 2$. Arguments similar to the previous ones, we obtain

$$\begin{aligned} \eta W-2 \underset{W \rightarrow \infty }{\propto }\eta W, \quad \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\underset{W\rightarrow \infty }{\propto }\left[ \frac{\pi ^2}{4}-1+ \frac{\eta ^2}{2}\right] ^{\frac{1}{2}}. \end{aligned}$$

(37)

and

$$\begin{aligned} R_2({\textbf {x}})&< \frac{1}{\eta } \left[ \frac{\pi ^2}{4}-1+ \frac{\eta ^2}{2}\right] \int _{0}^\infty \left( \frac{1}{W}\right) ^{n} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \hbox {d}W\\&=\frac{1}{\eta } \left[ \frac{\pi ^2}{4}-1+ \frac{\eta ^2}{2}\right] C_1({\textbf {x}}), \end{aligned}$$

where $C_1({\textbf {x}})$ is the same quantity defined in (15). So, it follows that $R_2({\textbf {x}})$ is finite for any $n\ge 2$. This completes the proof. $\square$

Theorem 8

The posterior mean of H relative to $\pi ^{PM}(H, W\vert {\textbf {x}})$ is finite for all $n\ge 3$.

Proof

$$\begin{aligned} E(H\vert {\textbf {x}})&= \int _0^\infty \int _{-\infty }^\infty H \pi ^{PM}(H,W \vert {\textbf {x}}) \,\hbox {d}H \,\hbox {d}W\nonumber \\&=\frac{1}{4}\int _{0}^{\infty }\int _{0}^{\infty }\frac{W^{\frac{n}{W}-n+2}}{\vert \eta W-2 \vert } \left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] ^{\frac{1}{2}} u^{\frac{n}{2}-1} \nonumber \\&\qquad \times \left( \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\ln u\right) \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}\right\} \,\hbox {d}u\,\hbox {d}W\nonumber \\&\qquad +\left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) R({\textbf {x}}), \end{aligned}$$

where $R({\textbf {x}})$ is defined in (35). From (14), it follows that

$$\begin{aligned} E(H \vert {\textbf {x}})&=2^{\frac{n}{2}-2}\Gamma \left( \frac{n}{2} \right) \left[ \left( \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\psi (\frac{n}{2})-\ln 2 \right) S_1({\textbf {x}})+2S_2({\textbf {x}})+S_3({\textbf {x}}) \right] \nonumber \\&\qquad +\left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) R({\textbf {x}}), \end{aligned}$$

where

$$\begin{aligned} S_1({\textbf {x}})&=\int _0^\infty \frac{\left( \frac{1}{W}\right) ^{n-2}}{|\eta W -2|} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W,\nonumber \\ S_2({\textbf {x}})&=\int _0^\infty \frac{\left( \frac{1}{W}\right) ^{n-1}}{|\eta W -2|} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} (\ln W) \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W,\nonumber \\ S_3({\textbf {x}})&=\int _0^\infty \frac{\left( \frac{1}{W}\right) ^{n-2}}{|\eta W -2|} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \ln \left( \sum _{i=1}^{n}x_{i}^{\frac{2}{W}} \right) \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W. \end{aligned}$$

Since, for $W>0, \vert \ln W \vert \le \frac{1}{2}(W+\frac{1}{W})$, it is readily seen that

$$\begin{aligned} |S_2({\textbf {x}})|&\le \frac{1}{2} \int _0^\infty \frac{\left( \frac{1}{W}\right) ^{n}}{|\eta W -2|} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W\nonumber \\&\quad +\frac{1}{2}S_1({\textbf {x}}). \end{aligned}$$

(38)

From (18), it follows that

$$\begin{aligned} |S_3({\textbf {x}}) |&\le 2 |\ln x_{(n)} |\int _0^\infty \frac{\left( \frac{1}{W}\right) ^{n-1}}{|\eta W -2|} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}}\hbox {d}W\nonumber \\&\quad +(\ln n) S_1({\textbf {x}}). \end{aligned}$$

(39)

From the proof of Theorem 7, $R({\textbf {x}})$ is finite for $n\ge 2$. Also, by adopting similar arguments to the one used in the proof of Theorem 7, it can be easily shown that $S_1({\textbf {x}})$ and integrals given in (38) and (39) and consequently $S_2({\textbf {x}})$ and $S_3({\textbf {x}})$ are finite for $n\ge 3$. Thus for $n\ge 3$,

$$\begin{aligned} |E(H\vert {\textbf {x}})|&\le 2^{\frac{n}{2}-2}\Gamma \left( \frac{n}{2} \right) \left[ \bigg |\left( \frac{\psi (\frac{1}{2})}{\sqrt{2}}-\psi (\frac{n}{2})-\ln 2 \right) \bigg |S_1({\textbf {x}})+2 |S_2({\textbf {x}})|+ |S_3({\textbf {x}})|\right] \nonumber \\&\qquad +\Bigg |\left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) \Bigg |R({\textbf {x}})<\infty . \end{aligned}$$

It has to be noticed that for $n=2,$ the posterior mean of H relative to $\pi ^{PM}(H, W\vert {\textbf {x}})$ does not exist. The proof is similar to that of Theorem 5 and is therefore omitted for brevity. $\square$

From (34), the marginal probability matching posterior of W and conditional probability matching posterior of H, can be expressed, respectively, as

$$\begin{aligned} \pi ^{PM}(W\vert {\textbf {x}})\propto \frac{1}{\vert \eta W-2\vert W^n} \frac{\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}}{\left( \sum _{i=1}^{n}x_i^{\frac{2}{W}} \right) ^{\frac{n}{2}}} \left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2\right] ^{\frac{1}{2}},~~W>0 \end{aligned}$$

and

$$\begin{aligned} \pi ^{PM}(H \vert W, {\textbf {x}})\propto \exp \left\{ -\frac{nH}{W}-\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right\} , ~~H\in (-\infty ,\infty ). \end{aligned}$$

2.4 Maximal Data Information (MDI) Prior

Zellner [30] introduced an entropy-based method for finding a prior distribution that is called MDI prior. For a density $f(x\vert \theta )$ with parameter of interest $\theta$, the MDI prior of $\theta$ is defined as

$$\begin{aligned} \pi ^{MDI}(\theta ) \propto \exp \Big \{E[\ln (f(x\vert \theta ))]\Big \}. \end{aligned}$$

(40)

Now, from (40), one can easily conclude that the MDI prior of (H, W) is as follows

$$\begin{aligned} \pi ^{MDI}(H,W)\propto \exp \Big \{-H \Big \},~~H\in (-\infty ,\infty ),~ W>0. \end{aligned}$$

Notice that the MDI prior is completely different with all prior distributions that discussed before. Because, it is the only prior distribution that contains information about H. But, this prior distribution leads to improper posterior of (H, W). Hence, its modified version is considered as

$$\begin{aligned} \pi ^{MDI}(H, W)\propto \exp \{-\vert H \vert \},~~H\in (-\infty ,\infty ),~ W>0. \end{aligned}$$

So, for $H\in (-\infty ,\infty )$ and $W>0$ the MDI posterior of (H, W) can be expressed as

$$\begin{aligned} \pi ^{MDI}(H, W\vert {\textbf {x}})\propto W^{\frac{n}{W}-n}\delta _{H, W}^n \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} \exp \left\{ -\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}}-|H |\right\} . \end{aligned}$$

(41)

Theorem 9

The posterior $\pi ^{MDI}(H, W \vert {\textbf {x}})$ is proper for all $n\ge 3$.

Proof

In order to simplify notation, let $\mathcal{{G}}({\textbf {x}})=\int _0^\infty \int _{-\infty }^\infty \pi ^{MDI}(H, W \vert {\textbf {x}}) \hbox {d}H \hbox {d}W$. Since

$$\begin{aligned} \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}} -|H |\right\} \le \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right\} , \end{aligned}$$

we have

$$\begin{aligned}&\mathcal{{G}}({\textbf {x}}) \le \frac{1}{2} \nonumber \\ {}&\int _{0}^{\infty }\int _{0}^{\infty }W^{\frac{n}{W}-n+1}\left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \exp \left\{ -\frac{1}{2}u\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right\} \,\hbox {d}u\,\hbox {d}W. \end{aligned}$$

(42)

It can be shown that for $n\ge 3$, quantity (42) is finite by similar proof to the $A({\textbf {x}})$ in (9). But, for $n=1, 2$, the MDI posterior can be shown to be improper by an argument similar to that of Theorem 5. $\square$

Theorem 10

The posterior mean H relative to $\pi ^{MDI}(H, W \vert {\textbf {x}})$ is finite for all $n\ge 4$.

Proof

Using the change of variable $\delta _{H,W}^2=u$, we have

$$\begin{aligned} \big |E(H \vert {\textbf {x}})\big |&= \Bigg |\left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) V_1({\textbf {x}})+\frac{\psi (\frac{1}{2})}{4\sqrt{2}} V_2({\textbf {x}})-\frac{1}{4} V_3({\textbf {x}})\Bigg |\\&\le \left( \frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) V_1({\textbf {x}})+ \Big |\frac{\psi (\frac{1}{2})}{4\sqrt{2}} \Big |V_2({\textbf {x}})+\frac{1}{4} V_3({\textbf {x}}), \end{aligned}$$

where

$$\begin{aligned} V_1({\textbf {x}})=&\frac{1}{2} \int _0^\infty \int _0^\infty W^{\frac{n}{W}-n+1} \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} u^{\frac{n}{2}-1}\exp \left\{ -\frac{u}{2}\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right. \\&\left. -\Big |\frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -(1-W)\frac{\psi (\frac{1}{2})}{4\sqrt{2}}-\frac{W}{2}\ln u \Big |\right\} \hbox {d}u~ \hbox {d}W, \\ V_2({\textbf {x}})=&\int _0^\infty \int _0^\infty W^{\frac{n}{W}-n+2} \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} u^{\frac{n}{2}-1}\exp \left\{ -\frac{u}{2}\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right. \\&\left. -\Big |\frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -(1-W)\frac{\psi (\frac{1}{2})}{4\sqrt{2}}-\frac{W}{2}\ln u \Big |\right\} \hbox {d}u\,\hbox {d}W, \end{aligned}$$

and

$$\begin{aligned} V_3({\textbf {x}})=&\int _0^\infty \int _0^\infty W^{\frac{n}{W}-n+2} \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \vert \ln u \vert \exp \left\{ -\frac{u}{2}\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right. \\&-\left. \Big |\frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }}\right) -(1-W)\frac{\psi (\frac{1}{2})}{4\sqrt{2}}-\frac{W}{2}\ln u \Big |\right\} \hbox {d}u\, \hbox {d}W. \end{aligned}$$

Since

$$\begin{aligned} V_1( {\textbf {x}})&\le \frac{1}{2} \int _0^\infty \int _0^\infty W^{\frac{n}{W}-n+1} \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \exp \left\{ -\frac{u}{2}\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right\} \hbox {d}u\, \hbox {d}W, \\ V_2( {\textbf {x}})&\le \int _0^\infty \int _0^\infty W^{\frac{n}{W}-n+2} \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \exp \left\{ -\frac{u}{2}\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right\} \hbox {d}u\,\hbox {d}W, \\ V_3( {\textbf {x}})&\le \int _0^\infty \int _0^\infty W^{\frac{n}{W}-n+2} \left( \prod _{i=1}^{n}x_i \right) ^{\frac{1}{W}} u^{\frac{n}{2}-1} \vert \ln u \vert \exp \left\{ -\frac{u}{2}\sum _{i=1}^{n}\left( W x_i\right) ^{\frac{2}{W}} \right\} \hbox {d}u\,\hbox {d}W, \end{aligned}$$

one can easily show that $V_1( {\textbf {x}})$ and $V_2( {\textbf {x}})$ are finite, respectively for $n\ge 3$ and $n\ge 4$ by the same procedures of $B({\textbf {x}})$ in (12). Also, similar to $C({\textbf {x}})$ from (13), the quantity $V_3( {\textbf {x}})$ is finite for $n\ge 4$. So, the proof is completed. $\square$

By (41), it can be shown that the marginal MDI posterior of W can be rewritten as

$$\begin{aligned}&\pi ^{MDI}(W \vert {\textbf {x}})\propto \left( \frac{1}{W} \right) ^n \left( \prod _{i=1}^{n}x_i\right) ^{\frac{1}{W}}\left( \frac{2}{\sum _{i=1}^{n}x_i^{\frac{2}{W}}}\right) ^{\frac{1}{2}(n+W)} \exp \Bigg \{\frac{\psi (\frac{1}{2})}{\sqrt{2}}(1-W) \Bigg \} \nonumber \\&\qquad \times \left[ \frac{W^2}{2^W} \left( \sum _{i=1}^{n}x_i^{\frac{2}{W}}\right) ^{W}\Gamma \left( \frac{n-W}{2}, \frac{1}{2}\sum _{i=1}^{n}(Wx_i)^{\frac{2}{W}}\right) \exp \Bigg \{-\frac{\psi (\frac{1}{2})}{\sqrt{2}}(1-W) \Bigg \}\right. \nonumber \\&\qquad + \left. \Gamma \left( \frac{n+W}{2}\right) F_G\left( 1,\frac{1}{2}(n+W),\frac{1}{2}\sum _{i=1}^{n}(Wx_i)^{\frac{2}{W}} \right) \right] ,~~W>0, \end{aligned}$$

(43)

where $\Gamma (a, b)$ is the upper incomplete gamma function defined as $\Gamma (a, b)=\int _{b}^{\infty } t^{a-1}e^{-t}\,\hbox {d}t$. Also, $F_G(a,b,c)$ is the CDF of gamma distribution with shape parameter b and rate parameter c, at point a. Moreover, the conditional MDI posterior of H can be obtained as

$$\begin{aligned} \pi ^{MDI}(H \vert W, {\textbf {x}})\propto \exp \left\{ -\frac{nH}{W}-\frac{1}{2}\delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}-\vert H\vert \right\} ,~~~~H\in (-\infty ,\infty ). \end{aligned}$$

(44)

3 Metropolis–Hastings Algorithm

For the various non-informative priors discussed in the previous section, the joint posterior distributions of (H, W) are not tractable and the computation of the BEs will be impossible. Consequently, we opt for stochastic simulation procedures, namely, the Metropolis–Hastings (M–H) samplers, to generate samples from the posterior distributions. It is worth mentioning that the BEs of W are not interesting because it is used as an auxiliary parameter to conduct the Jacobian transformation.

For each non-informative priors discussed early, the joint posterior distribution of (H, W) is decomposed into the marginal posterior distribution of W and the conditional posterior distribution of H given $W=w$. Based on this decomposition, the M–H algorithm is adopted to generate samples from the joint posterior distribution of (H, W). A non-negative random variable U is inverse gamma (IG) distributed if its PDF is given by

$$\begin{aligned} g(u;\beta , \lambda )=\frac{\lambda ^{\beta }}{\Gamma (\beta )}\left( \frac{1}{u}\right) ^{\beta +1}\exp \Big \{-\frac{\lambda }{u}\Big \}, \end{aligned}$$

where $\beta >0$ is the shape parameter and $\lambda >0$ is the scale parameter. Hereafter, it will be denoted by $IG(\beta , \lambda )$. Let $v=\ln \left( {x_{(n)}}/{x_{(1)}}\right) .$ In the $\ell$-th iteration of M–H algorithm we choose $IG({v}/{W^{(\ell -1)}}+1, v)$ as a proposal distribution to generate random sample from the marginal posterior distribution of W. It is noteworthy that the shape and scale parameters of IG distribution are selected in a such way that the mean of IG is $W^{(\ell -1)}$. We also choose the normal distribution, $N(H^{(\ell -1)}, \sigma ^2)$, as a proposal distribution to generate sample from the conditional posterior distribution of H. The mode of the marginal posterior distribution of W is used as initial value, say $W^{(0)}$. For example, let us consider the case of Jeffreys prior. On taking the natural logarithm of (20), differentiating with respect to W and equating to zero, we have the following non-linear equation:

$$\begin{aligned} (n+1)W-\frac{n\sum _{i=1}^{n}x_i^{\frac{2}{W}}\ln x_i}{\sum _{i=1}^{n}x_i^{\frac{2}{W}}}+\sum _{i=1}^{n}\ln x_i=0. \end{aligned}$$

(45)

The mode of posterior $\pi ^{J}(W \vert {\textbf {x}})$, say $\widetilde{W}$ can be computed by solving equation (45). Moreover, on taking the natural logarithm of (21), differentiating with respect to H and equating to zero, the initial value for H can be obtained as

$$\begin{aligned} \widetilde{H}=\frac{1}{2}-\ln \left( \sqrt{\frac{2}{\pi }} \right) -\frac{\psi (\frac{1}{2})}{2\sqrt{2}}(1-\widetilde{W})-\frac{\widetilde{W}}{2}\ln \left( \frac{n}{\sum _{i=1}^{n}\left( \widetilde{W}x_i \right) ^{\frac{2}{\widetilde{W}}}}\right) . \end{aligned}$$

The initial values for W and H in the cases of reference, probability matching and MDI priors can be obtained in a similar way. The M–H algorithm needed to generates samples from (8) can be described as follows:

• Algorithm 1: M–H algorithm within Gibbs

• Step 1. Set $W^{(0)}=\widetilde{W}, H^{(0)}=\widetilde{H}$ and $v=\ln \left( \frac{x_{(n)}}{x_{(1)}}\right) .$

• Step 2. Set $\ell =1$.

• Step 3. Generate $W^*$ from the proposal distribution $IG\left( {v}/{W^{(\ell -1)}}+1,v\right) .$

• Step 4. Calculate the acceptance probability

  $$\begin{aligned} \tau _1=\min \Bigg \{1,\frac{\pi ^{J}(W^*\vert {\textbf {x}})\,g\left( W^{(\ell -1)};{v}/{W^{*}}+1, v\right) }{\pi ^{J}(W^{(\ell -1)}\vert {\textbf {x}})\,g\left( W^*;{v}/{W^{(\ell -1)}}+1, v\right) } \Bigg \}. \end{aligned}$$

• Step 5. Generate $U_1$ from the standard uniform distribution.

• Step 6. If $U_1\le \tau _1$, accept $W^*$ and set $W^{(\ell )}=W^*$. Otherwise reject $W^*$ and set $W^{(\ell )}=W^{(\ell -1)}$.

• Step 7. Generate $H^*$ from the proposal distribution $N(H^{(\ell -1)}, \sigma ^2).$

• Step 8. Calculate the acceptance probability $\tau _2=\min \Bigg \{1, \frac{\pi ^{J}\left( H^*\vert W^{(\ell )}, {\textbf {x}}\right) }{\pi ^{J}\left( H^{(\ell -1)}\vert W^{(\ell )}, {\textbf {x}}\right) } \Bigg \}$.

• Step 9. Generate $U_2$ from the standard uniform distribution.

• Step 10. If $U_2\le \tau _2$, accept $H^*$ and set $H^{(\ell )}=H^*$. Otherwise reject $H^*$ and set $H^{(\ell )}=H^{(\ell -1)}$.

• Step 11. Set $\ell =\ell +1$.

• Step 12. Repeat Steps 3-11, N times.

Based on the resulting generated samples obtained using Algorithm 1, the BE of H under SEL function can be computed as

$$\begin{aligned} \widehat{H}^J=\frac{1}{N-M}\sum _{\ell =M+1}^{N} H^{(\ell )}, \end{aligned}$$

where M is burn-in period. In addition, for constructing the credible interval (CrI) of H, we sort all the $H^{(\ell )}, \ell =M+1, M+2, \ldots , N,$ in an ascending sequence, as $H_{(1)}, H_{(2)}, \ldots , H_{(N-M)}$. Then, for $0<\epsilon <1,$ a $100(1-\epsilon )\%$ CrI of H is specified by

$$\begin{aligned} \big ( H_{(k)},\, H_{(k+N-M-\lfloor (N-M)\epsilon +1\rfloor )} \big ),~~~k=1, 2, \ldots , \lfloor (N-M) \epsilon \rfloor , \end{aligned}$$

where $\lfloor x \rfloor$ is the largest integer less than or equal to x. Therefore, the $100(1-\epsilon )\%$ HPD CrI of H can be obtained as the $k_*$-th one satisfying

$$\begin{aligned} H_{(k_*+N-M-\lfloor (N-M)\epsilon +1\rfloor )} -H_{(k_*)}\le H_{(k+N-M-\lfloor (N-M)\epsilon +1\rfloor )} -H_{(k)}, \end{aligned}$$

for all $k=1, 2, \ldots ,\lfloor (N-M)\epsilon \rfloor$. For the reference prior, probability matching prior and MDI prior, the BEs and HPD CrIs of H can be obtained in a similar way.

4 Numerical Comparisons and Data Analysis

Here we perform a comprehensive simulation study to examine the performances of the sample-based estimates developed in the previous sections and conduct the analysis of two practical data sets with GHN fitting distribution. All the computations are performed using R Software package (R x64 4.0.3) and the R code can be obtained on request from the authors.

4.1 Numerical Comparisons

Here, a simulation study is mainly conducted to compare the performance of MLEs and BEs of the differential entropy measure H under the different non-informative priors discussed in previous sections. For this purpose, we first briefly mention how to obtain the MLE of H. The natural logarithm of LF given in (2) may be written as

$$\begin{aligned} \ell (H, W; {\textbf {x}}) \propto&\left( \frac{n}{W}-n\right) \ln W-\frac{n}{W} \left( H-\frac{1}{2}+\ln \sqrt{\frac{2}{\pi }} +(1-W)\frac{\psi (\frac{1}{2})}{2\sqrt{2}} \right) \nonumber \\&+\frac{1}{W}\sum _{i=1}^{n}\ln x_i-\frac{1}{2} \delta _{H, W}^2\sum _{i=1}^{n}\left( Wx_i\right) ^{\frac{2}{W}}. \end{aligned}$$

By setting the derivatives of $\ell (H, W; {\textbf {x}})$ with respective to H and W to zero, the MLE of W, say $\widehat{W}$, can be obtained from the equation $U(W)=0$, where

$$\begin{aligned} U(W)=W-\frac{\sum _{i=1}^{n}x_i^{\frac{2}{W}}(\ln x_i)}{\sum _{i=1}^{n}x_i^{\frac{2}{W}}}+\frac{1}{n}\sum _{i=1}^{n}\ln x_i. \end{aligned}$$

Since $U(W)=0$ does not admit an explicit solution, we propose a simple iterative scheme to compute $\widehat{W}$. Start with an initial guess of W, say $W^{(0)}$. Then, obtain $W^{(1)}=U\left( W^{(0)}\right)$. Continue this process until convergence is achieved. Once $\widehat{W}$ is obtained, $\widehat{H}$ can be obtained as follows:

$$\begin{aligned} \widehat{H}=H(\widehat{W})=\frac{1}{2}-\ln \sqrt{\frac{2}{\pi }}- (1-\widehat{W})\frac{\psi (\frac{1}{2})}{2\sqrt{2}} +\ln \widehat{W}-\frac{\widehat{W}}{2}\left( \ln n-\ln \left( \sum _{i=1}^{n}x_i^{\frac{2}{\widehat{W}}}\right) \right) . \end{aligned}$$

(46)

Since the MLEs of H and W are not obtained in closed form, it is not possible to derive the exact distributions of the MLEs. Now, the asymptotic confidence interval (CI) for H is obtained based on the asymptotic distributions of the MLEs $\widehat{H}$ and $\widehat{W}$.

Therefore, by applying the property of the asymptotic normality of MLEs, we have

$$\begin{aligned} \Big ((\widehat{H}-H), (\widehat{W}-W)\Big )^{T} \rightarrow {N}_2 ({\varvec{0}}, {\varvec{V}}), \end{aligned}$$

where ${\varvec{V}}$ is the asymptotic variance-covariance matrix of the MLEs $\widehat{H}$ and $\widehat{W}$. That is ${\varvec{V}}=\frac{1}{n}\varvec{\Sigma }^{-1}(\widehat{H}, \widehat{W})$. Consequently, the approximate $100(1-\epsilon )\%$ two sided CI for H is $\left( \widehat{H}- z_{{\epsilon }/{2}}\sqrt{V_{11}}, \widehat{H}+ z_{{\epsilon }/{2}}\sqrt{V_{11}}\right)$, where $0<\epsilon <1$, $z_{\epsilon /2}$ is the upper $(\epsilon /2)$th percentile of the standard normal distribution and

$$\begin{aligned} V_{11}=\frac{W^2}{n\left( \frac{\pi ^2}{2}-2 \right) }\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\frac{1}{W} \right) ^2 \right] . \end{aligned}$$

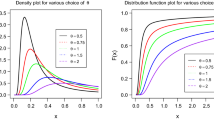
It is clearly noticed that as $\alpha$ changes for a fixed $\theta$, the PDF and hazard rate function of GHN have different properties. Hence, a simulation study based on various shapes of the PDF and hazard rate function of GHN distribution was carried out. We consider $\alpha =0.5, 0.75, 1.5, 2.17, 3$ and $\theta =0.25, 2, 5.$ According to Cooray and Ananda [11], for $0<\alpha <2.17$, GHN distribution is positively skewed and for $\alpha =2.17$ and $\alpha >2.17$ it is symmetric and negatively skewed, respectively. The hazard rate function of GHN decreases monotonically, concave up and approaches to 1/(2 scale parameter) as lifetime goes to $\infty$, for $\alpha =0.5$. Also, it is bathtub shape for $\alpha =0.75$. It increases monotonically, concave down and approaches $\infty$ as lifetime goes to $\infty$, for $\alpha =1.5$. Moreover, for $\alpha =2.17, 3$ it increases monotonically, concave up and approaches $\infty$ as lifetime goes to $\infty$. To compute the BEs of the differential entropy measure H using the M–H algorithm, we considered $\sigma =0.25$ and also ran the iterative process up to $N =5500$ iterations by discarding the first $M = 500$ iterations as burn-in-period. It was considered a thin parameter of 5 to diminish significant auto-correlation among sample draws. Moreover, to solve equation (45), Broyden Secant method of nleqslv package was used. The biases and mean squared errors (MSEs) of MLEs and BEs of the differential entropy measure H are computed for sample sizes $n=10, 20, 30, 40, 50, 70$ using 5000 simulated samples for different combinations of $\alpha$ and $\theta$ and are given in Tables 1, 2, 3, 4 and 5. The $95\%$ asymptotic CIs and HPD CIs for the differential entropy measure H were also obtained. The average lengths (ALs) and coverage probabilities (CPs) of the so obtained CrIs are presented in Tables 6, 7, 8, 9, and 10.

These results for MLEs and BEs under priors, Jeffreys, reference, probability matching and maximal data information are shown in tables with labels $\widehat{H}$, $\widehat{H}^J$, $\widehat{H}^R$, $\widehat{H}^{PM}$ and $\widehat{H}^{MDI}$, respectively. Since the CI is constructed based on the asymptotic normality of the MLE $\widehat{H}$, the corresponding AILs and CPs are reported for sample sizes greater than $n=10$.

By taking $\theta$ to be fixed and changing the shape parameter $\alpha$, we can observed from these tables that the BEs perform well when compared to the MLEs in the sense of bias and MSE criteria. The performance of all estimates behaves the same for large sample sizes. It is also observed that for $\alpha \le 1$, the BEs based on Jeffreys prior compete other BEs for small sample sizes. In this case, the BEs under MDI prior are the worse one. For $\alpha >1$, all BEs perform similarly. It is evident that for $\alpha \le 1$, the HPDs under PM prior work well in terms of the AIL and for $\alpha >1$, the CIs are shorter. By considering the CP criterion, the asymptotic CIs and HPDs are most valid intervals in the sense that the corresponding CPs tend to be high and close to the true confidence level $1-\epsilon =0.95$, especially for $\alpha > 1$.

In Fig. 1, the performance of the proposed M–H algorithm under different posterior distributions of the differential entropy is monitoring by inspecting the value of average acceptance rate(AAR). Figure 1 provides a limited summary when the parameters are $\alpha =0.5, 0.75, 1.5, 2.17, 3$ and $\theta =5$. In the cases where $\alpha =0.5, 0.75$, the ARRs are very good and high for all sample sizes. In the cases of $\alpha =1.5, 2.17, 3$ the ARRs lie within the intervals of $0.28-0.61$, $0.27-0.53$ and $0.21-0.45$, respectively. For $\alpha =0.5, 2.17, 3$, there is no a significant difference between the AARs of M–H algorithm when sample size n is greater than 10. Figure 1 also demonstrates how the ARR changes by changing sample size n. We observe that AAR decreases when sample size n increases. Three such plots would be required to consider full collections of AARs for all combinations of the parameters $\alpha$ and $\theta (\theta = 0.25, 2)$ that are omitted for the brevity’s sake, but it is worth mentioning that we get similar results for them.

Table 1 Biases and MSEs (between parentheses) of the MLE and BEs of H for $\alpha =0.5$

Table 2 Biases and MSEs (between parentheses) of the MLE and BEs of H for $\alpha =0.75$

Table 3 Biases and MSEs (between parentheses) of the MLE and BEs of H for $\alpha =1.5$

Table 4 Biases and MSEs (between parentheses) of the MLE and BEs of H for $\alpha =2.17$

Table 5 Biases and MSEs (between parentheses) of the MLE and BEs of H for $\alpha =3$

Table 6 AILs and CPs (between parentheses) of 95% CI/HPD of H for $\alpha =0.5$

Table 7 AILs and CPs (between parentheses) of 95% CI/HPD of H for $\alpha =0.75$

Table 8 AILs and CPs (between parentheses) of 95% CI/HPD of H for $\alpha =1.5$

Table 9 AILs and CPs (between parentheses) of 95% CI/HPD of H for $\alpha =2.17$

Table 10 AILs and CPs (between parentheses) of 95% CI/HPD of H for $\alpha =3$

4.2 Data Analysis

In this subsection, the proposed methods are illustrated by two real data sets. For both data sets, we apply Algorithm 1 to generate samples from the posterior densities and then compute the BEs. The simulation process is repeated 5500 iterations and initial 500 iterations are discarded as a burn-in period.

Data Set 1: First we discuss the analysis of real life data representing the lifetimes of Kevlar 49/epoxy strands which were subjected to constant sustained pressure at the 90% stress level until all had failed. The data set was initially reported by Barlow et al. [31]. It has been analyzed by many authors, among them, Cooray and Ananda [11] and Ahmadi et al. [13]. The failure times in hours are as follows:

Fig. 1

Average acceptance rate of M–H algorithm under different posterior distributions of the differential entropy: $\pi ^J(H\vert {\textbf {x}}), \pi ^R(H\vert {\textbf {x}}), \pi ^{PM}(H\vert {\textbf {x}}), \pi ^{MDI}(H\vert {\textbf {x}})$

Fig. 2

Auto-correlation graphs and trace plots of M–H algorithm under different posterior distributions of the differential entropy: $\pi ^J(H\vert {\textbf {x}}), \pi ^R(H\vert {\textbf {x}}), \pi ^{PM}(H\vert {\textbf {x}}), \pi ^{MDI}(H\vert {\textbf {x}})$

Based on the above observed data, we obtain the MLE of H as well as the corresponding BEs under Jeffreys, Reference, probability matching and maximal data information priors. The MLEs of H is computed numerically using Broyden Secant method to be $\widehat{H}=0.9867$. The asymptotic $95\%$ CI of H is (0.777, 1.196). We have generated 5500 observations to compute the BEs of H based on M–H samplers after discarding the initial 500 burn-in samples. Note that, for computing BEs and CrIs, we assume that the above four objective priors. The M–H algorithm with inverse gamma and normal proposal distributions(see Algorithm 1) is used to generate numbers from the target probability distribution. Here, we assume the initial value of H to be its MLE, $\widehat{H}$. To check the convergence of M–H algorithm, graphical diagnostics tools involving the auto-correlation function (ACF) and trace plots are used. Figure 2 displays ACF and trace plots of the simulated draws of H, under different posterior distributions. It is checked that the ACF plots show that chains are dissipating rapidly from sampling lag 8, for all posterior distributions. Hence, to eliminate high auto-correlations, we considered a thinning interval equal to 8 iterations. It is evident that the chains have very low autocorrelations. From the trace plots, we can easily observe a random scatter about some mean value represented by a solid line with a fine mixing of the chains for the simulated values of H. As a result, these plots indicate the rapid convergence of the M–H algorithm based on the proposed normal distribution of H. The results of the BEs of H using M–H samplers under different objective priors are computed to be

$$\begin{aligned} \widehat{H}^J=0.9815, \widehat{H}^R= 0.9871, \widehat{H}^{PM}= 0.9997, \widehat{H}^{MDI}= 0.9745. \end{aligned}$$

and the corresponding $95\%$ HPD CrIs of H under Jeffreys, reference, PM and MDI priors are also obtained and computed, respectively, as

$$\begin{aligned} (0.769, 1.183),\;(0.789, 1.199),\; (0.777, 1.211),\; (0.745, 1.210). \end{aligned}$$

Further, Geweke diagnostics (Geweke [32]) are used to confirm the convergence of chains under a confidence level of $95\%$. Its values under the difference priors are, respectively,

$$\begin{aligned} G^J=0.8352,\; G^R= 1.9351,\; G^{PM}= 0.4349,\; G^{MDI}=0.3041. \end{aligned}$$

Since the differential entropy of a system shows the degree of irregularity and randomness of that system, the small values of Bayesian point estimation of entropy H, $\widehat{H}^J=0.9815$ and $\widehat{H}^{PM}=0.9997$ with $95\%$ HPD CrIs (0.769, 1.183) and (0.777, 1.211) demonstrate good performance and stability in the production system.

Data Set 2: The COVID-19 pandemic has affected almost every country in the world. The monthly mean number of deaths from the pandemic of coronavirus disease in Iran since March, 1, 2020 till August, 29, 2021, based on the National Vital Statistics System (https://ourworldindata.org/coronavirus/country/iran) are as

Fig. 3

Auto-correlation graphs and trace plots of M–H algorithm under different posterior distributions of the differential entropy: $\pi ^J(H\vert {\textbf {x}}), \pi ^R(H\vert {\textbf {x}}), \pi ^{PM}(H\vert {\textbf {x}}), \pi ^{MDI}(H\vert {\textbf {x}})$

The Ljung-Box test is used to ensure that observations over time are independent. The values of its chi-squared statistic with one degree of freedom and p-value measure are 1.4709 and 0.2252, respectively. The p-value indicates that observations over time are independent. Here, we show that the GHN distribution is a correct fitting distribution. The MLEs of the unknown parameters $\alpha$ and $\theta$ are computed numerically to be $\hat{\alpha }=1.22019$ and $\hat{\theta }=251.704$. The Kolmogorov-Smirnov (K-S) distance between the fitted and the empirical distribution functions is $K-S=0.1355$, and the corresponding p value is 0.8527. Therefore, these values indicate that the two-parameter GHN distribution fits the data set well. The MLE of differential entropy measure is $\hat{H}=6.1803$ and the corresponding asymptotic $95\%$ CI of H is (5.908, 6.453). Based on 5500 iterations with discarding a burn-in period of 500 iterations, the ACF and trace plots of the generated samples using M–H algorithm are displayed in Figure 3. Under four posterior distributions, a thinning interval equal to 11 iterations was considered to obtain independent samples. From these plots, a rapid convergence of the M–H algorithm based on the proposed normal distribution can be observed clearly. For this, the BEs and $95\%$ HPD CrIs under Jeffreys, reference, PM and MDI priors using M–H algorithm are given by

$$\begin{aligned} \widehat{H}^J=6.2011,\; \widehat{H}^R= 6.2038,\; \widehat{H}^{PM}= 6.2165,\; \widehat{H}^{MDI}= 6.1797. \end{aligned}$$

and

$$\begin{aligned} (5.892, 6.442),\;(5.877, 6.487),\; (5.966, 6.564),\; (5.710, 6.561). \end{aligned}$$

The Geweke diagnostics are also computed, respectively, 0.4354, 0.2235, 1.2793, 1.2982. It worth mentioning that the point BEs H and corresponding CrIs tend to be relatively high. This shows that the available information content in this data is low. Therefore, it is suggested to further monitor the daily deaths for necessary decisions and actions.

5 Discussion and Conclusion

In the previous sections, we obtained the objective priors when H was the parameter of interest and W was a nuisance parameter. Now, by transforming back (H, W) into original parameters $(\alpha , \theta )$, the Jeffreys prior (7), reference prior (23) and probability matching prior (31) are respectively equivalent to

$$\begin{aligned} \pi ^{J}_*(\alpha , \theta )&\propto \frac{1}{\theta }, \end{aligned}$$

(47)

$$\begin{aligned} \pi ^{R}_*(\alpha , \theta )&\propto \frac{1}{\alpha \theta } \left[ \frac{\pi ^2}{4}-1+2\left( \frac{1}{2}-\alpha \right) ^2 \right] ^{\frac{1}{2}}, \end{aligned}$$

(48)

$$\begin{aligned} \pi ^{PM}_*(\alpha , \theta )&\propto {\left\{ \begin{array}{ll} \frac{1}{\alpha \theta (2\alpha -\eta )}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\alpha \right) ^2\right] ^{\frac{1}{2}} &{} \alpha > \frac{2}{\eta }\\ \frac{1}{\alpha \theta (\eta -2\alpha )}\left[ \frac{\pi ^2}{4}-1+2\left( \frac{\eta }{2}-\alpha \right) ^2\right] ^{\frac{1}{2}} &{} 0< \alpha <\frac{\eta }{2}. \end{array}\right. } \end{aligned}$$

(49)

A natural question is : “Are the priors (47)–(49) respectively Jeffreys, reference and probability matching priors for the original parameters $(\alpha , \theta )$ of GHN distribution?” To answer this question, we first consider the following theorem.

Theorem 11

Assume that $\alpha$ and $\theta$ are the parameters of interest.

• 1. The Jeffreys prior for the parameters of GHN distribution is ${\pi }^{J}_{**}(\alpha , \theta )\propto \frac{1}{\theta }.$

• 2. The probability matching prior for the parameters of GHN distribution is $\pi ^{PM}_{**}(\alpha , \theta )\propto \frac{1}{\alpha \theta }$.

• 3. The reference prior for the parameters of GHN distribution is $\pi ^{R}_{**}(\alpha , \theta )\propto \frac{1}{\alpha \theta }.$

Proof

(i): It is sufficient to calculate the square root of the determinant of $\mathcal {I}(\alpha , \theta )$ as is reported in (3).

(ii): Assume $\alpha$ is the parameter of interest and $\theta$ is a nuisance parameter. The second-order probability matching prior $\pi ^{PM}_\alpha (\alpha , \theta )$ can be obtained by solving the partial differential equation

$$\begin{aligned} \frac{\partial }{\partial \theta }\left( \frac{\mathcal {I}_{12}\pi ^{PM}_\alpha (\alpha , \theta )}{\mathcal {I}_{22}\sqrt{Q}}\right) - \frac{\partial }{\partial \alpha } \left( \frac{\pi ^{PM}_\alpha (\alpha , \theta )}{\sqrt{Q}}\right) =0, \end{aligned}$$

(50)

where

$$\begin{aligned} Q=\mathcal {I}^{-1}_{22}\,det(\mathcal {I}(\alpha , \theta ))=\frac{1}{2\alpha ^2}\left( \frac{\pi ^2}{2}-2\right) . \end{aligned}$$

Equation (50) becomes

$$\begin{aligned} \frac{\partial }{\partial \theta }\left( \theta \pi ^{PM}_\alpha (\alpha , \theta )\right) +\left( \frac{2\alpha }{2-\ln 2 -\gamma }\right) \frac{\partial }{\partial \alpha }\left( \alpha \pi ^{PM}_\alpha (\alpha , \theta ) \right) =0. \end{aligned}$$

(51)

Then, by applying Lemma A.1 of Sun [33], it follows that

$$\begin{aligned} \pi ^{PM}_\alpha (\alpha , \theta )=\frac{1}{\alpha \theta }h_1\left( \frac{2\ln \theta }{2-\ln 2-\gamma }+\frac{1}{\alpha }\right) , \end{aligned}$$

(52)

where $h_1(.)$ is some continuously differentiable function. Similarly, when $\theta$ is the parameter of interest and $\alpha$ is a nuisance parameter, the second-order probability matching prior $\pi ^{PM}_\theta (\alpha , \theta )$ is the solution of the partial differential equation

$$\begin{aligned} \frac{\partial }{\partial \theta }\left( \theta \pi ^{PM}_\theta (\alpha , \theta )\right) +\left( \frac{2(2-\ln 2-\gamma ) }{\frac{\pi ^2}{2}-2+(2-\ln 2 -\gamma )^2}\right) \frac{\partial }{\partial \alpha }\left( \alpha \pi ^{PM}_\theta (\alpha , \theta ) \right) =0. \end{aligned}$$

(53)

It follows that

$$\begin{aligned} \pi ^{PM}_\theta (\alpha , \theta )=\frac{1}{\alpha \theta }h_2\left( \frac{2(2-\ln 2-\gamma )\ln \theta }{\frac{\pi ^2}{2}-2+(2-\ln 2 -\gamma )^2}+\frac{1}{\alpha }\right) , \end{aligned}$$

(54)

where $h_2(.)$ is some continuously differentiable function. Now, we assume that $\alpha$ and $\theta$ are simultaneously the parameters of interest. Since second-order jointly matching prior $\pi ^{PM}(\alpha , \theta )$ should satisfy two Eqs. (51) and (53), it follows that $h_1(.)=h_2(.)\equiv 1$ in (52) and (54).

Now, let $\mathcal {I}^{-1}(\alpha , \theta )=(\kappa _{ij})$ be the inverse of the expected Fisher information $\mathcal {I}(\alpha , \theta )$. Define $\mathcal {M}=(m_{ij})$, where $m_{ij}=\frac{\kappa _{ij}}{\sqrt{\kappa _{ii}\kappa _{jj}}}, i,j=1, 2$. We get $m_{11}=m_{22}=1$ and

$$m_{12}=m_{21}=(2-\ln 2 -\gamma )\left[ \frac{\pi ^2}{2}-2+(2-\ln 2-\gamma )^2\right] ^{-\frac{1}{2}}.$$

According to Datta [34], since matrix $\mathcal {M}$ does not depend on $\alpha$ and $\theta$ it follows that $\pi ^{PM}_{**}(\alpha , \theta ) \propto \frac{1}{\alpha \theta }$ is the probability matching prior for the parameters of GHN distribution.

(iii) See Remark 3 of Kang et al. [12]. $\square$

It is observed that the prior in (47) is Jefferys prior for the original parameters $(\alpha , \theta )$, i.e. $\pi _*^{J}(\alpha , \theta )=\pi _{**}^{J}(\alpha , \theta ).$ This is to be expected, because the Jefferys prior is invariant with respect to one-to-one transformation. Part (ii) of Theorem 11 implies that $\pi _*^{PM}$ in (49) is not the probability matching prior for the GHN distribution parameters. For sufficient small and large $\alpha$, $\pi ^{PM}_*$ are only equivalent to $\pi ^{PM}_{**}$. According to part (iii) of Theorem 11, it is obvious that $\pi ^{R}_{*}$ in (48) is not the reference prior for the original parameters $(\alpha , \theta )$ of GHN distribution. For sufficient large $\alpha$, $\pi _*^{R}$ and $\pi _{**}^R$ are approximately similar and for sufficient small $\alpha$, $\pi ^{R}_*$ converges to $\pi ^{J}_*$. Thus, it is recommended to adopt the objective priors which obtained directly instead of non-informative priors based on the original parameters of GHN distribution in order to compute the BEs of the differential entropy H. In addition, based on the simulation results in Sect. 5, it can be said that such BEs are better than MLE in terms of biases and MSEs.

In this paper, we have discussed the estimation of differential entropy of the GHN distribution in a complete sample case. However in many practical situations, due to time constraint and cost reduction, censored samples may arise naturally. There are various schemes of censoring such as Type-I censoring, Type-II censoring, hybrid or progressive censoring. It may be mentioned, although we have provided the results mainly for complete samples but our method can be applied for other censoring mechanism also. More work is needed along these directions. Additionally, one may extend the work to include other non-informative priors such as copula prior, moment matching prior, and etc.