Slow Motion Past a Spheroid Implanted in a Brinkman Medium : Slip Condition

Abstract

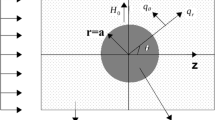
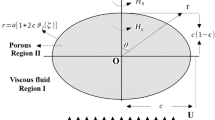
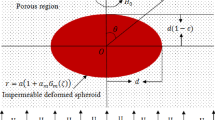
The current work deals with the Stokes incompressible flow past an impermeable spheroidal particle, a particle of slightly deformed spherical shape, implanted in a Brinkman’s porous media. The problem is perused by considering the slip flow boundary conditions at the interface. An analytical result for the drag force affecting on the spheroid is evaluated. Both the cases of an oblate and a prolate spheroids are analyzed. Dependence of drag coefficient in relation to different important dimensionless parameters including permeability, deformation, and slip are visualized using graphs and tables. The effect of slip is observed to have a remarkable impact in raising the drag. Several notable results are derived from the ongoing work.

A Appendix

Applying the boundary conditions (14)-(15) to the first order in $\beta _{m}$, we obtain the following system of algebraic equations

$$\begin{aligned}&\left[ \,1+a_{2}+b_{2}\,S_{2}\right] P_{1}(\zeta )+ \beta _{m}\xi _{1}(P_{1}(\zeta )\,\vartheta _{m}(\zeta )+\vartheta _{2}(\zeta )\,P_{m-1}(\zeta ))\nonumber \\&\quad + \sum _{n=3}^{\infty }\left[ \,A_{n}+B_{n}\,S_{3}\right] P_{n-1}(\zeta )=0 \end{aligned}$$

(A.1)

$$\begin{aligned}&\left[ 2\,\lambda -(\lambda +6)\,a_{2}-((6+\alpha ^2+\lambda )S_{2}+\alpha \,(2+\lambda )S_{1})\,b_{2}\right] \vartheta _{2}(\zeta )\nonumber \\&\quad + \beta _{m}\xi _{2}\vartheta _{2}(\zeta )\,\vartheta _{m}(\zeta )+\beta _{m}\xi _{3}\vartheta _{2}(\zeta )P_{1}(\zeta )P_{m-1}(\zeta )- \sum _{n=3}^{\infty }\left[ \xi _{4}\,A_{n}+\xi _{5}\,B_{n}\right] \vartheta _{n}(\zeta )=0\nonumber \\ \end{aligned}$$

(A.2)

$S_{1}=K_{1/2}(\alpha )$       $S_{2}=K_{3/2}(\alpha )$

$S_{3}=K_{n-1/2}(\alpha )$       $S_{4}=K_{n-3/2}(\alpha )$

$w_{1}=S_{2}+\alpha \,S_{1}$       $w_{2}=3\,S_{2}+\alpha \,S_{1}$

$$\begin{aligned} \xi _{1}=&2-a_{2}-b_{2}\,w_{1}\\ \xi _{2}=&2\lambda +2(\lambda +9)\,a_{2}+(\alpha ^2(\lambda +3)+2\lambda +18)S_{2}+\alpha (6+\alpha ^2)S_{1}\\ \xi _{3}=&-2(9a_{2}+3\,w_{2})\\ \xi _{4}=&\lambda (n-1)+2(n^2-1)\\ \xi _{5}=&(\xi _{4}+\alpha ^2)S_{3}+\alpha (2+\lambda )S_{4} \end{aligned}$$

On solving the leading terms of equations (A.1)-(A.2) we will get the values of $a_{2}$ and $b_{2}$. Since the expressions are very lengthy we are not presenting it here. To obtain the remaining arbitrary constants $A_{n}$ and $B_{n}$ we require the following identities

$$\begin{aligned}&\vartheta _{m}(\zeta )\,\vartheta _{2}(\zeta )={\bar{a}}_{m-2}\vartheta _{m-2}(\zeta )+ {\bar{a}}_{m}\vartheta _{m}(\zeta )-{\bar{a}}_{m+2}\vartheta _{m+2}(\zeta ) \end{aligned}$$

(A.3)

$$\begin{aligned}&\vartheta _{m}(\zeta )\,P_{1}(\zeta )+P_{m-1}(\zeta )\,\vartheta _2(\zeta )={\bar{a}}_{m-2}P_{m-3}(\zeta )+{\bar{a}}_{m}\,P_{m-1}(\zeta )- {\bar{a}}_{m+2}\,P_{m+1}(\zeta ) \qquad \end{aligned}$$

(A.4)

$$\begin{aligned}&P_1(\zeta )\,\vartheta _2(\zeta )\,P_{m-1}(\zeta )={\bar{b}}_{m-2}\vartheta _{m-2}(\zeta )+ {\bar{b}}_{m}\vartheta _{m}(\zeta )+ {\bar{b}}_{m+2}\vartheta _{m+2}(\zeta )\nonumber \\&{\bar{a}}_{m-2}=-\frac{(m-2)(m-3)}{2(2\,m-1)(2\,m-3)},\,\,{\bar{a}}_{m}=\frac{m(m-1)}{(2\,m+1)(2\,m-3)}\nonumber \\&{\bar{a}}_{m+2}=-\frac{(m+1)(m+2)}{2(2\,m-1)(2\,m+1)}\nonumber \\&{\bar{b}}_{m-2}=(m-1){\bar{a}}_{m-2},\,\,{\bar{b}}_{m}={\bar{a}}_{m}/2,\,\,{\bar{b}}_{m+2}=-m\,{\bar{a}}_{m+2} \end{aligned}$$

(A.5)

Using these in (A.1) and (A.2), we get $A_{n}=0$ and $B_{n}=0$, for $n\ne m-2, m, m+2$

and when $n=m-2, m, m+2$, we have the following system

$$\begin{aligned}&\xi _{1}\,{\bar{a}}_{n}+A_{n}+B_{n}\,S_{3}=0 \end{aligned}$$

(A.6)

$$\begin{aligned}&\xi _{2}\,{\bar{a}}_{n}+\xi _{3}\,{\bar{b}}_{n}-\xi _{4}\,A_{n}-\xi _{5}\,B_{n}=0 \end{aligned}$$

(A.7)