Abstract
We study the linear stability problem to gravitational and electromagnetic perturbations of the extremal, \( |Q|=M, \) Reissner–Nordström spacetime, as a solution to the Einstein–Maxwell equations. Our work uses and extends the framework [28, 32] of Giorgi, and contrary to the subextremal case we prove that instability results hold for a set of gauge invariant quantities along the event horizon \( {\mathcal {H}}^+ \). In particular, for associated quantities shown to satisfy generalized Regge–Wheeler equations we prove decay, non-decay, and polynomial blow-up estimates asymptotically along \( {\mathcal {H}}^+ \), the exact behavior depending on the number of translation invariant derivatives that we take. As a consequence, we show that for generic initial data, solutions to the generalized Teukolsky system of positive and negative spin satisfy both stability and instability results. It is worth mentioning that the negative spin solutions are significantly more unstable, with the extreme curvature component \( {\underline{\alpha }} \) not decaying asymptotically along the event horizon \( {\mathcal {H}}^+, \) a result previously unknown in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The question of stability of black holes, as solutions to the Einstein equation, has led to a vast interdisciplinary research work addressing this problem for various spacetime models. Some of the most recent results include the proof of non-linear stability of Schwarzschild, under polarized symmetry [34] and in full generality with no symmetry assumptions in [21], and Kerr for small angular momentum, i.e. \( \left|a\right|/M\ll 1 \), in a sequence of works [31, 35,36,37, 48]. This was done in the spirit of the seminal work of Christodoulou–Klainerman [15], proving the non-linear stability of Minkowski spacetime.
In this paper, we are interested in the Reissner–Nordström family of spacetimes \( ({\mathcal {M}}, g_{_{M,Q}}) \), which in local coordinates takes the form
and represent the spacetime outside a non-rotating, spherical symmetric, charged black hole of mass M and charge Q, with \( \left|Q\right|\le M. \) It stands as the unique spherically symmetric, asymptotically flat solution of the Einstein–Maxwell equations
where D is the Levi–Civita connection associated to the metric g, and the 2-form F is the electromagnetic tensor verifying the Maxwell equations.
In a series of papers [28,29,30, 32], the author concluded the linear stability of the full subextremal range of Reissner–Nordström spacetimes as solutions to the Einstein–Maxwell equations. Roughly, this means that all solutions to the linearized Einstein–Maxwell equations around a Reissner–Nordström solution, \( g_{_{M,Q}} \) with \( \left|Q\right|<M \), arising from regular asymptotically flat initial data remain uniformly bounded in the exterior, and decay to a linearized Kerr-Newman solution after adding a pure gauge solution. However, some of the results developed in this work no longer hold in the extremal case, \( \left|Q\right|=M, \) because of the degeneracy of the redshift effect at the event horizon \( {\mathcal {H}}^+\), a necessary ingredient in showing linear stability in [28, 32]. In addition, in view of the Aretakis instabilities that manifest on the horizon \( {\mathcal {H}}^+\) for the homogeneous wave equation [6, 7], one expects that similar instabilities arise in the linearized gravity as well.
The purpose of this paper is to address the linear stability problem for the extreme Reissner–Nordström (ERN) spacetime of maximally charged black holes. Our results are at the level of gauge–invariant quantities, characterized by the fact that they vanish in any pure gauge solution. We are looking at quantities that arise naturally in the linearization procedure and are shown to satisfy a generalized version of the so-called Teukolsky equation; see [28, 32]. These wave-type equations govern the gravitational and electromagnetic perturbations of Reissner–Nordström and decouple completely from the full set of linearized Einstein–Maxwell system when written in a null frame, and thus can be studied independently.
1.1 The Teukolsky System and the Instability Result
In the work of linear stability of Schwarzschild and Kerr spacetimes, or even in the case of Maxwell equations in these backgrounds, the resulting Teukolsky equations are independent for each corresponding extreme component (gravitational or electromagnetic); see [11, 16, 44, 49]. However, in the case of Reissner–Nordström, the Teukolsky equations obtained in [28, 32] are heavily coupled with each other. This is, roughly, due to the initiation of both gravitational and electromagnetic perturbations in the presence of charge. The Teukolsky system of \( \pm \) spin is satisfied by a pair of extreme curvature components \(\alpha _{AB}, {\underline{a}}_{AB}\), and two pairs \(\mathfrak {f}_{AB}, \underline{\mathfrak {f}}_{AB}, \ {\tilde{\beta }}_{A}, \underline{{\tilde{\beta }}}_{A}\), defined in terms of both Ricci coefficients and curvature/electromagnetic components. In particular, let  be a Teukolsky type operator with coefficients depending on M, Q, then the generalized Teukolsky system is schematically given by
be a Teukolsky type operator with coefficients depending on M, Q, then the generalized Teukolsky system is schematically given by

written with respect to a null frame \(\left\{ e_3,e_4,e_A \right\} _{_{A=1,2}} \), and by  we denote the projection of spacetime covariant derivative \( D_{e_i} \) on the section spheres.
we denote the projection of spacetime covariant derivative \( D_{e_i} \) on the section spheres.
As a central result in this paper, we obtain estimates for the Teukolsky system in the exterior of ERN spacetime, up to and including the event horizon \( {\mathcal {H}}^+. \) A set of conservation laws that hold for induced gauge–invariant quantities, along the event horizon \( {\mathcal {H}}^+,\) yields an analogue of Aretakis instability that carries up to the level of Teukolsky solution. Both stability and instability results coexist, which can be summarized in the following theorem.
Theorem
(Rough version) Let \( \alpha , \mathfrak {f} , {\tilde{\beta }} \) and \( {\underline{\alpha }}, \underline{\mathfrak {f}}, \underline{{\tilde{\beta }}} \) be solutions to the generalized Teukolsky system of \( \pm \) spin on the extreme Reissner–Nordström exterior, and let Y denote a transversal to the horizon \({\mathcal {H}}^+\) invariant derivative, then for generic initial data
-
1.
Away from the event horizon \( H^{+} \equiv \left\{ r=M \right\} , \) i.e. \( \left\{ r\ge r_0 \right\} \), \( r_0>M \), Teukolsky solutions decay with respect to the time function of a suitable foliation of the exterior,
-
2.
The following pointwise decay, non-decay and blow-up estimates hold asymptotically along the event horizon \( {\mathcal {H}}^+\)
-
(a)
For the positive spin solutions, we haveFootnote 1
-
 , and
, and 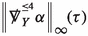 decay
decay -
 and
and  do not decay along \( {\mathcal {H}}^+. \)
do not decay along \( {\mathcal {H}}^+. \) -
 and
and  , as \( \tau \rightarrow \infty \), for any \( k\in {\mathbb {N}},\ \xi \in \left\{ \mathfrak {f},{\tilde{\beta }} \right\} . \)
, as \( \tau \rightarrow \infty \), for any \( k\in {\mathbb {N}},\ \xi \in \left\{ \mathfrak {f},{\tilde{\beta }} \right\} . \)
-
-
(b)
For the negative spin solutions, we have
-
\(\left\Vert \underline{\mathfrak {f}}\right\Vert _{\infty }\hspace{-0.1cm}(\tau ), \ \left\Vert \underline{{\tilde{\beta }}}\right\Vert _{\infty }\hspace{-0.1cm}(\tau ) \) decay
-
 and \( \left\Vert {\underline{\alpha }}\right\Vert _{S^{2}_{\tau ,M}} \) do not decay along \( {\mathcal {H}}^+, \)
and \( \left\Vert {\underline{\alpha }}\right\Vert _{S^{2}_{\tau ,M}} \) do not decay along \( {\mathcal {H}}^+, \) -
 and
and  , as \( \tau \rightarrow \infty \), for any \( k\in {\mathbb {N}},\ \xi \in \left\{ \underline{\mathfrak {f}},\underline{{\tilde{\beta }}} \right\} . \)
, as \( \tau \rightarrow \infty \), for any \( k\in {\mathbb {N}},\ \xi \in \left\{ \underline{\mathfrak {f}},\underline{{\tilde{\beta }}} \right\} . \)
-
where \(\tau \ge 1\) is an advanced time parameter on \({\mathcal {H}}^+\) defined explicitly in Chapter 2.
-
(a)
Remark 1.1
The extreme curvature component \( {\underline{\alpha }} \) does not decay, itselfFootnote 2, along \( {\mathcal {H}}^+\). This does not seem to be the case for axisymmetric linear perturbations of extreme Kerr, where it has been shown numerically [12] that \( {\underline{\alpha }} \) decays asymptotically on \( {\mathcal {H}}^{+}\); see relevant works [13, 38]. This suggests that ERN spacetimes are linearly more unstable than extreme Kerr ones in the axisymmetric setting.
Remark 1.2
For the positive spin equations, in both ERN and extreme Kerr (axisymmetric perturbations), it takes five transversal invariant derivatives of the curvature component \( \alpha \) not to decay asymptotically along \( {\mathcal {H}}^+\), as seen in [38]. Moreover, it is shown that any additional transversal derivative of \( \alpha \) yields asymptotic blow-up estimates with the same rates as in the Theorem above.
In order to obtain these estimates, we rely on the resolution introduced in the proof of linear stability of Schwarzschild [16], and then adapted in the case of Reissner–Nordström [28, 32]. The key part is a set of physical space transformations of Teukolsky solutions to higher order gauge invariant quantities which satisfy a system of generalized Regge–Wheeler equations (29). To study the latter, we follow standard techniques and ideas developed in the literature [17, 19, 20, 41].
1.2 Previous Works on Extreme Black Holes
A rigorous study of the scalar wave equation on extreme Reissner-Nordström spacetimes, uncovering the associated horizon instability, was initiated by Aretakis in [6, 7]. More results in this setting can be found at [3, 4, 22, 27], including the interior of the black hole [23, 26]. Works generalizing some of the above findings for a wide class of semilinear and nonlinear wave equations are given in [1, 2, 5], where we see that similar horizon instabilities persist.
For stability results of the scalar wave equation and the linearized gravity in the exterior of extreme Kerr spacetimes see [8, 25, 31, 51], and [24] for the interior. For horizon instabilities of extreme Kerr and Kerr-Newman see [9, 45], and [10] for an inclusive overview of extremal black holes.
At the same time, Aretakis’ work has inspired several heuristics and numerics that shed light on the stability and instability of extreme black holes. A variety of results in the case of extreme Reissner-Norström is found at [39, 40, 42, 43, 46, 52], while for extreme Kerr and other extreme black holes, we direct our readers to [12, 13, 33, 38, 47]. Closely related to our thesis are the results of [39], where the authors derive a horizon instability for Regge–Wheeler type equations in the linearized gravity of extreme Reissner–Nordström. The number of transversal invariant derivatives that appear in their corresponding Aretakis constants agree with the ones we obtain in Chapter 6. It would be interesting to see more numerics studying the associated Teukolsky system and obtaining data that can be compared to our findings.
1.3 Outline of the paper
We present the structure of this paper, along with the main theorems and results in each section.
In Section 2, we introduce the main coordinate systems and foliations we are using throughout the paper. In Section 3, we briefly review the set-up and the Teukolsky equations of [28, 32], on which our work is based. We write the transformation theory, adapted in the ERN case, which yields the Regge–Wheeler system, and after considering its spherical harmonic decomposition we decouple it.
In Section 4, we study the induced decoupled Regge–Wheeler equations, and we prove Morawetz type estimates in Theorems 4.1, 4.2, and a degenerate redshift estimate with a degeneracy of the transversal derivative on the horizon \( {\mathcal {H}}^+\), as in Theorem 4.3. In Section 5, we remove the aforementioned degeneracy as shown in Theorem 5.1.
In Section 6, we show that solutions to the Regge–Wheeler equations are subject to a conservation law on the horizon \( {\mathcal {H}}^+\), Theorem 6.1. We proceed with Section 7, where we obtain higher order transversal invariant derivative estimates, Theorem 7.1. Last, we derive \( r^{p}- \)hierarchy estimates in Section 8, which allows us to prove energy decay estimates in the exterior.
Using the energy decay results and the conservation laws, we prove pointwise decay, non-decay, and blow-up estimates along the event horizon \( {\mathcal {H}}^+\), as in Theorems 9.2, 9.3. As a consequence, in Proposition 9.3 we derive estimates for the initial Regge–Wheeler system.
Finally, in the last two Sections 10 and 11, we use the transformations of Section 3 to derive decay estimates for the Teukolsky system of \( \pm \) spin away from the horizon; Corollaries 10.3, 11.1. Estimates along the horizon \( {\mathcal {H}}^+\) are shown in Theorems 10.1, 10.2 and Theorems 11.1, 11.2.
2 Extreme Reissner–Nordström Spacetime
In this section, we introduce the main coordinate systems we will be working with, and the foliations we use to derive the energy estimates. In addition, we briefly go through relevant elliptic notions and identities that are frequently used throughout the paper.
2.1 Differential structure and metric
With respect to the Boyer–Lindquist coordinates \( (t,r,\vartheta ,\varphi ) \) the Reissner–Nordström metric takes the form \( g=g_{M,Q} = -D dt^2 + \frac{1}{D}dr^2 +r^2 g_{{\mathbb {S}}^2}\), where \( D(r)= 1- \frac{2M}{r}+\frac{\left|Q\right|^2}{r^2} \) and \( g_{{\mathbb {S}}^2} \) is the standard round metric on \( {\mathbb {S}}^2. \) In this paper, we are interested in the case where \( \left|Q\right| = M \), i.e the extremal Reissner–Nordström spacetime (ERN).
Our main goal is to capture the behavior of gauge–invariant quantities up to and including the event horizon \( {\mathcal {H}}^+\), \(\left\{ r=M \right\} \), so we work our way to introduce a different coordinate system that extends regularly on \( {\mathcal {H}}^+. \) To do so, we first define the so-called double null coordinates in ERN. Consider the tortoise coordinate \( r^{\star }(r):=r+2M\log (r-M)-\frac{M^2}{r-M}+C, \) for a constant C, and note \( r^{\star } \) satisfies \( \frac{\partial r^{\star }}{\partial r}= \frac{1}{D}. \) Then, the null coordinates are defined via \( u:=t-r^{\star }, \ v:=t+r^{\star }, \) with respect to which the ERN metric is given by
We use this coordinate system to produce the \( r^{p}- \)hierarchy estimates in Section 8, taking place at future null infinity \({\mathcal {I}}^{+}\): the limit points of future-directed null rays along which \(r\rightarrow \infty .\) For calculations that take place away from the event horizon \({\mathcal {H}}^+\) and future null infinity \({\mathcal {I}}^{+}\) we often work with the coordinate system \((t,r^{\star },\vartheta ,\varphi )\) where the ERN takes the form
However, both coordinate systems above do not extend regularly to the event horizon \( {\mathcal {H}}^+. \) One way to extend the metric beyond \({\mathcal {H}}^+\) is to consider the so-called ingoing Eddington–Finkelstein coordinates \( (v,r,\vartheta ,\varphi ) \) and with respect to that system the ERN metric is given by
In this setting, the event horizon is captured by \( {\mathcal {H}}^{+}\equiv \left\{ r=M \right\} \), while the coordinate \( v \in (-\infty , \infty )\) traverses it. While the ingoing coordinates are regular up to \( r>0, \) we focus on producing estimates only on the domain of outer communication \( {\mathcal {M}} \), where \( r\ge M,\) i.e.
Foliations. Here, we introduce the two foliations we are going to be using in this paper.
-
For the first one, let \( \Sigma _{0} \) be a flat \( SO(3)- \) invariant spacelike hypersurface terminating at \( i^{o} \), the spacelike infinity where \(r\rightarrow \infty \), and crossing the event horizon \( {\mathcal {H}}^+\) with \( \partial \Sigma _0 = \Sigma _0\cap {\mathcal {H}}^+.\) Note, \( \Sigma _0 \) can be chosen such that its unit normal future directed vectorfield \( n_{\Sigma _0} \), satisfies everywhere
$$\begin{aligned} \frac{1}{C}< -g(n_{\Sigma _0},n_{\Sigma _0})< C, \hspace{1cm} \frac{1}{C}< - g(n_{\Sigma _0},T) < C, \end{aligned}$$for a positive constant \( C>0 \), where \( T=\partial _v \) is the global Killing vector field in ERN, with respect to (3). Let \( \phi _{\tau }^{T} \) be the one-parameter family of isomorphisms corresponding to the Killing field T, and define the foliation \( \Sigma _{\tau } := \phi _{\tau }^T(\Sigma _0) \). Then, the hypersurfaces \( \Sigma _{\tau } \) are isometric to \( \Sigma _0 \) and the coercive relations above hold uniformly in \( \tau , \) for the same constant C. Estimates associated with this foliation take place in the region \( \quad {\mathcal {R}}(0,\tau ):= \cup _{0\le {\tilde{\tau }}\le \tau } \Sigma _{{\tilde{\tau }}} \)

-
Next, we introduce a foliation \( {\check{\Sigma }}_{\tau } \) that captures the radiating energy towards future null infinity \( {\mathcal {I}}^{+} \), and is ultimately used to obtain energy decay estimates. For that, fix \( R >2M \) and take the tortoise coordinate \( r^{\star } \) introduced earlier for \( C= -R-4M\log (R-M)- \frac{2M^2}{R-M}\). Define also the coordinate \( t^{\star }:=t+ 2M\log (r-M) - \frac{M^2}{r-M}, \) and consider the following hypersurfaces for all \( \tau \in {\mathbb {R}} \)
$$\begin{aligned} {\check{\Sigma }}_{\tau }:= {\left\{ \begin{array}{ll} \lbrace t^{\star }=\tau \rbrace , \hspace{1cm} \text {for }\ M\le r\le R \\ \\ \lbrace u = \tau \rbrace , \hspace{1.1cm} \text {for} \ \ r\ge R, \end{array}\right. } \end{aligned}$$where u is the advanced null coordinate we saw above. With the specific choice of C in the definition of the tortoise coordinate \( r^{\star }(r) \), the hypersurfaces \( {\check{\Sigma }}_{\tau } \) are well defined on \( \left\{ r=R \right\} \) for all \( \tau \in {\mathbb {R}}. \) Moreover, \( {\check{\Sigma }}_{\tau } \) crosses the event horizon \( {\mathcal {H}}^+ \) and terminates at future null infinity \( {\mathcal {I}}^+ \) for every \( \tau \in {\mathbb {R}} \), as seen in the figure below. Note, along \( {\mathcal {H}}^+\) the parameter of the foliation above satisfies: \( \tau = v+ (M + C)\).

For both foliations above, it is rather useful to consider a coordinate system associated to them. Of course, there is a natural way to define an induced one; for any \( P\in \Sigma _{\tau } \) (or \( {\check{\Sigma }}_{\tau } \)) with coordinates \( P=(v_P,r_P,\omega _P) \), let \( \rho = r_p \) and \( \omega = \omega _P \), where \( \omega _P \) corresponds to the spherical coordinates. Thus, for each point on the hypersurface there is an associated pair \( (\rho ,\omega ) \) for \(\rho \ge M, \ \omega \in {\mathbb {S}}^{2}. \) In addition, by the construction of the foliations, we have \( \partial _{\rho } = k(r)\cdot \partial _v + \partial _r \), for a bounded function k(r) . Hence, in view of \( [\partial _v,\partial _{\rho }]=[\partial _{\rho },\partial _{\theta }] = [\partial _{\rho },\partial _{\phi }]= [\partial _{\theta },\partial _{\phi }] = 0 , \) and Frobenius theorem, we have that \( (\rho ,\omega ) \) defines a Lie propagated coordinate system on the foliation \( \Sigma _{\tau } \) (similarly for \( {\check{\Sigma }}_{\tau } \)).
2.2 The \( S^2_{v,r} \)–tensor algebra and commutation formulae in ERN
We briefly present relevant angular operators for \( S^2_{v,r} -\)tensors and useful identities they satisfy, adopted on the ERN spacetime. We express everything with respect to the ingoing Eddington–Finkelstein coordinates \( (v,r,\vartheta ,\varphi ). \)
Let  be the covariant derivative associated to the round metric
be the covariant derivative associated to the round metric  on the spheres \( S^2_{v,r}. \) Next, we denote by
on the spheres \( S^2_{v,r}. \) Next, we denote by  the projection to \( S^2_{v,r} \) of the spacetime covariant derivative \( \nabla _{\frac{\partial }{\partial r}} \). For the following definitions of angular operators, let \( \xi _{A} \) be any one-form and \( \theta _{AB} \) be any symmetric traceless 2-tensor on \( S^2_{v,r} \) . Then,
the projection to \( S^2_{v,r} \) of the spacetime covariant derivative \( \nabla _{\frac{\partial }{\partial r}} \). For the following definitions of angular operators, let \( \xi _{A} \) be any one-form and \( \theta _{AB} \) be any symmetric traceless 2-tensor on \( S^2_{v,r} \) . Then,
- \( \diamond \):
-
 takes \( \xi \) to the pair of scalars
takes \( \xi \) to the pair of scalars  where
where 
- \( \diamond \):
-
 is the formal \( L^2- \)adjoint of
is the formal \( L^2- \)adjoint of  , which takes any pair of scalars (f, g) into the one-form
, which takes any pair of scalars (f, g) into the one-form  .
. - \( \diamond \):
-
 takes the tensor \( \theta \) to the one-form
takes the tensor \( \theta \) to the one-form  .
. - \( \diamond \):
-
 is the formal \( L^2- \)adjoint of
is the formal \( L^2- \)adjoint of  which takes a one form \( \xi \) to the symmetric traceless two tensor
which takes a one form \( \xi \) to the symmetric traceless two tensor 
The first set of identities relating the above operators to the Laplacian  on \( S^2_{v,r} \) can be easily checked
on \( S^2_{v,r} \) can be easily checked

where K is the Gauss curvature of \( S^2_{v,r} \) and  is the Laplacian acting on \( k- \)tensors respectively.
is the Laplacian acting on \( k- \)tensors respectively.
In addition, for any \( \xi _{A_1,\dots ,A_n} \), an \( n-\)covariant \( S^2_{v,r} \)-tensor, we have

from which we obtain the commutation identities

2.3 Spherical harmonics and elliptic identities
In this paragraph, we briefly recall the spherical harmonics, and using the operators introduced above we define the corresponding orthogonal decomposition of one forms \( \xi \) and traceless symmetric 2-tensors \( \theta \) on \( S_{v,r}^2 \).
Fix \( \ell \in {\mathbb {N}} \), \( \left|m\right|\le \ell \) and denote by \( \mathring{Y}_{m}^{\ell }(\vartheta ,\varphi ) \) the spherical harmonics on the unit sphere, i.e.

This family forms an orthogonal basis of \( L^2({\mathbb {S}}^2) \) with respect to the standard inner product on the sphere. Since we will be working on spheres of radius r, \( S^2_{v,r} \), we take the normalized spherical harmonics denoted by \( Y_{m}^{\ell } (r,\vartheta ,\varphi ) \) that satisfy

A function f is said to be supported on the fixed frequency \( \ell \) if the following projections vanish
for all \( {\tilde{\ell }}\ne \ell . \)
Now, we recall that any one-form \( \xi \) has a unique representation  for two functions f, g on the unit sphere with vanishing mean, i.e. \( f_{\ell =0}=g_{\ell =0}=0.\)
for two functions f, g on the unit sphere with vanishing mean, i.e. \( f_{\ell =0}=g_{\ell =0}=0.\)
Similarly, any traceless symmetric two-tensor \( \theta \) on \( S^2_{v,r} \) has a unique representation  , where both scalars f, g are supported on \( \ell \ge 2. \)
, where both scalars f, g are supported on \( \ell \ge 2. \)
We say that \( \xi , \) or \( \theta , \) are supported on the fixed frequency \( \ell \), if the scalars f, g in their unique representation are supported on the fixed frequency \( \ell . \) Now, using the identities from relation (4) we can show


where for any \( S^2_{v,r}-\) tensor of rank n, \( \xi _{A_1\dots A_n} \), we have

In addition, if \( \xi , \theta \) are supported on the fixed angular frequency \( \ell \), we have the following elliptic identities; see relations (24),(25) in [30]


In particular, for \( \xi \) supported on the fixed angular frequency \( \ell \ge 1 \), we have

and for a traceless symmetric tensor \( \theta \) supported on the angular frequency \( \ell \ge 2, \) using the above identity for  and then identities (8), (10) we obtain
and then identities (8), (10) we obtain

3 The generalized Teukolsky and Regge–Wheeler system and the gauge invariant hierarchy
The main goal of this paper is to study induced gauge–invariant quantities, arising from linear gravitational and electromagnetic perturbations of ERN spacetime. To do so, we rely on the set-up and resulting linearized equations obtained in [28, 32], however, we adapt all notions involved to the extremal case \( M = \left|Q\right| .\)
In the following subsections, we first give an overview of the general set-up used and briefly describe the quantities we will be working with throughout the paper. Next, we write down the generalized Teukolsky system that the aforementioned quantities satisfy; we also go through the transformation theory that allows us to study this system by reducing it to a set of generalized Regge–Wheeler equations. Finally, using operators introduced in Section 2, we derive the resulting scalar system from the tensorial one, and we show that it is subject to decoupling after we consider its spherical harmonics decomposition.
3.1 The set-up and the gauge–invariant quantities
Let \( ({\mathcal {M}},{\textbf{g}}) \) be a \( 3+1-\)dimensional Lorentzian manifold satisfying the Einstein–Maxwell equations
where \( \varvec{D} \) is the covariant derivative associated to the metric \( {\textbf{g}}_{\mu \nu } \), and \( \varvec{F}_{\mu \nu } \) is the electromagnetic tensor. The author in [29] builds upon the formalism of null frames and initiates a null decomposition of (13) for induced quantities, i.e. Ricci coefficients, curvature, electromagnetic components, and the equations they satisfy. This can be done since any Lorentzian manifold admits a foliation out of 2-surfaces ( ), where
), where  is the pullback metric of \( {\textbf{g}} \) on S, and at each point in \( {\mathcal {M}} \) we can associate a local null frameFootnote 3\( {\mathcal {N}} = \left\{ e_3,e_4, e_A \right\} \), with \( e_A\) tangent to S, for \( A\in \left\{ 1,2 \right\} \). We briefly express relevant quantities with respect to this null frame:
is the pullback metric of \( {\textbf{g}} \) on S, and at each point in \( {\mathcal {M}} \) we can associate a local null frameFootnote 3\( {\mathcal {N}} = \left\{ e_3,e_4, e_A \right\} \), with \( e_A\) tangent to S, for \( A\in \left\{ 1,2 \right\} \). We briefly express relevant quantities with respect to this null frame:
-
Ricci coefficients
$$\begin{aligned} \begin{aligned} \chi _{A B}&:={\textbf{g}}\left( {\textbf{D}}_A e_4, e_B\right) ,&{\underline{\chi }}_{A B}:={\textbf{g}}\left( {\textbf{D}}_A e_3, e_B\right) \\ \eta _A:&=\frac{1}{2} {\textbf{g}}\left( {\textbf{D}}_3 e_4, e_A\right) ,&{\underline{\eta }}_A:=\frac{1}{2} {\textbf{g}}\left( {\textbf{D}}_4 e_3, e_A\right) \\ \xi _A:&=\frac{1}{2} {\textbf{g}}\left( {\textbf{D}}_4 e_4, e_A\right) ,&{\underline{\xi }}_A:=\frac{1}{2} {\textbf{g}}\left( {\textbf{D}}_3 e_3, e_A\right) \\ \omega :&=\frac{1}{4} {\textbf{g}}\left( {\textbf{D}}_4 e_4, e_3\right) ,&{\underline{\omega }}:=\frac{1}{4} {\textbf{g}}\left( {\textbf{D}}_3 e_3, e_4\right) \\ \zeta _A&:=\frac{1}{2} {\textbf{g}}\left( {\textbf{D}}_A e_4, e_3\right) , \end{aligned} \end{aligned}$$and we also denote by \( \hspace{1cm}\kappa : = tr \chi , \hspace{1cm} {\underline{\kappa }} := tr {\underline{\chi }}. \)
-
Curvature components
$$\begin{aligned} \begin{aligned} \alpha _{A B}&:={\textbf{W}}\left( e_A, e_4, e_B, e_4\right) ,{} & {} {\underline{\alpha }}_{A B}:={\textbf{W}}\left( e_A, e_3, e_B, e_3\right) \\ \beta _A:&=\frac{1}{2} {\textbf{W}}\left( e_A, e_4, e_3, e_4\right) ,{} & {} {\underline{\beta }}_A:=\frac{1}{2} {\textbf{W}}\left( e_A, e_3, e_3, e_4\right) \\ \rho :&=\frac{1}{4} {\textbf{W}}\left( e_3, e_4, e_3, e_4\right) ,{} & {} \sigma :=\frac{1}{4}{ }^{\star } {\textbf{W}}\left( e_3, e_4, e_3, e_4\right) \end{aligned} \end{aligned}$$where \( {\textbf{W}} \) is the Weyl curvature of \( {\textbf{g}} \) and \( ^{\star }{\textbf{W}} \) denotes the Hodge dual.
-
Electromagnetic components
$$\begin{aligned} \begin{aligned}&^{(F)}\beta _{A}:={\textbf{F}}\left( e_A, e_4\right) , \quad ^{(F)}{\underline{\beta }}_{A}:={\textbf{F}}\left( e_A, e_3\right) \\&{ }^{(F)} \rho :=\frac{1}{2} {\textbf{F}}\left( e_3, e_4\right) , \quad { }^{(F)} \sigma :=\frac{1}{2}{ }^{\star } {\textbf{F}}\left( e_3, e_4\right) \end{aligned} \end{aligned}$$where \( ^{\star }{\textbf{F}} \) denotes the Hodge dual of \( {\textbf{F}}.\)
With the above in mind, consider a one-parameter family of Lorentian metrics \( \varvec{g}(\epsilon ) \), around the Reissner–Nordström (RN) solution, \( \varvec{g}(0)\equiv g_{M,Q} \), solving (13) and written in the following Bondi form; see [29].

with \( \varsigma (0)=1, \ {\underline{\Omega }}(0)= \left( 1-\frac{2M}{r} + \frac{Q^{2}}{r^{2}}\right) , \ {\underline{b}}_A(0)=0 \) and 
Initiating a linear gravitational and electromagnetic perturbation of RN spacetime corresponds to linearizing the full system of equations obtained from the null decomposition of (13) in terms of \( \epsilon \), with respect to the associated null frame \( {\mathcal {N}}_{\epsilon } = \left\{ \varvec{e}_3(\epsilon ),\varvec{e}_4(\epsilon ), \varvec{e}_A(\epsilon ) \right\} \) given by
For example, the linearization of the induced Bianchi equation satisfied by the extreme curvature component \( \varvec{\alpha }(\epsilon ) \equiv \ 0 \ + \epsilon \cdot \alpha \) yields the following equation for the linearized quantity \( \alpha \)

where all operators and scalars that appear above are taken with respect to the RN background metric; the rest are unknowns of the linearized system. For the complete set of linearized system and their list of unknowns, see section 4 in [29].
Gauge–invariant quantities. In this paper, we focus our analysis on a special set of derived unknowns called gauge–invariant quantities, identified as the ones that vanish in any pure gauge solution. Pure gauge solutions are derived from linearizing families of metrics that correspond to a smooth coordinate transformation of RN, preserving its Bondi form.
The first two such quantities are unknowns of the linearized system itself, \( \alpha \) and \( {\underline{\alpha }}, \) which correspond to the linearized quantities of the extreme curvature components \( \varvec{\alpha }(\epsilon )\), \( \underline{\varvec{\alpha }}(\epsilon ),\) respectively. In the linear theory of Einstein vacuum equations, these quantities satisfy decoupled wave equations, known as the Teukolsky equation, which is the starting point of the analysis. In the Einstein–Maxwell case, they no longer appear alone in these equations since there is a new set of gauge invariant quantities acting as a source. These new quantities were first defined in [28, 32] as

where \( {}^{(F)}\hspace{-0.08cm} {\beta }, {}^{(F)}\hspace{-0.08cm} {{\underline{\beta }}} \) and \( {\hat{\chi }}, \underline{{\hat{\chi }}} \) are unknowns of the linearized system, while  are to be taken with respect to the background RN metric. It is quite remarkable that also \( \mathfrak {f} \) and \( \underline{\mathfrak {f}} \) satisfy Teukolsky type equations themselves, however, coupled with \( \alpha \) and \( {\underline{\alpha }} \), respectively, acting as a source.
are to be taken with respect to the background RN metric. It is quite remarkable that also \( \mathfrak {f} \) and \( \underline{\mathfrak {f}} \) satisfy Teukolsky type equations themselves, however, coupled with \( \alpha \) and \( {\underline{\alpha }} \), respectively, acting as a source.
The last set of gauge invariant quantities that were also introduced are given by
where \( {}^{(F)}\hspace{-0.08cm} {\beta }, {}^{(F)}\hspace{-0.08cm} {{\underline{\beta }}} \) and \( \beta , {\underline{\beta }} \) are unknowns. In the case of Maxwell equations in Schwarzschild spacetime, we have \( {}^{(F)}\hspace{-0.08cm} {\rho } = 0\) and the quantities \( {}^{(F)}\hspace{-0.08cm} {\beta }, {}^{(F)}\hspace{-0.08cm} {{\underline{\beta }}} \) are gauge–invariant themselves, satisfying Teukolsky equations of \( \pm 1 \) spin. However, in our case where \( {}^{(F)}\hspace{-0.08cm} {\rho }\ne 0 \), we consider the modified quantities (15) which now are gauge–invariant and we will see they satisfy a generalized Teukolsky equation of \( \pm 1 \) spin.
3.2 Rescaled null frame and regular quantities
Throughout the papers [29, 30], the author uses the null frame \( {\mathcal {N}}_{\epsilon } \) defined in terms of the Bondi coordinates reducing to the outgoing Eddington–Finkelstein coordinates in the case of RN spacetime. However, much like the coordinate system itself, this null frame does not extend smoothly to the event horizon \( {\mathcal {H}}^+. \) Nevertheless, the rescaled null frame \( {\mathcal {N}}_{\star } : = \left\{ {\underline{\Omega }}^{-1}(\epsilon )\epsilon _{3}(\epsilon ), {\underline{\Omega }}(\epsilon ) e_{4}(\epsilon ), e_{A} \right\} \) extends smoothly to \( {\mathcal {H}}^+\), and so do all induced gauge–invariant quantities when expressed with respect to this frame.
Below, we write the rescaled frame in the extreme RN spacetime with respect to the ingoing Eddington-Finkelstein coordinates, and we give the appropriate rescalings of relevant quantities so that they extend smoothly on \( {\mathcal {H}}^+. \) In particular, in ERN we have \( {\underline{\Omega }} = D(r) = \left( 1-\frac{M}{r}\right) ^{2}\), and in the ingoing coordinates (3) the rescaled null vectors are given by
Then, the corresponding set of rescaled gauge–invariant quantities that extend smoothly on \( {\mathcal {H}}^+\), and the ones that we aim to obtain estimates for, are given by
From now on, all quantities with \( \star \) subscript are expressed with respect to the rescaled frame \( {\mathcal {N}}_{\star } \) defined above, and thus are regular up to and including the horizon \( {\mathcal {H}}^+. \)
3.3 The Teukolsky and Regge–Wheeler system of \( \pm \) spin
First, let us present the generalized Teukolsky equations of \( \pm 2 \) spin satisfied by the traceless, symmetric gauge–invariant quantities \( \alpha _{\star }, \mathfrak {f}_{\star } \), and \( {\underline{\alpha }}_{\star }, \underline{\mathfrak {f}}_{\star } \). We simply adapt the equations of [29] in the case of ERN and express them in terms of the \( {\mathcal {N}}_{\star } \) null frame. For the \( +2 \) spin equations, in view of Definition 5, p. 69, [30], we have

where \( \square _{{\textbf{g}}} = {\textbf{g}}^{\mu \nu } \nabla _{\nu }\nabla _{\mu } \) is taken with respect to the extreme Reissner–Nordström metric, and we denote  , and similarly for \( e_{4}^{\star } \). All coefficients above correspond to the background ERN values when expressed in the \( {\mathcal {N}}_{\star } \) null frame, given by
, and similarly for \( e_{4}^{\star } \). All coefficients above correspond to the background ERN values when expressed in the \( {\mathcal {N}}_{\star } \) null frame, given by
Similarly, we have the \( -2 \) spin equations

Regarding the \( \pm 1 \) spin generalized Teukolsky equations satisfied by \( {\tilde{\beta }}_{\star } \) and \( \underline{{\tilde{\beta }}}_{\star } \) we have

where here \( {}^{(F)}\hspace{-0.08cm} {\beta }_{\star }, \xi _{\star } \) and \( {}^{(F)}\hspace{-0.08cm} {{\underline{\beta }}}_{\star }, {\underline{\xi }}_{\star } \) are unknowns of the linearized system.
In addition to the Teukolsky equations above, the following relating equations have been derived at Lemma 6.1 [28], for \( \alpha , \mathfrak {f} \) and \( {\tilde{\beta }} \), and their underlined analogues.


We will use these relations to obtain estimates for \( \alpha _{\star } \) and \( {\underline{\alpha }}_{\star } \), after we control the quantities of the right-hand side.
Below, we present the transformation theory that allows us to obtain the generalized Regge–Wheeler equation. We write our equations in the ingoing coordinates of Section 2.
The transformation theory. For any \( n- \)rank \( S^{2}_{v,r}-\)tensor \( \xi \), consider the following operators


Using the above operators, the author of [28, 32] defines the following tensors


and similarly,


Note, the tensors \( \varvec{q}^{F}, \varvec{p}\) and \( \underline{\varvec{q}}^{F}, \underline{ \varvec{p}} \), are regular on the horizon \( {\mathcal {H}}^+. \) In [30], it has been shown that the above symmetric traceless tensors satisfy the following generalized Regge–Wheeler equations, adapted in ERN spacetime

where, g corresponds to the background ERN metric as in (3), and
The same equations hold for \( \underline{\varvec{q}}^{F} \) and \( \underline{\varvec{p}} \) as well. In the next subsection, we derive the associated scalar system and we show how to decouple it. This decoupling captures the dominant behavior of solutions to (29) asymptotically along the event horizon \( {\mathcal {H}}^+\); see discussion at the end of Section 6.
3.4 Derivation and decoupling of the scalar Regge–Wheeler system
System (29) involves two tensorial equations, of type 2 and 1. Instead, we use the \( S^{2}_{v,r} \) angular operators of Section 2 to derive the corresponding scalar system. From now on we only write the equations for the positive spin case, and all estimates we derive will automatically hold for the underline counterparts since they satisfy the same equations.
Proposition 3.1
The induced scalars  , and
, and  , satisfy the following coupled system
, satisfy the following coupled system

where K is the Gauss curvature of the section spheres, and \( V_1, V_2 \) as in (30).
Proof
We use Lemma A.1.4. of [32]:

In particular, commuting equations of system (29) with  and using the relations above we obtain the left hand side of the equations as seen above in (32).
and using the relations above we obtain the left hand side of the equations as seen above in (32).
For the right-hand side of the first equations we need to compute

We use the fact that  , from relation (4), and the last relation of the Lemma above to obtain
, from relation (4), and the last relation of the Lemma above to obtain

which concludes the proof. \(\square \)
Remark 3.1
We saw earlier that \( \varvec{p}, \varvec{q^{F}} \) are regular quantities on the horizon \( H^{+} \), and thus, \( \phi \) and \( \psi \) are regular on the horizon as well.
3.4.1 The Cauchy problem for the scalar coupled system
The Teukolsky system we introduced earlier admits a well-posed Cauchy initial value problem; see [28, 32]. However, we will be studying the induced coupled scalar system (32) independently as a system of its own. In particular, we consider general solutions \( (\phi ,\psi ) \) to system (32) arising from initial data
for any \( k\ge 2 \), with \( \Sigma _0 \) as in the foliation paragraph of Section 2, and \( n_{\Sigma _0} \) its future directed unit normal. Then, the solution \((\phi ,\psi )\) is unique in \( {\mathcal {R}}(0,\tau ) \), with \( (\phi ,\psi ) \in H_{loc}^{k}(\Sigma _{\tau })\times H_{loc}^{k}(\Sigma _{\tau }) \) and \( (n_{_{\Sigma }}\phi ,n_{_{\Sigma }}\psi ) \in H_{loc}^{k-1}(\Sigma _{\tau })\times H_{loc}^{k-1}(\Sigma _{\tau })\), for all \( \tau >0. \) Typically, we assume that k is sufficiently large such that all weighted norms appearing in our estimates are finite.
In order to obtain pointwise estimates, we also impose the extra assumptions
In this paper, by “generic initial data” we implicitly refer to those that are naturally derived from the above initial data satisfying the aforementioned assumptions.
We proceed with the following proposition, in which we show how to decouple the scalar system (32).
Proposition 3.2
Consider the spherical harmonic decomposition of (32), then the system of equations supported on the fixed frequency \( \ell \ge 2 \) decouple to
where \( \mu ^2= (\ell +2)(\ell -1)\) and
for \( {\tilde{\psi }}=\frac{1}{4} \mu \psi \quad \) and \(\quad {\tilde{\phi }} = M \phi \).
Proof
We project system (32) to their spherical harmonics \( \psi _{\ell },\phi _{\ell } \) and in view of  \( K=\frac{1}{r^2} \), they satisfy the system
\( K=\frac{1}{r^2} \), they satisfy the system
Now, consider the rescalings
and by writing \( \frac{8M}{r^3}= \frac{5M}{r^3}+\frac{3M}{r^3}, \ \ \frac{2M}{r^3} = \frac{5M}{r^3}-\frac{3M}{r^3} \) we obtain the following system
Let us denote by \( {\mathcal {P}} := \square _{g} + \left( \frac{5M}{r^3}-\frac{6M^2}{r^4}\right) \), the operator of the left-hand side above, and the above system now reads
The decoupling of system (32) will follow after we diagonalize the symmetric matrix \( {\mathcal {C}} = \left( {\begin{array}{c}-3M \quad 2M\mu \\ 2M\mu \quad 3M\end{array}}\right) , \) with \( \det ({\mathcal {C}}) = - M^2 \cdot (2\ell +1)^2 <0 \). In order to find the eigenvalues of \( {\mathcal {C}}, \) we compute its characteristic polynomial
and thus, we obtain the two eigenvalues \( \lambda _1 = M(2\ell +1) \), \( \lambda _2 = - M(2\ell +1). \) One can check directly that \( \left( {\begin{array}{c}2M\mu \\ 3M+\lambda _1\end{array}}\right) ,\ \left( {\begin{array}{c}3M-\lambda _2\\ -2M\mu \end{array}}\right) \) are two distinct non trivial eigenvectors of \( {\mathcal {C}}, \) thus the following two scalars
satisfy
which concludes the proof. \(\square \)
Corollary 3.1
Given the scalars \( \Psi _{i}^{^{(\ell )}} \), for \( \ell \ge 2 \) and \( i\in \left\{ 1,2 \right\} \) as above, it is immediate to check that
Remark 3.2
The above results also hold in the sub-extremal \(\left|Q\right|<M\) case, and such decoupling process in this setting first appeared in the work of Chandrasekhar [14].
4 Estimates for the decoupled scalar Regge–Wheeler equations
In this section, we prove estimates for each equation (35), (36) at the same time. Note, the decoupled system can be written as
where
By projecting the system (32) to the \( \ell =1 \) frequency we obtain only one equation, i.e
Note, the above wave equation can be included in the case \( \Psi _1^{(\ell =1)} \) with \( V_1^{(\ell =1)} \) as in (41). Thus, we will be studying solutions to the equation
with \( \Psi _i^{^{(\ell )}} \) supported on the fixed frequency \( \ell \ge i, \ i\in \left\{ 1,2 \right\} . \) For brevity, the superscript \( (\ell ) \) will be frequently dropped and inferred through the equations.
4.1 Preliminaries
In this section, we briefly recall the vector field method. First, consider the energy-momentum tensor associated to the wave equation (44)
Proposition 4.1
Consider a scalar \( \Psi _i \) verifying equation (44). Let X be a vectorfield, \( \omega \) a scalar function, and M a one form. Define the general current
then,
Proof
We begin by computing \( Div\left( {\mathcal {Q}}_{\mu \nu }\right) = \nabla ^{\mu } {\mathcal {Q}}_{\mu \nu } \)
We first treat the following term
Using the above relation and the fact that \( \nabla ^{\mu }\nabla _{\mu }\Psi _i = \square \Psi _i= V_i \Psi _i\) we obtain
On the other hand, we have
Last, we recall that \( ^{(X)}\pi ^{\mu \nu } := ({\mathcal {L}}_{X}g)^{\mu \nu } = (\nabla ^{\mu }X)^{\nu } + (\nabla ^{\nu }X)^{\mu } \) is the deformation tensor, thus we have
Combining all the above, we conclude the formula for \( K^{X,\omega ,M}[\Psi _i]. \) \(\square \)
Remark 4.1
If \( \Psi _i\) satisfies (44) with a non-homogeneous term on the right-hand side, i.e.
then we have
which can be easily checked by the calculations above when computing \( \nabla ^{\mu }Q_{\mu \nu }. \)
The Vector Field Method. The vector field method is the application of Stokes’ theorem in appropriate regions for the current \( J_{\mu }^{X,\omega ,M} \). In particular, given a (0,1) current \( P_{\mu } \), then Stokes’ theorem yields in the region \( {\mathcal {R}}(0,\tau ) \)
where all the integrals are with respect to the induced volume form and the unit normals \( n_{S} \) are future-directed.
4.2 Uniform Boundedness of Degenerate Energy
Let us apply the vectorfield method for \( X=T=\partial _v \), \( \omega =M=0, \) where T is written with respect to the coordinate system \( (v,r,\vartheta ,\varphi ) \). Since T is Killing, we have \( {}^{(T)}\pi =0 \) and \( T(V_i^{^{(\ell )}})=0 \) because \( V_i\) is a function of r alone, thus \( K^T[\Psi _i] =0\). Therefore, the divergence theorem in the region \( {\mathcal {R}}(0,\tau ) \) yields
On the event horizon \( {\mathcal {H}}^+ \) we can take \( n_{{\mathcal {H}}^+}^{\mu }=T\), thus
which proves the following proposition.
Proposition 4.2
For all solutions \( \Psi _i \) to equation (44) we have
The T-flux. We will see below that \( J_{\mu }^T[\Psi _i]n_{\Sigma _{\tau }}^{\mu } \) is non-negative definite only after we integrate on the spheres \(S^2_{v,r} \) and use Poincare’s Inequality due to the negative values of the potentials \( V_i^{^{(\ell )}}\), \( i=1,2. \) However, we also need to know how \( J_{\mu }^T[\Psi _i]n_{\Sigma _{\tau }}^{\mu } \) depends on the 1-jet of \( \Psi _i \). In particular, write \( n_{{\Sigma _{\tau }}}= n_{{\Sigma _{\tau }}}^v \partial _v + n_{\Sigma _{\tau }}^r\partial _r \) and note that the normal to the spacelike hypersurface \( \Sigma _0 \), \( n_{\Sigma _0} \), was chosen such that
for a positive constant \( C_1 \) depending only on \( M, \Sigma _0 \). Thus, the same holds for \( n_{\Sigma _{\tau }} \) since \( \Sigma _{\tau } = \phi _{\tau }(\Sigma _0) \), where \( \phi _{\tau } \) is the flow associated to the Killing vector field T. First, we recall the following inequality, p 33 [7],
Proposition 4.3
(Poincaré Inequality) Let \( \psi \in L^2 (S^2_{v,r}) \) and \( \psi _{\ell }=0 \) for all \( \ell \le L-1 \) for some finite natural number L, then

and equality holds if and only if \( \psi _{\ell }=0 \) for all \( \ell \ne L. \)
Proposition 4.4
Let \( \Psi _i^{^{(\ell )}} \) be a solution to equation (44), supported on the fixed frequency \( \ell \ge i,\ i\in \left\{ 1,2 \right\} \), then there exists a positive constant \( C=C(M, \Sigma _0) \) such that

Proof
Let \( n_{{\Sigma _{\tau }}}= n_{{\Sigma _{\tau }}}^v \partial _v + n_{\Sigma _{\tau }}^r\partial _r \), then direct computations yield

We argue that relations (52, 53) and Poincare inequality suffice to prove the proposition.
Away from the horizon \( \left\{ r\ge r_0 \right\} , \) for \( r_0 > M \), we might as well choose \( n_{\Sigma _{0}} \equiv T \). However, near the horizon \( {\mathcal {H}}^+\), the relations (52, 53) read
thus we must have \( n_{\Sigma _0}^r <0\) and \(n_{\Sigma _0}^v >0 \). On the other hand, squaring the second relation yields
and since the first term is positive from (52), we obtain that \( n^r \) is uniformly bounded. Hence, \( Dn^v-2n^r = (Dn^v-n^r) -n^r >\frac{1}{C_1} \) and bounded from above. Thus, using (52) we have
and as we saw \( \left( Dn^v-2n^r\right) \) is bounded from above, which makes \( n^v \) uniformly bounded from below by a positive constant. We put all the above together and we find a constant C depending on \( M, \Sigma _0 \) such that

However, the potential \( V_i^{^{(\ell )}}(r) \) takes negative values as well. To show that the \( T- \)flux is also coercive with respect to the zeroth order term we borrow from the angular derivative of \( \Psi _i\) using Poincare inequality. Integrating (56) along \( \Sigma _{\tau } \) and using the uniform boundedness of degenerate energy yields

Now, we write  , for some \( 0<a<1 \) to be determined later, and using Poincare we examine the following term
, for some \( 0<a<1 \) to be determined later, and using Poincare we examine the following term

It suffices to study the above coefficient for each \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \) and for each \( r\ge M. \)
-
If \( i=1, \) and for any \( \ell \ge 1 \) we have
$$\begin{aligned} a + \dfrac{V_1(r)\cdot r^2}{\ell (\ell +1)} = a - \dfrac{2M}{r}\dfrac{3\sqrt{D}}{\ell ( \ell +1)}+\dfrac{2M}{\ell \cdot r}\ge a + \dfrac{M}{\ell \cdot r}\left( 2-3\sqrt{D}\right) \end{aligned}$$The second term becomes negative only when \( r\ge 3M \), and it is easy to check that \( \frac{M}{r}(2-3\sqrt{D}) \ge -\frac{1}{3} \). Thus, it suffices to consider \( \frac{1}{3}<a<1, \) which works for all \( \ell \ge 1. \)
-
If \( i=2, \) for any \( \ell \ge 2 \) we have
$$\begin{aligned} a + \dfrac{V_2(r)\cdot r^2}{\ell (\ell +1)} = a- \dfrac{2M}{r}\dfrac{3\sqrt{D}}{\ell (\ell +1)} - \dfrac{2M}{(\ell +1)\cdot r} \ge a -\dfrac{1}{3} \dfrac{M}{r}\left( 2+3\sqrt{D}\right) \end{aligned}$$However, if we set \( x:= \sqrt{D} \in [0,1) \) we write the above as
$$\begin{aligned} a + \left( x^2-\dfrac{1}{3}x -\frac{2}{3}\right) \end{aligned}$$The quadratic polynomial above attains its minimum at \( x=\frac{1}{6} \) with value \( -\frac{25}{36} \sim 0.69 \). Thus, it suffices to consider \( 0.7< a <1. \)
We can see from the analysis above that \( a=0.7 \) is sufficient to get (57) uniformly positive for all \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \) and \( r\ge M. \) \(\square \)
4.3 Morawetz Estimates
We apply the vector field method for vector fields of the form \( X= f(r^{\star })\frac{\partial }{\partial r^{\star }}, \ \) written with respect to the coordinate system \( (t,r^{\star }) \). We will often differentiate with respect to the \( r-\)coordinate instead of \( r^{\star } \), and the two are related by \( \frac{\partial h}{\partial {r^{\star }}}=D\cdot \frac{\partial h}{\partial {r}} ,\) for any scalar function h. By \( h'= \frac{\partial h}{\partial r} \) we will denote the derivative with respect to the \( r-\)coordinate in the \( (t,r,\vartheta ,\varphi ) \) coordinate system.
The scalar current \( K^X \). Let us consider the following current
then using Proposition 4.1 we arrive at

However, there is no choice of scalar f such that all coefficients above are positive definite everywhere. Indeed, assume the coefficients of the first two terms of \( K^{X} \) are positive, then
On the other hand, if the coefficient of  is also non-negative we must have
is also non-negative we must have
Thus, going back to the coefficient of \( (\partial _t\Psi _i)^2 \) we obtain
Hence, in view of \( f'> 0 \) we have that \( \frac{f'}{2} + \frac{f}{r} \) becomes negative for \( r\ge r_{p}=2M. \)
Already, the above suggests that we modify the energy current by introducing more terms. The idea is to introduce a term with the effect of canceling \( (\partial _t\Psi _i)^2 \) when computing the scalar current. Nevertheless, we retrieve this term in the final Morawetz estimates of Proposition 4.6.
The scalar current \( K^{X,G}. \) Consider the following current
where \( G= r^{-2}\partial _{r^{*}}\left( f\cdot r^2\right) \). Consequently, this choice of G cancels the time derivative term when computing the scalar current. In particular, using Proposition 4.1 direct computations yield the expression

where \( P(r):= \sqrt{D}(2\sqrt{D}-1) = \frac{1}{r^2} (r-M)(r-2M) \). While, in view of the factor P(r) , the degeneracy of the angular derivative term at the photon sphere \(\left\{ r=r_p:= 2M \right\} \) is inevitable, we shall find functions f, G such that the coefficients of the two first terms in \( K^{X,G} \) are non-negative definite. In particular, it is imperative that we choose f that is increasing and changes sign from negative to positive at the photon sphere \( \left\{ r=r_p \right\} \).
The choice of G, f. In the extremal Reissner–Nordström spacetime, the wave operator with respect to the coordinate system \( (t,r^{\star },\vartheta ,\varphi ) \) reads

Since \( G= r^{-2}\partial _{r^{*}}\left( f\cdot r^2\right) \) is a function of \( r^{\star } \) alone, we have
Let us chooseFootnote 4
Then, direct computation yields
Therefore, we have
In addition, now that we have G we can find f using the transport equation \( G= r^{-2}\partial _{r^{*}}\left( f\cdot r^2\right) \) or equivalently \( \partial _{r}(f\cdot r^2)=\frac{r^2G}{D} \), thus integrating from \( r_p \) to r we obtain
As we can see, f is increasing and changes sign at the photon sphere and thus satisfies the requirements we were looking for. However, for both \( i=1,2 \), the zeroth order coefficient in \( K^{X,G} \) takes negative values as well, for all \( \ell \ge i \).
The zeroth order term of \(K^{X,G}\). Let’s first study the expression \( - \dfrac{1}{2}f\cdot \partial _r\Big (D\cdot V_i^{^{(\ell )}}\Big ). \) Denote by \( x:=\sqrt{D}\in [0,1) \) then using (63), direct computations yield
In this form, it is apparent that both \( z_i^{(\ell )} \) for all \( \ell \ge i, \ i\left\{ 1,2 \right\} ,\) are not positive definite. In addition, the term \( -\frac{1}{4} \square G = 3 \frac{x^2}{r^3}(1-x)(2x-1)\) comes to add extra "negativity" to the overall zeroth order term.
On the other hand, \( f(r)\cdot P(r) \) degenerates at the photon sphere to second order, as opposed to the two aforementioned terms, thus even after using Poincare inequality to borrow from the angular derivative coefficient, we cannot obtain a positive definite zeroth order term of the current \( K^{X,G} .\) Nevertheless, in what follows we show that there is a modified energy current that ultimately provides us with the required positive bulk for all terms.
4.3.1 The scalar current \( K^{X,G,h}\)
In view of the above discussion, we consider the following modified current
with the last term corresponding to the choice \(M_{\mu } = 2 h\left( \frac{\partial }{\partial _{r^{*}}}\right) _{\mu }\) in the relation (46). Then, applying Proposition 4.1, the corresponding scalar current is given by

Our goal is to find an appropriate function h(r) such that \( K^{X,G,h} \) is positive definite. However, we first need to treat the extra term \( h \Psi _i\partial _{r^{*}}\Psi _i \) such that only quadratic terms appear. We borrow from the coefficient of \( (\partial _{r^{*}} \Psi _i)^2 \) by writing
for some \( \nu \in (0,1) \) to be determined in the end, and we complete the square as
Therefore, using relation (68), we can now rewrite (67) as

Denote by \( \mathfrak {C}(h) \) the expression below
We simply focus on finding a function h(r) such that \( \mathfrak {C}(h) \) beats the negative values of \( z_i^{(\ell )} \), \( \forall \ell \ge i, \ i\left\{ 1,2 \right\} \), uniformly.
The coefficient \( \mathfrak {C}(h) \). In order to better understand the expression \( \mathfrak {C}(h) \) we rewrite it in a more concise way using relation (60), i.e.
Then we have
However, \( \partial _rG = 2r^{-2} \sqrt{D}(2-3\sqrt{D})\), and if we denote by \( x:=\sqrt{D} \in [0,1) \) and express \( \mathfrak {C}(h) = T(h(x(r))) \) we obtain
Now, consider the following choice
and using the fact that \( f'(r) = \frac{8(1-x)^2}{r} \), then \( \mathfrak {C}(h) \) becomes
Let \( \nu = \frac{15}{16} < 1 \), then \( \mathfrak {C}(h) \) becomes
We can already see that \( \mathfrak {C}(h) \) is positive definite around the photon sphere and becomes negative only for \( r> 5M. \) Nevertheless, with the help of Poincare inequality we will show that the zeroth order term of \( K^{X,G,h}[\Psi _i^{^{(\ell )}}] \) is positive definite uniformly in \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \), with a degeneracy only at the horizon \( {\mathcal {H}}^+\).
Proposition 4.5
Let h(r) be as in (71) and choose \( \nu =\frac{15}{16} \) in (69), then there exists a positive constant depending only on M, such that for all solutions \(\Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \), we have

Proof
After we integrate relation (69) on the spheres we obtain

Recall that \( f(r)\cdot P(r) = (2\sqrt{D}-1)(3-2\sqrt{D})\cdot (2\sqrt{D}-1)\sqrt{D} \), thus
In addition, the coefficient of \( (\partial _{r^{\star }}\Psi _i)^2 \) becomes
Finally, we need to treat the coefficient of the zeroth order term as well. For that, we consider each case \( i=1,2 \) separately because they pose different difficulties. We remind our readers that for the calculations below we express all functions in terms of \( x := \sqrt{D} \), and we produce estimates for all \( x\in [0,1), \) which corresponds to \( r\ge M. \)
The zeroth order term of \( K^{X,G,h}[\Psi _1^{^{(\ell )}}],\ \ell \ge 1.\) According to relation (72), the zeroth order coefficient reads
where
However, we may rewrite the quadratic polynomial as
Hence, \( z_1^{(\ell )} \) reads
We treat each term separately below.
-
The first term in (74) can be controlled using Poincare inequality by borrowing a fraction \( a \in (0,1) \) from the angular derivative coefficient. In particular, we have

Since \( f\cdot P \) has the correct sign, we are only interested in choosing a sufficient \( a \in (0,1) \) such that the discriminant of the quadratic expression is negative uniformly in \( \ell \ge 1 \), i.e.
$$\begin{aligned} a > \dfrac{(2\ell -7)^2}{36\ell (\ell +1)}, \hspace{1cm} \forall \ \ell \ge 1. \end{aligned}$$However, in view of the denominator growing quadratically in \( \ell \) with a higher rate than the numerator, we have
$$\begin{aligned} \dfrac{(2\ell -7)^2}{36\ell (\ell +1)}< \dfrac{(2\cdot 1-7)^2}{36(1+1)} < 0.35, \hspace{1cm} \forall \ell \ge 1, \end{aligned}$$thus \( a=0.35 \) is sufficient to make the first term of (74) non-negative definite for all \( \ell \ge 1. \)
-
We have a remaining fraction \( 0<b<0.65 \) of the angular derivative coefficient that we can use to control the second term of (74). Once again, using Poincare inequality we write
$$\begin{aligned}&\dfrac{(\ell +1)}{r^3}x^2(1-x)f + \dfrac{b}{r^3}\ell (\ell +1) f\cdot P \ge \dfrac{(\ell +1)}{r^3}x^2(1-x)f + \dfrac{b}{r^3}\ell (\ell +1)(1-x) f\cdot P \\&\quad = \dfrac{(\ell +1)}{r^3}x^2(1-x)(2x-1)(3-2x) + \dfrac{b}{r^3}\ell (\ell +1) x(2x-1)^2(3-2x) (1-x) \\&\quad = \dfrac{(\ell +1)}{r^3} x(1-x)(3-2x) (2x-1)\Big ((1+2b\ell )x-b\ell \Big ) \end{aligned}$$Clearly for \( x\ge \frac{1}{2} \) the expression above is non-negative. Let us focus on \( x<\frac{1}{2} \) and notice that the only interval where it takes negative values is \( N_{\ell }:= \left( x_{\ell }, \frac{1}{2}\right) \), where \( x_{\ell }:=\frac{b\ell }{1+2b\ell },\ \ell \ge 1, \) and \( x_{\ell } \xrightarrow {\ell \rightarrow \infty } \frac{1}{2} \). By studying the quadratic polynomial
$$\begin{aligned} p_{\ell }(x) := (2x-1)\Big ((1+2b\ell )x-b\ell \Big ) = (4b\ell +2)x^2 -(4b\ell +1)x+b\ell \end{aligned}$$we see that it attains its minimum at \( {\underline{x}}_{\ell } = \frac{(4b\ell +1)}{2(4b\ell +2)} \) with the value
$$\begin{aligned} p_{\ell }(x) \ge p_{\ell }({\underline{x}}_{\ell }) = - \dfrac{1}{4(4b\ell +2)}, \hspace{1cm} \forall x \in [0,1). \end{aligned}$$\( \diamond \) For all \( \ell \ge 2 \) we may choose \( b=\frac{1}{2}\in (0,0.65) \) and thus we have the lower bound
$$\begin{aligned} \dfrac{(\ell +1)}{r^3} x(1-x)(3-2x) p_{\ell }(x) \ge -\dfrac{1}{8r^3}x(1-x)(3-2x), \quad \forall x\in N_{\ell },\ \forall \ \ell \ge 2 \end{aligned}$$On the other hand, note that \( N_{\ell =2} \supset N_{\ell },\ \forall \ell \ge 2\) and thus, for all \( x \in N_{\ell =2}=\left( \frac{1}{3},\frac{1}{2}\right) \) we have
$$\begin{aligned} \mathfrak {C}(h) -\dfrac{1}{8r^3}x(1-x)(3-2x)&= \dfrac{1}{r^3} x \cdot \left( \dfrac{3}{10}x(4-5x) - \dfrac{1}{8}(1-x)(3-2x) \right) \\&=\dfrac{1}{r^3}\frac{x}{4}\left( -7x^2 +7.3x-1.5\right) , \end{aligned}$$and its easy to check that the quadratic polynomial is uniformly positive in \( N_{\ell =2}. \) \( \diamond \) For \( \ell = 1\), we need a little more help from Poincare inequality so we choose \( b = \frac{5}{8} = 0.625 <0.65 \) and now we have
$$\begin{aligned}&\dfrac{2}{r^3} x(1-x)(3-2x) p_{_{\ell =1}}(x) \ge -\dfrac{1}{9r^3}x(1-x)(3-2x), \\&\quad \forall x\in N_{_{\ell =1}}=\left( \frac{5}{18},\frac{1}{2}\right) . \end{aligned}$$Once again, one can check that the expression below is uniformly positive for \( x\in N_{_{\ell =1}} \),
$$\begin{aligned} \mathfrak {C}(h) -\dfrac{1}{9r^3}x(1-x)(3-2x) = \frac{1}{90 r^{3}} x \left( -155x^{2}+158x -30\right) \end{aligned}$$
Finally, regarding the region where \( \mathfrak {C}(h) \) becomes negative, i.e. \( r\ge 5M \), note that the Poincare inequality used earlier for \( b = \frac{1}{2} \) is sufficient to make it positive definite for all \( \ell \ge 1. \)
Combining all the above allows us to find a positive constant C that depends only on M such that
The zeroth order term of \( K^{X,G,h}[\Psi _2^{^{(\ell )}}],\ \ell \ge 2.\) We approach this case similarly and now have
-
Using Poincare inequality, we control the first term as
$$\begin{aligned}&-\dfrac{(2\ell +9x)}{r^3}(1-x)f\cdot P + \dfrac{a}{r^3}\ell (\ell +1)f\cdot P \\&\quad = \dfrac{1}{r^3}f\cdot P \Big ( -(1-x)(2\ell +9x) + a\ell (\ell +1) \Big ) \\&\quad = \dfrac{1}{r^3}f\cdot P \Big ( 9x^2+(2\ell -9)x + \ell (a(\ell +1)-2) \Big ) \end{aligned}$$and by checking the discriminant of the quadratic polynomial, it suffices to have \( a\in (0,1) \) such that
$$\begin{aligned}&(2\ell -9)^2-36\ell (a(\ell +1)-2)<0, \hspace{1cm} \forall \ \ell \ge 2 \\ \Leftrightarrow&a>\dfrac{(2\ell +9)^2}{36\ell (\ell +1)}, \hspace{1cm} \forall \ \ell \ge 2 \end{aligned}$$However, the right-hand side term satisfies for all \( \ell \ge 2 \)
$$\begin{aligned} \dfrac{(2\ell +9)^2}{36\ell (\ell +1)} \le \dfrac{(4+9)^2}{36\cdot 6} < 0.79, \end{aligned}$$thus \( a=0.79 \) is sufficient to make the first term of \( z_2^{(\ell )} \) non-negative for all \( \ell \ge 2. \)
-
There is a remaining fraction \( 0<b<0.21 \) we can use to bound the second term of \( z_2^{(\ell )} \) and with the help of \( \mathfrak {C}(h) \) we can show uniform positivity for the zeroth order term. In particular, we have
$$\begin{aligned}&- \dfrac{\ell }{r^3}x^2(1-x)f\ +\ b\ell (\ell +1) f\cdot P \ge - \dfrac{\ell }{r^3}x^2(1-x)f +b\ell (\ell +1)x f\cdot P \\&\quad = \dfrac{\ell }{r^3}x^2(3x-2) (2x-1)\Big (b(\ell +1)(2x-1)-(1-x)\Big ) \\&\quad := \dfrac{\ell }{r^3}x^2(3x-2)\cdot p_{\ell }(x) \end{aligned}$$Clearly, for \( x\le \frac{1}{2} \) the expression above is non-negative, and for \( x>\frac{1}{2} \) it is negative only in the interval \( N_{\ell }:=\left( \frac{1}{2},x_{\ell }\right) \), where \( x_{\ell }:= \frac{1+b(\ell +1)}{2b(\ell +1)+1}>\frac{1}{2} \) and we have \( x_{\ell } \xrightarrow {\ell \rightarrow \infty } \frac{1}{2}. \) It’s straight forward calculations to check that \( p_{\ell }(x) \) attains its minimum at \( {\underline{x}}_{\ell } = \frac{4b(\ell +1)+3}{2(4b(\ell +1)+2)}\) with the value
$$\begin{aligned} p_{\ell }(x)\ge p_{\ell }({\underline{x}}_{\ell }) = - \dfrac{1}{8\Big (2b(\ell +1)+1 \Big )}, \hspace{1cm} \forall \ell \ge 2, \ \forall x \in N_{\ell }. \end{aligned}$$We choose \( b=0.2<0.21 \) and thus we have for all \( \ell \ge 2,\ x\in N_{\ell }, \)
$$\begin{aligned} \ell \cdot p_{\ell }(x) \ge - \dfrac{1}{8} \cdot \dfrac{10}{4\left( 1+ \frac{7}{2\ell }\right) }&\ge - \frac{5}{16} \\ \Rightarrow \ \ \ \dfrac{\ell }{r^3}x^2(3x-2)\cdot p_{\ell }(x)&\ge - \dfrac{5}{16r^3}x^2(3x-2). \end{aligned}$$Hence, using \( \mathfrak {C}(h) \) we now have
$$\begin{aligned} \frac{3}{10r^3}x^2(4-5x) - \dfrac{5}{16r^3}x^2(3x-2) = \dfrac{x^2}{80r^3}\left( 146-195x\right) \end{aligned}$$which is uniformly positive for \( \frac{1}{2}< x < x_{\ell =2} = \frac{8}{11} \) for all \( \ell \ge 2. \)
Once again, in the region where \( \mathfrak {C}(h) \) is negative, the Poincare inequality used earlier is sufficient to make it positive definite, and thus there exists a positive constant depending on M such that
\(\square \)
4.3.2 Retrieving the \((\partial _t\Psi _i)^2\) term
Note that estimate (73) does not include any \( \partial _{t}\Psi _i \) term. To retrieve the \( \partial _{t}-\)derivative we introduce the current \( L_{\mu }^z = z(r) \Psi _i \nabla _{\mu }\Psi _i \) for an appropriate function z(r). In particular, we have the following proposition.
Proposition 4.6
There exists a positive constant C depending only on M, such that for all solutions \(\Psi _i^{^{(\ell )}} \) to (44), \( i\in \lbrace 1,2 \rbrace \), \( \ell \ge i\), we have

Proof
We compute

Consider
where again, \( x= \sqrt{D} \) and \( c>0 \) a scaling to be determined in the end. By Cauchy–Schwarz inequality, (76) yields

Note that \( z(r),\ z'(r),\ \dfrac{z}{D} \) are bounded functions everywhere including the horizon and all terms in (79) have the same degeneracy as \( K^{X,G,h} \) . The coefficient \( z(r)\cdot V_i(r) \) depends on \( \ell \) and thus can be controlled using Poincare inequality. Using Proposition 4.5 and choosing a small enough scaling \( c>0 \) of z(r) allows us to control the remaining negative terms. \(\square \)
Non-degenerate Morawetz Estimate. The estimate of Proposition 4.6 is degenerate with respect to the angular derivatives and \( \partial _t \Psi _i \) at the photon sphere. Below, we remove this degeneracy which will prove useful later on, however, at the cost of losing one derivative at the level of initial data.
First, by commuting equation (44) with the Killing vectorfield T and using Proposition 4.5 we obtain
where C depends only on M.
The remaining derivatives are obtained using the current
for \( w(r)= \dfrac{1}{r^3}D^{\frac{3}{2}} \). Indeed, taking the divergence of that current we obtain

By Cauchy Schwartz,
and choosing \( \varepsilon >0 \) small enough such that \( r/3\ge \varepsilon \sqrt{D}\), the last term above can be absorbed in the first term of \( Div(L_{\mu }^{w}) \). Thus, using the above and relation (80) we prove the following proposition
Proposition 4.7
There exits a positive constant C depending only on M such that for all solutions to (44), \( i\in \lbrace 1,2 \rbrace \) we have

Note, the decay rate for the angular derivative coefficient comes from Proposition 4.6.
4.3.3 Degenerate and non-degenerate X–estimate
We saw above that the modified scalar currents are positive definite, however, we also need to control the boundary terms that arise when applying the divergence identity in \( R(0,\tau ) \).
Proposition 4.8
Let \( X=f\partial _{r^{*}} \), where f(r) is bounded, then there exists a uniform positive constant C depending on \( M,\Sigma _0\) and \( \left\Vert f\right\Vert _{L^{\infty }({\mathcal {R}}(0,\tau ))} \) such that for all solutions \( \Psi _i^{^{(\ell )}}, \ \ell \ge i, \ i\in \left\{ 1,2 \right\} \) to (44)
for S being \( \Sigma _{\tau } \) or \( {\mathcal {H}}^{+} \), for all \( \tau >0. \)
Proof
Since our estimates involve the horizon as well, let us express everything in terms of the ingoing coordinate system \( (v,r,\vartheta ,\varphi ) \). In particular, we have \( \frac{\partial }{\partial {r^{\star }}}(r^{\star },t)=\frac{\partial }{\partial v}(v,r)+D\frac{\partial }{\partial r}(v,r) \), then

In addition, we have

Now, using Cauchy-Schwarz, the fact that \( f,n^u,n^r, h \) are bounded functions and that \( V_i \) is linear with respect to \( \ell \), Proposition 4.4 concludes the proof. \(\square \)
Now, we are in the position of proving the general Morawetz estimates of this main section. First, we proceed with the proof of a degenerate estimate that captures the trapping effect on both the photon sphere \( \left\{ r=2M \right\} \) and the horizon \( {\mathcal {H}}^+\).
Theorem 4.1
There exists a constant \( C>0 \) depending on \( M,\Sigma _0 \) such that for all solutions \(\Psi _i^{^{(\ell )}} \) to (44), \( i\in \lbrace 1,2 \rbrace \), \( \ell \ge i\) , we have

Proof
We apply Stoke’s Theorem in the region \( R(0,\tau ) \) to the currents
for a big enough constant \( A>0 \). Note, there will be no boundary terms on the horizon \( {\mathcal {H}}^+ \) since all quantities vanish there, thus applying Propositions 4.8, 4.6 and 4.2 we conclude the proof. \(\square \)
Similarly, using Proposition 4.7 we prove an estimate that does not degenerate at the photon sphere, however, requires higher regularity on the initial data.
Theorem 4.2
There exists a positive constant C depending on \( M,\Sigma _{0} \) alone such that for all solutions \( \Psi _i^{^{(\ell )}} \) to (44), \( i\in \lbrace 1,2 \rbrace \), \( \ell \ge i\), we have

4.4 The Vector Field N
In this section, we are looking for a timelike vectorfield N that captures the non-degenerate energy of a local observer near the horizon. However, in the extremal Reissner-Nordström case, the absence of redshift effect poses a difficulty since there is no analogous redshift vectorfield to Dafermos–Rodnianski’s [17]; for any timelike vectorfield N, the corresponding scalar current won’t be non-negative definite. Instead, we go around this by modifying appropriately the current \( J^N_{\mu }[\Psi _i]\) which allows us to obtain a non-negative local integrated estimate, however, still degenerate in the transversal invariant direction due to trapping on the horizon \( {\mathcal {H}}^+\). First, let’s take a closer look at why \( J^N_{\mu }[\Psi _i] \) alone won’t work. In this subsection, we work with respect to the coordinate system \( (v,r,\vartheta ,\varphi ) \) which is regular on the event horizon \( {\mathcal {H}}^+. \)
Absence of redshift effect. Let \( N= N^v(r)\partial _{v}+ N^r (r)\partial _r \) be a future-directed timelike \( \phi _{\tau }^T- \) invariant vector field. Then, if we consider \( J_{\mu }^N[\Psi _i] \) for a solution \( \Psi _i^{^{(\ell )}} \) to (44), \( i\in \lbrace 1,2 \rbrace \), \( \ell \ge i\), we obtain

where the coefficients are given by

Here we denote by \( N^i_r:= \frac{\partial N^i}{\partial _r}\) and \( D'= \frac{\partial D}{\partial r}. \) In hope of proving \( K^N \) is non-negative definite, we would like to control the term \( F_{vr}(\partial _{v}\Psi _i)(\partial _r \Psi _i) \) using the positivity of \( F_{rr}, F_{vv} \). However, note that \( F_{rr} \) vanishes on the horizon whereas \( F_{vr} \) doesn’t. Indeed, recall the relations (52), (53), so if we are looking for N timelike everywhere, it is necessary that \( N^r(M) \ne 0 \) on the horizon \( {\mathcal {H}}^+\). In particular, \( K^N[\Psi _i] \) is linear with respect to \( \partial _{r} \Psi _i \) on the horizon. In addition, the coefficient \( F_{00} \) becomes negative for low frequencies for both \( i=1,2. \) Therefore, no choice of timelike vectorfield N can make \( K^N[\Psi _i] \) non-negative definite.
A Locally Non-Negative Spacetime Current. In order to remedy the situation above, we need to introduce extra terms to our initial current. Consider \( J_{\mu }^{X,\omega ,M} [\Psi ] \) as in Proposition 4.1 for the (0,1)-form \( M_{\mu }:= h(\partial _r)_{\mu }, \) and \( \omega =\omega (r) \), \( h=h(r) \) functions of r alone. In particular, if
Then, we have

For simplicity, let us denote the above coefficients of \( (\partial _a\Psi _i \cdot \partial _b \Psi _i) \) by \( G_{ab} \) where  and define the vector field N in the region \( M\le r \le \frac{9M}{8} \) as
and define the vector field N in the region \( M\le r \le \frac{9M}{8} \) as
which is timelike. In view of the discussion of the previous paragraph, we define \( \omega \) such that \( G_{vr}\Big |_{r=M}=0, \) i.e. with the choice of N as above, we need \( \omega = -1 \) constant. Such choice of N vectorfield and function \(\omega \) was first seen in [7] for the homogeneous wave equation. However, in our case we have an extra zeroth order term \(G_{00}\) which we need to treat. Nevertheless, we will see in the proposition below, there is an appropriate function h which makes the coefficient \( G_{00} \) positive definite.
Proposition 4.9
Let \( h(r) := 6 \frac{\sqrt{D}(1+3\sqrt{D})}{r}\) and N as in (92), then there exists a positive constant C depending only on M such that for all solutions \( \Psi _{i}^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \), the current \( K^{N,-1,h}[\Psi _i] \) is non-negative definite in \( {\mathcal {A}}_{N}:= \left\{ M\le r\le \frac{9M}{8} \right\} \). In particular, we have

Proof
First, let’s write down the coefficients \( G_{ab} \) adapted to the choice of N as in (92):

Using Cauchy-Schwartz inequality we get
Similarly, we obtain
Therefore, going back to (91), we need to show that the new coefficients are non-negative definite in the region \( {\mathcal {A}}_N, \). For simplicity, we denote by \( x:=\sqrt{D} \) which in \( {\mathcal {A}}_{N} \) it satisfies \( 0\le x \le \frac{1}{9} \).
For the coefficient of \( (\partial _{v}\Psi _i)^2 \), which is \( 16-(16\sqrt{D}+2)^2 \), we have
The coefficient of \( (\partial _{r}\Psi _i)^2 \) is
which again for \( x\le \frac{1}{9} \), it is uniformly positive.
We already know that  , and it only remains to show positivity for the coefficient of \( \Psi _i^2 \). For that, we are going to need Poincare inequality but first, let’s examine the zeroth order coefficient closer. We have,
, and it only remains to show positivity for the coefficient of \( \Psi _i^2 \). For that, we are going to need Poincare inequality but first, let’s examine the zeroth order coefficient closer. We have,
For \( i=1 \), we write
The above expression is mostly negative, so borrowing from the coefficient of  by using Poincare Inequality we obtain the extra term
by using Poincare Inequality we obtain the extra term
Using the fact \( x\le \dfrac{1}{9} \), it is easy to see that the above expression is uniformly positive definite for all \( \ell \ge 3 \) in \( {\mathcal {A}}_N \). However, for \( \ell =1,2 \) we need the help of the extra positive term in (98). In particular,
Therefore, we obtain
which is positive for both \( \ell =1,2 \) in the region \( {\mathcal {A}}_N .\)
Similarly, we obtain the same result for the potential \( V_2^{^{(\ell )}}(r) \) for every \( \ell \ge 2 \) in \( {\mathcal {A}}_N \), which concludes the proof. \(\square \)
The \( J_{\mu }^{N,\delta ,{\tilde{h}}}[\Psi _i] \) current. Outside the region \( {\mathcal {A}}_N \), the scalar current \( K^{N,-1,h}[\Psi _i]\) takes negative values as well. We extend the current \( J_{\mu }^{N,-1,h} \) introducing cut-off functions so that the corresponding scalar current will be non-negative definite away from the horizon except maybe a compact region not including the photon sphere, in which we control it using Morawetz estimates.
In particular, we extend the vectorfield N outside \( {\mathcal {A}}_N \) as
and N remains an \( \phi _{\tau }^{T} \)- invariant timelike vectorfield.
Away from \( {\mathcal {A}}_N \), we extend both \( \omega (r)=-1 \) and h(r) by introducing the smooth cut-off functions \( \delta : [M, +\infty ) \rightarrow {\mathbb {R}} \) such that \( \delta =1 \) for \( r\in \left[ M, \frac{9M}{8}\right] \), and \( \delta (r)=0 \) for \( r \ge \frac{8M}{7} \), while also, \( {\tilde{h}}(r)= h(r)\) for \( r\in \left[ M, \frac{9M}{8}\right] \), and \( {\tilde{h}}(r)=0 \) for \( r\ge \frac{8M}{7}. \) Now, we consider the current
and we make the following observations,
-
1.
In the \( {\mathcal {A}}_N \) region, we have \( J_{\mu }^{N,\delta ,{\tilde{h}}}[\Psi _i] \equiv J_{\mu }^{N,-1,h}[\Psi _i] \), and thus \( K^{N,\delta ,{\tilde{h}}}[\Psi _i] =K^{N,-1,h}[\Psi _i] \).
-
2.
For \( r\ge \frac{8M}{7} \), we have \( K^{N,\delta ,{\tilde{h}}}[\Psi _i]= K^{T}= 0\).
-
3.
For \( \frac{9M}{8}\le r \le \frac{8M}{7} < 2M, \) the scalar current \( K^{N,\delta ,{\tilde{h}}}[\Psi _i]\) can be negative in general, however, it can be controlled by the Morawetz estimates which are non-degenerate away from the photon sphere and the event horizon.
4.4.1 N-multiplier boundary terms
In this section we treat the boundary terms that appear when applying the multiplier method for N. First, observe that the vectorfield N captures the non-degenerate energy of a local observer near the horizon. Indeed, since both \( N, n_{\Sigma _{\tau }}^{\mu } \) are timelike everywhere in \( R(0,\tau ) \), following exactly the same proof as in Proposition 4.4, we obtain

where the constant C depends only on M and \( \Sigma _0 \) since N is \( \phi _{\tau }^T -\) invariant. Now, regarding the current \( J_{\mu }^{N,\delta ,{\tilde{h}}}[\Psi _i] \), we have the following propositions.
Proposition 4.10
There exists a constant \( C>0 \) depending only on \( M,\Sigma _0 \) such that for all solutions \(\Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \) \( i\in \lbrace 1,2 \rbrace \) we have
Proof
To prove the left hand side inequality, notice that
and we use Cauchy-Schwartz inequality along with relation (105).
For the right-hand side inequality, using again Cauchy-Schwartz we can write
Doing the same for the term \( - \dfrac{1}{2}\delta \Psi _i \cdot \partial _{v}\Psi _i n^{v} \), and the fact that \( n^v,n^r, {\tilde{h}} \) are bounded, we choose \( \varepsilon >0 \) small enough such that relation (107) yields
Therefore, using Proposition 4.4 we obtain
for a big enough constant C, depending only on \( M,\Sigma _0 \). \(\square \)
We now control the boundary term over \( {\mathcal {H}}^+ \). In particular, we have the following proposition.
Proposition 4.11
For all solutions \(\Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i,\) \( i\in \lbrace 1,2 \rbrace \) we have
for a positive constant C depending only on \( M,\Sigma _0 \).
Proof
With the following convention in mind, \( n_{{\mathcal {H}}^+} \equiv T \), we write down equation (107) on the horizon \( {\mathcal {H}}^+ \) and we obtain
since \( n^r_{{\mathcal {H}}^+}={\tilde{h}}(M)=0 \) and \( \delta (M)=1. \) Using Cauchy Schwartz we write
for \( \varepsilon >0 \) sufficiently small, which concludes the proof. \(\square \)
Uniform Boundedness of Local Observer’s Energy and Integrated Local Energy. We combine our results above to obtain an integrated local energy estimate which captures the trapping effect at the horizon \( {\mathcal {H}}^+\) due to the degeneracy of the redshift effect.
Theorem 4.3
There exists a constant \( C>0 \) which depends on \( M,\Sigma _0 \) such that for all solutions \(\Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i,\) \( i\in \lbrace 1,2 \rbrace \)

Proof
We apply Stoke’s theorem for the current \( J_{\mu }^{N,\delta ,{\tilde{h}}}[\Psi _i] \) in the region \( {\mathcal {R}}(0,\tau ) \) to obtain
We have seen before that the spacetime term \( K^{N,\delta ,{\tilde{h}}} \) is non-negative definite everywhere, except in the region \( \frac{9M}{8}\le r \le \frac{8M}{7} < 2M. \) In that region, we control the spacetime term using Theorem 4.1 and we make it non-negative definite in terms of the \( 1- \)jet of \( \Psi _{i}^{^{(\ell )}},\) for all \( r\ge M \). Therefore, using also the left-hand side inequality of Proposition 4.10, we obtain
On the other hand, using the right-hand side inequality of Proposition 4.10 and Proposition 4.11 the above relation yields
for a sufficiently big constant \( C'>0 \) depending only on \( M, \Sigma _{0} \). However, note
which concludes the proof. \(\square \)
5 Energy Estimates for \(\partial _r\Psi _i\)
In the previous sections, we derived integrated local energy estimates that are degenerate with respect to \( (\partial _{r}\Psi _i^{^{(\ell )}})^2 \) on the horizon \( {\mathcal {H}}^+. \) In this section, we remove the aforementioned degeneracy near the horizon \( {\mathcal {H}}^+ \), at the cost of losing one derivative at the level of initial data. For that, we need to commute our equation (44) with the vectorfield \( \partial _r. \) In order to derive the instability that occurs along the horizon \( {\mathcal {H}}^+ \), we need to control \( \partial _r^k \Psi _i^{^{(\ell )}} \), for \( k\in {\mathbb {N}} \) depending on \( \ell . \)
The \(\partial _{r}- \)Commutator. For any scalar function \( \phi \) we have

The above relation can be justified by direct computation and using the fact that  Therefore, taking a \( \partial _r -\) derivative of equation (44) yields
Therefore, taking a \( \partial _r -\) derivative of equation (44) yields
Since \( \Psi _i^{^{(\ell )}} \) is supported on a fixed frequency \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \), we can write

Now, let’s define

Then, we obtain the following equations for \( \partial _r\Psi _i^{^{(\ell )}} \)
For simplicity, we will drop the \( (\ell ) \) superscript since each \(\Psi _i,V_i \) is defined in terms of \( \ell \ge i \) in the first place.
Control far from the horizon. Away from the horizon \( {\mathcal {H}}^+ \), the spacetime term \( \int _{R\cap \left\{ r\ge r_0 \right\} } (\partial _r\Psi _i)^2 \), \( r_0> M \), is already controlled in the previous section. In addition, commuting our equation (44) with T, using local elliptic estimates, and \( L^2 \) bounds obtained earlier we control all second order derivatives away from \( {\mathcal {H}}^+ \), for all solutions \( \Psi _i^{^{(\ell )}} \) to (44), \( \ell \ge i, \) \( i\in \lbrace 1,2 \rbrace \). In particular,
for a constant \( C>0 \) depending only on \( M,r_0, \Sigma _0. \) The same result holds for the bulk integrals where, however, we must exclude the photon sphere \( \lbrace r = 2M \rbrace \) due to trapping. Specifically, since T is timelike for \( r\ge r_0 \), using local elliptic estimates and Theorem 4.1 yield
5.1 Higher order control near the horizon
In view of the above, we now restrict our attention close to the horizon \( {\mathcal {H}}^+ \). In particular, we are looking for an \( \phi _{\tau }^T - \) invariant timelike vectorfield \( {\mathcal {X}}={\mathcal {X}}^{v} \partial _v + {\mathcal {X}}^ r \partial _r \) that will act as a multiplier for the function \( \partial _{r}\Psi _i. \)
Applying Stokes Theorem in the region \( R(0,\tau ) \) for the energy current \( J^{{\mathcal {X}}}_{\mu }[\partial _{r}\Psi _i]\) yields
Since \( {\mathcal {X}}\) is timelike in a region close to the horizon \({\mathcal {H}}^+ \), we have

for a constant \( C>0 \) depending only on \( M,\Sigma _0,{\mathcal {X}}\). In addition, on the horizon we have

where \( \ell \) is the fixed frequency support of \( \Psi _i^{^{(\ell )}}. \)
In what follows, we are studying the bulk term that appears in (120) and we define accordingly an appropriate vectorfield \( {\mathcal {X}}\) that will allow for control of the second order derivatives of \( \Psi _i \), while also for \( (\partial _r\Psi _i)^2 \) near the horizon \( {\mathcal {H}}^+. \) Specifically, from Proposition 4.1 we obtain
Note above, we have the extra third term since \( \partial _r\Psi _i \) satisfies the non-homogeneous wave equation (117). Now, similarly to Section 4.4, we have

where the coefficients \( F_{ij} \) are defined as in relation (89) for the vectorfield \( {\mathcal {X}}. \) Expanding also \( M_i[\Psi _i] \) we obtain altogether

with coefficients \( E_j \), \( j \in \left\{ 1,..,11 \right\} \)
First, let’s make some observations concerning the choice of \( {\mathcal {X}}\) and its consequence on the coefficients \( E_j. \) If \( {\mathcal {X}}\) is timelike everywhere, then \( {\mathcal {X}}^v(M)>0 \), \( {\mathcal {X}}^r(M)<0 \) and thus the same holds in a neighborhood of the horizon \( {\mathcal {H}}^+. \) This already ensures that \( E_2\ge 0 \), near the horizon, and it vanishes to first order on it. Indeed,
while the first term in the parenthesis is the dominant one and positive near \( {\mathcal {H}}^+. \)
Moreover, we have the freedom of choosing \( {\mathcal {X}}_r^v \) and \( -{\mathcal {X}}_r^r \) positive and sufficiently large such that \( E_1>0, \ E_3>0 \) near \( {\mathcal {H}}^+ \).
When it comes to controlling the coefficients \( E_j \) not corresponding to quadratic terms, part of the idea is to absorb them in the first three terms \( E_1,E_2,E_3, \) and for that we need \( -{\mathcal {X}}_r^r(M) \gg -\frac{{\mathcal {X}}_r(M)}{M} \), as well as \( {\mathcal {X}}^v_r(M) \gg \frac{{\mathcal {X}}^v(M)}{M}\).
For the reasons above, we restrict our attention to a region close to \( {\mathcal {H}}^+ \), \( {\mathcal {A}}_c := \left\{ M \le r \le r_c \right\} \) (Fig. 1) for an appropriate \( r_c\in (M,2M) \), to be determined at the end, and choose \( {\mathcal {X}}\) with the above requirements. Outside \( {\mathcal {A}}_c \) we extend \( {\mathcal {X}}\) as
for an \( r_d \) satisfying \( M<r_c<r_d<2M. \)
5.2 Hardy Inequalities and Lemmas
Before we treat the bulk terms in (125), we present a few lemmas that will prove useful later on when controlling boundary terms.
Lemma 5.1
(First Hardy Inequality) Consider \( r_c\in (M,2M) \), then for any scalar function \( \psi \) and \( \varepsilon >0 \) we have
for a constant \( C_{\varepsilon } \) depending only on \( M,\varepsilon ,r_c \) and \( \Sigma _{0} \).
Proof
Note that for any scalar \( \phi \) we have
In particular, if we choose \( \phi = r-r_c \) we obtain
Note \( \rho \) is bounded in the region \( \left\{ M\le r \le r_c \right\} \), thus integrating over \( {\mathbb {S}}^2 \) we obtain
\(\square \)
Lemma 5.2
(Second Hardy Inequality) Let \( M< r_c<r_d \), and consider the regions \({\mathcal {C}}:=R(0,\tau )\cap \left\{ M\le r\le r_c \right\} \) and \( {\mathcal {D}}=R(0,\tau )\cap \left\{ r_c\le r\le r_d \right\} \), then for any scalar function \( \psi \) we have
for a positive constant C depending on \( M, r_c, r_d, \) and \( \Sigma _0. \)
Proof
We apply relation (130) for \( \phi := \sqrt{D(r)} = \left( 1-\frac{M}{r}\right) \) and we obtain
However, by repeating the steps of the proof of the first Hardy Inequality, we can also show
for any \( \epsilon '>0 \) and a positive constant \( C_{\epsilon '} \) depending on \( \epsilon ', r_c, r_d. \) Let \( \epsilon '=1 \), then going back to the first relation and applying Cauchy-Schwarz we get
We choose \( \epsilon >0 \) small enough so that the coefficient of the left-hand side above is uniformly positive in \( \left\{ r_c\le r\le r_d \right\} \) and we obtain
for a positive constant depending on \( M,r_c, r_d. \) Integrating on the spheres \( {\mathbb {S}}^{2} \) and in time \( {\tilde{\tau }} \in [0,\tau ] \) while also using coarea formula yields the estimate of the assumption. \(\square \)
Remark 5.1
Note, \( \psi \) need not be a solution to a wave equation, i.e. the result above holds for any scalar in \(H^1_{loc}({\mathcal {R}}(0,\tau )). \)
Lemma 5.3
For any solution \( \Psi _i^{^{(\ell )}},\ \ell \ge i, \ i\in \left\{ 1,2 \right\} \) to (44), we have
where the constant \( C_{\varepsilon }>0 \) depends on \( M, r_c, r_d , \Sigma _0,\varepsilon . \)
Proof
We apply Lemma 5.2 for \( \partial _r\Psi _i \) and regions \( {\mathcal {C}}\equiv {\mathcal {A}}_c, \ {\mathcal {D}} \) and we get
Now, note that \( E_1>0 \) and \( E_2\ge 0 \) close to the horizon, with \( E_2 \) vanishing to first order on \( {\mathcal {H}}^+. \) On the other hand, \( C\cdot D \) vanish to second order on \( {\mathcal {H}}^+ \), thus for any \( \varepsilon >0 \) there exists a region close to the horizon \( A_{\varepsilon }:=\left\{ M\le r\le r_{\varepsilon }\le r_c \right\} \) such that
since all second-order derivatives are controlled away from the horizon in terms of the fluxes \( J^N_{\mu }[\Psi ], J^N_{\mu }[T\Psi ] \). On the other hand, since the region \( {\mathcal {D}} \) is away from the horizon, Theorem 4.3 yields
which concludes the proof. \(\square \)
We now state two more lemmas that allow us to treat boundary terms at the horizon.
Lemma 5.4
For all solutions \( \Psi _i^{^{(\ell )}},\ \ell \ge i, \ i\in \left\{ 1,2 \right\} \) to (44), we have
for any \( \varepsilon >0 \) where the constant \( C_{\varepsilon }>0 \) depends only on \( M,\Sigma _0,\varepsilon . \)
Proof
Using integration by parts we write
Now, since \( \square \Psi _i -V_i \Psi _i=0 \), on the horizon \( \left\{ r=M \right\} \) we have

Thus, we can write

However, using Cauchy Schwartz and the fact that \( V_i \) is linear with respect to \( \ell \), relation (105) and Theorem 4.3 allow us to control the integral above in terms of the flux \( \int _{\Sigma _{0}}J_{\mu }^{N}[\Psi _i]n^{\mu }_{\Sigma _{0}} \).
Finally, we have
and using Lemma 5.1 for \( \psi \equiv \Psi _i, \partial _r\Psi _i \) we obtain
which concludes the proof. \(\square \)
Lemma 5.5
For all solutions \( \Psi _i^{^{(\ell )}},\ \ell \ge i, \ i\in \left\{ 1,2 \right\} \) to (44), we have

for any \( \varepsilon >0 \) where the constant \( C_{\varepsilon }>0 \) depends only on \( M,\Sigma _0,\varepsilon . \)
Proof
Once again, we use the wave equation (44) evaluated on the horizon,  , and we write
, and we write

Since \( \Psi _i \) is supported on the \( \ell \)-frequency we have  , so
, so

For \( i=1 \), on the horizon \( {\mathcal {H}}^+\) we get
Similarly, for \( i=2 \),
Thus, going back to (142) we have

so using Lemma 5.4 and the first Hardy inequality (Lemma 5.1) we conclude the proof. \(\square \)
5.3 Estimates for the Spacetime Terms
We are now ready to control the bulk terms that appear in (125) in terms of the fluxes \( J^{N}_{\mu }[\Psi _i], J^{N}_{\mu }[T\Psi _i]\ \), and \(J^{{\mathcal {X}}}_{\mu }[\partial _r\Psi _i] \) or absorb them in known positive definite terms. Note, since the vectorfield \( {\mathcal {X}}(r)=0 \) for \( r\ge r_d \), then \( \nabla ^{\mu } J_{\mu }^{{\mathcal {X}}}[\partial _r\Psi _i]=0 \) for \( r\ge r_d \), so we focus our estimates in the region \( {\mathcal {R}}(0,\tau )\cap \left\{ r\le r_d \right\} \) only.
For any \( \varepsilon >0, \) Cauchy-Schwartz and Theorem 4.3 yield
for a constant \( C_{\varepsilon } \) depending on \( \varepsilon ,M,\Sigma _{0}. \)
Note, \( \left|E_5\right|= \left| {\mathcal {X}}^v(r)R'(r) \right| \) is uniformly positive and bounded in the region \( {\mathcal {A}}_c \), thus we have
for any \( \varepsilon >0 \). So, applying Lemma 5.3 for the second term above, for \( {\tilde{\varepsilon }}= \dfrac{\varepsilon ^2}{\max _{{\mathcal {A}}_c} (E_5)^2}>0 \) we obtain
for \( C_{\varepsilon }>0 \) depending on \( M, r_c, r_d , \Sigma _0,\varepsilon . \)
Here, we apply divergence theorem for \( P_{\mu }= E_6 (\partial _r\Psi _i)(\partial _v\Psi )(\partial _r)_{\mu } \), in the region \( R(0,\tau ). \)
First, we expand the left-hand side term and using the fact that \( Div(\partial _r)=\frac{2}{r} \) we get
Thus, we write
The boundary term over the horizon \({\mathcal {H}}^+ \) can be estimated using Lemma 5.4, and the term over \( \Sigma _{\tau } \), using Cauchy Schwartz and Theorem 4.3 to estimate it in terms of the N-flux on \( \Sigma _{0}. \)
Now, since \( \left|E_6\right| \) is uniformly positive in \( {\mathcal {A}}_c \), we estimate the spacetime term \( \int _{R}E_6(\partial _v\partial _r\Psi _i)(\partial _r\Psi _i) \) via exactly the same relation as in (147).
Finally, we control the remaining spacetime term \( \int _{R}\left( \partial _rE_6+ \frac{2E_6}{r}\right) (\partial _v\Psi _i)(\partial _r\Psi _i) \) by using Cauchy Schwartz, Lemma 5.3 and Theorem 4.3.

Divergence theorem for  in the region \( {\mathcal {R}}(0,\tau ) \) yields
in the region \( {\mathcal {R}}(0,\tau ) \) yields
and note there is no boundary term on the horizon \( {\mathcal {H}}^+ \), since \( (\partial _v)_{\mu }\cdot n_{{\mathcal {H}}^+}^{\mu }= 0 \) In particular, we obtain

First, note that since \( V_i'(r) \) is linear with respect to \( \ell \),\(\ E_7 \) is uniformly bounded with respect to \( \ell \) in the region \( {\mathcal {A}}_{c}. \)
Away from the horizon, the boundary terms are controlled by the fluxes \( J^N[\Psi _i], J^T[T\Psi _i] \). On the other hand, near the horizon, we have

with \( C_{\varepsilon }>0 \) depending on \( \Sigma _0,M,\varepsilon . \) As far as the last spacetime term, we estimate it as


Applying divergence theorem for  in the region \( {\mathcal {R}}(0,\tau ) \) yields
in the region \( {\mathcal {R}}(0,\tau ) \) yields

Again, we first show that \( E_8 \) is uniformly bounded in \( \ell \), since \( V_i'\cdot r^3 \) is linear in \( \ell \) and
for a positive constant C.
The boundary term over \( {\mathcal {H}}^+ \) is then controlled by Lemma 5.5 and using Cauchy Schwartz we also have in the region \( {\mathcal {A}}_c \)

Finally, for the remaining two spacetime integrals, using the fact that  , we obtain
, we obtain

The first integral in the right-hand side, is estimated as long as \( \left|E_8\right|\le E_3, \) however \( {\mathcal {X}}\) can be chosen such that
For the second integral on the right-hand side, Cauchy Schwartz yields

and \( \partial _rE_8 \) is uniformly bounded in \( \ell \) for the same reason \( E_8 \) was. So, \( J^N[\Psi _i] \) flux controls the latter integral.
Using the wave equations for \( \partial _v\partial _r\Psi _i \) we obtain

We use  and we rewrite the equation above as
and we rewrite the equation above as

The first integral on the right-hand is estimated in \( {\mathcal {A}}_c \) because of the D factor that degenerates to second order on the horizon, whereas \( E_2 \) degenerates to first order. Similarly, by Cauchy Schwartz, we have
and since \( R(r)^2 \sim D(r) \) the second integral is estimated, whereas the first integral is estimated by Lemma 5.3.
Next, note that \( -\dfrac{E_9}{r} \sim D + E_6 \), therefore the second integral at (148) is already estimated above.
Finally, in \( {\mathcal {A}}_c \) we have
and \( \left|E_9\right| \ll E_3 \) , so the last term at (148) can be estimated as in the \( E_8 \) case above.
Applying the divergence theorem for the current \( P_{\mu }: =E_{10} (\partial _r\Psi _i)^2(\partial _{r})_{\mu }\) in the region \( {\mathcal {R}}(0,\tau ), \) we obtain
The boundary terms over \( \Sigma _{\tau },\Sigma _{0} \) are estimated by the \( J^N[\Psi _i] \) flux, and the spacetime integral on the right is estimated by Lemma 5.3. Last, we need to deal with the boundary term on the horizon \( {\mathcal {H}}^+. \) In view of \( E_{10}(M)=-{\mathcal {X}}^r(M)\cdot R'(M)= -{\mathcal {X}}^r(M)\dfrac{2}{M^2}>0 \), the only way to control this term is to borrow from the horizon boundary term of (120).
In particular, we use Poincare Inequality

Thus, using the relation (122), it suffices to have
For \( i=1, \) we have \( \ell (\ell +1)\left( 1+\dfrac{2}{\ell }\right) =(\ell +1)(\ell +2)\ge 6 >2 \) for all \( \ell \ge 1. \)
For \( i=2 \), we get \( \ell (\ell +1)\left( 1-\dfrac{2}{\ell +1}\right) =\ell (\ell -1)\ge 2 \) for all \( \ell \ge 2. \)
Note, in the case \( i=2 \), \( \ell =2, \) we need to use the whole quantity (122) to control the last term of (149). Thus, there will be no  term in the boundary integral of \( {\mathcal {H}}^+ \) at (120). This is a manifestation of a conservation law that holds on the horizon \( {\mathcal {H}}^+ \) for \( \Psi _2^{(2)} \), which is supported on the \( \ell =2 \) frequency; see Section 6. We see later on that an analogous situation occurs when controlling higher-order estimates.
term in the boundary integral of \( {\mathcal {H}}^+ \) at (120). This is a manifestation of a conservation law that holds on the horizon \( {\mathcal {H}}^+ \) for \( \Psi _2^{(2)} \), which is supported on the \( \ell =2 \) frequency; see Section 6. We see later on that an analogous situation occurs when controlling higher-order estimates.
Let us first examine the coefficient \( E_{11} \). It’s straightforward computations to check that
Thus, we have
Note \( V_i \) depends on \( \ell , \) thus we cannot use Lemma 5.3 for an estimate since the constants will depend on \( \ell \) as well. Instead, we will show that \( \int _R E_{11}(\partial _r\Psi _i)^2 \) is positive definite for \( i=1, \) and while non-positive for \( i=2 \), Poincare inequality suffices to estimate it. In particular,
-
For \( i=1 \), we have
$$\begin{aligned}\begin{aligned} E_{11}&= \dfrac{M}{r^3}\left( \ell +1-3\sqrt{D}\right) \left( \dfrac{{\mathcal {X}}^r}{r}-{\mathcal {X}}^r_{r}\right) + \dfrac{3M^2}{r^5}{\mathcal {X}}^r \\&= \dfrac{M}{r^3}\left( -{\mathcal {X}}_r^r\big (\ell +1-3\sqrt{D}\big )+ \dfrac{{\mathcal {X}}^r}{r}\big (4-6\sqrt{D}+\ell \big )\right) \end{aligned} \end{aligned}$$In \( {\mathcal {A}}_c, \) we chose \( -{\mathcal {X}}_r^r(r)\gg -\dfrac{{\mathcal {X}}^r(r)}{r} \), thus
$$\begin{aligned} \begin{aligned} E_{11}>&-\dfrac{{\mathcal {X}}^r}{r}\dfrac{M}{r^3}\left( 25(\ell +1-3\sqrt{D})-4+6\sqrt{D}-\ell \right) \\&=- \dfrac{{\mathcal {X}}^r}{r}\dfrac{M}{r^3}\big ( 24 \ell +21 - 69\sqrt{D} \big ) \end{aligned} \end{aligned}$$which is positive definite for all \( \ell \ge 1 \) in \({\mathcal {A}}_c.\)
-
For \( i=2, \)
$$\begin{aligned} \begin{aligned} E_{11} =&-\dfrac{M}{r^3}(3\sqrt{D}+\ell )\left( \dfrac{{\mathcal {X}}^r}{r}-{\mathcal {X}}_r^r\right) + 3\dfrac{M^2}{r^4}\dfrac{{\mathcal {X}}^r}{r} \\ =&\dfrac{M}{r^3}\left( (3\sqrt{D}+\ell ){\mathcal {X}}_r^r + \dfrac{{\mathcal {X}}^r}{r}(3-6\sqrt{D}-\ell )\right) . \end{aligned} \end{aligned}$$(152)The dominant term \( {\mathcal {X}}_r^r \) has the wrong sign, so using Poincare inequality and borrowing a fraction \( \dfrac{2}{3}<\alpha <1 \) from
 we obtain
we obtain  (153)
(153)We will show that the coefficient of the right-hand side above, is positive definite uniformly in \( \ell \) in the region \({\mathcal {A}}_c. \) Indeed, for \( \ell \ge L \) where L is a fixed large enough integer,
$$\begin{aligned} \begin{aligned}&E_{11} + \dfrac{\alpha \cdot \ell (\ell +1)}{r^2}E_3 \\&= \dfrac{1}{r^2}\left( (1-x)\left( (3\sqrt{D}+\ell ){\mathcal {X}}_r^r + \dfrac{{\mathcal {X}}^r}{r}(3-6\sqrt{D}-\ell )\right) -\alpha \dfrac{\ell (\ell +1)}{2}{\mathcal {X}}^r_r \right) \end{aligned} \end{aligned}$$(154)and the \( {\mathcal {X}}_r^r \) term’s coefficient has the right sign everywhere in \( R(0,\tau ) \), due to the large value of \( -\ell (\ell +1). \) Thus, for \( \ell \ge L \), the term above is positive definite everywhere. For, \( 2\le \ell \le L-1 \), we evaluate the expression (154) on the horizon \( {\mathcal {H}}^+ \) and we obtain
$$\begin{aligned} \begin{aligned} E_{11} + \dfrac{\alpha \cdot \ell (\ell +1)}{r^2}E_3 \Big |_{\left\{ r=M \right\} }=\dfrac{1}{M^2}\left( \dfrac{\ell }{2}\left( 2 -\alpha (\ell +1)\right) {\mathcal {X}}_r^r(M)+\dfrac{{\mathcal {X}}^r(M)}{M}(3-\ell )\right) , \end{aligned} \end{aligned}$$(155)and for any \( 2/3< \alpha <1 \) the above expression is positive for all \( 2\le \ell \le L-1 \) in view of our choice \( -{\mathcal {X}}_r^r(M)\gg -\frac{{\mathcal {X}}^r(M)}{M} . \) Thus, for each \( 2\le \ell \le L-1 \) there exists a neighborhood \( A_\ell \) of the horizon where (154) is positive definite. By, choosing the intersection of all these neighborhoods we obtain a region including \( {\mathcal {A}}_c \) where (154) is positive definite for every \( \ell \ge 2 \) in the case \( i=2. \)
Conclusion As we can see from the analysis above, it suffices to consider \( -{\mathcal {X}}^r_r(M) \), \( {\mathcal {X}}^v_r(M) \) sufficiently large, \( r_d<2M \) and \( r_c \) close enough to the horizon \( {\mathcal {H}}^+ \equiv \lbrace r=M\rbrace \) in order to obtain the following estimate
Theorem 5.1
There exists a positive constant \( C >0 \) depending only on \( \Sigma _0, M \) such that for all solutions \( \Psi _i^{^{(\ell )}}\) to (44), supported on the fixed frequency \( \ell \ge i, \ i\in \lbrace 1,2 \rbrace \), the following estimate hold

where \( {\varvec{\chi }}_{i,2} = \left\{ \begin{array}{ll} 0, &{}\quad {\text {if}}\ \ i=\ell =2 \\ 1,&{}\quad \text {otherwise}. \end{array}\right. . \)
Proof
With \( {\mathcal {X}}\) chosen as described in the conclusion , we apply the energy identity (120) and using estimates (118, 119) while also all bulk estimates controlling \( E_{4-11} \) terms for an \( \varepsilon >0 \) small enough, we obtain a constant \( C>0 \) depending on \( M,\Sigma _0,r_c, r_{d}, {\mathcal {X}}\) satisfying (156). However, \( {\mathcal {X}},r_c \) and \( r_d \) depend solely on M and fixing specific values satisfying the restrictions of the conclusion we obtain a constant C that depends only on \( M, \Sigma _0. \)
Note, the right-hand side of (156) is justified since \( {\mathcal {X}}\sim n_{\Sigma _{\tau }} \) in the region \( {\mathcal {A}}_c \). In addition, we observe the degeneracy \( \varvec{\chi }_{2,2} \) at the horizon for the angular term of \( \Psi _2^{^{(\ell =2)}} \) only. We will see a similar degeneracy holds for higher order transversal derivatives of \( \Psi _i^{^{(\ell )}} \), \( \ell \ge i, \ i\in \left\{ 1,2 \right\} , \) close to \( {\mathcal {H}}^+ \) . \(\square \)
6 Conservation Laws Along the Event Horizon
In this section we show that solutions \( \Psi _i^{^{(\ell )}} \) to (44) satisfy conservation laws along the event horizon \( {\mathcal {H}}^+. \) The results developed here are used later on not only to produce higher order \( L^2 \) estimates but also to prove non-decay and growth of solutions to (44) asymptotically along the event horizon.
We start with a low-frequency example that will motivate the idea for the proof of the general case. Let us consider the solution to (44), \(\psi := \Psi _2^{(2)} \), i.e. \( i=2, \ell =2 ,\) and with respect to the ingoing coordinates \( (v,r,\vartheta ,\varphi ) \) the wave equation for \( \psi \) reads

where \( R = D' + \frac{2D}{r} \) and \( V_2 (r)= -\frac{2M}{r^3}(3\sqrt{D}-2) \). Since \( \psi \) is supported on the fixed frequency \( \ell =2 \) we have  , and in view of \( D(M)=R(M)=0 \), the wave equation on the horizon \( {\mathcal {H}}^+ \) yields
, and in view of \( D(M)=R(M)=0 \), the wave equation on the horizon \( {\mathcal {H}}^+ \) yields
Now, we take a \( \partial _r-\)derivative of the wave equation (44), i.e. \( \partial _{r}\left( \square _{g} \psi -V_2\psi \right) =0 \) and we obtain

Evaluating the equation above on the horizon \( {\mathcal {H}}^+ \) yields
In particular, note that the coefficient of \( \partial _r\psi \) is zero since
Now, using both (157,158) we obtain
Since the vectorfield T is tangent to the null generators of \( {\mathcal {H}}^+ \), we deduce from above that the expression
is conserved along the null geodesics of \( {\mathcal {H}}^+. \)
Similarly, one can show that for \( i=1, \ell =1 \) the corresponding conserved quantity along the horizon \( {\mathcal {H}}^+\) is
In fact, we show below that for any \( \ell \ge i, \ i \in \left\{ 1,2 \right\} \), there is a similar expression in terms of \( \Psi _i^{^{(\ell )}} \) denoted by \( H_{\ell }[\Psi _i] \) which is conserved along the null geodesics of \( {\mathcal {H}}^+. \)
Remark 6.1
The notation \( H_{\ell }[\Psi _i] \) comes from [7] where such conserved quantities were discovered by Aretakis in the case of homogeneous wave equations \( \square _g\psi =0 \), and they usually go by the name of Aretakis constants.
Before we proceed to the general case, we first need the following proposition.
Proposition 6.1
For any solution \( \Psi _i^{^{(\ell )}}\) to (44), supported on the fixed frequency \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \) and for any \( 0\le s \le (\ell -1) +(-1)^{i+1} \) we have
Proof
Let us fix a frequency \( \ell \ge i. \) Taking \( s- \)many \( \partial _r \) derivatives of (44), i.e. \( \partial _r^{s}(\square _g\Psi _i-V_i\Psi _i)=0 \), yields the equation

In view of \( D(M)=R(M)=0 \) and  , evaluating the above equation on the horizon \( {\mathcal {H}}^+ \) allows us to express the top order \( \partial _r- \)term, \( \partial _r^s \Psi _i\), in terms of lower order \( \partial _r-\) derivatives and \( T(\partial _r^m\Psi _i) \), for \( 0\le m\le s+1, \) as long as the coefficient of \( \partial _r^s\Psi _i \) does not vanish. The coefficient of \( \partial _r^s\Psi _i \) on the horizon \( {\mathcal {H}}^+ \) is given by
, evaluating the above equation on the horizon \( {\mathcal {H}}^+ \) allows us to express the top order \( \partial _r- \)term, \( \partial _r^s \Psi _i\), in terms of lower order \( \partial _r-\) derivatives and \( T(\partial _r^m\Psi _i) \), for \( 0\le m\le s+1, \) as long as the coefficient of \( \partial _r^s\Psi _i \) does not vanish. The coefficient of \( \partial _r^s\Psi _i \) on the horizon \( {\mathcal {H}}^+ \) is given by
By assumption we have \( s\le (\ell -1)+(-1)^{i+1} \), thus we see that the coefficient of \( \partial _r^s\Psi _i \) is not zero. Repeating the same procedure consecutively for all lower order terms \( \partial _r^k\Psi _i \), \( 0\le k< s, \) we finally express \( \partial _r^s\Psi _i \) only in terms of \( T(\partial _r^j\Psi _i) \), \( 0\le j \le s+1 \). \(\square \)
Theorem 6.1
Let \( \ell \in {\mathbb {N}} \), with \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \), then there exist constants \( c_i^j\), \(\ j=0,1,\dots ,\ell +(-1)^{i+1} \) depending on \( M,\ell , \) such that for all solution \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell , \) the quantities
are conserved along the null generators of \( {\mathcal {H}}^+. \)
Proof
We consider (161) for \( s=\ell +1 \) when \( i=1 \), and \( s=\ell -1 \) when \( i=2 \) and we evaluate it on the horizon \( {\mathcal {H}}^+. \) In view of (162) and \( D(M) =R(M)=0\), we have that the terms \( \partial _r^{\ell +3}\Psi _1,\ \partial _r^{\ell +2}\Psi _1, \ \partial _r^{\ell +1}\Psi _1 \), while also \( \partial _r^{\ell +1}\Psi _2,\ \partial _r^{\ell }\Psi _2, \ \partial _r^{\ell -1}\Psi _2 \) in the respected wave equation, vanish on \( {\mathcal {H}}^+. \)
In addition, using Proposition 6.1 we can express each \( \partial _r^p\Psi _1, \partial _r^q\Psi _2 \), for \( p\le \ell , \ q\le \ell -2 \) as a linear combination of \( T(\partial _r^m\Psi _i) \), \(\ m\le \ell +(-1)^{i+1} \) with coefficients depending on \( M,\ell \). Thus, we obtain altogether
for \( c_i^j \) depending on \( M,\ell \) alone, which concludes the proof. \(\square \)
At this point we mention that one can find a set of conservation laws by working directly with the coupled scalar system (32). In particular, if \((\phi _{\ell },\psi _{\ell })\) is a solution to (32), supported on the fixed frequency \(\ell \), then there are quantities
which are conserved along the null generators of \({\mathcal {H}}^+\), where \({\mathcal {L}}^{k}, \tilde{{\mathcal {L}}}^{k}\) are linear expressions of \(\partial _r-\)derivatives of \(\phi ,\psi \) up to order k, with coefficients depending only on \(\ell ,M.\)
In the coming sections, for any \(k\in {\mathbb {N}}\) we show the following blow-up rates \(\partial _r^{^{\ell +k}} \phi _{\ell } \sim \tau ^{k}, \ \partial _r^{^{\ell +k}} \psi _{\ell } \sim \tau ^{k} \), asymptotically along \({\mathcal {H}}^+\). However, in view of the second conservation law \( \tilde{{\mathcal {H}}}_{\ell }[\phi ,\psi ]\) of order \(\ell +2\) as seen above, there ought to be some cancellation asymptotically on \({\mathcal {H}}^+.\) Tracking down such cancellations can make the whole analysis unnecessarily chaotic. Instead, by first decoupling system (32), we manage to isolate the dominant linear expression \(\Psi _{2}^{^{(\ell )}}[\phi ,\psi ]\) along \( {\mathcal {H}}^+\). All non-decaying and blow-up estimates for the Regge–Wheeler and Teukolsky system to follow are understood in terms of that dominant scalar \(\Psi _2^{^{(\ell )}}\); see Theorems 10.1, 10.2, and Theorems 11.1, 11.2.
7 Higher order \( L^2\) Estimates
Similarly to Sect. 5, we derive energy estimates for \( \partial ^k_r\Psi _i^{^{(\ell )}} \), for all \( k\le \ell + (-1)^{i+1}\), \(\ \ell \ge i, \ i\in \left\{ 1,2 \right\} . \) We do so, by repeatedly commuting our wave equation (44) with the vector field \( \partial _r \) and using induction. By taking \( \partial _r^k \)-derivatives of (44) we obtain
where the Laplace Beltrami operator commutes with \( \partial _r^k \) according to

with \( R = \partial _rD + \frac{D}{2r}. \)
Since \( \Psi _i^{^{(\ell )}} \) is supported on the fixed frequency \( \ell , \) so is \( \partial _r^s\Psi _i \) for any \( s\ge 0, \) and using

we can absorb the potential term of \( M^k[\Psi _i] \) in the last term of \( \left[ \square _{g}, \partial _{r}^{k}\right] \Psi _i \). In particular, it is a direct computation to check by induction that for any \( j\ge 0 \) we have
thus, we can write

where
Energy Identity. Now that we have the wave equation for \( \partial _r^k\Psi _i \), i.e. \( (\square - V_i)\partial _r^k\Psi _i = M^k[\Psi _i] \), we can proceed with the energy identity of the current \( J_{\mu }^{{\mathcal {X}}_k}[\partial _r^k\Psi _i] \) for an appropriate vector field \( {\mathcal {X}}_k. \)
In this section, we are only interested in obtaining higher-order estimates in a region close to the horizon \( {\mathcal {H}}^+. \) However, if we were to stay away from the horizon and the photon sphere, we can easily control the \( L^2 \) norm of all k-derivatives by using local elliptic estimates, commuting the wave equation (44) with \( T^j, \ j \in \left\{ 1,\dots ,k-1 \right\} \) and using the Morawetz estimates from Theorem 4.1, to obtain
for any \( r_c,r_d \) satisfying \( M<r_c<r_d<2M, \) and \( \left|a\right|= k, \) where the constant C depends on \( M, \Sigma _0 \) and k. Thus, we restrict our attention to a region \( R(0,\tau )\cap \left\{ M\le r\le r_c \right\} \) for \( M<r_c<2M. \) In particular, we prove the following theorem
Theorem 7.1
There exists \( r_c\in (M,2M) \) and a positive constant \( C >0 \) depending only on \( M,\ \Sigma _{0}\ \text {and} \ k\) such that in the region \( {\mathcal {A}}_c = R(0,\tau )\cap \left\{ M\le r\le r_c \right\} \), for all solutions \( \Psi _i^{^{(\ell )}}\) of (44) supported on the fixed frequency \(\ \ell \ge i ,\ i\in \lbrace 1,2 \rbrace \), we have

for any \( k \le \ell + (-1)^{i+1} \), where here we define \( \varvec{\chi }_{i,k} := {\left\{ \begin{array}{ll} 0, \ \ \text {if}\ \ k=\ell + (-1)^{i+1} \\ 1,\ \ \text {otherwise}. \end{array}\right. }. \)
Proof
We prove this by induction on the number of derivatives \( k\le \ell + (-1)^{i+1} \). In particular, assume that for any \( 0\le s\le (\ell -1)+(-1)^{i+1} \) the estimate (169) holds for all \( k\le s \), then we will prove that it also holds for \( s= \ell + (-1)^{i+1}. \)
Note, both base cases \( s=0,\ s= 1 \) correspond to the results of Theorem 4.3 and Theorem 5.1 respectively.
Let us work with an \( \phi _{\tau }^T \)-invariant timelike vector field \( {\mathcal {X}}_k = {\mathcal {X}}_k^v \partial _v + {\mathcal {X}}_k^r \partial _r\) with constraints that will be apparent in the end, such that it vanishes in \( r\ge r_d \), for a choice of \( r_d,r_c \) with \( 2M>r_d>r_c>M \) determined later. Then, the energy identity for the current \( J_{\mu }^{{\mathcal {X}}_k}[\partial _r^k\Psi _i] \) is
where we use the abbreviated notation \( {\mathcal {H}}^+ \equiv {\mathcal {H}}^+(0,\tau ) .\ \) Regarding the energy fluxes we have

for a constant \( C>0 \) depending only on \( M,\Sigma _0,{\mathcal {X}}_k \). In addition, on the horizon \( {\mathcal {H}}^+ \) we have

where \( \ell \) is the frequency support of \( \Psi _i^{^{(\ell )}}. \) Note the expression above is positive definite since \( {\mathcal {X}}_k \) is timelike, i.e. \( {\mathcal {X}}_k^r<0. \)
We now focus on the bulk term of (170) and similarly to Section 5 we have
Again, the first term is given by

where the coefficients  are defined as in (89) for the vectorfield \( {\mathcal {X}}_k, \) i.e.
are defined as in (89) for the vectorfield \( {\mathcal {X}}_k, \) i.e.

Expanding also \( M^k[\Psi _i] \) yields

In what follows, we show that the bulk terms of (174, 176) are controlled by terms of the right-hand side of (169) for \( k\le (\ell -1)+(-1)^{i+1} \) of the inductive hypothesis, or they can be absorbed as a small \( \varepsilon >0 \) fraction in the positive definite terms of the left-hand side of (169).
First, we are going to prove the following lemma which will be frequently used in the estimates below.
Lemma 7.1
For solutions \( \Psi _i^{^{(\ell )}},\ \ell \ge i, \ i\in \left\{ 1,2 \right\} \) to (44), and for any \( 0\le j \le (l-1) - (-1)^{i} \), we have
for a positive constant \( C_{\varepsilon } \) depending on \( \varepsilon , M,\Sigma _0 \) and j.
Proof
In view of Proposition 6.1, we can work instead with the integrals
for \( 0\le s\le \ell - (-1)^i. \)
-
For \( s=\ell -(-1)^i \) we have
$$\begin{aligned} \int _{{\mathcal {H}}^+} (T\partial _r^{^{\ell - (-1)^i}}\Psi _i)(\partial _r^{^{\ell - (-1)^i}}\Psi _i)&= \dfrac{1}{2}\int _{{\mathcal {H}}^+} T\left( \partial _r^{^{\ell - (-1)^i}}\Psi _i\right) ^2 \\&= \dfrac{1}{2}\int _{\Sigma _{\tau }\cap {\mathcal {H}}^+} \left( \partial _r^{^{\ell - (-1)^i}}\Psi _i\right) ^2 \\&\quad - \dfrac{1}{2}\int _{\Sigma _{0}\cap {\mathcal {H}}^+}\left( \partial _r^{^{\ell - (-1)^i}}\Psi _i\right) ^2 \end{aligned}$$Thus, using Lemma 5.1 for each term above we obtain
$$\begin{aligned} \int _{\Sigma \cap {\mathcal {H}}^+}\left( \partial _r^{^{\ell - (-1)^i}}\Psi _i\right) ^2&\le \varepsilon \int _{\Sigma \cap A_c} \left[ \left( T\partial _r^{^{\ell - (-1)^i}}\Psi _i\right) ^2 + \left( \partial _r^{^{\ell +1 - (-1)^i}}\Psi _i\right) ^2\right] \\&\qquad + C_{\varepsilon }\int _{\Sigma \cap A_c}\left( \partial _r^{^{\ell - (-1)^i}}\Psi _i\right) ^2 \\&\quad \le \varepsilon \int _{\Sigma \cap A_c} J_{\mu }^{{\mathcal {X}}_k}[\partial _r^{^{\ell -(-1)^i}}\Psi _i]\cdot n _{\Sigma }^{\mu } \\&\qquad + C_{\varepsilon } \int _{\Sigma \cap A_c} J_{\mu }^{{\mathcal {X}}_k}[\partial _r^{^{(\ell -1)-(-1)^i}}\Psi _i]\cdot n _{\Sigma }^{\mu }, \end{aligned}$$where the last term above is estimated from the first term of the right-hand side of (177), due to the inductive hypothesis.
-
Now let \( 0\le s < \ell - (-1)^i, \) then integration by parts yields
$$\begin{aligned} \int _{{\mathcal {H}}^+}(T\partial _r^s\Psi _i)(\partial _r^{^{\ell - (-1)^i}}\Psi _i) =&\int _{{\mathcal {H}}^+\cap \Sigma _{\tau }}(\partial _r^s\Psi _i)(\partial _r^{^{\ell - (-1)^i}}\Psi _i) - \int _{{\mathcal {H}}^+\cap \Sigma _0} (\partial _r^s\Psi _i)(\partial _r^{^{\ell - (-1)^i}}\Psi _i) \\&- \int _{{\mathcal {H}}^+}\partial _r^s\Psi _i \left( T\partial _r^{^{\ell - (-1)^i}}\Psi _i \right) \end{aligned}$$After applying a Cauchy-Schwartz, the first two boundary terms are treated similarly to the \( s=\ell -(-1)^i \) case, using Lemma 5.1 and the inductive hypothesis.
For the last term, we have
and the first term on the right is estimated by the estimate (169), for \( 0\le s\le (\ell -1)+(-1)^{i+1} \). \(\square \)
Controlling the bulk terms. Now we are in the position of controlling the spacetime terms that appear in the energy identity.
\( \bullet \ \) For \( j=0, \) the coefficient of the bulk term \( (\partial _r^{k+1}\Psi _i)^2 \) is \( E_0^1 = F_{rr}^k - k{\mathcal {X}}_k^rD' \) and since \( {\mathcal {X}}_k \) is timelike, \( E_0^1 \ge 0 \) in \( A_c. \)
\( \bullet \ \) For \( j\ge 1, \) using integration by parts we obtain
Lemma 5.3 holds also for \( \partial _r^k\Psi _i \) with the corresponding right-hand side estimate, and the proof follows similarly. Thus, for any \( j\ge 1 \) the boundary terms over \( \Sigma _0,\Sigma _{\tau } \) and the last two spacetime terms are estimated using this Lemma, Cauchy-Schwartz, and the inductive hypothesis.
The boundary term over the horizon \( {\mathcal {H}}^+\) is estimated for \( j\ge 2 \) using Lemma 7.1 and it only remains to estimate it for \( j=1, \) in which case the coefficient is
Using Poincare inequality for the angular term of the event horizon \( {\mathcal {H}}^+\) integral in the energy identity (170), it suffices to have
For \( i=1 \) the above is equivalent to \( k(k+1)\le (\ell +1)(\ell +2) \ \Leftrightarrow \ k\le \ell +1 \) and for \( i=2 \), \( k(k+1)\le \ell (\ell -1)\ \Leftrightarrow \ k\le \ell -1 \).
Thus, we see that when \( k=\ell +(-1)^{i+1} \) we have to use the entire coefficient of the angular term  on horizon \( {\mathcal {H}}^+\) in order to close the above estimate, hence and the appearance of the factor \( \varvec{\chi }_{i,k} \) in (169).
on horizon \( {\mathcal {H}}^+\) in order to close the above estimate, hence and the appearance of the factor \( \varvec{\chi }_{i,k} \) in (169).
Let us first deal with the \( j\ge 2 \) case. Using integration by parts we obtain
Now, the boundary terms over \( \Sigma _0,\Sigma _{\tau } \) are estimated using Cauchy-Schwartz and the inductive hypothesis while the horizon \( {\mathcal {H}}^+\) term is treated using Lemma 7.1. The second last spacetime term is estimated by Cauchy-Schwartz, Lemma 5.3 (generalized) and the inductive hypothesis while the remaining last spacetime term is treated similarly where we use instead the \( \varepsilon \) variation of Cauchy-Schwartz and Lemma 5.3 for \( \varepsilon ' = \varepsilon ^2. \)
For the \( j=1 \) case, using the wave equation (44) for \( \Psi _i \) and  we have
we have

Thus, we write

where \( B_{\ell }(r) : = 1+\frac{r^2\cdot V_i(r)}{\ell (\ell +1)}. \)
-
The terms of first-line sum are estimated for \( s=0,1 \) in view of the degenerate coefficient \( D(r),D'(r) \) on the horizon \( {\mathcal {H}}^+\). The terms for \( s\ge 2 \) are treated similarly to estimates 178.
-
The terms of second-line are estimated as the \( j\ge 2 \) case studied above.
-
On the third line, the \( s=0 \) case is estimated in view of the degenerate coefficient R(r) on the horizon \( {\mathcal {H}}^+, \) and for \( s\ge 1 \) we work similarly to 178 estimates.
-
For the last line terms, it is direct a computation to check the following commutation for any \( m\in {\mathbb {N}} \)

Thus, terms of the fourth line can be expressed in the form of
 and such type of terms are estimated in the 183 paragraph below, as long as the coefficients of the corresponding terms are comparable. However, note that \( E_1^2=-k{\mathcal {X}}_k^vD'+D\partial _r({\mathcal {X}}_k^v)- \dfrac{2{\mathcal {X}}_k^r}{r} \) and \( \partial _r^sB_{\ell }(r) \) is uniformly bounded in \( A_c \) with respect to \( \ell , \) while \( E_j^6 \sim _k \left( - \dfrac{2{\mathcal {X}}_k^r}{r} \right) \) and uniformly bounded with respect to \( \ell \) for every \( j\ge 1 \). Thus, the estimates of Paragraph 183 yield estimates for the terms of the fourth line with uniform coefficients with respect to \( \ell . \)$$\begin{aligned} \boxed {\text {Estimates for the terms } \quad E_j^3 (\partial _r^{k-j+2}\Psi _i)(T\partial _r^k\Psi _i), \ j\ge 1. } \end{aligned}$$(180)
and such type of terms are estimated in the 183 paragraph below, as long as the coefficients of the corresponding terms are comparable. However, note that \( E_1^2=-k{\mathcal {X}}_k^vD'+D\partial _r({\mathcal {X}}_k^v)- \dfrac{2{\mathcal {X}}_k^r}{r} \) and \( \partial _r^sB_{\ell }(r) \) is uniformly bounded in \( A_c \) with respect to \( \ell , \) while \( E_j^6 \sim _k \left( - \dfrac{2{\mathcal {X}}_k^r}{r} \right) \) and uniformly bounded with respect to \( \ell \) for every \( j\ge 1 \). Thus, the estimates of Paragraph 183 yield estimates for the terms of the fourth line with uniform coefficients with respect to \( \ell . \)$$\begin{aligned} \boxed {\text {Estimates for the terms } \quad E_j^3 (\partial _r^{k-j+2}\Psi _i)(T\partial _r^k\Psi _i), \ j\ge 1. } \end{aligned}$$(180)
The \( j=1 \) case is treated already in the 179-estimates. For \( j\ge 2 ,\) we use Cauchy-Schwartz with \( \varepsilon >0 \), Lemma 5.3 (generalized) for \( \varepsilon '= \epsilon ^2>0 \) and the inductive hypothesis.
We simply use Cauchy-Schwartz with \( \varepsilon >0 \) and the inductive hypothesis.

We use induction on \( j\le k-1 \). For \( j=0 \), we use the wave equation (44) for \( \Psi _i\) and we express

Note, the coefficient of  satisfies
satisfies
for \( C_1,C_2 \) positive constants depending only on M, for all \( \ell \ge i,\ i\in \left\{ 1,2 \right\} , \) thus we can solve for  . Then, using Cauchy-Schwartz and the result obtained above we estimate each term.
. Then, using Cauchy-Schwartz and the result obtained above we estimate each term.
Now, assume we can estimate all terms of the form  for any \( s\le j-1 \), then we have
for any \( s\le j-1 \), then we have

However, after solving for  in the wave equation we take \( \partial _r^j \)-many derivatives of the equation and we use the results obtained previously to estimate the first term of the right-hand side above. Next, we have
in the wave equation we take \( \partial _r^j \)-many derivatives of the equation and we use the results obtained previously to estimate the first term of the right-hand side above. Next, we have

and we use the inductive hypothesis to estimate it, since \( j-s\le j-1 \) for all \( s\ge 1. \)

Once again, using integration by parts we obtain

Now, the first two boundary terms \( \Sigma _0,\Sigma _{\tau } \) and the second last spacetime term are estimated using Stokes’ theorem for the angular derivative on the sphere \( S^2(r) \), applying Cauchy-Schwartz and using the inductive hypothesis. For the last spacetime term, we write

so all the sum terms are estimated using Cauchy-Schwartz and the inductive hypothesis, for any \( j\ge 1 \). The first term on the left-hand side is estimated the same for \( j\ge 2 \), while for \( j=1 \) we use Stokes’s theorem and we obtain

which can be absorbed in the  term of (174) as long as \( \left|E_1^6\right|< -\frac{1}{2}\partial _r{\mathcal {X}}_k^r. \) However, in view of \( A_{j,\ell }(r) \) being uniformly bounded in \( A_c \) with respect to \( \ell \), it suffices to choose \( -{\mathcal {X}}_k^r \ll -\frac{1}{2}\partial _r{\mathcal {X}}_k^r. \)
term of (174) as long as \( \left|E_1^6\right|< -\frac{1}{2}\partial _r{\mathcal {X}}_k^r. \) However, in view of \( A_{j,\ell }(r) \) being uniformly bounded in \( A_c \) with respect to \( \ell \), it suffices to choose \( -{\mathcal {X}}_k^r \ll -\frac{1}{2}\partial _r{\mathcal {X}}_k^r. \)
Finally, we will estimate the horizon \( {\mathcal {H}}^+\) boundary term by induction. In particular, it suffices to estimate

for any \( 0\le m \le k-1. \) For \( m=0, \) using the wave equation (44) for \( \Psi _i\) we have

where \( \frac{1}{3}\le \left( 1+\frac{M^2\cdot V_i(M)}{\ell (\ell +1)}\right) \le 3 \) for all \( \ell \ge i. \) Thus, using Lemma 7.1 we obtain an estimate for the \( m=0 \) case. Now, assume we also have an estimate for any \( m\le k-2 \), then we write

The terms of the sum are all estimated by the inductive hypothesis for \( m\le k-2. \) For the first term, using the wave equation and taking \( \partial _r^{k-1} \)-derivatives we obtain

In view of \( D(M)=D'(M)=R(M)=0,\) the non-vanishing terms on the horizon \( {\mathcal {H}}^+\) of the above sums are estimated using Lemma 7.1 and the inductive hypothesis. All coefficients in the estimates are independent of \( \ell \) since \( \partial _r^sB_{\ell }(r) \) is uniformly bounded with respect to \( \ell \) for all \( s\ge 0. \)
This term is estimated precisely in the same way as \( E_{11}(\partial _r\Psi _i) \) in Section 5.
Conclusion. Thus, in order to conclude the proof of Theorem 7.1, it suffices to consider a timelike vectorfield \( {\mathcal {X}}_k \), i.e. \( {\mathcal {X}}_k^v(M)>0 , {\mathcal {X}}_k^r(M)<0,\) such that \( -\partial _r{\mathcal {X}}_k^r(M)\gg -{\mathcal {X}}_k^r(M) \) and \( \partial _r{\mathcal {X}}_k^v(M) \) to be sufficiently large. Then, choosing \( r_c \) close enough to the horizon \( {\mathcal {H}}^+\) and \( \varepsilon >0 \) sufficiently small, allows us to obtain the estimate (169) for \( k=\ell +(-1)^{i+1} \), and thus closing the induction argument. \(\square \)
8 The \( r^p\)–hierarchy estimates
In this section, we aim to derive decay for both the degenerate and non-degenerate energy flux leading to pointwise decay estimates for \( \Psi _{i}^{^{(\ell )}}, \ \forall \ \ell \ge i, \ i\in \left\{ 1,2 \right\} \). The key part is to produce the so-called \( r^p- \)hierarchy estimates by applying the vector field method for vectorfields of the form \( Z=r^{q} \partial _v \), written with respect to the double null coordinate system (u, v) . All results in this section are expressed in the double null coordinate system and we work with the foliation \( {\check{\Sigma }}_{\tau } \) introduced in Section 2.
Let us make some notation remarks regarding regions where these estimates take place. For any \( \tau _1< \tau _2 \) we define the following regions, as seen in the Penrose diagram of Fig. 2,
We proceed with the following proposition.
Proposition 8.1
Let \( 0 < p \le 2 \), then there exists a positive constant \( C>0 \) depending only on \( M,{\check{\Sigma }}_0 \), such that for any solution \( \Psi _{i}^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \), the rescaled quantity \( \Phi _i := r \Psi _i \) satisfies the following estimate

Proof
As described in the introduction, we apply the vectorfield method in the \( {\check{I}}_{\tau _1}^{\tau _2} \) region, for the multiplier \( Z = r^q \partial _v \), where \( q=p-2. \) In order to avoid timelike boundary terms we also fix a smooth cut-off function of r alone, such that \( \zeta _R(r) \equiv 0 \) for \( r\le R \) and \( \zeta _R(r)\equiv 1 \) for \( r\ge R+1 \). Then, the energy identity associated to \( \zeta _R\cdot \Phi _i \) reads
However, for \( r\ge R+1 \) we have \( \zeta _R\cdot \Phi _i = \Phi _i \) and for solutions \( \Psi _i \) to equation (44), it is immediate computations to check that \( \Phi _i = r\Psi _i\) satisfies the following non-homogeneous equation
Therefore, from Proposition 4.1 we have

To treat the non-positive cross term we use Stoke’s theorem and we write
Note, the boundary integral over \( {\check{I}}_{\tau _1}^{\tau _2}\cap \lbrace r=R \rbrace \) vanishes since \( \zeta _R \equiv 0 \) on \( \lbrace r=R\rbrace \), whereas the remaining terms are positive definite in \( {\check{I}}_{\tau _1}^{\tau _2} \) for \( p \le 2 \) and R large enough.
Now, when it comes to the error terms in equations (187, 190) coming from the region \( R\le r\le R+1 \), as quadratic terms of the 1st-order jet of \( \Psi _i \), we control them in terms of the T-flux by Theorem 4.1, as long as \( R> 2M \).
Finally, for the boundary terms on the right-hand side of (187) we have

and seeing that the last two terms have the right sign, we conclude the proof. \(\square \)
Estimates for the non-degenerate energy near null infinity \( {\mathcal {I}}^+ \). Using the proposition above, we obtain local integrated energy decay estimates near future null infinity \( {\mathcal {I}}^{+}.\)
Proposition 8.2
There exists a positive constant C depending on \( {\check{\Sigma }}_{\tau _0}, \ M \), such that for all solution \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \(\ell \ge i, \ i\in \lbrace 1,2 \rbrace \), we have
Proof
Using Proposition 8.1 for \( p=1 \) we obtain

However, in view of \( V_i = {\mathcal {O}}\left( \frac{1}{r^3}\right) \), choosing R large enough and using Poincare inequality we can absorb the last term of the left-hand side in the angular derivative term. In addition, the first term expands as
and in order to treat the last term above, using the cut-off smooth function introduced earlier, we write
The middle term in the last line vanishes, and since \( \partial _v (D/r) = D\sqrt{D}(2-3\sqrt{D})/2r^2 <0 \) for large values of R, the remaining two terms above are positive definite.
All error terms that occur in the region \( \left\{ R\le r\le R+1 \right\} \) are controlled in terms of the \( T-\)flux along \( {\check{\Sigma }}_{\tau _{1}} \) using Theorem 4.1, and combining all estimates above we show

On the other hand, since \( n _{{\check{O}}_{\tau }} \equiv \frac{\partial }{\partial v}, \) we have

thus using the coarea formula for the spacetime term of (197) we conclude the proof of (192). \(\blacksquare \)
In order to prove (193), we use Proposition 8.1 for \( p=2 \) and we obtain

By Poincare’s inequality, we write

for all \( \ell \ge i \). Thus, the last two terms of (198) are bounded by the right-hand side of (197) which concludes the proof. \(\square \)
8.1 Decay of Energy
With the above estimates in hand, we are ready to show decay for the non-degenerate energy of \( \Psi _i^{^{(\ell )}} \), for all \( \ell \ge i. \) First, Theorem 5.1 and coarea formula yield near the event horizon \( {\mathcal {H}}^+ \)
On the other hand, close to future null infinity \( {\mathcal {I}}^+ \) we have estimate (192) and using Theorem 4.2 to control the energy in the intermediate region \( \lbrace r_c\le r \le R \rbrace \cap {\check{\Sigma }}_{\tau } \), we obtain
for a positive constant \( C = C(M,{\check{\Sigma }}_0)\), where
Last, in order to improve the decay of the non-degenerate energy we also need an estimate for
Theorem 7.1 for \( k=2 \) and coarea formula yield
for all \( \ell \ge 2+(-1)^{i} \). Thus, applying (200) for both \( \Psi _i, T \Psi _i \) (note \( T\Psi _i \) also satisfies (44)), using (193) and the estimate above, we obtain
for all \( \ell \ge 2+(-1)^{i} \). Note, the above estimate holds for all frequencies \( \ell \ge 1 \) in the \( i=1 \) case, however, in the \( i=2 \) case it holds only for \( \ell \ge 3.\) Thus, using an effective method introduced by Dafermos-Rodnianski in [18], we obtain the following inverse polynomial energy decay estimates.
Proposition 8.3
There exists a positive constant C depending only on \({\check{\Sigma }}_0, M \) such that for all solutions \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \ i \in \left\{ 1,2 \right\} \), the following inverse linear decay holds
Moreover, if \( \ell \ge 2 + (-1)^i \), we have the improved inverse polynomial decay
where \( \bar{{\mathcal {E}}}[\Psi _i](0) \) is equal to the right-hand side of (201) for \( \tau _1=0. \)
Proof
Applying (200) for \( \tau _1 = 0 \) and \( \tau _2=\tau \) for any \( \tau \ge 0, \) we obtain
Using the fundamental theorem of calculus and the uniform boundedness of the non-degenerate energy of Theorem 4.3, i.e.
we obtain
which readily proves (202).
Now, let \( \ell \ge 2 +(-1)^i \) and considering (201) for \( \tau _1=0 \) while taking \( \tau _2 \rightarrow +\infty \) and we obtain
This allows us to find a sequence \(\lbrace \tau _n \rbrace _{n\in {\mathbb {N}}}\) with \( \tau _0\ge 1 \) and \( 2\tau _n\le \tau _{n+1}\le 3\tau _n \) such that
Note, the above sequence has the property that \( \tau _n \sim \tau _{n+1}\sim (\tau _{n+1}-\tau _n )\), uniformly for any \( n\in {\mathbb {N}}, \) which also makes it unbounded, i.e. \( \tau _{n} \xrightarrow {n\rightarrow \infty } \infty \).
So, applying (200) for the interval \( [\tau _n,\tau _{n+1}] \) and using relation (207) we get
Thus, using the fundamental theorem of calculus and uniform energy boundedness we obtain
where we used the dyadic property of the sequence above. Now, note that for any \( \tau \ge 1 \), there exists \( n\in {\mathbb {N}} \) such that \( \tau _n\le \tau \le \tau _{n+1} \) and using the above estimate we finally get
\(\square \)
In order to prove pointwise decay estimates that are \( L^2(\tau _0,\infty ) \) integrable in time, we need the non-degenerate energy to decay like \( 1/\tau ^2 \). However, we see above that we don’t have such decay for the energy of \( \Psi _2^{(2)} \), i.e. \( i=2,\ \ell =2. \) We remedy this situation by working with the degenerate energy, \( J_{\mu }^T[\Psi _i] \), which we show decays like \( \frac{1}{\tau ^{2}} \), and using certain interpolation inequalities we manage to show adequate pointwise decay for all frequencies \( \ell \ge i,\ i\in \left\{ 1,2 \right\} \).
Proposition 8.4
There exists a positive constant C depending only on \({\check{\Sigma }}_0, M \) such that for all solutions \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i \), \( i\in \lbrace 1,2 \rbrace \), the following decay estimate holds
where \(\bar{{\mathcal {E}}}^T[\Psi _i](\tau ) \) is defined in the proof below.
Proof
Using Proposition 4.9, Theorem 4.3 and coarea formula we obtain for any \( \tau _1<\tau _2 \)

However, since \( \sqrt{D}\ge D \) for all \( r\ge M \), we have
Thus, using the above estimate, Theorem 4.2 and (192) for \( T\sim N \) readily yields
with
In addition, note
where,
Thus, using the uniform boundedness of degenerate energy and following the same idea for a dyadic sequence \( \lbrace \tau _n\rbrace _{n\in {\mathbb {N}}} \) as the proposition above we prove the corresponding decay result. \(\square \)
9 Decay, Non-Decay and Blow-up for Regge–Wheeler solutions
We have reached the point where we can finally state and prove pointwise estimates for solutions to the Regge–Wheeler system. First, we show how to obtain pointwise decay estimates for solutions \( \Psi _i^{^{(\ell )}}, \ \ell \ge i, \ i \in \left\{ 1,2 \right\} \) to (44), in the exterior up to and including the event horizon \( {\mathcal {H}}^+. \) We then generalize the energy results of the previous section to obtain higher-order pointwise estimates accordingly. Such findings are essential later on when we prove non-decay and growth estimates for translation invariant derivatives of \( \Psi _i^{^{(\ell )}} \), asymptotically along the event horizon \( {\mathcal {H}}^+. \) Finally, using elliptic identities we pass these estimates to the corresponding gauge invariant quantities \( \varvec{q}^{F}, \varvec{p} \) (and \( \underline{\varvec{q}}^{F}, \underline{\varvec{p}} \)) satisfying the Regge–Wheeler system (29).
9.1 Pointwise estimates
With the energy decay results obtained in the previous section, we can now prove pointwise estimates for \( \Psi _i^{^{(\ell )}}, \) \( i\in \lbrace 1,2\rbrace \), for all \( \ell \ge i. \) The results are based on the Sobolev inequality and the spherical symmetry of our spacetime that allow us to use the angular momentum operators \( \Omega _j \), \( j\in \left\{ 1,2,3 \right\} \) as commutators.
Working on the foliation \( \Sigma _{\tau } \) (or \( {\check{\Sigma }}_{\tau } \)) with the associated coordinate system \( (\rho ,\omega ) \), for any \( r\ge M \) we have
where in the last equality we used that \( \partial _{\rho } = k(r)\partial _v + \partial _{r} \), for k(r) bounded; see Section 2. Then, Cauchy-Schwartz and Hölder inequality (for both \( p=\infty , q=1 \) and \( p=q=2 \) cases) yield
for a constant C depending only on \( M,\Sigma _0. \) Thus, integrating upon the sphere \( {\mathbb {S}}^2 \) and using again Hölder inequality (\( p=2,q=2 \)) for the last term above, we obtain
Note, we are using the non-degenerate flux \( J^{N}_{\mu }[\Psi _i] \) in the last term above since \( \partial _r\Psi _i \) appears without a D(r) factor in front of it. Thus, using Proposition 8.3 and relation (211) we show that for all \( r\ge M \),
where \( {\mathcal {E}}_1[\Psi _i] \) is an expression involving initial data of \( \Psi _i^{(\ell )}. \) Note the above decay estimate holds for all \( \ell \ge i, \ i\in \left\{ 1,2 \right\} . \) We now present our first pointwise estimate.
Theorem 9.1
There exists a positive constant C depending only on \(M,{\check{\Sigma }}_0 \) such that for all solutions \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \ i \in \left\{ 1,2 \right\} \), there are expressions \( {\mathcal {E}}_1, {\mathcal {E}}_2 \) in terms of norms of initial data of \( \Psi _i^{^{(\ell )}} \) such that
Moreover, for any \( \ell \ge 2 + (-1)^{i} \) we have instead
Proof
Commuting the wave equation (44) with the Killing angular momentum operators \( \Omega _j \) we obtain the corresponding estimate (214) and using the Sobolev embedding theorem on the sphere \( {\mathbb {S}}^2 \), we get
where \( {\mathcal {E}}_1 \,= \sum _{\left|a\right|\le 2}\sum _{j}{\mathcal {E}}_1[\Omega _j^a \Psi _i] \).
Now, consider \( \ell \ge 2 + (-1)^i \) and using Hölder inequality we write for any \( r\ge M \)
Integrating upon the sphere \( {\mathbb {S}}^2 \) we obtain
Thus, using (203) and (217) we obtain
Once again, from Sobolev embedding theorem we get
for \( {\mathcal {E}}_2 := \sum _{\left|a\right|\le 2}\sum _{j}\bar{{\mathcal {E}}}[\Omega _j^a \Psi _i](0). \) \(\square \)
9.2 Higher order pointwise estimates
Using the ideas introduced earlier we show pointwise decay results for the derivatives \( \partial _r^k\Psi _i^{^{(\ell )}} \), for all \( \ell \ge i, \ i\in \left\{ 1,2 \right\} \) and \( k\le \ell +(-1)^{i+1}, \) near and including the event horizon \( {\mathcal {H}}^+. \) Again, pointwise decay will follow from showing energy decay first. In particular, we have the following proposition
Proposition 9.1
Let us fix \( {\bar{R}}>M, \ \ell \in {\mathbb {N}},\ \ell \ge i,\ i\in \left\{ 1,2 \right\} \) and consider \( \tau \ge 1, \) then there exists a positive constant C depending on \( M,k,{\bar{R}} \) and \( {\check{\Sigma }}_0 \) such that for all solutions \( \Psi _i^{^{(\ell )}}\) to (44), supported on the fixed frequency \( \ell \ge i, \) there exist norms \( {\mathcal {E}}^{k}_{i,\ell } \) of the initial data such that
Proof
For any \( r_c>M \), in the region \( {\check{\Sigma }}_{\tau }\cap \left\{ r_c\le r\le {\bar{R}} \right\} \) we can produce the above decay results by commuting the wave equation (44) with the Killing vector field T, applying local elliptic estimates and using the decay results obtained in Proposition 8.3. Thus, we focus on showing decay in \( {\check{\Sigma }}_0\cap {\mathcal {A}} \), for \( {\mathcal {A}} \) an \( \phi ^T_{\tau }- \)invariant neighborhood of \( {\mathcal {H}}^+. \)
Using estimate (169) of Theorem 7.1 for all \( s \le \ell -(-1)^{i}\) and coarea formula yields the estimate
for any \( T\ge 0 \), where
This allows us to find a sequence \(\lbrace \tau _n \rbrace _{n\in {\mathbb {N}}}\) with \( \tau _0\ge 1 \) and \( 2\tau _n\le \tau _{n+1}\le 3\tau _n , \ \forall n\in {\mathbb {N}}, \) such that
On the other hand, commuting the wave equation (44) with \( T^{s} \) for all \( s < \ell -(-1)^{i} \) and using the corresponding estimate of relation (202) we obtain
Then, for any \( \tau \ge 1 \) we can find \( n\in {\mathbb {N}} \) such that \( \tau _n\le \tau \le \tau _{n+1} \) and applying estimate (169) in \( {\mathcal {R}}(\tau _n,\tau ) \) for \(k=(\ell -1)-(-1)^i \) while using (221, 222) yields
where \( {\mathcal {E}}_{i}^{^{\ell }} \) involves norms of initial data of \( \Psi _i^{^{(\ell )}} \) only, and C is a positive constant that depends on \( M, {\bar{R}}, {\check{\Sigma }}_{0} \) and \( k=\ell -1-(-1)^{i} \).
Now, fix \( k\le (\ell -2)-(-1)^i \) and apply (169) in \( {\mathcal {R}}(a_n,b_{n}) \), where \( a_n :=\tau _{n}+\frac{\tau _{n+1}-\tau _n}{3}, \ b_{n}:=\tau _{n+1}- \frac{\tau _{n+1}-\tau _n}{3} \), along with coarea formula to obtain
where the latter estimate comes from the analysis above. By fundamental theorem of calculus, there exists \( \xi _n \in (a_n,b_n) \) such that
However, \( b_n-a_n= \frac{\tau _{n+1}-\tau _n}{3}, \ \forall n \in {\mathbb {N}}, \) and using the property of \( \left\{ \tau _n \right\} _{n\in {\mathbb {N}}} \), i.e. \( \tau _n \sim \tau _{n+1} \sim (\tau _{n+1}-\tau _{n}) \), relation (223) yields
for all \( n\in {\mathbb {N}}. \) It’s a direct computation to check that the sequence \( \left\{ \xi _n \right\} _{n\in {\mathbb {N}}} \) satisfies
which also corresponds to an unbounded dyadic sequence with \( \xi _n \sim \xi _{n+1}\sim (\xi _{n+1}-\xi _{n}), \) uniformly \( \forall n \in {\mathbb {N}} \). Thus, for any \( \tau \ge 1 \) we can find \( n\in {\mathbb {N}} \) such that \( \xi _n\le \tau \le \xi _{n+1} \) and applying estimate (169) in \( {\mathcal {R}}(\xi _n,\tau ) \) and using estimate (224) with the results of Proposition 8.3, we conclude the proof of (219). \(\square \)
Theorem 9.2
Let \( {\bar{R}}>M, \ \tau \ge 1 \) and fix \( \ell \ge i, \ i\in \left\{ 1,2 \right\} , \) then for any \( k\le \ell - (-1)^{i} \) there exists a positive constant C depending on \( M,\ k,\ {\bar{R}} \) and \( {\check{\Sigma }}_0 \) such that for all solution \( \Psi _i^{(\ell )} \) to (44), supported on the fixed frequency \( \ell , \) the following pointwise decay estimates hold
in \( \left\{ M\le r \le {\bar{R}} \right\} , \) where \( {\mathcal {I}}_{k,\ell }[\Psi _i] \) are norms of initial data of \( \Psi _i^{^{(\ell )}}. \)
Proof
Consider a smooth-cutoff function \( \chi _{_{{\bar{R}}+1}} : [M, {\bar{R}}+1]\rightarrow [0,1] \) of r alone, such that \( \chi _{_{{\bar{R}}+1}}(r)=1 \) for \( M\le r\le {\bar{R}} +\frac{1}{4} \) and \( \chi _{_{{\bar{R}}+1}}(r)=0 \) for \( r\ge {\bar{R}}+\frac{1}{2}. \) Let \( r \in [M,{\bar{R}}] \), then we write
Now, integrating on the sphere \( {\mathbb {S}}^2 \) and since \( \chi _{_{{\bar{R}}+1}} \) is smooth, we obtain
with C depending on \( M, {\check{\Sigma }}_0. \) Thus, using the results of Proposition 9.1 we have that for \( k\le (\ell -2)-(-1)^i \) all integrals of the right-hand side decay at the rate of \( \frac{1}{\tau ^2} \). For \( k=\ell -1 -(-1)^i \) the first integral of the right-hand side decays like \( \frac{1}{\tau ^2} \), whereas the last integral decays like \( \frac{1}{\tau }. \) Finally, for \( k=\ell -(-1)^i \) the first integral decays like \( \frac{1}{\tau } \) and from Theorem 7.1, the last integral is bounded.
Thus, repeating the same estimates after we commute with the angular momentum operators \( \Omega \) and using the Sobolev inequality on the sphere \( {\mathbb {S}}^2 \) we prove the decay rates of the assumption. \(\square \)
Non-Decay and Blow-up Estimates
Proposition 9.2
For all solutions \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i, \ i \in \left\{ 1,2 \right\} ,\) we have the following non decay estimates
asymptotically along the event horizon \( {\mathcal {H}}^+\), where \( H_{\ell }[\Psi _i] \) are the conserved quantities of Theorem 6.1 . In addition, for generic initial data of \( \Psi _{i}^{^{(\ell )}} \), \( H_{\ell }[\Psi _i](\vartheta ,\varphi ) \) is almost everywhere non-zero on \( {\check{\Sigma }}_0\cap {\mathcal {H}}^+. \)
Proof
Using Theorem 6.1, we know the expressions below are conserved along the null generators of \( {\mathcal {H}}^+, \)
Thus, using the pointwise decay estimates of Theorem 9.2 along the event horizon \( {\mathcal {H}}^+\), we deduce that all terms of the sum above converge to zero asymptotically as \( \tau \rightarrow \infty , \) and so the limits of the assumption follow.
In addition, as in [7], we may introduce a new hypersurface \( {\tilde{\Sigma }}_0 \) formed by ingoing null hypersurfaces in an \( \phi ^{T}- \)invariant neighborhood of the horizon \( {\mathcal {H}}^+\), and prescribed initial data for \( \Psi _i\) on \( {\tilde{\Sigma }}_0 \) can be compared to initial data prescribed on \( {\check{\Sigma }}_0 \) using energy boundedness results obtained already. In view of \( H_{\ell }[\Psi _i] \) involving only transversal derivatives to \( {\mathcal {H}}^+\), we see that it is completely determined on \( {\check{\Sigma }}_{0}\cap H \) by the initial data prescribed on \( {\tilde{\Sigma }}_0 \). Hence, generic initial data for \( \Psi _i\) on \( {\tilde{\Sigma }}_0 \) produces generic eigenfunctions \( H_{\ell }[\Psi _i] \) of order \( \ell \) of  on \( {\check{\Sigma }}_0 \), and thus almost everywhere non-zero. \(\square \)
on \( {\check{\Sigma }}_0 \), and thus almost everywhere non-zero. \(\square \)
Theorem 9.3
Let \( k,\ell \in {\mathbb {N}} \), then for all solutions \( \Psi _i^{^{(\ell )}} \) to (44), supported on the fixed frequency \( \ell \ge i \), \( i\in \left\{ 1,2 \right\} \), we have
as \( \tau \rightarrow \infty \) along the event horizon \( {\mathcal {H}}^+\), where
Proof
We use induction on \( k\in {\mathbb {N}}.\) To show the \( k=1 \) case, we consider (161) for \( s=\ell +1 - (-1) ^{i}\) and we evaluate it on the horizon \( {\mathcal {H}}^+\) to obtain
where \( L_{\le q}[\Psi _i],\ {\tilde{L}}_{\le q}[\Psi _i]\) is a linear combination of \( \partial _r-\)derivatives of \( \Psi _i\) up to order q, with coefficients depending on \( \ell ,q,M. \) However, in view of the pointwise estimates of Theorem 9.2 we have
Thus, using the conserved expressions of Theorem 6.1 and integrating (231) along the null geodesics of \( {\mathcal {H}}^+\) we obtain
which proves the \( k=1 \) case. Now, assume the relation of the assumption holds for all \(q \le k-1\), then evaluating (161) for \( s=\ell +k-(-1) ^{i}\) on the horizon \( {\mathcal {H}}^+\) yields accordingly
However, using the inductive hypothesis we obtain
Thus, integrating the above relation along the null generators of \( {\mathcal {H}}^+\) and using the inductive hypothesis we conclude the proof. \(\square \)
Remark 9.1
The proposition above holds also for \( k=0 \) which corresponds to the non-decaying result of Proposition 9.2.
Corollary 9.1
Let \( (\phi ,\psi ) \) be a solution to the coupled system (32), then for generic initial data, the following decay estimates hold in the exteriorFootnote 5
for all \( r\ge M \) and \( \tau \ge 1. \) Moreover, the following decay, non-decay and blow up estimates hold asymptotically on \( {\mathcal {H}}^+\), as \( \tau \rightarrow \infty \). For any \( \ell \ge 2, \) we have
-
Decay:
$$\begin{aligned} \left|\partial _r^{\ell -1}\phi _{\ell }\right|&\lesssim _{_{\ell ,M}} \dfrac{1}{\tau ^{\frac{1}{4}}}, \hspace{2cm} \left|\partial _r^{\ell -1}\psi _{\ell }\right| \lesssim _{_{\ell ,M}} \dfrac{1}{\tau ^{\frac{1}{4}}} , \end{aligned}$$(234)$$\begin{aligned} \left|\partial _r^{\ell -2}\phi _{\ell }\right|&\lesssim _{_{\ell ,M}} \dfrac{1}{\tau ^{\frac{3}{4}}}, \hspace{2cm} \left|\partial _r^{\ell -2}\psi _{\ell }\right| \lesssim _{_{\ell ,M}} \dfrac{1}{\tau ^{\frac{3}{4}}}, \end{aligned}$$(235)$$\begin{aligned} \left|\partial _r^k \phi _{\ell }\right|&\lesssim _{_{k,M}} \dfrac{1}{\tau }, \hspace{2cm} \left|\partial _r^k \psi _{\ell }\right| \lesssim _{_{k,M}} \dfrac{1}{\tau } \hspace{1cm} \forall \ k\le \ell -3 \end{aligned}$$(236) -
Non-decay
$$\begin{aligned} \partial _r^{\ell }\phi _{_{\ell }}(\tau ,\omega )&\xrightarrow {\tau \rightarrow \infty } \dfrac{1}{2M^2(2\ell +1)}H_{\ell }[\Psi _2](\omega ), \end{aligned}$$(237)$$\begin{aligned} \partial _r^{\ell }\psi _{_{\ell }}(\tau ,\omega )&\xrightarrow {\tau \rightarrow \infty } -\dfrac{2}{M(2\ell +1)(\ell +2)}H_{\ell }[\Psi _2](\omega ), \end{aligned}$$(238) -
Blow up:
$$\begin{aligned}&\partial _r^{k+\ell }\phi _{\ell }(\tau ,\omega ) = (-1)^{k} \dfrac{a_{2,k}^{^{(\ell )}}}{2M^{2}(2\ell +1)}H_{\ell }[\Psi _2](\omega ) \cdot \tau ^{k}+ {\mathcal {O}}(\tau ^{k-\frac{1}{4}}), \hspace{1cm} k\ge 0, \end{aligned}$$(239)$$\begin{aligned}&\partial _r^{k+\ell }\psi _{\ell }(\tau ,\omega ) = -(-1)^{k}\frac{2a_{2,k}^{^{(\ell )}}}{M(\ell +2)(2\ell +1)} H_{\ell }[\Psi _2](\omega ) \cdot \tau ^{k}+ {\mathcal {O}}(\tau ^{k-\frac{1}{4}}), \hspace{1cm} k\ge 0, \end{aligned}$$(240)where the constants \( a_{i,k}^{^{(\ell )}} \) are given in Theorem 9.3.
Proof
We recall from Corollary 3.1 the following expressions for any \( \ell \ge 2 \)
Thus, the proof follows immediately from Theorem 9.2, 9.2, and 9.3. Note, \( \psi _{\ell =1} = \Psi _1^{^{(\ell =1)}}\), thus we already have estimates for \( \psi _{\ell =1} \). \(\square \)
9.3 Estimates for \( \mathbf {q^F, p} \)
Using elliptic identities of Section 2 we can show that a similar hierarchy of estimates also holds for the gauge–invariant quantities \( \varvec{q^F}\) and \(\varvec{p} \) in \( L^2(S^2_{\tau ,M}). \) First, let us prove the following lemma that allows us to do so.
Lemma 9.1
Let \( \xi _{A}, \theta _{AB} \) be a one tensor and a symmetric traceless 2-tensor on \( S^2_{v,r} \), respectively, and consider the scalars  . Then,
. Then,
-
For any \( k\in {\mathbb {N}} \), we have
 (241)
(241) -
The following elliptic estimates hold for any \( k\in {\mathbb {N}} \)
 (242)
(242)
Proof
From the definition of  and the commutations (6) we have
and the commutations (6) we have  which shows (241). For example,
which shows (241). For example,

To show (242), we use identities (7),(8) and for motivation, we only look at the second estimate, i.e.

where in the last equation we used relation (241). \(\square \)
In the propositions that follow, we define the \( L^2(S^{2}_{v,r}) \)-norm of any \( S^2_{v,r}- \)tensor \( \xi \) as
Proposition 9.3
Let \( (\varvec{q^{F}}, \varvec{p}) \) and \( (\underline{\varvec{q}}^{F}, \underline{\varvec{p}}) \) be a solutions to the coupled system (29), then for generic initial data, we have
Also, the following decay, non-decay and blow-up results hold asymptotically along the event horizon \( {\mathcal {H}}^+\)
-
Decay:
 (244)
(244) (245)
(245) -
Non-Decay:
 (246)
(246) (247)
(247) -
Blow-up:
 (248)
(248) (249)
(249)
where \( {\mathcal {H}}_{\ell =2}[\Psi _2] :=\left\Vert H_{2}[\Psi _2]\right\Vert _{S^{2}_{\tau ,M}}, \ \forall \ \tau \ge 1, \) and \( a_{2,k}^{^{(2)}} \) is given in Theorem 9.3. The same estimates hold for \( (\underline{\varvec{q}}^{F}, \underline{\varvec{p}}). \)
Proof
We recall the definitions  and
and  . Let us motivate the idea of showing decay by working with \( \varvec{q^{F}}\) only, and let \( k\le 1 \), then using the elliptic identity (12) and relation (241) we write
. Let us motivate the idea of showing decay by working with \( \varvec{q^{F}}\) only, and let \( k\le 1 \), then using the elliptic identity (12) and relation (241) we write

However, in view of the decay estimates of Corollary 9.1 we obtain

for a constant C that depends only on \( M, {\check{\Sigma }}_{0} \).
Now, fix \( k\ge 2 \) and working with equation (250) we have that for any \( \ell > k \) the corresponding term decays in view of Corollary 9.1, i.e.
for a positive constant depending on \( k, M, {\check{\Sigma }}_0. \) On the other hand, for the remaining \( k-1 \) first terms of the sum we see from Corollary 9.1 that the \( \ell =2 \) term is the dominant one and we write
for
Note for \( k=2 \), we simply obtain a non-decaying term while the others decay in the expression above. We work similarly to obtain the decay, non-decay, and blow-up estimates of \( \varvec{p}. \) \(\square \)
10 The positive spin Teukolsky equations instability
With the results of the previous section in hand, we can now show estimates for the Teukolsky solutions in the exterior up to and including the event horizon \( {\mathcal {H}}^+. \) In particular, in this section we are interested in the positive spin gauge invariant quantities \( \alpha , \mathfrak {f}, {\tilde{\beta }} \) which satisfy the relating equation

Note that \( \rho \) and \({}^{(F)} \rho \) are regular quantities on the horizon \( {\mathcal {H}}^+\), while \(\alpha , \ {\tilde{\beta }}, \ \mathfrak {f}, \ {\underline{\kappa }} \) are not. However, the rescaled quantities \(\alpha _{\star }= D^2 \cdot \alpha ,\ \mathfrak {f}_{\star } = D \cdot \mathfrak {f}, \ {\tilde{\beta }}_{\star } = D \cdot {\tilde{\beta }}, \ {\underline{\kappa }}_{\star } = D^{-1}{\underline{\kappa }} \) extend regularly on \( {\mathcal {H}}^+\). With respect to the ingoing Eddington–Finkelstein coordinates \(\left\{ v,r \right\} \), the quantities involved in the relating equation (251) are given in the ERN spacetime by
In addition, we recall the transformation identities relating \( \mathfrak {f},{\tilde{\beta }} \) to the Regge–Wheeler solutions \( \varvec{q}^{F}, \varvec{p} \) respectively

We first write the induced scalars we will be working with and after we obtain estimates for those, we pass them to the respected tensors using standard elliptic identities. Let

and after we project to the \( E_{\ell } \) eigenspace and using the commutation formulae (6), i.e.  , the relating equation (251) now reads
, the relating equation (251) now reads

Moreover, the transport equations (252) yield
10.1 Energy and decay estimates for \( \mathfrak {f}_{\star }, \ {\tilde{\beta }}_{\star }, \ \alpha _{\star } \) in the exterior
In this section, we use the transport equations to produce energy decay estimates that ultimately lead to pointwise control in the exterior up to and including the event horizon \( {\mathcal {H}}^+. \) First, we present the following lemma.
Lemma 10.1
Let f, F be two scalar functions satisfying
with respect to the double null coordinate system \( (u,v,\vartheta ,\varphi ) \) introduced in Sect. 2, then the following estimates hold near future null infinity
for any \( \tau _1<\tau _2 \) and \( k>0 \), where \( C>0 \) depends on M, k and R of Sect. 8.
Proof
Multiplying (256) with \( 2r^m\cdot f \) we obtain
To obtain the best possible decay in r we multiply the above relation with a factor of \( r^{q} \) which yields
Then, for \( \varepsilon = \frac{q+2}{2} >0 \) we obtain
Now, in view of \( div\left( \frac{\partial }{\partial _u}\right) = - \frac{\sqrt{D}}{r} \) we may rewrite the above estimate as
Thus, integrating in \( {\check{I}}_{\tau _1}^{\tau _2}\) and applying the divergence theorem readily yields
for a positive constant C depending on R. In particular, in view of \( q+2>0 \), we can consider \( q=k-2 \) for \( k > 0 \) and conclude the estimate. \(\square \)
It is clear that using the transport equation (256), we also control \( \partial _u f \) in terms of F and f. In addition, by taking a \(\partial _v-\)derivative of relation (256) we obtain
Thus, using Lemma 10.1 for \( \partial _vf \) with \( k+2 \) instead of k, and using Cauchy Schwartz yields
Finally, in view of  , we can obtain estimates for the angular derivatives of f in terms of F using (256) as
, we can obtain estimates for the angular derivatives of f in terms of F using (256) as
Using the above relations, we apply Lemma 10.1 twice to obtain

With the above results in mind, we proceed to producing local integrated energy estimates for \(h_{\mathfrak {f}},h_{{\tilde{\beta }}}\) and \(h_{\alpha }\). We break the analysis to three distinct regions which require different handling.
10.1.1 Energy estimates near null infinity \( {\check{I}}_{\tau _1}^{\tau _2}\)
Using Lemma 10.1 we obtain estimates for \( h_{\mathfrak {f}},\ {h_{{\tilde{\beta }}_{\ell }}}\) which satisfy (255), and with respect to the double null coordinate system they read
In order to obtain bounds with respect to initial data of \( \Psi _i^{^{(\ell )}} \), we will be working with the spherical harmonics decomposition of the scalars above. In particular, using the results of the previous paragraph we arrive at
Corollary 10.1
For any \(0<p<2\) and \(\tau _1<\tau _2\), there is a positive constant C depending on \({\check{\Sigma }}_{\tau _1}, M\) such that

and

Proof
By Lemma 10.1 and the calculations below it we arrive at

and we conclude the estimate using Proposition 8.1. Similarly we show it for \(h_{{\tilde{\beta }}}\). \(\square \)
10.1.2 Energy estimates in the intermediate trapping region
For any \(\tau _1<\tau _2\), let us denote \({\mathcal {D}}(\tau _1,\tau _2):=R(\tau _1,\tau _2)\cap \left\{ r_c\le r\le R \right\} ,\) for \( r_c\in (M,2M) \) and \( R>2M \). To obtain local integrated energy estimates in \({\mathcal {D}}(\tau _1,\tau _2)\) we no longer need to pay attention in the weights in r, however, we do have to mind for the trapping manifesting at the photon sphere \(\left\{ r=2M \right\} \) for the Morawetz estimates. Our goal is to produce estimates without loss of derivatives, at the level of initial data, whenever is possible.
Denote \(f : = r^{2}h_{\mathfrak {f}}\) and \(b:= r^{4}h_{{\tilde{\beta }}}\), then, in Boyer—Lindquist coordinates \((t,r^{\star },\theta ,\phi )\), the projection of (255) on a fixed spherical harmonic is
Using Lemma 10.1 and the Morawetz estimate of Theorem 4.1 for \(\Psi _i\), we obtain
while commuting relation (265) with \(\partial _{r^{\star }}\) and repeating the lemma for \(\partial _{r^{\star }}f_{\ell }\) yields
Similarly, the above estimates are shown for \(h_{{\tilde{\beta }}_{\ell }}\). Note, there is no loss of derivative here since the Morawetz estimates are not degenerate with respect to \(\partial _{r^{\star }}\), whereas there is trapping for the angular and the \(\partial _t\) derivative.
Moving on, to control the \(\partial _t-\)derivative we simply use relation (265) to write
and by Cauchy–Schwarz we obtain
Controlling the angular terms. To control the angular derivatives of f and b we use the Teukolsky equations they satisfy and we isolate the elliptic operator within. In particular, Corollary A.2 in [32] states

where  and \(\psi _3 = r^{2}{\underline{\kappa }}\cdot \mathfrak {f}.\) In addition, using relation (237) of [32], and Corollary A.2. of [28], we obtain the following equation for the laplacian of \(\psi _5:= r^{4}{\underline{\kappa }}{\tilde{\beta }}\)
and \(\psi _3 = r^{2}{\underline{\kappa }}\cdot \mathfrak {f}.\) In addition, using relation (237) of [32], and Corollary A.2. of [28], we obtain the following equation for the laplacian of \(\psi _5:= r^{4}{\underline{\kappa }}{\tilde{\beta }}\)

By relation (128) of [28]

we now write (270) in the form of

In order to control the angular derivative of \(f_{\ell }\) in the trapping region we use both relations (269) and (271). However, first we need estimates for the angular derivative of \(b_{\ell }\) which is already controlled as a consequence of the Lemma below.
Lemma 10.2
The induced scalar  satisfies the following local integrated estimates for any \(\tau _1<\tau _2\)
satisfies the following local integrated estimates for any \(\tau _1<\tau _2\)

for a constant \(C=C(M,{\check{\Sigma }}_{\tau _1})\).
Proof
We recall the transformation in Corollary 3.1 relating \(\psi _{\ell }\) to the decoupled quantities \(\Psi _i^{^{(\ell )}}\)
Applying Cauchy-Schwarz and divergence theorem on the sphere we have

where \(\mu ^{2} = (\ell +2)(\ell -1).\) Thus, integrating with respect to t and \(r^{\star }\) and using Morawetz estimates we obtain the estimate of the assumption. \(\square \)
Corollary 10.2
The following local integrated estimates hold for \(b_{\ell }\) satisfying (265)

Proof
We simply commute transport equation (265) with the angular derivatives and we apply Lemma 10.1 and 10.2. \(\square \)
The  term. We begin by deriving the elliptic equations for the scalars \(f_{\ell }\) and \(b_{\ell }\) using their corresponding tensorial equations (269),(271). First, to obtain the related scalar equation for (269) we also need the relating equation (251)
term. We begin by deriving the elliptic equations for the scalars \(f_{\ell }\) and \(b_{\ell }\) using their corresponding tensorial equations (269),(271). First, to obtain the related scalar equation for (269) we also need the relating equation (251)

Then, applying the operator  to (269) and using standard elliptic identities, we obtain
to (269) and using standard elliptic identities, we obtain

Quite similarly, we work with equation (271) and we obtain

for some functions of coordinate r alone, \(B_i(r)\), \(i\in \left\{ 0,3 \right\} \). The purpose of the later equation is not to control  , which was already controlled earlier, but to express \(h_{\alpha }\) of (275) in terms of controllable terms. Specifically, using the equation above, we substitute \(h_{\alpha }\) in (275) to obtain
, which was already controlled earlier, but to express \(h_{\alpha }\) of (275) in terms of controllable terms. Specifically, using the equation above, we substitute \(h_{\alpha }\) in (275) to obtain

where \({\mathcal {L}}[*,... ,*]\) is a linear expression of its arguments with coefficients functions of r alone.
We are ready to control the angular derivative of \(f_{\ell }\) in the trapping region without any loss of derivatives. Note that in \((t,r_{\star })\)-coordinates, \(e_{4^{ \star }} = \partial _t + \partial _{r^{\star }}\), and \(\partial _t\phi _{\ell }\), \(\partial _t{\psi }\) are trapped in that region. Hence, after we multiplying (277) with \(f_{\ell }\), we differentiate by parts to transfer the \(\partial _{t}\)-derivative to \(f_{\ell }\) which we already control. Specifically,

An application of the divergence theorem for the current \(P_{\mu } = \frac{1}{r}\big (\phi _{\ell }\cdot f_{\ell }+F_{0}(r)\psi _{\ell }\cdot f_{\ell }\big ) \cdot (\partial _t)_{\mu }\), in the \({\mathcal {D}}(\tau _1,\tau _2)\) region yields
Thus, using equation (278), the above relation yields

Note, there are no timelike boundary terms since \(\partial _t \cdot (\nabla r) =0\). Hence, using Cauchy–Schwarz, divergence theorem on the sphere, and the local integrated estimates obtained earlier we arrive at

for any \(\epsilon >0\) and \(C=C(M,{\check{\Sigma }}_{\tau _1})\). Integrating also equation (278) along \({\check{\Sigma }}_{\tau _2}\) and choosing \(\epsilon >0\) small enough yields

Remark 10.1
Observe that all estimates in the trapping region above have a timelike boundary term on the right hand side, i.e. \({\mathcal {D}}\cap \left\{ r=R \right\} \). These terms will be controlled by the right hand side of Corollary 10.1 when we combine all estimates together, see Proposition 10.1.
10.1.3 Energy estimates near and including the event horizon \( {\mathcal {H}}^+\)
In this paragraph, we use the \( (v,r,\vartheta ,\varphi ) \) coordinate system which is regular on the horizon \({\mathcal {H}}^+. \) Using the transport equations (255) we obtain the corresponding Lemma 10.1, where all scalars involved are regular on the horizon \( {\mathcal {H}}^+. \) Simply by repeating the ideas above we obtain the following estimates in the region \( {\mathcal {A}}_c := {\mathcal {R}}(0,\tau ) \cap \left\{ M\le r\le r_c \right\} \)

Then, using Proposition 4.4 and Theorem 4.3 we obtain

Combining all estimates above. Now, in order to write all the above estimates more concisely we introduce the following energy quantities. For any scalar h regular up to and including the horizon \( {\mathcal {H}}^+\), we consider



where in each region we use the associated coordinate system as done earlier. In addition, we also denote by
Proposition 10.1
Let \( \mathfrak {f}, {\tilde{\beta }} \) be solutions to the Teukolsky system and consider the induced scalars  ,
,  then
then
where \( {\tilde{E}}^{3-\delta }[h_{\mathfrak {f}_{\ell }}](0)\) is the right-hand side of (289) at \( {\check{\Sigma }}_{0}. \) Similarly, we have
Proof
Let \( 0<\delta \ll 1 \), then using Corollary 10.1 for \( p=1-\delta \), relation (280), the estimates of Subsection 10.1.2, and coarea formula, we obtain for any \(\tau _1<\tau _2\)
Let us denote by \( {\tilde{E}}^{2-\delta }[h_{\mathfrak {f}_{\ell }}](\tau ) \) the right-hand side of the above relation with \( \tau \) instead \( \tau _1. \) Then, we also need an estimate for
However, applying the same steps as above along with the estimates of Proposition 8.1 for \( p=2-\delta \), and using (200) we obtain
Therefore, repeating the argument of a dyadic sequence of Proposition 8.3 we show decay for the energy fluxes of the assumption. \(\square \)
Remark 10.2
Note, we had to give some \( \delta >0 \) “space" when obtaining estimates for \( E^{1-\delta }[h_{\mathfrak {f}_{\ell }}]\) and \( E^{5-\delta }[h_{{\tilde{\beta }}_{\ell }}] \). That is because if we take \( p=2 \), instead of \( p=2-\delta \), in the proof of Corollary 10.1, then we cannot control the right-hand side \( \phi _{\ell },\psi _{\ell } \) terms using Proposition 8.1.
To obtain local integrated energy estimates for \(h_{\alpha }\) we repeat the ideas of this section for the relation equation (254). In particular, we substitute (276) to the relating equation and we obtain
Finally, we repeat the \( L^2({\mathbb {S}}^{2}) \) estimates of Section 9 for the scalars \( \left( r^{\frac{4-\delta }{2}}h_{\mathfrak {f}}\right) , \left( r^{\frac{8-\delta }{2}}h_{{\tilde{\beta }}}\right) , \left( r^{\frac{3-\delta }{2}}h_{\alpha }\right) \), and we commute with the angular momentum operators to obtain the pointwise estimates below by using Sobolev inequalities.
Corollary 10.3
For any \( 0<\delta \ll 1 \), there exists \( C>0 \) depending on \( M, {\check{\Sigma }}_0, \delta \) and norms of initial data such that
for all \( r\ge M, \ \tau \ge 1,\) and all admissible frequencies \( \ell \in {\mathbb {N}}. \) Using standard elliptic identities of Section 2, and Sobolev inequalities we obtain the following pointwise estimates
for all \( r\ge M \) and \( v>0. \)
10.2 Decay, Non-decay and Blow-up for \(\mathfrak {f}_{\star }, {\tilde{\beta }}_{\star }\), and \( \alpha _{\star }\) along the horizon \({\mathcal {H}}^+\)
We derive estimates for both \( \mathfrak {f}_{\star }, {\tilde{\beta }}_{\star } \) and their transversal derivatives along the event horizon \( {\mathcal {H}}^+. \) In addition, using the relating equation (254) we also prove estimates for the extreme curvature component \( \alpha \) along \({\mathcal {H}}^+. \)
Theorem 10.1
Let \( \mathfrak {f}_{\star }, {\tilde{\beta }}_{\star } \) be solutions to the generalized Teukolsky equations of positive spin, then for generic initial data the following estimates hold asymptotically along \( {\mathcal {H}}^+\) for all \( \tau \ge 1 \)
-
Decay

-
Non-decay

-
Blow-up

where \( {\mathcal {H}}_{\ell =2}[\Psi _2] :=\left\Vert H_{2}[\Psi _2]\right\Vert _{S^{2}_{\tau ,M}}, \ \forall \ \tau \ge 1, \) and \( a_{2,k}^{^{(2)}} \) is given in Theorem 9.3.
Proof
Using the decay estimates we have acquired for \( h_{\mathfrak {f}} \), we produce estimates for \( \partial _r^k(h_{\mathfrak {f}}) \). Going back to (255), we can write it as
By induction, it is immediate to check for all \( k\in {\mathbb {N}} \)
where \( \mathfrak {D}^{k}(\phi ) \) is an expression involving \( \partial _r- \)derivatives of \( \phi \) of order less than k and \( A_k(r) \) is a function of r alone, for any k. Thus, Corollary 9.1 and relation (290) yield the following decay estimates asymptotically on \( {\mathcal {H}}^+\)
for any \( \ell \ge 2. \) In addition, we deduce the following estimates for higher order derivatives along \( {\mathcal {H}}^+\)
Now, using the elliptic identity (12) and relation (241) we write

In view of \( h_{\mathfrak {f}_{\ell =2}} \) having the dominant behavior along \( {\mathcal {H}}^+, \) we obtain the decay results for \( k\le 2 \), and for \( k>3 \) we see that the infinite sum for \( \ell \ge k \) decays uniformly in \( \ell \) while the first remaining terms of the sum inherit the dominant asymptotic of \( \partial _r^{k}h_{\mathfrak {f}_{\ell =2}}. \)
To produce the estimates of the assumption for \( {\tilde{\beta }}_{\star } \), we work similarly as above, however, we use the elliptic identity (11) instead. \(\square \)
We conclude the study of the positive spin gauge invariant components by proving estimates for the extreme curvature tensor \( \alpha _{\star } \), using the estimates obtained for \( \mathfrak {f}_{\star } \) and \( {\tilde{\beta }}_{\star }. \)
Theorem 10.2
Let \( \alpha _{\star }\) be a solution to the generalized Teukolsky equation of \( +2 \) spin, then for generic initial data the following estimates hold asymptotically along \( {\mathcal {H}}^+\) for all \( \tau \ge 1 \)

where \( {\mathcal {H}}_{\ell }[\Psi _2] :=\left\Vert H_{\ell }[\Psi _2]\right\Vert _{S^{2}_{\tau ,M}}, \ \forall \ \tau \ge 1, \) and the constant \( c_k \) are given by
Proof
Once again, we work with the rescaled quantities \(f : = r^{2}h_{\mathfrak {f}}\) and \(b:= r^{4}h_{{\tilde{\beta }}}\), then, we rewrite the relating equation (254) as
By taking k many \( \partial _r-\)derivatives of the above relation and by writing explicitly the first two top order terms only, we obtain the following expression
where \( {\mathcal {D}}^{\le s}[\ \cdot \ ] \) is a linear expression involving up to \( s-\)many \( \partial _r-\)derivatives of its arguments. However, in view of the transport equations that f, b satisfy, i.e.
relation (297) reads
where \( A_i(r),\ i\in \left\{ 1,2,3 \right\} \) are scalar functions of r alone.
In view of the estimates obtained for \( \Psi _i^{^{(\ell )}}, \ i \in \left\{ 1,2 \right\} \) in Section 9, it suffices to study the low frequencies \( h_{\alpha _{\ell }} \), \( \ell = 2,3 \), which give the dominant behavior of \( \alpha _{\star } \) along the event horizon \( {\mathcal {H}}^+. \) Using the estimates of Corollary 9.1 and relation (298), we obtain the following decay estimates
and in particular, for \( \ell =2 \) we have
Next, the first non-decay estimate occurs at the level of five transversal invariant derivatives for both the \( \ell =2, \ \ell =3 \) frequencies. For the \( \ell =2\) frequency, relation (298) yields along the event horizon \( {\mathcal {H}}^+\)
However, \(( M\psi _{\ell =2} + \phi _{\ell =2} )\) is a scalar multiple of \( \Psi _1^{^{(\ell =2)}} \) and thus the dominant term in the expression above is \( \frac{8k}{M^5} \partial _r^{k-2} \phi _{_{\ell =2}}.\) Hence, for \( k=4 \) we obtain
Similarly, for \( \ell =3 \) and \( k=4 \) relation (298) yields
For the blow-up estimates, we can see from the non-decaying results above that both frequencies \( \ell =2\) and \(\ell =3 \) ought to contribute to the leading term of the asymptotics. In particular, for \( \ell =2 \) we have established above that
Thus, using Theorem 9.3 we obtain the following asymptotic along \( {\mathcal {H}}^+\)
On the other hand, we consider relation (298) for \( \ell =3 \) and we obtain quite similarly as above
Now, we pass the above estimates for the scalar \( h_{\alpha } \) to the corresponding tensor \( \alpha _{\star } \) using the elliptic identity below

For \( k\le 4 \), we use the decay estimates (299-301) and the equation above to obtain \( L^2- \)decay for  . The \( L^{\infty }(S^{2}_{\tau ,M}) \) estimate comes from commuting with the angular momentum operators and using the Sobolev inequality on the sphere.
. The \( L^{\infty }(S^{2}_{\tau ,M}) \) estimate comes from commuting with the angular momentum operators and using the Sobolev inequality on the sphere.
Now let \( k \ge 5 \), then note that the tail of the sum (306) decays uniformly in \( \ell \) for frequencies \( \ell \ge k-1 \) and we only have to deal with the first \( k-2 \) terms of the sum. However, the dominant behavior comes from the frequencies \( \ell =2 \) and \( \ell =3 \) along \( {\mathcal {H}}^+\) and thus we obtain

Thus, by changing the parameter k we can write the above estimate as

where
\(\square \)
Remark 10.3
As opposed to the gauge invariant quantities \( \mathfrak {f}_{\star },{\tilde{\beta }}_{\star } \), which their behavior is dominated by their \( \ell =2 \) frequency asymptotically along \( {\mathcal {H}}^+\), the extreme curvature component \( \alpha _{\star } \) is dominated by both \( \ell =2 \) and \( \ell =3 \) frequencies.
11 The negative spin Teukolsky equations instability
We show that solutions to the negative spin Teukolsky system exhibit an even more unstable behavior compared to the positive spin case. In particular, the \( L^2(S^{2}_{v,M})- \)norm of the extreme curvature component \( {\underline{\alpha }}_{\star } \) does not decay asymptotically along the even horizon \( {\mathcal {H}}^+. \) In other words, no transversal derivative of the aforementioned quantity is required for the instability to manifest.
First, we obtain decay estimates outside the event horizon \( {\mathcal {H}}^+\) using the transport equations, and then, we derive decay, non-decay, and blow-up estimates asymptotically along \( {\mathcal {H}}^+. \) As opposed to the positive spin case, where we obtained estimates using only the Regge–Wheeler system and their transport equations, for the corresponding negative spin quantities we need to use the coupled Teukolsky system they satisfy in order to close the estimates.
11.1 The negative spin components
We are interested in obtaining estimates for the gauge invariant quantities \( {\underline{\alpha }}_{\star }, \underline{\mathfrak {f}}_{\star } \) and \( {\underline{\beta }}_{\star } \) in the exterior up to and including the event horizon \( {\mathcal {H}}^+\), which satisfy the following relations with respect to the Regge–Wheeler solutions

They also satisfy the following relating equation, which we use later on to obtain estimates for \( {\underline{\alpha }}_{\star } \)

Here, all quantities with star subscript are expressed in the rescaled frame \( {\mathcal {N}}_{\star } \), and we recall that
Once again, it will be more convenient to work with the corresponding scalar quantities derived by the tensors above. In particular, we introduce the following notations

Using standard elliptic identities from Section 2, (307) yields the following equations for the above scalars
while the relating equation (308) yields for the scalar \( h_{{\underline{\alpha }}}\), after we project to the \( E_{\ell }\) eigenspace,
One final rescaling of the above scalars allows us to write all equations to follow more concisely and perform computations more easily. In particular, let
then we may write (311) as
Moreover, the relating equation (312) now reads
11.2 Negative spin Teukolsky system
We write the Teukolsky equations of Section 3.3 with the coefficients expanded in the \( {\mathcal {N}}_{\star } \) frame and we obtain

where \( {\mathcal {A}}[\underline{{\tilde{\beta }}}, {\underline{\alpha }}] \) is an expression depending on  and up to one \( e_{3^{\star }} \)–derivative of \( \underline{{\tilde{\beta }}}_{\star } \); see p. 41, [28], pp. 133-134 [29]. Using elliptic identities from Section 2, we obtain the corresponding Teukolsky system for the scalar rescaled quantities \( {\underline{a}}, {\underline{f}} \) and \( {\underline{b}}, \) as defined in (313), when supported on the fixed frequency \( \ell \). With respect to the ingoing Finkelstein-Eddington coordinates the system reads
and up to one \( e_{3^{\star }} \)–derivative of \( \underline{{\tilde{\beta }}}_{\star } \); see p. 41, [28], pp. 133-134 [29]. Using elliptic identities from Section 2, we obtain the corresponding Teukolsky system for the scalar rescaled quantities \( {\underline{a}}, {\underline{f}} \) and \( {\underline{b}}, \) as defined in (313), when supported on the fixed frequency \( \ell \). With respect to the ingoing Finkelstein-Eddington coordinates the system reads
Using the relating equation (315) we can rewrite the Teukolsky equation for \( {\underline{f}} \) so that it is coupled only with \( {\underline{b}} \) modulo a term with a factor of D(r) in it, i.e.
11.3 Decay for \(\underline{\mathfrak {f}}_{\star }, \underline{{\tilde{\beta }}}_{\star }\) and \( {\underline{\alpha }}_{\star } \) away from the horizon \( {\mathcal {H}}^+. \)
We repeat the ideas of Section 10.1 for the transport equations (307) and the relating equation (308). This time we omit most of the details involved as the procedure is identical to that of Section 10.1, however, we examine more carefully the two main differences that manifest when controlling the negative spin quantities. First, we prove the following lemma.
Lemma 11.1
Let f, F be two scalar functions satisfying
then the following energy estimates hold near future null infinity \( {\check{I}}_{\tau _1}^{\tau _2}\)
for a constant \( C>0 \) depending on M, k and R of Section 8.
Proof
We multiply relation (319) with \( r^{m}\kappa _{\star }^{n} f\) and we obtain
Now, dividing by \( r^{q} \) for \( q>0 \) we have
However, \( div (e_{4^{\star }}) =\frac{2\sqrt{D}}{r} \), and note \( e_{4^{\star }}= 2\partial _v + D\partial _r \), in ingoing coordinates, thus we write
Let \( q = k + 2 \), for \( k>0 \), and pick \( \epsilon = \frac{k}{4} \), then obtain
Note \( \kappa _{\star } = \frac{2D}{r} \), and thus there exists R large enough such that
for a constant \( C>0 \) depending on k, M and R. We apply the divergence theorem on the \( {\check{I}}_{\tau _1}^{\tau _2}\) region to conclude the proof. Note, the null vector \( e_{4^{\star }} \) is normal to the boundary null hypersurfaces \( {\check{O}}_{\tau } \), and thus no such terms appear in the estimate. \(\square \)
Estimates near future null infinity \( {\check{I}}_{\tau _1}^{\tau _2}. \) Already, comparing the above lemma to the corresponding Lemma 10.1 of Section 10, we see that k appears with the opposite sign. This leads to weaker decay rates in r for the negative spin Teukolsky solutions. In particular, the transport equations (307) yield for the corresponding scalars
We see that for \( h_{\underline{\mathfrak {f}}} \) we have \( m=3, n=1, \) and thus, applying the above lemma for \( k=\delta \), where \( 0<\delta \ll 1, \) we obtain
The second term of the right-hand side above is controlled in Proposition 8.2 for any \( \delta >0 \), while the timelike boundary term is treated by applying the divergence theorem in the region \( {\mathcal {D}}(\tau _1,\tau _2):={\mathcal {R}}(\tau _1,\tau _2) \cap \left\{ r_c \le r\le R \right\} . \) Using also the transport equations for \( h_{\underline{{\tilde{\beta }}}}, \) \( h_{{\underline{\alpha }}} \), and coarea formula we obtain
The remaining first-order derivatives are controlled similarly as in Section 10.1, and so do we obtain estimates in the intermediate region \( {\mathcal {D}}(\tau _1,\tau _2). \) In the following paragraph, we examine a degeneracy that manifests close to the event horizon \( {\mathcal {H}}^+\).
Estimates near the event horizon \( {\mathcal {H}}^+. \) The main issue we are faced with near the horizon can be already seen in the proof of Lemma 11.1, where the estimates degenerate on \( {\mathcal {H}}^+. \) This is due to the occurrence of stronger trapping on \( {\mathcal {H}}^+\) for the negative spin Teukolsky solutions, which also leads to a stronger instability as we will see in the coming Section 11.4. Nevertheless, we show how to obtain pointwise estimates in the exterior which degenerate, however, on the horizon. In this paragraph, we will be working with the transport equations (314). Fix \( M<r_c<2M \) and let \( {\mathcal {A}}_c := {\mathcal {R}}(\tau _1,\tau _2) \cap \left\{ M\le r\le r_c \right\} \), then we have the following lemma.
Lemma 11.2
Let f, F be two scalar functions satisfying
with respect to the ingoing coordinates \( (v,r,\theta ,\phi ), \) then for any \( a\in \left[ \frac{1}{2},1\right) \) and \( \tau _1\le \tau _2 \), we have
for a constant \( C>0 \) depending on \( M, r_c, a \) and \( \Sigma _{\tau _1}. \)
Proof
Let \(a\in \left[ \frac{1}{2},1\right) \), then we multiply relation (324) with \( D^{a} \cdot f\) and we obtain
Now, using the fact that \( div(\partial _v) =0 \) and \( div(\partial _r) = \frac{2}{r} \), we obtain
By simplifying the above expression and applying Cauchy-Schwarz on the right-hand side, we get
Thus, choosing \( \epsilon = \frac{a}{3}>0 \) and \( r_c \) close enough to \( r=M \), we apply the divergence theorem in \( {\mathcal {A}}_{c} \) and we find a positive constant C depending on \( M, r_c, a \) such that the estimate of the assumption holds. \(\square \)
Remark 11.1
Note, \( a=\frac{1}{2} \) is the smallest value for which the above lemma holds, for if we take \( a<\frac{1}{2} \), then \( D^{2a} > D^{\frac{1}{2}+a} \) near \( {\mathcal {H}}^+\) and the term we obtain after applying Cauchy-Schwarz in the last line cannot be absorbed in left-hand side one.
With the help of the second Hardy inequality (Lemma 5.2) we show a slightly stronger estimate which allows us to obtain better pointwise decay for the negative spin Teukolsky solutions in the exterior.
Lemma 11.3
Let f, F be as in the assumptions of Lemma 11.2, then there exists \( \delta _0>0 \) such that for any \( 0<\delta \le \delta _0 \) the following estimate hold
for a positive constant C depending on \( M,r_c,r_d, \delta _0, \) and \( \Sigma _{\tau _1}. \)
Proof
Let \( \delta >0 \) to be determined in the end, then repeating the steps of the previous lemma for \( a=\frac{1}{2}-\delta \) we arrive at
Now, choosing \( \epsilon >0 \) small enough we can absorb the first term of the right-hand side in the left one. However, we still need to treat the second term of the right-hand side. For that, we apply the second Hardy inequality for the regions \( {\mathcal {A}}_c \), \( {\mathcal {D}}(\tau _1,\tau _2) \) and we obtain
where the constant \( {\tilde{C}} \) depends only on \( M,r_c,r_d=R \) and \( \Sigma _0 \). However, we have
Thus going back to (327) we obtain
Thus, there exists a small enough \( \delta _0>0 \) such that \( \left( 1-{\tilde{C}}\left( \delta /2\right) ^{2}\right) \) is uniformly positive definite for any \( 0<\delta \le \delta _0 \). Hence, for any \( 0<\delta \le \delta _0 \), applying the divergence theorem for the relation at the beginning concludes the proof. \(\square \)
In view of the transport equations (314) for \( {\underline{f}} \) and \( {\underline{b}} \), we apply Lemma 11.2 for \( a=1-\delta \), \( 0<\delta \ll 1 \), and using coarea formula we obtain
Next, we apply Lemma 11.3, coarea formula, and Theorem 4.2 to get
Using the transport equations (314) and commuting them with the Killing vector field T and the angular derivatives we derive estimates for the first-order derivatives of \( {\underline{f}},{\underline{b}}. \) With these local integrated energy estimates in hand, we use the above lemmas (slightly modified) for the transport equation (315) to show energy estimates for \( {\underline{a}} \) as well. Using as ingredients the energy estimates in each respected region above and applying the dyadic sequence argument we show quadratic decay for the energy of \( h_{\underline{\mathfrak {f}}}, h_{\underline{{\tilde{\beta }}}} \) and \( h_{{\underline{\alpha }}}. \)
Corollary 11.1
Let \( 0<\delta \ll 1 \), then there exists \( C>0 \) depending on \( M, {\check{\Sigma }}_0, \delta \) and norms of initial data such that
for all \( r> M, \ \tau \ge 1,\) and all admissible frequencies \( \ell \in {\mathbb {N}}. \) In addition, fix \( r_0> M \), then using standard elliptic identities of Section 2, and Sobolev inequalities we obtain the following pointwise decay estimates away from the horizon \( {\mathcal {H}}^+\)
for all \( r\ge r_0\) and \( v>0. \)
11.4 Estimates for \(\underline{\mathfrak {f}}_{\star }, \underline{{\tilde{\beta }}}_{\star }\) and \( {\underline{\alpha }}_{\star } \) along the event horizon \( {\mathcal {H}}^+\)
First, we prove estimates for \( \underline{\mathfrak {f}}_{\star }, \tilde{{\underline{\beta }}}_{\star } \) along the event horizon \( {\mathcal {H}}^+. \) For that, we use the Teukolsky equations they satisfy and the transport equations relating them to the Regge–Wheeler solutions \( \underline{\varvec{q}}^{F}, \ \underline{\varvec{p}} \), for which we have already obtained estimates in the previous sections. In view of \( \underline{\varvec{q}}^{F}, \ \underline{\varvec{p}} \) satisfying the same equations as the positive spin equivalent, \( \varvec{q}^{F}, \varvec{p}\), the same estimates holds for the negative spin scalar quantities \( {\underline{\phi }} , {\underline{\psi }}\) as in Section 9. As far as the tensor \( {\underline{\alpha }}_{\star } \) is concerned, we obtain estimates by using the induced relating equation (315) in addition to the above.
In order to understand the dominant behavior of Teukolsky solutions of negative spin asymptotically along the event horizon \( {\mathcal {H}}^+\), it suffices to only study the quantities \( {\underline{f}}_{\ell =2}, {\underline{b}}_{\ell =2}\) and \( {\underline{a}} _{\ell =2}\) supported on the fixed harmonic frequency \( \ell =2.\) For shortness, we will often neglect the “\( \ell =2 \)” subscript in the equations.
Theorem 11.1
Let \( \underline{\mathfrak {f}}_{\star }, \underline{{\tilde{\beta }}}_{\star } \) be solutions to the generalized Teukolsky equations of negative spin, then for generic initial data the following estimates hold asymptotically along \( {\mathcal {H}}^+\), for all \( \tau \ge 1 \)
-
Decay
$$\begin{aligned} \left\Vert \underline{\mathfrak {f}}_{\star }\right\Vert _{L^{\infty }(S^{2}_{\tau ,M})}&\lesssim _{_{M}} \tau ^{-\frac{1}{4}}, \\ \left\Vert \underline{{\tilde{\beta }}}_{\star }\right\Vert _{L^{\infty }(S^{2}_{\tau ,M})}&\lesssim _{_{M}} \tau ^{-\frac{1}{4}} \end{aligned}$$ -
Non-Decay and Blow up

for all \( k\ge 0, \) where \( {\mathcal {H}}_{2}[{\underline{\Psi }}_2] :=\left\Vert H_{\ell =2}[{\underline{\Psi }}_2]\right\Vert _{S^{2}_{\tau ,M}}\), \( \forall \ \tau \ge 1 \), and the coefficients \( f_k,b_k \) are given by
Proof
We begin by studying the induced scalars \( {\underline{f}} _{\ell =2} \) and \( {\underline{b}}_{\ell =2} \). First, we show the decay estimates. We evaluate the Teukolsky equation for \( {\underline{f}} \) on the horizon \( {\mathcal {H}}^+\) and we obtain
On the other hand, differentiating the transport equation for \( {\underline{f}} \) and evaluating it on \( {\mathcal {H}}^+\) yields
Combining the equations above and the transport equation for \( {\underline{f}} \) produces
Following the same procedure for the Teukolsky and transport equations satisfied by \( {\underline{b}} \), we obtain
Thus, solving the system (333,334) yields the expressions
and using Corollary 9.1 we obtain the decay rates of \( {\underline{f}}, {\underline{b}} \) along the event horizon \( {\mathcal {H}}^+. \)
To show the non-decay estimates we consider a \( \partial _r\)-derivative of the Teukolsky system and we consider sufficiently many \( \partial _r-\)derivatives of the transport equations to express all components in terms of \( {\underline{f}}, {\underline{b}}, {\underline{\phi }} \) and \( {\underline{\psi }}. \) In particular, the equation for \( {\underline{f}} \) yields
Using the same approach for the equations of \( {\underline{b}} \) we obtain
Note that the coefficients of \( \partial _r{\underline{f}}, \partial _r{\underline{b}} \) terms in the equations above are the same with the top order ones in (333,334). Solving the system once again yields
Consider the decomposition of \( {\underline{\phi }}, {\underline{\psi }} \) in terms of \( \Psi _1^{^{(\ell =2)}}, \Psi _2^{^{(\ell =2)}} \)
then, using the conservation laws of Theorem 6.1 and the decay estimates of Theorem 9.2 for the expressions in (337) we obtain
and thus concluding the non-decay estimates of the proposition.
Finally, to obtain the blow-up estimates we use induction on the number of derivatives. Note that the \( k=0 \) case corresponds to the non-decay estimates shown above. Assume the expression of the assumption holds for all \( s\le k \), \( k\ge 1, \) then we consider \( \partial _r^{k+1}-\)derivatives of the Teukolsky system and we use the same procedure as above. In particular, for the equations of \( {\underline{f}} \) we obtain
where \( {\mathcal {L}}[{\underline{f}}^{^{\le k}},{\underline{b}}^{^{\le k}}, {\underline{a}}^{^{\le k-2}}]\) is an expression involving \( \partial _r-\) derivatives of the underline quantities up to the order of their respective superscript. Differentiating the transport equation for \( {\underline{f}} \) as well we obtain
and thus the previous equation yields
Note that the term of \( \partial _r^{k-1} {\underline{a}}\) in (338) was absorbed in the \( {\mathcal {L}}[{\underline{f}}^{^{\le k}},{\underline{b}}^{^{\le k}}] \) term. We can do this by taking \( \partial _r^{k-1}- \) derivatives of the Teukolsky equation for \( {\underline{a}} \) and using the relating equation (315) we express \( \partial _r^{k-1} {\underline{a}} \) in terms of lower derivatives of itself and derivatives up to order k of both \( {\underline{f}},{\underline{b}}. \) By consecutively repeating the same procedure for the remaining lower order derivative of \( {\underline{a}} \) we eventually write it only in terms of derivatives of \( {\underline{f}},{\underline{b}}. \)
We repeat these steps for the equations of \( {\underline{b}} \) and we obtain
Once again, after solving the system formed by (339,340), using the induction assumption for all derivatives up to order k and using Theorem 9.3, we obtain
asymptotically along the event horizon \( {\mathcal {H}}^+, \) for any \( k\ge 1. \)
One can proceed similarly to show estimates for \(\underline{\mathfrak {f}}_{\ell }\) and \( {\underline{b}}_{\ell } \), for all frequencies \( \ell \). Of course, the higher the frequency \( \ell \) the more \( \partial _r- \)derivatives we must take for the non-decay and blow estimates to manifest. Nevertheless, using standard elliptic identities and the results of the dominant frequency projection \( \ell =2 \) we conclude the estimates of the assumption. \(\square \)
11.5 Non-decay and blow up estimates for \( {\underline{\alpha }}_{\star } \) on \( {\mathcal {H}}^+. \)
Now that we understand the behavior of \( {\underline{f}}, {\underline{b}} \) asymptotically along the event horizon \( {\mathcal {H}}^+\), we can prove estimates for the rescaled scalar extreme curvature component \( {\underline{a}} \) of spin -2. In particular, we see that it does not decay along the event horizon, and any transversal invariant derivative we consider leads to blow-up asymptotically on \( {\mathcal {H}}^+. \) Then, estimates for \( {\underline{\alpha }}_{\star } \) follow by standard elliptic identities.
Theorem 11.2
Let \( {\underline{\alpha }}_{\star } \) be solutions to the generalized Teukolsky equation of -2–spin, then for generic initial data the following estimates hold asymptotically along \( {\mathcal {H}}^+\), for all \( \tau \ge 1 \)
-
Non-decay
$$\begin{aligned} \left\Vert {\underline{\alpha }}_{\star }\right\Vert _{S^{2}_{\tau ,M}}&=\ \dfrac{1}{\sqrt{12}M^{2}} \dfrac{1}{30}\cdot {\mathcal {H}}_{2}[{\underline{\Psi }}_2] + {\mathcal {O}}\left( \tau ^{-\frac{1}{4}}\right) , \end{aligned}$$ -
Blow-up

where \({\mathcal {H}}_{2}[{\underline{\Psi }}_2] :=\left\Vert H_{\ell =2}[{\underline{\Psi }}_2]\right\Vert _{S^{2}_{\tau ,M}}, \ \forall \ \tau \ge 1\) and
Proof
First, we show the corresponding estimates for the induced scalar \( {\underline{a}} \) supported on the fixed frequency \( \ell =2. \) For the non-decay estimate, we begin by taking one \( \partial _r- \)derivative of the relating equation (315) and after we evaluate it on the horizon \( \left\{ r=M \right\} \) we obtain
On the other hand, we write down the Teukolsky equation for \( {\underline{a}} \) and evaluate it on the horizon \( {\mathcal {H}}^+\) to get
while evaluating the Teukolsky equation for \( {\underline{f}} \) on \( {\mathcal {H}}^+\), written as in (317), yields
Thus, plugging in the last two relations to (341) and using the transport equation for \( {\underline{f}} \) gives us
However, from Proposition 11.1 we have that the last four terms decay; taking the limit for the first two yields
In view of \( H_{2}[\Psi _2] \) being almost everywhere non-zero on \( S^{2}_{v,M} \) for generic initial data, we obtain the non-decay result of \( {\underline{a}}. \) To obtain the higher-order blow-up estimates we use induction on the number of derivatives. The base case \( k=0 \) corresponds to the non-decay results proved earlier. Assume the proposition holds for all \( s\le k-1 \), \( k\ge 1 \), then we consider k many \( \partial _r- \)derivatives of the Teukolsky equation for \( {\underline{a}} \) and evaluate it on the horizon \( {\mathcal {H}}^+\) to obtain
On the other hand, we may write the relating equation (315) as
and by taking \( k+1 \)-many derivatives of the above and evaluating on \( {\mathcal {H}}^+\) we obtain
Thus, plugging the above expression in (343) for all \( s\le k+1 \) yields
Now we can use the blow-up estimates of Proposition 11.1 and the inductive hypothesis to get
and in view of \( \frac{2}{3} b_k = c_k\) we conclude the estimates for \( {\underline{a}}. \) Finally, using standard elliptic identities we show the estimates of the assumption for the tensor \( {\underline{\alpha }}_{\star }. \) \(\square \)
Notes
Here, \( \left\Vert \xi \right\Vert _{\infty }(\tau ) := \left\Vert \xi \right\Vert _{L^{\infty }(S^{2}_{\tau ,M})}\), \( \left\Vert \xi \right\Vert _{S^{2}_{\tau ,M}} := \left\Vert \xi \right\Vert _{L^{2}(S^{2}_{\tau ,M}).} \), and \( f(\tau ) \sim _{_{p}} g(\tau )\) if \(\displaystyle \lim _{\tau \rightarrow \infty } \frac{f(\tau )}{g(\tau )} = c,\) with c depending on p. Also,
 refers to
refers to  , for all integers \(0\le k\le m.\)
, for all integers \(0\le k\le m.\)This is due to the appearance of a transversal invariant derivative of \( \underline{\mathfrak {f}} \) on the right-hand side of the Teukolsky equation satisfied by \( {\underline{\alpha }} \), which acts as a source and it does not decay along the horizon \( {\mathcal {H}}^+. \)
A null frame is one that satisfies: \( g(e_3,g_3)=g(e_4,e_4)=0, \hspace{0.2cm} g(e_3,e_4)=-2\ \) and

A detailed analysis on how to arrive at this G(r) first appeared in the thesis of J. Stogin [50]. The author arrives at the same function for the Morawetz estimates of the scalar wave equation on the Schwarzschild and subextremal Kerr background.
If \( f(x)\lesssim _{p} g(x) \) then there exists a constant \( C>0 \) depending on p, such that \( f(x) \le C \cdot g(x)\).
References
Angelopoulos, Yannis: Global spherically symmetric solutions of non-linear wave equations with null condition on extremal Reissner-Nordström spacetimes. International Mathematics Research Notices 2016(11), 3279–3355 (2016)
Angelopoulos, Yannis, Aretakis, Stefanos, Gajic, Dejan: “Asymptotic blow-up for a class of semilinear wave equations on extremal Reissner-Nordström spacetimes”. In: arXiv preprint arXiv:1612.01562 (2016)
Angelopoulos, Yannis, Aretakis, Stefanos, Gajic, Dejan: “The trapping effect on degenerate horizons”. Annales Henri Poincaré. Vol. 18(5). Springer, pp. 1593–1633, (2017)
Angelopoulos, Yannis, Aretakis, Stefanos, Gajic, Dejan: A non-degenerate scattering theory for the wave equation on extremal Reissner-Nordström. Communications in Mathematical Physics 380(1), 323–408 (2020)
Angelopoulos, Yannis, Aretakis, Stefanos, Gajic, Dejan: Nonlinear scalar perturbations of extremal Reissner-Nordström spacetimes. Annals of PDE 6(2), 1–124 (2020)
Aretakis, Stefanos: “Stability and instability of extreme Reissner–Nordström black hole spacetimes for linear scalar perturbations II”. In: Annales Henri Poincaré. Vol. 12. 8. Springer. (2011), pp. 1491–1538
Aretakis, Stefanos: Stability and instability of extreme Reissner-Nordström black hole spacetimes for linear scalar perturbations I. Communications in mathematical physics 307(1), 17–63 (2011)
Aretakis, Stefanos: Decay of axisymmetric solutions of the wave equation on extreme Kerr backgrounds. Journal of Functional Analysis 263(9), 2770–2831 (2012)
Aretakis, Stefanos: “Horizon instability of extremal black holes”. In: arXiv preprint arXiv:1206.6598 (2012)
Aretakis, Stefanos: Dynamics of extremal black holes, vol. 33. Springer, Berlin (2018)
Blue, Pieter: Decay of the Maxwell field on the Schwarzschild manifold. Journal of Hyperbolic Differential Equations 5(04), 807–856 (2008)
Burko, Lior M., Khanna, Gaurav, Sabharwal, Subir: Scalar and gravitational hair for extreme Kerr black holes. Physical Review D 103(2), L021502 (2021)
Casals, Marc, Gralla, Samuel E., Zimmerman, Peter: Horizon instability of extremal Kerr black holes: nonaxisymmetric modes and enhanced growth rate. Physical Review D 94(6), 064003 (2016)
Chandrasekhar, Subrahmanyan, Chandrasekhar, Subrahmanyan: Selected Papers, Volume 6: The Mathematical Theory of Black Holes and of Colliding Plane Waves. Vol. 6. University of Chicago Press, (1991)
Christodoulou, Demetrios, Klainerman, Sergiu: “The global nonlinear stability of theMinkowski space”. In: Séminaire Équations aux dérivées partielles (Polytechnique) dit aussi” Séminaire Goulaouic-Schwartz” (1993), pp. 1–29
Dafermos, Mihalis, Holzegel, Gustav, Rodnianski, Igor: The linear stability of the Schwarzschild solution to gravitational perturbations. Acta Mathematica 222(1), 1–214 (2019)
Dafermos, Mihalis, Rodnianski, Igor: The red-shift effect and radiation decay on black hole spacetimes. Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences 62(7), 859–919 (2009)
Dafermos, Mihalis, Rodnianski, Igor:“A new physical-space approach to decay for the wave equation with applications to black hole spacetimes”. In: XVIth International Congress On Mathematical Physics: (With DVD-ROM). World Scientific. (2010), pp. 421–432
Dafermos, Mihalis, Rodnianski, Igor:“Decay for solutions of the wave equation on Kerr exterior spacetimes I-II: The cases \(|a| << M\) or axisymmetry”. In: arXiv preprint arXiv:1010.5132 (2010)
Dafermos, Mihalis, Rodnianski, Igor: Lectures on black holes and linear waves. Clay Math. Proc 17, 97–205 (2013)
Dafermos, Mihalis, et al.:“The non-linear stability of the Schwarzschild family of black holes”. In: arXiv preprint arXiv:2104.08222 (2021)
Dain, Sergio, Dotti, Gustavo: The wave equation on the extreme Reissner-Nordstör black hole. Classical and Quantum Gravity 30(5), 055011 (2013)
Gajic, Dejan: Linear waves in the interior of extremal black holes I. Communications in Mathematical Physics 353(2), 717–770 (2017)
Gajic, Dejan:“Linear waves in the interior of extremal black holes II”. In: Annales Henri Poincaré. Vol. 18. 12. Springer. (2017), pp. 4005–4081
Gajic,Dejan:“Late-time asymptotics for geometric wave equations with inverse-square potentials”. In: arXiv preprint arXiv:2203.15838 (2022)
Gajic, Dejan, Luk, Jonathan: The interior of dynamical extremal black holes in spherical symmetry. Pure and Applied Analysis 1(2), 263–326 (2019)
Gajic, Dejan, Warnick, Claude: Quasinormal modes in extremal Reissner-Nordstör spacetimes. Communications in Mathematical Physics 385(3), 1395–1498 (2021)
Giorgi, Elena: Boundedness and decay for the Teukolsky equation of \({{\rm spin}}\pm 1\) on Reissner. Nordstör spacetime: the spherical mode. Classical and Quantum Gravity 36(20), 205001 (2019)
Giorgi, Elena: The linear stability of Reissner-Nordstör spacetime for small charge. Annals of PDE 6(2), 1–145 (2020)
Giorgi, Elena: The Linear Stability of Reissner-Nordstör Spacetime: The Full Subextremal Range \(|Q| < M\). Communications in Mathematical Physics 380(3), 1313–1360 (2020)
Giorgi, Elena, Klainerman, Sergiu, Szeftel Jeremie:“Wave equations estimates and the nonlinear stability of slowly rotating Kerr black holes”. In: arXiv preprint arXiv:2205.14808 (2022)
Giorgie, Elena:“Boundedness and Decay for the Teukolsky System of \({{\rm Spin}}\pm 2\) on Reissner–Nordstör Spacetime: The Case \(|Q|<<M\)”. In: ANNALES HENRI POINCARE. Vol. 21(8). SPRINGER INTERNATIONAL PUBLISHING AG GEWERBESTRASSE 11, CHAM, CH-6330 . . . 2020, pp. 2485–2580
Gralla, Samuel E., Zimmerman, Peter: Scaling and universality in extremal black hole perturbations. Journal of High Energy Physics 2018(6), 1–39 (2018)
Klainerman, Sergiu, Szeftel, Jérémie: Global Nonlinear Stability of Schwarzschild Spacetime under Polarized Perturbations:(AMS-210). Vol. 395. Princeton University Press, (2020)
Klainerman, Sergiu, Szeftel, Jérémie.: Construction of GCM spheres in perturbations of Kerr. Annals of PDE 8(2), 17 (2022)
Klainerman, Sergiu, Szeftel, Jérémie.: Effective results on uniformization and intrinsic GCM spheres in perturbations of Kerr. Annals of PDE 8(2), 18 (2022)
Klainerman, Sergiu, Szeftel, Jeremie:“Kerr stability for small angular momentum”. In: arXiv preprint arXiv:2104.11857 (2021)
Lucietti, James, Reall, Harvey S.: Gravitational instability of an extreme Kerr black hole. Physical Review D 86(10), 104030 (2012)
Lucietti, James, et al.: On the horizon instability of an extreme Reissner-Nordstör black hole. Journal of High Energy Physics 2013(3), 1–44 (2013)
Marolf, Donald: The dangers of extremes. General Relativity and Gravitation 42(10), 2337–2343 (2010)
Moschidis, Georgios: The \(\text{ r }\hat{\,}\, \text{ p }\) rp-weighted energy method of Dafermos and Rodnianski in general asymptotically flat spacetimes and applications. Annals of PDE 2, 1–194 (2016)
Murata, Keiju, Reall, HarveyS., Tanahashi, Norihiro: What happens at the horizon (s) of an extreme black hole? Classical and Quantum Gravity 30(23), 235007 (2013)
Ori, Amos: Late-time tails in extremal Reissner–Nordstrom spacetime. In: arXiv preprint arXiv:1305.1564, (2013)
Pasqualotto, Federico:“The \({{\rm Spin}}\pm {1}\) Teukolsky Equations and the Maxwell System on Schwarzschild”. In: Annales Henri Poincaré. Vol. 20. 4. Springer. (2019), pp. 1263–1323
Reiris, Martin: Instability of the extreme Kerr-Newman black-holes. In: arXiv preprint arXiv:1311.3156, (2013)
Richartz, Mauricio: Quasinormal modes of extremal black holes. Physical Review D 93(6), 064062 (2016)
Richartz, Mauricio, Herdeiro, Carlos AR., Berti, Emanuele: Synchronous frequencies of extremal Kerr black holes: resonances, scattering, and stability. Physical Review D 96(4), 044034 (2017)
Shen, Dawei: Construction of GCM hypersurfaces in perturbations of Kerr. Annals of PDE 9(1), 1–112 (2023)
Shlapentokh-Rothman, Yakov, da Costa, Rita Teixeira:“Boundedness and decay for the Teukolsky equation on Kerr in the full subextremal range \(|a| < M\): frequency space analysis”. In: arXiv preprint arXiv:2007.07211 (2020)
Stogin, John: “Nonlinear wave dynamics in black hole spacetimes”. PhD thesis. Princeton University, (2017)
da Costa, Rita Teixeira: Mode stability for the Teukolsky equation on extremal and subextremal Kerr spacetimes. Communications in Mathematical Physics 378(1), 705–781 (2020)
Zimmerman, Peter: Horizon instability of extremal Reissner-Nordström black holes to charged perturbations. Physical Review D 95(12), 124032 (2017)
Acknowledgements
I would like to express my gratitude to Aretakis Stefanos for introducing me to this problem and for his fruitful advice, insights, and comments. I am particularly grateful to Elena Giorgi for her constant support and invaluable ideas while this paper was being written. Finally, I would like to thank Mihalis Dafermos and Gustav Holzegel for assisting with helpful discussions and suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
Apetroaie Marios Antonios wrote the main manuscript text and prepared figures 1-4. I reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Apetroaie, M.A. Instability of Gravitational and Electromagnetic Perturbations of Extremal Reissner–Nordström Spacetime. Ann. PDE 9, 22 (2023). https://doi.org/10.1007/s40818-023-00158-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40818-023-00158-5




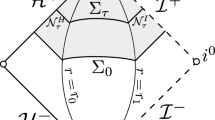
 , and
, and 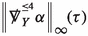 decay
decay and
and  do not decay along
do not decay along  and
and  , as
, as  and
and  and
and  , as
, as 

 takes
takes  where
where 
 is the formal
is the formal  , which takes any pair of scalars (f, g) into the one-form
, which takes any pair of scalars (f, g) into the one-form  .
. takes the tensor
takes the tensor  .
. is the formal
is the formal  which takes a one form
which takes a one form 


 we obtain
we obtain 

 and such type of terms are estimated in the
and such type of terms are estimated in the 













 refers to
refers to  , for all integers
, for all integers 