Two Approaches to the Concept of Area in Calculus

Imagine Maria – an undergraduate, sitting her final exam in a first-year mathematics course. One of its calculus problems asks her to find the area enclosed by the function \(y=2x-{x}^{2}\) and the \(x\)-axis over the interval \(\left[\mathrm{0,3}\right]\). Maria is not surprised by this problem as its variations were discussed in the course under the topic of definite integrals. But then she notices that the assigned function changes its sign within the interval, meaning that she better recall accurately how the concept of area has been approached in her course.

In the Concise Encyclopedia of Mathematics, Weisstein (2003) distinguishes between the area integral and the area of a surface. Regarding the former, Weisstein explains that “if a plane curve is given by \(y=f\left(x\right)\), then the area between the curve and the \(x\)-axis from \(x=a\) to \(x=b\) is given by \(A={\int }_{a}^{b}f\left(x\right)dx\)” (p. 118). Other sources refer to this approach as “signed area”, “net area”, and “net signed area”. In turn, “the area of a surface is the amount of material needed to ‘cover’ it completely” (Weisstein, 2003, p. 118). From this viewpoint, Maria should not take a single definite integral, but sum the absolute values of area measures of the regions that the graph of the assigned function captures above and below the \(x\)-axis.

Bajracharya et al. (this issue) and Hall Jr (2010) are among very a few mathematics education studies that discuss these two occasionally conflicting approaches to areas. Other researchers often adhere to one approach, while omitting the alternative. For instance, Grundmeier et al. (2006) maintain that \({\int }_{0}^{2\pi }\mathrm{sin}xdx\) “gives an area of 0” (p. 185), and Sealey (2006) posits that “[o]f course, area under a curve and Riemann sums are mathematically equivalent”. This area-integral approach seems especially useful in contextual situations, where positive and negative areas have specialized meanings, such as displacement and energy (e.g., McDermott et al., 1987; Sealey, 2006). On the other hand, many other studies consider the notion of area in a purely geometrical sense. This approach also features in many calculus textbooks. Stewart (1999) explains that “if we are asked to find the area between the curves \(y=f\left(x\right)\) and \(y=t\left(x\right)\) where \(f\left(x\right)\ge t\left(x\right)\) for some values of \(x\) but \(t\left(x\right)\ge f\left(x\right)\) for other values of \(x\), then we split the given region \(S\) into several regions […]. We then define the area of the region \(S\) to be the sum of the areas of the smaller regions” (p. 418).

Worldwide, many Marias encounter the surface approach to areas in their studies of calculus, and this is the approach that they are expected to implement when asked about areas enclosed by functions (e.g., see Huang, 2013 for Taiwan; Kouropatov & Dreyfus, 2013 for Israel; Orton, 1983 for the US; Rasslan & Tall, 2002 for the UK). This is also the conventional approach in many first-year calculus courses in New Zealand, where this study was carried out. I return to the tension between the two approaches to the concept of area in the last section of this paper.

Taking Single Integrals to Find Areas

Maria’s question in the previous section comes from Orton (1983) – arguably the first study to document students’ issues with the area-integral relations. In that question, 33 out of 110 Orton’s participants were convinced that the integral must be calculated in separate parts but could not explain why. A further seven students separated between two integrals to compute the contributing areas but suggested that they could work out a single integral instead. Five additional students maintained that a single integral \({\int }_{0}^{3}\) yields the answer. More recent studies point to similar issues with students’ use of definite integrals to calculate areas (e.g., Grundmeier et al., 2006; Huang, 2013; Machín et al., 2010; Kontorovich & Li, 2022; Kontorovich & Locke, 2022; Nilsen & Knutsen, this issue; Rasslan & Tall, 2002; Sofronas et al., 2011).

In secondary school and first-year calculus courses, students are often asked to calculate the area enclosed by graphs of single-variable functions (find-the-area-problems hereafter). The routineness of these problems should not overshadow their significance. From Archimedes and ancient Greek mathematicians, through Valerio, Kepler, and Cavalieri, to Newton and Leibniz, calculus development has been instigated by the interest to measure “curvy” objects (for a short review see Rosenthal, 1951 and Thompson, 1994). This significance goes beyond mathematics: computing the overall distance traveled given the velocity function, calculating the total work based on the applied forces, deducing the size of a bacteria population from its rate of growth – these are only a few contextualized instances where it is instrumental to find the “area” in its totality and avoid a common claim that “the area is simply a definite integral”. In this way, students’ use of single integrals as a model (or a tool) for areas (SImA hereafter) over an interval where a function changes its sign appears research-worthy.Footnote 1

At first glance, SImA may appear as one of those didactical issues that are “easy to fix”. For example, teachers can explicitly tell their students that definite integrals do not calculate surface but net-signed areas. However, the findings on SImA come from research varying in students’ mathematical backgrounds, teachers, educational contexts, languages of instruction, et cetera. In terms of Dreyfus (2017), SImA appears as a robust research finding, i.e. one that has been “repeatedly observed or confirmed in many studies reporting the same or similar results leading to the same (general) conclusions” (p. 59). Thus, it seems unlikely that such a robust model of reasoning can be “fixed” by a single instructional move. This unlikeness is also in accord with broader research that highlights the complexity of the relations between teachers’ instruction and students’ learning (e.g., Schoenfeld, 2000; Sfard, 2008). To understand SImA as a complicated cognitive phenomenon that is typical to the study of calculus, I zoom into fine-grained actions that students undertake when adhering to this reasoning model. Mapping the model’s “building blocks”, will afford educators to relate to students’ ways of thinking and offer telic support that meets students “where they are” (e.g., Schouten, 2017).

Generally speaking, the findings on students’ adherence to SImA come from two types of studies. The first type usually involves dozens of student participants, who are given a questionnaire asking them to explain the notion of definite integral and/or to compute the area between a function and the \(x\)-axis over an interval where the function changes its sign (e.g., Orton, 1983). The findings emerge from students’ written responses, and they are typically categorized as “the area under the curve”-conception of definite integrals (e.g., Jones, 2015; Rasslan & Tall, 2002; Sealey, 2014). In the studies of the second type, a smaller number of students are interviewed in depth around tasks that are not very different from those in the first type. These studies offer more detailed accounts of students’ work with an emphasis on specific issues that emerge as part of their solutions (e.g., Nilsen & Knutsen, this issue; Machín et al., 2010; Sealey, 2006).

Three methodological specificities of the accumulated body of knowledge on SImA are noteworthy. First, often coming from a deficit viewpoint (e.g., Adiredja & Louie, 2020), research has been concerned with what students do not do and should do. In this study, I take an alternative approach, aiming to identify the actions that students undertake when implementing SImA. Second, the number of research participants in the described studies rarely exceeds one hundred (to my knowledge, Orton’s, 1983 remains the largest one). This confines the discussion on how widespread SImA can be among students. Third, in most cases, SImA emerged in “laboratory” research conditions, where students were expected to find areas “here, now, and on their own”. This summons questions concerning whether students would resort to SImA in less constrained settings, for instance, where external mathematical resources are accessible. Accordingly, another aim of this study is to explore SImA in authentic learning environments and with large student cohorts.

Theoretical Framework

The theoretical framework of this study bridges between Fischbein’s theories (3.1) and the literature on mathematical modeling (3.2).

Figural Concepts, Conceptual Control, and Tacit Models

Drawing on cognitive theories, Fischbein (1993) distinguishes between concepts and images. He maintains that “in mathematics, a concept is an absolute expression of its definition” (Fischbein, 1996, p. 113), which makes any concept ideal, abstract, perfect, and universal. On the other hand, images constitute sensorial representations or material models, but not copies or avatars of a concept. Having that said, Fischbein (1996) argues that geometrical figures, such as points, lines, and surfaces, have a blended identity. He refers to them as figural concepts and explains that

“The properties of geometrical figures imposed by, or derived from definitions in the realm of a certain axiomatic system […] A geometrical figure may, then, be described as having intrinsically conceptual properties. Nevertheless, a geometrical figure is not a mere concept. It is an image, a visual image. It possesses a property which usual concepts do not possess, namely, it includes the mental representation of space property” (Fischbein, 1993, p. 141, italics in the original).

Fischbein (1993) maintains that in the mathematically trained mind, the fusion between figurative and conceptual components of a figural concept is absolute. However, when the complete symbiosis does not exist, figural constraints can impose interpretations that are visually consistent but contradicting to conceptual properties. Fischbein refers to such situations as an escape of the conceptual control or as a concept that does not control the figure in full. In a similar vein, Kontorovich (2019) proposes that many mathematical problems ask solvers to find an instance of a specific concept or a combination of concepts. Accordingly, once an answer to a problem has been obtained, it could be checked for critical attributes and potential contradictions with the definitions and properties of these concepts. For instance, in find-the-area-problems, the non-positive answers can be discarded instantly. Assuming that the assigned function is continuous in the interval, the sought-after area should be smaller than the area of the rectangle with the interval as the “width” and the “length” being determined by the maximum and the minimum of the function in that interval. Checks of this sort can be associated with one’s enactment of conceptual control.

Fischbein (1989) argues that “the main psychological problem is that we are not naturally equipped to manipulate concepts and operations, the consistency of which is not supported by some empirical evidence” (p. 9, italics in the original). He suggests that this issue is often resolved by producing mental models that can confer meanings and factually replace abstract concepts. By a model, he refers to “a global, unitary, meaningful interpretation of a phenomenon or a concept” (Fischbein, 1989, p. 12). Formally speaking, Fischbein defines a system B as a mental model of a system or a concept A if a person construes the two as “isomorphic” – a metaphor he uses to refer to situations where one systematically reasons in terms of \(B\) when asked to solve problems about \(A\) (e.g., when students compute definite integrals when asked to find areas). The appeal of such B-models is ingrained in their properties, which often are antipodal to the properties of the corresponding concepts (i.e. A). Specifically, mental models can be more familiar, more accessible, simpler, better structured, and easier to manipulate mentally and practically. Fischbein (1996) suggests that while some models are produced and used consciously, “very often models may play an active, even decisive, role in the reasoning process in a tacit way” (p. 110).

Fischbein and his followers mostly concentrated on intuitive tacit models that influence learners’ reasoning “behind the scenes” without the learner being aware of their impact (e.g., Fischbein et al., 1985; Kontorovich, 2018a; Stavy & Tirosh, 2000). Fischbein (1989) proposes six characteristics of such models: (i) they constitute a structural entity providing a global cluster of rules for coping with a concept; (ii) they have a concrete, practical, behavioral nature that enables learners to operate with a concept; (iii) they have a simple character that instigates economical actions; (iv) they impose a number of constraints for application; (v) if the circumstances are met, such models become autonomous and their behavior does not depend on external constraints; and (vi) they are robust to tensions with formal knowledge acquired by an individual. I draw on these six characteristics in the last section to discuss whether SImA identified in this study can be considered as a tacit model.

Proposing a model that is consistent with one’s reasoning about a mathematical concept is not the same as growing this model analytically based on the steps that this one undertakes when asked about that concept. To make sense of these steps, I turn to the literature on modeling for conceptual and analytical tools.

Modeling Cycles

Mobilizing modeling literature in a study around find-the-area-problems comes with an acknowledgment that these problems can barely be considered authentic, realistic, open-ended, or client-driven, which are typical characteristics of modeling tasks (e.g., Hamilton et al., 2008). Indeed, modeling has often been associated with tasks in which students use mathematics to tackle real-life problems or at least those problems involving a real-life context (e.g., Lesh & Doerr, 2003; Yoon et al., 2010). Notwithstanding, “realism” can have different weights in the educational discourse on modeling. For instance, Lehrer and Schauble (2003) view a model as an analogy between an unfamiliar (and usually complex) system and a familiar one (note the similarity to Fischbein’s, 1989 mental models). Chevallard et al. (1997) posit that “most of the mathematical activity can be identified […] with a mathematical modelling activity” (p. 51). García et al. (2006) elaborate that “the idea of modelling is not limited only to ‘mathematization’ of non-mathematical issues, that is, when the intra-mathematical modelling is considered as an essential and inseparable aspect of mathematics” (p. 232, italics in the original). Therefore, I suggest that the phenomenon in the focus of this study can be considered in terms of modeling in an intra-mathematical sense.

One of the often-cited modeling cycles comes from Blum and Leiss (2005), and it consists of iterative actions that generate one model after another. The researchers explain that initial problem needs to be understood, which yields the construction of a situation model. Its simplification, structuring, and precision produces a real model. The action of mathematization transforms the real model to a mathematical one, working on which entails mathematical results. Their interpretation with respect to the original situation arrives at real results, and a validation of these results may yield a new modeling route. Alternative approaches to modeling processes can be found in the literature, but the usefulness of Blum and Leiss’s cycle has been repeatedly acknowledged (e.g., Borromeo Ferri, 2006). These categories provided a baseline for the analysis in this study.

The Study

Frame and Questions

I suggest that surface areas in the focus of this paper constitute a figural concept. Its conceptual character stems from being defined by objects in the axiomatic realm of calculus, such as functions’ graphs, intervals, and axes (cf. Fischbein, 1993). These objects are figural concepts themselves, and their displacement on a plane forms the focal concept.

Mathematics and mathematics education literature often refers to the described concept as “area under the curve” (e.g., Orton, 1983; Rasslan & Tall, 2002; Sealey, 2006; Stewart, 1999). I refrain from this term for two reasons: First, the directional preposition “under” implies that the curve is positive and that the area is necessarily “beneath it”. Second, the term is silent regarding “how far under the curve” the area goes. Then, I use enclosed areas to highlight that the focal concept is rarely formed by a single curve but by a combination of other concepts (e.g., axes, intervals, graphs of other functions).

Fischbein (1996) maintains that mathematical concepts are not independent of each other. In his words,

“A concept has no meaning and no functional validity by itself. A concept simply does not exist as an isolated entity. The genuine nature of a concept is to be able to entertain various dynamic relationships with a vast network of the other concepts” (p. 103).

In relation to enclosed areas, I distinguish between two conceptual networks. The figural network contains visually perceptual shapes formed by calculus concepts (e.g., graphs, points of intersections). Some attributes of these shapes can be determined with purely algebraic and geometrical methods, when others require turning to the integral network. This network can be characterized by terms such as “integral” and “integrand”, symbols such as “\({\int}_{\blacksquare}^{\blacksquare}\blacksquare\)” and “dx”, and a range of integration techniques.Footnote 2 Accordingly, in terms of 3.2, SImA can be construed as an intra-mathematical modeling process, in which students cycle through the figural and integral networks.

Given the above framing, I operationalize the first aim of this study into a research question: “what modeling routes do students take when implementing SImA?” As argued in Section "Taking Single Integrals to Find Areas", previous research has been rather limited in the number of participants that it involved. Thus, I turn to a large student cohort to ask “how widespread is this model of reasoning among undergraduates on the completion of their first-year courses?”.

Context, Data, and Analysis

This study is contextualized in a first-semester service course in mathematics, offered at a large New Zealand university. The course is typically taken by large student cohorts majoring in statistics, business, economics, and commerce. Nearly a third of the course syllabus is dedicated to integral calculus where students engage with standard topics, such as antiderivatives, the Fundamental Theorem of Calculus, and integration methods. The coursebook introduces definite integrals via Riemann sums, explaining that the definite integral gives the displacement between the \(x\)-axis and a function’s graph. The integral of the absolute value of a function is proposed as the advised approach to find-the-area-problems “since it makes all the negative parts positive again”. This method is illustrated with a worked example featuring a function that changes its signs in the assigned interval. Similar find-the-area-problems are typically assigned for homework and tutorials each semester. Being aware of students’ adherence to SImA, the course lecturers and tutors explicitly address it in their instruction. These teaching moves can be viewed as purposeful attempts to support students in developing a conventional area-integral relationship.

This study’s data was structured in two corpuses. Corpus A contained the answers of nearly twelve thousand students to find-the-area-problems that appeared in 17 in-person closed-book invigilated final exams in the last decade. The exams were multiple-choice, and they came in four versions: each version containing the same sequence of problems and the same set of four options for an answer, but the order of the options was alternated in each version. Each exam contained a single find-the-area-problem, in which a function changes its sign in the assigned interval. One of the options for an answer could be obtained with SImA (the SImA-option hereafter). The number of students who selected this option was traced throughout the exams.

To support students’ preparation for the final exam, the course teachers designed a novel homework assignment. They went over the problems from past exams with the lowest success rates, constructed a set of 30 problems, asked the students to choose one of them, and “produce a video no shorter than one minute and no longer than five minutes in which you will fully explain your answer to the problem. […] Try and explain your answer as if you were talking to a friend in the class”. The four problems relevant to this study are presented in the Appendix. This assignment was published in the last week of the semester and the students had nearly two weeks to upload their solutions to the course managing system. Over four semesters, 190 students video-recorded their solutions, to which I refer as Corpus B. Then, the students sat the final exams, and they answers were considered as part of Corpus A.

To analyze Corpus B, all video clips were reviewed in a search for students’ usage of SImA. The solutions featuring the model were transcribed and divided into episodes corresponding to the main solution steps. In an iterative inductive process (Denzin & Lincoln, 2011), a constant comparison technique (Glaser & Strauss, 1967) was applied to identify the intermediate models that students generated as part of their route towards the final answer. Drawing on the previously presented conceptualization, these models were initially associated with the figural and integral networks, and then generalized into analytical categories that were informed by Blum and Leiss (2005). In this process, I also drew on Sfard (2021), who distinguished between “area” as a concrete geometrical shape (or a region) and “area” as a positive number of measuring units. This distinction led to the observations that when working on a find-the-area-problem, a student could create a visual of the area in the focus of the problem (cf. situation model in Blum & Leiss, 2005), before generating an integral-based formula and obtaining a numerical result. Then, conceptual control was required to decide whether this result should be taken as the measure of the area in question. The categories emerging from initial analytical rounds were repeatedly applied to the whole Corpus B, which led to their further development.

To enhance the analysis, a graduate mathematics education student was involved. I discussed the preliminary categories with them, and we applied the categories together on the random sample of about 7% of Corpus B. Then, the student independently analyzed another random sample of about 20% of the data. Our inter-rater agreement was 87%, and we discussed the remaining instances separately. These discussions resulted in further refinements of the categories, and eventually led to the construction of the SImA-cycle. Section "SImA-cycle and Routes in Students’ Solutions" presents this cycle with illustrative excerpts from students’ solutions.

Findings

This section is structured in accordance with the research questions: the first sub-section presents the modeling routes that students undertook in their solutions, and the second sub-section focuses on students’ adherence to the SImA-options in their final exams.

SImA-cycle and Routes in Students’ Solutions

Table 1 offers an overview of students’ final answers to the four focal problems of Corpus B. The table shows that the SImA-option was consistently obtained by students each semester, accumulating to 53% overall. Problem III was especially triggering with more than 55% of the students reasoning in terms of SImA. In one semester, the SImA-options were derived by more students than the expected answers in each problem.

Table 1 Overview of students’ answers in video-recorded solutions
Full size table

To handle the diversity of students’ routes through the figural and integral networks, the SImA-cycle was developed (see Fig. 1 for a visual representation). As a whole, the cycle does not depict a specific route that a particular student took in their solution. Instead, it is a structured set of analytically developed categories that were accumulated from the similarities of actions that students exhibited at similar solution points. In other words, the vast majority of students’ routes could be described with a subset of categories presented in the cycle (see the next subsections for examples).

Fig. 1
figure 1

SImA-cycle

Full size image

The SImA-cycle includes five models (cf. Blum & Leiss, 2005). The figural model featured at the beginnings of students’ solutions, and it encapsulated the images, graphically representing the find-the-area-problem of their choice (this category can be construed as a situation model in terms of Blum & Leiss, 2005). The examples in Table 2 show that students’ figural models varied not only in their accuracy (e.g., the functions’ graphs, intersections with the axes), but also in the elements of the problem that they represented (e.g., axes, intervals). More often than not, these models contained an enclosed figure with a marked area; an area that the students addressed as “the area” in the focus of the problem. However, in some cases, the students referred to their “pictures”, “images”, and “graphs” in rather general terms. Then, a region model was introduced to capture instances where students marked, or verbally indicated, the enclosed figures whose areas they wanted to find, as opposed to cases where the specific regions of interest were not explicated.

Table 2 Illustrations of figural and region models from students’ solutions
Full size table

The relation model bridges between the figural and integral networks. This model captures students’ descriptions of the connection between areas and integrals (e.g., “Area is just a definite integral”) and of actions that need to be taken to find areas (e.g., “To find the area we are going to anti-differentiate the function”).

The integral formula captures symbolic expressions that students used. Overall, students’ formulas ranged in their generality and extent of elaboration. In some solutions, the students instantly presented a specific formula that corresponded to the focal problem (e.g., \({\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}x\mathrm{cos}xdx\) in Problem I); in other cases, the students referred to the function’s anti-derivates and the Fundamental Theorem of Calculus before presenting the definite integral they were using in a particular case. Taking the integral yields integral results, and together with an integral formula, these categories can be seen as contextualized versions of “mathematical results” and “mathematical model” in terms of Blum and Leiss (2005). These numerical results were often positioned as an answer to the focal problem, which completed the cycle and provided the area measure. In some rare cases, the unsatisfaction with the result led the students to a new round through the SImA-cycle.

To exemplify how the students cycled through these models, I present three solutions. They were chosen based on the potential to illustrate the nuances of the described models and the typicality of actions that the students undertook. In the analysis, I notice the opportunities for taking conceptual control that the students seized and missed.

A Route Without a Figure and with a Single Integral

The first illustration comes from Kate,Footnote 3 who worked on Problem II. Kate opened her clip with self-introduction and showing a card where the problem was printed. She read its formulation out loud and embarked on its solution (see Table 3 for the transcript).

Table 3 Transcript of Kate’s solution
Full size table

Kate’s solution is illustrative of many others, where the students did not operate in the figural network, leaving the focal enclosed area behind the integral scenes. Drawing on the relation model of “area equals the integral” in [1], Kate instantly generates a formula that involves a single integral of the function over the assigned interval. In [2], she develops the formulae’s elements in steps: with a reference to an indefinite integral at first, but in [3] Kate explains why what normally “would be important […is] going to cancel out”. After completing her calculations in [5–6], some of which contains mistakes, in [7], Kate turns to the options for an answer that accompany the problem. Her “\(e-\frac{e}{1}-2\)” and the problem’s “\(e-\frac{1}{e}-2\)” differ, but, in [8], Kate marks this SImA-option as correct. Accordingly, [7–8] can be interpreted as Kate endorsing her integral result as the numerical measure of the sought-after area. There are no evidence of Kate checking or addressing the viability of her result. This is representative of the solutions in this category that underscored the details of integration and calculation, while making no moves that can be construed as taking conceptual control over the obtained results.

A Route with an Accurate Figure, Non-conventional Region, and Two Integrals that do the Same Thing

To illustrate how the SImA-cycle can pass through the figural network, I turn to Jamie’s work on Problem III. He opened his solution with reading the problem out loud and declaring that his answer is “\(\frac{2}{3}\)”, which is the SImA-option. Table 4 presents a transcript of the work that followed. As part of it, Jamie displayed a piece of paper with a handwritten text. Due to the poor visibility of the text, I reproduced it and assigned letters to the lines that Jamie was referring to in his utterances.

Table 4 Transcript of Jamie’s solution
Full size table

Jamie’s route starts with the figural model of the problem in [3–4]. The model’s elements seem accurate and appear as being generated with a computer software. Concerning the region model, only the area enclosed by the positive part of the function’s graph and the \(x\)-axis is colored, and, in [3], Jamie explicates that this is the area the measure of which needs to be found. And while it is unclear why Jamie posited that the “yellow part” is “the area between the curve and the interval”, it is possible that it relates to his confusion between the interval \(\left[\mathrm{0,2}\right]\) and the point \(\left(\mathrm{2,0}\right)\) through which the right boundary of the enclosed area passes.

In [3], Jamie explains that “the definite integral from two to zero” is needed to find the area, implying that this should be the usual integral formula. However, since “there are two things” the integral is separated. This statement in [4] is noteworthy because it suggests that for Jamie the figural model is the one to shape the formula of the definite integral rather than the region model. On the one hand, this move can be interpreted through the lens of a missed opportunity for conceptual control: if the focal area is the highlighted one, then why doesn’t it correspond to the limits in the integral formula? On the other hand, Jamie may have assumed that the vertical line through \(\left[\mathrm{2,0}\right]\) in his notation is the figural version of the assigned interval \(\left[\mathrm{0,2}\right]\). Indeed, note that in the utterances [2–3], he refers to the interval as “two to zero”. From this perspective, Jamie controlled the concept of area by ensuring that the interval in the assigned problem had corresponding elements in the figural model, the region model, and the integral formula.

The integral model is articulated in [5] and developed in [6]. This model pertains to the line (e) – the sum of two integrals of \(f\left(x\right)\) over the two intervals that correspond to the “two things” in the figural model. In other words, while Jamie does split his formula into two parts, both of them conduct the same operation and lead to the result that could be obtained if the integral was taken over the whole interval (cf. Orton, 1983). Notably, the partial cancelation of areas is reflected in Jamie using \(F\left(1\right)\) in both definite integrals – by adding it in [6] and then instantly subtracting it in [7]. These places can be associated with opportunities for conceptual control to either challenge the integral formula, or at least ask “how come” the cancellation of \(F\left(1\right)\) is embedded in the formula’s simplification.

A Route Where Control Over the Integral Result Yields Another Modeling Round

In the previous illustrations, I pointed at the opportunities that Kate and Jamie had to take conceptual control over their integral results. In this illustration, I turn to Benny’s work on Problem IV to demonstrate how such opportunities can be seized. Benny opened with reading the problem out loud and mentioning that it requires integration by parts. Table 5 presents a transcript of what followed, when the right column shows the handwritten pre-written text that Benny used.

Table 5 Transcript of Benny’s solution
Full size table

Benny’s route starts with him displaying the figural model of the problem, where the focal region is marked. Nevertheless, the region model is not acknowledged verbally at this point. Benny’s first utterances in [1–2] revolve around the “building blocks” of the forthcoming integration by parts, which links to the relation model in [4] (i.e., “to find the area under a curve, we do a definite integral”) and the integral formula (b). The integration is carried out in [5–7] and it yields zero, which is labelled in (h) as the result of the definite integral. In turn, this result is rejected in [8] since “as we know we are talking about area”, which I construe as Benny’s act of control over the concept of area. The act completes the first round of Benny’s route through the SImA-cycle, and it opens a new round that is explicitly focused on areas.

In the second round in [8–12], Benny attends to his model of the focal region, recognizing that the enclosed figure consists of two components both of which should be considered as “area underneath the curve”. In [10], he even mentions the notion of modulus that needs to be involved “to add the two areas together”. However, Benny does not introduce a new integral formula, and capitalizes on his last step from the previous round instead. The move in [11] suggests that Benny associates \(\frac{\pi }{2}\) and \(-\frac{\pi }{2}\) from (g) with the two measures corresponding to the components of the focal area. Then, taking the modulus of the negative component leads to a positive result of \(\pi\), which is presented in (j) as the measure of the “area under curve”.

SImA in Final Exams

Table 6 presents an overview of students’ performance in the find-the-area-problems in the analyzed final exams. The table shows that the overall success rate in these problems was 41.7%, and it ranged from nearly 24% to 64% in different exam sittings. The SImA-options were selected by 28.5% of the students, and this measure varied between 14 and 64%. In five exams, the SImA-options were chosen by more students than the expected answers, and in all but four cases, the SImA-options were the most popular among the three alternative possibilities. It is also worth mentioning that in one problem, the SImA-option was 0, and yet, it was chosen by 149 students. This might be interpreted as an issue of conceptual control since this option lacked a critical attribute of the concept of area (Kontorovich, 2019).

Table 6 Overview of students’ responses in find-the-area-problems in final exams
Full size table

Table 7 provides an overview of students’ selections with a focus on functions involved in the find-the-area-problems. This table demonstrates that more than half of the students successfully coped with cubic functions and functions with roots, compared to the cases with exponential and trigonometrical functions where a third of the students selected the expected answers. Interestingly, the choice of the SImA-options was rather similar in all the four cases, ranging from 20% to nearly 26%. The popularity of the SImA-options was the highest for quadratic and linear functions. In both cases, these options were selected by a compatible percentage of students as the expected answers. The linear cases are notable since there students could compute areas through mobilizing the figural models of triangles and rectangles, without having to pass through the integral network. Possibly this is what helped at least some of the 40% of the students to choose the expected answers. In turn, the other nearly 31% did not succeed to avoid the SImA-options.

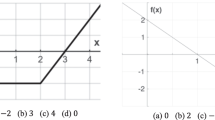
Table 7 Overview of students’ performance with a focus on involved functions
Full size table

Eight exams in Corpus A corpus contained what I call tandem problems – pairs, where the first problem asked students to calculate \({\int }_{a}^{b}f\left(x\right)dx\) for particular \(a\), \(b\), and \(f\left(x\right)\), and the subsequent problem asked that they find the area enclosed by the x-axis and the same \(f\left(x\right)\) over the same interval \(\left[a,b\right]\). The options for an answer to these problems corresponded: they were either the same or had the same absolute value (e.g., Fig. 2). Table 8 shows that between some 20% and nearly 60% of the students selected corresponding answers in the tandem problems. This supports the proposal that for many students, the selection of the SImA-option was not an arbitrary choice but a result of implementing some variation of SImA.

Fig. 2
figure 2

Example of a tandem problem from a final exam

Full size image
Table 8 Overview of students’ answers in tandem problems
Full size table

Summary and Discussion

In their overview of research on calculus teaching and learning, Bressoud et al. (2016) maintain that one of its most important issues relates to the tension between students’ actual thinking and institutional expectations. This study has focused on SImA – a particular model of reasoning that can emerge when students compute areas enclosed by functions in a single-variable calculus (i.e. a surface area in terms of Weisstein, 2003). Students’ adherence to SImA has been documented in previous research. The theoretical innovation of this study pertains to considering this phenomenon through the lens of Fischbein (1989, 1993) and intra-mathematical modeling.

Research has shown that calculus students struggle with topics of conceptual nature (cf. Hiebert & Lefevre, 1986), which require making connections and sense-making (e.g., Mahir, 2009; Orton, 1983). Some may argue that this meta-finding is relevant to this study as well; for instance, SImA might be interpreted as an algebraic manipulation where students “operate with symbols without any regard to their possible contextual meaning” (White & Mitchelmore, 1996, p. 91). This interpretation appears especially appealing in cases where issues with conceptual control were identified (e.g., when students responded with non-positive values for areas, like Kate and 149 students who maintained that the area is zero). However, in addition to the broadly discussed deficiencies of a deficit discourse (e.g., Adiredja & Louie, 2020), I argue that this interpretation of SImA is not viable: find-the-area-problems are typical to calculus courses and, at least in the case of problems used in this study, students could solve them rather procedurally through reproducing the methods demonstrated by their course teachers. True, some studies show that many undergraduates are unsuccessful in reproducing standard procedures (e.g., Kontorovich, 2020). Yet, students’ adherence to SImA, draws attention to the characteristics of this reasoning model; characteristics that could cast light on its cognitive appeal.

I proposed that find-the-area-problems revolve around a figural concept, the area of which can be determined by taking a modeling route through the figural and integral networks (cf. Fischbein, 1993). This proposal summons the consideration of SImA in terms of the six characteristics of tacit models (see the "Theoretical Framework" section), those which are renowned for their impact on students’ reasoning “behind the scenes”. Let me start with the first five. Through the lens of the analytically developed cycle, SImA emerges as a well-structured frame that equips students with practical actions that need to be taken and concrete models that need to be generated as part of the route from the assigned problem to its result. The route is not always simple since taking a definite integral may be technically challenging for first-year students. Notwithstanding, the transition from “Find the area between \(f\left(x\right)\) and the \(x\)-axis over the interval \(\left[a,b\right]\)” to its integral version of “\({\int }_{a}^{b}f\left(x\right)dx=?\)” appears relatively straightforward. Compared to the conventional method, this transition is economical as it skips finding the function’s zeroes, subdividing the assigned interval, computing the corresponding integrals, and combining the results. These actions are sensitive to the number of function’s zeros, its sign changes, et cetera. The invariance of SImA to the givens of the assigned problem (e.g., the function, the interval) fuels the autonomy of this model of reasoning. In turn, the model’s constraints become about the technicalities of taking the definite integral rather than considering whether SImA is adequate for determining the sought-after area in the first place. Indeed, in their video clips, the students dedicated substantial chunks of time to taking the integral (e.g., see examples in the "Findings" section), when relation models and integral formulas were often mentioned quickly and casually. Fischbein (1989) maintains that a model can “replace, tacitly, the original [concept] in our reasoning process” (p. 9), and I suggest that this may be an accurate description of SImA’s impact on many students.

The empirical component of this study contributes to the existing research by showing that SImA is not a single model with which all students reason in the same way. Instead, it emerges as an umbrella notion that encapsulates a range of modeling routes. The analytically developed SImA-cycle demonstrates that these routes can differ in terms of the kinds of models students construct, the models themselves, and their order of construction. Particularly, the findings indicate that unconventional models can feature at every station on a student’s route (e.g., the figural model, the region model), and not only when generating the formula of a definite integral.

Another contribution of this study taps into SImA’s widespread nature and robustness, with the latter being the sixth characteristic of tacit models. These aspects were explored with two complementary sources. The first one encompassed multiple-choice problems in invigilated final exams that were sat over a decade by nearly twelve thousand non-mathematics majors. The SImA-option has been consistently selected by a large proportion of students each semester. It was often the most popular alternative response, and, occasionally, students chose it more often than the expected one. Clearly, the selection of the SImA-option in multiple-choice problems does not necessarily imply that this model underlies each student's reasoning. Yet, in tune with Schoenfeld (2000), SImA appears as a research-informed explanatory model with which students’ selections were consistent. Furthermore, students’ selection of SImA-options in final exams echoes the findings of previous questionnaire-based studies with smaller numbers of participants (e.g., Grundmeier et al., 2006; Orton, 1983; Rasslan & Tall, 2002).

The repeated featuring of SImA-options in students’ responses in the final exams cannot be taken for granted given the myriad of didactical changes that the focal course went through over the years. For instance, the course instructors were aware of the issue, they explicitly addressed SImA in their teaching, and systematically engaged students with the find-the-area-problems in the tutorials and homework assignments. True, for many participants the first encounter with area-integral relations occurred in secondary school. Fischbein (1989) argues that many “representations of certain mathematical, abstract notions, […] develop themselves at an initial stage of the learning process and […] continue to influence, tacitly, the interpretations and the solving decisions of the learner” (p. 9). Yet, in New Zealand calculus curriculum, areas are also approached as areas of surfaces. All in all, the consistency of students’ answers with SImA in final exams speaks to the robustness of this reasoning model to formal instruction (cf. Fischbein, 1989).

Students’ reliance on SImA in non-examinational conditions, such as when solving problems in the homework assignment, is noteworthy. A basic online search leads to a variety of conventional explanations for finding areas, not to mention advanced resources that not only output final answers but also explicate the solution steps. Yet, it was easier for some students to email their course instructors arguing that the published answers contained a mistake rather than to entertain the possibility that their SImA-based solutions could be flawed. This is not a criticism of students’ knowledge or actions, but an illustration of what Fischbein (1989) describes as the tacit grip of a model over one’s reasoning, to the extent that they are not aware of it.

Let me cautiously offer four teaching-oriented comments based on this descriptive study. First, previous research has recognized that students often draw on areas when reasoning about definite integrals (e.g., Rasslan & Tall, 2002; Sealey, 2006). This study invites calculus teachers to introduce and promote this reasoning model with care, leading students towards a rich web of area-integral relations (cf. Machín et al., 2010) and away from the oversimplified “definite integral is the area under a curve”. Such instruction can entail a consistent engagement with problems where areas comprise regions above and below the \(x\)-axis as well as the use of terminology foregrounding the figural concepts the areas of which the problems are targeting (e.g., “Find the area enclosed by …”). A recent study shows how digital resources can be utilized to this end (Kontorovich & Locke, 2022).

The above comment is inseparable from a broader debate on the productivity of different conceptualizations of definite integrals (e.g., Bajracharya et al., this issue; Hall Jr, 2010). Specifically, Jones (2015) notices that the commonly referenced conceptualization of “adding up pieces” highlights the adding aspect only. Then, the researcher proposes to reframe this conceptualization as “multiplicative-based summation” to emphasize the multiplication between the integrand and the differential (for developments see Jones & Ely, this issue; Stevens & Jones, this issue). Given this study’s findings, I support Jones’s proposal: the integrated function can be either positive or negative, and as such, it makes a signed contribution to the resulting quantity rather than simply measures the encapsulated area. In this way, multiplicative-based take on definite integrals may support teachers when addressing SImA in a classroom.

Second, in my experience, find-the-area-problems are often introduced to illustrate the applicatory power of the Fundamental Theorem of Calculus. This introduction may come at the expense of explicit discussions about the figural concepts whose areas the theorem helps to measure. And while an accurate image of the figure is not required to undertake the computation, a visual that preserves critical attributes of the area (e.g., points where a function changes its sign in the assigned interval) may be instrumental for students to make sense of what the problem is all about and whether SImA is viable. Indeed, to draw on the famous phrase about all models being wrong but some being useful (Box & Draper, 1987), SImA is useful as long as the function is positive or does not change its sign in the assigned interval. That being said, Table 2 illustrates that sketching such images and identifying the intended areas, i.e. “finding the areas” in the geometrical sense (cf. Sfard, 2021), may not be trivial for many students. Accordingly, when discussing find-the-area-problems, it might be worthwhile for instructors to deliberate on all the stations that need to be visited in the area-integral cycle, both in the figural and integral networks.

Third, the previous comments stem from the assumption that an instructor approaches areas as those attributed to surfaces (Weisstein, 2003). Adhering to this approach in first-year calculus can allow students to apply their previous mathematical knowledge and experiences of conceptual control to the integration. In the words of Bender (1991), “the act of measuring area has always clearly had elements of everyday life” (p. 51); hence, I suggest that this everyday-life interpretation can be mobilized, expanded, and formalized in calculus classrooms.

Finally, it is essential to keep in mind that the integral or the net-signed approach to areas dominates many disciplinary contexts (e.g., Bajracharya et al., this issue; McDermott et al., 1987; Sealey, 2006). As one of the reviewers pointed out, there are myriad problems in which it is didactically desirable for students not to be distracted by the function’s sign change inside the limits of integration. These problems can also involve the term “area” and instructors can use it to discuss net-signed-based solutions (e.g., see Kontorovich, 2018b for polysemous concepts). Accordingly, I believe that it is important for calculus instructors to be cognizant of both approaches and provide students with opportunities to appreciate the value of each of them.