Online motion planning of mobile cable-driven parallel robots for autonomous navigation in uncertain environments

Abstract

Mobile cable-driven parallel robots (MCDPRs) offer expanded motion capabilities and workspace compared to traditional cable-driven parallel robots (CDPRs) by incorporating mobile bases. However, additional mobile bases introduce more degree-of-freedom (DoF) and various constraints to make their motion planning a challenging problem. Despite several motion planning methods for MCDPRs being developed in the literature, they are only applicable to known environments, and autonomous navigation in unknown environments with obstacles remains a challenging issue. The ability to navigate autonomously is essential for MCDPRs, as it opens up possibilities for the robot to perform a broad range of tasks in real-world scenarios. To address this limitation, this study proposes an online motion planning method for MCDPRs based on the pipeline of rapidly exploring random tree (RRT). The presented approach explores unknown environments efficiently to produce high-quality collision-free trajectories for MCDPRs. To ensure the optimal execution of the planned trajectories, the study introduces two indicators specifically designed for the mobile bases and the end-effector. These indicators take into account various performance metrics, including trajectory quality and kinematic performance, enabling the determination of the final following trajectory that best aligns with the desired objectives of the robot. Moreover, to effectively handle unknown environments, a vision-based system utilizing an RGB-D camera is developed, allowing for precise MCDPR localization and obstacle detection, ultimately enhancing the autonomy and adaptability of the MCDPR. Finally, the extensive simulations conducted using dynamic simulation software (CoppeliaSim) and the on-board real-world experiments with a self-built MCDPR prototype demonstrate the practical applicability and effectiveness of the proposed method.

Introduction

Cable-driven parallel robots (CDPRs) have emerged as a promising class of robotic devices for a wide range of industrial and service applications. Typically, CDPRs are parallel robotic manipulators that employ multiple flexible cables to control the motion of a moving platform (or end-effector). The cables are wound around fixed motorized winch systems to control the position of the end-effector by adjusting their lengths. CDPRs can provide several advantages such as low inertia, large workspace, and high load capacity making them suitable for a variety of tasks of such robots in large-scale construction [1], painting [2] and rehabilitation mechanisms [3].

In spite of the promising performance of CDPRs in numerous applications, several challenges still remain. One of the major drawbacks of classical CDPR is the fixed cable layout, i.e, fixed pulley position and winch system which significantly increases the probability of collision between the cable and the surrounding environment, thereby the available workspace of CDPRs was reduced [4]. Moreover, the fixed cable layout leads to the position of the pulleys must be carefully optimized in order to maximize the workspace [5]. Consequently, Reconfigurable Cable-Driven Parallel Robots (RCDPRs) have been developed by researchers in which cable robots have the ability to change their configurations [6,7,8]. However, the reconfigurability of most existing RCDPRs is limited due to they still require manually adjusted cable layouts and the base frame cannot be freely moved.

Fig. 1

A self-built MCDPR prototype with a vision system

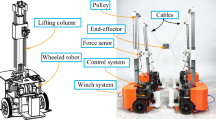
To achieve autonomous reconfigurability of RCDPRs, mobile cable-driven parallel robots (MCDPRs) were developed by researchers [9], in which the additional mobile bases were introduced to mobilize the cable layout and the base frame. The MCDPR developed in this work is shown in Fig. 1, it consists of a classical CDPR with eight cables and a six degree-of freedom (DoF) end-effector mounted on four mobile bases. A mobile base consists of a differential wheeled robot with three wheels and a lifting column. Moreover, an RGB-D camera (Intel RealSense$^{\hbox {TM}}$ Depth Camera D435i) is mounted on the mobile base to sense the environment. However, additional mobile bases involve complex constraints and high-dimensional configuration space, resulting in motion planning of MCDPRs becoming a challenging issue and requiring to be addressed.

Accordingly, sampling-based motion planning methods have demonstrated promising performance in addressing high-dimensional problems and accommodating various constraints by randomly sampling the configuration space [10]. One of the representative sampling-based path planning algorithms is the Rapidly exploring Random Tree (RRT) method, and some variants of RRT such as RRT* and RRT-connect are proposed [11,12,13]. In recent years, researchers have developed different RRT-based online motion planning methods for a wide range of robotic systems, including self-driving cars, unmanned aerial vehicles (UAVs), and unmanned ground vehicles (UGVs). Sotirios et al. [14] developed an RRT*-NH method to generate real-time paths for nonholonomic self-driving cars in quasi-static unknown environments. Lin et al. [15] developed a closed-Loop RRT method for UAV dynamic obstacle collision avoidance. Wen et al. [16] developed a heuristic dual sampling domain reduction-based RRT* method to complete the online planning of an unmanned surface vehicle (USV). However, MCDPR consists of multiple mobile bases and CDPR, presenting a unique challenge compared to the aforementioned conventional robotic systems. The mobile bases collaborate and coordinate their movements to achieve a common objective, which involved multi-agent motion planning problem, and high-dimensional state spaces are required to be considered.

One of the main advantages of the RRT algorithm is that it can be easily extended to multidimensional spaces [17]. Zhang et al. [16] proposed an optimization-based map exploration strategy by extending the RRT algorithm, enabling multiple robots to actively explore and construct environment maps. In a similar vein, Lau et al. [18] introduced a temporal memory-based RRT (TM-RRT) exploration strategy designed for multi-robot systems to execute robust exploration tasks within unknown environments. Additionally, Neto et al. [19] presented a Multi-agent Rapidly-exploring Pseudo-random Tree (MRPT) approach, which combines rapid exploration and pseudo-random tree construction, providing real-time motion planning and control for under-actuated robots. While the aforementioned methods have showcased their adaptability and potential in multi-robotic systems, the CDPR brings forth additional constraints that necessitate careful consideration. Specifically, in the context of CDPR, there are unique challenges related to cable interference and the intricate kinematics of the robots, which are required to be considered in the present study.

In the pursuit of generating safe trajectories for CDPRs, an adaptive RRT method was proposed in [20] to facilitate the moving obstacle avoidance of moving obstacles. Xiang et al. [21] developed an RRT-based dynamic trajectory planning method specifically tailored for three degrees-of-freedom (DOFs) suspended CDPRs. Mishra et al. [22] introduced the AFG-RRT* method, which considers multiple performance constraints to generate optimized paths for CDPRs. However, these studies only generate feasible trajectories for classic CDPRs. In the case of MCDPRs, Rasheed et al. [23] proposed a sampling-based algorithm that generates collision-free paths while maximizing the wrench capability. Furthermore, the Direct Transcription method was proposed in [24] to provide an optimized path for mobile bases and the end-effector by minimizing the cost function with a series of given constraints. However, the scope of previous MCDPR studies is restricted to scenarios where the environmental information is known a priori. Most recently, Liu et al. [25] introduced a novel approach based on reinforcement learning (RL) to address dynamic obstacle avoidance in real time for CDPRs with mobile bases, further expanding the possibilities for motion planning in the context of MCDPRs.

In this work, we propose an online motion planning method for navigating Mobile Cable-Driven Parallel Robots (MCDPRs) in uncertain environments. Our approach utilizes RGB-D camera data and introduces a novel multi-time-based RRT algorithm. While recent learning-based approaches have gained attention, they suffer from computational complexity and limited transferability to different environments [26, 27]. Additionally, optimal cascade control for parallel robot platforms has been developed in prior works [28,29,30], where heuristic algorithms were employed. We also highlight the potential use of a novel exploration-exploitation-based policy for model-free control [31]. However, to simplify the analysis, we have designed two controllers based on the kinematic models of the mobile base and CDPR. The specific contributions of this paper are as follows:

• (1) An online motion planning algorithm for MCDPR navigation in real-world scenarios. To address the diverse constraints inherent to MCDPRs and ensure real-time performance, our developed approach employs a continuously constructed time-based tree for the four mobile bases through forward simulation. Consequently, a set of reference trajectories can be generated, allowing for effective motion planning of the MCDPR system.

• (2) The novel heuristic functions were designed to determine the final following trajectory for MCDPR in each time interval. These heuristic functions take into account multiple performance metrics, including kinematics stability and distance to the goal, to ensure the generation of a favorable trajectory. Once the trajectories for the four mobile bases have been obtained, we employ a developed partial sampling method to generate the trajectory for the end-effector. This approach allows for the efficient planning of the MCDPR’s motion while considering the unique requirements and characteristics of the end-effector.

• (3) A vision-based system is developed for MCDPR localization and detecting obstacles by using the RGB-D camera. The system incorporates the proposed method, and we conducted real-world experiments to validate its performance. The experimental results demonstrate the compelling performance of the proposed approach, highlighting its efficacy in accurately localizing the MCDPR and effectively detecting obstacles in a real-world environment.

The remainder of this paper is organized as follows: Robot parameterization and problem formulation are introduced in Sect. “System Modeling”. The kinematics and stability model for MCDPRs is established in Sect. “Method Description”. In Sect. “Method Validation”, the proposed path planning method for MCDPRs is introduced in detail. The method validation is carried out in Sect. “Conclusion and Future Work”. Finally, Section 6 concludes the research work.

System modeling

MCDPR parameterization

As shown in Fig. 2, the MCDPR studied in this work consists of $m=8$ cables and $p=4$ mobile bases. For j-th mobile base, denoted as ${\mathscr {M}}_j$, $j = 1,...,4$ carries two cables ($m_{j}=2$) and has three wheels ($c=3$) including one caster wheel and two driven wheels. The cable exit points are dependent on the position and orientation of the mobile base. The origin of the global coordinate system is represented as $O_{0}$ and the local coordinate system located at the center of the end-effector is denoted as $O_{e}$. The mobile bases enable autonomous reconfiguration of the CDPR within a plane parallel to the ground. It should be noted that the mobile base operates as a planar robot, thus limiting the reconfiguration of the plane. As a result, the height of the cable exit points remains constant.

Fig. 2

Structural diagram of MCDPR

In this study, cables are treated as massless line segments for simplicity. Let i-th cable exit point and anchor point associated with ${\mathscr {M}}_j$ denote as $A_{ij}$ and $B_{ij}$, respectively. Moreover, $A_{ij}$ is designed to lie on the axis ${}^{pj}z$ of ${\mathscr {M}}_j$. Based on the properties of parallel robots, i-th cable vector attached onto ${\mathscr {M}}_j$, ${\varvec{l}}_{ij}$, can be expressed as follows

$$\begin{aligned} {\varvec{l}}_{ij}= {\varvec{a}}_{ij}-{\varvec{P}}-{{\varvec{{R}}}}{\cdot }{}^{e}{\varvec{b}}_{ij} \end{aligned}$$

(1)

where ${\varvec{a}}_{ij}$ is the position vector of $A_{ij}$ in $O_{0}$ coordinate system. ${}^{e}{\varvec{b}}_{ij}$ represents the position vector of $B_{ij}$ in the moving coordinate system $O_{e}$. ${\varvec{P}}$ and $\varvec{{R}}$ is a three-dimensional position vector and rotation matrix of the end-effector, respectively. Hence, the velocity relationship between the cable vector and the end-effector can be obtained via the differentiation of (1) with respect to time

$$\begin{aligned}{} & {} {{\dot{{\varvec{l}}}_{i,j}}}=\text {-}{{{\varvec{J}}}^{{T}}}\varvec{\dot{P}} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} {\varvec{J}}({\varvec{X}})=\left[ \begin{matrix} {{{\varvec{u}}}_{1,1}} &{} \cdots &{} {{{\varvec{u}}}_{2,j}} \\ {{{\varvec{u}}}_{1,1}}\times {({{\varvec{R}}}}\cdot {}^{e}{{{\varvec{b}}}_{1,1})} &{} \cdots &{} {{{\varvec{u}}}_{2,j}}\times {({{\varvec{R}}}}\cdot {}^{e}{{{\varvec{b}}}_{m,j})} \\ \end{matrix} \right] \end{aligned}$$

(3)

where ${\varvec{J}}\in {\mathbb {R}}^{n\times {m}}$ is the Jacobian matrix of the carried CDPR. ${\varvec{u}}_{i,j}$ is the unit vector of ${\varvec{l}}_{ij}$. In this work, we limit the end-effector to perform only translational motion. By using (1) and (3), the position and the velocity of the end-effector can be controlled by varying the length of the cable.

Problem formulation

To accomplish autonomous navigation of MCDPR in unknown environments, the sampling-based motion planning method requires searching the state space to construct a graph. We first define the state of j-th mobile base and the end-effector at k-th time step is ${\varvec{m}}_{j,k}=[{}^{0}{{x}_{{{j,k}}}}, {}^{0}{{y}_{{{j,k}}}}]$ and ${\varvec{P}}_{k}=[{}^{0}{{x}}_{k},{}^{0}{{y}}_{k},{}^{0}{{z}}_{k}]$, $k=1,...,N$, respectively. The system state was constructed by multiple mobile bases at kth time step is ${\varvec{M}}_{k}=[{\varvec{m}}_{1,k}^T, {\varvec{m}}_{2,k}^T, {\varvec{m}}_{3,k}^T,{\varvec{m}}_{4,k}^T]^T$. Therefore, the system state of MCDPR at kth time step can be expressed as ${{{\varvec{X}}}_{k}}=[{\varvec{P}}_{k}^{T}, {\varvec{M}}_{k}^{T}]^T$.

The MCDPR involves planning the movement of multiple mobile bases in a constrained environment with internal and external constraints. To simplify the computation, the mobile bases and obstacles are modeled as cylindrical structures. At each time step, the path planning algorithm takes into account the following constraints for the jth mobile base:

$$\begin{aligned}{} & {} \left\| {{{\varvec{m}}}_{h,k}}-{{{\varvec{m}}}_{j,k}} \right\| >L_m, \,\text {for}\ h=1,..,4,\, {h}\ne {j} \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \left\| {{{\varvec{m}}}_{j,k}}-{{{\varvec{o}}}_{q}} \right\| >r_m+r_o, \,\text {for}\ q=1,..,s, \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \beta _{j,k}=\text {cos}^{-1}\frac{{\varvec{d}}_{j,k-1}\cdot {\varvec{d}}_{j,k}}{\Vert {\varvec{d}}_{j,k-1}\Vert \Vert {\varvec{d}}_{j,k}\Vert }<\beta _\textrm{max} \end{aligned}$$

(6)

where (4)–(6) impose the distance and angle constraints of mobile bases. Equation (4) imposes a distance constraint between the current mobile base position ${\varvec{m}}_{j,k}$ and the positions of other mobile bases ${\varvec{m}}_{h,k}$, ensuring a minimum separation distance $L_m$ between them and promotes safe navigation for the MCDPR. Equation (5) represents a distance constraint between the mobile base position ${\varvec{m}}_{j,k}$ and the positions of obstacles ${\varvec{o}}_q$, which ensures that the distance between the mobile base and any obstacle is greater than the sum of their respective radii, $r_m$ and $r_o$, to prevent collision between the MCDPR and obstacles. To address the nonholonomic constraints, the algorithm uses directional vectors ${\varvec{d}}_{k}={\varvec{m}}_{j,k}-{\varvec{m}}_{j,k-1}$ in Eq. (6), which represent the movement of the mobile base between adjacent states ${\mathscr {M}}_{j}$. The algorithm ensures smooth and continuous movement of mobile bases by imposing a limit on the maximum turning angle, denoted by $\beta _\textrm{max}$. Moreover, due to the limited workspace and cable length of the CDPR, the end-effector requires to satisfy the following constraints

$$\begin{aligned}{} & {} \left\| {{{\varvec{c}}}_{k}}-{{{\varvec{b}}}_{k}} \right\| >L_c \end{aligned}$$

(7)

$$\begin{aligned}{} & {} l_\textrm{min}\le \left\| [{{{\varvec{m}}}_{j,k}}^T \;{{{h}}_{i}}]^T - {\varvec{P}}_{k} \right\| \le l_\textrm{max}, \,\text {for}\; i=1,2 \end{aligned}$$

(8)

$$\begin{aligned}{} & {} {\varvec{P}}_k \in {\mathcal {W}}_k \end{aligned}$$

(9)

where $\varvec{c_k}$ and $\varvec{b_k}$ denotes the two closest point between cables and obstacles at kth time step, respectively. Therefore, Eq. (7) ensures a safe distance $L_c$ between the cables and obstacles, preventing collisions and maintaining the safety of the MCDPR system. Equation (12) imposes a constraint on the cable lengths by limiting them to lie within the range $l_\textrm{min}$ and $l_\textrm{max}$, which ensures that the cable lengths are within acceptable limits and facilitates the proper functioning of the MCDPR. Moreover, Eq. (9) specifies that the end-effector’s position ${\varvec{P}}_k$ should lie within the defined workspace ${\mathcal {W}}_k$ to ensure the end-effector to operate within the designated workspace, allowing the MCDPR to perform its intended tasks effectively.

Let ${\mathcal {X}}({\varvec{M}},{\varvec{P}}) \subset {\mathbb {R}}^{2p+3}$ denotes the state space of MCDPR and the obstacle space ${\mathcal {X}}_{obs}\subseteq {\mathcal {X}}$ refers to the states that the robot collides with the obstacle. The free space that satisfy (4)–(9) contraints given by ${\mathcal {X}}_{free}\subseteq {\mathcal {X}}/{\mathcal {X}}_{obs}$. Let $\Sigma _{k}$ denote the set of feasible trajectories obtained by the proposed method at time k. The autonomous navigation problem for MCDPR can be defined by

$$\begin{aligned} \begin{aligned}&{{\sigma }^{{*}}} = \underset{\sigma \in \!\!\Sigma _{k}\!\!}{\mathop {\text {argmin}}}\,c(\sigma ) \\&\text {s}\text {.t}\text {. }\sigma \text {(0)} = {{{\mathcal {X}}}_{{init}}} \\&\quad \, \sigma \text {(}{{t}_{f}}\text {)}\in {\mathcal {X}}_{goal}\\&\quad \, \sigma \text {(}t\text {)}\in {{{\mathcal {X}}}_{free}}(t),\forall t \,\,\in \,\, [\text { 0,}{{t}_{f}}]{.} \\ \end{aligned} \end{aligned}$$

(10)

where ${\mathcal {X}}_\textrm{init}$ and ${\mathcal {X}}_\textrm{goal}$ denote the initial and goal state of mobile bases. $c:\Sigma \mapsto {\mathbb {R}}\ge 0$ is the defined cost function for MCDPR. In the next section, we will discuss the details of the aforementioned problem and propose the sampling-based motion planning method to solve it in real-time.

Method description

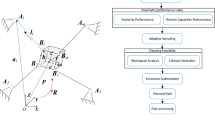
We now present the sampling-based method to deal with the autonomous navigation problem for MCDPR. The proposed method utilizes RRT-based approach to generate feasible trajectories at each time step by constructing a tree-structured graph, denoted by $\mathcal {T(V,E)}$, where V is the set of nodes representing the state of mobile bases ${\varvec{M}}$ and ${\mathcal {E}}$ is the set of edges connecting them with state transition. The proposed method is summarized in Algorithm 1.

Algorithm 1

Multi Time-based RRT (MTB-RRT)

In Algorithm 1, the complete loop of the suggested method includes several steps or stages that are carried out in a specific sequence. Checking the feasibility of the initial state is the first step in this process, and it is essential for ensuring that the method can proceed successfully. If the initial state satisfies (4)–(9), the initial state has been assigned as the root of the tree ${\mathcal {T}}$. If the goal point has not been reached, we observe the current state of MCDPR ${\mathcal {X}}_{k}({\varvec{M}}_{k},{\varvec{P}})$, which can be done by using vision-based simultaneous localization and mapping (SLAM) technique and also the state of obstacles can be estimated using RGB-D camera. Based on the observed state of both MCDPR and the environment, the tree ${\mathcal {T}}_{k}$ is constructed during limited time step $\Delta t$. After the tree has been constructed, a series of feasible trajectories of mobile bases ${\varvec{M}}_{k}^P$ are obtained by continuously propagating the sub-node of the parent node and the optimized trajectories with minimum cost, ${\varvec{M}}_{k}^{P^*}$, can be generated.

Consequently, each state in ${\varvec{M}}_{k}^{P^*}$ represents a specific configuration of four mobile bases and is denoted as ${\varvec{M}}_{k}$. For each ${\varvec{M}}_{k}$, a sequence of potential end-effector positions ${\varvec{P}}_{k}^{M}$ are sampled and the best end-effector position ${\varvec{P}}_{k}^{*}$ is obtained by minimizing the given cost. By continuously accumulating nodes ${\varvec{P}}_{k}^{*}$, the final path of the end-effector ${\varvec{P}}_{k}^{P^{*}}$ can be generated, and the trajectory for MCDPR that minimizes a given cost function $\sigma _{k}^{*}$ can be found. In cases where the set $\sigma _{k}^{*}$ is found to be empty, indicating the absence of a feasible trajectory, the Brake() function is invoked to bring the robot to a halt until a new viable trajectory can be generated. This mechanism ensures that the robot does not proceed with an invalid or unsafe trajectory, thereby preventing any undesired actions or potential hazards. Otherwise, the tree will be updated to obtain a new tree ${\mathcal {T}}_{k+1}$ for the next loop. Finally, the MCDPR is controlled to follow $\sigma _{k}^{*}$ for one-time step.

Fig. 3

Illustrations of proposed sampling-based path planning method for CDPR moving obstacle avoidance. Every node on the tree is feasible in its time stamp according to the prediction of the moving obstacle. a Time-based tree was constructed with a certain depth. b Optimal trajectory was obtained from the tree. c Delete additional branches and move one step

The proposed tree construction method was illustrated in Fig. 3. For more clarity and to avoid overlap, we only show two trees associated with ${\mathcal {M}}_{1}$ and ${\mathcal {M}}_{2}$, in which $^q{\varvec{M}}_{i,j}$ represent the qth node on the ith tree of jth mobile base. For every time interval, the feasible tree is constructed shown in Fig. 3a, and the depth of the tree is limited to accommodate the unknown environment. Hence, a series of feasible trajectories can be generated by continuously propagating from the leaf node to the root node. As shown in Fig. 3b, five feasible trajectories can be found and the final following trajectory is obtained by using the cost function. During the MCDPR follow the trajectory in one step, the tree is pruned and unnecessary branches are removed for growing a new tree, as shown in Fig. 3c.

Multiple tree extension and rewiring

In this subsection, the tree extension algorithm is presented in detail. As shown in Algorithm 2, the feasibility of the remained tree ${\mathcal {T}}_{k}$ is checked. In certain situations where the environment significantly changes, some branches of the algorithm may not be feasible or practical to execute, which can negatively impact the real-time performance of the algorithm.

After the feasibility of the ${\mathcal {T}}_{k}$ is checked, the algorithm proceeds in a loop, where in each iteration, it generates a new state ${\varvec{M}}_\textrm{new}$ for the robot using adaptive sampling, which is a sampling strategy that attempts to bias the sampling towards unexplored areas of the state space. As a result, for the case of four mobile bases, we only need to sample an 8-dimensional vector, and for each subtree comprising the mobile bases, a two-dimensional vector suffices for sampling. This dimension reduction enables the acquisition of valid nodes within small time intervals, addressing the challenges associated with handling such high-dimensional data in the algorithm. Then, the algorithm attempts to connect this new state to the nearest node in the tree ${\varvec{M}}_\textrm{nearest}$ using a steering function, which generates a path from the nearest node to the new state. Moreover, ${\varvec{M}}_\textrm{new}$ are obtained with a fixed expansion angle ${\varvec{M}}_\textrm{new}={\varvec{M}}_\textrm{near}+\eta *[\cos (\theta ), \sin (\theta )]$. If ${\varvec{M}}_\textrm{new}$ is feasible by checking constraints (Eqs. 4–9), then the new state is added to the tree as a new node, and an edge is added to connect it to the nearest node.

Algorithm 2

MultiTreeExtend

Furthermore, the heuristic method of Algorithm 2 was introduced, which aims to optimize the path by utilizing neighbor vertices. After generating a feasible new node ${\varvec{M}}_\textrm{new}$, its neighbor vertices were obtained, denoted as ${\mathcal {M}}_\textrm{near}$, by employing a search radius $r^*$. Specifically, each ${\varvec{m}}_{\textrm{near},j}$ that is directly connected to ${\varvec{m}}_{\textrm{new},j}$ and attempts to minimize the heuristic cost. Here, $h({\varvec{M}}_\textrm{new})$ represents the total path length from the initial node ${\varvec{M}}_\textrm{init}$ to ${\varvec{M}}_\textrm{new}$. However, assigning ${\varvec{m}}_{\textrm{near},j}$ as the parent node may disrupt the tree structure, leading to vertex disjunction. To address this issue, ReSetParent() method was proposed, which resets the passed vertices on the edge (${\varvec{m}}_{\textrm{near},j}$, ${\varvec{m}}_{\textrm{new},j}$) while preserving the parent node. By adopting this approach, we ensure the stability of the tree structure and maintain the integrity of the graph. The Heuristic method and the ReSetParent() technique are specifically designed to enhance the algorithm’s efficiency and reliability. Through careful selection of neighbor vertices and preservation of the tree structure, our algorithm is capable of generating high-quality paths that satisfy the given constraints and objectives.

Finally, the algorithm iteratively executes this process until the time limit is reached. The resulting final tree represents a feasible path from the current root state to the goal state, providing guidance for the robot to traverse along the determined trajectory. This approach ensures that the robot can navigate the environment effectively and reach the desired goal state.

Feasible paths generation for the end-effector

After the RRT tree ${\mathcal {T}}_k$ is obtained from Algorithm 2, the path for mobile bases ${\varvec{M}}_{k}^{P^*}$ can be generated by consecutively finding ${\varvec{M}}_\textrm{parent}$ from the root of the tree. In this work, the grid sampling method is developed to generate the feasible path for the end-effector, and the proposed method is shown in Algorithm 3.

Algorithm 3

Grid Sampling Method

Fig. 4

illustration of the path planning for end-effector

Fig. 5

Results of simulation and verification in CoppeliaSim. The red, green, blue, yellow, and black represent the ${\mathscr {M}}_1$, ${\mathscr {M}}_2$, ${\mathscr {M}}_3$, ${\mathscr {M}}_4$ and the end-effector a, b t = 0 s. c, d t = 6 s. e, f t = 12 s. g, h t = 18 s. i, j t = 24 s. k, l t = 30 s

The Algorithm 3 takes two inputs: ${\varvec{P}}_{P}^{k}$ and Q. ${\varvec{P}}_{P}^{k}$ represents the current state of an end-effector, which denotes the three-dimensional coordinates of the end-effector. Q is a user-defined parameter that specifies the number of cells to be generated in the search area. The algorithm first checks the current state of the end-effector, denoted as ${\varvec{M}}{k}^{*}$. This step is necessary to determine the starting position for the search. The algorithm then determines the search area, denoted as ${\mathcal {S}}{p}$, which is a circular region around the current end-effector position with a radius of $r_s$. Next, the algorithm discretizes the search area into Q cells, denoted as ${c_{1},...,c_{Q}}$. Each cell represents a possible location for the end-effector. The algorithm then iterates over each cell to determine if it is a feasible location for the end-effector to move to. If a cell is not feasible, the algorithm skips it and moves on to the next cell. If a cell is feasible, it is added to the output set ${\varvec{P}}_{k}^{M}$, which contains all the feasible locations for the end-effector to move to. Finally, the algorithm returns ${\varvec{P}}_{k}^{M}$ as the output.

Cost function

In this subsection, the cost functions for generating the optimal path for the mobile bases and the end-effector are presented. For mobile bases, the $\text {FindCheapest}({\varvec{M}}_{k}^P,{\mathcal {X}}_\textrm{goal}, {\mathcal {X}}_\textrm{obs}$) function in Algorithm 1 was used to obtain the optimal paths for mobile bases by minimizing the following cost function ${c}_{m}$, which consists of three terms, considering the state error, potential collision avoidance, and the distance to the target.

$$\begin{aligned} {{c}_{m}}=\sum \limits _{k=1}^{Q}{{{J}_{r}}({\varvec{M}}_{k}^{p}, {\varvec{M}}_{{{k}_\textrm{ref}}}^{p})+{{J}_{c}}({\varvec{M}}_{k}^{p}, {\mathcal {X}}_\textrm{obs})+{{J}_{g}}({\varvec{M}}_{l}^{p},{\mathcal {X}}_\textrm{goal})} \end{aligned}$$

(11)

Where the first term ${J}_{r}({\varvec{M}}_{k}^{p},{\varvec{M}}_{{k}_\textrm{ref}}^{p})$ penalizes the deviation of the predicted state ${\varvec{M}}_{k}^{p}$ from the desired state vector ${\varvec{M}}_{{k}_\textrm{ref}}^{p}$ in a quadratic sense. It measures the difference between these two states using the $Q_{m}$-weighted Euclidean norm, encouraging the mobile bases to closely follow the desired trajectory as shown follows

$$\begin{aligned} {J}_{r}({\varvec{M}}_{k}^{p},{\varvec{M}}_{{k}_{ref}}^{p})=\Vert {\varvec{M}}_{k}^{p}-{\varvec{M}}_{{k}_\textrm{ref}}^{p} \Vert _{Q_{m}}^2 \end{aligned}$$

(12)

The collision cost term in (11), $J_{c}({\varvec{M}}_{k}^{p},{\mathcal {X}}_\textrm{obs})$, is shown in (13) and designed to avoid collisions with obstacles. It is computed as a sum over all obstacles, where each term considers the distance between the predicted state ${\varvec{M}}_{k}^{p}$ and a specific obstacle. This term utilizes the logistic function to create a smooth and bounded cost function, with $Q_{c,q}$ and $k_{q}$ as tuning parameters controlling its shape and sensitivity.

$$\begin{aligned} J_c=\sum \limits _{q=1}^{s}{\frac{{{Q}_{c,q}}}{1+\exp {{k}_{q}}(\left\| {\varvec{M}}_{k}^{p}-{{{\varvec{o}}}_{q}} \right\| -{{r}_{m}}-{{r}_{o}})}} \end{aligned}$$

(13)

Moreover, the cost-to-go function is given by ${{J}_{g}}({\varvec{M}}_{l}^{p},{\mathcal {X}}_\textrm{goal})$ can be expressed in (14). aims to guide the mobile bases to reach the goal state quickly. It measures the distance between the leaf node ${\varvec{M}}_{l}^{p}$ in the path ${\varvec{M}}_{k}^{p}$ and the goal state ${\mathcal {X}}_\textrm{goal}$. The $G_{m}$-weighted Euclidean norm is used to compute this cost, providing a measure of how close the mobile bases are to reaching the goal.

$$\begin{aligned} J_g=\Vert {\varvec{M}}_{l}^{p}-{\varvec{M}}_\textrm{goal} \Vert _{G_{m}}^2 \end{aligned}$$

(14)

After obtaining the final following path of the mobile bases, denoted as ${\varvec{M}}_{k}^{P^*}$, the path for the end-effector can be obtained using the GridSampling (${\varvec{M}}_{k}$) function. The optimal path for the end-effector, denoted as ${\varvec{P}}_{k}^*$, is then determined by the FindBest(${\varvec{M}}_{k}$) function by using following equation

$$\begin{aligned} J_{e}=\alpha \gamma _{k}+\beta \gamma _{s} \end{aligned}$$

(15)

where kinematic cost, $\gamma _{k}=\sqrt{\det ({\varvec{J}}{\varvec{J}}^T)}$, measures the manipulability of the robot along the trajectory, which is computed based on the determinant of the Jacobian matrix, providing information about the robot’s ability to perform desired tasks effectively. Moreover, The smoothness cost, $\gamma _{s}$, characterizes the smoothness of the trajectory. It evaluates the squared differences between consecutive points in the path, ${\varvec{P}}_{k+1}^{M} - 2{\varvec{P}}_{k}^{M} + {\varvec{P}}_{k-1}^{M}$, where ${\varvec{P}}{k}^{M}$ represents the position of the end-effector at time step k. This term promotes smooth and continuous motion of the end-effector. The weighting factors $\alpha$ and $\beta$ determine the relative importance of dexterity, obstacle avoidance, and smoothness costs in the overall evaluation. These factors can be adjusted according to the specific requirements of the application, allowing customization of the optimization process based on desired priorities.

Method validation

Initialization set-up and results

Within this section, we present a series of simulations aimed at demonstrating the effectiveness and efficiency of our proposed algorithm. The cluttered environment in which the simulations are performed consists of the dynamic model of our MCDPR prototype, developed through the utilization of the CoppeliaSim (formerly V-REP) robot simulator software [32]. Specifically, we have implemented ten obstacles within the environment, all of which are modeled as cylinders with varying radii of 0.15 m, 0.25 m, and 0.4 m. These obstacles possess an equivalent height of 0.4 m and are randomly positioned throughout the environment. Additionally, five distinct goal points have been designated around the dark blue obstacle, which serves as the target obstacle where the robot executes tasks, such as picking and/or releasing operations.

Fig. 6

Simulation environment developed using CoppeliaSim software [32]

Table 1 Simulation parameter

The proposed method is initialized using the parameters listed in Table 1. To achieve high accuracy during the consecutive state transition from ${\varvec{X}}_{k}$ to ${\varvec{X}}_{k+1}$, a relatively small $\Delta t$ of 0.5 s is used in this work. If $\Delta t$ is too large, more nodes can be explored, but there is also a higher likelihood of overskipping or overlooking obstacles in the environment. Moreover, $\Delta t$ is a constant in this work to maintain the integrity and coherence of the tree structure, as changes in sample spacing may disrupt connectivity and introduce computational complexity. For each ${\varvec{M}}_{k}^{p}$, a set of pulleys’ coordinates can be determined using $h_1=0.285$ m and $h_2=0.926$ m. As a result, the mass center of the mobile base can be directly obtained from the MCDPR dynamic model in CoppeliaSim, which is given by $[0.12, 0.34, 0.36]^T$ with respect to $O_pj$ coordinate system. Therefore, $\gamma _{k}$ and $\gamma _{s}$ can be computed based on the configuration of the mobile bases.

The results of the simulation depicted in Fig. 5 demonstrate the generation of feasible paths for both the mobile bases and end-effector in each time interval. The final paths for both the end-effector and mobile bases are highlighted in bold and determined by minimizing Eqs. 11 and (15). As the maximum tree length is constrained, it is observed that the tree’s predicted distance during growth is limited by assuming the tree is confined by the unknown aspects of the environment and sensor accuracy. Furthermore, in this simulation, we can acquire specific states of the robot and obstacles through the software, which allows for the direct acquisition of feasibility detection within the algorithm. Figure 7 illustrates the variation of the end-effector’s z-coordinate. One should note that the end-effector’s z-coordinate is determined by using the cost function (15). In order to illustrate the impact of path optimization, we conducted a comparative analysis of the performance change in the end-effector movement with and without optimization. As all obstacles were set to the same height of 0.4 ms, the non-optimized process involved fixing the Z-coordinate of the end-effector at 0.43 m to ensure collision avoidance and the results were shown in Fig. 9. The behavior of $J_e$ with respect to a fixed Z-coordinate exhibits an initial marginal increase followed by a subsequent decline with oscillatory patterns. Conversely, with the implementation of optimization processes, $J_e$ experiences a rapid escalation and oscillates at higher levels. This phenomenon exemplifies the efficacy of the optimization techniques utilized.

Fig. 7

z-coordinate of the end-effector

Fig. 8

Relative distance change with time

Fig. 9

Performace $J_e$ Comparison

To streamline the problem, the end-effector is represented as a single point to facilitate collision detection. Figure 8 depicts the three minimum distances that pertain to mobile bases/mobile bases, mobile bases/obstacles, and cables/obstacles. It is noteworthy that the distance constraints specified by Eqs. (4), (5), and (7) can be met by adhering to the aforementioned distances.

Fig. 10

Velocity profiles of MCDPR during the simulation

MCDPR verification in CoppeliaSim

In this section, we demonstrate the resulting MCDPR trajectories $\sigma ^*$ in each iteration are simulated in the CoppeliaSim environment to verify the proposed method. The software simulation framework is depicted in Fig. 11, which describes a process for simulating the proposed method for MCDPR. The process begins with the input of parameters required for the simulation. These parameters could include the robot’s physical characteristics, the properties of the environment, and the initial conditions of the simulation. Once the parameters have been inputted, the next step is to create the simulation environment and load the MCDPR model in which the simulation will take place. Then, the simulation will continue to run until the robot has reached the target.

Fig. 11

Software simulation framework

In the course of the simulation, the state of the robot is acquired periodically and a path is generated by using the proposed MTB-RRT method for the robot to follow. Next, control commands are computed based on the generated path. Then, control directives are derived based on the path that was generated. To control the mobile bases, the continuous velocity profiles of the mobile bases are transformed into the rotational velocities of the mobile base’s wheels via its kinematic model. As demonstrated in Fig. 10, the continuity of the velocity profiles of the mobile bases and the end-effector is guaranteed in each iteration. In addition, to control the end-effector, we use (1) and (2) to regulate the length and speed of the cables shown in Fig. 12. The obtained rotational velocities of the wheels are dispatched to the revolute joints linked with the wheels to control the mobile bases in the simulation software CoppeliaSim. Besides, the length of the cable can be regulated via prismatic joints connected with the cables. As a result, the MCDPR model is actuated by these joints. The state of the MCDPR can be directly obtained from the CoppeliaSim throughout the movement, which will be compared with the intended path to obtain the error.

The simulation clips presented in Fig. 5 demonstrate that the MCDPR effectively adheres to desired paths while successfully avoiding collisions. Additionally, Fig. 13 depicts the discrepancy between the simulated MCDPR’s actual path and the desired path, revealing a maximum error of roughly 3.8 cm at both the mobile base and end-effector. These findings confirm the validity and stability of the proposed motion planning method. These results demonstrate the feasibility of utilizing the MCDPR for complex tasks requiring precise control and maneuverability in dynamic environments.

Experimential verification

Experimental setup

The proposed approach has been experimentally validated using a self-built MCDPR. A specific scenario was designed, wherein the MCDPR passed through the first obstacle illustrated in Fig. 5. The MCDPR system in our study utilized the NVIDIA Jetson Nano Developer Kit as the control computer, which plays a crucial role in orchestrating the operation of the MCDPR by transmitting the prescribed cable lengths and mobile base velocities necessary for its functioning. To enhance the system’s perception capabilities, an RGB-D camera was strategically mounted on the mobile base. This camera facilitated environment sensing, enabling the MCDPR to capture visual and depth information about its surroundings. Prior to conducting the experiment, the cables were pre-tensed to 20 N to ensure that cable tension remained positive during MCDPR movement. Moreover, the MCDPR incorporates two primary control systems. First, for the end-effector control, an inverse kinematic approach (equation 2) was employed to regulate its position accurately, which enables the determination of joint angles or cable lengths necessary to achieve the desired end-effector position, considering the kinematic constraints of the system. The control strategy for the mobile base systems involved the utilization of a differential drive control algorithm. This algorithm facilitates the tracking of a reference path by computing the required velocities of the left and right wheels of the robot.

Fig. 12

Cable length change

Fig. 13

Error between the actual and the desired position

Vision system

In this work, a vision system was designed to enable the MCDPR to accurately perceive its surroundings and determine its location. By leveraging the acquired self-state and environmental data, the proposed MTB-RRT algorithm consistently generates feasible paths for the MCDPR to navigate. To detect the obstacle, the YOLOv5 pre-trained model was employed, which can detect 80 different object categories [33]. YOLOv5 is a popular object detection algorithm that builds upon the success of the YOLO (You Only Look Once) family of models. It is a state-of-the-art real-time object detection system that achieves high accuracy and fast inference speeds. The YOLOv5 pre-trained model will output bounding boxes that indicate the location and size of each detected object. Moreover, the visual odometry simultaneous localization and mapping(OdoSLAM) was used [34]. In visual OdoSLAM, visual features such as corners or edges are detected and tracked over time to estimate the camera or robot’s motion. By comparing the location of visual features between consecutive frames, visual OdoSLAM can estimate the relative pose of the camera with respect to the environment and thus the location of MCDPR can be realized.

Experimental results

The experimental results presented in Fig. 17 provide compelling evidence of the effectiveness of the MTB-RRT algorithm in acquiring accurate information about the robot’s state and detecting the presence of obstacles. In the depicted scenario, as illustrated in Fig. 17a, the algorithm demonstrates its capability to identify the green static obstacle. Subsequently, by employing sampling and tree construction techniques in the state space, the algorithm successfully generates an optimal path that enables the robot to avoid the obstacle, as depicted in Fig. 17b. These experimental findings serve as a testament to the robustness and efficacy of the proposed algorithm in addressing obstacle avoidance challenges. The consistent acquisition of pertinent information and the ability to generate obstacle-free trajectories further validate the performance and potential of the MA-RRT algorithm.

Fig. 14

Illstruation of YOLOv5

Fig. 15

Illstruation of OdoSLAM

Fig. 16

Framework of vision system

Fig. 17

Experimental results

Evaluation

Within this section, the comparative analysis of our proposed online motion planning method for MCDPRs against existing approaches was conducted. To ensure a fair evaluation, we specifically selected sampling-based online path planning methods for comparison. Our assessment encompassed three key aspects: path length, simulation time, and kinematic performance ($J_e$). To account for the stochastic nature of the proposed method, a comprehensive batch evaluation consisting of 1000 simulations was conducted. To ensure the realism and complexity of the scenarios, the environment was randomly generated for each simulation, carefully controlling the location, size, and number of obstacles. The maximum number of obstacles was limited to nine, and their sizes were randomly assigned across three distinct scenarios. However, the starting and target points remained consistent throughout. This deliberate manipulation of obstacle characteristics aimed to create diverse and challenging environments, allowing for the evaluation of the proposed online motion planning approach’s robustness and adaptability. By incorporating varying obstacle sizes and configurations, the study aimed to assess the method’s performance in handling complex and unpredictable scenarios that resemble real-world conditions. The random generation of the environment provided a comprehensive assessment of the method’s effectiveness, offering valuable insights into its capabilities for navigating through diverse and challenging environments encountered in MCDPR applications. Finally, the average values resulting from these simulations were used to evaluate the performance of the proposed method. All simulations were performed using MATLAB, utilizing the CPU computations of an Intel i7-9750 CPU @ 2.60 GHz with a 32 GB RAM Windows 10 system. To ensure consistency and comparability, the initialization parameters employed in the previous simulations were retained for these evaluations.

Table 2 The evaluation result

The results of the batch evaluation are summarized in Table 2. The proposed method outperforms the other methods with a significantly reduced CPU time, which can be primarily attributed to the introduction of the proposed cost function (Eq. 11). This improvement represents an impressive enhancement of approximately 18.6% when compared to the fastest competitor, MRPT. Furthermore, the proposed method exhibits a shorter path length with a reduction of 26.8% compared to CL-RRT. Although Reduction-based RRT* has the shortest path length, it is important to acknowledge that its optimization process detrimentally affects real-time performance, thereby limiting its practicality for online motion planning scenarios. Furthermore, since the proposed algorithm takes into account the kinematic performance of the robot (Eq. 15), the kinematic performance of the proposed method is the highest compared to other methods, especially compared to Adaptive RRT, with an improvement of 86.3%. Unlike another recent method that may rely on extensive training processes or data-driven models in [25], the proposed algorithm can be directly implemented without requiring such preparatory steps. These results serve as compelling evidence, validating the effectiveness and superiority of the proposed approach in the realm of online motion planning for MCDPRs.

Conclusion and future work

This paper presents an online motion planning method tailored for MCDPR systems, enabling them to generate feasible trajectories in unknown environments. The method involves the continuous generation of a time-based tree through a sampling of the state space as the MCDPR moves. The heuristic approach was employed in each iteration to determine the final path. By considering various constraints and employing designed cost functions, the proposed method ensures constraint satisfaction while maximizing system performance. Simulation in a complex environment using CoppeliaSim demonstrates that the technique creates practical trajectories for mobile bases and the end-effector within a shorter duration, resulting in enhanced kinematic performance and path quality. Empirical testing on a self-built MCDPR prototype, incorporating a vision system with YOLOv5 for environment perception and OdoSLAM for self-localization, validates the approach’s validity. The simulation and experimental results substantiate the reliability of the proposed method.

Despite the promising performance of the proposed approach in real-world operations such as picking and releasing, there are several challenges that require further attention. Limited computational resources can impact execution time and overall performance. Environmental disturbances, including uneven terrain, dynamic obstacles, and varying lighting conditions, complicate trajectory planning. The parameter settings of the proposed method were based on experience and algorithm generality, necessitating further experiments and simulations to optimize performance. The assumption of prior knowledge of obstacle locations in simulations reduces viable trajectories in real-world scenarios. Imposed speed limits on mobile base and end-effector motions were necessary for localization accuracy, but exploring safe higher-speed operation remains a future research direction. Future work aims to enhance the intelligence and adaptability of MCDPR systems in navigating complex environments, contributing to their versatility and applicability in real-world operations.