Introduction

Cable-driven parallel robots (CDPRs) are categorized as a particular type of parallel manipulator. In CDPRs, multiple flexible cables that reel around a fixed winch-pulley system are responsible for actuating the end-effector to the desired position. Owing to the large workspace and higher payload-to-weight ratio, CDPRs are promising for several industrial applications such as picking and placing heavy loads, grasping, space and terrestrial applications [1,2,3].

Although CDPRs provide significant advantages in numerous applications, several challenges still exist. As an example, CDPRs are generally available with a large workspace, which imposes a strong requirement for the safety issue [4]. The radiate structure of cables increases the risks of cable–cable and cable–environment interferences, especially when CDPRs have a large number of cables in a cluttered environment [5]. Due to the conventional CDPRs having a fixed frame, the cable span dominates a large space during the motion of the end-effector [6], which results in restricted flexibility for CDPR.

Fig. 1
figure 1

A self-built MCDPR prototype that is designed to perform a variety of manipulation tasks in a complex environment

Full size image

Consequently, CDPRs require further development to improve adaptation to environmental and task requirements [7]. Based on the concept of reconfiguration, reconfigurable cable-driven parallel robots (RCDPRs) were developed, in which the cable’s attachment points on the frame and the cable’s anchor points on the end-effector of pulleys can be altered [8]. However, the existing RCDPR systems have limited reconfigurability, such as having a guideway with limited length or requiring manual intervention. These drawbacks of conventional RCDPRs lead the reconfigurable operations to be time-consuming and costly to use.

To extend the reconfigurability of RCDPRs, as shown in Fig. 1, a mobile cable-driven parallel robot (MCDPR) is developed in this work to make it automatically be configured according to the desired task. The developed MCDPR is composed of a six degree-of-freedom (DoF) end-effector pulled by eight cables mounted on four mobile bases. A mobile base consists of a differential wheeled robot and a lifting column. Thus, MCDPR can be moved freely with the wheeled robots, and the position of the pulley can be adjusted by using the lifting column.

However, the kinematical redundancy of MCDPRs is increased due to more DoF given by additional mobile bases. These mobile bases are coupled to each other by multiple cables, resulting in complex constraints and a high-dimension regime. In addition, the mobile base is susceptible to cable tension and becomes unstable, which also affects the available workspace for MCDPRs [9]. Hence, the path planning of MCDPRs becomes a challenging problem and requires to be addressed. In consequence, for displacing the end-effector from the starting point to its destination, feasible and optimal paths are required to be generated for each mobile base and the end-effector simultaneously.

For CDPRs, path planning is a challenging issue due to various constraints such as cable tension, workspace, collisions, and obstacle avoidance. In particular, MCDPRs involve in the high-dimensional cooperative pathfinding problem as a result of the coupled mobile bases and end-effector. Accordingly, Jiang et al [10] developed a dynamic point-to-point trajectory planning point trajectory planning method for a CDPR with six DoF. More recently, Idà et al. [11] proposed a rest-to-rest trajectory planning method of CDPRs with the given motion time and path profile. However, these studies only considered an underactuated CDPR in an environment without obstacles.

In a cluttered environment, it is critical for CDPRs to avoid obstacles. However, MCDPRs involve multiple moving parts such as cables and the end-effector must avoid the obstacles simultaneously. Furthermore, the multiple mobile bases of MCDPRs introduce more constraints increasing the complexity of the path planning problem. On the other hand, the sampling-based path planning algorithms perform well to deal with various constraints by randomly sampling the state space [12, 13]. Compared with other path planning techniques, they need less time to conduct the computation and can avoid obstacle accurately. The most representative sampling-based path planning algorithm is the Rapidly exploring Random Tree (RRT) method, which relies on a feasible checking module to generate a series of candidate trajectories for constructing a graph framework [14]. However, the conventional RRT method generally generates a path that comprises a significant number of redundant nodes. To address the optimality issue, some extensions of RRT like RRT* and informed RRT* are developed to obtain an asymptotically optimal solution [15, 16].

Accordingly, Bak et al. [17] proposed a modified RRT method to generate feasible paths for CDPRs, which takes advantage of the goal-biased sampling method and post-processing to mitigate the length of the path. Zhang et al. [18] designed a new dexterity-based cost function to accomplish collision-free path planning for CDPR by combining RRT* and potential field guidance (PFG) methods. Recently, Mishra et al. [19] proposed an AFG-RRT* method to generate optimized paths for CDPRs in cluttered environments. However, the above-cited methods only deal with the path planning for the end-effector, the multiple mobile bases and additional constraints are not involved.

For MCDPRs, the additional mobile bases lead to kinematical redundancy, and the path planning problem for MCDPRs becomes incrementally challenging. Rasheed et al. [20] developed an iterative algorithm to generate available paths for MCDPR. This approach is straightforward to traverse all possible pre-defined states of each mobile base, and the next state is identified by maximizing the wrench capacity. However, the traversal time cost increases exponentially with the possible states of the mobile bases and the quality of the obtained path is not desirable. To improve the path quality, the Direct Transcription method was proposed in [21], in which the trajectory is discretized according to the specific time step and the resulting paths are obtained by minimizing the goal function with a set of given constraints, but the optimization-based method is commonly time-consuming in terms of convergence.

In this work, we present an optimal sampling-based path planning algorithm for MCDPR. The proposed approach is capable of efficiently handling the multiple constraints and kinematic redundancies associated with the robot. In summary, the contributions of this paper are listed as follows:

  1. (1)

    First, an innovative high-dimensional tree structure is proposed in this paper. A distinctive characteristic is that we maintain the tree growth in the high-dimensional state space while preserving the tree to share information in the low-dimensional domain. Based on the growth state of the tree, we deploy a heuristic cost that allows the tree to be sampled adaptively in the subspace. Hence, the proposed method can generate the feasible path in a short time.

  2. (2)

    Second, various constraints of MCDPR such as mobile base/mobile base, mobile base/obstacle, cable/obstacle collisions, and the available configuration are considered. The dynamic control checking method is developed to smooth the path and satisfy kinodynamic constraints of the robot. Moreover, the heuristic method is designed to optimize the path and ensure the continuity of parent nodes. The optimal and smooth path can thus be obtained.

  3. (3)

    Third, two performance metrics are developed considering the stability and kinematics of MCDPR. Based on the performance metrics, the path of the end-effector is generated by using the proposed grid-search method. Finally, the resulting paths are simulated in complex scenarios using the MCDPR dynamic model developed by CoppeliaSim software and validated by prototype experiments.

The remainder of this paper is organized as follows: Robot parameterization and problem formulation are introduced in Section “System modeling” . The kinematics and stability model for MCDPRs is established in Section “Consideration” . In Section “Method description”, the proposed path planning method for MCDPRs is introduced in detail. The method validation is carried out in Section “Method validation”. Finally, Section “Conclusion and future work” concludes the research work.

System modeling

MCDPR parameterization

The self-bulit MCDPR in this work is composed of a classical redundantly constrained CDPR with eight cables (\(m=8\)) and a six DoF moving-platform (\(n=6\)) mounted on four mobile bases (\(p=4\)). As depicted in Fig. 2, the origin of the global coordinate system is represented as \(O_{0}\) and the local coordinate system located at the center of the end-effector is denoted as \(O_{e}\). The j-th mobile base, denoted as \(\mathscr {M}_j\), \(j = 1,...,4\) carries two cables (\(m_{j}=2\)) and has three wheels (\(c=3\)) including one caster wheel and two driven wheels. The local coordinate system attached to \(\mathscr {M}_j\) is denoted as \(O_{pj}\). The mobile base is characterized as the non-holonomic differential drive mechanism, it can provide two DoF translational motions and one DoF rotational motion.

Fig. 2
figure 2

Structural diagram of MCDPR

Full size image

Cables are assumed to be straight and massless. The end-effector is modeled as a cube. The cable exit point and the anchor point are represented as \(A_{ij}\) and \(B_{ij}\), respectively. Thus, i-th cable vector attached onto \(\mathscr {M}_j\) is denoted as \({\varvec{l}}_{ij}\), \(i=1,...m_{j}\).

Selecting the i-th closed-loop vector branch, \({\varvec{l}}_{ij}\) can be expressed as follows

$$\begin{aligned} {\varvec{l}}_{ij}= {\varvec{a}}_{ij}-{\varvec{P}}-{{\varvec{{R}}}}{\cdot }{}^{e}{\varvec{b}}_{ij} \end{aligned}$$
(1)

where \({\varvec{a}}_{ij}\) is the position vector of \(A_{ij}\) in \(O_{0}\) coordinate system. \({\varvec{P}}\) and \(\varvec{{R}}\) is a three-dimensional position vector and rotation matrix of the end-effector, respectively. \({}^{e}{\varvec{b}}_{ij}\) represents the position vector of \(B_{ij}\) in the moving coordinate system \(O_{e}\). To simplify the problem, we restrict the end-effector only perform the translational motion in this work.

Problem formulation

Due to the MCDPR is designed such that \(A_{ij}\) is lie on the axis \({}^{pj}z\) of \(\mathscr {M}_j\), the rotational of \(\mathscr {M}_j\) has no effect on \({\varvec{u}}_{ij}={\varvec{l}}_{ij}/\Vert {\varvec{l}}_{ij}\Vert \), which is the unit vector along the cable \({\varvec{l}}_{ij}\). We consider the state of mobile bases \(\mathscr {M}_j\) at k-th time step is \({\varvec{m}}_{j,k}=[{}^{0}{{x}_{{{j,k}}}}, {}^{0}{{y}_{{{j,k}}}}]\), \(k=1,...,N\). The state of the muti-robot system constructed by mobile bases at k-th time step is represented as \({\varvec{M}}_{k}=[{\varvec{m}}_{1,k}^T, {\varvec{m}}_{2,k}^T, {\varvec{m}}_{3,k}^T,{\varvec{m}}_{4,k}^T]^T \) in \(\mathbb {R}^{2p}\) and the state of the end-effector at k-th time step is \({\varvec{P}}_{k}=[{}^{0}{{x}}_{k},{}^{0}{{y}}_{k},{}^{0}{{z}}_{k}]\). Consequently, the state of MCDPR at k-th time step can be denoted as \({{{\varvec{X}}}_{k}}=[{\varvec{P}}_{k}^{T}, {\varvec{M}}_{k}^{T}]^T\).

Fig. 3
figure 3

MCDPR configurations

Full size image

The MCDPR involves various internal and external constraints that require to be considered during the path planning. To facilitate the computation, the mobile base and the obstacles are modeled as cylindrical structures. Hence, at each time step, the following constraints are imposed for j-th mobile base

$$\begin{aligned}{} & {} \!\!\!\left\| {{{\varvec{m}}}_{h,k}}-{{{\varvec{m}}}_{j,k}} \right\| >L_m, \,\text {for}\ h=1,..,4,\, {h}\ne {j} \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \!\!\!\left\| {{{\varvec{m}}}_{j,k}}-{{{\varvec{o}}}_{q}} \right\| >r_m+r_q, \,\text {for}\ q=1,..,s, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \!\!\!\left\| {{{\varvec{c}}}_{k}}-{{{\varvec{b}}}_{k}} \right\| >L_c \end{aligned}$$
(4)
$$\begin{aligned}{} & {} l_{min}\le \left\| [{{{\varvec{m}}}_{j,k}}^T \;{{{h}}_{i}}]^T - {\varvec{P}}_{k} \right\| \le l_{max}, \,\text {for}\; i=1,2 \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \!\!\!{\varvec{P}}_k \in {\mathcal {W}}_k \end{aligned}$$
(6)

Where (2–4) impose the distance constraints of the MCDPR in terms of mobile base/mobile base, mobile base/obstacle and cable/obstacle. \(L_m\) denotes the safety distance between two mobile bases. \(r_m\) and \(r_q, q=1,...,s\), represent the radius of the mobile base and the q-th obstacle, respectively. \({\varvec{o}}_q\) represents the position of q-th obstacle. \(\varvec{c_k}\) and \(\varvec{b_k}\) denotes the two closest point between MCDPR and obstacles at kth time step, respectively. Hence, (2) and (3) prevent the collision between mobile bases/mobile bases and mobile bases/obstacles. (4) prevent the collision between cables/end-effector with obstacles by using the minimum acceptable distance \(L_c\). Furthermore, (5) and (6) indicate that the CDPR have limited workspace and cable length, respectively. Let \(l_{min}\) and \(l_{max}\) denote the minimum and maximum length of cable. \(h_l,l=1,2\), denotes two constant heights of exit point \(A_{i,j}\) in the \(O_{0}\) coordinate system. For each \({\varvec{M}}_{k}\), the available workspace of the end-effector is given by \({\mathcal {W}}_k\).

Additionally, the MCDPR also requires to satisfy the nonholonomic and configuration constraints. Let \({\varvec{d}}_{k}={\varvec{m}}_{j,k}-{\varvec{m}}_{j,k-1}\) denotes the directional vector of \(\mathscr {M}_{j}\) between two adjacent states, (7) prevents the abrupt direction change of the mobile base to satisfy the non-holonomic constraints by using the maximum turning angle \(\beta _{max}\). As a result of mobile bases are coupled with cables, the MCDPR should maintain the initial formation shown in Fig. 3a, and the infeasible formation illustrated in Fig. 3b and c should be prevented to cause internal interferences, which indicates that the intersection of the line segment formed by connecting two mobile bases. We consider \(\theta _{j}\in [0,2\pi ]\) is the interior angle of \(\mathscr {M}_{j}\) shown in Fig. 3a is defined by (9), and \(\theta _{j}=\theta _{j}+2\pi \) if \(\theta _{j}<0\), (8) ensures the mobile bases do not cross each other during the motion.

$$\begin{aligned}{} & {} \!\!\beta _{j,k}=\text {cos}^{-1}\frac{{\varvec{d}}_{j,k-1}\cdot {\varvec{d}}_{j,k}}{\Vert {\varvec{d}}_{j,k-1}\Vert \Vert {\varvec{d}}_{j,k}\Vert }<\beta _{max} \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \!\!\theta _{j,k}\in [0,\pi ] \end{aligned}$$
(8)
$$\begin{aligned} \!\!{} & {} \theta _{j}= \text {atan2}({\varvec{u}}_{j,y},{\varvec{u}}_{j,x})-\text {atan2}({\varvec{u}}_{h,y},{\varvec{u}}_{h,x}) \end{aligned}$$
(9)

The composite state space of MCDPR \({\varvec{X}}={\varvec{M}}\times {\varvec{P}} \subset \mathbb {R}^{2p+3}\) is the Cartesian product of the individual spaces. We denote the free composite state space that satisfies constraints defined in (2–8) is \({\varvec{X}}_{free}\subseteq {\varvec{X}}\). Then, the optimal path planning problem for MCDPR is to find the feasible trajectory \(\pi :[0,t]\rightarrow {\varvec{X}}_{free}\) from an initial state \(\pi (0)={\varvec{X}}_{init}\) to the goal region \(\pi (t)\in {\varvec{X}}_{goal}\) that minimizes a given optimal function and obeys the system dynamics. In this work, the optimal function is defined to minimize the total path length.

Consideration

Kinematics performance

Due to additional mobile bases lead the kinematical redundancy of the MCDPR, the kinematics performance indicator is designed in this subsection to ensure excellent kinematics performance. Derivative of (1) with respect to time and lead the end-effector only perform translational motion, the velocity of the end-effector \(\dot{{\varvec{P}}}=[{}^{0}\dot{x}_{e}, {}^{0}\dot{y}_{e}, {}^{0}\dot{z}_{e}]^T\) can be expressed as follows

$$\begin{aligned} \left[ \begin{matrix} {{{\varvec{J}}}_{1}} \\ {{{\varvec{J}}}_{2}} \\ \vdots \\ {{{\varvec{J}}}_{j}} \\ \end{matrix} \right] \varvec{\dot{P}}=\left[ \begin{matrix} {{{\varvec{\dot{l}}}}_{1}} \\ {{{\varvec{\dot{l}}}}_{2}} \\ \vdots \\ {{{\varvec{\dot{l}}}}_{j}} \\ \end{matrix} \right] \end{aligned}$$
(10)

where \(\varvec{\dot{l}}_{j}=[\varvec{\dot{l}}_{1j},...,\varvec{\dot{l}_{m_{j}j}} ]^T\) denotes the speed vector of the cables on \(\mathscr {M}_j\), and \({\varvec{J}}_{j}\) can be expressed as

$$\begin{aligned} {{{\varvec{J}}}_{j}}=\left[ \begin{matrix} {{{\varvec{u}}}_{1,j}}^T \\ \vdots \\ {{{\varvec{u}}}_{{{m}_{j}}j}}^T \\ \end{matrix} \right] \end{aligned}$$
(11)

where \({\varvec{J}}_{j}\in \mathbb {R}^{m_j\times {2}}\) is the sub-Jacobian matrix associated with the cable actuation wrench on \(\mathscr {M}_j\). The kinematic jacobian matrix of the carried CDPR can be expressed as \({\varvec{J}}=[{\varvec{J}}_{1},...,{\varvec{J}}_{j}]^T\), which is associated with a specific position of the end-effector to map relationship from the end-effector velocity to the cable velocities.

Based on the kinematic jacobian matrix of the carried CDPR, the kinematic performance indicator is defined as the dexterity of the mechanism, which measures the accuracy of transmission between cable space and the Cartesian space of the end-effector. The dexterity of the robot can be obtained by the condition number of \({\varvec{J}}\), denoted as

$$\begin{aligned} \kappa= & {} ||{\varvec{J}}||\cdot ||{\varvec{J}}^{-1}|| \end{aligned}$$
(12)
$$\begin{aligned}{} & {} ||{\varvec{J}}|| =\sqrt{\lambda _{max}({\varvec{J}}^T{\varvec{J}})}=\sigma _{max}({\varvec{J}}) \end{aligned}$$
(13)

where, \({\lambda }_{max}\) is the maximum eigenvalues of square matrix \({\varvec{J}}^{T}{\varvec{J}}\), and \({\sigma }_{max}\) is the maximum singular value of \({\varvec{J}}\). The condition number of kinematic Jacobian matrix \(\kappa \in [1,\infty )\). Thus, \(\kappa \) is normalized to define the kinematics performance index \(\gamma _{k} \) expressed as

$$\begin{aligned} \gamma _{k}=1/\kappa \in [0,1] \end{aligned}$$
(14)

The better the kinematics performance can be obtained when \(\gamma _{k}\) is closer to 1, and the robot loses its control when \(\gamma _{k}=0\). Consequently, the larger \(\gamma _{k}\) should be remained during the path planning.

Stability performance

The additional mobile bases lead the MCDPR highly flexible. However, the mobile base is susceptible to cable tension and becomes unstable. Thus, the static equilibrium of the mobile base with its tipping condition is analyzed in this section to guarantee the better stability performance.

Fig. 4
figure 4

a Free body diagram of j-th mobile base. b Distribution of wheel contact points

Full size image

Figure (4) illustrates the free body diagram of j-th mobile base. \({\varvec{t}}_{ij}=-t_{ij}{\varvec{u}}_{ij}\) denote the cable tension vector along the cable \({\varvec{l}}_{ij}\), and \(t_{ij}\) is the cable tension. We define the wheel contact points of the mobile base \(\mathscr {M}_{j} \) as \(C_{nj}\), \(n=1,2,3\), in a counter-clockwise direction, and \({\varvec{c}}_{nj}\) denotes the Cartesian coordinate vector of \(C_{nj}\). The boundary between two successive contact points \(C_{nj}\) and \(C_{n+1j}\) is expressed as the \(\mathscr {L}_{C_{nj}}\), and the direction is described by \({\varvec{u}}_{C_{nj}}\). The equilibrium towards the tipping of a wheeled robot can be calculated by using Zero-Moment Point (ZMP) method [22], which depends on the moments generated at the boundaries. We consider \({\varvec{m}}_{C_{nj}}\) is the moment when \(\mathscr {M}_{j} \) loses contact with the ground that does not constitute the boundary \(\mathscr {L}_{C_{nj}}\),

$$\begin{aligned} \begin{aligned} {\varvec{m}}_{C_{nj}}=&{{\varvec{u}}_{c_{nj}}^T}(({{\varvec{g}}_{j}}-{{\varvec{c}}_{kj}})\times {{\varvec{w}}_{gj}})\\ {}&+\sum \limits _{i=1}^{m_{j}}{{{\varvec{u}}_{C_{nj}}^T}(({{\varvec{c}}_{kj}}-{\varvec{P}})\times {{\varvec{u}}_{ij}})}{t}_{ij} \end{aligned} \end{aligned}$$
(15)

where \({\varvec{g}}_{j}\) denotes the Cartesian coordinate vector of the center of gravity in \(\mathscr {M}_{j} \). \({\varvec{w}}_{gj}\) is the weight vector of \(\mathscr {M}_{j} \). To guarantee \(\mathscr {M}_{j} \) in static equilibrium, the following constraints are required to be satisfied.

$$\begin{aligned} {{m}_{C_{nj}}}<0,\;n=1,2,3 \end{aligned}$$
(16)

Equation (16) denotes the tipping conditions of \(\mathscr {M}_{j} \), it can be regarded as linear constraints in terms of the cable tensions \(t_{ij}\). In general, the cable tensions are all bounded between a minimum and positive tension \(t_{min}\) and a maximum tension \(t_{max}\). The feasible tension space of \(\mathscr {M}_{j} \) is represented as a square with side length \(\Delta t=t_{max}-t_{min} \). However, as shown in Fig. 5, the linear constraints in (16) reduce the feasible tension space to form the feasible tension polygon. We denote the area of \(\mathscr {M}_{j} \)’s feasible tension polygon is \(\mathscr {F}_{j} \). Since the cable tension has infinite solutions due to redundant actuation, we define the riskiest feasible tension polygon as

Fig. 5
figure 5

Feasible cable tension polygon of \(\mathscr {M}_{1},...,\mathscr {M}_{4}\)

Full size image
$$\begin{aligned} \mathscr {F}_{r}=\text {min}(\mathscr {F}_{r}),j=1,...,4 \end{aligned}$$
(17)

where \(\mathscr {F}_{r}\) indicates the feasible tension polygon with the smallest area, which can be obtained by corresponding vertices(i.e., \({\textbf {v}}_{13},{\textbf {v}}_{23},{\textbf {v}}_{33}\) in Fig. 5c). This polygon corresponds to a mobile base that is the most unstable to the cable tension and has a risk of tipping phenomenon. Hence, the stability performance of MCDPR can be defined as

$$\begin{aligned} {\gamma }_{s}={\mathscr {F}_{r}}/{\Delta t^{2}}\in [0,1] \end{aligned}$$
(18)

It can be observed from (18) that MCDPR is at the nest stability performance when \(\gamma _{s}=1\). However, when \(\gamma _{s}=0\), the MCDPR will tip and lose control due to the cable tension solution not satisfying the static equilibrium.

Method description

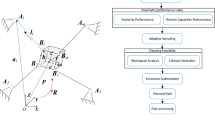
In this section, the path planning method of MCDPRs is described in detail. In Algorithm 1, the muti-agent RRT is proposed to generate feasible path \({\varvec{M}}_{path}=(^p{\varvec{M}}_{1},^p{\varvec{M}}_{2},...,^p{\varvec{M}}_{N})\) for mobile bases. For each state of mobile bases on the path \(^p{\varvec{M}}_{k}\), the position of end-effector \(^p{\varvec{P}}_{k}\) is determined by using the grid-based search method presented in Algorithm 3 with considering kinematic stability. Moreover, the corresponding high-level diagram of the proposed method is depicted in Fig. 6.

Path planning for mobile bases

The proposed multi-agent method aims to build a tree-structured graph \({\mathcal {T}}({\mathcal {V}},{\mathcal {E}})=({\mathcal {T}}_1,...,{\mathcal {T}}_4)\) by randomly sampling the state space. The vertices \({\mathcal {V}}\) represent feasible states of mobile bases \({\varvec{M}}_k\), and the edge \({\mathcal {E}}\) denotes the feasible transitions of two adjacent states. \({\mathcal {T}}_j,j=1,...,4\), denotes a sub-tree of \(\mathscr {M}_j\).

figure a
Fig. 6
figure 6

High-level diagram of the proposed method

Full size image

In Algorithm 1, the feasibility of the initial and goal state of mobile bases are checked first. Then, some attributes are assigned to vertices. \( {\varvec{M}}_{new}.\text {GoalArrived}\) is used to determine the arrival status of four mobile bases. The j-th element of \( {\varvec{M}}_{new}.\text {GoalArrived}\) is changed to 1 when \(\mathscr {M}_j\) arrive its goal point, and \(\mathscr {M}_j\) becomes fixed. \(M_{new}.\text {FailureRate}\) is the ratio of the number of failed expansions to total expansions. \({\varvec{M}}_{new}.\text {GoalExtend}\) is used to record whether the node can expand toward the goal point, and it changes to 1 if the expansion fails.

figure b

To solve the high-dimensional state space and increase efficiency, the adaptive sampling method (line 6 of Algorithm 1) is designed in Algorithm 2. The random node of \(\mathscr {M}_j\),\({\varvec{m}}_{rand,j}\), is assigned as the goal point if the parent node can successfully expand to the goal point. Otherwise, the proposed method can adaptively select two sampling methods based on \({\varvec{M}}_{parent}.\text {GoalExtend}\) and \({\varvec{M}}_{parent}.\text {FaiureRate}\). It should be noted that the proposed method is sampling in the subspace for each mobile base and integrated into high-dimensional space.

The ForwardSector(\({\varvec{m}}_{goal,j}\), \(r_{s}\),\(\theta _s\)) expands the sampling space to a sector to guide the tree towards the goal space in which the vertex is the goal point and \({\varvec{m}}_{c,j}\) denotes the subnode with maximum cost. \(r_{s}\) and \(\theta _s\) represent the radius and angle of the sector, representatively.The BackwardBall(\({\varvec{m}}_{centor}\), \(r_b\)) represents uniformly sampling in a circular area centered on the \({\varvec{m}}_{centor}\) with radius \(r_{b}\), and \({\varvec{m}}_{f}\) is the sub-node with maximum failure rate. Thus, the proposed method favors BackwardBall(\({\varvec{m}}_{centor}\), \(r_b\)) with the \({\varvec{M}}_{parent}.\text {FaiureRate}\) increasing.

Fig. 7
figure 7

Illustrations of proposed sampling-based path planning method for MCDPR. Every node on the tree is feasible in its time stamp according to the prediction of the moving obstacle. a Tree growth by using adaptive sampling and DCC method. b Tree was optimized by using the heuristic method. c One subtree reached its target. d Tree is constructed successfully after all subtrees reached the target

Full size image

Dynamic control checking and heuristic path optimization

In contrast to the conventional RRT, the Nearest( \({\varvec{M}}_{rand}\),\({\mathcal {T}}\),\(V_j\)) function (line 7 of Algorithm 1) returns a node \({\varvec{M}}_{nearest}\) closest to \({\varvec{M}}_{rand}\) by searching the remained tree to lead the mobile base fixed after it reaches the target, and the starting node of the remained tree is recorded as \(V_j\) (line 29 of Algorithm 1). In addition, to smooth the path and satisfy the kinodynamic constraints, the Steer(\({\varvec{M}}_{nearest}\),\({\varvec{M}}_{rand}\)) function in Algorithm 1 is developed based on the dynamic control checking method. As shown in Fig. 7a, each node on the tree has a set of possible control output \({\mathcal {U}}(u_k,\epsilon )\), which is constrained by the control input from the parent node and the inherent control constraints of the mobile base. According to the kinematic model of the mobile base [23], each control output \(u_k\) corresponds to an expected state \({\varvec{M}}_k\), which is determined by

$$\begin{aligned} {\varvec{m}}_{check,j}= & {} \underset{{{\varvec{m}}_{k,j}}}{\mathop {\text {argminCost}}}\,({{\varvec{m}}_{k,j}},{{\varvec{m}}_{rand,j}}) \end{aligned}$$
(19)
$$\begin{aligned} \text {Cost}( {\varvec{m}}_{1}, {\varvec{m}}_{2})= & {} \omega _1\Vert {\varvec{m}}_{1}- {\varvec{m}}_{2}\Vert \nonumber \\{} & {} \quad +\, \omega _2\text {arccos}\frac{\overrightarrow{ {\varvec{v}}_{1}}\cdot \overrightarrow{ {\varvec{m}}_{1}{ {\varvec{m}}_{2}}}}{\Vert \overrightarrow{{\varvec{v}}_{1}}\Vert \Vert \overrightarrow{{\varvec{m}}_{1}{{\varvec{m}}_{2}}}\Vert } \end{aligned}$$
(20)

where \({\varvec{m}}_{check,j}\) is a temporary control checking node associated with \(\mathscr {M}_j\) in the new node \({\varvec{M}}_{new}\). \({\varvec{m}}_{1}\) and \({\varvec{m}}_{2}\) are the two arbitrary node, \({\varvec{v}}_{1}\) is the unit vector with angle of \({\varvec{m}}_{1}\). This cost function evaluates the distance and smoothness between two nodes. Hence, by using (19) and (20), \({\varvec{M}}_{new}\) and the optimal control output \(u_{new}\) is obtained. One should note that \({\mathcal {U}}(u_k,\epsilon )\) is assigned as null if \({\varvec{M}}_{parent}.\text {GoalArrived}[j]=1\) to ensure the mobile base is fixed once it reaches goal points.

In line 11-20 of Algorithm 1, the Heuristic method is proposed to optimize the path by using neighbor vertices. After a feasible new node \({\varvec{M}}_{new}\) is generated. The neighbor vertices of \({\varvec{M}}_{new}\), \({\mathcal {M}}_{near}\) are obtained by using a given search radius \(r_c\). Each \({\varvec{m}}_{near,j}\) directly connected to \({\varvec{m}}_{new,j}\) and the \({\varvec{m}}_{near,j}\) with minimum heuristic cost remained, in which \(h({\varvec{M}}_{new})\) indicates the total path length from \({\varvec{M}}_{init}\) to \(h({\varvec{M}}_{new})\). However, setting \({\varvec{m}}_{near,j}\) as the parent node could change the structure of the tree causing vertices disjunction. In this work, we propose ReSetParent() to reset the passed vertices on the edge ( \({\varvec{m}}_{near,j}\), \({\varvec{m}}_{new,j}\)), which is not change the parent node and thereby ensure the stability of the tree structure.

The proposed heuristic method in this study differs from the conventional neighborhood optimization method used in the RRT* algorithm in two key aspects. Firstly, the RRT* algorithm typically utilizes path length as its cost function without considering the feasibility of robot control, but the MCDPR is significantly more flexible and incorporates multiple constraints. As a result, the cost function in this study was enhanced, and control feasibility was taken into account. Secondly, the rewiring process in RRT* has the potential to change the parent node and thus alter the timestamp. To ensure the stability of the tree structure, the ReSetParent() function was introduced. This function enables us to reset the passed vertices on the edge, preventing changes to the parent node while maintaining the integrity of the tree structure. By implementing this additional step, we can effectively address the issue of changing timestamps that may arise during the rewiring process.

Figure 7 illustrates the proposed method, we use two sub-trees to represent two mobile bases for simplicity. As shown in Fig. 7a, the neighbor vertices of \({\varvec{m}}_{8,1}\) and \({\varvec{m}}_{8,2}\) is obtained to optimize path. Thus, two path (\({\varvec{m}}_{3,1}\),\({\varvec{m}}_{8,1}\)) and (\({\varvec{m}}_{3,2}\),\({\varvec{m}}_{8,2}\)) with minimum cost can be found. The parent vertices \({\varvec{m}}_{7,1}\), \({\varvec{m}}_{7,2}\) is reset and check in Fig. 7b by using \({\varvec{m}}_{reset,j}={\varvec{m}}_{reset,j}.parent+\eta ({\varvec{m}}_{reset,j}.child-{\varvec{m}}_{reset,j}.parent)\), in which \(\eta \) is initialized to 1/2. However, if \({\varvec{m}}_{reset,j}\) is not feasible, \(\eta \) is a random number ranging from 0 to 1. Moreover, due to the adaptive sampling method, the tree tends to grow toward the goal. As shown in Fig. 7c, the first tree has arrived but the second tree is not. In this case, the next sampling will be expanded on the remained vertices \({\varvec{m}}_{10,2}\) on the second tree. Finally, the algorithm is terminated when each tree has reached its target point shown in Fig. 7d.

Generation of the end-effector optimal path

After the RRT tree \({\mathcal {T}}\) is obtained from Algorithm 1, the path for mobile bases \({\varvec{M}}_{path}\) can be generated by consecutively finding \({\varvec{M}}_{parent}\) from the root of the tree. In this work, a kinematic stability index \(\gamma \) is used to determine the position of the end-effector, which is expressed as follows

$$\begin{aligned} \gamma =\gamma _{k}+\gamma _{s} \in [0,2] \end{aligned}$$
(21)

Based on the kinematic stability index \(\gamma \), a grid-based search method is developed in Algorithm 3 to generate the path for the end-effector \({\varvec{P}}_{path,p},p=1,...,N\). The proposed algorithm traverses each state on the path of mobile bases \({\varvec{M}}_{path,p}\) that corresponds to a specific CDPR configuration to maximize \(\gamma \). For each configuration, we first determine a search area \({\mathcal {S}}_p\) with radius \(r_s\), and the center of the \({\mathcal {S}}_p\) depends on the last end-effector position \({\varvec{P}}_{path,n-1}\). Thus, \({\mathcal {S}}_p\) is different in each \({\varvec{M}}_p\), which ensures smoothness and continuity of the path. For each \({\mathcal {S}}_p\), we discrete \({\mathcal {S}}_p\) to obtain \(Q_{p}\) cells \(\{c_{1},...,c_{Q}\}\), and traverse each cell find the largest \(\gamma \). It should be noted that some cells may not be feasible due to the cable/end-effector colliding with obstacles, which is considered in line 6 of Algorithm 3.

figure c

The path obtained through the end-effector is optimal due to the use of the grid-based search method and a kinematic stability index. Specifically, the kinematic stability index \(\gamma \) is used to determine the position of the end-effector, and a grid-based search method is developed to generate the path for the end-effector by maximizing \(\gamma \) at each configuration along the path of the mobile bases. By maximizing \(\gamma \), the algorithm ensures that the end-effector is positioned in a kinematically stable configuration at each point along the path. Additionally, the use of the grid-based search method ensures that the path is smooth and continuous. Together, these factors suggest that the path obtained through the end-effector is optimal in terms of kinematic stability and smoothness/continuity.

Fig. 8
figure 8

Simulation environment developed using CoppeliaSim software [24]

Full size image

Method validation

Initialization set-up and results

In this section, we conduct a number of simulations to demonstrate the effectiveness and efficiency of the proposed algorithm. Figure 8 illustrates the cluttered environment with the dynamic model of our MCDPR prototype developed using CoppeliaSim (formerly known as V-REP) robot simulator software [24]. The cluttered environment is composed of ten obstacles and these obstacles are modeled as cylinders with three different radii, 0.15 m, 0.25 m, and 0.45 m. These obstacles have an identical height 0.4 m, and the position of obstacles is randomly assigned. The five goal points for the MCDPR are given around the dark blue obstacle that is denoted as a target obstacle in which the robot can perform the task on it, i.e., picking and/or releasing operations.

Table 1 Simulation parameter
Full size table

The proposed method is initialized using parameters given in Table 1. For the consecutive state transition from \({\varvec{X}}_{k}\) to \({\varvec{X}}_{k+1}\), \(\Delta T\) should be relatively small to obtain high accuracy, thereby \(\Delta T=0.2\) is used in this work. For each \(^p{\varvec{M}}_{path}\), it could determine the coordinates of a set of pulleys by using \(h_1=0.285\) m and \(h_2=0.926\) m. Accordingly, the mass center of the mobile base can be directly obtained from the MCDPR dynamic model in CoppeliaSim given by \([0.12, 0.34, 0.36]^T\) with respect to \(O_pj\) coordinate system. Hence, \(\gamma _{k}\) and \(\gamma _{s}\) can be computed in each \(^p{\varvec{M}}_{path}\). The simulation result is illustrated in Fig. 9, it is found that a feasible path is generated for each mobile base to reach their goal points and the path of the end-effector is determined by maximizing \(\gamma \). Due to the limitation of the length of the cable making MCDPR impossible to separate through large obstacles, one should note that the MCDPR adaptively performs integration mode and separation modes in Fig. 9.

Fig. 9
figure 9

Resulted path in a constrainted environment

Full size image
Fig. 10
figure 10

z-coordinate of the end-effector

Full size image

To simplify the problem, the end-effector is modeled as a point to perform collision detection. Due to the end-effector was restricted to only perform the translational motion in x, y, and z direction, and the rotation of the end-effector is not considered. The x and y motion of the end-effector were depicted in Fig. 9 and the z-coordinate of the end-effector was shown in Fig. 10. The MCDPR is a type of parallel robot for which the inverse kinematics, as expressed in equations (1) and (10), can be readily determined. As a result, when given a set of three-dimensional coordinates for the end-effector, it is possible to calculate the corresponding cable length and cable speed using these equations. This enables precise control of the end-effector’s translational motion through the manipulation of cable length and speed.

The three minimum distances about mobile bases/mobile bases, mobile bases/obstacles, and cables/obstacles is illustrated in Fig. 11, it can be found that the distance constraints of (2), (3), and (4) can be satisfied. Moreover, the change of four interior angles is shown in Fig. 12, it can be seen that \(\theta _1,\theta _2,\theta _3,\theta _4\in [0,\pi ]\), thereby the MCDPR configuration constraints defined by (4) is thus fulfilled.

Fig. 11
figure 11

Relative distance change with time

Full size image
Fig. 12
figure 12

Interior angles change with time

Full size image

MCDPR Verification in CoppeliaSim and experiments

In this section, the resulting MCDPR trajectories obtained from the last section are simulated in CoppeliaSim environment to verify the proposed method and the corresponding experiment is carried out. The software simulation framework is depicted in Fig. 14. For controlling the mobile bases, the continuous velocity profiles of the mobile bases are converted into the rotational velocities of the mobile base’s wheels by using its kinematic model. As shown in Fig. 13, the continuous velocity profiles of the mobile bases and the end-effector are guaranteed due to the post-processing. One should note that these mobile bases do not arrive at the goal points at the same time. Moreover, for controlling the end-effector, we utilize (1) and (10) to adjust the length and speed of cables shown in Fig. 15.

The obtained wheels’ rotational velocities are sent to the revolute joints associated with wheels to control the mobile bases in CoppeliaSim. Additionally, the length of the cable can be adjusted by prismatic joints associated with cables. Hence, the MCDPR model is actuated by these joints. The state of MCDPR can be directly obtained from the CoppeliaSim during the motion, it will be compared with the desired path to obtain the error.

Fig. 13
figure 13

Velocity profiles of mobile bases

Full size image
Fig. 14
figure 14

Software simulation framework

Full size image
Fig. 15
figure 15

Cable length change

Full size image
Fig. 16
figure 16

Error between the actual and the desired position

Full size image
Fig. 17
figure 17

Simulation in CoppeliaSim. a \(t=21\) s b \(t=49\) s c \(t=61\) s

Full size image

The clips of the simulation in CoppeliaSim are shown in Fig. 17, it can be seen that the MCDPR can follow the desired paths and avoid the collision. Moreover, Fig. 16 illustrates the error between the actual path of the MCDPR from the simulation and the desired path, the maximum error about the mobile base and the end-effector is approximately 3.8 cm. Thus, the feasibility and stability of the proposed path planning method can be verified.

Fig. 18
figure 18

Experimental results. a \(t=6\) s b \(t=12\) s a \(t=18\) s b \(t=24\) s

Full size image
Fig. 19
figure 19

Cable tension change in experiment

Full size image

The proposed approach is validated experimentally on our self-built MCDPR, a scenario is designed as the MCDPR pass through the first obstacle shown in Fig. 9. The NVIDIA Jetson Nano\(^TM\) Developer Kit is adopted as a control computer to operate our MCDPR system, in which the designed cable length and mobile base velocities are sent to control MCDPR. The experimental results are shown in Fig. 18, it can be seen that the MCDPR is smooth and stable passing the obstacle and the total time is 24 s. Before the experiment, the cable was pre-tensed to 20 N, and the cable tension change measured from the load cell sensor during the experiment is shown in Fig. 19. It can be seen that the cable tension remains positive in the experiment and has a continuous profile. These results verify that the proposed method is feasible and effective.

Batch evaluation

In this section, the proposed path planning method for MCDPRs is compared with other existing methods. Due to the stochastic nature of the proposed method, a batch evaluation of 1000 simulations is performed and the proposed method is evaluated using the average value. All the simulations are performed using \(\textcircled {c}\)MATLAB with CPU computations on an Intel ®i7-9750 CPU@2.60GHz and 32GB RAM Windows 10 system. The identical initialization parameters defined in the previous simulations are used in these simulations.

Table 2 The evaluation result
Full size table

The results of the batch evaluation are summarized in Table 2. Comparing the proposed method with the Iterative Algorithm and Direct Transcription, the proposed method reduced the CPU time by 88.7% and 79.8%, respectively. This is due to the developed adaptive sampling strategy leading the tree to grow towards the goal points. Iterative Algorithm and Direct Transcription require complex iterative processes for optimization which may become computationally more expensive with the increase of obstacles in the environment. However, the proposed method does not require an iterative search but constructs the feasible tree by adaptively exploring the state space. It should be noted that the Iterative algorithm and the Direct Transcription method resulted in the mobile base and the end-effector reaching the target point simultaneously. In our method, the growth of the subtree is terminated when it reaches the goal point. Furthermore, it can be observed that the average global performance index \(\gamma \) of the total path is improved by 56.12% and 34.21% with respect to the Iterative Algorithm and Direct Transcription. Therefore, the proposed path planning method can contribute to better stability and kinematic performance of MCDPRs.

The proposed algorithm incorporates a heuristic optimization approach to enhance the efficiency of the MCDPR path. The results demonstrate a 46.81% decrease in path length compared to the Iterative Algorithm. Although the Direct Transcription method outperforms the proposed algorithm in terms of path length due to its broader optimization radius and iterative process, the proposed method only differs by 4.51% from Direct Transcription. Moreover, the proposed algorithm offers several advantages, including faster CPU time and improved average \(\gamma \), which offset the minor difference in path length. These results highlight the ability of the proposed method to optimize path, enhance computational efficiency, and ensure kinematics stability simultaneously.

Conclusion and future work

In this work, an optimal path planning method is proposed for MCDPRs to generate feasible paths in constrainted environments with considering kinematic stability. The proposed method utilizes a heuristic approach to optimize the path, and the adaptive sampling method is developed to enhance efficiency. Hence, the various constraints of MCDPR can be considered in detail and the kinematic stability is maximized by using designed performance indicators. The proposed method was validated by simulations and subject to real-world testing on a self-built MCDPR prototype. The results show that the proposed approach can generate feasible paths for mobile bases and the end-effector in a shorter time. Compared to other existing methods, the proposed method provides better kinematic stability performance and efficiency on the premise of minimizing the path length. Therefore, the reliability of the proposed method was verified.

One should note that the proposed method is developed in a static environment in which the position of the obstacle is known. Moreover, the proposed method can be extended to a variety of multi-agent systems, such as UAVs. However, it is imperative for individuals to tailor the algorithm to the specific system by adjusting the cost function and constraint equations as necessary. This enables the algorithm to effectively accommodate the distinct characteristics and demands of the system. In future work, it is desirable to develop the real-time path planning method for MCDPR in a dynamic environment with the moving obstacle. To fulfill this purpose, a continuous localization system for MCDPR is also required to be designed in the future.