A collaborative path planning method for mobile cable-driven parallel robots in a constrained environment with considering kinematic stability

Abstract

Mobile cable-driven parallel robot (MCDPR) is a variant of cable-driven parallel robots (CDPRs) by mounting several mobile bases to replace the conventional fixed frame. The novel modification of adding mobile bases leads MCDPRs being highly flexible and have great potential for complex environments. However, the issue of coupled mobile bases introduces actuated kinematic redundancies which present challenges for path planning. In this paper, we propose a collaborative path planning method for MCDPRs, and it allows the robot to deal with complex internal and external constraints in a high-dimensional state space efficiently. The proposed method quickly generates feasible paths for coupled mobile bases using the adaptive goal-biased rapidly exploring random tree (RRT) method, in which the adaptive sampling method is developed to enhance efficiency. Based on the feasible path of the mobile base, we proposed a grid-based search method to determine the position of the end-effector with considering the stability and kinematic performances. Furthermore, the planned paths are post-processed with the cubic splines to obtain continuous profiles for the robot. Finally, the proposed method is validated through the dynamic simulation software (CoppeliaSim) and experiments based on a MCDPR prototype with an eight-cable-driven parallel robot mounted on four mobile bases.

Introduction

Cable-driven parallel robots (CDPRs) are a particular type of parallel robots actuated by multiple cables; these cables are guided by the fixed winch–pulley system to connect the end-effector. The pose of the end-effector is controlled by adjusting the cable length between the anchor point of the end-effector and the pulley. CDPRs are promising for various industrial applications, such as pick and place tasks, works over a large workspace, and manipulations of heavy payload [1,2,3].

Despite CDPRs have distinct advantages in numerous applications, several challenges have not been addressed. CDPRs are composed of multiple cables, which results in strong demand for avoiding interference with the environment [4]. Besides, due to cables being attached to a fixed frame, the cable span volume takes up significant space when the end-effector is moving [5]. Consequently, there is a need for CDPRs to tune their geometry structure for adapting to the environment and performing tasks. Based on the concept of reconfiguration, reconfigurable cable-driven parallel robots (RCDPRs) were developed, in which the position of pulleys can be altered [6]. However, the most of proposed RCDPRs still have a fixed frame, and their extensibility is limited due to the winch–pulley system cannot be freely moved.

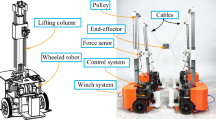
To extend the reconfigurability of RCDPRs, mobile cable-driven parallel robots (MCDPRs) have been developed by mounting several mobile bases on the base frame [7]. The mobile bases carry the winch–pulley system to discretize CDPR, thereby involving more degree-of-freedom (DoF). Compared with CDPRs, MCDPRs are capable of arranging the layout of pulleys automatically, which can be adapted based on the desired task. Moreover, MCDPRs can move freely to interact with other objects or the environment, and makes effective use of task space. The MCDPR prototype studied in this work is depicted in Fig. 1, and each mobile base provides two additional DoF, resulting in the system capable of satisfying complex task requirements.

Fig. 1

Self-built MCDPR prototype with 8 cables and 4 mobile bases

However, the added mobile bases cause the kinematic redundancy of MCDPRs. For this reason, the path planning of MCDPRs becomes increasingly difficult with the additional DoF introduced by mobile bases [8]. In addition, these mobile bases are coupled to each other by multiple cables, resulting in complex constraints and high dimension regime. Furthermore, the mobile base is especially susceptible to becoming unstable due to the effect of the applied cable tension changed by the difference in relative position between mobile bases [9]. As a consequence, for displacing the end-effector from the starting point to the destination, feasible paths are required to be obtained for each mobile base and the end-effector simultaneously.

For the single-agent system, existing path planning methods such as A* [10] and Dijkstra [11] are available to generate an optimal path in the discretized map, but the performance gradually became worse when more agents are involved. To address the high-dimensional state and environmental constraints, optimization-based approaches can be adopted. Rasheed et al. [12] presented a method for the trajectory planning of MCDPRs based on Direct Transcription method, in which the trajectory was discretized based on a given timestep and the solution was obtained by minimizing the objective function with respect to a range of defined constraints. However, the optimization-based approaches are generally time-consuming for converging.

Accordingly, sampling-based path planning methods can be adapted to solve high-dimensional path planning problems with various constraints [13].One of the famous representative methods is rapidly exploring random tree (RRT), in which a tree is built from a given start state by randomly sampling the configuration space [14]. To improve the performance of RRT, RRT* approach and its variants have been explored for generating optimized results [15,16,17]. Zhang et al. [18] completed the optimal collision-free path planning of CDPR based on RRT* and the dexterity of the robot. Bak et al. [19] proposed a modified goal-biased RRT method to obtain the feasible path for CDPR in a cluttered environment. More recently, Mishra et al. [20] generated the optimal path for CDPRs by deploying the combination of the artificial field guide (AFG) method and RRT*. However, the aforementioned studies were restricted to CDPR. For MCDPR, RRT searching process might be progressively slower due to complex state space. Rasheed et al. [21] proposed an Iterative Algorithm to generate feasible paths for MCDPR. This method directly traversed all possible pre-defined states for each mobile base, and the next state was determined by maximizing the wrench capacity. However, the traversal time increases exponentially with possible states of the mobile base that will cause the direct traverse method to be unreliable.

In this paper, we present a collaborative path planning algorithm for MCDPR. The proposed sampling-based method reduces the dimensionality by planning separately for the mobile base and the end-effector, and then the final path is obtained by post-processing. Hence, various constraints and kinematic redundancy associated with MCDPRs can be effectively dealt with. Furthermore, two evaluation indices are designed to optimize the path of the end-effector by considering the kinematic and stability performance of MCDPR simultaneously. The kinematic performance of MCDPR is defined as the dexterity of the robot and the stability performance of MCDPR is optimized by considering the tipping condition of the mobile base. Contrary to the Iterative Algorithm and Direct Transcription method, the proposed method algorithm pre-defined goal points, and thus the goal-biased sampling method is developed to quickly generate the feasible path in high-dimensional state space. The results are verified by the simulation and experiments in a complex scenario based on the dynamic model of MCDPR developed using the CoppeliaSim software.

The remainder of this paper is organized as follows: Robot parameterization and problem formulation are introduced in the next section. The kinematics and stability model for MCDPRs is established in the third section. In the fourth section, the proposed path planning method for MCDPRs is introduced in detail. The method validation is carried out in the fifth section. Finally, last section concludes the research work.

MCDPR parameterization and problem formulation

MCDPR parameterization

In this work, we focus on a MCDPR composed of a classical redundantly constrained CDPR with eight cables ($m=8$) and a six DoF end-effector ($n=6$) mounted on four mobile bases ($p=4$), as shown in Fig. 2. The origin of the global coordinate system is denoted as $O_{0}$ and the local coordinate system located at the center of the end-effector is expressed as $O_{e}$. The jth mobile base, denoted as ${\mathscr {M}}_j$, $j = 1,\ldots ,4$ carries two cables ($m_{j}=2$) and has three wheels ($c=3$) including one caster wheel and two driven wheels. The local coordinate system attached to ${\mathscr {M}}_j$ is denoted as $O_{pj}$. The characteristics of the non-holonomic two-wheeled differential drive mechanism implicate that ${\mathscr {M}}_j$ is the planar robot, it can generate two DoF translational motions and one DoF rotational motion.

Fig. 2

a Structural diagram of MCDPR. b Structural diagram of ${\mathscr {M}}_j$

The ith cable vector attached onto ${\mathscr {M}}_j$ is named as ${\varvec{l}}_{ij}$, $i=1,\ldots m_{j}$. As a result, the cable exit point and the anchor point are denoted as $A_{ij}$ and $B_{ij}$, respectively. According to the characteristics of parallel robots, selecting the ith closed-loop vector branch, ${\varvec{l}}_{ij}$ can be expressed by

$$\begin{aligned} {\varvec{l}}_{ij}= {\varvec{a}}_{ij}-{\varvec{P}}-{}^{e}{\varvec{b}}_{ij} \end{aligned}$$

(1)

where ${\varvec{a}}_{ij}$ represents the position vector of $A_{ij}$ in $O_{0}$ coordinate system. ${\varvec{P}}=[{}^{0}{x},{}^{0}{{y}},{}^{0}{{z}}]^T$ is a three-dimensional position vector of the end-effector, and the rotation of the end-effector is not considered. ${}^{e}{\varvec{b}}_{ij}$ denotes the position vector of $B_{ij}$ in the moving coordinate system.

Let ${\varvec{u}}_{ij}={\varvec{l}}_{ij}/\Vert {\varvec{l}}_{ij}\Vert$ be the unit vector pointing from $B_{ij}$ to $A_{ij}$ of the cable ${\varvec{l}}_{ij}$. The MCDPR is designed that $A_{ij}$ lies on the axis ${}^{pj}z$ of ${\mathscr {M}}_j$, the rotation motion of ${\mathscr {M}}_j$ has no impact on ${\varvec{u}}_{ij}$. Hence, for a certain pose of the end-effector, ${\varvec{u}}_{ij}$ can be obtained by determining the position of $O_{pj}$ in $^{0}x{^{0}y}$ plane. The position of the mobile base is controlled by sending the velocity commands to two wheels, and the pose of the end-effector can be adjusted by changing the cable length.

Problem formulation

To specify the MCDPR path planning problem more precisely, let ${\varvec{P}}_{k}$, $k=1,\ldots ,N$, be the position vector of the end-effector at the kth time step. Correspondingly, the state of mobile bases ${\mathscr {M}}_j$ at the kth time step is denoted as ${\varvec{m}}_{j,k}=[{}^{0}{{x}_{{{j,k}}}}, {}^{0}{{y}_{{{j,k}}}}]$. Therefore, the state of four mobile bases and MCDPR at the kth time step is denoted as ${\varvec{M}}_{k}=[{\varvec{m}}_{1,k}^T , {\varvec{m}}_{2,k}^T , {\varvec{m}}_{3,k}^T ,{\varvec{m}}_{4,k}^T]^T$ and ${{{\varvec{X}}}_{k}}=[{\varvec{P}}_{k}^{T} , {\varvec{M}}_{k}^{T}]^T$, respectively.

One of the basic requirements for the feasible paths of MCDPR is to ensure mobile bases without colliding with each other or obstacles in the environment. For simplification purposes, the mobile bases and obstacles are modeled as cylindrical shaped structures. Therefore, for each time step, the position of the jth, $j=1,\ldots ,4$, the mobile base needs to satisfy constraints as follows:

$$\begin{aligned}{} & {} \left\| {{{\varvec{m}}}_{h,k}}-{{{\varvec{m}}}_{j,k}} \right\| >L_m, \,\text {for}\ h=1,\ldots ,4,\, {h}\ne {j} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \left\| {{{\varvec{m}}}_{j,k}}-{{{\varvec{o}}}_{q}} \right\| >r_m+r_o, \,\text {for}\ q=1,\ldots ,s, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \text {cos}^{-1}\frac{{\varvec{d}}_{j,k}\cdot {\varvec{d}}_{j,k+1}}{\Vert {\varvec{d}}_{j,k}\Vert \Vert {\varvec{d}}_{j,k+1}\Vert }<\beta _{\textrm{max}} \end{aligned}$$

(4)

where $L_m$ represents the safety distance between two mobile bases and $r_m$ is the radius of the mobile base. ${\varvec{o}}_{q}$ denotes the position of the qth obstacle on $^{0}{x}^{0}{y}$ plane with radius $r_o$. ${\varvec{d}}_{k}={\varvec{m}}_{j,k+1}-{\varvec{m}}_{j,k}$ is the directional vector of the mobile base in two adjacent states, and $\beta _{\textrm{max}}$ is the maximum turning angle. Equation (2) aims to keep safety distance between each two mobile bases, (3) ensure that the mobile base does not collide with obstacles, and (4) prevents the abrupt direction change of the mobile base.

Since the mobile base carried CDPR is composed of multiple cables and the interference of cables/obstacles and end-effector/obstacles should be considered in the path planning of MCDPR. In this paper, the cables between $A_{i,j}$ and $B_{i,j}$ are simplified as line segments, and the end-effector is modeled as a cube. Let $\varvec{c_k}$ and $\varvec{b_k}$ denotes the two closest point between CDPR and obstacles at kth time step. It should be noted that $\varvec{c_k}$ is either on the end-effector or cables, and $\varvec{b_k}$ is on the obstacle. Therefore, to prevent the collision between CDPR and obstacles, let $L_c$ be the minimum acceptable distance between CDPR and obstacles. We have the following equation:

$$\begin{aligned} \left\| {{{\varvec{c}}}_{k}}-{{{\varvec{b}}}_{k}} \right\| >L_c. \end{aligned}$$

(5)

In addition, we consider the carried CDPR have limited workspace and cable length. For each configuration of mobile bases ${\varvec{M}}_{k}$, we can identify a corresponding workspace ${\mathcal {W}}_k$. Thus, the following constraints are conducted:

$$\begin{aligned}{} & {} l_{\textrm{min}}\le \left\| [{{{\varvec{m}}}_{j,k}}^T \;{{{h}}_{i}}]^T - {\varvec{P}}_{k} \right\| \le l_{\textrm{max}}, \,\text {for}\; i=1,2 \end{aligned}$$

(6)

$$\begin{aligned}{} & {} {\varvec{P}}_k \in {\mathcal {W}}_k \end{aligned}$$

(7)

where $l_{\textrm{min}}$ and $l_{\textrm{max}}$ denote the minimum and maximum length of cable, respectively. $h_l$ represent two constant heights of exit point $A_{i,j}$ in the $O_{0}$ coordinate system. $h_1$ and $h_{2}$ represents the height of $A_{1,j}$ and $A_{2,j}$, $j=1,\ldots ,4$, respectively.

In summary, MCDPR path planning is a problem that is concerned about finding feasible paths for the end-effector and multiple mobile bases from their given start locations to a sufficiently small area of their target locations ${\varvec{M}}_{goal}=[{\varvec{m}}_{goal,1}^T , {\varvec{m}}_{goal,2}^T , {\varvec{m}}_{goal,3}^T ,{\varvec{m}}_{goal,4}^T]^T$ while satisfying the constraints defined in (2)–(7) and optimizing the objective function.

Consideration

Kinematics performance

Due to the kinematical redundancy of the MCDPR, ensuring excellent kinematics performance is the basic premise for studying the MCDPR path planning problem. We consider the classical CDPR carried by mobile bases, the velocity of the end-effector $\dot{{\varvec{P}}}=[{}^{0}{\dot{x}}_{e}, {}^{0}{\dot{y}}_{e} , {}^{0}{\dot{z}}_{e}]^T$ due to the motion of cables can be expressed as

$$\begin{aligned} \left[ \begin{matrix} {{{\varvec{J}}}_{1}} \\ {{{\varvec{J}}}_{2}} \\ \vdots \\ {{{\varvec{J}}}_{j}} \\ \end{matrix} \right] \varvec{{\dot{P}}}=\left[ \begin{matrix} {{{\varvec{{\dot{l}}}}}_{1}} \\ {{{\varvec{{\dot{l}}}}}_{2}} \\ \vdots \\ {{{\varvec{{\dot{l}}}}}_{j}} \\ \end{matrix} \right] \end{aligned}$$

(8)

where $\varvec{{\dot{l}}}_{j}=[\varvec{{\dot{l}}}_{1j},\ldots ,\varvec{{\dot{l}}_{m_{j}j}} ]^T$ indicates the speed vector of the cables mounted on the mobile base ${\mathscr {M}}_j$, and ${\varvec{J}}_{j}$ is expressed as

$$\begin{aligned} {{{\varvec{J}}}_{j}}=\left[ \begin{matrix} {{{\varvec{u}}}_{1,j}}^T \\ \vdots \\ {{{\varvec{u}}}_{{{m}_{j}}j}}^T \\ \end{matrix} \right] \end{aligned}$$

(9)

where ${\varvec{J}}_{j}$ is associated with the cable actuation wrench on ${\mathscr {M}}_j$. According to (8) and (9), the kinematic Jacobian matrix of the carried CDPR can be defined by ${\varvec{J}}=[{\varvec{J}}_{1},\ldots ,{\varvec{J}}_{j}]^T$, which maps the end-effector velocity to the actuated cable velocities. Thus, kinematic performance is defined as the sensitivity of kinematic Jacobian matrix ${\varvec{J}}$, which can be obtained by the condition number $\kappa$, denoted as

$$\begin{aligned} \kappa =\frac{\sqrt{{{\lambda }_{\textrm{max}}}({{{\varvec{J}}}^{T}}{\varvec{J}})}}{\sqrt{{{\lambda }_{\textrm{min}}}({{{\varvec{J}}}^{T}}{\varvec{J}})}} \end{aligned}$$

(10)

where ${\lambda }_{\textrm{max}}$ and ${\lambda }_{\textrm{min}}$ are the maximum and minimum eigenvalues of square matrix ${\varvec{J}}^{T}{\varvec{J}}$. The condition number of kinematic Jacobian matrix $\kappa$ also describes the dexterity of the robot. Since $\kappa \in [1,\infty )$, we normalized $\kappa$ to define the kinematics performance index $\gamma _{k} \in [0,1]$ expressed as

$$\begin{aligned} \gamma _{k}=1/\kappa . \end{aligned}$$

(11)

Thus, for guaranteeing the better kinematics performance of MCDPR, the larger $\gamma _{k}$ should remain.

Stability performance

One major drawback of MCDPR is that the structure of the mobile base combined with the lifting column is susceptible to cable tension. The mobile base could be vibrated or tipped if the cable tension beyond a specific range. These unstable mobile base could increase the position error of the end-effector and lead to task failure. To prevent the MCDPR becoming unstable, the stability performance is defined in this section.

Fig. 3

a Free body diagram of jth mobile base. b Distribution of wheel contact points

The free body diagram of jth mobile base is illustrated in Fig. 3a; it can be observed that the stability of the mobile base is influenced by both cable tension and its gravity. As shown in Fig. 3b, we define the wheel contact points of the mobile base ${\mathscr {M}}_{j}$ as $C_{nj}$, $n=1,2,3$, in a counter-clockwise direction, and the position vector of nth wheel contact point denotes as ${\varvec{c}}_{nj}=[{\varvec{c}}_{nj,x},{\varvec{c}}_{nj,y},{\varvec{c}}_{nj,z}]^T$. The left and right driven wheels of the mobile base are defined based on the forward direction (i.e., $C_{2j}$ and $C_{3j}$). According to the Zero-Moment Point (ZMP) method, the static equilibrium of the mobile base relies on the moments generated at the boundaries of the wheel contact points [22]. The boundary between the two consecutive contact $(C_{nj},C_{n+1j})$ is denoted as ${\mathscr {L}}_{C_{nj}}$ of the directional vector ${\varvec{u}}_{C_{nj}}$. Thus, the moment ${\varvec{m}}_{C_{nj}}$ generated at the instant when ${\mathscr {M}}_{j}$ is about to tipping can be formulated as

$$\begin{aligned} \begin{aligned} {\varvec{m}}_{C_{nj}}&={{\varvec{u}}_{c_{nj}}^T}(({{\varvec{g}}_{j}}-{{\varvec{c}}_{kj}})\times {{\varvec{w}}_{gj}})\\&\quad +\,\sum \limits _{i=1}^{m_{j}}{{{\varvec{u}}_{C_{nj}}^T}(({{\varvec{c}}_{kj}}-{\varvec{P}})\times {{\varvec{u}}_{ij}})}{t}_{ij} \end{aligned} \end{aligned}$$

(12)

where ${\varvec{g}}_{j}=[\varvec{g_{j,x}},\varvec{g_{j,y}},\varvec{g_{j,z}}]^T$ is the position vector of ${\mathscr {M}}_{j}$’s center of mass. ${\varvec{w}}_{gj}$ denotes the weight vector of ${\mathscr {M}}_{j}$. ${t}_{ij},i=1,\ldots ,m_{j}$, represents the cable tension associated ${\mathscr {M}}_{j}$. The first and second term of (12) denote the moment generated by the gravity and cable tension, respectively. To prevent negative tension and deformation of the cable, ${t}_{ij}$ is bounded between a minimum tension $t_{\textrm{min}}$ and $t_{\textrm{max}}$. Accordingly, the tipping constrains for ${\mathscr {M}}_{j}$ is to ensure the negative ${\varvec{m}}_{C_{nj}}$. It means that each boundary ${\mathscr {L}}_{C_{nj}}$ requires to satisfy the following constraints:

$$\begin{aligned} {{m}_{C_{nj}}}<0,\;n=1,2,3. \end{aligned}$$

(13)

The feasible interval of the cables tension of ${\mathscr {M}}_{j}$ could form an area called feasible tension polygon (FTP), denoted by ${\mathscr {F}}_{j}$. For the FTP without considering the tipping condition, ${\mathscr {F}}_{j}$ is a square with side length $\Delta t=t_{\textrm{max}}-t_{\textrm{min}}$ shown in Fig. 4a. However, according to (12) and (13), the tipping condition is the function of cable tension which causes the linear constraints to cut the original FTP shown in Fig. 4b. Since the cable tension has infinite solutions, we define a riskiest feasible tension polygon ${\mathscr {F}}_{r}=\text {min}({\mathscr {F}}_{r}),j=1,\ldots ,4$. The stability performance of MCDPR, $\gamma _{s}$, can be defined as

Fig. 4

Feasible cable tension polygon of ${\mathscr {M}}_{j}$: a without considering the tipping condition; b with considering the tipping condition

$$\begin{aligned} {\gamma }_{s}={{\mathscr {F}}_{r}}/{\Delta t^{2}} \end{aligned}$$

(14)

where ${\mathscr {F}}_{r}$ can be obtained by getting the point of intersection (i.e., ${{\textbf {v}}}_1,{{\textbf {v}}}_2,{{\textbf {v}}}_3$ in Fig. 4b). It can be seen from (14) that $\gamma _{s} \in [0,1]$, $\gamma _{s}=1$ indicates the tipping constraints has no effects on the original ${\mathscr {F}}_{j}$ so that MCDPR is at the stability performance. In contrast, when $\gamma _{s}=0$, the MCDPR will be tipping due to a cable tension solution that satisfies the static equilibrium does not exist.

Method description

In this section, the path planning method of MCDPRs is presented. In Algorithm 1, the feasible paths of mobile bases are generated using the adaptive goal-biased RRT method. For each state of mobile bases ${\varvec{M}}_k$, the position of end-effector is determined using the grid-based search method presented in Algorithm 4. Therefore, the final paths of mobile bases and the end-effector can be obtained by continuously tracing the parent node when Algorithm 1 ends.

Path planning for mobile bases

Due to the high-dimensional state space and various coupled constraints of mobiles, the adaptive goal-biased (RRT) is proposed to generate feasible paths for mobile bases. The proposed RRT-based method is to find a set of feasible paths by building a tree-structured graph ${\mathcal {T}}({\mathcal {V}},{\mathcal {E}})$. The vertices ${\mathcal {V}}$ represents possible collision-free states of mobile bases ${\varvec{M}}_k$, and the edge ${\mathcal {E}}$ denotes the feasible transitions of mobile bases between two adjacent states.

Algorithm 1 summarizes the proposed approach, if the initial and goal state of mobile bases are feasible, the root tree is initialized with the initial state ${\varvec{M}}_{init}$, then the initial state is assigned to the first vertices ${\varvec{M}}_{new}$. Some important attributes are also initialized to vertices, ${\varvec{M}}_{new}.\text {Goal\_arrived}$ indicates the arrival status of four mobile bases. In proposed method, once ${\mathscr {M}}_j$ reaches its target location, it is stays fixed and does not move, and the jth element of ${\varvec{M}}_{new}.\text {Goal\_arrived}$ is changed to 1. Therefore, the algorithm proceeds with all elements in ${\varvec{M}}_{new}.\text {Goal\_arrived}$ are not equal to 1.

Lines 5–31 of Algorithm 1 describe the execution process of the proposed method. For dealing with the high-dimensional state space of mobile bases and increase efficiency, the adaptive goal-biased sampling is designed (line 6 of Algorithm 1) to generate random state ${\varvec{M}}_{rand}=[{\varvec{m}}_{rand,1}^T , {\varvec{m}}_{rand,2}^T , {\varvec{m}}_{rand,3}^T ,{\varvec{m}}_{rand,4}^T]^T$ and its specific steps is given in Algorithm 2. The developed adaptive sampling strategy can guide the tree towards the goal region and the volume of the sampling space is reduced by adaptively adjusting the sampling strategy in a subspace for each mobile base. The ${\varvec{M}}_{partent}$ and ${\varvec{M}}_{goal}$ are the inputs of Algorithm 2. The elements in ${\varvec{M}}_{partent}.\text {Goal\_extended}$ is checked to decide whether to assign the goal of jth mobile base ${\varvec{m}}_{goal,j}$ to ${\varvec{m}}_{rand,j}$ or not. If the element in parent vertices ${\varvec{M}}_{parent}$ fails to expand to its goal point directly, the adaptive sampling method is implemented in lines 5–11. GoalCircle(${\varvec{m}}_{goal,j}$, $r_{gc,j}$) represents uniformly sampling in a circular area centered on the ${\varvec{m}}_{goal,j}$ with radius $r_{gc,j}=\Vert {\varvec{m}}_{goal,j}-{\varvec{m}}_{r,j} \Vert$, and ${\varvec{m}}_{r,j}$ denotes a sub-vertices with a maximum expansion failure rate. Uniform(${\mathcal {W}}_{m}$) represents uniformly sampling in the workspace for mobile bases ${\mathcal {W}}_{m}$. The choice of which method for sampling depends on the ${\varvec{M}}_{parent}.\text {Failure\_rate}$.

To increase the robustness of the algorithm, the current number of vertices is stored in each iteration function (line 25 of Algorithm 1) once one of the mobile bases reach the goal point. In the beginning of the proposed method, $V_j=0$, the function Nearest( ${\varvec{M}}_{rand}$,${\mathcal {T}}$,$V_j$) return a vertices ${\varvec{M}}_{nearest}=[{\varvec{m}}_{nearest,1}^T , {\varvec{m}}_{nearest,2}^T , {\varvec{m}}_{nearest,3}^T ,{\varvec{m}}_{nearest,4}^T]^T$ closest to ${\varvec{M}}_{rand}$ by searching the vertices of entire tree $\mathcal {T.V}$. However, after the one mobile base reaches the goal point, the search range is changed to $\mathcal {T.V}[V_j\ldots ]$ to prevent the car from moving after reaching the target.

After ${\varvec{M}}_{nearest}$ is obtained, a new vertices ${\varvec{M}}_{new}=[{\varvec{m}}_{new,1}^T , {\varvec{m}}_{new,2}^T , {\varvec{m}}_{new,3}^T ,{\varvec{m}}_{new,4}^T]^T$ is generated using Steer(${\varvec{M}}_{rand}$,${\varvec{M}}_{nearest}$,${\varvec{M}}_{parent}$) function (line 8 of Algorithm 1), shown in Algorithm 3. The input ${\varvec{M}}_{parent}$ is used to determine if the mobile base has reached the goal point. Moreover, the inputs $M_{rand}$ and ${\varvec{M}}_{nearest}$ is used to obtain a new node ${\varvec{M}}_{new}$. It is noted that the step size $\eta$ depends on the state of ${\varvec{M}}_{parent}.\text {Goal\_arrived}[j]$, indicates ${\mathscr {M}}_j$ is fixed after arriving the goal point and returned variables ${\varvec{M}}_{new}$ have four components corresponding to the four mobile bases.

For each ${\varvec{M}}_{new}$, its feasibility is checked by using (2), (3), and (4) in “MCDPR parameterization and problem formulation” section. If ${\varvec{M}}_{new}$ is feasible according to previous constraints, an optimization strategy similar to RRT* is applied. The neighbor vertices of ${\varvec{M}}_{new}$ is obtained with a given radius $r_c$, and if the edge from ${\varvec{M}}_{near}$ to ${\varvec{M}}_{new}$ is feasible, ${\varvec{M}}_{parent}$ is replaced by ${\varvec{M}}_{near}$ with a better cost (lines 12–20 of Algorithm 1). However, if ${\varvec{M}}_{new}$ is not feasible, some properties of ${\varvec{M}}_{nearest}$ and ${\varvec{M}}_{new}$ are updated to inspire the next iteration process (lines 21–30 of Algorithm ). In this work, the cost function is defined as total path length and $\text {Dist}({\varvec{M}}_{new},{\varvec{M}}_{nearest})$ denotes the distance between two nodes:

$$\begin{aligned} \text {Cost}=\sum \limits _{i=2}^{N}{\sum \limits _{j=1}^{4}{\left\| {{\textrm{m}}_{j,i}}-{{\textrm{m}}_{j,i-1}} \right\| }}. \end{aligned}$$

(15)

Generate path for the end-effector

Once the RRT tree ${\mathcal {T}}$ is constructed in the last section, the path for mobile bases $^p{\varvec{M}}_{path}=[^p{\varvec{m}}_{path,1}^T , ^p{\varvec{m}}_{path,2}^T , ^p{\varvec{m}}_{path,3}^T, ^p{\varvec{m}}_{path,4}^T]^T, p=1,\ldots ,Q$, ${\varvec{M}}_{path}=[{\varvec{M}}_1, {\varvec{M}}_2,\ldots ,{\varvec{M}}_Q]^T$can be generated by consecutively finding ${\varvec{M}}_{parent}$ from the end of the tree, and Q denotes the number of vertices on the path. It should be noted that the first vertices on the path $^1{\varvec{M}}_{path}$ ${\varvec{M}}_{path,1}$ represents the initial state of mobile bases ${\varvec{M}}_{init}$, and the last vertices $^Q{\varvec{M}}_{path}$ ${\varvec{M}}_{path,Q}$ is the goal state ${\varvec{M}}_{goal}$.

For each state on the path, ${\varvec{M}}_{path,p},p=1,\ldots ,Q$, it corresponds to a specific CDPR structure in which the position of pulleys is determined. Therefore, a global performance index $\gamma$ with considering the stability and kinematic performance of MCDPR is formulated to generate the path ${\varvec{P}}_{path}=[{\varvec{P}}_{1},{\varvec{P}}_{2},\ldots ,{\varvec{P}}_{Q}]^T$for the end-effector, namely

$$\begin{aligned} \gamma =\gamma _{k}+\gamma _{s} \in [0,2]. \end{aligned}$$

(16)

To obtain ${\varvec{P}}_{path}$ with (16), a grid-based search method is developed in Algorithm 4. The pth element of ${\varvec{P}}_{path}$, ${\varvec{P}}_{path,p}$ is generated by maximizing $\gamma$ in the mobile bases configuration ${\varvec{M}}_{path,p}$. According the definition in “Kinematics performance” and “Stability performance” sections, $\gamma$ can be considered as a function of the end-effector position. Therefore, as shown in Fig. 5, we can obtain the distribution map of $\gamma$ after gridding ${\mathcal {C}}_p$, and the cell with the maximum $\gamma$ will be recorded. Hence, for each cell $c_n$, it corresponds to a specific end-effector position and its feasibility is checked using (5)–and (7), which is considered in line 6 of Algorithm 4.

Fig. 5

The proposed grid-based search method. a Gridded search space. b $\gamma$ distribution map in 2D

Post-processing

According to Algorithm 1 and , the final paths of the mobile bases and the end-effector are the sequences of straight line segments. Thus, the cubic splines [23] is adopted to smooth paths of the robot, whose geometric is constructed of piecewise third-order polynomials through each specified position point obtained from the proposed method. In this case, we define a single cubic spline for smoothing each independent path of the mobile base and the end-effector by connecting path points. Thus, the continuous motion profiles of the MCDPR can be guaranteed. Moreover, the boundary conditions are also imposed in which the velocities and accelerations at initial and final position points are null.

Method validation

Initialization setup and results

In this section, the proposed MCDPR path planning method is simulated in a cluttered environment. As shown in Fig. 6, a dynamic model of our MCDPR prototype is developed using CoppeliaSim (formerly known as V-REP) robot simulator software [24], to verify our proposed method. One should note that the end-effector is modeled as a point with a mass of 0.4 kg. We define 10 cylindrical obstacles with random positions in the environment. These obstacles have an identical radius and the height is 0.4 m. The dark blue obstacle is denoted as a target obstacle, where the MCDPR needs to move to this obstacle for performing a task action, i.e., picking and/or releasing an object. Therefore, goal points for each mobile base and the end-effector are defined around the target obstacle.

Fig. 6

Simulation environment developed using CoppeliaSim software [24]

Table 1 Simulation parameter

The proposed method is initialized using parameters given in Table 1, and the tree grows with a constant step size $\eta =0.2$ m. Thus, a constant timestep $\Delta T$ is required to transition the MCDPR state ${\varvec{X}}_{k+1}$ from the previous state ${\varvec{X}}_{k}$. In this work, $\Delta T=0.2$ s is used to obtain high accuracy. Accordingly, the mass center of the mobile base can be directly obtained from the CoppeliaSim given by $[0.12, 0.34, 0.36]^T$ with respect to $O_pj$ coordinate system. The simulation result is depicted in Fig. 7, and it is found that a collision-free path is generated for each mobile base to reach their goal points, and a path of the end-effector is also obtained by maximizing $\gamma$. It should be noted that the safe region around obstacles is defined and its radius is given by $r_m+r_o$. As a consequence, the mobile bases can be considered as a point to perform collision detection.

Fig. 7

The proposed grid-based search method

The velocity profiles of the end-effector and the mobile bases are shown in Fig. 8. As we can see, the continuous velocity profiles are guaranteed due to the post-processing. One should note that the mobile bases do not arrive the goal points at the same time. Thus, the total trajectory time 63 s due to ${\mathscr {M}}_{3}$ being the last one to reach its goal point. Moreover, Fig. 9 illustrates the three distance changes given by (2), (3), and (5). On account of the sampling characteristics of the proposed algorithm, the nodes will be retained only if they satisfy the given constraints. As a result, it can be found that MCDPR satisfies the distance constraints defined by these equations at each timestep, the collision-free trajectory is thus fulfilled.

Fig. 8

MCDPR velocity profiles

Fig. 9

Relative distance change with time

MCDPR verification in CoppeliaSim and experiments

In this section, the resulting MCDPR trajectories obtained from the last section is simulated in CoppeliaSim environment to verify the proposed method and the corresponding experiment is carried out. The software simulation framework is depicted in Fig. 10. For controlling the mobile bases, the resulting MCDPR trajectories are converted into the rotational velocities of the mobile base’s wheels using its kinematic model [25]. As shown in Fig. 11, due to the cubic splines are adopted, the continuous rotational velocities of wheels can be obtained, in which $v_l$ and $v_r$ represent the rotational velocities of the left and right wheels, respectively. For controlling the end-effector, we utilize (1) and (8) to adjust the length and speed of cables shown in Fig. 12. The obtained wheels’ rotational velocities are sent to CoppeliaSim to control the MCDPR model. The state of MCDPR can be directly obtained from the simulator, it will be compared with the desired path to obtain the error in evaluating the simulation results.

Fig. 10

Software simulation framework

Fig. 11

Wheel velocity profiles of mobile bases

Fig. 12

Cable length change

Fig. 13

Simulation in CoppeliaSim. a $t=29$ s, b $t=30$ s

The clips of the simulation in CoppeliaSim are shown in Fig. 13, it can be seen that the MCDPR can follow the resulting paths and avoid the collision. In addition, the actual position of the MCDPR in CoppeliaSim is obtained to compute the error with the desired paths. As shown in Fig. 14, the maximum error about the mobile base and the end-effector is approximately 2.8 cm and 4.1 cm, respectively. The planned path is validated experimentally using a second scenario one obstacle as shown in Fig. 15, in which NVIDIA Jetson Nano$^{\textrm{TM}}$ Developer Kit is adopted as a control computer to operate our MCDPR system. These results verify that the proposed method is feasible and effective.

Batch evaluation

The proposed path planning method for MCDPRs is compared with other existing methods in this section. Due to the random characteristics of the proposed path planning algorithm, a batch evaluation with 1000 simulations is conducted, and the average value is used to evaluate the proposed method. These simulations use the identical environment and parameters defined in the previous simulation. All the simulations are performed using $\copyright$MATLAB with CPU computations on an Intel ^®i7-9750 CPU@2.60 GHz and 32 GB RAM Windows 10 system. The results of the batch evaluation are presented in Table 2.

Fig. 14

Error between the actual and the desired position

Comparing the proposed method with the Iterative Algorithm and Direct Transcription, our method reduced the time costs by 93.3% and 84.7%, respectively. This is due to goal points being pre-defined for each mobile base and the end-effector. In addition, our adaptive sampling method reduces the time cost by 76.6% compared to the conventional goal-biased sampling method in which the sampling probability of the goal point is given as 0.5. Thus, the adaptive goal-biased sampling strategy can be deployed to improve the efficiency of our method. Moreover, Iterative Algorithm and Direct Transcription require continuous iterative processes for optimization, it may become computationally more expensive with more complex environments. On the contrary, the proposed method does not need to perform an iterative search, but rather finds a suitable solution by adaptive sampling the state space. One should note that the Iterative Algorithm and Direct Transcription lead mobile bases and the end-effector to reach goal points at the same time. However, in our method, once one mobile base reaches the goal point, it will be fixed to wait for all mobile bases to reach goal points. Finally, we can observe that the average global performance index $\gamma$ of the total path is improved by 31.1% and 14.4% with respect to the Iterative Algorithm and Direct Transcription. The average global performance index $\gamma$ of the proposed method with and without adaptive sampling have almost identical value, which is due to the grid-based search algorithm performed by both all of them. Hence, the proposed method can bring greater stability and kinematic performance for MCDPRs during the motion of the end-effector.

Despite the better performance in the evaluation results, the path quality of the proposed method, i.e., lengths of the MCDPR path, may not be as good as Iterative Algorithm or Direct Transcription. However, the proposed method has higher efficiency and better comprehensive performance, these provide the possibility of real-time implementation. The path quality can be somewhat mitigated by performing additional sampling. Moreover, the post-processing using the cubic splines add additional discrete points between the two consecutive nodes, this might not satisfy all constraints. This problem may be resolved using a smaller step size $\eta$ and increasing the safety region of obstacles.

Fig. 15

Experimental results. a $t=19$ s, b $t=22$ s, a $t=25$ s, b $t=28$ s

Table 2 The evaluation result

Conclusion and future work

In this work, we developed a collaborative path planning method for MCDPRs to generate feasible paths in cluttered environments. The various constraints such as external and internal interferences resulting from cables and mobile bases are considered to enforce the quality of the path. Moreover, the proposed method ensures adaptive exploration maximizes kinematic and stability performance stability and achieves fast convergence. Finally, the planned paths are post-processed to generate continuous motion profiles using cubic splines. The proposed approach was validated by simulations and subject to real-world testing on a self-built MCDPR prototype composed of eight cables and four mobile bases. The simulation results indicate that the proposed method can generate the feasible path for MCDPR effectively. Compared to other existing methods, the proposed method provides higher efficiency and better performance. Therefore, the reliability of the proposed method was demonstrated.

It is noteworthy that the proposed method is generally applied in an environment where we have complete knowledge about obstacles and the robot’s state. Hence, in future work, it is desirable that the trajectory of MCDPR towards the goal is calculated online during the motion of mobile bases and the end-effector, to provide more flexibility for MCDPRs to adapt to the environment. In addition, the velocity profiles of the robot show a little vibration, which may be because the sequence of line segments changes the direction frequently. In future work, we will further improve the algorithm to make the speed more stable.