Analysis of Hamming and Hausdorff 3D distance measures for complex pythagorean fuzzy sets and their applications in pattern recognition and medical diagnosis

Abstract

Similarity measures are very effective and meaningful tool used for evaluating the closeness between any two attributes which are very important and valuable to manage awkward and complex information in real-life problems. Therefore, for better handing of fuzzy information in real life, Ullah et al. (Complex Intell Syst 6(1): 15–27, 2020) recently introduced the concept of complex Pythagorean fuzzy set (CPyFS) and also described valuable and dominant measures, called various types of distance measures (DisMs) based on CPyFSs. The theory of CPyFS is the essential modification of Pythagorean fuzzy set to handle awkward and complicated in real-life problems. Keeping the advantages of the CPyFS, in this paper, we first construct an example to illustrate that a DisM proposed by Ullah et al. does not satisfy the axiomatic definition of complex Pythagorean fuzzy DisM. Then, combining the 3D Hamming distance with the Hausdorff distance, we propose a new DisM for CPyFSs, which is proved to satisfy the axiomatic definition of complex Pythagorean fuzzy DisM. Moreover, similarly to some DisMs for intuitionistic fuzzy sets, we present some other new complex Pythagorean fuzzy DisMs. Finally, we apply our proposed DisMs to a building material recognition problem and a medical diagnosis problem to illustrate the effectiveness of our DisMs. Finally, we aim to compare the proposed work with some existing measures is to enhance the worth of the derived measures.

Introduction

Similarity and dissimilarity are important because they are used by a number of data mining techniques, such as clustering nearest neighbor classification and anomaly detection. The term proximity is used to refer to either similarity or dissimilarity. The similarity between two objects is a numeral measure of the degree to which the two objects are alike. Consequently, similarities are higher for pairs of objects that are more alike. Similarities are usually non-negative and are often between 0 (no similarity) and 1 (complete similarity). The dissimilarity between two objects is the numerical measure of the degree to which the two objects are different. Dissimilarity is lower for more similar pairs of objects. Frequently, the term distance is used as a synonym for dissimilarity. Dissimilarities sometimes fall in the interval [0, 1, but it is also common for them to range from 0 to $\infty$. Certain people have diagnosed the theory of similarity measures and distance measures for classical information and because of this reason, we loss a lot of information. For managing with such sort of issues, Zadeh [46] introduced the concept of fuzzy set (FS) by using a function from the universe of discourse to [0, 1], which was called the membership degree function, to describe the importance of an element in the universe of discourse. Then, Zadeh’s fuzzy set theory constitutes the basis of fuzzy decision-making [10, 11, 19]. However, the FS can only deal with the situation containing two opposite responses. Therefore, it failed to deal with the situation with hesitant/neutral state of “this and also that”. According to this, Atanassov [8] generalized Zadeh’s fuzzy set by proposing the concept of intuitionistic fuzzy sets (IFSs), characterized by a membership function and a non-membership function meeting the condition that their sum at every point is less than or equal to 1. In the theory of IFSs, the condition that the sum of the membership degree and the non-membership degree is less than or equal to 1 induces some decision evaluation information that cannot be expressed effectively. Hence, the range of their applications is limited. To overcome this shortcoming, Yager [42,43,44] proposed the concepts of Pythagorean fuzzy sets (PFSs) and q-rung orthopair fuzzy sets (q-ROFSs). These sets satisfy the condition that the square sum or the qth power sum of the membership degree and the non-membership degree is less than or equal to 1. It is determined from the aforementioned in-depth research and DMPs that their use is restricted to handling only the data’s uncertainty while failing to address its fluctuations at a particular point in time. But data derived from “medical research, a database for biometric and facial recognition” are constantly updated in tandem with time. Thus, a range of MD is expanded from a real subset to the unit disc of the complex plane to cope with these kinds of difficulties, which developed the idea of the complex fuzzy sets (CFSs) Ramot et al. [31]. Further, Alkouri and Salleh [7] introduced the concepts of complex intuitionistic fuzzy sets (CIFSs). To enlarge the representing domain, Ullah et al. [36] proposed the concept of complex Pythagorean fuzzy sets (CPyFSs), and Liu et al. [20] introduced the concept of complex q-rung orthopair fuzzy sets (Cq-ROFSs). Since then, CIFSs, CPyFSs, and Cq-ROFSs have been widely applied to various fields, such as MCDM/MADM [1,2,3,4,5,6, 12, 15, 20,21,22, 24, 25, 32, 38, 40], medical diagnosis [13, 27,28,29, 32], pattern recognition [12, 13, 27, 36], cluster analysis [12, 47], and image processing [16].

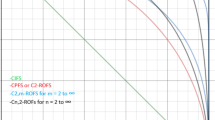
It is necessary to gauge the degree of discriminating between the pairs of sets due to the intricate decision-making process. The most effective tools for this purpose are instant messengers. The decision-maker have the ability to assess the degree of discriminating between the sets among the many measures like entropy, similarity, inclusion, etc. The major goal of this work is to create some exponential-based decision-makers to quantify the information, which is encouraged by the CPyFS model’s characteristics and the quality of decision-maker. In order to achieve this, the data was designated under the CPyFS model to quantify the data using the suggested metric for resolving the decision-making procedures. The qualities of a few axioms are studied in detail. Later, an algorithm was developed based on the proposed investigation, to assess the differences for various types of complex fuzzy sets, the normalized distance measure (DisM) and the similarity measure (SimM), being a pair of dual concepts, are important tools for decision-making and pattern recognition under CPyFSs and CIFSs frameworks. For the CIFSs, Rani and Garg [32] presented a few two-dimensional (2D) CIFDisMs by using the Hamming, Euclidean, and Hausdorff distances. Then, Garg and Rani [12] proposed some new CIF information measures, including SimMs, DisMs, entropies, and inclusion measures) and obtained the transformation relationships among them. Meanwhile, they [12] developed a CIF clustering algorithm. For Cq-ROFSs, Garg et al. [13] gave the notion of Cq-ROF dice SimM and weighted Cq-ROF dice SimM and derived some new Cq-ROF dice SimMs. Liu et al. [21] proposed some cosine DisMs and SimMs for Cq-ROFSs and obtained developed a TOPSIS method under Cq-ROFS framework. To distinguish different Cq-ROFSs with high similarity, Mahmood and Ali [25] obtained some new SimMs for Cq-ROFSs. For CPyFSs, Aldring and Ajay [5] developed a MCGDM method by introducing a new CPyF projection measure between the alternatives and the relative CPyF ideal point. Based on the Hamming distance and the Hausdorff distance, Ullah et al. [36] developed two parametric DisMs for CPyFSs and applied to a building material recognition problem. However, because the different weights are assigned to the degrees of membership, non-membership, and hesitancy for the 3D DisM $D^{2}_{{\textrm{CPyFS}}}$ of Ullah et al. [36], the may cause an unreasonable result that the DisM $D^{2}_{{\textrm{CPyFS}}}$ does not satisfy the axiomatic definition of complex Pythagorean fuzzy DisM (see Example 1). The geometrical shape of the proposed work is described in the form of Fig. 1.

Fig. 1

Geometrical representation of the proposed work

To overcome the drawback of Ullah et al.’s DisM $D^{2}_{\textrm{CPyFS}}$ in [36], we introduce a new 3D DisM for CPyFSs by combining the 3D Hamming distance with the Hausdorff distance and prove that it satisfies the axiomatic definition of CPyFDisM. Moreover, similarly to the DisMs for IFSs in [14, 34, 37, 39, 45], we propose some other new CPyFDisMs. Finally, we give the comparative analysis by using our proposed DisMs to a building material recognition problem and a medical diagnosis problem to illustrate the effectiveness of our DisMs. The comparative analysis results also indicate the unreasonableness of Ullah et al.’s DisM $D^{2}_{_{\textrm{CPyFS}}}$.

Preliminaries

This section gives some elements on IFS, PFS, CIFS, and CPyFS. Throughout this paper, let ${\mathscr {O}}_{_{\mathbb {C}}}=\{z\in \mathbb {C} \mid |z|\le 1\}$.

Intuitionistic fuzzy set (IFS)

Definition 2.1

([9, Definition 1.1]). An intuitionistic fuzzy set (IFS) I in ${\mathfrak {X}}$ is defined as

$$\begin{aligned} I=\left\{ \langle \vartheta , {\mathfrak {P}}_{_{I}}(\vartheta ), {\mathfrak {O}}_{_{I}}(\vartheta )\rangle \mid \vartheta \in {\mathfrak {X}}\right\} , \end{aligned}$$

(1)

where the functions ${\mathfrak {P}}_{_{I}}: {\mathfrak {X}} \longrightarrow [0,1]$ and ${\mathfrak {O}}_{_{I}}: {\mathfrak {X}} \longrightarrow [0,1]$ define the degree of membership and the degree of non-membership of the element $\vartheta \in {\mathfrak {X}}$ to the set I, respectively, and for every $\vartheta \in {\mathfrak {X}}$, ${\mathfrak {P}}_{_{I}}(\vartheta ) +{\mathfrak {O}}_{_{I}}(\vartheta )\le 1$. Moreover, the hesitancy degree ${\mathfrak {H}}_{_{I}}(\vartheta )$ of an element $\vartheta$ belonging to I is defined by ${\mathfrak {H}}_{_I}(\vartheta )=1-{\mathfrak {P}}_{_I}(\vartheta ) -{\mathfrak {O}}_{_I}(\vartheta )$. The pair $\langle {\mathfrak {P}}_{_I}(\vartheta ), {\mathfrak {O}}_{_I}(\vartheta )\rangle$ is called an intuitionistic fuzzy number (IFN) by Xu [41]. Let $\Theta$ be the set of all IFNs, i.e., $\Theta =\{\langle {\mathfrak {P}}, {\mathfrak {O}} \rangle \in [0, 1]^{2} \mid {\mathfrak {P}}+{\mathfrak {O}} \le 1\}$.

Pythagorean fuzzy set (PFS)

Definition 2.2

([42]). A Pythagorean fuzzy set (PFS) P in ${\mathfrak {X}}$ is defined as

$$\begin{aligned} P=\left\{ \langle \vartheta , {\mathfrak {P}}_{_{P}}(\vartheta ), {\mathfrak {O}}_{_{P}}(\vartheta )\rangle \mid \vartheta \in {\mathfrak {X}}\right\} , \end{aligned}$$

(2)

where the functions ${\mathfrak {P}}_{_{P}}: {\mathfrak {X}} \longrightarrow [0,1]$ and ${\mathfrak {O}}_{_{P}}: {\mathfrak {X}} \longrightarrow [0,1]$ define the degree of membership and the degree of non-membership of the element $\vartheta \in {\mathfrak {X}}$ to the set P, respectively, and for every $\vartheta \in {\mathfrak {X}}$, ${\mathfrak {P}}^{2}_{_{P}}(\vartheta ) +{\mathfrak {O}}^{2}_{_{P}}(\vartheta )\le 1$. Moreover, the hesitancy degree ${\mathfrak {H}}_{_{P}}(\vartheta )$ of an element $\vartheta$ belonging to P is defined by ${\mathfrak {H}}_{_P}(\vartheta )=\sqrt{1-{\mathfrak {P}}^{2}_{_P}(\vartheta ) -{\mathfrak {O}}^{2}_{_P}(\vartheta )}$.

Complex intuitionistic fuzzy set (CIFS)

Definition 2.3

([7, Definition 3.1], [36, Definition 6]). A complex intuitionistic fuzzy set (CIFS) C in ${\mathfrak {X}}$ is defined as

$$\begin{aligned} {\small C=\left\{ \langle \vartheta , {\mathfrak {P}}_{_{C}}(\vartheta ), {\mathfrak {O}}_{_{C}}(\vartheta )\rangle \mid \vartheta \in {\mathfrak {X}}\right\} ,} \end{aligned}$$

(3)

where the functions ${\mathfrak {P}}_{_{C}}: {\mathfrak {X}} \longrightarrow {\mathscr {O}}_{_{\mathbb {C}}}$ and ${\mathfrak {O}}_{_{C}}: {\mathfrak {X}} \longrightarrow {\mathscr {O}}_{_{\mathbb {C}}}$ define the degree of membership and the degree of non-membership of the element $\vartheta \in {\mathfrak {X}}$ to the set C, respectively, and for every $\vartheta \in {\mathfrak {X}}$, ${\mathfrak {P}}_{_{C}}(\vartheta )= T_{_C}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{_C}}(\vartheta )}$ and ${\mathfrak {O}}_{_{C}}(\vartheta )=F_{_C}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{_C}}(\vartheta )}$ satisfying that $0\le T_{_C}(\vartheta ), F_{_C}(\vartheta ) \le 1$, $0\le W_{T_{_C}}(\vartheta ), W_{F_{_C}}(\vartheta ) \le 1$, and $T_{_C}(\vartheta )+ F_{_C}(\vartheta ) \le 1$, $W_{T_{_C}}(\vartheta )+W_{F_{_C}}(\vartheta ) \le 1$. Moreover, the hesitancy degree ${\mathfrak {H}}_{_{C}}(\vartheta )= R_{_C}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{R_{_C}}(\vartheta )}$ of the element $\vartheta$ belonging to C is defined by $R_{_C}(\vartheta )=1-T_{_C}(\vartheta )- F_{_C}(\vartheta )$ and $W_{R_{_C}}(\vartheta )=1-W_{T_{_C}}(\vartheta )-W_{F_{_C}}(\vartheta )$.

Complex pythagorean fuzzy set (CPyFS)

Definition 2.4

([36, Definition 7]). A complex Pythagorean fuzzy set (CPyFS) ${\mathfrak {C}}$ in ${\mathfrak {X}}$ is defined as

(4)

where the functions ${\mathfrak {P}}_{_{{\mathfrak {C}}}}: {\mathfrak {X}} \longrightarrow {\mathscr {O}}_{_{\mathbb {C}}}$ and ${\mathfrak {O}}_{_{{\mathfrak {C}}}}: {\mathfrak {X}} \longrightarrow {\mathscr {O}}_{_{\mathbb {C}}}$ define the degree of membership and the degree of non-membership of the element $\vartheta \in {\mathfrak {X}}$ to the set ${\mathfrak {C}}$, respectively, and for every $\vartheta \in {\mathfrak {X}}$, ${\mathfrak {P}}_{_{{\mathfrak {C}}}}(\vartheta )= T_{{\mathfrak {C}}}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}}}(\vartheta )}$ (${\textbf{i}}=\sqrt{-1}$) and ${\mathfrak {O}}_{_{{\mathfrak {C}}}}(\vartheta )=F_{{\mathfrak {C}}}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}}}(\vartheta )}$ satisfying that

$$\begin{aligned}{} & {} 0\le T_{{\mathfrak {C}}}(\vartheta ), F_{{\mathfrak {C}}}(\vartheta ) \le 1, \ 0\le W_{T_{{\mathfrak {C}}}}(\vartheta ), W_{F_{{\mathfrak {C}}}}(\vartheta ) \le 1, \nonumber \\{} & {} \quad \text { and } T^{2}_{{\mathfrak {C}}}(\vartheta )+ F^{2}_{{\mathfrak {C}}} (\vartheta ) \le 1,\ W^{2}_{T_{{\mathfrak {C}}}}(\vartheta )+W^{2}_{F_{{\mathfrak {C}}}}(\vartheta ) \le 1.\nonumber \\ \end{aligned}$$

(5)

Moreover, the hesitancy degree ${\mathfrak {H}}_{_{{\mathfrak {C}}}}(\vartheta )= R_{{\mathfrak {C}}}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{R_{{\mathfrak {C}}}}(\vartheta )}$ of the element $\vartheta$ belonging to ${\mathfrak {C}}$ is defined by $R_{{\mathfrak {C}}} (\vartheta )=\sqrt{1-T^{2}_{{\mathfrak {C}}}(\vartheta )- F^{2}_{{\mathfrak {C}}}(\vartheta )}$ and $W_{R_{{\mathfrak {C}}}}(\vartheta )=\sqrt{1-W^{2}_{T_{{\mathfrak {C}}}}(\vartheta ) -W^{2}_{F_{{\mathfrak {C}}}}(\vartheta )}$. Let $\textrm{CPyFS}({\mathfrak {X}})$ denote the set of all CPyFSs in ${\mathfrak {X}}$.

In [36], the pair $(T_{{\mathfrak {C}}}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}}}(\vartheta )}, F_{{\mathfrak {C}}}(\vartheta )\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}}}(\vartheta )})$ satisfying the condition in (5) is called a complex Pythagorean fuzzy set (CPyFN). For convenience, use ${\mathfrak {C}}=(T_{{\mathfrak {C}}}\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}}}}, F_{{\mathfrak {C}}}\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}}}})$ to represent a CPyFN ${\mathfrak {C}}$, which satisfies $0\le T_{{\mathfrak {C}}}, F_{{\mathfrak {C}}} \le 1$, $0\le W_{T_{{\mathfrak {C}}}}, W_{F_{{\mathfrak {C}}}} \le 1$, and $T^{2}_{{\mathfrak {C}}}+ F^{2}_{{\mathfrak {C}}}\le 1$, $W^{2}_{T_{{\mathfrak {C}}}}+W^{2}_{F_{{\mathfrak {C}}}}\le 1$. Let ${\mathscr {C}}_{_{\textrm{PyFN}}}$ denote the set of all CPyFNs, i.e., ${\mathscr {C}}_{_{\textrm{PyFN}}}=\{(T_{{\mathfrak {C}}}\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}}}}, F_{{\mathfrak {C}}}\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}}}}) \mid 0\le T_{{\mathfrak {C}}}, F_{{\mathfrak {C}}} \le 1,\ 0\le W_{T_{{\mathfrak {C}}}}, W_{F_{{\mathfrak {C}}}} \le 1, \text { and } T^{2}_{{\mathfrak {C}}}+ F^{2}_{{\mathfrak {C}}}\le 1,\ W^{2}_{T_{{\mathfrak {C}}}}+W^{2}_{F_{{\mathfrak {C}}}}\le 1\}$.

Meanwhile, Ullah et al. [36] introduced the following basic operations for CPyFSs and CPyFNs.

Definition 2.5

([36, Definition 8]). (1) Let ${\mathfrak {C}}_1=(T_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_1}}}, F_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_1}}})$ and ${\mathfrak {C}}_2=(T_{{\mathfrak {C}}_2} \cdot e^{2\pi {\textbf{i}}\cdot W_{T_{{\mathfrak {C}}_2}}}, F_{{\mathfrak {C}}_2} \cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_2}}})$ be two CPyFNs. Define

• (i) (Inclusion) ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2$ if and only if $T_{{\mathfrak {C}}_1} \le T_{{\mathfrak {C}}_2}$, $F_{{\mathfrak {C}}_1}\ge F_{{\mathfrak {C}}_2}$, and $W_{T_{{\mathfrak {C}}_1}}\le W_{T_{{\mathfrak {C}}_2}}$, $W_{F_{{\mathfrak {C}}_1}} \ge W_{F_{{\mathfrak {C}}_2}}$;

• (ii) ${\mathfrak {C}}_1={\mathfrak {C}}_2$ if and only if $T_{{\mathfrak {C}}_1} =T_{{\mathfrak {C}}_2}$, $F_{{\mathfrak {C}}_1}= F_{{\mathfrak {C}}_2}$, and $W_{T_{{\mathfrak {C}}_1}}= W_{T_{{\mathfrak {C}}_2}}$, $W_{F_{{\mathfrak {C}}_1}} = W_{F_{{\mathfrak {C}}_2}}$;

• (iii) (Complement) $({\mathfrak {C}}_1)^\complement =(F_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_1}}}, T_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_1}}})$.

(2) Let ${\mathfrak {C}}_1$ and ${\mathfrak {C}}_2$ be two CPyFSs in ${\mathfrak {X}}$. Define

• (i) (Inclusion) ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2$ if and only if, for any $\vartheta \in {\mathfrak {X}}$, ${\mathfrak {C}}_1(\vartheta )\subseteq {\mathfrak {C}}_2(\vartheta )$;

• (ii) ${\mathfrak {C}}_1={\mathfrak {C}}_2$ if and only if, for any $\vartheta \in {\mathfrak {X}}$, ${\mathfrak {C}}_1(\vartheta ) = {\mathfrak {C}}_2(\vartheta )$;

• (iii) (Complement) $({\mathfrak {C}}_1)^\complement =\{\langle \vartheta , ({\mathfrak {C}}_1(\vartheta ))^\complement \mid \vartheta \in {\mathfrak {X}}\rangle \}$.

Distance and similarity measures on $\textrm{CPyFSs}$

Definition 2.6

A function $D: \textrm{CPyFS}({\mathfrak {X}})\times \textrm{CPyFS}({\mathfrak {X}}) \longrightarrow \mathbb {R}$ is a normalized distance measure (DisM) on $\textrm{CPyFS}({\mathfrak {X}})$ if it satisfies the following conditions: for any ${\mathfrak {C}}_1$, ${\mathfrak {C}}_2$, ${\mathfrak {C}}_3\in \textrm{CPyFS}({\mathfrak {X}})$,

• (1) $0\le D({\mathfrak {C}}_1, {\mathfrak {C}}_2)=D({\mathfrak {C}}_2, {\mathfrak {C}}_1)\le 1$;

• (2) $D({\mathfrak {C}}_1, {\mathfrak {C}}_2)=0$ if and only if ${\mathfrak {C}}_1={\mathfrak {C}}_2$;

• (3) $D({\mathfrak {C}}_1, {\mathfrak {C}}_3)\le D({\mathfrak {C}}_1, {\mathfrak {C}}_2)+D({\mathfrak {C}}_2, {\mathfrak {C}}_3)$;

• (4) If ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$, then $D({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D({\mathfrak {C}}_1, {\mathfrak {C}}_2)$ and $D({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D({\mathfrak {C}}_2, {\mathfrak {C}}_3)$.

Definition 2.7

A function ${\textbf{S}}: \textrm{CPyFS}({\mathfrak {X}})\times \textrm{CPyFS}({\mathfrak {X}}) \longrightarrow \mathbb {R}$ is a similarity measure (SimM) on $\textrm{CPyFS}({\mathfrak {X}})$ if it satisfies the following conditions: for any ${\mathfrak {C}}_1$, ${\mathfrak {C}}_2$, ${\mathfrak {C}}_3\in \textrm{CPyFS}({\mathfrak {X}})$,

• (1) $0\le {\textbf{S}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)={\textbf{S}}({\mathfrak {C}}_2, {\mathfrak {C}}_1)\le 1$;

• (2) ${\textbf{S}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)=1$ if and only if ${\mathfrak {C}}_1={\mathfrak {C}}_2$;

• (3) If ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$, then ${\textbf{S}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\le {\textbf{S}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$ and ${\textbf{S}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\le {\textbf{S}}({\mathfrak {C}}_2, {\mathfrak {C}}_3)$.

Drawback of DisM of Ullah et al. [36]

Let ${\mathfrak {X}}=\{\vartheta _1, \vartheta _2, \ldots , \vartheta _{\ell }\}$ and ${\mathfrak {C}}_1=\{(T_{{\mathfrak {C}}_1}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_1}}(\vartheta _j)}, F_{{\mathfrak {C}}_1}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_1}}(\vartheta _j)}) \mid 1\le j\le \ell \}$ and ${\mathfrak {C}}_2=\{(T_{{\mathfrak {C}}_2}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_2}}(\vartheta _j)}, F_{{\mathfrak {C}}_2}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_2}}(\vartheta _j)}) \mid 1\le j\le \ell \}$ be two CPyFSs on ${\mathfrak {X}}$. Recently, Ullah et al. [36] introduced two DisMs $D^1_{_{\textrm{CPyFS}}}$ and $D^2_{_{\textrm{CPyFS}}}$ for CPyFSs as follows (see [36, Definition 12]):

$$\begin{aligned} \begin{aligned} D^1_{_{\textrm{CPyFS}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right)&= \frac{1}{2\ell }\sum _{j=1}^{\ell } \big [ a_1 \cdot |T_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -T_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) | \\&\quad +b_1 \cdot |F_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -F_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) | +c_1\cdot \max \{|T_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) \\&\quad -T_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |, |F_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -F_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |\}\\&\qquad a_2 \cdot |W^{2}_{T_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{T_{{\mathfrak {C}}_2}}\left( x_{j}\right) |\\&\quad +b_2 \cdot |W^{2}_{F_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{F_{{\mathfrak {C}}_2}}\left( x_{j}\right) |\\&\quad +c_2 \cdot \max \big \{|W^{2}_{T_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{T_{{\mathfrak {C}}_2}}\left( x_{j}\right) |,\\&\qquad |W^{2}_{F_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{F_{{\mathfrak {C}}_2}}\left( x_{j}\right) |\big \}\big ], \end{aligned} \end{aligned}$$

(6)

and

$$\begin{aligned} D^2_{_{\textrm{CPyFS}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right)&= \frac{1}{2\ell }\sum _{j=1}^{\ell } \big [ a_1 \cdot |T_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -T_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) | \nonumber \\&\quad +b_1 \cdot |F_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -F_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |\nonumber \\&\quad +r_1 \cdot |R_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -R_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |\nonumber \\&\quad +c_1\cdot \max \{|T_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -T_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |,\nonumber \\&\quad |F_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -F_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |, \nonumber \\&\quad \times |R_{{\mathfrak {C}}_1}^{2}\left( x_{j}\right) -R_{{\mathfrak {C}}_2}^{2}\left( x_{j}\right) |\} a_2 \cdot |W^{2}_{T_{{\mathfrak {C}}_1}}\left( x_{j}\right) \nonumber \\&\quad -W^{2}_{T_{{\mathfrak {C}}_2}}\left( x_{j}\right) | +b_2 \cdot |W^{2}_{F_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{F_{{\mathfrak {C}}_2}}\left( x_{j}\right) |\nonumber \\&\quad +r_2 \cdot |W^{2}_{R_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{R_{{\mathfrak {C}}_2}}\left( x_{j}\right) |\nonumber \\&\quad +c_2 \cdot \max \{|W^{2}_{T_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{T_{{\mathfrak {C}}_2}}\left( x_{j}\right) |, \nonumber \\&\quad |W^{2}_{F_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{F_{{\mathfrak {C}}_2}}\left( x_{j}\right) |,\nonumber \\&\quad |W^{2}_{R_{{\mathfrak {C}}_1}}\left( x_{j}\right) -W^{2}_{R_{{\mathfrak {C}}_2}}\left( x_{j}\right) |\}\big ], \end{aligned}$$

(7)

where $0\le a_i$, $b_i$, $c_i$, $r_i\le 1$ and $a_i+b_i+c_i+r_i=1$.

Meanwhile, Ullah et al. [36] proved that DisM $D^2_{_{\textrm{CPyFS}}}$ has the following property.

Property

If ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$, then $D^2_{_{\textrm{CPyFS}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D^2_{_{\textrm{CPyFS}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$ and $D^2_{_{\textrm{CPyFS}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D^2_{_{\textrm{CPyFS}}}({\mathfrak {C}}_2, {\mathfrak {C}}_3)$.

The following example shows that Property 3 does not hold, and thus the DisM $D^2_{_{\textrm{CPyFS}}}$ does not satisfy the axiomatic definition of complex Pythagorean fuzzy DisM.

Example 1

Let ${\mathfrak {X}}=\{\vartheta \}$ and ${\mathfrak {C}}_1=(0\cdot e^{2\pi {\textbf{i}} \cdot 0}, 1\cdot e^{2\pi {\textbf{i}} \cdot 0})$, ${\mathfrak {C}}_2=(0\cdot e^{2\pi {\textbf{i}} \cdot 0}, 0\cdot e^{2\pi {\textbf{i}} \cdot 0})$, and ${\mathfrak {C}}_3=(1\cdot e^{2\pi {\textbf{i}} \cdot 0}, 0\cdot e^{2\pi {\textbf{i}} \cdot 0})$ be three CPyFSs on ${\mathfrak {X}}$ and choose $a_1=a_2=b_1=b_2=c_1 =c_2=0.1$ and $r_1=r_2=0.7$. Clearly, ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$. By direct calculation, we have

$$\begin{aligned} D^2_{_{\textrm{CPyFS}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right) =0.1\times 0+0.1\times 1+0.7\times 1+0.1\times 1 =0.9, \end{aligned}$$

and

$$\begin{aligned} D^2_{_{\textrm{CPyFS}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_3\right) =0.1\times 1+0.1\times 1+0.7\times 0+0.1\times 1 =0.3, \end{aligned}$$

implying that $D^2_{_{\textrm{CPyFS}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)<D^2_{_{\textrm{CPyFS}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$. This means that Property 3 does not hold because ${\mathfrak {C}}_1\subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$.

A new complex Pythagorean fuzzy DisM

A novel DisM on ${\mathscr {C}}_{_{\textrm{PyFN}}}$

Let ${\mathfrak {C}}_1=(T_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_1}}}, F_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_1}}})$ and ${\mathfrak {C}}_2=(T_{{\mathfrak {C}}_2} \cdot e^{2\pi {\textbf{i}}\cdot W_{T_{{\mathfrak {C}}_2}}}, F_{{\mathfrak {C}}_2} \cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_2}}})$ be two CPyFNs. Define the DisM $D_{_{\textrm{Wu}}}$ between ${\mathfrak {C}}_1$ and ${\mathfrak {C}}_2$ by

$$\begin{aligned} D_{_{\textrm{Wu}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right){} & {} = \frac{1}{2} \left[ \frac{1}{4} \cdot \left( |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|\right. \right. \nonumber \\ {}{} & {} \qquad \left. \left. +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\right) \right. \nonumber \\{} & {} +\frac{1}{2}\cdot \max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|,\nonumber \\{} & {} \qquad |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}\nonumber \\{} & {} +\frac{1}{4} \cdot \left( |W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|\right. \nonumber \\ {}{} & {} \qquad \left. +|W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|\right) \nonumber \\{} & {} \left. +\frac{1}{2} \cdot \max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|,\right. \nonumber \\ {}{} & {} \qquad \left. |W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|\}\right] . \end{aligned}$$

(8)

Proposition 4.1

$0\le D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)\le 1$.

Proof

From $T_{{\mathfrak {C}}_1}^{2}+F_{{\mathfrak {C}}_1}^{2}+R_{{\mathfrak {C}}_1}^{2}=1$, $T_{{\mathfrak {C}}_2}^{2}+F_{{\mathfrak {C}}_2}^{2}+R_{{\mathfrak {C}}_2}^{2}=1$, $W^{2}_{T_{{\mathfrak {C}}_1}}+ W^{2}_{F_{{\mathfrak {C}}_1}}+ W^{2}_{R_{{\mathfrak {C}}_1}}=1$, and $W^{2}_{T_{{\mathfrak {C}}_2}}+ W^{2}_{F_{{\mathfrak {C}}_2}}+ W^{2}_{R_{{\mathfrak {C}}_2}}=1$, it follows that $|T_{{\mathfrak {C}}_1}^{2} -T_{{\mathfrak {C}}_2}^{2}|+|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\le 2$, $\max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}\le 1$, $|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}| +|W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|\le 2$, and $\max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|, |W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|\}\le 1$, and thus $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)\le 1$ by Eq. (8). $\square$

Proposition 4.2

• (1) $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2) =D_{_{\textrm{Wu}}}({\mathfrak {C}}_2, {\mathfrak {C}}_1)$.

• (2) $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)=0$ if and only if ${\mathfrak {C}}_1={\mathfrak {C}}_2$.

Proof

It follows directly from Eq. (8). $\square$

Proposition 4.3

For ${\mathfrak {C}}_1$, ${\mathfrak {C}}_2$, ${\mathfrak {C}}_3\in {\mathscr {C}}_{_{\textrm{PyFN}}}$, $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\le D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)+D_{_{\textrm{Wu}}}({\mathfrak {C}}_2, {\mathfrak {C}}_3).$

Proof

It follows directly from Eq. (8) and triangle inequality. $\square$

Proposition 4.4

Let ${\mathfrak {C}}_1$, ${\mathfrak {C}}_2$, ${\mathfrak {C}}_3\in {\mathscr {C}}_{_{\textrm{PyFN}}}$. If ${\mathfrak {C}}_1 \subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$, then $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$ and $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_2, {\mathfrak {C}}_3).$

Proof

By ${\mathfrak {C}}_1 \subseteq {\mathfrak {C}}_2 \subseteq {\mathfrak {C}}_3$, it follows that $T_{{\mathfrak {C}}_1}^{2}\le T_{{\mathfrak {C}}_2}^{2} \le T_{{\mathfrak {C}}_3}^{2}$ and $F_{{\mathfrak {C}}_1}^{2} \ge F_{{\mathfrak {C}}_2}^{2} \ge F_{{\mathfrak {C}}_3}^{2}$. To prove $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$, we consider the following four cases:

(i) If $R_{{\mathfrak {C}}_2}^{2}\ge R_{{\mathfrak {C}}_1}^{2}$ and $R_{{\mathfrak {C}}_3}^{2} \ge R_{{\mathfrak {C}}_1}^{2}$, then

$$\begin{aligned} |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}| =&\left( 1-T_{{\mathfrak {C}}_2}^{2}-F_{{\mathfrak {C}}_2}^{2}\right) - \left( 1-T_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_1}^{2}\right) \\ =&\left( F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\right) +\left( T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}\right) \\&\le F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2},\\ |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}| =&\left( 1-T_{{\mathfrak {C}}_3}^{2}-F_{{\mathfrak {C}}_3}^{2}\right) - \left( 1-T_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_1}^{2}\right) \\ =&\left( F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}\right) +\left( T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}\right) \\&\le F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2},\\ |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|&+|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\\&= T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2} +F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}+R_{{\mathfrak {C}}_2}^{2}-R_{{\mathfrak {C}}_1}^{2}\\&= T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}+F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2} +\left( 1-T_{{\mathfrak {C}}_2}^{2}-F_{{\mathfrak {C}}_2}^{2}\right) \\&\quad -\left( 1-T_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_1}^{2}\right) \\&= 2\left( F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\right) , \end{aligned}$$

and

$$\begin{aligned} |T_{{\mathfrak {C}}_1}^{2}&-T_{{\mathfrak {C}}_3}^{2}| +\quad |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +\quad |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\\&= T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2} + \quad F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}+ R_{{\mathfrak {C}}_3}^{2}-R_{{\mathfrak {C}}_1}^{2}\\&= T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}+F_{{\mathfrak {C}}_1}^{2} -F_{{\mathfrak {C}}_3}^{2}+\left( 1-T_{{\mathfrak {C}}_3}^{2}-F_{{\mathfrak {C}}_3}^{2}\right) \\&\quad -\left( 1-T_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_1}^{2}\right) \\&= 2\left( F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}\right) . \end{aligned}$$

These, together with $T_{{\mathfrak {C}}_1}^{2}\le T_{{\mathfrak {C}}_2}^{2} \le T_{{\mathfrak {C}}_3}^{2}$ and $F_{{\mathfrak {C}}_1}^{2} \ge F_{{\mathfrak {C}}_2}^{2} \ge F_{{\mathfrak {C}}_3}^{2}$, imply that

$$\begin{aligned}{} & {} |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}| \\{} & {} \quad \le |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}|\\{} & {} \qquad +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|, \end{aligned}$$

and

$$\begin{aligned} \max&\{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}\\ =&\max \{T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\}\\ \le&\max \{T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}\}\\ =&\max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\}. \end{aligned}$$

And thus, $\frac{1}{4} \cdot (|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|)$$+\frac{1}{2}\cdot \max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}\le \frac{1}{4} \cdot$$(|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|) +\frac{1}{2}\cdot \max \{|T_{{\mathfrak {C}}_1}^{2}$$-T_{{\mathfrak {C}}_3}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\}$. Similarly, it can be verified that $\frac{1}{4} \cdot (|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}| +|W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|)$$+\frac{1}{2} \cdot \max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|, |W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|\}$$\le \frac{1}{4} \cdot (|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_3}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_3}}| +|W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_3}}|)$$+\frac{1}{2} \cdot \max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_3}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_3}}|, |W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_3}}|\}$. Therefore,

$$\begin{aligned} D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2). \end{aligned}$$

(ii) If $R_{{\mathfrak {C}}_2}^{2}\le R_{{\mathfrak {C}}_1}^{2}$ and $R_{{\mathfrak {C}}_3}^{2} \le R_{{\mathfrak {C}}_1}^{2}$, similarly to the proof of (i), it can be verified that

$$\begin{aligned}&|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}| \le T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}| \le T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2},\\&\quad |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\\&\quad = 2(T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}), \end{aligned}$$

and

$$\begin{aligned} |T_{{\mathfrak {C}}_1}^{2}&-T_{{\mathfrak {C}}_3}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\\ =&2\left( T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}\right) . \end{aligned}$$

These, together with $T_{{\mathfrak {C}}_1}^{2}\le T_{{\mathfrak {C}}_2}^{2} \le T_{{\mathfrak {C}}_3}^{2}$ and $F_{{\mathfrak {C}}_1}^{2} \ge F_{{\mathfrak {C}}_2}^{2} \ge F_{{\mathfrak {C}}_3}^{2}$, imply that

$$\begin{aligned}{} & {} |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\\{} & {} \quad \le |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}|\\{} & {} \qquad +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|, \end{aligned}$$

and

$$\begin{aligned} \max&\{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}\\ =&\max \{T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\}\\ \le&\max \{T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}\}\\ =&\max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\}. \end{aligned}$$

And thus, it can be similarly verified that

$$\begin{aligned} D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2). \end{aligned}$$

(iii) If $R_{{\mathfrak {C}}_2}^{2}\ge R_{{\mathfrak {C}}_1}^{2}$ and $R_{{\mathfrak {C}}_3}^{2} \le R_{{\mathfrak {C}}_1}^{2}$, i.e., $1-T_{{\mathfrak {C}}_2}^{2}-F_{{\mathfrak {C}}_2}^{2} \ge 1-T_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_1}^{2}$ and $1-T_{{\mathfrak {C}}_3}^{2}-F_{{\mathfrak {C}}_3}^{2} \le 1-T_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_1}^{2}$, then, by $F_{{\mathfrak {C}}_1}^{2} \ge F_{{\mathfrak {C}}_2}^{2} \ge F_{{\mathfrak {C}}_3}^{2}$, we have $F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2} \ge T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}$ and $F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\le F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2} \le T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}$. Meanwhile, by (i) and (ii), we have

$$\begin{aligned}&|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}| \le F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}, \\&|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}| \le T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}, \\&|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\\&\quad = 2\left( F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\right) , \end{aligned}$$

and

$$\begin{aligned}&|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\\&\quad \quad = 2(T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}). \end{aligned}$$

These, together with $F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2} \le T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}$ and $T_{{\mathfrak {C}}_1}^{2}\le T_{{\mathfrak {C}}_2}^{2} \le T_{{\mathfrak {C}}_3}^{2}$ and $F_{{\mathfrak {C}}_1}^{2} \ge F_{{\mathfrak {C}}_2}^{2} \ge F_{{\mathfrak {C}}_3}^{2}$, imply that

$$\begin{aligned}{} & {} |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}| \le |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}|\\{} & {} \quad +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|, \end{aligned}$$

and

$$\begin{aligned}&\max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}\\&\quad =\max \{T_{{\mathfrak {C}}_2}^{2}-T_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}\}\\&\quad \le \max \{T_{{\mathfrak {C}}_3}^{2}-T_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}\}\\&\quad = \max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_3}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_3}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_3}^{2}|\}. \end{aligned}$$

And thus, it can be similarly verified that

$$\begin{aligned} D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2). \end{aligned}$$

(iv) If $R_{{\mathfrak {C}}_2}^{2}\le R_{{\mathfrak {C}}_1}^{2}$ and $R_{{\mathfrak {C}}_3}^{2} \ge R_{{\mathfrak {C}}_1}^{2}$, similarly to the proof of (iii), it is not difficult to check that $D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_3)\ge D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2).$ $\square$

Summing Propositions 4.1–4.4, we have the following result.

Theorem 4.1

• (1) The function $D_{_{\textrm{Wu}}}$ defined by Eq. (8) is a normalized distance measure on ${\mathscr {C}}_{_{\textrm{PyFN}}}$.

• (2) The function ${\textbf{S}}_{_{\textrm{Wu}}}$ defined by ${\textbf{S}}_{_{\textrm{Wu}}} ({\mathfrak {C}}_1, {\mathfrak {C}}_2)=1-D_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$ is similarity measure on ${\mathscr {C}}_{_{\textrm{PyFN}}}$.

Remark 1

(1) Park et al. [30] propose a similar distance formula to Eq. (8) for IFNs as follows: for $\alpha _1=\langle {\mathfrak {P}}_1, {\mathfrak {O}}_1 \rangle$, $\alpha _2=\langle {\mathfrak {P}}_2, {\mathfrak {O}}_2 \rangle \in \Theta$,

$$\begin{aligned} d_{_{\textrm{P}}}\left( \alpha _1, \alpha _2\right)&=\frac{1}{4}\left( |{\mathfrak {P}}_1-{\mathfrak {P}}_2| +|{\mathfrak {O}}_1-{\mathfrak {O}}_2|+|{\mathfrak {H}}_1-{\mathfrak {H}}_2|\right) \\&\quad +\frac{1}{2} \max \{|{\mathfrak {P}}_1-{\mathfrak {P}}_2|, |{\mathfrak {O}}_1-{\mathfrak {O}}_2|, |{\mathfrak {H}}_1-{\mathfrak {H}}_2|\}, \end{aligned}$$

where ${\mathfrak {H}}_1=1-{\mathfrak {P}}_1-{\mathfrak {O}}_1$ and ${\mathfrak {H}}_2=1-{\mathfrak {P}}_2 -{\mathfrak {O}}_2$, and proved that $d_{_{\textrm{P}}}$ is a DisM on $\Theta$ (see [30, Theorem 1]). In the proof of [30, Theorem 1], they claimed that, for $\alpha _1$, $\alpha _2$, $\alpha _3\in \Theta$ with $\alpha _1\subseteq \alpha _2 \subseteq \alpha _3$, one has ${\mathfrak {H}}_1\ge {\mathfrak {H}}_2\ge {\mathfrak {H}}_3$. However, the claim does not hold, leading to the result that the proof of [30, Theorem 1] is not right. In fact, choose $\alpha _1=\langle 0, 1\rangle$, $\alpha _2=\langle 0, 0\rangle$, and $\alpha _3=\langle 1, 0\rangle$. Clearly, $\alpha _1\subseteq \alpha _2 \subseteq \alpha _3$ and ${\mathfrak {H}}_2>{\mathfrak {H}}_1={\mathfrak {H}}_3$, which contradicts the claim.

(2) If we consider the imaginary part as zero in Eq. (8) and replace the constraint ${\mathfrak {P}}^2+{\mathfrak {O}}^2\le 1$ by ${\mathfrak {P}}+{\mathfrak {O}}\le 1$, then the distance $D_{_{\textrm{Wu}}}$ reduces to IF environment. By Theorem 4.1, we know that $d_{_{\textrm{P}}}$ is a DisM on $\Theta$.

Motivated by the DisMs for IFNs in [14, 34, 37, 39, 45], we introduced the following new DisMs for CPyFNs.

Let ${\mathfrak {C}}_1=(T_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_1}}}, F_{{\mathfrak {C}}_1}\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_1}}})$ and ${\mathfrak {C}}_2=(T_{{\mathfrak {C}}_2} \cdot e^{2\pi {\textbf{i}}\cdot W_{T_{{\mathfrak {C}}_2}}}, F_{{\mathfrak {C}}_2} \cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_2}}})$ be two CPyFNs. Then, define

• (1) Szmidt and Kacprzyk’s complex Pythagorean fuzzy DisMs ( [34]):

  $$\begin{aligned}{} & {} D_{_{\textrm{SK}}}^{\textrm{H}}({\mathfrak {C}}_1, {\mathfrak {C}}_2) = \frac{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}| +|R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|}{4}\nonumber \\{} & {} \quad +\frac{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}| +|W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|}{4},\nonumber \\ \end{aligned}$$

  (9)

  and

  $$\begin{aligned} D_{_{\textrm{SK}}}^{\textrm{E}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)&= \frac{\sqrt{\frac{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|^2 +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|^2}{2}}}{2}\nonumber \\&\quad +\frac{\sqrt{\frac{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|^{2} +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|^{2}}{2}}}{2}.\nonumber \\ \end{aligned}$$

  (10)

• (2) Wang and Xin’s complex Pythagorean fuzzy DisMs ([37]):

  $$\begin{aligned} D_{_{\textrm{WX1}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right)&= \frac{1}{2} \left[ \frac{1}{4} \cdot \left( |T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|\right) \right. \nonumber \\&\quad +\frac{1}{2}\cdot \max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|\}\nonumber \\&\quad +\frac{1}{4} \cdot \left( |W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|\right) \nonumber \\&\quad \left. +\frac{1}{2} \cdot \max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|\}\right] ,\nonumber \\ \end{aligned}$$

  (11)

  and

  $$\begin{aligned} D_{_{\textrm{WX2}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)&= \frac{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}| +|F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|}{4}\nonumber \\&\quad +\frac{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}| +|W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|}{4}.\nonumber \\ \end{aligned}$$

  (12)

• (3) Grzegorzewski’s complex Pythagorean fuzzy DisM ([14]):

  $$\begin{aligned}{} & {} D_{_{\textrm{G}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)= \,\,\frac{1}{2} \left[ \max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|\}\right. \nonumber \\{} & {} \quad \quad \left. + \max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|\}\right] ,\nonumber \\ \end{aligned}$$

  (13)

• (4) Yang and Chiclana’s complex Pythagorean fuzzy DisM ( [45]):

  $$\begin{aligned}&D_{_{\textrm{YC}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)\nonumber \\&\quad = \frac{\max \{|T_{{\mathfrak {C}}_1}^{2}-T_{{\mathfrak {C}}_2}^{2}|, |F_{{\mathfrak {C}}_1}^{2}-F_{{\mathfrak {C}}_2}^{2}|, |R_{{\mathfrak {C}}_1}^{2}-R_{{\mathfrak {C}}_2}^{2}|\}}{2}\nonumber \\&\quad \quad +\frac{\max \{|W^{2}_{T_{{\mathfrak {C}}_1}}-W^{2}_{T_{{\mathfrak {C}}_2}}|, |W^{2}_{F_{{\mathfrak {C}}_1}}-W^{2}_{F_{{\mathfrak {C}}_2}}|, |W^{2}_{R_{{\mathfrak {C}}_1}}-W^{2}_{R_{{\mathfrak {C}}_2}}|\}}{2}.\nonumber \\ \end{aligned}$$

  (14)

• (5) Wu et al.’s complex Pythagorean fuzzy DisM ([39]):

  $$\begin{aligned}&D_{_{\textrm{Wu}}}^{\left( 1\right) }\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right) \nonumber \\&\quad = \frac{\sqrt{\frac{1}{2}\left( L\left( 1-T_{{\mathfrak {C}}_1}^{2}, 1-T_{{\mathfrak {C}}_2}^{2}\right) +L\left( F_{{\mathfrak {C}}_1}^{2}, F_{{\mathfrak {C}}_2}^{2}\right) \right) }}{2}\nonumber \\&\qquad \frac{\sqrt{\frac{1}{2}\left( L\left( 1-W_{T_{{\mathfrak {C}}_1}}^{2}, 1-W_{T_{{\mathfrak {C}}_2}}^{2}\right) +L\left( W_{F_{{\mathfrak {C}}_1}}^{2}, W_{F_{{\mathfrak {C}}_2}}^{2}\right) \right) }}{2},\nonumber \\ \end{aligned}$$

  (15)

  where $L(p, q)=p\cdot \log _{2}\frac{2p}{p+q}+q\cdot \log _{2}\frac{2q}{p+q}$.

According to the proof in [14, 34, 37, 39, 45], by Propositions 4.1–4.4, it can be verified that the above DisMs $D_{_{\textrm{SK}}}^{\textrm{H}}$, $D_{_{\textrm{SK}}}^{\textrm{E}}$, $D_{_{\textrm{WX1}}}$, $D_{_{\textrm{WX2}}}$, $D_{_{\textrm{G}}}$, $D_{_{\textrm{YC}}}$, and $D_{_{\textrm{Wu}}}^{(1)}$ are normalized distance measures on ${\mathscr {C}}_{_{\textrm{PyFN}}}$.

A novel DisM on CPyFSs

Let ${\mathfrak {X}}=\{\vartheta _1, \vartheta _2, \ldots , \vartheta _{\ell }\}$ and ${\mathfrak {C}}_1=\{{\mathfrak {C}}_1(\vartheta _j)=(T_{{\mathfrak {C}}_1}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_1}}(\vartheta _j)}, F_{{\mathfrak {C}}_1}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_1}}(\vartheta _j)}) \mid 1\le j\le \ell \}$ and ${\mathfrak {C}}_2=\{{\mathfrak {C}}_2(\vartheta _j)=(T_{{\mathfrak {C}}_2}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{T_{{\mathfrak {C}}_2}}(\vartheta _j)}, F_{{\mathfrak {C}}_2}(\vartheta _{j})\cdot e^{2\pi {\textbf{i}} \cdot W_{F_{{\mathfrak {C}}_2}}(\vartheta _j)}) \mid 1\le j\le \ell \}$ be two CPyFSs on ${\mathfrak {X}}$. Define a DisM ${\tilde{D}}_{_{\textrm{Wu}}}$ for CPyFSs as follows:

$$\begin{aligned} \begin{aligned} {\tilde{D}}_{_{\textrm{Wu}}}\left( {\mathfrak {C}}_1, {\mathfrak {C}}_2\right) = \sum _{j=1}^{\ell } \omega _{j}\cdot D_{_{\textrm{Wu}}}\left( {\mathfrak {C}}_1\left( \vartheta _j\right) , {\mathfrak {C}}_2\left( \vartheta _j\right) \right) , \end{aligned} \end{aligned}$$

(16)

where $\omega =(\omega _1, \omega _2, \ldots , \omega _n)^{\top }$ is the weight vector of $\omega _{j}$ ($j=1, 2, \ldots , \ell$) with $\omega _j\in (0, 1]$ and $\sum _{j=1}^{\ell }\omega _j=1$.

Table 1 CPF information about known and unknown materials in Example 2

By Theorem 4.1, we have the following result.

Theorem 4.2

• (1) The function ${\tilde{D}}_{_{\textrm{Wu}}}$ defined by Eq. (16) is a normalized distance measure on $\textrm{CPyFS}({\mathfrak {X}})$.

• (2) The function $\tilde{{\textbf{S}}}_{_{\textrm{Wu}}}$ defined by ${\textbf{S}}_{_{\textrm{Wu}}} ({\mathfrak {C}}_1, {\mathfrak {C}}_2)=1-{\tilde{D}}_{_{\textrm{Wu}}}({\mathfrak {C}}_1, {\mathfrak {C}}_2)$ is similarity measure on $\textrm{CPyFS}({\mathfrak {X}})$.

Applications

Building material recognition problem

Example 2

([36, Example 1]). Consider the following 4 building materials: ${\mathscr {M}}_1$–sealant; ${\mathscr {M}}_2$–floor varnish; ${\mathscr {M}}_3$–wall paint, and ${\mathscr {M}}_{4}$–polyvinyl chloride flooring, which are expressed by CPyFNs for attribute set denoted by ${\mathfrak {A}}=\{{\mathfrak {A}}_{1}, {\mathfrak {A}}_{2}, {\mathfrak {A}}_{3}, {\mathfrak {A}}_{4}, {\mathfrak {A}}_{5}, {\mathfrak {A}}_{6}, {\mathfrak {A}}_{7}\}$ in Table 1. Given an unknown building material ${\mathscr {M}}$, which is expressed by CPyFNs for the above 7 attributes in Table 1. We want to determine to which building material the unknown material ${\mathscr {M}}$ belongs.

If we take the weight vector $\omega$ of 7 attributes as $\omega =(0.11, 0.14, 0.1, 0.18, 0.21, 0.10, 0.16)^{\top }$, the SimMs calculated by Eq. (16) are given in Table 2. By the principle of the maximum degree of SimMs, the unknown building material belongs to the class ${\mathscr {M}}_{4}$–polyvinyl chloride flooring.

The pattern classification results by using different DisMs/SimMs are listed in Table 3. Observing from Table 3, we know that (1) our result listed in Table 1 is consistent with the results obtained by the DisM $\textrm{WD}^{1}_{_{\textrm{CPyFS}}}$ in [36] and DisMs defined by Eqs. (9)–(15); (2) because the DisM $\textrm{WD}^{2}_{_{\textrm{CPyFS}}}$ in [36] does not satisfy the axiomatic definition of complex Pythagorean fuzzy DisM, the pattern classification result obtained by this DisM is ${\mathscr {M}}_1$–sealant, which is unreasonable.

Table 2 SimMs between ${\mathscr {M}}_{i}$ ($i=1, 2, 3, 4$) and ${\mathscr {M}}$ in Example 2 using $\tilde{{\textbf{S}}}_{_{\textrm{Wu}}}$

Table 3 Comparative analysis by different SimMs/DisMs in Example 2

Observing from Table 3, we notice that the existing measures are provided the different ranking results such as ${\mathscr {M}}_1$ and ${\mathscr {M}}_4$. But, we also notice that the proposed all measures are given the same ranking measures. Further, we aim to consider some measures which was proposed by different scholars, for this, Rani and Garg [32] presented a few two-dimensional (2D) CIFDisMs by using the Hamming, Euclidean, and Hausdorff distances. Then, Garg and Rani [12] proposed some new CIF information measures, including SimMs, DisMs, entropies, and inclusion measures and obtained the transformation relationships among them. Meanwhile, they [12] developed a CIF clustering algorithm. But these all measures are not able to resolve our selected information because of their limitations, where the computed measures of Rani and Garg [32] have been failed because these measures are the particular case of the proposed measures.

A medical diagnosis problem

The medical diagnostic data in the following example comes from [32, Example 4.2], which were equivalently expressed by using CIFNs.

Example 3

([32, Example 4.2]). Consider a medical diagnosis problem for a patient $\mathbb {P}$ with the symptoms ${\mathfrak {S}}=\{\text {Temperature, Headache, Stomach pain, Cough}\}$ represented by using CPyFNs, as listed in Table 4. The symptom characteristics for diagnosis ${\mathfrak {D}}=\{\text {Viral fever, Malaria, Typhoid,}$ $\text {Stomach problem}\}$ are represented by using CPyFNs, as shown in Table 5.

Table 4 CPF representation of symptoms for the patient

Table 5 CPF representation of symptom characteristics for diagnosis

Table 6 Diagnostic results by different SimMs/DisMs with $\omega =(0.25, 0.25, 0.25, 0.25)^{\top }$ in Example 3

By the principle of the maximum degree of SimMs, observing from Table 6, we know that the diagnostic result is that $\mathbb {P}$ suffers from ‘Viral fever’, which is consistent with the result in [32, Example 4.2].

Observing from Table 6, we notice that the existing measures are provided the same ranking results such as $\textrm{Vf}$. But, we also notice that the proposed all measures are given the same ranking measures. Further, we aim to consider some measures which was proposed by different scholars, for this, Rani and Garg [32] presented a few two-dimensional (2D) CIFDisMs by using the Hamming, Euclidean, and Hausdorff distances. Then, Garg and Rani [12] proposed some new CIF information measures, including SimMs, DisMs, entropies, and inclusion measures) and obtained the transformation relationships among them. Meanwhile, they [12] developed a CIF clustering algorithm. But these all measures are not able to resolve our selected information because of their limitations, where the computed measures of Rani and Garg [32] have been failed because these measures are the particular case of the proposed measures.

Conclusion

Complex Pythagorean fuzzy set is very effective and realistic for evaluating awkward and complex information in real-life problems. Keeping the advantages of the CPyFS, the main theme of this analysis is described below:

• (1) Ullah et al. [36] introduced the notion of CPyFS to deal with uncertain information and proposed a 2D CPyFDisM $D^{1}_{_{\textrm{CPyFS}}}$ and a 3D CPyFDisM $D^{2}_{_{\textrm{CPyFS}}}$.

• (2) The DisM $D^{2}_{_{\textrm{CPyFS}}}$ does not satisfy the axiomatic definition of CPyFDisM (see Example 1).

• (3) To overcome the drawback of the DisM $D^{2}_{_{\textrm{CPyFS}}}$ in [36], we constructed a novel 3D DisM ${\tilde{D}}_{_{\textrm{Wu}}}$ for CPyFSs based on the 3D Hamming distance and the Hausdorff distance for IFSs and show that it satisfies the axiomatic definition of CPyFDisM.

• (4) Based on the DisMs for IFSs in [14, 34, 37, 39, 45], we proposed some other new CPyFDisMs.

• (5) We illustrated the effectiveness of our DisMs, we give the comparative analysis by using our proposed DisMs to a building material recognition problem and a medical diagnosis problem.

In the future, we aim to develop some new ideas such as averaging or geometric aggregation operators [26], Maclaurin symmetric mean operators [35], Aczel–Alsina operators [18], information measures [33], similarity measures [23], Einstein aggregation operators, Hamacher aggregation operators, improved Dombi aggregation operators [17], interaction aggregation operators, similarity measures, distance measures, many techniques based on CPyFSs and try to justify it with the help of some suitable applications such as road signals, computer networks, game theory, artificial intelligence, and decision-making theory.