A new outranking method for multicriteria decision making with complex Pythagorean fuzzy information

Abstract

This article contributes to the advancement and evolution of outranking decision-making methodologies, with a novel essay on the ELimination and Choice Translating REality (ELECTRE) family of methods. Its primary target is to unfold the constituents and expound the implementation of the ELECTRE II method for group decision making in complex Pythagorean fuzzy framework. This results in the complex Pythagorean fuzzy ELECTRE II method. By inception, it is intrinsically superior to models using one-dimensional data. It is designed to perform the pairwise comparisons of the alternatives using the core notions of concordance, discordance and indifferent sets, which is then followed by the construction of complex Pythagorean fuzzy concordance and discordance matrices. Further, the strong and weak outranking relations are developed by the comparison of concordance and discordance indices with the concordance and discordance levels. Later, the forward, reverse and average rankings of the alternatives are computed by the dint of strong and weak outranking graphs. This methodology is supported by a case study for the selection of wastewater treatment process, and by a numerical example for the selection of the best cloud solution for a big data project. Its consistency is confirmed by an effectiveness test and comparison analysis with the Pythagorean fuzzy ELECTRE II and complex Pythagorean fuzzy ELECTRE I methods.

1 Introduction

Multicriteria decision making (MCDM) or multi criteria group decision making (MCGDM) defines a process that aggregates data in order to reach a befitting solution meeting the requirements of a problem. Crisp set theory used to be the only competent tool to model information, which was therefore assumed to be exact and precise. Many researchers stepped forward to propose a number of decision approaches that recommend decisions in classical set theory [1,2,3,4,5,6]. These techniques were bound to capture exact data only, disregarding imprecise data altogether. The uncertainty of human knowledge, being an essential part of daily life decisions, exposed the limitations of the crisp set theory and highlighted the need of a new model with the passage of time.

In this context, ELECTRE [7] refers to a whole family of outranking methods. A common feature of these methods is that they work by pairwise comparison of alternatives relying on the primary notions of concordance and discordance sets, which are further used to point out the best possible alternative with the help of outranking graphs. The credit for the development of these reliable and influential strategies goes to Benayoun et al. [2], who put forward the ELECTRE method in 1966. This was later renamed as ELECTRE I. Its popularity made the way for other more evolved approaches, namely the ELECTRE II, ELECTRE III, ELECTRE IV and ELECTRE TRI methods among others. Evolution was imperative as the ELECTRE I method may not provide a ranking of the alternatives. For this reason, in this article we are concerned with the ELECTRE II technique which was developed to rank the alternatives in decision-making scenarios (cf., Grolleau and Tergny [8]). Many evidences speak for the benefits of this particular strategy. For example, Recently, Liu and Ma [9] analyzed the rank reversal problem for the ELECTRE II method. Jun et al. [10] took advantage of this method to select the appropriate site for wind/solar hybrid station. Huang and Chen [11] employed it to investigate differentiation theory. Wen et al. [12] opted the best techniques for coal gasification to promote cleaner production through ELECTRE-II method.

Let us now motivate the informational basis of our evolved outlook to the ELECTRE II strategy.

1.1 Related work

After observing the deficiencies of classical set theory, Zadeh [13] took the initiative to establish a new theory for imprecise information and set up the innovative model of fuzzy sets (FSs). Inexact information abounds nowadays, and it needs to be processed in a proper manner, which creates a new demand for decision making in imprecise environments. For example, Dasc$\breve{a}$l [14] worked on the widely used ELECTRE II approach using the fuzzy numbers. Mir et al. [15] merged the fuzzy TOPSIS method with the fuzzy ELECTRE II approach to compute the most suitable process for lithium extraction from brines and seawater.

Later on, Atanassov [16] expanded the theory of fuzzy sets so that the new theory would separate truthness from falseness. This model, which comprised non-membership along with membership grades, was named as intuitionistic fuzzy set (IFS). In relation with outranking methods, Wu and Chen [17] proposed the procedure of intuitionistic fuzzy ELECTRE method along with practical applications. Mishra et al. [18] proposed the intuitionistic fuzzy divergence measure-based ELECTRE method. They applied it to find the most adequate cellular mobile telephone service provider. Devadoss and Rekha [19] showcased a study of the inequality of women in society that made full use of the extended version of the ELECTRE II method for IFSs.

As the study of ambiguous information progressed, the IFSs were perceived insufficient due to the tight restriction on the sum of truthness and falseness degrees that they impose. A solution to this problem was provided by Yager [20, 21] who expanded the literature with an even superior model, namely Pythagorean fuzzy sets (PFSs). Later, Riaz et al. [22] and Yager [23] proposed the linear Diophantine fuzzy set (LDFS) and q-rung orthopair fuzzy set (q-ROFS), respectively. Correspondingly, Chen [24] extended the ELECTRE method to the Pythagorean fuzzy (PF) environment by employing the Chebyshev metric. Akram et al. [25,26,27] merged the theoretical backgrounds of the ELECTRE method with the numerous features and advantageous structure of PFSs and Hesitant Pythagorean fuzzy sets. Sitara et al. [28] proposed some decision-making approaches on the basis of graphs for ambiguous information. Xian et al. [29] presented an outranking methodology for interval-valued Pythagorean fuzzy linguistic sets.

Numerous applications of the traditional models of FS theory were found for many years. Nevertheless, these studies were unable to accommodate two-dimensional vague data because of their restriction to real-valued membership grades. To deal with such situation, the work of Ramot et al. [30, 31] proved to be the cornerstone of an improved, competent model, namely complex fuzzy sets (CFS).

Thanks to CFSs, one can choose membership grades from the complex unit circle [32]. This domain allows us to describe a membership grade in terms of its amplitude and phase terms. But the seminal structure of CFSs was limited, in the sense that it narrates the two-dimensional information only in terms of its satisfaction degree. Alkouri and Salleh [33] incorporated the non-membership grades to the original CFSs. Not surprisingly, their extension of the CFSs was named as complex intuitionistic fuzzy set (CIFS). In a CIFS, the sum of amplitude and phase terms of the membership and non-membership grades is bounded. Recently, Almagrabi et al. [34] and Ali et al. [35] initiated new models for inexact data with a linguistic component, namely the complex linear Diophantine uncertain linguistic sets and q-linear Diophantine fuzzy sets, respectively.

To further broaden the space of CIFSs, Ullah et al. [36] laid the foundations of complex Pythagorean fuzzy sets (CPFSs). The complex Pythagorean fuzzy (CPF) model possesses an innovative structure that relaxes some constraints of CIFSs and henceforth it also outperforms other preceding models in the fuzzy literature. Akram et al. [37, 38] established some aggregation operators and a competent decision-making approach for CPFS.

Concerning decisions in the CPFS framework, Akram et al. [39] focused on the extension of the competent theory of the ELECTRE I method to this case. Ma et al. [40] also contributed to expand the literature on CPFSs by developing a decision-making approach for two-dimensional uncertain data.

The innovative features of the CPFS overturned the deficiencies of existing extensions of fuzzy set theory including CIFS, PFS, q-ROFS, LDFS, and many others. The CPFS dominates over “traditional” models (like PFS, q-ROFS or LDFS) that take membership and non-membership values from the unit interval, simply because its complex-valued membership grades allow CPFSs to represent the ambiguity associated with two-dimensional phenomena. Notice that even though the LDFS model includes two additional parameters along with membership and non-membership, this feature broadens the admissible space without allowing for two-dimensional data. Similarly, the structure and space of membership grades for PFSs and q-ROFSs are limited to model one-dimensional inconsistent information only.

1.2 Motivation of the proposed methodology

The outranking approaches are widely adopted to pinpoint the most favorable alternative in a variety of decision-making scenarios. Initially, they were drawn up for accurate outcomes. The ELECTRE methods, a family of well-known and easily executable outranking approaches, found many applications also to address vaguely defined problems in decision-making environments. Even so, they fail to accommodate the two-dimensional information that has gained the attention of many researchers in recent years. Specifically, none of the ELCTRE methods has been adapted to deal with two-dimensional inexact information, except for the CPF-ELECTRE I method. But CPF-ELECTRE I is hampered by the fact that it may or may not provide a ranking of the alternatives.

These facts prompted us to propose the CPF-ELECTRE II approach. To summarize our motivation:

• The imperfections and limitations of CIFSs and other weaker models diverted our attention to the ample applicability of CPFSs, as this general model is crafted to encapsulate the two-dimensional ambiguous data by means of a wide space of truthness and falseness degrees.

• The capacity of the CPF-ELECTRE I approach was limited, as it does not necessarily provide a ranking of the alternatives. This fact encouraged us to employ the working principle of ELECTRE II technique to develop a more significant approach that yields both an optimal alternative and a complete ranking of alternatives.

• The Pythagorean fuzzy ELECTRE II (PF-ELECTRE II) method searches the most favorable solution and yields a ranking of the alternatives; however, it applies only to the problems defined from one-dimensional data only. The failure of the PF-ELECTRE II strategy in implementing the two-dimensional information in decision making proves to be a major incentive for the proposed methodology.

• The decision-making abilities of the ELECTRE II method depend on the classification of criteria on the basis of concordance, indifference and discordance sets, plus the graphical explanation of weak and strong outranking relations.

All these considerations persuaded us to propose a modified version of the ELECTRE II method befitting the structure of CPFSs.

1.3 Contribution of this article

As hinted above, we set forth a competent decision-making strategy which improves upon the PF-ELECTRE II method so that it can operate in an environment with two-dimensional information while retaining the reliability of that strategy. Thus, the new procedure performs the pairwise comparisons of alternatives to classify the criteria that indicate the concordance, discordance and indifferent relations among the alternatives. The concordance and discordance sets are further employed to evaluate the concordance and discordance indices which lead to the construction of strong and weak outranking relations. Finally, the ranking is obtained by exploitation of the strong and weak outranking graphs.

The main contributions of this article are:

• First and foremost, we produce an advanced, versatile and practical mathematical approach for group decision making under the advantageous environment of CPFSs.

• A flowchart diagram provides a quick and comprehensive overview of this novel methodology.

• A case study for the selection of the best wastewater treatment process highlights the efficiency of the proposed tactic in decision-making scenarios.

• The applicability of the proposed technique is further illustrated with the help of two explanatory numerical examples.

• Its reliability is tested by conducting a comparative study with two related techniques, namely the PF-ELECTRE II and CPF-ELECTRE I methods.

• An effectiveness test is applied to check the competency and adequacy of the proposed methodology.

1.4 Structure of this article

The remaining of this article is organized as follows: Sect. 2 comprises the primary notions related to CPFSs, inclusive of basic definitions, fundamental operations, associated operators like the score degree and accuracy degree and a comparison rule. Section 3 presents the stepwise procedure of the CPF-ELECTRE II method as well as the corresponding flowchart diagram. Section 4 elaborates the case study for the selection of optimal wastewater treatment process. A numerical example, highlighting the practical application of the proposed approach, is given in Sect. 5. Section 6 presents the comparative analysis of the proposed tactic with the PF-ELECTRE II and CPF-ELECTRE I methods. The validity of the proposed technique is checked by an effectiveness test in Sect. 7. Section 8 unfolds the insights and limitations of the proposed methodology. The purpose of Sect. 9 is to conclude with a concise discussion.

2 Preliminaries

The structure of the model that we investigate in this article is as follows:

Definition 1

[36] For any universe of discourse V, a complex Pythagorean fuzzy set (CPFS) ${\mathcal {F}}$ is an object of the form

$$\begin{aligned} {\mathcal {F}}=\{(v, x_{{\mathcal {F}}}(v)e^{{i}\zeta _{{\mathcal {F}}}(v)}, y_{{\mathcal {F}}}(v)e^{{i}\sigma _{{\mathcal {F}}}(v)}): v\in V \}, \end{aligned}$$

where ${i} =\sqrt{-1}$. Further, membership and non-membership grades in a CPFS consist of two terms, namely amplitude term ($x_{{\mathcal {F}}}(v), y_{{\mathcal {F}}}(v) \in [0, 1]$) and phase term ($\zeta _{{\mathcal {F}}}(v), \sigma _{{\mathcal {F}}}(v) \in [0, 2\pi ]$). These terms are restricted by the conditions $0 \le x_{{\mathcal {F}}}^{2}(v)+y_{{\mathcal {F}}}^{2}(v) \le 1$  and  ${0 \le (\frac{\zeta _{{\mathcal {F}}}(v)}{2\pi })^2+(\frac{\sigma _{{\mathcal {F}}}(v)}{2\pi })^2 \le 1}$. For simplicity, the pair $(xe^{{i}\zeta }, ye^{{i}\sigma })$ is called complex Pythagorean fuzzy number (CPFN).

Definition 2

[39] Let $\xi =(x_{\xi }e^{{i}\zeta _{\xi }}, y_{\xi }e^{{i}\sigma _{\xi }})$, $\xi _{1}=(x_{\xi _{1}}e^{{i}\zeta _{\xi _{1}}}, y_{\xi _{1}}e^{{i}\sigma _{\xi _{1}}})$ and $\xi _{2}=(x_{\xi _{2}}e^{{i}\zeta _{\xi _{2}}}, y_{\xi _{2}}e^{{i}\sigma _{\xi _{2}}})$ be three CPFNs. The operations corresponding to these three CPFNs can be defined as follows:

• $\mu \xi =\left( \sqrt{1-(1-x_{\xi }^{2})^{\mu }}e^{{i}2\pi \sqrt{1-\left(1-\Big (\dfrac{\zeta _{\xi }}{2\pi }\Big )^{2}\right)^{\mu }}}, y_{\xi }^{\mu }e^{{i}2\pi \left (\dfrac{\sigma _{\xi }}{2\pi }\right)^{\mu }}\right), (\mu >0);$

• $\xi ^{\mu } = \left( {x_{\xi }^{\mu } e^{{i2\pi (\frac{{\zeta _{\xi } }}{{2\pi }})^{\mu } }} ,} \sqrt {1 - (1 - y_{\xi }^{2} )^{\mu } e} ^{{i2\pi \left( {\sqrt {1 - \left( {1 - \left( {\frac{{\sigma _{\xi } }}{{2\pi }}} \right)^{2} } \right)\mu } } \right)}} \right),(\mu > 0)$;

• $$\xi _{1}\oplus \xi _{2}=\left( \sqrt{x_{\xi _{1}}^{2}+x_{\xi _{2}}^{2}-x_{\xi _{1}}^{2}x_{\xi _{2}}^{2}}e^{{i}2\pi \sqrt{\Big (\dfrac{\zeta _{\xi _{1}}}{2\pi }\Big )^{2}+\Big (\dfrac{\zeta _{\xi _{2}}}{2\pi }\Big )^{2}-\Big (\dfrac{\zeta _{\xi _{1}}}{2\pi }\Big )^{2}\Big (\dfrac{\zeta _{\xi _{2}}}{2\pi }\Big )^{2}}}, y_{\xi _{1}}y_{\xi _{2}}e^{{i}2\pi \Big (\dfrac{\sigma _{\xi _{1}}}{2\pi }\Big )\Big (\dfrac{\sigma _{\xi _{2}}}{2\pi }\Big )}\right);$$
• $$\xi _{1}\otimes \xi _{2}=\left( x_{\xi _{1}}x_{\xi _{2}}e^{{i}2\pi \Big (\dfrac{\zeta _{\xi _{1}}}{2\pi }\Big )\Big (\dfrac{\zeta _{\xi _{2}}}{2\pi }\Big )}, \sqrt{y_{\xi _{1}}^{2}+y_{\xi _{2}}^{2}-y_{\xi _{1}}^{2}y_{\xi _{2}}^{2}}e^{{i}2\pi \sqrt{\Big (\dfrac{\sigma _{\xi _{1}}}{2\pi }\Big )^{2}+\Big (\dfrac{\sigma _{\xi _{2}}}{2\pi }\Big )^{2}-\Big (\dfrac{\sigma _{\xi _{1}}}{2\pi }\Big )^{2}\Big (\dfrac{\sigma _{\xi _{2}}}{2\pi }\Big )^{2}}}\right).$$

Definition 3

[37] Let $\xi _{{\mathfrak {b}}} =(x_{{\mathfrak {b}}}e^{{i}\zeta _{{\mathfrak {b}}}}, y_{{\mathfrak {b}}}e^{{i}\sigma _{{\mathfrak {b}}}})(\mathfrak {}=1,2,\ldots ,{\mathfrak {p}})$ be a finite family of CPFNs. ${{\mathfrak {g}}=({\mathfrak {g}}_{1}, {\mathfrak {g}}_{2},\ldots , {\mathfrak {g}}_{{\mathfrak {p}}})^T}$ represents the normalized weight vector of given family of CPFNs where ${\mathfrak {g}}_{{\mathfrak {b}}} \in [0, 1]$ and $\sum\nolimits_{{{\mathfrak{b}} = 1}}^{{\mathfrak{p}}} {{\mathfrak{g}}_{{\mathfrak{b}}} = 1}$. The complex Pythagorean fuzzy weighted averaging (CPFWA) operator can be defined as:

$$\begin{aligned}&CPFWA_{{\mathfrak {g}}}(\xi _{1}, \xi _{2},\ldots ,\xi _{{\mathfrak {p}}})={\mathfrak {g}}_{1}\xi _{1}\oplus {\mathfrak {g}}_{2}\xi _{2}\oplus \cdots \oplus {\mathfrak {g}}_{{\mathfrak {p}}}\xi _{{\mathfrak {p}}}\nonumber \\&\quad =\left( \sqrt{1-\prod _{{\mathfrak {b}}=1}^{{\mathfrak {p}}}(1-(x_{\xi _{{\mathfrak {b}}}})^{2})^{{\mathfrak {g}}_{{\mathfrak {b}}}}}e^{{i}2\pi \sqrt{1-\underset{{\mathfrak {b}}=1}{\overset{{\mathfrak {p}}}{\prod }}\Big (1-\big (\dfrac{\zeta _{\xi _{{\mathfrak {b}}}}}{2\pi }\big )^{2}\Big )^{{\mathfrak {g}}_{{\mathfrak {b}}}}}} ,\nonumber \right. \\&\qquad \left. \prod _{{\mathfrak {b}}=1}^{{\mathfrak {p}}}(y_{\xi _{{\mathfrak {b}}}})^{{\mathfrak {g}}_{{\mathfrak {b}}}}e^{{i}2\pi \underset{{\mathfrak {b}}=1}{\overset{{\mathfrak {p}}}{\prod }}\big (\dfrac{\sigma _{\xi _{{\mathfrak {b}}}}}{2\pi }\big )^{{\mathfrak {g}}_{{\mathfrak {b}}}}}\right) . \end{aligned}$$

(1)

The complex Pythagorean fuzzy weighted geometric (CPFWG) operator can be defined as:

$$\begin{aligned}&CPFWG_{{\mathfrak {g}}}(\xi _{1}, \xi _{2},\ldots , \xi _{n})={\mathfrak {g}}_{1}\xi _{1}\otimes {\mathfrak {g}}_{2}\otimes _{2}\otimes \cdots \otimes {\mathfrak {g}}_{{\mathfrak {p}}}\xi _{{\mathfrak {p}}}\nonumber \\&\quad =\left( \prod _{{\mathfrak {b}}=1}^{{\mathfrak {p}}}(x_{\xi _{{\mathfrak {b}}}})^{{\mathfrak {g}}_{{\mathfrak {b}}}}e^{{i}2\pi \underset{{\mathfrak {b}}=1}{\overset{{\mathfrak {p}}}{\prod }}\left (\dfrac{\zeta _{\xi _{{\mathfrak {b}}}}}{2\pi }\right )^{{\mathfrak {g}}_{{\mathfrak {b}}}}} ,\nonumber \right. \\&\left. \quad \sqrt{1-\prod _{{\mathfrak {b}}=1}^{{\mathfrak {p}}}(1-(y_{\xi _{{\mathfrak {b}}}})^{2})^{{\mathfrak {g}}_{{\mathfrak {b}}}}}e^{{i}2\pi \sqrt{1-\underset{{\mathfrak {b}}=1}{\overset{{\mathfrak {p}}}{\prod }}\Big (1-\big (\dfrac{\sigma _{\xi _{{\mathfrak {b}}}}}{2\pi }\big )^{2}\Big )^{{\mathfrak {g}}_{{\mathfrak {b}}}}}}\right) . \end{aligned}$$

(2)

Definition 4

[39] Let $\xi _{1}=(x_{\xi _{1}}e^{{i}\zeta _{\xi _{1}}}, y_{\xi _{1}}e^{{i}\sigma _{\xi _{1}}})$ and $\xi _{2}=(x_{\xi _{2}}e^{{i}\zeta _{\xi _{2}}}, y_{\xi _{2}}e^{{i}\sigma _{\xi _{2}}})$ be two CPFNs. The normalized Euclidean distance between $\xi _{1}$ and $\xi _{2}$ can be defined as:

$$\begin{aligned} d(\xi _{1}, \xi _{2})=\sqrt{\frac{(x_{\xi _{1}}^{2}-x_{\xi _{2}}^{2})^{2}+(y_{\xi _{1}}^{2}-y_{\xi _{2}}^{2})^{2}+(w_{\xi _{1}}^{2}-w_{\xi _{2}}^{2})^{2}+ \frac{1}{16\pi ^{4}}\left( (\zeta _{\xi _{1}}^{2}-\zeta _{\xi _{2}}^{2})^{2}+(\sigma _{\xi _{1}}^{2}-\sigma _{\xi _{2}}^{2})^{2}+(\gamma _{\xi _{1}}^{2}-\gamma _{\xi _{2}}^{2})^{2}\right) }{2}}. \end{aligned}$$

(3)

Definition 5

[37] Let $\xi =(xe^{{i}\zeta }, ye^{{i}\sigma })$ be a CPFN. The score degree of a CPFN is given by:

$$\begin{aligned} s(\xi )=(x^{2}-y^{2})+\frac{1}{4\pi ^{2}}(\zeta ^{2}-\sigma ^{2}). \end{aligned}$$

(4)

Definition 6

[37] Let $\xi =(xe^{{i}\zeta }, ye^{{i}\sigma })$ be a CPFN. Then, accuracy degree of a CPFN is given by

$$\begin{aligned} h(\xi )=(x^{2}+y^{2})+\frac{1}{4\pi ^{2}}(\zeta ^{2}+\sigma ^{2}). \end{aligned}$$

(5)

Definition 7

[37] For the comparison of any two CPFNs $\xi _{1}=(x_{1}e^{{i}\zeta _{1}},y_{1}e^{{i}\sigma _{1}})$ and $\xi _{2}=(x_{2}e^{{i}\zeta _{2}},y_{2}e^{{i}\sigma _{2}})$

• 1. If $s(\xi _{1}) > s(\xi _{2})$, then $\xi _{1} \succ \xi _{2}$ ($\xi _{1}$ is superior to $\xi _{2}$);

• 2. If $s(\xi _{1}) = s(\xi _{2})$, then

  • If $h(\xi _{1})>h(\xi _{2})$, then $\xi _{1}\succ \xi _{2}$ ($\xi _{1}$ is superior to $\xi _{2}$);

  • If $h(\xi _{1})=h(\xi _{2})$, then $\xi _{1} \sim \xi _{2}$ ($\xi _{1}$ is equivalent to $\xi _{2}$).

3 Complex Pythagorean fuzzy ELECTRE II method

In this section, we elaborate the stepwise methodology of the CPF-ELECTRE II method which employs the concordance and discordance sets to observe the superiority or inferiority of alternatives over each other. The method is further portrayed with the help of a flowchart diagram.

Let ${\mathcal {D}}=\{{\mathcal {D}}_{1}, {\mathcal {D}}_{2}, {\mathcal {D}}_{3},\ldots ,{\mathcal {D}}_{p}\}$ be the set of p feasible alternatives which are to be evaluated in accordance with the set of s criteria, represented by ${\mathcal {Z}}=\{{\mathcal {Z}}_1, {\mathcal {Z}}_2, {\mathcal {Z}}_3, \ldots , {\mathcal {Z}}_s\}.$ For the proceedings of the MCGDM, a panel of k decision-making experts is designated to assess the competency of alternatives as well as the relative importance of the decision criteria. The initial assessments of the decision-making experts are provided by means of linguistic terms. The procedure of the CPF-ELECTRE II method is elaborated in the following steps:

3.1 Construction of independent decision matrices

The panel of decision-making experts evaluates capacity of the available alternatives relative to some particular criterion and assigns them linguistic terms in reference to each criterion. These linguistic terms can be represented in the form of CPFN to precisely capture the vague decisions. In short, an individual decision matrix ${\mathfrak {P}}^{(g)}$ is formed corresponding to the judgment of the decision maker ${\mathfrak {N}}_{g}.$ In the similar fashion, we obtain k independent decision matrices corresponding to k experts working in the decision-making panel. The complex Pythagorean fuzzy decision matrix (CPFDM) of the expert ${\mathfrak {N}}_{g}$ is of the form

Any entry of the decision matrix ${\mathfrak {P}}^{(g)}$ is of the form $B_{er}^{(g)}=(x_{er}^{(g)}e^{i\zeta _{er}^{(g)}}, y_{er}^{(g)}e^{i\sigma _{er}^{(g)}})$ which indicates the CPFN given to the alternative ${\mathcal {D}}_{e}$ by the expert ${\mathfrak {N}}_{g}$ regarding the criterion ${\mathcal {Z}}_{r}.$

3.2 Construction of aggregated complex Pythagorean fuzzy decision matrix

To specify the collective opinion of the decision-making panel, our next task is to merge all individual decisions with the help of aggregation operators. Here, the independent opinions are cumulated with the help of CPFWA operator to construct the aggregated complex Pythagorean fuzzy decision matrix (ACPFDM) using the normalized weights of all experts, given by weight vector $\theta =(\theta _{1}, \theta _{2}, \cdots , \theta _{k})^T$. The entries of the ACPFDM are again CPFNs which are determined using the following formula:

$$\begin{aligned} B_{er} &=\, {} CPFWA_{\theta }( B_{er}^{(1)}, B_{er}^{(2)},\ldots , B_{er}^{(k)})\nonumber \\ &= \, {} \theta _{1} B_{er}^{(1)}\oplus \theta _{2} B_{er}^{(2)}\oplus \ldots \oplus \theta _{k} B_{er}^{(k)}\nonumber \\&=\, {} \left( \sqrt{1-\prod _{g=1}^{k}(1-(x_{er}^{(g)})^{2})^{\theta _{g}}}e^{i2\pi \sqrt{1-\underset{g=1}{\overset{k}{\prod }}\Big (1-\big (\dfrac{\zeta _{er}^{(g)}}{2\pi }\big )^{2}\Big )^{\theta _{g}}}} ,\nonumber \right. \\&\left.\quad \prod _{g=1}^{k}(y_{er}^{(g)})^{\theta _{g}}e^{i2\pi \underset{g=1}{\overset{k}{\prod }}\big (\dfrac{\sigma _{er}^{(g)}}{2\pi }\big )^{\theta _{g}}}\right) , \end{aligned}$$

(6)

where $B_{er}=(x_{er}e^{i\zeta _{er}}, y_{er}e^{i\sigma _{er}})$ shows the cumulative opinion of all the experts in the decision panel regarding the alternative ${\mathcal {D}}_{e}$ corresponding to the criterion ${\mathcal {Z}}_{r}.$

Furthermore, these aggregated opinions are organized in a proper way to determine the ACPFDM ${\mathfrak {P}}=(B_{er})_{p\times s}$, given by

3.3 Computation of the criteria weights

To find out the normalized weights of criteria, each expert in the decision-making panel expresses his opinion by the means of linguistic terms which can be further represented by CPFNs. Let $\gamma _{r}^{(g)}=(x_{r}^{(g)}e^{i\zeta _{r}^{(g)}}, y_{r}^{(g)}e^{i\sigma _{r}^{(g)}})$ be the CPF weight assigned to the criterion ${\mathcal {Z}}_r$ by the expert ${\mathfrak {N}}_{g}.$ The individual decision of the experts regarding the significance of the criteria needs to be merged for the sake of authentic decision making. The cumulative CPF weight $\gamma _{r}=(x_{r}e^{i\zeta _{r}}, y_{r}e^{i\sigma _{r}})$ of the criterion ${\mathcal {Z}}_{r}$ can be evaluated using the CPFWA operator as follows:

$$\begin{aligned} \gamma _{r}=\, & {} CPFWA_{\theta }( \gamma _{r}^{(1)}, \gamma _{r}^{(2)},\ldots , \gamma _{r}^{(k)})\nonumber \\= \,& {} \theta _{1} \gamma _{r}^{(1)}\oplus \theta _{2} \gamma _{r}^{(2)}\oplus \cdots \oplus \theta _{k} \gamma _{r}^{(k)}\nonumber \\=\, & {} \left( \sqrt{1-\prod _{g=1}^{k}(1-(x_{r}^{(g)})^{2})^{\theta _{g}}}e^{i2\pi \sqrt{1-\underset{g=1}{\overset{k}{\prod }}\Big (1-\big (\dfrac{\zeta _{r}^{(g)}}{2\pi }\big )^{2}\Big )^{\theta _{g}}}} ,\nonumber \right. \\&\left. \prod _{g=1}^{k}(y_{r}^{(g)})^{\theta _{g}}e^{i2\pi \underset{g=1}{\overset{k}{\prod }}\big (\dfrac{\sigma _{r}^{(g)}}{2\pi }\big )^{\theta _{g}}}\right). \end{aligned}$$

(7)

Finally, the normalized weights of the criteria can be computed by dint of the following formula:

$$\begin{aligned} \gamma _{r}^{*} = \frac{{x_{r} + z_{r} \left( {\frac{{x_{r} }}{{x_{r} + y_{r} }}} \right) + \frac{{\zeta _{r} }}{{2\pi }} + \frac{{\rho _{r} }}{{2\pi }}\left( {\frac{{\frac{{\zeta _{r} }}{{2\pi }}}}{{\frac{{\zeta _{r} }}{{2\pi }} + \frac{{\sigma _{r} }}{{2\pi }}}}} \right)}}{{\sum\nolimits_{{r = 1}}^{s} {\left( {x_{r} + z_{r} \left( {\frac{{x_{r} }}{{x_{r} + y_{r} }}} \right) + \frac{{\zeta _{r} }}{{2\pi }} + \frac{{\rho _{r} }}{{2\pi }}\left( {\frac{{\frac{{\zeta _{r} }}{{2\pi }}}}{{\frac{{\zeta _{r} }}{{2\pi }} + \frac{{\sigma _{r} }}{{2\pi }}}}} \right)} \right)} }}.\end{aligned}$$

(8)

3.4 Construction of aggregated weighted complex Pythagorean fuzzy decision matrix

The aggregated weighted complex Pythagorean fuzzy decision matrix (AWCPFDM) is computed by operating the entries of the ACPFDM with respect to the CPF weights of the criteria. In short, an entry ${\widetilde{B}}_{er}=({\widetilde{x}}_{er}e^{i{\widetilde{\zeta }}_{er}}, {\widetilde{y}}_{er}e^{i{\widetilde{\sigma }}_{er}})$ can be evaluated by the dint of the following formula:

$$\begin{aligned} {\widetilde{B}}_{er}= & {} B_{er}\otimes \gamma _{r}\nonumber \\= & {} \left( x_{er}x_{r}e^{i2\pi \left( \dfrac{\zeta _{er}}{2\pi }\right) \left( \dfrac{\zeta _{r}}{2\pi }\right) },\nonumber \right. \\&\left. \sqrt{y_{er}^{*^2}+y_{r}^2-y_{er}^{*^2}y_{r}^2}e^{i2\pi \sqrt{\Bigg (\dfrac{\sigma _{er}}{2\pi }\Bigg )^2+\Bigg (\dfrac{\sigma _{r}}{2\pi }\Bigg )^2-\Bigg (\dfrac{\sigma _{er}}{2\pi }\Bigg )^2\Bigg (\dfrac{\sigma _{r}}{2\pi }\Bigg )^2}}\right) . \end{aligned}$$

(9)

Finally, AWCPFDM can be constructed as follows:

3.5 Construction of complex Pythagorean fuzzy concordance, discordance and indifferent sets

At this stage, the pairwise comparison of alternatives with respect to decision criteria is made to construct the concordance, discordance and indifferent sets. The comparison is made on the basis of score degree, accuracy degree and hesitancy to figure out the edge or inferiority of an alternative over the other. In a nutshell, the concordance sets serve as a scale to check the dominance of an alternative over the other. In the similar manner, discordance sets being the complements of concordance sets represent the counter property.

3.5.1 Complex Pythagorean fuzzy concordance sets

The dominance of the alternative over other alternatives can be examined through the concordance sets. The concordance sets are categorized in three categories, namely CPF strong concordance set, CPF midrange concordance set and CPF weak concordance set. These concordance sets consist of the subscripts of all those criteria that predict the edge of an alternative over the other.

For any pair of $({\mathcal {D}}_{\eta }, {\mathcal {D}}_{\varrho }),$ the concordance sets can be constructed as follows:

• (i) The CPF strong concordance set ${{\mathfrak {K}}_{\eta \varrho }}$ can be defined as:

  $$\begin{aligned}&{{\mathfrak {K}}_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}\ge {\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}\ge {\widetilde{\zeta }}_{\varrho r}, {\widetilde{y}}_{\eta r}< {\widetilde{y}}_{\varrho r}, \nonumber \\&\quad {\widetilde{\sigma }}_{\eta r}< {\widetilde{\sigma }}_{\varrho r}, {\widetilde{w}}_{\eta r}< {\widetilde{w}}_{\varrho r}, \gamma '_{\eta r}< \gamma '_{\varrho r}\}. \end{aligned}$$

  (10)

• (ii) The CPF midrange concordance set ${{\mathfrak {K}}^*_{\eta \varrho }}$ can be defined as:

  $$\begin{aligned}&{{\mathfrak {K}}^*_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}\ge {\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}\ge {\widetilde{\zeta }}_{\varrho r}, {\widetilde{y}}_{\eta r}< {\widetilde{y}}_{\varrho r}, \nonumber \\&{\widetilde{\sigma }}_{\eta r}< {\widetilde{\sigma }}_{\varrho r},{\widetilde{w}}_{\eta r}\ge {\widetilde{w}}_{\varrho r},\gamma '_{\eta r}\ge \gamma '_{\varrho r}\}. \end{aligned}$$

  (11)

• (iii) The CPF weak concordance set ${{\mathfrak {K}}^{**}_{\eta \varrho }}$ can be defined as:

  $$\begin{aligned}&{{\mathfrak {K}}^{**}_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}\ge {\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}\ge {\widetilde{\zeta }}_{\varrho r}, \nonumber \\&\quad {\widetilde{y}}_{\eta r}> {\widetilde{y}}_{\varrho r}, {\widetilde{\sigma }}_{\eta r}>{\widetilde{\sigma }}_{\varrho r}\}. \end{aligned}$$

  (12)

3.5.2 Complex Pythagorean fuzzy discordance sets

The inferiority of an alternative over the alternatives can be examined through the discordance sets. The discordance sets are further categorized in three categories, namely strong discordance set, midrange discordance set and weak discordance set. These discordance sets consist of the subscripts of all those criteria that predict the inadequacy of an alternative over the other alternatives.

For any pair of $({\mathcal {D}}_{\eta }, {\mathcal {D}}_{\varrho }),$ the discordance sets can be constructed as follows:

• (i) The CPF strong discordance set ${{\mathfrak {L}}_{\eta \varrho }}$ can be defined as:

  $$\begin{aligned}&{{\mathfrak {L}}_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}<{\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}< {\widetilde{\zeta }}_{\varrho r}, {\widetilde{y}}_{\eta r}\ge {\widetilde{y}}_{\varrho r}, \nonumber \\&{\widetilde{\sigma }}_{\eta r}\ge {\widetilde{\sigma }}_{\varrho r}, {\widetilde{w}}_{\eta r}\ge {\widetilde{w}}_{\varrho r}, \gamma '_{\eta r}\ge \gamma '_{\varrho r}\}. \end{aligned}$$

  (13)

• (ii) The CPF midrange discordance set ${{\mathfrak {L}}^*_{\eta \varrho }}$ can be defined as:

  $$\begin{aligned}&{{\mathfrak {L}}^*_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}< {\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}< {\widetilde{\zeta }}_{\varrho r}, {\widetilde{y}}_{\eta r}\ge {\widetilde{y}}_{\varrho r}, \nonumber \\&{\widetilde{\sigma }}_{\eta r}\ge {\widetilde{\sigma }}_{\varrho r},{\widetilde{w}}_{\eta r}< {\widetilde{w}}_{\varrho r},\gamma '_{\eta r}<\gamma '_{\varrho r}\}. \end{aligned}$$

  (14)

• (iii) The CPF weak discordance set ${{\mathfrak {L}}^{**}_{\eta \varrho }}$ can be defined as:

  $$\begin{aligned}&{{\mathfrak {L}}^{**}_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}< {\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}< {\widetilde{\zeta }}_{\varrho r}, \nonumber \\&{\widetilde{y}}_{\eta r}\le {\widetilde{y}}_{\varrho r}, {\widetilde{\sigma }}_{\eta r}\le {\widetilde{\sigma }}_{\varrho r}\}. \end{aligned}$$

  (15)

3.5.3 Complex Pythagorean fuzzy indifferent set

The CPF indifferent set expresses the indifference relation between two alternatives. It contains the subscripts of all those criteria in reference to which two alternatives exhibit the same performance. The CPF indifference set is constructed as follows:

$$\begin{aligned}&{{\mathfrak {T}}_{\eta \varrho }}=\{r:{\widetilde{x}}_{\eta r}={\widetilde{x}}_{\varrho r}, {\widetilde{\zeta }}_{\eta r}= {\widetilde{\zeta }}_{\varrho r}, {\widetilde{y}}_{\eta r}= {\widetilde{y}}_{\varrho r},\nonumber \\&{\widetilde{\sigma }}_{\eta r}= {\widetilde{\sigma }}_{\varrho r}, {\widetilde{w}}_{\eta r}= {\widetilde{w}}_{\varrho r}, \gamma '_{\eta r}= \gamma '_{\varrho r}\}. \end{aligned}$$

(16)

3.6 Construction of complex Pythagorean fuzzy concordance and discordance matrices

After the construction of CPF concordance and discordance sets, the next step is to measure the extent to which an alternative dominate or precede over the other alternative. Here, the measures, representing the dominance or inferiority of an alternative over the other, are named as CPF concordance index and CPF discordance index, respectively. These indices further led us to the construction of CPF concordance matrix and CPF discordance matrix.

3.6.1 Construction of complex Pythagorean fuzzy concordance matrix

The CPF concordance index $C_{\eta \varrho }$ corresponds to the degree to which the alternative ${\mathcal {D}}_{\eta }$ is loftier than the alternative ${\mathcal {D}}_{\varrho }$. In simple words, the CPF concordance index is a measure to reveal the amount or level of dominance of an alternative over the other. For the pair of alternative $({\mathcal {D}}_{\eta }, {\mathcal {D}}_{\varrho }),$ the CPF concordance index can be computed using the following formula:

$$\begin{aligned} C_{\eta \varrho }=\, & {} \gamma _{{\mathfrak {K}}}\sum _{r\in {\mathfrak {K}}}\gamma ^{*}_{r}+ \gamma _{{\mathfrak {K}}^*}\sum _{r\in {\mathfrak {K}}^{*}}\gamma _{r}^{*}+ \gamma _{{\mathfrak {K}}^{**}} \sum _{r\in {\mathfrak {K}}^{**}}\gamma _{r}^{*}\nonumber \\&+\gamma _{{\mathfrak {T}}} \sum _{r\in {\mathfrak {T}}}\gamma _{r}^{*}, \end{aligned}$$

(17)

where $\gamma _{{\mathfrak {K}}},$ $\gamma _{{\mathfrak {K}}^*},$ $\gamma _{{\mathfrak {K}}^{**}}$ and $\gamma _{{\mathfrak {T}}}$ denote the weights of the CPF strong, midrange, weak concordance sets and CPF indifferent set, respectively. Furthermore, $\gamma _{r}^{*}$ represents the normalized weightage of the criterion ${\mathcal {Z}}_{r}.$ The CPF concordance matrix, comprising all the concordance indices, can be constructed as follows:

$$\begin{aligned} {\mathfrak {C}}=\left( \begin{array}{cccccc} - &\quad C_{12} &\quad C_{13}&\quad \cdots &\quad C_{1(p-1)}&\quad C_{1p} \\ &\quad &\quad &\quad &\quad &\\ C_{21} &\quad - &\quad C_{23}&\quad \cdots &\quad C_{2(p-1)} &\quad C_{2p} \\ &\quad &\quad &\quad &\quad &\\ C_{31} &\quad C_{32} &\quad -&\quad \cdots &\quad C_{3(p-1)}&\quad C_{3p} \\ \vdots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots &\quad \vdots \\ C_{(p-1)1}&\quad C_{(p-1)2}&\quad C_{(p-1)3}&\quad \cdots &\quad -&\quad C_{(p-1)p}\\ &\quad &\quad &\quad &\quad &\\ C_{p1} &\quad C_{p2} &\quad C_{p3} &\quad \cdots &\quad C_{p(p-1)} &\quad - \end{array}\right) . \end{aligned}$$

A larger value of $C_{\eta \varrho }$ predicts that the alternative ${\mathcal {D}}_{\eta }$ is more preferable than the alternative ${\mathcal {D}}_{\varrho }.$

3.6.2 Construction of complex Pythagorean fuzzy discordance matrix

The CPF discordance index $D_{\eta \varrho }$ corresponds to the degree to which the alternative ${\mathcal {D}}_{\eta }$ is subordinate than the alternative ${\mathcal {D}}_{\varrho }$. In simple words, the CPF discordance index is a measure to the reveal the amount or level of subordination of an alternative over the other. For the pair of alternative $({\mathcal {D}}_{\eta }, {\mathcal {D}}_{\varrho }),$ the CPF discordance index can be computed using the following formula:

$$\begin{aligned} D_{\eta \varrho }=\frac{\underset{r\in {{\mathfrak {L}}}\cup {{\mathfrak {L}}^*}\cup {{\mathfrak {L}}^{**}}}{\max }\{\gamma _{{\mathfrak {L}}}\times d({\tilde{B}}_{\eta r}, {\tilde{B}}_{\varrho r}), \gamma _{{\mathfrak {L}}^*}\times d({\tilde{B}}_{\eta r}, {\tilde{B}}_{\varrho r}), \gamma _{{\mathfrak {L}}^{**}}\times d({\tilde{B}}_{\eta r}, {\tilde{B}}_{\varrho r})\}}{\underset{r}{\max }~d({\tilde{B}}_{\eta r}, {\tilde{B}}_{\varrho r})}, \end{aligned}$$

(18)

where $\gamma _{{\mathfrak {L}}},$ $\gamma _{{\mathfrak {L}}^*}$ and $\gamma _{{\mathfrak {L}}^{**}}$ denote the weights of the CPF strong, midrange and weak discordance sets, respectively. The normalized Euclidean distance $d({\tilde{B}}_{\eta r}, {\tilde{B}}_{\varrho r})$ between the alternatives ${\mathcal {D}}_{\eta }$ and ${\mathcal {D}}_{\varrho }$ with respect to the criterion ${\mathcal {Z}}_{r}$ can be evaluated as follows:

$$\begin{aligned} d({\tilde{B}}_{\eta r}, {\tilde{B}}_{\varrho r})=\sqrt{\frac{(x_{\eta r}^{2}-x_{\varrho r}^{2})^{2}+(y_{\eta r}^{2}-y_{\varrho r}^{2})^{2}+(z_{\eta r}^{2}-z_{\varrho r}^{2})^{2}+ \frac{1}{16\pi ^{4}}\left( ({\tilde{\zeta }}_{\eta r}^{2}-{\tilde{\zeta }}_{\varrho r}^{2})^{2}+({\tilde{\sigma }}_{\eta r}^{2}-{\tilde{\sigma }}_{\varrho r}^{2})^{2}+(\aleph _{\eta r}^{2}-\aleph _{\varrho r}^{2})^{2}\right) }{2}}. \end{aligned}$$

(19)

The CPF discordance matrix, comprising all the discordance indices, can be represented as follows:

$$\begin{aligned} {\mathfrak {D}}=\left( \begin{array}{cccccc} - &{}\quad D_{12} &{}\quad D_{13}&{}\quad \cdots &{}\quad D_{1(p-1)}&{}\quad D_{1p} \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\\ D_{21} &{}\quad - &{}\quad D_{23}&{}\quad \cdots &{}\quad D_{2(p-1)} &{}\quad D_{2p} \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\\ D_{31} &{}\quad D_{32} &{}\quad -&{}\quad \cdots &{}\quad D_{3(p-1)}&{}\quad D_{3p} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ D_{(p-1)1}&{}\quad D_{(p-1)2}&{}\quad D_{(p-1)3}&{}\quad \cdots &{}\quad -&{}\quad D_{(p-1)p}\\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\\ D_{p1} &{}\quad D_{p2} &{}\quad D_{p3} &{}\quad \cdots &{}\quad D_{p(p-1)} &{}\quad - \end{array}\right) . \end{aligned}$$

A larger value of $D_{\eta \varrho }$ suggests that the alternative ${\mathcal {D}}_{\eta }$ is less significant than the alternative ${\mathcal {D}}_{\varrho }.$

3.7 Outranking relation

In this step, we establish two types of outranking relations, namely strong outranking relation ${\mathbb {R}}^{{\mathfrak {s}}}$ and weak outranking relation ${\mathbb {R}}^{w}$, by comparing the evaluated indices with the threshold parameters. The purpose of this comparison is to check the effectiveness of the concordance and discordance indices among any pair of alternatives. Further, the threshold values are specified by appointed decision-making experts which lead to the construction of three concordance levels and two discordance levels to authentically inspect the dominance of an alternative over the other.

Let $k^{-},$ $k^{\circ}$ and $k^{*}$ be three strictly increasing levels of the concordance such that 0<$k^{-}<$$k^{\circ}<$$k^*{<}1$ and the indicated concordance levels can be labeled as low, average and high level, respectively. Let $\c{d}^{*}$ and $\c{d}^\circ$ be the strictly increasing discordance levels such that $0<$$\c{d}^*<$$\c{d}^\circ <1$ and these discordance levels can be labeled as low and average level, respectively. An alternative ${\mathcal {D}}_{\eta }$ strongly outranks the alternative ${\mathcal {D}}_{\varrho }$, i.e., ${\mathcal {D}}_{\eta }{\mathbb {R}}^{{\mathfrak {s}}}{\mathcal {D}}_{\varrho }$ if and only if one or both of these conditions hold

Likewise, the alternative ${\mathcal {D}}_{\eta }$ weakly outranks the alternative ${\mathcal {D}}_{\varrho }$, i.e., ${\mathcal {D}}_{\eta }{\mathbb {R}}^{w}{\mathcal {D}}_{\varrho }$ if and only if the following condition holds

3.8 Construction of outranking graph

To specify the ranking of the alternatives on the basis of outranking relations, two outranking graphs, namely strong outranking graph $\mathrm {G}^{{\mathfrak {s}}}=({\mathcal {D}},\mathrm {E}^{{\mathfrak {s}}})$ and weak outranking graph $\mathrm {G}^{w}=({\mathcal {D}},\mathrm {E}^{w})$, are portrayed to depict the pairwise strong and weak outranking relations, respectively. Here, $\mathrm {E}^{{\mathfrak {s}}}$ and $\mathrm {E}^{w}$ denote the corresponding edge sets in reference to strong and weak outranking relations, respectively, and ${\mathcal {D}}$ is the set of all available alternatives. Further, the forward ranking and reverse ranking of the alternatives are predicted by deployed these graphs in an iterative manner which further lead to the establishment of average ranking.

3.8.1 Forward ranking $\psi ^{F}$

Let ${\mathcal {D}}(t)$ be any subcollection of ${\mathcal {D}}.$ The forward ranking of the potential alternative can be obtained as

• 1. Construct the non-dominated set of the feasible alternatives ${\mathbb {H}}(t)$, consisting of all those vertices having no incoming or precedent flow, by exploration of the strong outranking graph $\mathrm {G}^{{\mathfrak {s}}}=({\mathcal {D}},\mathrm {E}^{{\mathfrak {s}}}).$

• 2. Construct the edge set $\widetilde{\mathrm {E}}^{{\mathfrak {s}}}$, consisting of all those edges which have both extremities in ${\mathbb {H}}(t)$, by exploration of the weak outranking graph $\mathrm {G}^{w}=({\mathcal {D}},\mathrm {E}^{w}).$

• 3. Construct the set ${\mathcal {P}}(t)$, consisting of all those edges having no incoming edge, by the exploration of the graph $\mathrm {G}=({\mathbb {H}}(t),\widetilde{\mathrm {E}}^{{\mathfrak {s}}}).$

• 4. The following iterative procedure is adopted to find out the forward ranking $\psi ^{F}$:

  • (i) Let $t=1$ and ${\mathcal {D}}(1)={\mathcal {D}}.$

  • (ii) Construct the sets ${\mathbb {H}}(t)$ and ${\mathcal {P}}(t)$ by following the steps 1,2,3 and 4(iv).

  • (iii) Assign the ranking to alternative ${\mathcal {D}}_{e}$ by $\psi ^{F}({\mathcal {D}}_{e})=t$ for all ${\mathcal {D}}_{e}\in {\mathcal {P}}(t).$

  • (iv) Delete the forwardly ranked alternative from the original set and the corresponding edges from $\mathrm {G}^{w}$ and $\mathrm {G}^{{\mathfrak {s}}}.$ In other words, construct the set ${\mathcal {D}}(t+1)={\mathcal {D}}(t)-{\mathcal {P}}(t).$ If ${\mathcal {D}}(t+1)=\phi$, then all the alternatives are ranked; otherwise, proceed further by taking $t=t+1$ in the step 4(ii).

3.8.2 Reverse ranking $\psi ^{R}$

• 1. To obtain the mirror image of the direct outranking relations, the direction of the edges of the weak outranking graph $\mathrm {G}^{w}$ and strong outrank graph $\mathrm {G}^{{\mathfrak {s}}}$ is reversed.

• 2. Now, the procedure of the forward ranking is adopted to these graph to obtain a ranking $\psi ^{'}$ of the alternatives.

• 3. The authentic order of reverse ranking can be obtained via the formula:

  $$\begin{aligned} \psi ^R({\mathcal {D}}_{e})=1+\max _{{\mathcal {D}}_{e}\in {\mathcal {D}}}\psi ^{'}({\mathcal {D}}_{e})-\psi ^{'}({\mathcal {D}}_{e}). \end{aligned}$$

  (22)

3.8.3 Average ranking

The average ranking of the alternatives can be determined by the dint of the following formula:

$$\begin{aligned} \psi ({\mathcal {D}}_{e})=\frac{\psi ^F({\mathcal {D}}_{e})+\psi ^R({\mathcal {D}}_{e})}{2} \end{aligned}$$

(23)

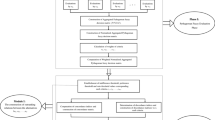
The flowchart of the proposed procedure is shown in Fig. 1.

Fig. 1

Flowchart of CPF-ELECTRE II method

3.9 Algorithm

The complete algorithm of the proposed strategy is described in Table 1.

Table 1 Algorithm for the CPF-ELECTRE II method

4 A case study

Water is a complementary part of human life which is necessarily needed for drinking, industry, plants, animals, agriculture, cleaning and other purposes. In short, water is one of the main necessities of life on earth. Water quality is judged on the basis of some key factors including the concentration of oxygen, bacteria levels, salinity and turbidity. The depletion of water resources and water pollution, caused by industrial waste, sewage, wastewater, mining activities, acid rain, animal waste, global warming, radioactive waste, urban development, chemical fertilizers, burning of fossil fuels and marine dumping, is emerging as a serious and noticeable issue. This situation captivated the attentions of the researchers who presented the wastewater treatment processes (WWTPs) as a solution of the above problem. Wastewater treatment refers to a process designed to remove contaminants and harmful pollutants from wastewater to make the treated water a part of the water cycle again for reuse. In this MCGDM, our task is to select the most suitable WWTP from a set of available choices. This study [41] is carried out by three stake holder groups:

• ${\mathfrak {N}}_{1}$: Researchers: This group consists of eight researchers inclusive of two professors, two PhD, one postdoctoral and three senior researchers working on WWTPs.

• ${\mathfrak {N}}_{2}$: Administrators: This group consists of three administrators, two from local environmental protection bureau and one from sector of wastewater treatment of the coal-fired power company.

• ${\mathfrak {N}}_{3}$: Local resident of the city: This group consists of six local residents contributing in this study.

Each group has a director to collect the information and represent the assessment. The normalized weights of the decision makers are given by the weight vector $\theta =(0.3455, 0.3365, 0.3180)^T$. After a deep analysis, the decision-making panel considers the following four WWTPs as potential alternatives:

• ${\mathcal {D}}_{1}$: Anaerobic-Anoxic-Oxic ($\mathbb {AAO}$): This presents a well-known WWTP which is widely used for the removal of nitrogen and phosphorus organic compounds to improve the quality of water. The process is implemented using a combination of anaerobic, anoxic and oxic tanks. A major pitfall of the $\mathbb {AAO}$ process is the high capital cost for the establishment of the plant.

• ${\mathcal {D}}_{2}$: Triple oxidation ditch ($\mathbb {TOD}$): This is an effective WWTP that alternates between aerobic, anoxic and settling phases to decrease the nitrogen amount up to desired level without employing internal recycle streams or external clarifiers. The prominent advantages of this procedure are its reliability and ease of operation, whereas this procedure is not effective for sludge treatment and its plants require more land for operation.

• ${\mathcal {D}}_{3}$: Anaerobic single-ditch oxidation ($\mathbb {ASD}$): This WWTP exhibits very good performance for the removal of nitrogen and phosphorus organic compounds. But it occupies more land for the establishment of the plant.

• ${\mathcal {D}}_{4}$: Sequencing batch reactor activated sludge process ($\mathbb {SBR}$): This WWTP performs equalization, biological treatment and secondary clarification by employing a timed control sequence, while it shows poor potential for the removal of nitrogen and phosphorus organic compounds. The advantageous features of this WWTP include low capital cost and less occupied land. The drawbacks of this process include low maturity and reliability.

Further, the decision-making panel considers the following economical, environmental, technological and social–political aspects as decision criteria:

• ${\mathcal {Z}}_{1}$: Capital cost (${{\mathbb {CC}}}$): Capital cost represents the initial amount required for the establishment of the water treatment plant.

• ${\mathcal {Z}}_{2}$: Operation and maintenance cost (${{\mathbb {OM}}}$): Operational and maintenance cost includes the human resource, energy used, fuel, electricity, repairing cost, etc.

• ${\mathcal {Z}}_{3}$: Effect on water quality improvement (${{\mathbb {WQ}}}$): Water quality is an indicator to check the caliber of the wastewater treatment. Water quality depends upon amount of nitrogen, phosphorus, pollutant, solid waste and salinity.

• ${\mathcal {Z}}_{4}$: Occupied land (${{\mathbb {OL}}}$): Occupied land refers to the total piece of land required for the implementation and operation of the WWTP.

• ${\mathcal {Z}}_{5}$: Operability and simplicity (${{\mathbb {OS}}}$): This criterion refers to the ease of the continuous operation and implementation of the WWTP.

• ${\mathcal {Z}}_{6}$: Maturity (${\mathbb {M}}$): This criterion is an indicator of the utilization level of the WWTP nationally and internationally.

• ${\mathcal {Z}}_{7}$: Reliability (${\mathbb {R}}$): Reliability refers to the durability and precision of results of the WWTP.

• ${\mathcal {Z}}_{8}$: Public acceptability (${{\mathbb {PA}}}$): This criterion indicates the acceptability of the nearby residents for the WWTP.

The solution of the narrated MCGDM problem is derived by methodology of CPF-ELECTRE II technique in the following steps:

Step 1::

The linguistic terms, employed to represent the assessments of each decision maker, are arranged in Table 2.

Table 2 Linguistic term to rate the water treatment procedures

Table 3 provides a comprehensive view of the judgments of the decision-making panel regarding the aptitude of the WWTPs in reference to each criterion.

Table 3 Linguistic terms assigned to water treatment processes

These linguistic terms, representing the independent decisions of all experts, can be interpreted as CPFNs. The corresponding independent CPFDMs ${\mathfrak {P}}^{(1)}$, ${\mathfrak {P}}^{(2)}$ and ${\mathfrak {P}}^{(3)}$ are organized in Tables 4, 5 and 6, respectively.

Table 4 Complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(1)}$

Table 5 Complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(2)}$

Table 6 Complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(3)}$

Step 2::

The independent opinions are cumulated by operating the entries of the individual CPFDMs and the weight vector $\theta$ according to Eq. (6). The entries of ACPFDM are tabulated in Table 9.

Step 3::

The linguistic terms, employed to express the expert’s opinion relative to importance of criteria, are organized in Table 7.

Table 7 Linguistic term for the importance of criteria

The opinions of the decision-making experts in reference to importance of decision criteria are expressed in terms of linguistic terms. Further, Table 8 comprises the CPF weight and normalized weight of each criterion which are evaluated with the help of Eqs. (7) and (8), respectively.

Table 8 Criteria weights

Step 4::

The AWCPFDM, evaluated by means of Eq. (9), is shown in Table 10.

Table 9 Aggregated complex Pythagorean fuzzy decision matrix

Table 10 Aggregated weighted complex Pythagorean fuzzy decision matrix

Step 5::

The CPF strong concordance set, determined by Eq. (10), is given by

$$\begin{aligned} {\mathfrak {K}}=\left( \begin{array}{cccc} - &{}\quad \{3, 6\} &{}\quad \{6\} &{}\quad \{3, 6\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{3\} &{}\quad \{3, 6, 8\} &{}\quad - &{}\quad \{3, 6\} \\ \{1,4,7\} &{}\quad \{1,7\} &{}\quad \{1,7\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF midrange concordance set, determined by Eq. (11), is given by

$$\begin{aligned} {\mathfrak {K}}^*=\left( \begin{array}{cccc} - &{}\quad \{2, 4\} &{}\quad \{2, 4\} &{}\quad \{2, 8\} \\ \{1, 5, 8\} &{}\quad - &{}\quad \{5\} &{}\quad \{5, 8\} \\ \{1, 5, 8\} &{}\quad \{2\} &{}\quad - &{}\quad \{2, 5, 8\}\\ \{\} &{}\quad \{2, 4\} &{}\quad \{4\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF weak concordance set, determined by Eq. (12), is given by

$$\begin{aligned} {\mathfrak {K}}^{**}=\left( \begin{array}{cccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF indifference set, determined by Eq. (16), is given by

$$\begin{aligned} {\mathfrak {T}}=\left( \begin{array}{cccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{5\} \\ \{\} &{}\quad - &{}\quad \{4, 7\} &{}\quad \{3\} \\ \{\} &{}\quad \{4, 7\} &{}\quad - &{}\quad \{\} \\ \{5\} &{}\quad \{3\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF strong discordance set, determined by Eq. (13), is given by

$$\begin{aligned} {\mathfrak {L}}=\left( \begin{array}{cccc} -- &{}\quad \{\} &{}\quad \{3\} &{}\quad \{1, 4, 7\} \\ \{3, 6\} &{}\quad -- &{}\quad \{3, 6, 8\} &{}\quad \{1,7\} \\ \{6\} &{}\quad \{\} &{}\quad -- &{}\quad \{1, 7\} \\ \{3, 6\} &{}\quad \{\} &{}\quad \{3, 6\} &{}\quad -- \end{array}\right) . \end{aligned}$$

The CPF midrange discordance set, determined by Eq. (14), is given by

$$\begin{aligned} {\mathfrak {L}}^*=\left( \begin{array}{cccc} - &{}\quad \{1, 5, 8\} &{}\quad \{1, 5, 8\} &{}\quad \{\} \\ \{2, 4\} &{}\quad - &{}\quad \{2\} &{}\quad \{2, 4\} \\ \{2, 4\} &{}\quad \{5\} &{}\quad - &{}\quad \{4\} \\ \{2, 8\} &{}\quad \{5, 8\} &{}\quad \{2, 5, 8\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF weak discordance set, determined by Eq. (15), is given by

$$\begin{aligned} {\mathfrak {L}}^{**}=\left( \begin{array}{cccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

Step 6::

For the evaluation of the concordance indices, the decision-making panel assigns weights to the CPF concordance and indifference sets as follows:

$$\begin{aligned} (\gamma _{{\mathfrak {K}}}, \gamma _{{\mathfrak {K}}^*}, \gamma _{{\mathfrak {K}}^{**}}, \gamma _{{\mathfrak {T}}})=\left( 1, \frac{3}{4}, \frac{2}{4}, \frac{1}{4}\right) . \end{aligned}$$

The complex Pythagorean fuzzy concordance matrix (CPFCM) ${\mathfrak {C}}$, determined in the light of concordance sets by deploying Eq. (17), is given as follows:

$$\begin{aligned} {\mathfrak {C}}=\left( \begin{array}{cccc} - &{}\quad 0.4489 &{}\quad 0.3003 &{}\quad 0.5013\\ 0.2776 &{}\quad - &{}\quad 0.1264 &{}\quad 0.2121 \\ 0.4262&{}\quad 0.5498 &{}\quad - &{}\quad 0.5479 \\ 0 .3860 &{}\quad 0.4676 &{}\quad 0.3374 &{}\quad - \end{array}\right) . \end{aligned}$$

The normalized Euclidean distance between the entries of AWCPFDM, evaluated by Eq. (19), is shown in Table 11.

Table 11 Distance measures

The weights of strong, midrange and weak discordance sets are given by,

$$\begin{aligned} (\gamma _{{\mathfrak {L}}}, \gamma _{{\mathfrak {L}}^*}, \gamma _{{\mathfrak {L}}^{**}})=\left( 1, \frac{3}{4}, \frac{2}{4}\right) . \end{aligned}$$

The CPF discordance indices, evaluated by Eq. (18), are arranged to construct the complex Pythagorean fuzzy discordance matrix (CPFDSM) as follows:

$$\begin{aligned} {\mathcal {D}}=\left( \begin{array}{cccc} -&{}\quad 0.5063 &{}\quad 0.9411 &{}\quad 1\\ 0.9755 &{}\quad -&{}\quad 1 &{}\quad 0.4247 \\ 0.4180&{}\quad 0.2013&{}\quad - &{}\quad 0.6173 \\ 0.9119 &{}\quad 0.7500 &{}\quad 0.7500&{}\quad - \end{array}\right) . \end{aligned}$$

Step 7::

Table 12 represents the strong and weak outranking relations which are established by the comparison of concordances and discordance indices with reference to the concordance levels ($k^{-}$, $k^{\circ}$, $k^{*}$)=(0.4, 0.5, 0.6) and discordance levels ($\c{d}^*$ , $\c{d}^\circ$)= (0.6, 0.7).

Table 12 Outranking relations

Step 8::

The strong and weak outranking graphs as well as reverse strong and weak outranking graphs, represented in Figs. 2 and 3, respectively, are portrayed to visualize the outranking relations in a comprehensive way. These strong and weak outranking graphs are employed in an iterative way to specify the forward and reverse rankings which are helpful to evaluate average ranking. Table 13 comprises the forward, reverse and average rankings of the feasible alternatives.

Table 13 Forward, reverse and average rankings

Thus, we conclude that anaerobic single-ditch oxidation is the most suitable WWTP.

Fig. 2

Strong (a) and weak (b) outranking graphs

Fig. 3

Reverse strong (a) and weak (b) outranking graph

5 Selection of appropriate cloud solution to manage big data projects

The term “big data” corresponds to the large increase in the amount of data which cannot be stored, managed, processed and analyzed by traditional technologies as the traditional technologies require expensive hardware devices, storage devices and complex softwares to compile the data. The four major characteristics of big data include volume, variety (audio, video, figures or other files), speed of data transfer and specification of required hidden value from the clumped data. The stored data serves as a key tool for the relevant person to keep a record of the previous events, to predict new trend on basis of previous data sheet and to estimate the profit in business, medical, engineering, industries and other fields. With the advancement in information technology, the need of timely implementation of the new, advanced and smart data storing technology has been increased with exponential growth in amount of stored data. Cloud computing is the accessibility of computing services, including servers, storage, databases, networking, software, analytics and intelligence over the internet to facilitate the users with its innovative infrastructure. In the modern era, cloud computing is a rapid growing innovative technology which is replacing the traditional technologies due to low capital cost, high speed, productivity, performance, reliability and security. In this MCGDM problem, adapted from Sachdeva et al. [42], we aim to figure out the most beneficial and efficient cloud solution to manage big data projects. For the sake of authentic decision, a panel of three decision makers is designated to exhibit their opinions in terms of linguistic terms after taking a deep review of performance of the alternatives. The weightage of decision-making experts in the panel is given by the normalized weight vector $\theta =(0.4060, 0.2380, 0.3560)^T.$ The following cloud solutions are considered as potent alternatives:

• ${\mathcal {D}}_{1}$: Amazon (${{\mathcal {AM}}}$): Amazon web services (AWS) is a secure, authentic and affordable platform for business sector which is providing its services in almost 190 countries. The user friendly infrastructure and tremendous features of AWS, which are designed to deliver best security and other business advantages to customers, make it more popular and adaptable.

• ${\mathcal {D}}_{2}$: HP cloud (${{\mathcal {HP}}}$): HP Cloud, based on openstack technology, presents a set of cloud computing services inclusive of public cloud, private cloud, hybrid cloud, managed private cloud, pay-as-you-go cloud and other cloud services. HP cloud finds abundant application in enterprise organizations to merge the public cloud services with their internal IT resources to develop a fruitful blend of different clouding environments. Other prominent features of HP cloud include storage, platform, computation, compilation and orchestration.

• ${\mathcal {D}}_{3}$: Google cloud platform (${{\mathcal {GO}}}$): Google cloud platform delivers cloud computing services following the same infrastructure as used by other Google applications including Gmail, file storage and YouTube. The notable services of Google cloud platform include computing, load balancing data storage, faster persistent disk, data analytics, extended support for operating systems and machine learning.

• ${\mathcal {D}}_{4}$: Rackspace (${{\mathcal {RS}}}$): Rackspace cloud offers cloud storage, virtual private server, databases, backup and monitoring. Owing to the Rackspace cloud, the developers and service managers are capable to provide excellent services with smaller advance investments without the dedicated hardware.

• ${\mathcal {D}}_{5}$: Microsoft azure (${{\mathcal {MA}}}$): Microsoft azure provides cloud computing services which are utilized for the sake of building, testing, deploying, supporting disaster recovery, managing applications and services through Microsoft-managed data centers. Microsoft azure is competent to support many different programming languages, innovative features and frameworks, including both Microsoft-specific and third-party software and systems.

Three aspects, treated as decision criteria to check the performance of available alternatives, are given as follows:

• ${\mathcal {Z}}_{1}$: e-Governance $({{\mathcal {EG}}})$

• ${\mathcal {Z}}_{2}$: Business continuity $({{\mathcal {BC}}})$

• ${\mathcal {Z}}_{3}$: Security $({{\mathcal {SC}}})$

The complete solution of narrated MCGDM problem is comprised in the following steps:

Step 1::

Table 14 comprises the linguistic terms to describe the decision-maker’s preferences regarding the performance of the alternatives.

Table 14 Linguistic terms for the assessment of cloud solutions

The independent decisions of each decision maker, expressed in terms of linguistic terms, are compiled in Table 15.

Table 15 Assessments of the decision-making panel

The individual CPFDMs ${\mathfrak {P}}^{(1)},$ ${\mathfrak {P}}^{(2)}$ and ${\mathfrak {P}}^{(3)}$, comprising the independent assessments of decision maker ${\mathfrak {N}}_{1},$ ${\mathfrak {N}}_{2}$ and ${\mathfrak {N}}_{3}$, are organized in Tables 16, 17 and 18, respectively.

Table 16 Complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(1)}$

Table 17 Complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(2)}$

Table 18 Complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(3)}$

Step 2::

The entries of the individual matrices are merged to construct the ACPFDM by dint of Eq. (6), shown in Table 19.

Table 19 Aggregated complex Pythagorean fuzzy decision matrix ${\mathfrak {P}}$

Step 3::

Table 20 is comprised of the linguistic terms, expressing the decision-maker’s preference about the relative importance of the decision criteria.

Table 20 Linguistic terms for weightage of criteria

The opinions of the decision makers concerning the importance of decision criteria as well as CPF and normalized weights of the criteria, computed by Eqs. (7) and (8), are embedded in Table 21.

Table 21 Criteria weights

Step 4::

The AWCPFDM, determined by the help of Eq. (9), is arranged in Table 22.

Table 22 Aggregated weighted complex Pythagorean fuzzy decision matrix $\widetilde{{\mathfrak {P}}}$

Step 5::

The CPF strong concordance set, evaluated in the light of Eq. (10), is given by

$$\begin{aligned} {\mathfrak {K}}=\left( \begin{array}{ccccc} - &{}\quad \{1,2,3\} &{}\quad \{3\} &{}\quad \{1,2,3\} &{}\quad \{1,2,3\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{2\} &{}\quad \{1,2\} \\ \{1,2\} &{} \quad \{1,2,3\} &{}\quad - &{}\quad \{1,2,3\} &{}\quad \{1,2,3\} \\ \{\} &{}\quad \{1,3\} &{}\quad \{\} &{}\quad - &{}\quad \{1,2,3\}\\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF midrange concordance set, evaluated in the light of Eq. (11), is given by

$$\begin{aligned} {\mathfrak {K}}^*=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF weak concordance set, evaluated in the light of Eq. (12), is given by

$$\begin{aligned} {\mathfrak {K}}^{**}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF indifference set, evaluated in the light of Eq. (16), is given by

$$\begin{aligned} {\mathfrak {T}}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF strong discordance set, evaluated in the light of Eq. (13), is given by

$$\begin{aligned} {\mathfrak {L}}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{1,2\} &{}\quad \{\} &{}\quad \{\} \\ \{1,2,3\} &{}\quad - &{}\quad \{1,2,3\} &{}\quad \{1,3\} &{}\quad \{\} \\ \{3\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{1,2,3\} &{}\quad \{2\} &{}\quad \{1,2,3\} &{}\quad - &{}\quad \{\}\\ \{1,2,3\} &{}\quad \{1,2\} &{}\quad \{1,2,3\} &{}\quad \{1,2,3\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF midrange discordance set, evaluated in the light of Eq. (14), is given by

$$\begin{aligned} {\mathfrak {L}}^*=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF weak discordance set, evaluated in the light of Eq. (15), is given by

$$\begin{aligned} {\mathfrak {L}}^{**}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

Step 6::

For the evaluation of the concordance indices, the decision-making panel assigns weights to the CPF concordance and indifference sets as follows:

$$\begin{aligned} (\gamma _{{\mathfrak {K}}}, \gamma _{{\mathfrak {K}}^*}, \gamma _{{\mathfrak {K}}^{**}}, \gamma _{{\mathfrak {T}}})=(1, \frac{3}{4}, \frac{2}{4}, \frac{1}{4}). \end{aligned}$$

The CPFCM ${\mathfrak {C}}$, determined in the light of concordance sets by deploying Equation (17), is given as follows:

$$\begin{aligned} {\mathfrak {C}}=\left( \begin{array}{ccccc} - &{}\quad 1 &{}\quad 0.3181 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad - &{}\quad 0 &{}\quad 0.3373 &{}\quad 0.6819 \\ 0.6819&{}\quad 1&{}\quad - &{}\quad 1 &{}\quad 1 \\ 0 &{}\quad 0.6627 &{}\quad 0 &{}\quad - &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad - \end{array}\right) . \end{aligned}$$

The normalized Euclidean distances between the entries of the AWCPFM are arranged in Table 23.

Table 23 Distance measures

For the evaluation of the discordance indices, the decision-making panel assigns weights to the CPF discordance sets as follows:

$$\begin{aligned} (\gamma _{{\mathfrak {L}}}, \gamma _{{\mathfrak {L}}^*}, \gamma _{{\mathfrak {L}}^{**}})=\left(1, \frac{3}{4}, \frac{2}{4}\right). \end{aligned}$$

Further, Eq. (18) is employed to find the CPF discordance indices which are organized to form CPFDSM as follows:

$$\begin{aligned} {\mathcal {D}}=\left( \begin{array}{ccccc} - &{}\quad 0 &{}\quad 1&{}\quad 0 &{}\quad 0\\ 1 &{}\quad - &{}\quad 1 &{}\quad 1 &{}\quad 0 \\ 0.0581 &{}\quad 0 &{}\quad -&{}\quad 0 &{}\quad 0 \\ 1&{}\quad 0.8908 &{}\quad 1&{}\quad -&{}\quad 0 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad - \end{array}\right) . \end{aligned}$$

Step 7::

The strong and weak outranking relations, established by the comparison of concordances and discordance indices with reference to the concordance levels ($k^{-}$, $k^{\circ}$, $k^{*}$)=(0.6, 0.7, 0.8) and discordance levels ($\c{d}^*$ , $\c{d}^\circ$)= (0.7, 0.8), are comprised in Table 24.

Table 24 Outranking relations

Step 8::

The strong and weak outranking graphs as well as reverse strong and weak outranking graphs, represented in Figs. 4 and  5, respectively, are portrayed to visualize the outranking relations in a comprehensive way. The strong and weak outranking graphs are employed in an iterative way to specify the forward and reverse rankings which are helpful to evaluate average ranking. Table 25 comprises the forward, reverse and average rankings of the feasible alternatives.

Table 25 Forward, reverse and average rankings

Thus, Google is the best cloud solution for the management of big data projects.

Fig. 4

Strong (a) and weak (b) outranking graphs

Fig. 5

Reverse strong (a) and weak (b) outranking graph

6 Comparative analysis

This section presents a comprehensive comparison of the proposed technique with two existing approaches to showcase its validity and adequacy. Furthermore, the merits of the proposed procedure over the compared approaches are unfolded to highlight the efficiency of CPF-ELECTRE II method in decision-making scenarios.

6.1 Selection of the best wastewater treatment process by complex Pythagorean fuzzy ELECTRE I method

To prove the consistency of the proposed procedure, we solve the numerical example “selection of best wastewater treatment process” using CPF-ELECTRE I method, proposed by Akram et al. [39]. The stepwise solution is given as follows:

Step 1::

The linguistic terms for the evaluation of the creditability of decision makers and decision criteria are shown in Table 7. The normalized weights along with the linguistic terms assigned to decision maker in reference of their capabilities are shown in Table 26.

Table 26 Weightage of decision makers in the decision-making panel

Step 2::

The linguistic terms to evaluate the potential of feasible alternatives are arranged in Table 2. Table 3 represents the individual decision of all the experts in the panel of decision makers. These opinions are embedded in more organized form in terms of CPFNs to form the individual decision matrices ${\mathfrak {P}}^{(1)},{\mathfrak {P}}^{(2)}$ and ${\mathfrak {P}}^{(3)}$, shown in Tables 4, 5 and 6, respectively. Further, the individual judgments of all the experts are combined to get the more authentic opinion for the construction of ACPFDM, shown in Table 9.

Step 3::

The linguistic terms to rate the creditability of decision criteria are given in Table 7. The individual decision of experts as well as CPF weights of criteria is tabulated in Table 8.

Step 4::

The AWCPFDM, determined by deploying the ACPFDM and weights of the criteria, is organized in Table 10.

Step 5::

The CPF strong concordance set is given by

$$\begin{aligned} {\mathfrak {K}}=\left( \begin{array}{cccc} - &{} \{3, 6\} &{} \{6\} &{} \{3, 6\} \\ \{\} &{} - &{} \{\} &{} \{\} \\ \{3\} &{} \{3, 6, 8\} &{} - &{} \{3, 6\} \\ \{1,4,7\} &{} \{1,7\} &{} \{1,7\} &{} - \end{array}\right) . \end{aligned}$$

The CPF midrange concordance set is given by

$$\begin{aligned} {\mathfrak {K}}^*=\left( \begin{array}{cccc} - &{}\quad \{2, 4\} &{}\quad \{2, 4\} &{}\quad \{2, 8\} \\ \{1, 5, 8\} &{}\quad - &{}\quad \{5\} &{}\quad \{5, 8\} \\ \{1, 5, 8\} &{}\quad \{2\} &{}\quad - &{}\quad \{2, 5, 8\}\\ \{\} &{}\quad \{2, 4\} &{}\quad \{4\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF weak concordance set is given by

$$\begin{aligned} {\mathfrak {K}}^{**}=\left( \begin{array}{cccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{5\} \\ \{\} &{}\quad - &{}\quad \{4, 7\} &{}\quad \{3\} \\ \{\} &{}\quad \{4, 7\} &{}\quad - &{}\quad \{\} \\ \{5\} &{}\quad \{3\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF strong discordance set is given by

$$\begin{aligned} {\mathfrak {L}}=\left( \begin{array}{cccc} - &{}\quad \{\} &{}\quad \{3\} &{}\quad \{1, 4, 7\} \\ \{3, 6\} &{}\quad - &{}\quad \{3, 6, 8\} &{}\quad \{1,7\} \\ \{6\} &{}\quad \{\} &{}\quad - &{}\quad \{1, 7\} \\ \{3, 6\} &{}\quad \{\} &{}\quad \{3, 6\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF midrange discordance set is given by

$$\begin{aligned} {\mathfrak {L}}^*=\left( \begin{array}{cccc} - &{}\quad \{1, 5, 8\} &{}\quad \{1, 5, 8\} &{}\quad \{\} \\ \{2, 4\} &{}\quad - &{}\quad \{2\} &{}\quad \{2, 4\} \\ \{2, 4\} &{}\quad \{5\} &{}\quad - &{}\quad \{4\} \\ \{2, 8\} &{}\quad \{5, 8\} &{}\quad \{2, 5, 8\} &{}\quad - \end{array}\right) . \end{aligned}$$

The CPF weak discordance set is given by

$$\begin{aligned} {\mathfrak {L}}^{**}=\left( \begin{array}{cccc} - &{} \quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

Step 6::

The CPF concordance indices are tabulated in Table 27 to construct the CPFCM in which each index indicates the eminence of an alternative over the other.

Table 27 Complex Pythagorean fuzzy concordance matrix

Step 7::

The CPFDSM ${\mathcal {D}}$ is given by

$$\begin{aligned} {\mathcal {D}}=\left( \begin{array}{cccc} -&{}\quad 0.5063 &{}\quad 0.9411 &{}\quad 1\\ 0.9755 &{}\quad -&{}\quad 1 &{}\quad 0.4247 \\ 0.4180&{}\quad 0.2013&{}\quad - &{}\quad 0.6173 \\ 0.9119&{}\quad 0.7500 &{}\quad 0.7500&{}\quad - \end{array}\right) . \end{aligned}$$

Step 8::

The CPF concordance level can be evaluated as follows:

$$\begin{aligned} \tilde{{\mathcal {C}}}=\, & {} \frac{1}{p(p-1)}\max _{\eta \varrho }C_{\eta \varrho }^{'}\\=\, & {} \frac{1}{(4)(3)}(0.9925e^{i2\pi (0.9915)}, 0.0028e^{i2\pi (0.0039)})\\=\, & {} (0.5436e^{i2\pi (0.5368)}, 0.6127e^{i2\pi (0.6299)}). \end{aligned}$$

The CPF effective concordance matrix $\Phi$ is given by

$$\begin{aligned} \Phi =\left( \begin{array}{cccc} - &{}\quad 1&{}\quad 1&{}\quad 1\\ 1 &{}\quad -&{}\quad 1 &{}\quad 1\\ 1&{}\quad 1 &{}\quad - &{}\quad 1\\ 1&{}\quad 1&{}\quad 1&{}\quad - \end{array}\right) . \end{aligned}$$

Step 9::

The CPF discordance level can be evaluated as follows:

$$\begin{aligned} \tilde{{\mathcal {D}}}=\, & {} \frac{1}{p(p-1)}\sum _{\eta ,\eta \ne \varrho }\sum _{\varrho ,\eta \ne \varrho }D_{\eta \varrho }\\=\, & {} 0.7080. \end{aligned}$$

The CPF effective concordance matrix $\Psi$ is given by

$$\begin{aligned} \Psi =\left( \begin{array}{cccc} - &{}\quad 1&{}\quad 0&{}\quad 0\\ 0 &{}\quad -&{}\quad 0 &{}\quad 1\\ 1&{}\quad 1 &{}\quad - &{}\quad 1\\ 0&{}\quad 0&{}\quad 0&{}\quad - \end{array}\right) . \end{aligned}$$

Step 10::

The aggregated outranking Boolean matrix is given by

$$\begin{aligned} \Lambda =\left( \begin{array}{cccc} - &{}\quad 1&{}\quad 0&{}\quad 0\\ 0 &{}\quad -&{}\quad 0 &{}\quad 1\\ 1&{}\quad 1 &{}\quad - &{}\quad 1\\ 0&{}\quad 0&{}\quad 0&{}\quad - \end{array}\right) . \end{aligned}$$

Step 11::

To observe the pairwise outranking relations, outranking graph ${\mathbb {G}}=({\mathbb {V}},{\mathbb {E}})$ is shown in Fig. 6. After the detailed exploration of outranking graph, the necessary information is organized in Table 28.

Table 28 Analysis of outranking graph

Thus, we conclude that anaerobic single-ditch oxidation is the optimal and most suitable WWTP.

Fig. 6

Outranking graph

6.2 Selection of the best cloud solution for big data projects by Pythagorean fuzzy ELECTRE II method

In this subsection, we solve the numerical example “selection of best cloud solution for big data projects” by employing the using the advantageous procedure of PF-ELECTRE II method, proposed by Akram et al. [25]. For the sake of comparison analysis, the CPFNs have been converted to Pythagorean fuzzy numbers (PFNs) by taking the phase terms equal to zero. The stepwise solution is elaborated in the following steps:

Step 1::

The linguistic terms, used to narrate the relative importance of criteria and decision-making experts, which are expressible in PFNs, are shown in Table 29.

Table 29 Linguistic terms for weightage of experts and criteria

The linguistic terms as well as the normalized weights assigned to the experts in the decision-making panel are organized in Table 30.

Table 30 Weightage of decision makers in the decision-making panel

Step 2::

The linguistic terms and the corresponding PFNs, used to assign the experts preference to alternatives, are tabulated in Table 31.

Table 31 Linguistic terms for the assessment of cloud solutions

The Pythagorean fuzzy decision matrices (PFDMs) ${\mathfrak {P}}^{(1)}$, ${\mathfrak {P}}^{(2)}$ and ${\mathfrak {P}}^{(3)}$ are shown in Tables 32, 33 and 34, respectively.

Table 32 Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(1)}$

Table 33 Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(2)}$

Table 34 Pythagorean fuzzy decision matrix ${\mathfrak {P}}^{(3)}$

The individual opinions are merged with the help of weight vector $\theta =(0.3754, 0.2552, 0.3694)^T$ to construct the aggregated PFDM, shown in Table 35

Table 35 Aggregated Pythagorean fuzzy decision matrix ${\mathfrak {P}}$

Step 3::

All the decision criteria in this MCGDM problem are benefit type criteria, so normalized aggregated PFDM ${\mathfrak {P}}^{'}$ is same as aggregated Pythagorean fuzzy decision matrix, as shown in Table 35.

Step 4::

The opinions of the decision-making experts relative to the importance of criteria, PF-weight and normalized weights of the criteria are embedded in Table 36.

Table 36 Criteria weights

Step 5::

Table 37 comprises the entries of weighted normalized aggregated PFDM $\widetilde{{\mathfrak {P}}}$.

Table 37 Weighted normalized aggregated Pythagorean fuzzy decision matrix $\widetilde{{\mathfrak {P}}}$

Step 6::

The PF strong concordance set is given by

$$\begin{aligned} {\mathfrak {K}}=\left( \begin{array}{ccccc} - &{}\quad \{1,2,3\} &{}\quad \{3\} &{} \quad \{1,2,3\} &{}\quad \{1,2,3\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{2\} &{}\quad \{1,2\} \\ \{1,2\} &{}\quad \{1,2,3\} &{}\quad - &{}\quad \{1,2,3\} &{}\quad \{1,2,3\} \\ \{\} &{}\quad \{1,3\} &{}\quad \{\} &{}\quad - &{}\quad \{1,2,3\}\\ \{\} &{}\quad \{3\} &{}\quad \{\} &{} \quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The PF midrange concordance set is given by

$$\begin{aligned} {\mathfrak {K}}^*=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{} \quad \{\} &{} \quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The PF weak concordance set is given by

$$\begin{aligned} {\mathfrak {K}}^{**}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The PF indifference set is given by

$$\begin{aligned} {\mathfrak {T}}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{} \quad \{\} \\ \{\} &{}\quad \{\} &{} \quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

The PF strong discordance set is given by

$$\begin{aligned} {\mathfrak {L}}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{1,2\} &{}\quad \{\} &{}\quad \{\} \\ \{1,2,3\} &{}\quad - &{} \quad \{1,2,3\} &{}\quad \{1,3\} &{} \quad \{3\} \\ \{3\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{1,2,3\} &{}\quad \{2\} &{}\quad \{1,2,3\} &{}\quad - &{}\quad \{\}\\ \{1,2,3\} &{}\quad \{1,2\} &{}\quad \{1,2,3\} &{}\quad \{1,2,3\} &{}\quad - \end{array}\right) . \end{aligned}$$

The PF midrange discordance set is given by

$$\begin{aligned} {\mathfrak {L}}^*=\left( \begin{array}{ccccc} - &{}\quad \{\} &{} \quad \{\} &{} \quad \{\} &{}\quad \{\} \\ \{\} &{} \quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{} \quad - &{}\quad \{\} &{} \quad \{\} \\ \{\} &{} \quad \{\} &{}\quad \{\} &{}\quad - &{} \quad \{\} \\ \{\} &{} \quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - \end{array}\right) \end{aligned}$$

The PF weak discordance set is given by

$$\begin{aligned} {\mathfrak {L}}^{**}=\left( \begin{array}{ccccc} - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{}\quad - &{}\quad \{\} \\ \{\} &{}\quad \{\} &{}\quad \{\} &{} \quad \{\} &{}\quad - \end{array}\right) . \end{aligned}$$

Step 7::

For the evaluation of the concordance indices, the decision-making panel assigns weights to the PF concordance and indifference sets as follows:

$$\begin{aligned} (\gamma _{{\mathfrak {K}}}, \gamma _{{\mathfrak {K}}^*}, \gamma _{{\mathfrak {K}}^{**}}, \gamma _{{\mathfrak {T}}})=\left(1, \frac{3}{4}, \frac{2}{4}, \frac{1}{4}\right). \end{aligned}$$

The PF concordance matrix ${\mathfrak {C}}$, determined in the light of concordance sets, is given as follows:

$$\begin{aligned} {\mathfrak {C}}=\left( \begin{array}{ccccc} - &{}\quad 1 &{}\quad 0.3168 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad - &{}\quad 0 &{}\quad 0.3380 &{}\quad 0.6832 \\ 0.6832&{}\quad 1&{}\quad - &{}\quad 1 &{}\quad 1 \\ 0 &{}\quad 0.6620 &{}\quad 0 &{}\quad - &{}\quad 1 \\ 0 &{}\quad 0.3168 &{}\quad 0 &{}\quad 0 &{}\quad - \end{array}\right) . \end{aligned}$$

Step 8::

The weights of the PF discordance, assigned by the decision-making experts, are given as follows:

$$\begin{aligned} (\gamma _{{\mathfrak {L}}}, \gamma _{{\mathfrak {L}}^*}, \gamma _{{\mathfrak {L}}^{**}})=\left(1, \frac{3}{4}, \frac{2}{4}\right). \end{aligned}$$

Distance measures between the entries of the weighted normalized aggregated PFDM are arranged in Table 38.

Table 38 Distance measures

The PF discordance matrix is given by

$$\begin{aligned} {\mathcal {D}}=\left( \begin{array}{ccccc} - &{}\quad 0 &{}\quad 1&{}\quad 0 &{}\quad 0\\ 1 &{}\quad - &{}\quad 1 &{}\quad 1 &{}\quad 0.1483 \\ 0.0557 &{}\quad 0 &{}\quad -&{}\quad 0 &{}\quad 0 \\ 1&{}\quad 0.8683 &{}\quad 1&{}\quad -&{}\quad 0 \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 &{}\quad - \end{array}\right) . \end{aligned}$$

Step 9::

The strong and weak outranking relations, established by the comparison of concordances and discordance indices with reference to the concordance levels (ķ$^-$, ķ$^\circ$, ķ$^*$)=(0.6, 0.7, 0.8) and discordance levels ($\c{d}^*$ , $\c{d}^\circ$)= (0.7, 0.8), are organized in Table 39.

Table 39 Outranking relations

Step 10::

To comprehend the forward, reverse and average rankings, the strong and weak outranking graphs along with the reverse strong and weak outranking graphs are shown in Figs. 4 and 5, respectively. These strong and weak outranking graphs are employed in an iterative way to specify the forward and reverse rankings which are helpful to evaluate average ranking. Table 25 comprises the forward, reverse and average rankings of the feasible alternatives. Thus, Google is the best cloud solution to manage the big data project.

6.3 Discussion

• In Sect. 6.1, the numerical example “selection of the most appropriate wastewater treatment strategy” has been solved by the CPF-ELECTRE I method [39]. The results are summarized in Table 40.

  Table 40 Comparison analysis

  Table 40 shows that the result of the proposed method is consistent with the results obtained from existing approaches, which speaks for its authenticity.

• Furthermore, notice that the results in Table 40 highlight the inadequacy of the CPF-ELECTRE I approach, as it is unable to provide a complete ranking of the alternatives. The reason is the existence of an incomparable pair of alternatives. For comparison, we emphasize that the proposed technique always provides us with ranking of the alternatives.

• In Sect. 6.2, the numerical example “selection of the best cloud solution for big data projects” has been solved by the PF-ELECTRE II method [25]. The results are summarized in Table 41.

  Table 41 Comparison analysis

  Table 41 shows that the result of the proposed method is consistent with the results obtained from existing approaches, which speaks for its authenticity.

• The proposed methodology enjoys a vast area of application, and it can be conveniently utilized with IF and PF information in order to meet a fruitful decision, owing to the amenability of CPFSs. We only need to associate them with a phase term equal to zero, as the structure of CPFSs coincides with PFSs in the absence of phase terms, and IFSs can be embedded into the PFS model. Clearly, however, the PF-ELECTRE II method and other existing methodologies for the IF and PF environments are unable to operate in the presence of two-dimensional inexact information.

• The proposed CPF-ELECTRE II method is more privileged as it takes the advantage of five threshold values (including three types of concordance levels and two types of discordance levels) to identify two different outranking relations, namely the strong and weak outranking relation. Besides, the CPF-ELECTRE I method only accounts for two threshold values, including a concordance level and a discordance level, to unfold the outranking relations. In simple words, the theory of ELECTRE II method is competent enough to incorporate the small amount of preference through the weak outranking relation, but the performance of the ELECTRE I procedure is limited in this scenario.

• Furthermore, the presented CSF-ELECTRE II strategy explicitly considers the indifferent sets along with concordance sets, but the CSF-ELECTRE I method does not take account of the indifferent set explicitly in case that two alternatives exhibit the same performance.

7 Effectiveness test

We proceed to check the effectiveness and competency of the CPF-ELECTRE II method by applying three specific tests, as proposed by Wang and Triantaphyllou [43], on the numerical Example 5. Let us recall these three criteria:

Test criterion 1: A MCGDM method is effective if the replacement of a non-optimal alternative by another worse alternative (without changing the weights of the decision criteria) does not effect the ranking position of the best alternative.

Test criterion 2: The ranking results of an effective MCGDM method should always obey transitivity.

Test criterion 3: A MCGDM method is effective if the combined ranking of a smaller subproblem of the original MCGDM problem, when solved by the same technique, coincides with the ranking prescribed by the original undecomposed MCGDM problem.

We now refer to the numerical Example 5 in order to test these features.

Effectiveness test by criterion 1: For this test, replace the alternative ${{\mathcal {HP}}}$ by a worse alternative $\widetilde{{{\mathcal {HP}}}}$ by changing the preferences of the alternative ${{\mathcal {HP}}}$ by the preferences given in Table 42.

Table 42 Preference for the alternative $\widetilde{{{\mathcal {HP}}}}$

For the remaining alternatives, the same data are considered as in Example 5. By applying the proposed CPF-ELECTRE II method, we obtain the following rankings of the potential alternatives:

$$\begin{aligned} {{\mathcal {GO}}}\succ {{\mathcal {AM}}}\succ {{\mathcal {RS}}}\succ {{\mathcal {MA}}}\succ \widetilde{{{\mathcal {HP}}}}. \end{aligned}$$

The keen analysis of the above problem shows that the best alternative is still “Google,” which was also top ranked in the original MCGDM problem.

Effectiveness test by criteria 2 and 3: To test criteria 2 and 3, we split the original MCGDM problem into smaller subproblems, namely ${\mathcal {S}}_{1},{\mathcal {S}}_{2},{\mathcal {S}}_{3}, {\mathcal {S}}_{4},$ by taking into account only three alternatives from the available five choices as follows: ${\mathcal {S}}_{1}=\{{{\mathcal {AM}}}, {{\mathcal {HP}}}, {{\mathcal {GO}}}\}$, ${\mathcal {S}}_{2}=\{{{\mathcal {HP}}}, {{\mathcal {GO}}}, {{\mathcal {RS}}}\}$, ${\mathcal {S}}_{3}=\{{{\mathcal {GO}}}, {{\mathcal {RS}}}, {{\mathcal {MA}}}\}$ and ${\mathcal {S}}_{4}=\{{{\mathcal {RS}}}, {{\mathcal {MA}}}, {{\mathcal {AM}}}\}$. Now, we apply the procedure of CPF-ELECTRE II method to each subproblem by considering the linguistic ratings of alternatives same as in Example 5. The results of all subproblems are compiled in Table 43.

Table 43 Rankings of the subproblems

Table 43 confirms that the combined ranking of all the subproblems is same as the ranking prescribed for the original MCGDM problem. Moreover, it also follows that the transitive law holds true for the ranking of alternatives. Relying on these evidences, we claim that the proposed technique is effective with respect to both criteria.

As the CPF-ELECTRE II method satisfies all the criteria of this renowned effectiveness test, we can declare that it is a competitive, advanced and authentic procedure which can be used for the sake of reliable decision making in two-dimensional scenarios.

8 Merits and limitations of the CPF-ELECTRE II method

8.1 Insights into the proposed methodology

The remarkable insights of the presented methodology are listed as follows:

• The ELECTRE II method, an improvement of the traditional ELECTRE I method, is a distinguished outranking approach that performs aptly both for the choice of a best alternative and the design of a complete ranking of the alternatives. However, within the stream of the literature initiated by fuzzy set theory, it is not fully adequate, as it does not recognize the need for a two-dimensional informational framework.

• In this regard, the PF-ELECTRE II method [25] served as a chief methodology to deal with one dimensional uncertain information. Its aptitude is nevertheless limited, as it does not deal with two-dimensional information. With the materialization of our CPF-ELECTRE II method, this shortcoming of the PF-ELECTRE II method has been overturned.

• Further, there exists another outranking approach in the literature for interval-valued Pythagorean fuzzy linguistic sets that merges the theories of VIKOR and ELECTRE methods [29]. The design of this hybrid approach disregards two-dimensional ambiguous information. Thus, the proposed methodology has an edge over it in the treatment of two-dimensional inconsistent data. Moreover, interval-valued Pythagorean fuzzy linguistic sets employ intervals as membership and non-membership grades that define the level of satisfaction and dissatisfaction, respectively. On the other hand, specific complex-valued membership and non-membership grades are assigned to each object in CPFS, thus enhancing the authenticity and precision of decision results.

• Also, the CPF-ELECTRE I method [39] had incorporated two-dimensional data competently. The scope of this strategy is limited to pinpoint the most efficient alternative. Incomparable pairs of alternatives might exist, thus preventing the production of a complete ranking of the set of alternatives. In contrast, the theory of the CPF-ELECTRE II approach is equipped with an iterative procedure to rank the alternatives.

• These facts convinced us to design a CPF-ELECTRE II strategy which might overcome these fundamental drawbacks. In short, the new CPF-ELECTRE II technique is conceived of as a modern, advanced and general tactic whose merits include the incorporation of two-dimensional information and the production of complete rankings of the set of alternatives.

• Moreover, the successful and favorable analysis of the effectiveness tests leads us to conclude that this strategy is a reliable approach that supposes a productive enhancement of the body of knowledge around the extended FS theories.

8.2 Limitations of the proposed methodology

Besides the numerous benefits of the proposed methodology, it still suffers from limitations and deficiencies, which are elaborated as follows:

• Although the presented variant of ELECTRE II method yields authentic results for the wide space of CPFSs, the procedure is not applicable outside the boundaries of CPFSs, where the square sum of membership and non-membership grades exceeds 1.

• The imperfection of the proposed method is apparent when there exist some neutral opinions along with satisfaction and dissatisfaction degrees in two-dimensional scenarios. The application of the proposed methodology in such situation may lead to an unreasonable decision, as the CPFNs are unable to incorporate the neutral part of human decisions.

9 Conclusion and future directions

This paper has combined two ingredients whose main features ensure a remarkable performance.

On the one hand, owing to their innovative features and broader structure, CPFSs exhibit a precise and well-suited framework for the representation of ambiguous data far beyond the structure of CIFSs and other preceding models. One of the premium and salient characteristics of the prevalent model is its aptitude to model the two-dimensional phenomena competently.

On the other hand, the ELECTRE II method excels among the outranking procedures because it compares the alternative in a systematic way in order to distinguish the criteria representing the concordance and discordance relations among each pair of alternatives. The main incentive behind the advent of the ELECTRE II method was the deficiency of its predecessor, the ELECTRE I approach, regarding the complete ranking of the alternatives. Furthermore, ELECTRE II method derives the final decision by deploying two different types of outranking relations to avoid the loss of any worthy information, but traditional ELECTRE I method is equipped with only one outranking relation.

To achieve the primary goal, CPF-ELECTRE II method, presenting a perfect blend of salient features of CPFS with theoretical background and accuracy of renowned ELECTRE II procedure, has been proposed as an authentic group decision-making strategy to deal two-dimensional imprecise information. In the proposed procedure, three categories of concordance and discordance sets, and an indifferent set have been employed to classify the criteria exhibiting the vantage, inferiority and equality of the alternatives, respectively. Finally, a complete ranking has been obtained by operating on the strong and weak outranking graphs in an iterative way. Moreover, demonstration of the proposed strategy has been provided by means of a case study and an explicatory numerical application and comparative study. An effectiveness test has been carried out to verify the authenticity of the procedure proposed in this paper.

In a nutshell, the proposed methodology retains the essential features of the ELECTRE method while extending its scope. These characteristics justify that it is a consistent and reliable approach for solving MCGDM problems.

Furthermore, we are planning to work on the following related projects in the future:

• A near target is to unfold the application of the proposed methodology in different fields, including medical sciences, engineering, business, chemical and other industries, for managing the two-dimensional data to reach a trustworthy decision.

• We are further planning to expand the literature on outranking approaches by merging the broader structure of CPFS with other outranking approaches based on the ELECTRE method. This should allow us to propose new MCGDM strategies inclusive of CPF-ELECTRE III and CPF-ELECTRE IV methods.

• The restrictions of the CPFSs hinder the applicability of our methodology, and we shall strive to extend the ELECTRE II method under the yet more general framework of complex q-rung orthopair fuzzy sets.

• We are also pondering the benefits of a blend of the ELECTRE methods with the more general environment of complex spherical fuzzy sets, which are able to address the neutral part of two-dimensional obscure information by the dint of neutral membership grade along with the traditional membership grades of PFSs.