Introduction

The system uncertainty or mismatch is considered as one of the most important challenges in the area of nonlinear systems by now. It is to note that the uncertainty can be observed in the system parameters or the external disturbances that apply to the system. One of the popular approaches to deal with the uncertainties is known as the SMC strategy [1]. The SMC has indicated acceptable results since 1970, and comprises two parts: in the first part stable surfaces (sliding surfaces) are designed and in the second part, the control law for the trajectory of the closed-loop system is designed to converge the sliding surfaces in a finite time. The obvious feature of the SMC is the rapid response of the system, which leads to high overshoot. There exist contradictions between these characteristics; therefore, a tradeoff should be considered. The CNF is an efficient and simple approach which is employed to improve transient performance (small overshoot and acceptable settling time) and overcome the contradiction of simultaneous achievement of the mentioned transient performances. The CNF strategy is a relatively new approach that consists of a linear and a nonlinear section. The linear section plays an acceptable role in the closed-loop system stabilization and fast response. The nonlinear part attempts to change the damping ratio and decrease the steady state error according to the definition of the nonlinear function and the settling time response.

Recently, several types of research are established based on the CNF approach for the purpose of improving the performance of the closed-loop system [2,3,4,5]. In [6], the CNF method is applied to synchronize the master/slave nonlinear systems with time-varying delays in chaotic systems with nonlinearities. In [7], for a particular type of vehicle suspension, a CNF with a band and a layer is used to reduce the chattering phenomenon. Then, the proportional-integral controller and intelligent algorithm have been used to improve the error situation and optimization. Combination of the CNF strategy with intelligent algorithms has been illustrated with acceptable results in recent years. In [8,9,10], the nonlinear system of level tank and electromagnetism suspension system has been described by Takagi–Sugeno (T–S) model then the stability of closed-loop system has been proved by the CNF strategy with the parallel distributed compensation and the LMI. In [11], the combination of the CNF with the SMC has been applied to a class of nonlinear systems.

To the best knowledge of recent considerations, a few investigations are applied to the underactuated and the nonlinear systems through the CNF approach. Tracking and regulation problem for practical systems has experienced a sweeping change over 1 decade. This paper proposes the SMC based on CNF approach for tracking control of a nonlinear magnetic ball suspension system and stabilization of an inverted pendulum system. The final object in a magnetic ball suspension system is to move a mass in a space without physical contact by magnetic characteristics. It is widely used in magnetic trains, accelerometers, etc. [12]. These systems have high nonlinearity and instability in the open-loop situation. Therefore, stabilization and tracking of the system are one of the engineering challenges. Several methods have been proposed to design a suitable control for linear and nonlinear types of the magnetic ball suspension system. In addition, investigation of underactuated systems has rapidly expanded in recent years. The underactuated systems are characterized by the fact that they have fewer actuators than the degrees of freedom to be controlled. The inverted pendulum is an example of an underactuated system with two degrees of freedom [13]. In these systems, the pendulum should be kept upright, meanwhile the cart must even be at the center of the line. It should be possible to control the position of the cart and the pendulum angle only with one control signal input. In fact, this model is a single input and two output (SIMO) system. In this paper, the idea of the CNF controller to the inverted pendulum system and nonlinear magnetic ball suspension system has been extended by the SMC and GC algorithm [14,15,16,17]. The cuckoo search (CS) is a global random interactive search algorithm inspired by nature. The basis of this algorithm is the combination of the behavior of a particular species of cuckoo birds with the behavior of flying levy birds [18,19,20,21,22]. The Cuckoo search is applied owing to the fact that it is a simple, fast and efficient algorithm, which uses only a single parameter for search. The elimination of the genetic algorithm difficulty and providing global results are the main advantages of the cuckoo search algorithm; also, it does not trap in local optima and represents the proper coefficients for the sliding surfaces. Finally, it is theoretically proved that the trajectory of the closed-loop system converges to the sliding surface in a finite time manner in these cases.

The rest of the paper is organized as follows: in the next section, the formulation and preliminary concerning the incremental SMC-based CNF strategy is first studied and subsequently the genetic-cuckoo (GC) algorithm has been introduced to minimize tracking errors for the purpose of finding the suitable sliding surface coefficients. In following section, the main results regarding this research including the stability of the closed-loop system for magnetic ball suspension and inverted pendulum systems are proposed. In the section before the conclusion, the simulation results are carried out and finally, in last section, concluding remarks are provided.

The formulation and preliminary

The formulation and preliminary of the CNF in connection with the SMC control strategy with its application to the magnetic ball suspension system tracking and stabilization as well as the inverted pendulum system has been now presented. The SMC is in fact designed to stabilize the closed-loop system and provides the fast system response convergence, high overshoot and long settling time; meanwhile, the main objective of the aforementioned CNF is to reduce the settling time and eliminate the overshoot corresponding to the SMC fast response. Now, the cuckoo search algorithm has been used to set the parameters, to reach the optimum condition. The rapid response is the obvious feature of the SMC, which leads to high overshoot. To solve this problem, the overall proposed controller is proposed as follows by the combination of the SMC and the CNF approach:

$$ \begin{aligned} &U_{T} = u_{\text{SMC}} + u_{\text{CNF}} , \hfill \\ &u_{\text{SMC}} = u_{\text{eq}} + u_{\text{sw}} , \hfill \\ \end{aligned} $$
(1)

where UCNF and Ueq are the CNF controller and equivalent law for state variables, respectively. The equivalent law is not enough to guarantee rapid convergence of state variables to the sliding surface. Usw is the switch control law for the sliding surface which provides a smooth control signal to remove chattering. Figure 1 illustrates the total control structure.

Fig. 1
figure 1

The proposed control strategy

Full size image

The SMC-based CNF approach for the magnetic ball suspension system

This section of the research proposes the SMC-based CNF approach to deal with the nonlinear magnetic ball suspension system. The magnetic systems are floating systems in which the main target of control is the preservation of the ball at the desired point with a certain distance from the core without any physical contact. Figure 2 shows the magnetic suspension system which includes a ferromagnetic ball, a sensor for position detestation of the ball, an actuator and flow controller.

Fig. 2
figure 2

The magnetic ball suspension system

Full size image

Consider the following magnetic ball suspension system:

$$ \begin{aligned}& \begin{array}{ll}& {\mathop {x_{1} }\limits^{ \bullet } = x_{2} } \\ &{\mathop {x_{2} }\limits^{ \bullet } = g - \frac{{(1/L)^{2} u^{2} }}{{m.d(x_{1} )}}} \\ \end{array} \hfill \\ &d(x_{1} ) = a_{4} .x^{4} + a_{3} .x^{3} + a_{2} .x^{2} + a_{1} .x + a_{0} , \hfill \\ \end{aligned} $$
(2)

where \( x \) and \( u \) are the state vector and the control input vector, respectively. d(x1) obtained in the laboratory is a polynomial in x1 which illustrates the ratio between the amount of flow and the position of the ball. m is the mass of the ball and g is the gravitational force, L shows induction. x1 and x2 are the ball position and the velocity of ball, respectively.

The equivalent law control is obtained from the time derivative of the sliding surface. The sliding surface is defined as the following equation in which E, c and s illustrate error, sliding surface coefficient, and sliding surface, respectively.

$$ \begin{aligned} &s = c.E\,,\,\,\,E = x_{d} - x \hfill \\ & s = [\begin{array}{*{20}ll} {c_{1} } & {c_{2} ]\left[ {\begin{array}{*{20}c} {x_{1d} - x_{1} } \\ {x_{2d} - x_{2} } \\ \end{array} } \right] \to s = c_{1} (x_{1d} - x_{1} ) + c_{2} (x_{2d} - x_{2} )} \\ \end{array} \hfill \\ &\mathop s\limits^{ \bullet } = 0 \to c_{1} \mathop {x_{1d} }\limits^{ \bullet } - c_{1} \mathop {x_{1} }\limits^{ \bullet } + c_{2} \mathop {x_{2d} }\limits^{ \bullet } - c_{2} \mathop {x_{2} }\limits^{ \bullet } = 0 \hfill \\ & - c_{1} x_{2} - c_{2} \left(g - \frac{{G^{2} .u^{2} }}{{m.d(x_{1} )}}\right) + c_{1} \mathop {x_{1d} }\limits^{ \bullet } + c_{2} \mathop {x_{2d} }\limits^{ \bullet } = 0 \hfill \\ & u_{\text{eq}} = \frac{{\sqrt {m.d(x_{1} ) \left[g - \frac{{c_{1} }}{{c_{2} }} ( {{x_{1d}}^{ \bullet }} - x_{2} ) - {{x}_{2d}^{ \bullet }} \right]} } }{G}. \hfill \\ \end{aligned} $$
(3)

The equivalent law guarantees rapid convergence of state variables to the sliding surface, but to remain on the sliding surface it is assumed that the usw is defined as follows:

$$ u_{\text{sw}} = g - \frac{{c_{1} }}{{c_{2} }}(x_{2d} - x_{2} ) - \mathop {x_{2d} }\limits^{ \bullet } . $$
(4)

The sliding surface coefficients (ci) can be computed by the GC algorithm. Finally, the total control signal is defined as follows. In addition, the CNF strategy is applied to Eq. (1) in which \( \psi (s) \) is a semi-positive function and arbitrary:

$$ \begin{aligned}& \mathop s\limits^{ \bullet } = - c_{2} k.{\text{sat}}(s/\varphi ) - c_{2} \psi (s).{\text{sat}}(s/\varphi ) \hfill \\& u_{T} = \frac{{\sqrt {m.d(x_{1} )(u_{s} - (k + \psi (s)).{\text{sat}}(s/\varphi )} )}}{G}. \hfill \\ \end{aligned} $$
(5)

It should be noted that the \( \psi (s) \) function increases the degree of freedom of the control rule [23]. Therefore, in this case, the CNF-based SMC approach is realized.

The incremental SMC-based CNF strategy for the inverted pendulum

The inverted pendulum system is known as one of the popular and important laboratory models for teaching underactuated systems, as shown in Fig. 3. The underactuated systems do not have the ability to control a trajectory, in its own operating point, due to different causes. One of the common problems of controlling underactuated systems is the numerical difference between the degrees of freedom of system and number of its actuator. For these systems, designing a conventional sliding mode surface is not appropriate, because the parameters of the sliding mode surface cannot be obtained directly according to the Hurwitz condition [13]. Therefore, the incremental SMC based on CNF has been proposed in this paper.

Fig. 3
figure 3

The inverted pendulum model

Full size image

The general form of an underactuated system is presented as follows:

$$ \begin{aligned} &\dot{x}_{{1}{2n - 1}} = x_{2n} \hfill \\ & \dot{x}_{{1}{2n}} = f_{n} (X) + b_{n} (X)u \hfill \\ \end{aligned} $$
(6)

where \( X = \left[ {x_{1} ,x_{2} , \ldots x_{2n} } \right]^{T} \) is the state variable, u illustrated the system input, and fn and bn are bounded nominal functions. Also, for inverted pendulum, fi and bi have been defined as follows [12]:

$$ \begin{aligned} & f_{1} = \frac{{mL\dot{\theta }^{2} \sin \theta + mg\sin \theta \cos \theta }}{{M + m\sin^{2} \theta }}; \quad b_{1} = \frac{1}{{M + m\sin^{2} \theta }} \hfill \\ &f_{2} = - \frac{{(m + M)g\sin \theta + mL\dot{\theta }^{2} \sin \theta \cos \theta }}{{(M + m\sin^{2} \theta )L}}; \quad b_{2} = - \frac{\cos \theta }{{(M + m\sin^{2} \theta )L}}. \hfill \\ \end{aligned} $$
(7)

The main advantage of the incremental SMC-based CNF approach is to collect all the sliding surfaces on the final surface. In fact, the problems of dividing the system into several subsystems and controlling a high-order SMC and determining the coefficients with the Hurwitz polynomials almost disappear. The first surface is defined as follows:

$$ \begin{aligned} &s_{1} = c_{1} x_{1} + c_{2} x_{2} \quad \dot{s}_{1} = 0 \to \hfill \\ &0 = c_{1} \mathop x\limits^{ \bullet }_{1} + c_{2} \mathop x\limits^{ \bullet }_{2} \to c_{1} x_{2} + c_{2} (f_{1} + b_{1} u) \to \hfill \\ & u_{{{\text{eq}}(1)}} = - \frac{{c_{2} f_{1} + c_{1} x_{2} }}{{c_{2} b_{1} }}. \hfill \\ \end{aligned} $$
(8)

For the state variables of the i-th subsystem, the sliding mode surface is defined as follows:

$$ \begin{aligned} &s_{2} = c_{3} x_{3} + s_{1} , \hfill \\ &s_{i} = c_{i + 1} x_{i + 1} + s_{i - 1} . \hfill \\ \end{aligned} $$
(9)

The total equivalent law control is obtained from \( \dot{s}_{i} = 0 \). The usw with the CNF strategy is defined as follows:

$$ \begin{aligned} & \mathop s\nolimits^{\bullet }_{i} = \sum\limits_{j = 1}^{m} {c_{2j - 1} .x_{2j} + \sum\limits_{j = 1}^{m} {c_{2j} } } (f_{j} + b_{j} u + d_{j} )\,\,;\\&m = \left\{ {\begin{array}{ll} {(i + 1)/2\,\,\,i\,\,{\text{is}}\,\,\,{\text{odd}}} \\ {i/2\,\,\,\,\,\,\,\,\,\,\,i\,\,\,\,{\text{is}}\,\,\,\,{\text{even}}} \\ \end{array} } \right. \hfill \\ & u_{{{\text{sliding}}(i)}} = - \frac{{\sum\nolimits_{j = 1}^{m} {c_{2j - 1} .x_{2j} + \sum\nolimits_{j = 1}^{m} {c_{2j} } } f_{j} }}{{\sum\nolimits_{j = 1}^{m} {c_{2j} b_{j} } }} \hfill \\ & u_{{{\text{sw}}(i)}} = \left\{ {\begin{array}{ll} 0 & {i = 1} \\ {\sum\limits_{j = 1}^{i} {\eta_{j} \text{sgn} (s_{j} )/{\text{den}}(i)} } & {i > 1} \\ \end{array} } \right. \hfill \\ & {\text{den}}(i) = c_{2} b_{1} + \sum\limits_{j = 2}^{m} {(c_{2j} } .(b_{j} + \psi (s_{2j - 1} )).\text{sgn} (s_{2j - 1} )) \hfill \\ \end{aligned} $$
(10)

The nonlinear \( \psi \,(s) \) function in the CNF

The nonlinear \( \psi (s) \) function selection method is expressed in [8, 30,31,32]. Arbitrary choice of \( \psi (s) \) function leads to an acceptable response. The main purpose of adding this nonlinear function to the control low is improving the settling time and reducing the tracking error. This function must be selected in such a way that supplies the following features: when the system state variables are far from the desired value, the reference input from the nonlinear term is diminished; hence the nonlinear effect of the control low is very limited. Also, when the system state variables reach the desired value, the reference input from the nonlinear term enlarges, thus the nonlinear section of the control low will be effective. A nonlinear \( \psi (s) \) function is defined as an exponential function as follows:

$$ \psi (s) = - \beta e^{ - \alpha \parallel s\parallel } , $$
(11)

where \( \alpha \) and \( \beta \) are the two positive parameters designed by GC algorithm. According to the Eq. (11), when s is large, \( \psi (s) \) is small and vice versa.

The optimization

In the control low, there are three constants: C1 and C2 are sliding surface coefficients and k is the coefficient of switching low. The nonlinear \( \psi (s) \) function contains two parameters (\( \alpha \), \( \beta \)). With respect to the stability equation, the limits of these coefficients can be determined; it is very time consuming to set the parameters to reach the optimum condition. Therefore, by defining the cost function in the form of the following equation and using the GC algorithm, the suitable coefficients with the least error rate are introduced [24,25,26]:

$$ j = \sum\limits_{i = 0}^{n} {(x_{i}^{T} rx + } u_{i}^{T} qu), $$
(12)

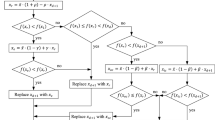
where j, x and u are taken as the cost function, the state variables, and the control input, respectively. Also, r and q are also taken as the identity square matrix. The main characteristic of the genetic algorithm is the simultaneous evaluation of several solutions. The cuckoo search algorithm is a global random interactive search algorithm inspired by nature. The basis of the aforementioned algorithm is the combination of the behavior of a particular species of cuckoo birds with the behavior of flying levy birds. This particular species of cuckoo birds have the ability to select new spawned nests and eliminate their eggs, which increases the probability of the birth of their babies. Therefore, their eggs are placed in the nest of host birds. On the other hand, some host birds are able to fight this parasitic behavior of cuckoo birds and throw out foreign eggs, discover or build new nests in the new place. The process of reproduction of cuckoo birds is described by three simple rules [27,28,29].

  1. 1.

    Each cuckoo bird collects an egg at a time and randomly places it in a selected nest.

  2. 2.

    High-quality nests are selected for re-laying.

  3. 3.

    The number of host nests is constant and a host with a certain probability identifies a foreign egg.

The motivation behind the development of the hybrid CS-GA algorithm is to combine the benefits of both cuckoo search and genetic algorithm. The GC algorithm is summarized as follows:

  1. 1.

    Setting: production number is selected \( t = 1 \). Based on the cuckoo algorithm, the primary population is produced.

  2. 2.

    Population update: as long as the conditions for the moratorium are not established, the new population is being implemented.

The cost function is calculated on the basis of the levy’s flight for each population.

The main results

In this section, the finite time stability for magnetic ball suspension and inverted pendulum system has been proved.

The magnetic ball suspension system stability

For the system stability, the Lyapunov function is defined as \( V = \frac{1}{2}\parallel S\parallel \) which is a positive function. Given the Lyapunov stability, if \( \dot{V} < - \eta ,\,\,\,\eta > 0 \), then it will be established as finite time stability, and each state variable on the sliding surface will move in a finite time to zero [11, 30].

$$ \mathop V\limits^{ \bullet } = \frac{1}{\parallel s\parallel }s.\mathop s\limits^{ \bullet } = \frac{1}{\parallel s\parallel }s.c.E,\,\,\,\,\frac{1}{\parallel s\parallel }s.[c_{1} (\mathop {x_{1d} }\limits^{ \bullet } - \mathop {x_{1} }\limits^{ \bullet } ) + c_{2} (\mathop {x_{2d} }\limits^{ \bullet } - \mathop {x_{2} }\limits^{ \bullet } )] $$
(13)

By applying the magnetic ball suspension system model and the SMC-CNF approach to (13), \( \mathop V\limits^{ \bullet } \) is obtained as follows:

$$ \begin{aligned} &= \frac{1}{\parallel s\parallel }s.\left[c_{1} \mathop {x_{1d} }\limits^{ \bullet } - c_{1} x_{2} + c_{2} \mathop {x_{2d} }\limits^{ \bullet } - c_{2} \left(g - \frac{{G^{2} .u^{2} }}{{m.d(x_{1} )}}\right)\right] \hfill \\ &= s.\left[c_{1} \mathop {x_{1d} }\limits^{ \bullet } - c_{1} x_{2} + c_{2} \mathop {x_{2d} }\limits^{ \bullet } \,\,\,;\,\,\, - c_{2} \left(g - \left(u_{s} - k.{\text{sat}}(s/\varphi\right )\right)\right] \hfill \\ & = \frac{1}{\parallel s\parallel }s.\left[c_{1} \mathop {x_{1d} }\limits^{ \bullet } - c_{1} x_{2} + c_{2} \mathop {x_{2d} }\limits^{ \bullet } - c_{2} g\right.\\ & \quad \left.+ c_{2} \left(g - \frac{{c_{1} }}{{c_{2} }}\left(x_{1d} - x_{2} \right) - \mathop {x_{2d} }\limits^{ \bullet } - k.{\text{sat}}\left(s/\varphi \right) \right) - \psi (s).{\text{sat}}(s/\phi )\right], \hfill \\ \end{aligned} $$

where \( (\mathop {x_{2d} }\limits^{ \bullet } - \mathop {x_{2} }\limits^{ \bullet } ) = - \frac{{c_{1} }}{{c_{2} }}(x_{2d} - x_{2} ) \), if \( \frac{{c_{1} }}{{c_{2} }} > 0 \) then the stability condition will be as follows:

$$ \mathop V\limits^{ \bullet } < - \frac{{c_{2} (k + \psi (s))}}{\parallel s\parallel }s.{\text{sat}}(s/\varphi )). $$
(14)

If \( \varphi \) is large enough to be selected, then \( {\text{sat}}(s/\varphi ) \cong \text{sgn} (s) = \frac{s}{\parallel s\parallel } \) and the following equation is obtained:

$$ \begin{aligned} \mathop V\limits^{ \bullet } < - k.c_{2} .\frac{{s^{2} }}{{\parallel s\parallel^{2} }} = - k.c_{2} - c_{2} .\psi (s) \hfill \\ < - k.c_{2} < 0. \hfill \\ \end{aligned} $$
(15)

Given that the time derivative V is less than a constant negative value, V tends to be asymptotically zero. To calculate the T convergence time to zero, it is sufficient to integrate from Eq. (15).

$$ \int_{0}^{T} {\mathop V\limits^{ \bullet } (t){\text{d}}t} \le - \int_{0}^{T} {k.c_{2} {\text{d}}t \to V(T) - V(0) \le - k.c_{2} .T} $$
(16)

As a result of \( V(T) = 0 \):

$$ T \le \frac{V(0)}{{c_{2} .k}}. $$
(17)

Equation (17) will be established, which means that \( \dot{V} \) has a negative value and ensures that the system is stable for a finite time.

The stability analysis

To analyze the stability of underactuated systems, the Lyapunov function is considered as follows:

$$ \begin{aligned} & V_{2n - 1} = \frac{1}{{2\parallel s_{2n - 1} \parallel }}s^{2}_{2n - 1} \hfill \\ & \to \mathop V\limits^{ \bullet }_{2n - 1} = \frac{{s_{{_{2n - 1} }} .\dot{s}_{{_{2n - 1} }} }}{{\parallel s_{2n - 1} \parallel }} = \frac{{s_{{_{2n - 1} }} }}{{\parallel s_{2n - 1} \parallel }}(c_{{_{2n - 1} }} \dot{x}_{2n} + {\dot{s}_{2n - 2}} ) \hfill \\& = \frac{{s_{2n - 1} }}{{\parallel s_{2n - 1} \parallel }}\left( {c_{2n - 1} [f_{n} + b_{n} u] + c_{2n - 2} x_{2n} + } \right.c_{2n - 3} [f_{n - 1} + b_{n - 1} u] + \ldots + c_{1} x_{2} + f_{1} + b_{1} u]\left. {} \right) \hfill \\ &= \frac{{s_{2n - 1} }}{{\parallel s_{2n - 1} \parallel }}\left\{ \sum\limits_{i = 2}^{n} {(c_{2i - 1} f_{i} + c_{2i - 2} x_{2i} )} + (f_{1} + c_{1} x_{2} ) + \left[\sum\limits_{i = 2}^{n} {(c_{2i - 1} b_{i} )} + b_{1} \right]u\right\} \hfill \\ \end{aligned} $$
(18)

By applying the total controller in Eq. (1), the relationships will be as follows:

$$ \begin{aligned} \mathop V\limits^{ \bullet }_{2n - 1} &= \frac{{s_{{_{2n - 1} }} }}{{\parallel s_{2n - 1} \parallel }}\Bigg\{ \sum\limits_{i = 2}^{n} {(c_{2i - 1} f_{i} + c_{2i - 2} x_{2i} )} + (f_{1} + c_{1} x_{2} ) + \Bigg[\sum\limits_{i = 2}^{n} {(c_{2i - 1} b_{i} )} + b_{1} \Bigg](u_{eq} + u_{sw} \Bigg\} \hfill \\ &= \frac{{s_{{_{2n - 1} }} }}{{\parallel s_{2n - 1} \parallel }}\Bigg\{ \sum\limits_{i = 2}^{n} {(c_{2i - 1} f_{i} + c_{2i - 2} x_{2i} )} + (f_{1} + c_{1} x_{2} ) + \Bigg[\sum\limits_{i = 2}^{n} {(c_{2i - 1} b_{i} ) + b_{1} \Bigg]u_{eq} } + \Bigg [\sum\limits_{i = 2}^{n} {(c_{2i - 1} b_{2i} ) + b_{1}\Bigg ]u_{sw} } \Bigg\} . \hfill \\ \end{aligned} $$
(19)

Considering the values of usw and \( u_{sliding} \) assumptions \( \eta ,k > 0 \) then:

$$\begin{aligned} \mathop V\limits^{ \bullet }_{2n - 1} &= - \frac{{s_{{_{2n - 1} }} }}{{\parallel s_{2n - 1} \parallel }}.(\eta + \psi (s_{sj - 1} )).{\text{sgn}}(s_{2n - 1} ) - k.s^{2}_{2n - 1} \\ & \quad = - \eta - \psi (s_{sj - 1} ) - k.s^{2}_{2n - 1} \le - \eta . \end{aligned}$$
(20)

As a result, the closed-loop system will have finite time stability.

The simulation results

In this section, the examples illustrate the advantages of the proposed control strategy. In the first example, the SMC based on CNF is applied to the magnetic ball suspension system. In the second example, the inverted pendulum is given and the proposed controller designed in Eq. (10) is employed to stabilize the closed-loop system.

The magnetic ball suspension system parameters are introduced in Table 1. By MATLAB simulation, the state variables are illustrated in Figs. 4, 5, 6, and 7; Fig. 4 shows the tracking path, as \( x_{d1} = 0.06 + 0.015{ \sin }(0.7\pi t) \) for the arbitrary position of the track. d−(x1) coefficients and correlation are obtained experimentally as Table 2.

Table 1 The constant parameters in the magnetic ball suspension system
Full size table
Fig. 4
figure 4

Tracking the desired path with the laboratory coefficients (m = 1.65)

Full size image
Fig. 5
figure 5

The xd tracking with optimal coefficients (m = 1.65 gr)

Full size image
Fig. 6
figure 6

The xd tracking with the disturbance (m = 16.5 gr)

Full size image
Fig. 7
figure 7

The control signal

Full size image
Table 2 Relative displacement and required current
Full size table
$$\begin{aligned} &f(i,x_{1} ) = \frac{{i^{2} }}{{d(x_{1} )}}, \end{aligned}$$
$$ \begin{aligned} & \begin{array}{ll} &{\begin{array}{ll}& {\mathop {x_{1} }\limits^{ \bullet } = x_{2} } \\ & {\mathop {x_{2} }\limits^{ \bullet } = g - \frac{{(1/L)^{2} u^{2} }}{{m.d(x_{1} )}}} \\ \end{array} } \\ & {d(x_{1} ) = a_{4} .x^{4} + a_{3} .x^{3} + a_{2} .x^{2} + a_{1} .x + a_{0} } \\ \end{array} \end{aligned}$$
$$\begin{aligned} & \begin{array}{ll} {a_{4} = - 176896.25\begin{array}{ll} {} & {a_{3} = 84793.69\begin{array}{ll} {} & {} \\ \end{array} } \\ \end{array} } \\ & {a_{2} = 7685.55\begin{array}{ll} {} & {a_{1} = 284.79\begin{array}{ll} {} & {a_{0} = - 3.7} \\ \end{array} } \\ \end{array} } \\ \end{array} \end{aligned}$$
$$ u_{T} = \frac{{\sqrt {m.d(x_{1} )(u_{s} - (k + \psi (s)).sat(s/\varphi )} )}}{G}, $$
$$ s = c_{1} (x_{1d} - x_{1} ) + c_{2} (x_{2d} - x_{2} ), $$
$$ \psi (s) = - \beta e^{ - \alpha \parallel s\parallel } . $$

In Fig. 5, using the GC algorithm, the most suitable compromise between the amount of input to the coil and the displacement of the ball is investigated, which indicates that the tracking error has been reduced significantly.

$$ \begin{array}{ll} &{a_{4} = - 1225.25\begin{array}{ll} {} & {a_{3} = 3150} \\ \end{array} } \\ & {a_{2} = 7720\begin{array}{ll} {} & {a_{1} = 522\begin{array}{ll} {} & {a_{0} = - 4.2} \\ \end{array} } \\ \end{array} } \\ \end{array} $$

Figure 6 shows that the SMC-CNF control is not sensitive to the system parameters changing, because there is no significant change in the system response even with a tenfold mass.

Figure 7 shows the control signal input, which is smooth.

Assuming the initial conditions below and determining the coefficients by the GC algorithm, the simulation results are shown in Figs. 8 through 11 for the inverted pendulum. The inverted pendulum system parameters are introduced in Table 3.

Fig. 8
figure 8

The sliding surfaces

Full size image
Table 3 The constant parameters in the inverted pendulum system
Full size table
$$\begin{aligned} x_{1} & = 0,\;x_{2} = 0,\;x_{3} = pi{\text{/}}3,\;x_{4} = 0 \\ c & = {\text{ }}\left[ {\begin{array}{*{20}l} { - 0.3643} & { - 0.7448} & {3.9157} & {0.7355} & { - 0.4195} & {0.0412} & {0.7938} & {5.1554} \\ \end{array} } \right] \\ s_{1} & = c_{1} x_{1} + c_{2} x_{2} \\ s_{2} & = c_{3} x_{3} + s_{1} \\ s_{3} & = c_{4} x_{4} + s_{2} \\ \end{aligned}$$

As can be seen, the sliding surfaces converge to the zero very fast.

By applying UT controller in Eq. (1) to the model of the inverted pendulum, Eqs. (6) and (7) the cart and the pendulum position are obtained. As it can be seen, the SMC strategy stabilizes the closed-loop system and provides the high overshoot and long settling time; meanwhile, using the CNF-SMC the settling time has been reduced and the overshoot has been eliminated.

The closed-loop inverted pendulum system state variables are illustrated in Figs. 9 and 10; the proposed approach can effectively stabilize and improve the closed-loop system and the transient performance. The overshoot and settling time of the closed-loop system states in Table 4 reveal that the proposed approach provides favorable transient performance. Finally, Fig. 11 illustrates the control signal. Comparison of the results indicates that the control effort of the proposed approach is smaller and smoother than the SMC and there is no chattering in the proposed approach.

Fig. 9
figure 9

The cart position with the SMC-CNF and the GS algorithm

Full size image
Fig. 10
figure 10

The pendulum position with the SMC-CNF and the GS algorithm

Full size image
Table 4 Transient response performance
Full size table
Fig. 11
figure 11

The control signal

Full size image

Conclusion

In the investigation presented here, a kind of incremental SMC-based CNF strategy is newly designed considering the magnetic ball suspension and the inverted pendulum systems to be handled. The selection of all the tuning parameters regarding the aforementioned SMC-based CNF strategy is turned into a minimization problem and solved automatically by the GC algorithm. It should be noted that the Lyapunov stability theory is used to prove the finite time closed-loop stability of the magnetic ball suspension system and also the inverted pendulum system. By the proposed control approach, the convergence of the state variables to the sliding surfaces and the equilibrium points in the finite time is guaranteed. The main advantage of the proposed approach is that the controller does not show any sensitivity to the system parameters changing, such as ball mass and the sensors inaccuracy in determining the ball position for the tracking. The simulation results illustrate that adding the CNF approach improves the transient performance of the closed-loop system. Also, by applying the incremental SMC-based CNF strategy to the inverted pendulum system, the states variables converge to their equilibrium point with acceptable overshoot and its settling time. Using other control techniques such as the fuzzy-based solutions or in general, the intelligent control approaches instead of the SMC can be a new approach to the nonlinear systems via the CNF. Applying the CNF strategy to the singular systems and also the hybrid systems is the other suggestion in this area for the future researches.