Introduction

Nowadays, with regard to improvement in use of space capabilities, the process to design spatial robots regarding removal of human parameter keeps expanding, under which is expected that robotic systems play a major role in the future of space applications [1]. Therefore, the design of dynamic models from space robots has been increasingly drawn into attention [2,3,4].

Long time has passed from lifetime of fixed-wing vehicles that such vehicles due to optimization of energy consumption have been widely drawn into attention, yet they have constantly suffered from the lack of power of maneuverability, at the affairs pertaining to unmanned vehicles. For instance, small air flasks can easily be controlled so far as there do not exist wind and turbulence. Under this state, natural lifting force causes moving aerial vehicle, yet causes decreasing its power of maneuverability. Helicopters have numerous advantages than fixed-wing vehicles and balloons especially at control and the reason for this can be known in their ability in take off and land at small area of space as well as high power of maneuverability. In addition, static flight (hover) has been regarded as one of the capabilities of aerial vehicles, mentioned top of aims. On the other hand, these advantages lead to difficulty in control of helicopters for which different sensors as well as rapid processing boards are required. Unmanned aerial robots have been regarded as efficient and practical solutions to cope with this challenge in helicopters. Building unmanned aerial robots include synergic combination at different stages including design, selection of sensors and development of controllers. All the stages are fulfilled in an integrative and parallel way, so that, each one affects another one. To build autonomous unmanned aerial robots, high information on position and direction is required. Such information is provided through self-stabilizing sensors such as inertial navigation system (INS). Global positioning system (GPS) and/or sensors such as sound navigation and ranging (SONAR) [5]. With regard to increasing trend of research at the area of unmanned vehicles especially quadrotors, the present research will intend to examine, simulate and control aerial robots [6].

In recent years, aerial robots or unmanned aerial vehicles (UAVs) regarding removal of human operator have been drawn into attention as the aerial instruments with wide applications and capabilities [1]. With regard to high potential of aerial instruments for flying at points that the manned aerial vehicles fail to access them, investigation, analysis and control of such system have been transformed to an important issue. Nowadays, UAVs develop an important part of scientific studies pertaining to military industries. Unmanned aerial vehicles compared to the systems that are conducted by man’s intervention can have a high protective role in human’s life at hazardous environments.

Autonomous aerial vehicles have been witnessed with numerous commercial applications. Recent advancements at areas of energy storage with high density, integrated miniature operators. Micro-electromechanical systems (MEMS), construction of miniature unmanned aerial robots has come to realize. This has opened the way towards complicated applications at military and non-military markets. Currently, military applications propose the leading part of UAVs with huge increasing in industrial sector. With regard to growing increase of research at the area of UAVs especially quadrotor, the present research seeks to examine, simulate and control these UAVs [5].

Quadrotor has been mentioned as a useful tool for researchers at universities to engage in examining new ideas at different areas including flight control theory, guidance and navigation, real-time and robotic systems. In recent years, most of universities have conducted research on complex aerial maneuvers through quadrotors for which different controllers have been designed. Since quadrotors are so maneuverable, they can be beneficial under any environmental conditions quadrotors with the flight ability in an independent way can assist for removal of required manpower at hazardous situations, whereby this ability represents the main reason for increasing research on these systems in recent years [6].

With regard to significance of topic of this research, to date numerous activities have been conducted at the area of optimization of UAVs via nonlinear controllers, so that there are numerous ways to control an UAVs [4, 7, 8]. Use of fuzzy logic regarding capabilities of this method in controlling nonlinear systems is one way to control UAVs. For instance, in long lost past, a variety of research to improve membership functions in fuzzy controllers which had been used in UAVs have been conducted via genetic algorithm, that also this theory has been used to detect status of system, indicating such a theory as a suitable method to detect status of aerial robot. An adaptive neuro-fuzzy inference system to control position of an aerial robot at three-dimensional space has been designed in reference [9], and a new idea which has integrated advantages of neural network method with advantages of fuzzy logic to control an aerial robot has been proposed in [10].

To date, numerous studies have been conducted at the area of control of quadrotor unmanned aerial robots. According to reference [11], sliding-mode control approach has been used to regulate the force at quadrotor engines. This is in a way that a sliding surface entitled as the suitable return for force at four engines has been defined, aiming at sliding force to this sliding surface so far as the force at each of these engines removes from this return. These controllers due to sustainability of system at nonlinear models have been mentioned as a suitable item for control. Yet, the phenomenon of chattering has been found as a defect in these controllers for which no solution has been represented to cope with it.

In [12, 13], an output feedback adaptive fuzzy model following controller is proposed for a nonlinear and uncertain airplane model. The unknown nonlinear functions are approximated by fuzzy systems based on universal approximation theorem, where both the premise and the consequent parts of the fuzzy rules are tuned with adaptive schemes. Thus, prior knowledge and the number of fuzzy rules for designing fuzzy systems are decreased effectively. Also, to cope with fuzzy approximation error and external disturbances an adaptive discontinuous structure is used to make the controller more robust, as long as due to adaptive mechanism attenuates chattering effectively. All the adaptive gains are derived via Lyapunov approach thus asymptotic stability of the closed-loop system is guaranteed.

Type-2 fuzzy neural networks have a high ability to detect and control nonlinear systems and change systems over time as well as systems with uncertainties. In [14], the method of designing type-2 fuzzy neural adaptive (inverse) controller has been studied in order to control on-line an example of a nonlinear dynamical system of flying robot. In this reference, the class structure of interval type-2 fuzzy neural networks of T-S model has been displayed first. It has seven layers that fuzzy operation is carried out by the first two layers, which contains type-2 fuzzy nerves with uncertainty in the center of the Gaussian member functions. The third layer is the layer of rules and in the fourth layer, the operation of reducing degree is performed by matching nodes. Layers of fifth, sixth and seventh include the resulting layer, layers of calculating the center of gravity and layers of output, respectively. To teach network, decreasing gradient algorithm was used with adaptive training rate. Finally, in the section of the simulation of adaptive inverse on-line control with interval type-2 fuzzy neural network of model T-S and adaptive neuro-fuzzy inference system (ANFIS) for nonlinear dynamic system, a robot sample drone with certain parameters and with uncertain parameters were compared. The results of simulation show the effectiveness of the proposed method in this reference.

In [15], type-2 fuzzy neural network with fuzzy clustering method is used to identify structures and update the parameters of the condition and the gradient algorithm is used to update the parameters of the result. Also in this reference, it has been indicated that the method of fuzzy clustering is not appropriate for identifying and on-line controlling. In recent years, various methods for training type-2 fuzzy neural networks have been suggested, such as genetic algorithm [16] and PSO [17]. With the expansion of research in the field of type-2 fuzzy systems, these systems have found wide applications, including the prediction of time series [18], linear motor control [19], sliding-mode control [20] and control of robots [21].

For the first time Han et al. [22] have proposed an adaptive fuzzy-based control of sliding mode, which estimates input and output parameters of member functions by means of matching rules that are extracted from a Lyapunov function. But in their approach, asymptotic stability is not guaranteed and it results in an error of permanent state. Recently, Lin and Hsu [23] designed a new method of controlling adaptive fuzzy sliding mode for controlling a servo motor in a manner that estimates the parameters of member functions of input and output by means of matching rules that are extracted from a Lyapunov function and they do not need to be specified by a designer. Furthermore, at the expense of having discontinuous control, they have asymptotic stability. But the method is only applicable to a particular motor system. Peng and Shi [24] presented a new and direct method of controlling adaptive fuzzy of sliding mode for a class of flying robots that estimates the parameters of member functions in input and output by means of matching rules that are extracted from a Lyapunov function. Therein a proportional-integral adaptive controller is used to increase the consistency that ensures asymptotic stability.

In this investigation, with regard to an overview on the research in the area of modeling of the UAVs via Newton/Euler equation, a model has been proposed for quadrotor robot with 6 degrees of freedom. In following, the capability of fuzzy-based sliding-mode control approach, optimized by the genetic algorithm has been used to assure the sustainability of system.

This research has organized in line with five sections, while after introducing the key materials, in the second section, based on the equation of 6 degrees of freedom through Newton–Euler equation of rigid body, a nonlinear model for the drone robot of quadrotor UAV is extracted. It is to note that in the third section, the hybrid fuzzy-based sliding-mode control approach is realized to address the weaknesses of the structure of the traditional sliding-mode control approach. In fact, there is the idea of combining it with the genetic algorithms and also fuzzy-based approach to be newly proposed. Subsequently, in the fourth section, the results of the simulations regarding the hybrid fuzzy-based sliding-mode control approach, optimized by the above-referenced genetic algorithm on UAV quadrotor model have been described and finally the last section is dedicated to conclusions.

The representation of a nonlinear dynamic model for quadrotor UAVs

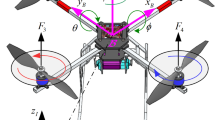
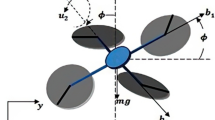
It should be first noted that quadrotor uses four separate engines to create driving forces and movement, at three-dimensional space, in general. Figure 1 represents a general schematic of a quadrotor.

Fig. 1
figure 1

A schematic of quadrotor [25]

Full size image

Height and angle for setting robot in space are controlled through regulating speed of circulation at each of engines. Propellers at backward and forward rotate counterclockwise, yet the propellers at left and right sides rotate clockwise. This way for rotating blades meets the need to tail rotor. Four basic movements based on speed at rotation of engines are considered for a quadrotor. Movements roll, pitch, yaw and movement alongside axis z or height. To move alongside axis z, speed of four engines must be equal with each other, yet speed of the left engine is greater than the specified extent and speed of right engine is under the specified extent in movement roll, yet rest of engines have fixed speed, causing rotation around axis x, at movement pitch which rotates around axis y, the backward engine rotates with higher speed and the forward engine rotates with lower speed and rest of two engines rotate at fixed speed. Ultimately, at movement yaw, the left and right engines will rotate at lower speed and the backward and forward engines will rotate at higher speed at counterclockwise rotation by an angle \(\theta \) about the z-axis. At all basic movements, all the forces raised through engines must be equal to the force at first state which is movement alongside z-axis [26, 27].

Quadrotor is a flying vehicle with rotary wings. This flying aircraft receives various physical effects from the fields of aerodynamics and mechanics; therefore, the quadrotor model should consider all the important effects, including gyroscopic effects that enter it. This model can be evaluated and analyzed based on kinematic and dynamic relationships. Quadrotors contain 6 degrees of freedom follows [28]:

  1. 1.

    x: Quadrotor’s movement in the direction of the axis x (surge);

  2. 2.

    y: Quadrotor’s movement in the direction of the axis y (sway);

  3. 3.

    z: Quadrotor’s movement in the direction of the axis z (heave);

  4. 4.

    \(\phi \): Quadrotor’s rotation around the axis x (roll), where \(\phi \in \left( {-\frac{\pi }{2}\cdot \frac{\pi }{2}}\right) \);

  5. 5.

    \(\theta \): Quadrotor’s rotation around the axis y (pitch), where \(\theta \in \left( {-\frac{\pi }{2}\cdot \frac{\pi }{2}}\right) \);

  6. 6.

    \(\Psi \): Quadrotor’s rotation around the axis z (yaw), where \(\Psi \in ({-\pi \cdot \pi })\).

For modeling, it is required to extract the equation with 6 degrees of freedom pertaining to the rigid body among Newton–Euler equations. The model derived from the flying robot quadrotor is as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} {\ddot{x} = \frac{1}{m}(\cos \phi \,\sin \theta \,\cos \psi + \sin \phi \sin \psi ){u_1} - \frac{{{K_1}\dot{x}}}{m}\,}\\ {\ddot{y} = \frac{1}{m}(\cos \phi \,\sin \theta \,\sin \psi - \sin \phi \cos \psi ){u_1} - \frac{{{K_2}\dot{y}}}{m}\,}\\ {\ddot{z} = \frac{1}{m}(\cos \phi \cos \theta ){u_1} - g - \frac{{{K_3}\dot{z}}}{{m}}}\\ {\ddot{\phi }= \dot{\theta }\dot{\psi }\left( {\frac{{{I_y} - {I_z}}}{{{I_x}}}} \right) + \frac{{{J_r}}}{{{I_x}}}\dot{\theta }{\Omega _r} + \frac{l}{{{I_x}}}{u_2} - \frac{{{K_4}l}}{{{I_x}}}\dot{\phi }}\\ {\ddot{\theta }= \dot{\psi }\dot{\phi }\left( {\frac{{{I_z} - {I_x}}}{{{I_y}}}} \right) - \frac{{{J_r}}}{{{I_y}}}\dot{\phi }{\Omega _r} + \frac{l}{{{I_y}}}{u_3} - \frac{{{K_5}l}}{{{I_y}}}\dot{\theta }}\\ {\ddot{\psi }= \dot{\phi }\dot{\theta }\left( {\frac{{{I_x} - {I_y}}}{{{I_z}}}} \right) + \frac{1}{{{I_z}}}{u_4} - \frac{{{K_6}}}{{{I_z}}}\dot{\psi }}. \end{array}\right. \end{aligned}$$
(1)

In model (1), \(\Omega _r \) has been defined as \(\Omega _r =\Omega _1 -\Omega _2 +\Omega _3 -\Omega _4 \), where:

  • \(\Omega _1\) represents the impeller speed at the front part of the quadrotor;

  • \(\Omega _2 \) represents the impeller speed on left side of the quadrotor;

  • \(\Omega _3 \) represents the impeller speed at the back of the quadrotor;

  • \(\Omega _4 \) represents the impeller speed on left side of the quadrotor.

In model (1), \(u_1\) represents the total propulsive force in the body of quadrotor in parallel with axes z. \(u_2\) and \(u_3\) which, respectively, show such inputs as roll, pitch and \(u_4\) yawing moment and are defined as the following relations:

$$\begin{aligned}&u_1 =( {F_1 +F_2 +F_3 +F_4 })\nonumber \\&u_2 =( {-F_2 +F_4 } )\nonumber \\&u_3 =( {-F_1 +F_3 } )\nonumber \\&u_4 ={d( {-F_1 +F_2 +F_3 +F_4 } )}/b, \end{aligned}$$
(2)

where \(F_i=b\Omega _i^{2}\) represents the generated thrust on part of the four rotors existing in the structure of the quadrotor robot and are considered as real control input signals, which are applied to the system dynamics model. Other parameters of the model (1) and relation (2) are as follows:

  • m: total mass of the quadrotor;

  • \(K_{i}\): constant coefficients of the drag;

  • g: gravity acceleration of the ground;

  • l: distance between the center of each rotor from the center of quadrotor mass;

  • \(I_{x},I_{y}\) and \(I_{z}\): the quadrotor’s moment of inertia;

  • \(J_{r}\): moment of inertia belonging to the impellers of each rotor;

  • b: the quadrotor’s ascending coefficient;

  • d: coefficient of drag for moment sampling.

In the simulations, for fixed values of the parameters that exist in the quadrotor dynamic equations, the values of a sample quadrotor are used in [28] and are all tabulated in Table 1.

Now, in this research, the first step is to model the behavior of the robot quadrotor and validate dynamic equations of the system for open-loop. In Fig. 2, the response time of the state variables regarding the robot system without the presence of controller is shown.

By a close look at Fig. 2, it can be concluded that the state variables of the present robot system are unstable and its open-loop strategy is incapable of meeting the key needs of the designer in case of the system.

Table 1 The parameter’s values regarding the UAV model
Full size table
Fig. 2
figure 2

The response time of the state variables regarding the quadrotor system for open-loop simulation

Full size image

The hybrid fuzzy-based sliding-mode control approach realization

At first, to design the sliding-mode control approach, the UAV robot in (1) is divided into two subsystems as follows:

$$\begin{aligned} \left[ {\begin{array}{l} {\ddot{z}}\\ {\ddot{\psi }} \end{array}} \right] = \left[ {\begin{array}{c} {\frac{{{u_1}\cos \phi \cos \theta }}{m} - g}\\ {\frac{1}{{{I_z}}}{u_4}} \end{array}} \right] + \left[ {\begin{array}{c} { - \frac{{{K_3}\dot{z}}}{m}}\\ {\dot{\phi }\dot{\theta }\frac{{{I_x} - {I_y}}}{{{I_z}}} - \frac{{{K_6}}}{{{I_z}}}\dot{\psi }} \end{array}} \right] \end{aligned}$$
(3)
$$\begin{aligned} \left\{ {\begin{array}{l} { {\left[ {\begin{array}{l} {\ddot{x}}\\ {\ddot{y}} \end{array}} \right] = \frac{{{u_1}}}{m}\left[ {\begin{array}{ll} {\cos \psi }&{}{\sin \psi }\\ {\sin \psi }&{}{ - \cos \psi } \end{array}} \right] \left[ {\begin{array}{c} {\cos \phi \sin \theta }\\ {\sin \phi } \end{array}} \right] } + \left[ {\begin{array}{l} { - \frac{{{K_1}\dot{x}}}{m}}\\ { - \frac{{{K_2}\dot{y}}}{m}} \end{array}} \right] }\\ {\left[ {\begin{array}{l} {\ddot{\phi }}\\ {\ddot{\theta }} \end{array}} \right] = \left[ {\begin{array}{ll} {\frac{l}{{{I_x}}}}&{}0\\ 0&{}{\frac{l}{{{I_y}}}} \end{array}} \right] \left[ {\begin{array}{l} {{u_2}}\\ {{u_3}} \end{array}} \right] + \left[ {\begin{array}{ll} {\dot{\theta }\dot{\psi }\frac{{{I_y} - {I_z}}}{{{I_x}}}}&{}{ - \frac{{{K_4}l}}{{{I_x}}}\dot{\phi }}\\ {\dot{\psi }\dot{\phi }\frac{{{I_z} - {I_x}}}{{{I_y}}}}&{}{ - \frac{{{K_5}l}}{{{I_y}}}\dot{\theta }} \end{array}} \right] }. \end{array}} \right. \end{aligned}$$
(4)

The first step in implementing the sliding-mode control approach is the design of this controller for subsystem (3). To this end, new variables are defined as follows:

$$\begin{aligned} \begin{array}{l} {\left\{ {\begin{array}{l} {{x_1} = z}\\ {{x_3} = \psi } \end{array} \Rightarrow {X_1}} \right. = \left[ { \begin{array}{l} {{x_1}}\\ {{x_3}} \end{array}} \right] }\\ {\left\{ { \begin{array}{l} {{x_2} = \dot{z}}\\ {{x_4} = \dot{\psi }} \end{array} \Rightarrow {X_2}} \right. = \left[ { \begin{array}{l} {{x_2}}\\ {{x_4}} \end{array}} \right] } \end{array} \Rightarrow \left\{ { \begin{array}{l} {{{\dot{X}}_1} = {X_2}}\\ {{{\dot{X}}_2} = {f_1} + {g_1}{U_1} + {d_1}}, \end{array}} \right. \nonumber \\ \end{aligned}$$
(5)

where

$$\begin{aligned} {U_1} = \left[ { \begin{array}{l} {{u_1}}\\ {{u_4}} \end{array}} \right] . \end{aligned}$$
(6)

Now, the sliding surfaces are defined as follows in order to follow the desired paths by the system states:

$$\begin{aligned}&{{s_1} = {z_d} - z}\nonumber \\&{s_2} = {{\dot{s}}_1} + {\omega _1}{s_1} + {\xi _1} {s_1}^{m^{\prime }_1/n^{\prime }_1}\nonumber \\&{{s_3} = {\psi _d} - \psi }\nonumber \\&{{s_4} = {{\dot{s}}_3} + {\omega _2}{s_3} + {\xi _2}{s_3}^{m^{\prime }_2/n^{\prime }_2}}. \end{aligned}$$
(7)
Table 2 The parameter’s values regarding the realized sliding-mode control
Full size table

In relation (7), \(m_1^{{\prime }},n_1^{\prime },m_2^{{\prime }}\) and \(n_2^{{\prime }}\) are positive odd integers wherein the relations \(m_1^{{\prime }}<n_1^{{\prime }}\) and \(m_2^{{\prime }}<n_2^{{\prime }}\) hold true. Consideration of sliding surfaces as (7) is focused on the time limit for the detection of the states, which is the main objective in UAV quadrotor systems. In the following, the control rules pertinent to \(u_1\) and \(u_4\) are calculated using the equivalent control method in sliding mode (i.e., \({\dot{s}}=0)\) as follows:

$$\begin{aligned} {u_1}= & {} \frac{m}{{\cos \phi \cos \theta }}\left[ {{\ddot{z}}_d} + g + {\omega _1}{{\dot{s}}_1}+{\xi _1}\frac{m^{\prime }_1}{n^{\prime }_1}{s_1}^{\left( {{m^{\prime }_1} - {n^{\prime }_1}} \right) /{n^{\prime }_1}}{{\dot{s}}_1}\right. \nonumber \\&\left. +\,{\varepsilon _1}{s_2} + {\eta _1}{s_2}^{{m_1}/{n_1}} \phantom {\frac{m^{\prime }_1}{n^{\prime }_1}}\right] \nonumber \\ {u_4}= & {} {I_z}\left[ {{\ddot{\psi }}_d} + {\omega _2}{{\dot{s}}_3} + {\xi _2}\frac{m^{\prime }_2}{n^{\prime }_2}{s_3}^{\left( {{m^{\prime }_2} - {n^{\prime }_2}} \right) /{n^{\prime }_2}}{{\dot{s}}_3} \right. \nonumber \\&\left. +\,{\varepsilon _2}{s_4}+{\eta _2}{s_4}^{{m_2}/{n_2}} \phantom {\frac{m^{\prime }_2}{n^{\prime }_2}}\right] . \end{aligned}$$
(8)
Fig. 3
figure 3

The state variable x(t) in the presence of the sliding-mode control approach

Full size image
Fig. 4
figure 4

The state variable y(t) in the presence of the sliding-mode control approach

Full size image
Fig. 5
figure 5

The state variable z(t) in the presence of the sliding-mode control approach

Full size image
Fig. 6
figure 6

The state variable \(\phi (t)\) in the presence of the sliding-mode control approach

Full size image
Fig. 7
figure 7

The state variable \(\theta (t)\) in the presence of the sliding-mode control approach

Full size image
Fig. 8
figure 8

The state variable \(\psi (t)\) in the presence of the sliding-mode control approach

Full size image

In the following, the equations pertaining to the subsystem (4) can be examined to control other system states. To this end, a series of new definitions in this case is presented as follows:

$$\begin{aligned} \begin{array}{l} {{Y_1} = {Q^{ - 1}}{{\left[ { \begin{array}{l} X\\ Y \end{array}} \right] }}}\\ {{Y_2} = {{\dot{Y}}_1} = {Q^{ - 1}}{{\left[ { \begin{array}{l} {\dot{X}}\\ {\dot{Y}} \end{array}} \right] }}}\\ {{Y_3} = {{\left[ { \begin{array}{l} \phi \\ \theta \end{array}} \right] }}}\\ {{Y_4} = {{\dot{Y}}_3} = {{\left[ { \begin{array}{l} {\dot{\phi }}\\ {\dot{\theta }} \end{array}} \right] }}} \end{array} \end{aligned}$$
(9)

where

$$\begin{aligned} Q=\frac{u_1 }{m}\left[ {{\begin{array}{l@{\quad }l} {\cos \Psi }&{} {\sin \Psi } \\ {\sin \Psi }&{} {-\cos \Psi } \\ \end{array} }} \right] . \end{aligned}$$
(10)

With the new definition of the states, the subsystem (4) is now changed as follows:

$$\begin{aligned} \begin{array}{l} {{{\dot{Y}}_1} = {Y_2}}\\ {{{\dot{Y}}_2} = {f_2} + {d_2}}\\ {{{\dot{Y}}_3} = {Y_4}}\\ {{{\dot{Y}}_4} = {f_3} + {g_2}{U_2} + {d_3}}, \end{array} \end{aligned}$$
(11)

where

$$\begin{aligned}&f_2 =\left[ {{ \begin{array}{l} {\cos \phi \sin \theta } \\ {\sin \phi } \\ \end{array} }} \right] \nonumber \\&d_2 =Q^{-1}\hbox {diag}\left[ {{ \begin{array}{l@{\quad }l} {\frac{K_1 }{m}}&{} {\frac{K_2 }{m}} \\ \end{array} }} \right] QY_2\nonumber \\&f_3 =0\nonumber \\&g_2 =\hbox {diag}\left[ {{ \begin{array}{l@{\quad }l} {\frac{l}{I_x }}&{} {\frac{l}{I_y }} \\ \end{array} }} \right] \nonumber \\&U_2 =\left[ {{ \begin{array}{l} {u_2 } \\ {u_3 } \\ \end{array} }} \right] \nonumber \\&d_3 =\hbox {diag}\left[ {{ \begin{array}{l@{\quad }l} {\frac{-lK_4 }{I_x }}&{} {\frac{-lK_5 }{I_y }} \\ \end{array} }} \right] Y_4. \end{aligned}$$
(12)

Then, the tracking error has been defined as follows:

$$\begin{aligned}&{e_1} ={Y_1}^{d} -{Y_1}\nonumber \\&{e_2} = {{\dot{e}}_1}\nonumber \\&{e_3} = {{\dot{e}}_2}\nonumber \\&{e_4} = {{\dot{e}}_3}. \end{aligned}$$
(13)

Now, sliding surface can be defined in linear mode for the achievement of stability in the states of the subsystem (4):

$$\begin{aligned} S=\left[ {{\begin{array}{l} {s_5 } \\ {s_6 } \\ \end{array} }} \right] =c_1 e_1 +c_2 e_2 +c_3 e_3 +e_4. \end{aligned}$$
(14)

Thereafter, the control rule \(U_2 =\left[ {{\begin{array}{l} {u_2 } \\ {u_3 } \\ \end{array} }} \right] \) has been calculated as follows through the equivalent control method in sliding mode (i.e., \({\dot{s}}=0)\):

$$\begin{aligned} {U_2} = {\left[ \frac{\partial {f_2}}{\partial {y_3}}{g_2}\right] ^{ - 1}}\left\{ { \begin{array}{l} {{c_1}{e_2} + {c_2}{e_3} + {c_3}{e_4} + \ddot{Y}_1^d - \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{\partial {f_2}}}{{\partial {y_1}}}{Y_2}} \right] }\\ {\quad - \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{\partial {f_2}}}{{\partial {y_2}}}{f_2}} \right] - \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{\partial {f_2}}}{{\partial {y_3}}}} \right] }{Y_4}\\ {\quad -\frac{\partial {f_2}}{\partial {y_3}} ( {{f_3} + {d_3}}) + M{\mathrm{sgn}} \left( s \right) + \lambda s} \end{array}} \right\} .\nonumber \\ \end{aligned}$$
(15)

For applying the rules of the sliding-mode control approach (8) and (15) to the robot model of quadrotor UAV, the software MATLAB is accurately carried out. The numerical values of the parameters of the sliding-mode control approach are acquired [28] and are presented in Table 2. The results for this controller are illustrated in Figs. 3, 4, 5, 6, 7 and 8.

The results of applying the sliding-mode control to the quadrotor UAV in Figs. 3, 4, 5, 6, 7 and 8 illustrate that the aforementioned sliding-mode control designed in this research about subsystem (3) namely, the state variables z(t) and \(\psi (t)\) has acceptable performance, while regarding subsystem (4), namely, the state variables x(t),  y(t),  \(\phi (t)\) and \(\theta (t),\) it suffered a serious overshoot and had no optimal performance. Absence of sufficient flexibility in the nonlinear behavior can be considered as a major cause of inefficiency of sliding-mode control in the stabilizing state variables of subsystem (4). In the following section, in order to deal with the weaknesses in the structure of the sliding-mode controller, the idea of combining the controllers with intelligent algorithms will be implemented.

The fuzzy-based control approach shows high flexibility due to the lack of limitation on part of control signals to the mathematical absolute values. Hence, the idea of combining the sliding-mode control approach and fuzzy-based control approach can be an efficient way to improve the weaknesses of the above-referenced one against the nonlinear behaviors in the systems with uncertainty. Due to optimal performance of the sliding-mode control approach in the stabilizing states of z(t) and \(\psi (t),\) the fuzzy-based control is designed in this study to concentrate on the upgraded performance of control signal \(U_2 =\left[ {{\begin{array}{l} {u_2 } \\ {u_3 } \\ \end{array} }} \right] \) (subsystem (4)). By considering the fuzzy-based control in the structure of the sliding-mode control approach, the new control signal \({U}_2\) can be of the following forms:

$$\begin{aligned} {U_{2\_\mathrm{new}}}= & {} {\left[ { \frac{\partial {f_2}}{\partial {y_3}}{g_2}} \right] ^{ - 1}}\nonumber \\&\quad \times \left\{ { \begin{array}{l} {{c_1}{e_2} + {c_2}{e_3} + {c_3}{e_4} + \ddot{Y}_1^d - \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{\partial {f_2}}}{{\partial {y_1}}}{Y_2}} \right] }\\ {\quad - \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{\partial {f_2}}}{{\partial {y_2}}}{f_2}} \right] - \frac{\mathrm{d}}{{\mathrm{d}t}}\left[ {\frac{{\partial {f_2}}}{{\partial {y_3}}}} \right] }{Y_4}\\ {\quad - \begin{array}{*{20}{c}} {\partial {f_2}}\\ {\partial {y_3}} \end{array}({{f_3}+{d_3}})} \end{array}} \right\} \nonumber \\&\quad +\,\lambda \hbox {FSM}\left[ { \begin{array}{l} {{s_5}/{s_{5M}}}\\ {{s_6}/{s_{6M}}} \end{array}} \right] , \end{aligned}$$
(16)
Fig. 9
figure 9

The structure of hybrid fuzzy-based sliding-mode control approach

Full size image
Fig. 10
figure 10

The membership function of the fuzzy-based control inputs

Full size image
Fig. 11
figure 11

The membership function of the fuzzy-based control output

Full size image

where FSM denotes the output signal of the fuzzy-based control and the signals pertaining to \(s_{iM},i=5.6\) have been proposed to normalize the fuzzy-based control and hold true in the following relation:

$$\begin{aligned} \hbox {If}\quad s_{iM} < s_i (t)\quad \hbox {then}\quad s_{iM} =s_i (t). \end{aligned}$$
(17)

Therefore, one can argue that the proposed structure of the fuzzy-based control includes two inputs, namely \(s_5 /s_{5M} \) and \(s_6 /s_{6M} \) and one output, namely FSM. The structure of hybrid fuzzy-based sliding-mode control approach is illustrated in Fig. 9.

To implement the fuzzy-based control approach, the fuzzy logic designer toolbox in Matlab software is directly used. Membership functions of the inputs and its output of the present control approach are shown in Figs. 10 and 11.

Despite the optimal impact of fuzzy-based control on the performance of the sliding-mode control approach, one of the weaknesses in the structure of the controller is lack of access to accurate information, in order to design the optimal system. Given that considering the model of quadrotor UAV, in this research, such information is not available; therefore, the designed fuzzy-based sliding-mode control approach is incomplete and its performance is not optimal. To deal with this problem, a lot of resources are analyzed, which led to the idea of adding the genetic algorithm optimization to the structure of hybrid fuzzy-based sliding-mode control approaches. The reason to choose the genetic algorithms is regarding their parallel nature of random search on the problem situation because each of the chromosomes randomly generated by this one is considered, as a new starting point to search for a part of the problem situation and search on all of them takes place, simultaneously. In addition, there is no limit on the search path and choosing random answers. In fact, the main purpose of implementing a genetic algorithm is to determine the rules of designing fuzzy-based control approach in such a way that the control does not need information of the expert and be able to work, efficiently.

In this investigation, each of the two inputs and only output of the fuzzy-based control contains five membership functions. In order to optimize the fuzzy sliding control by means of intelligent fuzzy algorithm, fuzzy-based control inputs and output are replaced with binary numbers as follows:

$$\begin{aligned}&\hbox {Inputs and output}{:}\nonumber \\&\left\{ {{ \begin{array}{l} {{\begin{array}{lll} \hbox {NB}&{} \rightarrow &{} {111} \\ \end{array} }} \\ {{\begin{array}{lll} \hbox {NS}&{} \rightarrow &{} {101} \\ \end{array} }} \\ {{\begin{array}{lll} \hbox {ZE}&{} \rightarrow &{} {000} \\ \end{array} }} \\ {{\begin{array}{lll} \hbox {PS}&{} \rightarrow &{} {001} \\ \end{array} }} \\ {{\begin{array}{lll} \hbox {PB}&{} \rightarrow &{} {011} \\ \end{array} }}. \\ \end{array} }} \right. \end{aligned}$$
(18)

As it can be observed, all membership functions of the fuzzy-based control have been replaced 3-bit binary numbers. It is necessary to mention that the first bit in these numbers represent the sign; indeed, if it equals one, it will be a negative number; and if it is zero, it will be a positive number. In the following structure, this model has been shown for one of the membership functions of fuzzy control.

$$\begin{aligned} \hbox {NS}:\underbrace{1}_{\mathrm{Sign}\,\mathrm{Bit}} 0\ 1. \end{aligned}$$
(19)

It is obvious that fuzzy rules are created as a result of the combination of the membership functions of fuzzy control. As an example, the first rule of fuzzy-based control can be defined as follows:

$$\begin{aligned}&\hbox {if}\quad (s_5 /s_{5M},\ \hbox {is NB})\quad \hbox {and}\quad ({s_6 /s_{6M} \ \hbox {is NB}})\quad \hbox {then}\nonumber \\&\quad \quad (\hbox {FSM is NB}). \end{aligned}$$
(20)

Equivalently, each of the fuzzy rules can be expressed as the binary numbers attributed to them. For example, fuzzy rule (20) goes as follows:

$$\begin{aligned} \underbrace{111}_{s_5 /s_{5M} (\mathrm{NB})} \underbrace{111}_{s_6 /s_{6M} (\mathrm{NB})} \underbrace{111}_{\mathrm{FSM}(\mathrm{NB})}. \end{aligned}$$
(21)

In this study, each of the fuzzy rules expressible in the design of fuzzy sliding control is defined in the form of a chromosome in order to design the intelligent genetic algorithm. In this way, the number of \(5\times 5\times 5=125\) is defined as follows:

$$\begin{aligned} \left\{ \begin{array}{c} \hbox {chromosome }1=\left[ 111 \quad 111 \quad 111 \right] _{1\times 9} \\ \hbox {chromosome }2=\left[ 111 \quad 101 \quad 111 \right] _{1\times 9} \\ \vdots \\ \hbox {chromosome }125=\left[ 011 \quad 011 \quad 011 \right] _{1\times 9} \end{array}\right\} . \end{aligned}$$
(22)

According to Eq. (22), there are three binary numbers in each 9-bit chromosome which mutually represent the input-output modes.

In this study, for the conduct of optimization by the genetic algorithm, the objective function has been selected out regarding fitness functions and the main goal is the minimization of these functions. The objective functions used in this study are as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} {f_1 (k)=\int _0^{t_{\max } }|{e(t)}|\mathrm{d}t} \\ {f_2 (k)=f_1 (k)-\min _{i=1,2,\ldots ,N_p}({f_1(i)})} \\ {f_3 (k)=\left( {\frac{f_2(k)}{\frac{1}{N_p }\sum _{i=1}^{N_p } f_2 (i)}}\right) ^{3}} \\ \end{array} }}. \right. \end{aligned}$$
(23)

The performance of the genetic algorithms in simulation is such that, after the determination of the results for each chromosome in each stage, the best one, which includes the chromosome with the fastest response is transferred to the next generation as the elite and the remaining ones are integrated together using mutation and hybrid methods to produce the next generation.

The results of the simulations

In order to implement the proposed control strategy, it is necessary to calculate the design parameters for the genetic algorithm. These values are tabulated in Table 3. In this work, the initial random population is considered based on the total number of defined rules for fuzzy-based control (the number of chromosomes in the genetic algorithm). The rest of the Table 3 was obtained by the information contained in the conducted study in [29] or by trial and error methods.

Table 3 The designed parameters in the genetic algorithm
Full size table
Table 4 The best fuzzy rules obtained for the fuzzy-based sliding mode control approach from the genetic algorithm
Full size table
Fig. 12
figure 12

The quadrotor’s movement in the direction of the axis x,  fuzzy-type 2 control and fuzzy-based sliding-mode control approach

Full size image

Finally, after the implementation of the genetic algorithms in the software Matlab, top chromosomes (optimized fuzzy rules) are obtained according to member functions defined in Figs. 10 and 11 which are shown in Table 4.

Fig. 13
figure 13

The quadrotor’s movement in the direction of the axis y,  fuzzy-type 2 control and fuzzy-based sliding-mode control approach

Full size image
Fig. 14
figure 14

The quadrotor’s movement in the direction of the axis z,  fuzzy-type 2 control and fuzzy-based sliding-mode control approach

Full size image
Fig. 15
figure 15

The quadrotor’s rotation around the axis x (roll), fuzzy-type 2 control and fuzzy-based sliding-mode control approach

Full size image
Fig. 16
figure 16

The quadrotor’s rotation around the axis y (pitch), fuzzy-type 2 control and fuzzy-based sliding-mode control approach

Full size image
Fig. 17
figure 17

The quadrotor’s rotation around the axis z (yaw), fuzzy-type 2 control and fuzzy-based sliding-mode control approach

Full size image

By applying the optimized results obtained from the genetic algorithm in the structure of designed fuzzy-based sliding-mode control approach, it is expected that improvements can be made in the objectives of the control system. To prove this claim, the results obtained in this study are compared with the results of research carried out in [30], where type-2 fuzzy-based control is realized to stabilize the robot of quadrotor, and are illustrated in terms of the state variables of six systems in Figs. 12, 13, 14, 15, 16 and 17.

Due to the limitations of the mechanical structure in modeled robot of quadrotor, the results obtained can be analyzed. The mission of the studied robot is that in a vertical axis it can be as high as 3 m from the ground and have a minor rotation around it (0.5 radians). According to Figs. 12, 13, 14, 15, 16 and 17, it can be argued that the designed control strategy in this article has been able to achieve these goals. Since the intended robot does not have the ability to move or rotate around the x-axis and y-axis, thus in order to prevent the diversion of robots from the required route and also for the realization of the desired control objectives, it is essential that other state variables of system converge to zero. The results indicate that these demands have been met when robot was flying. Importantly, the state variables of system are stabilized without the need for expert information for designing fuzzy control. Therefore, we can conclude that the proposed genetic algorithm in this article has implemented its task properly.

Since the practical issues of control, sustained pressure on the actuators is very important, being aware of the control efforts is essential. Therefore, in the following, the signals generated by the fuzzy-based sliding-mode control approach, optimized by genetic algorithm, in order to apply to existing engines in structure of the quadrotor robot are shown in Fig. 18.

Fig. 18
figure 18

The fuzzy-based sliding-mode control approach

Full size image
Table 5 Comparing the results with respect to the potential benchmarks
Full size table

To compare the results obtained in this study with previous potential similar benchmarks, the implemented control algorithm for fuzzy-type 2 in the study [30] is investigated, in order to stabilize a drone robot of quadrotor. After the survey was conducted, the control parameters for both methods are extracted and compared with each other in Table 5. After integrating the absolute value of the output level for each controller in the designed method in this article and presented method in this study [30], the following results were achieved. As can be seen, the designed control strategy in this study could perform better both in reducing the amount of control efforts and in achieving of the control objectives.

Conclusion

In order to direct a sample of quadrotor robot automatically, in this paper, the capacities of hybrid fuzzy-based sliding-mode control approach optimized by genetic algorithm was used. The main advantages of this approach are the following:

  • ensuring the stability of nonlinear system of robot due to the use of sliding-mode control;

  • ability to deal with the disturbance and uncertainty in the system due to the use of fuzzy control;

  • lack of need for expert information about the robot system so as to control design phase because of the use of genetic optimization algorithm.

Finally, the cited procedure for experimental model is a sample robot of simulated quadrotor. By comparing the results, it can be concluded that it is in line with previous similar studies and indicated that the proposed method has attempted to control signals of u2, u3 and u4, but the control signal of u1 was weak. Also it could dramatically improve the control parameters of maximum overshoot and landing time of state variables system. Some disadvantages of the proposed approach can be a high volume of computing and slow process of simulation compared with earlier work, which can be caused by a combination of the proposed algorithm. To cope with such a phenomenon, the use of intelligent algorithms such as optimization of multi-purpose development as part of future work in this area is suggested.