Numerical studies to detect chaotic motion in the full planar averaged three-body problem

Abstract

In this paper, the author deals with a well-known problem of Celestial Mechanics, namely the three-body problem. A numerical analysis has been done in order to prove existence of chaotic motions of the full-averaged problem in particular configurations. Full because all the three bodies have non-negligible masses and averaged because the Hamiltonian describing the system has been averaged with respect to a fast angle. A reduction of degrees of freedom and of the phase-space is performed in order to apply the notion of covering relations and symbolic dynamics.

1 Introduction

The three-body problem is one of the most studied issues in Celestial Mechanics. It deals with the motion of three bodies interacting by only the gravitational force. The problem is, generally, non-integrable, namely, no analytical closed solutions exist to describe the dynamics of the model. Many analytical and numerical studies have been done in order to acquire information about the motions of the associated dynamical system, proving existence of both stable, unstable, regular and chaotic dynamics (see, for example, [3] for a complete treatment of the problem).

The purpose of the current paper is to collect and to link two recent works (we refer to papers [8, 9]) where the onset of chaos is numerically proved in two different configurations of the three-body problem. In both the works, we aim to write the Hamiltonian describing the model as the sum of a Keplerian part ruling the motion of two of three bodies plus a part depending on all the three bodies. In principle, we do not have dominant interactions between the three bodies but we choose a region of the phase-space, where the remaining part of the Hamiltonian becomes a perturbation, so we deal with a “perturbed Keplerian problem”. It can be possible by introducing new coordinates associated to the three bodies (see [15] for a detailed study of the new coordinates) and through suitable rescalings of variables and time. In works [8, 9], two different configurations and phase-spaces are considered and in both cases we use symbolic dynamics to prove, numerically, the existence of chaotic motions. In Sect. 1.1, we aim to write the Hamiltonian of the two different configurations in the same way, in order to have a generic treatment of the problem. Indeed, the goal of the current paper is to show a method to apply to the perturbed Keplerian problem when some conditions are satisfied. Afterwards, the two different cases of papers [8, 9] are described.

1.1 The general setting

Let us consider 3 bodies $P_0,P_1,P_2$ with masses $m_0, m_1, m_2$ interacting by only the gravitational force. By fixing an orthonormal reference frame (i, j, k) in the Euclidean space identified with ${\mathbb {R}}^3$, the Hamiltonian $\mathcal {H}_\textrm{3b}$ describing the system can be written as

$$\begin{aligned} \mathcal {H}_\textrm{3b}= \frac{{\vert y_0\vert }^2}{2 m_{0}} + \frac{{\vert y_1\vert }^2}{2 m_1}+\frac{{\vert y_2\vert }^2}{2 m_{2}}-\frac{ m_{0} m_1}{\vert x_0-x_1\vert }-\frac{ m_{0} m_2}{\vert x_0-x_2\vert }-\frac{m_1 m_2}{\vert x_1-x_2\vert } \, , \end{aligned}$$

(1)

where $x_0,x_1,x_2 \in {\mathbb {R}}^3$ and $y_0,y_1,y_2 \in {\mathbb {R}}^3$ are, respectively, the positions and the impulses of the three bodies; $\vert \cdot \vert$ stands for the Euclidean distance and the gravity constant has been fixed to one. At the beginning, we do not impose any restrictions on the masses of the bodies and for this reason we can refer to the Hamiltonian (1) as full three-body problem, where full is opposed, in this case, to restricted where one of the three bodies has negligible mass and it does not affect the motion of the other two bodies. Moreover, in our study, we consider the planar problem, i.e. the motion is restricted to a plane by choosing positions and impulses $x_0,x_1,x_2, y_0,y_1,y_2 \in {\mathbb {R}}^2$. After a suitable change of the Cartesian coordinates and a rescaling of coordinates and Hamiltonian itself, we aim to write the Hamiltonian $\mathcal {H}_\textrm{3b}$ in the following way:

$$\begin{aligned} H_\textrm{3b}(y',y,x',x) =\frac{{\vert y \vert }^2}{2}-\frac{1}{{\vert x \vert }} + {\hat{H}}(y',y,x',x;\eta ) \end{aligned}$$

(2)

where $(x,y),(x',y') \in {\mathbb {R}}^2 \times {\mathbb {R}}^2$ are Cartesian positions and impulses of two of the bodies whose origin is set in a suitable point¹ and $\eta = \eta (m_0,m_1, m_2)$ is a mass parameter. The first two terms $\frac{{\vert y \vert }^2}{2}-\frac{1}{{\vert x \vert }}$ are called Keplerian part and, assuming it takes negative values, it generates motions for the body of coordinates (x, y) on an ellipse. The term ${\hat{H}}$ is the remaining part of the Hamiltonian. In principle, we do not ask that ${\hat{H}}$ is necessarily a perturbation since the coordinates are not centered at the most massive body, although we will work in regions of the phase-space such that ${\hat{H}}$ is small. An analysis of this point will be addressed in the following sections.

The Hamiltonian (2) has four degrees of freedom and in the following steps we aim to reduce it to a two degrees of freedom system. First of all, the Hamiltonian $H_\textrm{3b}$ is invariant under the group of transformations SO(2), namely, orthogonal rotations. Introducing a set of canonical coordinates in a suitable rotating system we reduce this symmetry obtaining a three degrees of freedom system. To this aim, we introduce the total angular momentum, which is a constant of motion, as

$$\begin{aligned} \textrm{C} = x \times y \cdot k + x' \times y' \cdot k \end{aligned}$$

where $k = i \times j$ is the unit vector orthogonal to the plane where motions take place, and then, we define a six-dimensional “rotation-reduced phase space”  introducing 6 new canonical coordinates

$$\begin{aligned} (\Lambda ,R,G,\ell , r,g). \end{aligned}$$

To define this set of coordinates we denote as “first body”  the body $P_1$ of Cartesian coordinates (x, y) and as “second body”  the body $P_2$ of Cartesian coordinates $(x',y')$. We denote by ${\mathbb {E}}$ the ellipse generated by the Keplerian term of Eq. (2) for given values of (x, y). Finally, we define two pairs of Delaunay variables $(\Lambda ,G,\ell ,g) \in {\mathbb {R}}^2 \times {\mathbb {T}}^2$ for the first body $P_1$ as follows:

• $\Lambda = \sqrt{a} \quad \text {where } a \text { is the semi-major axis of }{\mathbb {E}},$

• $G = x \times y \cdot k \text { is the angular momentum of the first body},$

• $\ell \text { is } \text {the mean anomaly of } x \text { from the pericenter } P \text { of }{\mathbb {E}},$

• $g \text { is } \text {the angle detecting the pericenter of } {\mathbb {E}} \text { with respect the direction of } x',$

and a radial-polar pair of coordinates $(R,r) \in {\mathbb {R}}^2$ for the second body $P_2$ as

• $R = y' \cdot \frac{x'}{\vert x' \vert },$

• $r = \vert x' \vert ,$

namely, R is the radial velocity of $x'$ and r is the Euclidean length of $x'$. We underline that the coordinates $(R, G,\Lambda ,r,g,\ell )$ refer to a reference frame which is not inertial with respect to the “second body”  and they have been introduced to reduce the symmetry of rotations (see [15] for a complete and detailed discussion about these variables). The Hamiltonian (2) written in the new coordinates appears as

$$\begin{aligned} H_\textrm{3b,C} = -\frac{1}{2\Lambda ^2} + H_{\textrm{C}, \eta }(\Lambda ,R,G,\ell ,r,g) \, , \end{aligned}$$

(3)

where the first term $-1/ (2\Lambda ^2)$ is the Keplerian term and the total angular momentum $\textrm{C}$ is considered as parameter. The next step consists in averaging Eq. (3) with respect to the fast angle, the mean anomaly $\ell$, in order to reduce again the degrees of freedom from three to two. The new averaged Hamiltonian

$$\begin{aligned} {\overline{H}}_{\textrm{3b,C}} = \frac{1}{2 \pi }\int _0^{2\pi } H_{\textrm{3b,C}} \, d\ell \end{aligned}$$

takes the form:

$$\begin{aligned} {\overline{\mathcal {H}}}_{\textrm{3b, C}} = -\frac{1}{2 \Lambda ^2} + \overline{H}_{\mathrm{C, \eta }}=-\frac{1}{\Lambda ^2} + \Big ( K_{\textrm{C}}(R,r)+ {\widetilde{K}}_{\textrm{C}}(G,r) +U(r,G,g)\Big ). \end{aligned}$$

(4)

The three terms in parentheses—in which, for the moment, we omit the dependence on the mass parameter $\eta$—will be named as kinetic term, disturbing term and Newtonian potential term, respectively. Under two explicit assumptions about the terms appearing in Hamiltonian (4), namely,

$$\begin{aligned} \Big \vert -\frac{1}{2 \Lambda ^2} \Big \vert \gg \, \vert \overline{H}_{\textrm{C},\eta }\vert \end{aligned}$$

(5)

and

$$\begin{aligned} \vert K_\textrm{C} \vert \gg \vert U \vert \gg \vert {\widetilde{K}}_\textrm{C} \vert \, , \end{aligned}$$

(6)

we claim that, at first approximation, the motion of $(\Lambda (t),R(t),G(t),\ell (t),r(t),g(t))$ under the Hamiltonian flow (4) is described by the following three rules:

(a):

$\Lambda (t)$ remains almost constant and $\ell (t)\approx t$ moves fast;

(b):

the motion (R(t), r(t)) is ruled by $K_\textrm{C}$;

(c):

the motion (G(t), g(t)) is ruled by the non-autonomous Hamiltonian $U(r(t),\cdot ,\cdot )$.

Precise computations and assumptions on each term will be addressed in the following sections where two explicit examples will be numerically analyzed.

Fig. 1

Contour lines of the Euler integral function for fixed r: a $0<r<1$; b $1<r<2$; c $r>2$

1.2 Euler integral function

Let us recall some important properties about the function U (as it has been proved in [15]). Its general formula is given by:

$$\begin{aligned} U(r,G,g) = \frac{1}{2 \pi }\int _0^{2\pi } \frac{d \ell }{\vert x' -x \vert }, \end{aligned}$$

and we remark that it is integrable; in particular, there exists a function F of two arguments, such that

$$\begin{aligned} U(r,G,g) = F(r,E(r,G,g)) \, , \end{aligned}$$

(7)

where

$$\begin{aligned} E(r,G,g) = G^2 -r\sqrt{1-G^2}\cos g. \end{aligned}$$

The function E(r, G, g) is called Euler integral, because it appears in the integration of the two-fixed centers problem. By Eq. (7), the level sets of E are also level sets of U and the phase portrait of E can be easily studied (see [17]): in fact, the level sets of E are given by the curves

$$\begin{aligned} {{\mathcal {S}}}({ r}, {{\mathcal {E}}}):=\Big \{({ G}, { g}):\quad { G}^2-{ r}\sqrt{1- G^2}\cos { g}={{\mathcal {E}}}\Big \} \, \end{aligned}$$

where r is fixed and ${{\mathcal {E}}}$ takes different values; by periodicity of g, we consider as domain for the coordinates (g, G), the rectangle $[0,2\pi )\times (-1,1)$. Then, according to the fixed value of the variable r, three different phase portraits appear: a first case if $0<r<1$, the second case if $1<r<2$ and the third if $r>2$. Let us recall that, the variable r is the norm of the vector $x'$, thus, the three different cases stand for different configurations of the third body $P_2$ with respect to the first two bodies $P_0$ and $P_1$, whose motion is ruled by the Keplerian part of the Hamiltonian. Let us now show in detail the phase space of the Euler integral function. In Fig. 1, we can distinguish three completely different phase portraits. In panel (a) the case $0<r<1$ is represented. The point (0, 0) is a minimum, then there are two symmetric (with respect to $G=0$) maxima in $\biggl ( \pi , \pm \sqrt{1-\frac{r^2}{4}}\biggr )$ and finally the point $(\pi , 0)$ is a saddle. Two separatrices split the phase space in different regions: the first separatrix is the curve $\mathcal{S}_r ({ r}):=\Big \{({ G}, { g}):\quad { G}^2-{ r}\sqrt{1- G^2}\cos { g}=r\Big \}$ passing through the saddle point $(\pi ,0)$ and the second is the curve ${{\mathcal {S}}}_1 ({ r}):=\Big \{({ G}, { g}):\quad { G}^2-{ r}\sqrt{1- G^2}\cos { g}=1\Big \}$ passing through the points $(\frac{\pi }{2},\pm 1)$. The curve ${{\mathcal {S}}}_r ({ r})$ delimits a region of librational motions around the minimum (0, 0); between ${{\mathcal {S}}}_r ({ r})$ and ${{\mathcal {S}}}_1 ({ r})$ a region of rotational motions exists. Finally, ${{\mathcal {S}}}_1 ({ r})$ delimits a region of librational motions around the two maxima. In panel (b) the case $1<r<2$ is shown. The minimum (0, 0) persists as well as the two symmetric maxima, the saddle point and the two separatrices $\mathcal{S}_r ({ r})$ and ${{\mathcal {S}}}_1 ({ r})$. Rotational motions disappear, ${{\mathcal {S}}}_r ({ r})$ delimits libration areas around the two maxima, other librational motions surround the separatrix ${{\mathcal {S}}}_r ({ r})$ and thus, the maxima and the saddle point, up to the separatrix ${{\mathcal {S}}}_1 ({ r})$ which delimits the area with librational motion around the minimum. The structure completely changes in panel (c) representing the case $r>2$. The saddle point and the separatrix ${{\mathcal {S}}}_r ({ r})$ disappear; $(\pi ,0)$ turns to be the only maximum and (0, 0) remains a minimum. The separatrix ${{\mathcal {S}}}_1 ({ r})$ still exists and it delimits two regions of librational motions around the minimum and the maximum, respectively.

The analysis of the dynamics of the three-body problem ruled by Hamiltonian (4) has been deeply developed in the last years. In particular, from an analytical point of view it has been studied by using normal form theory in order to prove stability estimates. For a complete treatment of the subject we refer the reader to the articles [4, 6, 16, 17]. At the same time, the problem has been studied from a numerical point of view in order to prove existence of chaotic motions under particular initial configurations. We refer, in particular to papers [8, 9].

The two numerical studies will be presented and compared in this paper as follow: in Sect. 2 we present two different configurations and write how the respective Hamiltonian functions are reduced; in Sect. 3, we explicitly define the Poincaré maps and study the hyperbolic structures of the two models; in Sect. 4 we provide some definitions and properties of covering relations and symbolic dynamics; in Sect. 5, we prove, numerically, the existence of symbolic dynamics and the onset of chaos in the two studied models. Finally, in Sect. 6, we provide conclusions and ongoing works.

2 Two different configurations

We want to present two different cases related to two different configurations of the three-body problem where chaos appears. The two cases have been studied, separately, in papers [9] and [8], respectively.

2.1 First case: $0<r<1$

Let us show the first model. We fix three bodies $P_0,P_1,P_2$ with masses, respectively, $m_0 =\mu$, $m_1 = \kappa$, $m_2=1$, with $\mu ,\kappa <1$. Through a translation of coordinates, we center the reference system in the body $P_0$ with mass $\mu$ and write the Hamiltonian (1) where x and $x'$ are, respectively, the positions of bodies $P_1$ and $P_2$ with masses $\kappa$ and 1. The Hamiltonian takes the form:

$$\begin{aligned} H_\textrm{3b}(y',y,x',x)= \frac{\kappa +\mu }{\kappa \mu } \frac{\vert y \vert ^2}{2}-\frac{\kappa \mu }{\vert x\vert } + \frac{\mu +1}{\mu } \frac{\vert y'\vert ^2}{2} - \frac{\mu }{\vert x'\vert }-\frac{\kappa }{\vert x-x'\vert } + \frac{1}{\mu } y\cdot y'. \end{aligned}$$

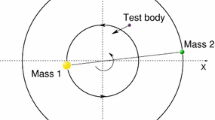
We underline that this Hamiltonian is not centered in the more massive body: the reference frame has the origin in the body $P_0$ with mass $\mu$, thus, the Hamiltonian describes the motions of the bodies $P_1,P_2$ with masses $\kappa , 1$, respectively. Figure 2 shows the model.

Fig. 2

Configuration of the three-body problem described in Sect. 2.1 when $0<r<1$

A suitable rescaling of variables $(y',y,x',x)$ and of Hamiltonian through a rescaled time provides the new Hamiltonian in the form given by Eq. (2) as

$$\begin{aligned} H_\textrm{3b}(y',y,x',x) = \frac{\vert y\vert ^2}{2}-\frac{1}{\vert x\vert } + \delta \biggl (\frac{\vert y'\vert ^2}{2} -\frac{\alpha }{\vert x-x'\vert } -\frac{\beta }{\vert x'\vert } + \gamma \, y\cdot y' \biggr )\, , \end{aligned}$$

(8)

with

$$\begin{aligned} \alpha := \frac{\kappa +\mu }{\kappa \mu (\mu +1)}, \quad \beta := \frac{\kappa +\mu }{\kappa ^2(\mu +1)}, \quad \gamma := \frac{1}{\mu +1}, \quad \delta := \frac{\kappa (\mu +1)}{\kappa +\mu }. \end{aligned}$$

From now on, in our computations, we choose $\alpha$ and $\beta$ as independent mass parameters. Hamiltonian (8) has four degrees of freedom and, as it has been discussed in Sect. 1.1, we reduce one degree of freedom by exploiting the rotational invariance and using the conservation of the total angular momentum $\textrm{C}$. We introduce the Delaunay variables $(\Lambda , G, \ell , g)$ relative to the Keplerian motion of $P_1$ with respect to $P_0$, and the couple (R, r) of radial coordinates relative to the body $P_2$. In the new coordinates, Hamiltonian (8) can be written as Eq. (3), with $\eta = \eta (\alpha ,\beta )$. To reduce one more degree of freedom, we average the Hamiltonian with respect the fast angle $\ell$, obtaining Eq. (4). Without loss of generality, we choose $\Lambda = 1$ (which implies that the semimajor axis a is equal to 1) and consider the Keplerian term $-1/(2\Lambda ^2)$ as an additive constant which does not change the equations of motion; thus, we will study the motion ruled by the averaged Hamiltonian:

$$\begin{aligned} {\overline{H}} = K_{\textrm{C}}( R, r)+{\widetilde{K}}_{\textrm{C}}( G, r) -\alpha \, U(r, G, g), \end{aligned}$$

where

$$\begin{aligned} K_\textrm{C}( R, r)= & {} \frac{ R^{2}}{2} + \frac{\textrm{C}^{2}}{2 {r}^{2}} -\frac{\beta }{r}, \\ {\widetilde{K}}_{\textrm{C}}( G, r)= & {} \frac{{G^2-2 C G}}{2 {r}^2} \, \end{aligned}$$

and

$$\begin{aligned} U= & {} \frac{{ G}^3}{2 \pi } \int _0^{2 \pi } \frac{d \nu }{(1 + e \cos \nu )\sqrt{{r}^2(1 + e \cos \nu )^2 - 2{ G}^2{ r}(1 + e \cos \nu ) \cos ({ g}+\nu )+{ G}^4}}\nonumber \\= & {} \frac{1}{2 \pi } \int _0^{2 \pi } \frac{(1-e\cos \xi )d \xi }{\sqrt{(1 - e \cos \xi )^2 - 2{ \,r}(\cos \xi -e)\cos { g}+2{\, r}{\, G} \sin \xi \sin { g}+{ r}^2}} \end{aligned}$$

with $\,e=\sqrt{1-{G}^2}$ being the eccentricity, $\nu$ the true anomaly and $\xi$ the eccentric anomaly related with the mean anomaly $\ell$ by means of the Kepler equation

$$\begin{aligned} \xi -e \sin \xi = \ell \, . \end{aligned}$$

(9)

Let us recall some properties of the function U(r, G, g) (the reader can refer to papers [4, 9, 16, 17] for more details):

• the function U is singular if and only if $0<r<2$ and $(g,G) \in {{\mathcal {S}}}_1 ({ r})$;

• the rate of divergence of U is logarithmic with respect to the distance from ${{\mathcal {S}}}_1 ({ r})$.

In this section we are dealing with the case $0<r<1$ and, moreover, we require that r be less than the radius of the Keplerian ellipse, meaning that $P_2$ is moving inside the Keplerian ellipse which is defined by the motion of $P_1$ (consider again Fig. 2). Being r small, the potential U can be expanded in power series of r as

$$\begin{aligned} U_N(r,G,g) = \sum _{n=0}^N P_n (G,g) \cdot r^n \end{aligned}$$

where N is a suitable order of truncation.

Let us now choose values of parameters² fulfilling assumptions (5) and (6):

$$\begin{aligned} \left\{ \begin{array}{lll} C &{} = &{} 1.6 \\ \alpha &{} = &{} 50 \\ \beta &{} = &{} 20 \end{array} \right. \,; \end{aligned}$$

we fix an energy level ${\overline{H}}_\textrm{fix}$ and, on such level, we find initial conditions

$$\begin{aligned}{} & {} \Gamma _\textrm{e}:\qquad \left\{ \begin{array}{lll} R_\textrm{e} &{} = &{} -11.367\\ G_\textrm{e} &{} = &{} 0.993\\ r_\textrm{e} &{} = &{} 0.132\\ g_\textrm{e} &{} = &{} 2.759 \end{array} \right. , \end{aligned}$$

(10)

such that the orbit starting at $(R_\textrm{e},G_\textrm{e},r_\textrm{e},g_\textrm{e})$ and evolving under the Hamiltonian ${\overline{H}}$ is periodic in the four-dimensional phase space (R, G, r, g). The projection of such orbit on the three-dimensional phase space (G, r, g) is still periodic. Now, we are ready to study the hyperbolic structure of this problem by introducing a suitable Poincaré map. Before continuing, we introduce a new model and then, we proceed with the definition of first return maps on Sect. 3.

2.2 Second case: $r>2$

Let us now present a new model: recalling again Hamiltonian (1), we choose $m_1 = \mu m_0$ and $m_2 = \kappa m_0$ with $\mu =1 \ll \kappa$ so that $P_0,P_1$ are bodies with equal mass and much smaller than the body $P_2$. The Hamiltonian (1) is translational invariant, so we rapidly switch to a translation-free Hamiltonian by applying the well-known Jacobi reduction (see, for example, [12]). We recall that this reduction consists of using, as position coordinates, the centre of mass of the system (which moves linearly in time), the relative position vector x of two of the three bodies and the position vector $x'$ of the third body with respect to the centre of mass of the former two. Without loss of generality, we choose $m_0=1$ and rescale the coordinates and Hamiltonian as described in [8] to transform Hamiltonian (2) in the following explicit expression³:

$$\begin{aligned} H_\textrm{3b}(y',y,x',x) =\frac{{\vert y \vert }^2}{2}-\frac{1}{{\vert x \vert }} + \sigma \Bigg ( \frac{{\vert y' \vert }^2}{2} -\frac{1}{\vert x'+{\bar{\beta }} x \vert } -\frac{{\bar{\beta }}}{\beta }\frac{1}{\vert x'- \beta x \vert } \Bigg ), \end{aligned}$$

where

$$\begin{aligned} \beta = \frac{\kappa ^2 (1+\mu )}{\mu ^2 (1+\mu +\kappa )}\,\quad \bar{\beta } =\frac{\kappa ^2 (1+\mu )}{\mu (1+\mu +\kappa )}\, \quad \sigma = \frac{\kappa ^3 {(1+\mu )}^2}{\mu ^3 (1+\mu +\kappa )}. \end{aligned}$$

The choice $\kappa \gg \mu =1$ gives $\beta ={\bar{\beta }}\gg 1$ and simplifies $H_\textrm{3b}(y',y,x',x)$ to

$$\begin{aligned} H_\textrm{3b}(y',y,x',x) = \frac{ {\vert y\vert }^2}{2} -\frac{1}{\vert x\vert } +\sigma \Bigg ( \frac{ {\vert y'\vert }^2}{2} - \frac{1 }{\vert x' + \beta x \vert }- \frac{1}{\vert x' - \beta x \vert } \Bigg ). \end{aligned}$$

(11)

From now on, we regard $\beta$ as mass parameter, with $\beta \sim \kappa$ and $\sigma \sim \beta ^2$. By choosing a region of the phase-space where

$$\begin{aligned} \vert x'\vert >\vert \beta x\vert , \end{aligned}$$

(12)

we ensure the denominators of the last two terms in (11) to be different from zero.

All the assumptions made until now lead to a configuration where two bodies $P_0$, $P_1$ with the same mass (for example two asteroids) move around their barycenter b and a third much more massive body $P_2$ (a planet) moves far from the first two. A schematic representation can be seen in Fig. 3.

Fig. 3

Configuration of three-body problem described in Sect. 2.2 with $r>2$

As it has been described in Sect. 1.1, we introduce the couples of Delaunay variables $(\Lambda ,G,\ell ,g)$ for the asteroid relatively to $x'$ (the angle g is the angle of pericenter between the line passing through b, P and $x'$ direction) and the radial-polar coordinates (R, r) for the planet. More precisely, the variables are defined as follows:

$$\begin{aligned} \left\{ \begin{aligned} \Lambda&= \sqrt{a} \\ G&= x \times y \cdot k \\ \ell&= 2 \pi \frac{S}{S_{tot}} \\ g&= \alpha _{x',P}\\ R&= y' \cdot \frac{x'}{\vert x'\vert }\\ r&= \vert x'\vert \end{aligned} \right. , \end{aligned}$$

where, considering the instantaneous ellipse generated by the first two terms in Hamiltonian (11), a is the semimajor axis, S and $S_{tot}$ are, respectively, the area of the ellipse spanned from the pericenter P and the total area. With this notation, G is the projection of the angular momentum of $P_0,P_1$ on the direction orthogonal to the plane where motions take place, $\ell$ is the mean anomaly of $P_1$, g is the argument of pericenter, R is the radial velocity of $P_2$ and r is its distance from the center of mass of $P_0$ and $P_1$.

In the new coordinates the Hamiltonian reads:

$$\begin{aligned} H_\textrm{3b,C}= & {} -\frac{1}{2\Lambda ^2} + \sigma \Big (\frac{R^2}{2}+ \frac{(G-C)^2}{2 r^2}\Big ) - \frac{\sigma }{\sqrt{r^2+2\beta a r p + \beta ^2 a^2 \varrho ^2}} \nonumber \\{} & {} - \frac{\sigma }{\sqrt{r^2-2\beta a r p + \beta ^2 a^2 \varrho ^2}}, \end{aligned}$$

(13)

where

$$\begin{aligned} \varrho= & {} \varrho (\Lambda ,G,\ell )=1-e \cos \xi (\lambda , G, \ell ), \\ p= & {} p(\Lambda ,G,\ell ,g)= (\cos \xi -e) \cos g - \frac{G}{\Lambda } \sin \xi \sin g \end{aligned}$$

and

$$\begin{aligned} e=e(\Lambda ,G)=\sqrt{1-\frac{G^2}{\Lambda ^2}} \end{aligned}$$

is the eccentricity; $\xi =\xi (\Lambda , G, \ell )$ denotes the eccentric anomaly, defined as the solution of Kepler’s equation (9). In the new coordinates, the assumption (12) takes the form:

$$\begin{aligned} \frac{\beta \, a}{r} < \frac{1}{2}. \end{aligned}$$

Thus, the last two terms of Eq. (13) can be expanded in powers of the small parameter $\beta \, a /r$; then, the Hamiltonian can be averaged with respect to the fast angle $\ell$ in order to reduce the system from three to two degrees of freedom and to study the secular (averaged) problem. Let us write Equation (4) for this case:

$$\begin{aligned} {\overline{H}}_\textrm{3b, C} = -\frac{1}{\Lambda ^2} + {\overline{H}}_\mathrm{C, \eta }=-\frac{1}{\Lambda ^2} +\sigma \, \Big ( K_\textrm{C}(R,r)+ {\widetilde{K}}_\textrm{C}(G,r) +U(r,G,g)\Big ) \, , \end{aligned}$$

(14)

with

$$\begin{aligned} \left\{ \begin{aligned} K_\textrm{C}&= \frac{R^2}{2} + \frac{C^2}{2 r^2} - \frac{2}{r}\\ {\widetilde{K}}_\textrm{C}&= \frac{G^2 - 2CG}{2 r^2} \\ U&= U_+ + U_- +\frac{2}{r} \end{aligned} \right. \end{aligned}$$

(15)

where

$$\begin{aligned} U_{\pm }(r,G,g) = - \frac{1}{2 \pi } \int _0^{2 \pi } \frac{d \ell }{\sqrt{r^2\pm 2\beta a r p + \beta ^2 a^2 \varrho ^2}}. \end{aligned}$$

After expanding $U_{\pm }$ in power series of $\beta \, a /r$ and averaging with respect to $\ell$, we replace the series of the Newtonian potential with a finite sum given explicitly by:

$$\begin{aligned} U_k=\sum _{\nu =1}^{k} q_{\nu }(G,g,r) \Big (\beta \frac{a}{r}\Big )^{\nu } \end{aligned}$$

(16)

where $q_{\nu }(G,g,r)$ are the Taylor coefficients in the expansion of U with $\nu =1$, $\ldots$, k. Using the parity of U as a function of r, these coefficients have the form

$$\begin{aligned} q_{\nu }(G,g,r) =\left\{ \begin{array}{ll} \frac{m_0^2}{r} \sum _{p=0}^{\nu /2} {\tilde{q}}_{p}(G) \cos (2\,p\,g) &{}\quad \textrm{if}\ \nu \ \mathrm{is\ even} \, \\ 0 &{}\quad \textrm{otherwise} \end{array} \right. \end{aligned}$$

(17)

In our numerical implementation, we truncate Eq. (16) at $k=k_{\max }=10$, so as to balance accuracy and number of produced terms. In this work we do not provide rigorous estimates to prove that the averaged problem is a good model for the full problem, but we fulfill some requirements which guarantee that the averaged problem well describes the full one. In a work in progress, we are better comparing the averaged and non-averaged problems.

Neglecting the Keplerian term in Eq. (14) (being an additive constant) and rescaling time to get the parameter $\sigma = 1$, Hamiltonian (14) becomes

$$\begin{aligned} {\overline{H}}(G,R,g,r)= K_\textrm{C}(R,r)+ {\widetilde{K}}_\textrm{C}(G,r) +U(r,G,g)\, , \end{aligned}$$

(18)

with $K_\textrm{C}, \widetilde{K}_\textrm{C}, U$ as in (15). From now on, we will deal with the secular Hamiltonian (18). The dependence on $\beta , \Lambda , \textrm{C}$ does not appear in an explicit way being they considered as parameters.

Let us now show how the initial conditions for (G, R, g, r) and the parameters $\textrm{C},\Lambda , \beta$ are chosen. The aim is to find a region of the phase space and a range of parameters such that the terms in Eq. (18) become weakly coupled. The choice $\beta \gg 1$ has been already made, as well as $\frac{\beta \, a}{r} < \frac{1}{2}$. To ensure that the averaged problem well describes the full one, we also, heuristically, require that $r\gg \beta ^{3/2} a$ (see [8] for further details). Then, we take $\Lambda$ and $\textrm{C}$ such that $\Lambda \ll \textrm{C}$, which implies also $\vert G \vert \ll \textrm{C}$ (being $\vert G \vert < \Lambda$). Moreover, we consider a region of the phase space where $r = r_0 \sim \textrm{C}^2/2$ and $R \sim 0$, which allow the term $K_\textrm{C}$ to reach its minimum, so that the coupling between the term $K_\textrm{C}$ and the two terms ${\widetilde{K}}_\textrm{C}, U$ is weaker and at a first approximation the motion of (G, g) is ruled by $({\widetilde{K}}_\textrm{C} + U)\vert _{r=r_0}$. In Fig. 4, we plot the phase portrait of the function $({\widetilde{K}}_\textrm{C} + U)\vert _{r=r_0}$ on the plane (g, G), with $U = U(r,G,g)$ truncated up to the order $1/r^3$ and parameters as in Eq. (19). Such plot approximates the motion of the variables (g, G) replacing panel (c) of Fig. 1.

Fig. 4

Phase portrait of the function $({\widetilde{K}}_\textrm{C} + U)\vert _{r=r_0}$ with parameters as in Eq. (19) on the plane (g, G)

According to assumptions (5) and (6), we choose the following values for the parameters⁴:

$$\begin{aligned} \left\{ \begin{array}{lll} C &{} = &{} 24.394 \\ \beta &{} = &{} 80 \\ \Lambda &{} = &{} 1 \end{array} \right. \, , \end{aligned}$$

(19)

and the following initial conditions:

$$\begin{aligned} \left\{ \begin{array}{lll} {\hat{G}} &{} = &{} -0.804 \\ {\hat{R}} &{} = &{} -0.006\\ {\hat{g}} &{} = &{} 1.4524 \\ {\hat{r}} &{} = &{} 625.256 \end{array} \right. \, . \end{aligned}$$

(20)

We do not choose $r=r_0$ and $R=0$ but values close to them, in order to well define, in the following, a section plane transversal to the orbit (as it will be described in Sect. 3). Moreover, G and g are chosen such that the orbit starting from $({\hat{G}}, {\hat{R}}, {\hat{g}}, {\hat{r}})$ under the flow of ${\overline{H}}$ is periodic in the four-dimensional phase space (G, R, g, r).

3 Poincaré map and hyperbolic structure

In this section we define a first return map in order to reduce the dimension of the phase space of the models introduced in Sect. 2. The simple idea is to start from the four-dimensional phase space (R, G, r, g), fix an energy level ${\overline{H}}_\textrm{fix}$ to derive R as a function of $(\overline{H}_\textrm{fix}, G,r,g)$ and consider the three-dimensional space (g, G, r). In such a space, we consider the projection of propagated orbits under the flow of ${\overline{H}}$, which are unidimensional curves in the three-dimensional space (g, G, r). Then, we fix a two-dimensional plane section orthogonal to a given orbit in a given point and study the first return map of orbits on such a plane.

We introduce a generalized first return map as follows: consider a compact domain $D \subset {\mathbb {R}}^2$; fix a two-dimensional plane $\Pi$ in the three-dimensional space (g, G, r) and define a two-dimensional map $\mathcal {P}_{\Pi }$ as

$$\begin{aligned} \mathcal {P}_{\Pi }: D\rightarrow & {} D \\ z\mapsto & {} z'= \mathcal {P}(z) \end{aligned}$$

where $z= (z_1,z_2) \in D$ is an unordered couple of combinations of variables (g, G, r), namely, $z = (z_1,z_2) \in \{(g,G),(g,r),(G,r) \}$; we call $z_3$ the remaining variable such that $(z_1,z_2,z_3) \in \Pi$; then we consider the initial condition $(z_1,z_2,z_3, R({\overline{H}}_\textrm{fix}, G,r,g))$ and propagate it under the flow $\Phi _{{\overline{H}}}^t$ obtaining the orbit $\Phi _{{\overline{H}}}^t (z_1,z_2,z_3, R)= (z_1(t),z_2(t),z_3(t), R(t))$ where $t \in {\mathbb {R}}$ is time. Moreover, we define $\mathcal {P}(z) =(z_1(\tau ),z_2(\tau ))$ where $(z_1(\tau ),z_2(\tau ))$ is such that $(z_1(\tau ),z_2(\tau ),z_3(\tau )) \in \Pi$ and $\tau = \inf \{t \in {\mathbb {R}}_+ \quad \vert \quad ((z_1(\tau ),z_2(\tau ),z_3(\tau )) \in \Pi \}$, namely, $\tau$ is the time of the first return on the plane $\Pi$.

The aim is to find a suitable Poincaré map of the flow $\Phi _{{\overline{H}}}^t$ and look for fixed points (corresponding to periodic orbits of the flow). If some hyperbolic fixed points exist, it is possible to construct stable and unstable manifolds of such points finding homoclinic or heteroclinic intersections which are the base to apply symbolic dynamics as described in Sect. 4.

In the following subsections we define suitable Poincaré maps for the two cases described in Sect. 2 (studied, respectively, in papers [9] and [8]).

3.1 A case of homoclinic intersection

Let us continue introducing first return maps for the model described in Sect. 2.1. The initial condition (10), corresponds to a periodic orbit in the four dimensional space. We consider the projection of such orbit in the three-dimensional space (g, G, r) and define a plane $\Pi _e$, in such a space, orthogonal to the orbit at the point $(g_e,G_e,r_e)$. We construct the two-dimensional map:

$$\begin{aligned} \mathcal {P}_{{\overline{H}}, \Pi _e}:[0;2 \, \pi ] \times [-1;1]\rightarrow & {} [0;2 \, \pi ] \times [-1;1] \\ (g,G)\mapsto & {} (g',G') \end{aligned}$$

where $(g',G')$ is the first return value on the plane $\Pi _e$. We take a grid of initial conditions (g, G) on the domain $D= [0;2 \, \pi ] \times [-1;1]$ and complete it so that the initial point $(g,G,r)\in \Pi _e$ and (R, G, r, g) has a fixed energy level; then, we iterate the first return map many times (in the order of $10^3$) to get a Poincaré section as shown in Fig. 7; we implement a Newton method in order to find fixed points of the map $\mathcal {P}_{{\overline{H}}, \Pi _e}$. We found two fixed points: $(g_e,G_e)$ and $(g_h,G_h)$. Studying the linear part of $\mathcal {P}_{{\overline{H}}, \Pi _e}$ and computing its eigenvalues, we see that the former is an elliptic point and the latter is a hyperbolic point (having real eigenvalues, one greater and one smaller than 1). The two points correspond to periodic orbits in the three-dimensional space (g, G, r). The first one, $\Gamma _e$, called elliptic, has a rotational behavior in the variable g while in the second, $\Gamma _h$, called hyperbolic, the variable g librates around the value $\pi$ (see the propagated variables in Figs. 5 and 6, respectively). In Fig. 7, we provide a visualization of the Poincaré section: on the upper panel, the two dimensional map is shown, and the elliptic and hyperbolic fixed points are represented in blue and red, respectively: we can see elliptic islands surrounding the elliptic point, rotational curves corresponding to regular tori and some chaos in the bottom part of the plot; on the bottom panel, we represent a three-dimensional visualization where the plane section $\Pi _e$ and the two periodic orbits are shown (the elliptic one in blue and the hyperbolic one in red).

We want to focus on the hyperbolic orbit to prove, numerically, existence of chaos. Let us recall Fig. 1a: level curves of the Euler integral function are shown for a fixed value of the variable $r\in (0,1)$. We define two-dimensional manifolds in the three-dimensional space (r, G, g) as:

$$\begin{aligned} {{\mathcal {M}}}({{\mathcal {E}}})=\{({r}, {G}, {g}):\ E({r}, {G}, {g})={{\mathcal {E}}}\} \, \end{aligned}$$

which, as the ${{\mathcal {E}}}$ changes, are essentially surfaces where the Euler integral E(r, G, g) remains equal to the constant value ${{\mathcal {E}}}$:

$$\begin{aligned} {{\mathcal {M}}}({{\mathcal {E}}}): r= \frac{G^2 -{\mathcal {E}}}{\sqrt{1-G^2}\cos g}. \end{aligned}$$

We are also interested in the manifold corresponding to the separatrix ${{\mathcal {S}}}_r ({ r})$, namely, ${{\mathcal {M}}}({r}) = {{\mathcal {M}}}_r =\{({ r}, {G}, {g}):\ {E}({r}, {G}, {g})=r\}$:

$$\begin{aligned} {{\mathcal {M}}}_r: r= \frac{G^2}{1+\sqrt{1-G^2}\cos g}. \end{aligned}$$

We analyze the relation between the hyperbolic orbit and the manifold ${{\mathcal {M}}}_r$ to show the presence of chaos close to this manifold as we shown in Fig. 8: let us start by comparing the variation of the variable r and the variation of the Euler integral versus time along the hyperbolic orbit: the value of the Euler integral is always greater than the value of the variable r, and in particular the minimum value $\mathcal {E}_{\min }$ of the Euler integral is greater than the maximum value $r_{\max }$ of the variable r. The values are very close and they are reached when $g= \pi$. This implies that the hyperbolic orbit touches the surface ${{\mathcal {M}}}({\mathcal {E}_{\min }})$ (in particular it lies on the surface in $g=\pi$ being tangent on that point) and never touches the surface ${{\mathcal {M}}}_r$ being the orbit always above this surface. In Fig. 9, it is possible to see a three-dimensional visualization of the hyperbolic orbit and of the two surfaces ${{\mathcal {M}}}({\mathcal {E}_{\min }})$ and $\mathcal{M} _r$.

Fig. 5

Evolution of the elliptic periodic orbit: panels a–d show, respectively, variables R, G, r, g versus time (figures already used in paper [9])

Fig. 6

Evolution of the hyperbolic periodic orbit: panels a–d show, respectively, variables R, G, r, g versus time (figures already used in paper [9])

Fig. 7

Upper: Poincaré section of map $\mathcal {P}_{{\overline{H}}, \Pi _e}$ is depicted in purple; the elliptic and hyperbolic fixed points are represented with blue and red dots, respectively. Bottom: spatial visualization of the section plane $\Pi _e$ with the section map in purple, the periodic orbits $\Gamma _e$, $\Gamma _h$ in blue and in red, respectively (figures already used in paper [9]) (color figure online)

Fig. 8

Orbit $\Gamma _h$: the variation of the variable r and of the Euler integral function E versus time are depicted in red and green, respectively. The constant values $r_{\max }$ and $\mathcal {E}_{\min }$ are represented in magenta and blue, respectively (color figure online)

Fig. 9

Three-dimensional visualization of the hyperbolic orbit $\Gamma _h$ in red is plotted; in magenta and in blue, respectively, the surfaces ${{\mathcal {M}}}({\mathcal {E}_{\min }})$ and ${{\mathcal {M}}} _r$ are represented (color figure online)

Observing the orbit numerically, we see that the maximum value $r_{\max } = 0.274496$ and the minimum value $r_{\min } = 0.022$ of the variable r, are both reached when $g=\pi$. The section plane $\Pi _e$ intersects the orbit $\Gamma _h$ in an intermediate point being the associated quadruplet (R, G, r, g) given by:

$$\begin{aligned} \Gamma _h:\qquad \left\{ \begin{array}{lll} R_h =10.331\\ G_h =0.718\\ r_h =0.132\\ g_h =5.699 = 1.8 \, \pi \end{array}. \right. \end{aligned}$$

We study, initially, the stable and unstable⁵ manifolds of the hyperbolic fixed point $(g_h,G_h)$ of the Poincaré map $\mathcal {P}_{{\overline{H}}, \Pi _e}$ and we claim (see Numerical Evidence 5.1 in [9]) that a Transverse Homoclinic Intersection between the stable and unstable manifolds for $\mathcal {P}_{{\overline{H}}, \Pi _e}$ exists.⁶ In fact, the two manifolds have a transverse intersection at the point $(g_h,G_h)$. Then, we consider different planes $\Pi _{h}^i$ orthogonal to $\Gamma _{h}$ at different points $({g}_{ i},{G}_{ i},{r}_{ i} )$ on the curve. We consider first return maps

$$\begin{aligned} {{\mathcal {P}}}_{{\overline{H}}, \Pi _{h}^i}:\qquad (g, G)\rightarrow (g', G') \end{aligned}$$

(21)

on $\Pi _h^i$. We denote as $\Pi _*$ the plane orthogonal to $\Gamma _h$ at

$$\begin{aligned} (g_*, G_*, r_*)=(1.27\,\pi , 0.346, 0.270)\, . \end{aligned}$$

(22)

This point of $\Gamma _h$ has been chosen for being “close” to ${{\mathcal {M}}}_r$. With this choice, we detect a homoclinic tangency⁷ and absence of splitting⁸ and claim (see Numerical Evidence 5.2 in [9]) that as soon as $r_{ i}$ is chosen closer and closer to ${r}_{\max }$ the stable tori zone becomes smaller and smaller. For $\Pi _{h}^i=\Pi _*$, stable motions are not numerically detected, and the unstable, stable manifolds have a homoclinic tangency at $(g_*, G_*)$. In other words a splitting of such manifolds (which have the shape of ${{\mathcal {S}}}_0(r_*)$) is not numerically detected. The idea is that the “near-homoclinic tangency”  in $(g_*, G_*)$ becomes a “homoclinic tangency”  in $(\pi , G_{**})$ (where $G_{**}$ is such that the point $(\pi ,G_{**}, r_{\max }) \in \Gamma _h$). We consider sections up to the point (22) and not up to $(\pi ,G_{**}, r_{\max })$ because this point is a cuspid for $\Gamma _h$ so that it is not possible to construct an orthogonal plane there. In Fig. 10, four first return maps (21) are shown where we represent the following objects:

• the elliptic (dark-blue dot) and the hyperbolic (dark-red dot) fixed points;

• rotational tori (purple curves);

• chaotic motions (dotted purple);

• the transverse/near-tangent homoclinic intersection between the stable (blue curve) and unstable (red curve) manifolds from $(g_i,G_i)$.

Fig. 10

First return maps on the planes $\Pi _h^i$ orthogonal to $\Gamma _h$ at $({g}_{ i},{G}_{ i},{r}_{ i} )\in \Gamma _h$, for $i=1, \dots ,4$ where, a–d correspond to $r_1 =0.13165,\,r_2 = 0.242432,\,r_3 = 0.252024,\,r_4 = r_* = 0.26987$, respectively (we recall that $r_{\max }= 0.274496$); note that in the panel d, the stable manifold (blue curve) is completely overlaid by the unstable manifold (red curve) at the hyperbolic fixed point. Figures already used in paper [9] (color figure online)

The last step we propose in this section in order to prove numerically the detection of chaos is to define a new first return map on the curve $\Gamma _h$ at the point $(g_*, G_*, r_*)$. The new section plane is taken to be vertical and in particular we consider the plane $\Pi ^*=\{g=g_*\}$. The two-dimensional first return map

$$\begin{aligned} {{\mathcal {P}}}_{{\overline{H}},\Pi ^*}:\qquad ({G}, {r})\rightarrow ({G}', {r}') \end{aligned}$$

(23)

is depicted in Fig. 11. The aspect of the stable and unstable manifolds changes drastically, but homoclinic intersections are present.

Fig. 11

In the upper panel, the first return map on the plane $\Pi ^*=\{ g= g_*\}$ is plotted; the section map is represented in purple, and the stable and unstable manifolds in blue and in red, respectively. In the center panel a three-dimensional visualizations on the space (g, G, r) is presented, while in the bottom panel we show the projection on the (g, r)-plane. In both panels the elliptic and hyperbolic fixed points are represented, respectively, with dark-blue and dark-red dots; the elliptic and hyperbolic orbits, respectively, with dark-blue and dark-red curves and the stable and unstable manifolds appear in blue and red, respectively. Note that, in bottom panel the stable and unstable manifolds appear as a segment because they belong to a vertical plane parallel to the plane (G, r) (figures already used in paper [9]) (color figure online)

3.2 A case of heteroclinic intersection

Let us consider now the model described in Sect. 2.2 and introduce the first return map as it has been done in the previous section. The initial condition (20) corresponds to a periodic orbit in the four dimensional space. We consider the projection of such orbit in the three-dimensional space (g, G, r) and define a plane $\Pi$, in such a space, orthogonal to the orbit at the point $({\hat{g}},{\hat{G}}, {\hat{r}})$. We construct a two-dimensional map $\mathcal {P}_{{\overline{H}}, \Pi }$ as:

$$\begin{aligned} \mathcal {P}_{{\overline{H}}, \Pi }:[0; \pi ] \times [-1;1]\rightarrow & {} [0; \pi ] \times [-1;1] \nonumber \\ (g,G)\mapsto & {} (g',G') \end{aligned}$$

(24)

where $(g',G')$ is the first return value on the plane $\Pi$. Note that the domain of the variable g is, in this case, $[0; \pi ]$ instead of $[0; 2 \,\pi ]$ due to the $\pi$-periodicity of Eq. (17). We take a grid of initial conditions (g, G) on the domain $D= [0; \pi ] \times [-1;1]$ and complete the quadruplet of the initial conditions such that $(g,G,r)\in \Pi$ and (R, G, r, g) has a fixed energy level; then, we iterate the first return map many times (in the order of $10^3$) to get a Poincaré section and we implement a Newton method in order to find fixed points of the map $\mathcal {P}_{{\overline{H}}, \Pi }$. This case is completely different from the previous one because, here, many hyperbolic and many elliptic fixed points are found. In Fig. 12 the following objects can be recognized:

• elliptic fixed points as blue dots;

• hyperbolic fixed points as red crosses;

• rotational tori in dark;

• librational islands in dark;

• chaotic motions as dotted dark.

Fig. 12

First return map on the plane $\Pi$. In black the section map is represented; elliptic and hyperbolic fixed points are depicted in blue and red, respectively (figures already used in paper [8]) (color figure online)

Fig. 13

Finite pieces of stable and unstable manifolds are depicted in blue and red, respectively. Left: homoclinic intersections between stable and unstable manifolds related to a hyperbolic fixed point. Right: heteroclinic intersections between stable and unstable manifolds of two different hyperbolic fixed points (figures already used in paper [8]) (color figure online)

We computed stable and unstable manifolds of some hyperbolic fixed points. In Fig. 13 left, we consider one fixed point and show finite pieces of stable (in blue) and unstable (in red) manifolds of such a point. In this case, many homoclinic intersections can be seen. In Fig. 13 right, we choose two hyperbolic fixed points $q_1$ and $q_2$ and show a small region of their stable (in blue) and unstable (in red) manifolds. In such figure the heteroclinic transversal intersections between the manifolds of the two points are detected and well visible.

4 Symbolic dynamics

In this section we recall some important definitions of covering relations and we remark the link with symbolic dynamics and existence of chaotic motions. It has been done following papers [11, 18, 19], and as in [8, 9], here we give a simplified version of the subject: in particular the results are valid in ${\mathbb {R}}^n$, while we restrict them to ${\mathbb {R}}^2$, being our first return maps defined on such a space.

Definition 1

(h-sets, [11, 19]) Let $N \subset {\mathbb {R}}^2$ be a compact set and let

$$\begin{aligned} c_{N}: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2 \end{aligned}$$

be a homeomorphism such that $c_N(N) = [-1,1]^2$.

• (i) The couple $(N, c_N)$ is called a h-set; N is called support of the h-set.

• (ii) Put

  $$\begin{aligned} N_c:=[-1,1]^2,\quad N_c^-:=\{-1,1\} \times [-1,1],\quad N_c^+:= [-1,1]\times \{-1,1\} \end{aligned}$$

and

$$\begin{aligned} S(N)_c^l:= & {} (-\infty , -1) \times {\mathbb {R}},\quad S(N)_c^r:=(1,\infty ) \times {\mathbb {R}}, \\ N_{c}^\textrm{le}:= & {} \{-1\}\times [-1,1],\quad N_{c}^\textrm{ri}:=\{1\}\times [-1,1]. \end{aligned}$$

The sets

$$\begin{aligned} N^- = c_N^{-1}(N_c^-),\quad N^+= c_N^{-1}(N_c^+) \end{aligned}$$

are called, respectively, the exit set and the entry set; the sets

$$\begin{aligned} N^\textrm{le} = c_N^{-1}(N_c^\textrm{le}),\quad N^\textrm{ri}=c_N^{-1}(N_c^\textrm{ri}) \end{aligned}$$

are called, respectively, the left edge and the right edge of N; the sets

$$\begin{aligned} S(N)^l:= c_N^{-1}(S(N)_c^l),\quad S(N)^r = c_N^{-1}(S(N)_c^r) \end{aligned}$$

are called, respectively, the left side and the right side of N.

The following definition is fitted to the special case (realised in our study) that the unstable manifold has dimension 1. The simplification compared to the general definition in [11, 19] is based on [19, Theorem 16].

Definition 2

(Covering relation, [11, 19]) Let $f: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ be a continuous map and N and M the supports of two h-sets. We say that M f-covers N and we denote it by $M {\mathop {\Longrightarrow }\limits ^{f}}N$ if:

(1):

$\exists \, q_0\in [-1, 1]$ such that $f(c^{-1}_{M}([-1, 1]\times \{q_0\}))\subset \textrm{int}( S(N)^l \bigcup N \bigcup S(N)^r)$;

(2):

$f(M) \bigcap N^+ = \emptyset$;

(3):

$f(M^\textrm{le})\subset S(N)^\textrm{l}\quad \textrm{and}\quad f(M^\textrm{ri})\subset S(N)^\textrm{r}$ or

(3)$'$:

$f(M^\textrm{le})\subset S(N)^\textrm{r}\quad \textrm{and}\quad f(M^\textrm{ri})\subset S(N)^\textrm{l}$.

If $M=N$, we say that f self-covers N.

Conditions (2) and (3) are called, respectively, exit and entry condition.

In Fig. 14, we represent a schematic example of covering and self-covering relation.

Fig. 14

Examples of covering (left) and self-covering (right) relations are represented: in red the entry sets and their image are represented, while in blue the exit sets and their images are represented (figures already used in paper [8]) (color figure online)

Let us now proceed by defining a topological horseshoe as follows:

Definition 3

Let $N_{0}$ and $N_{1}$ be the supports of two disjoint h-sets in ${\mathbb {R}}^2$. A continuous map $f: {\mathbb {R}}^2 \rightarrow \mathbb R^2$ is said to be a topological horseshoe for $N_0$ and $N_1$ if

$$\begin{aligned} N_0 {\mathop {\Longrightarrow }\limits ^{f}}N_0, \quad N_0 {\mathop {\Longrightarrow }\limits ^{f}}N_1, \quad N_1 {\mathop {\Longrightarrow }\limits ^{f}}N_0, \quad N_1 {\mathop {\Longrightarrow }\limits ^{f}}N_1. \end{aligned}$$

Topological horseshoes are associated to symbolic dynamics as presented in Theorem 2 in [11] and Theorem 18 in [19], where the authors show that the existence of a horseshoe for a map f provides a semi-conjugacy between f and a shift map $\{0,1\}^{{\mathbb {Z}}}$, meaning that for any sequence of symbols 0 and 1 there exists an orbit generated by f passing through the sets $N_1$ and $N_2$ in the order given by the sequence, guaranteeing the existence of “any kind of orbit” (periodic orbits, chaotic orbits, etc.). Let us also generalize the notion of symbolic dynamics, giving a weaker definition:

Definition 4

Let $D\subset {{\mathbb {R}}}^2$

$$\begin{aligned} {f }:\qquad D\rightarrow {{\mathbb {R}}}^2, \end{aligned}$$

we say that f has m-symbolic dynamics if there exist compact subsets with non-empty interior $N_0$, $N_1\subset D$ such that,

for every $n\in {\mathbb {N}}$ and any finite sequence $(\sigma _0$, $\ldots$, $\sigma _n)$ of symbols $\sigma _i\in \{0,\ 1\}$ having length $n+1$, one can find $x_0\in N_{\sigma _0}$ such that the orbit of $x_0$ under f, namely, $x_j:={f }^j(x_0)$ is well defined for $j=0$, $\ldots$, nm, and $x_{mj}\in N_{\sigma _j}\quad \forall \ j=0,\ldots , n$.

1-SYMBOLIC dynamics in $N_0\cup N_1$ is also called horseshoe.

In Fig. 15, we represent a schematic example of a 1-symbolic dynamics and a 3-symbolic dynamics in $N_0\cup N_1$.

Fig. 15

Schematic examples of 1-symbolic dynamics, namely, a topological horseshoe (left) and of a 3-symbolic dynamics (right) of the map f for $N_{0},N_{1}$. In red tones the entry sets and their images are depicted, while in blue tones the exit sets and their images are represented (figures already used in paper [8]) (color figure online)

Let us continue by provide the following important results:

Theorem 1

([18]) Let $N_i$, $i=0$, $\ldots$, k, be h-sets such that $N_0=N_k$. Let

$$\begin{aligned} f_i:\ N_{i-1}\rightarrow {{\mathbb {R}}} \qquad \forall \ i=1,\ldots , k\, \end{aligned}$$

be a continuous map such that

$$\begin{aligned} N_{0} {\mathop {\Longrightarrow }\limits ^{f_1 }}N_1{\mathop {\Longrightarrow }\limits ^{f_2 }}\cdots {\mathop {\Longrightarrow }\limits ^{f_k }}N_{k}=N_0. \end{aligned}$$

Then, there exists $x_0\in N_0$ such that

• (i) $f_i\circ f_{i-1}\circ \cdots \circ f_1(x_0)\in N_{i}\quad \forall \ i=1,\ldots , k\,;$

• (ii) $f_k\circ f_{k-1}\circ \cdots \circ f_1(x_0)= x_0.$

We shall use Theorem 1 in the following form:

Corollary 1

([9]) Let

$$\begin{aligned} {f }:\quad D\rightarrow {{\mathbb {R}}}^2 \end{aligned}$$

with $D\subset {{\mathbb {R}}}^2$ and let $N_0$, $N_1$ be h-sets in D. Assume that there exist h-sets $M^{(\sigma , \sigma ')}_i$, with $i=1$, $\ldots$, $m-1$ and $\sigma$, $\sigma '\in \{0, 1\}$, such that

$$\begin{aligned} N_\sigma {\mathop {\Longrightarrow }\limits ^{f }}M^{(\sigma , \sigma ')}_1 {\mathop {\Longrightarrow }\limits ^{f }}M^{(\sigma , \sigma ')}_2\cdots {\mathop {\Longrightarrow }\limits ^{f }}M^{(\sigma , \sigma ')}_{m-1}{\mathop {\Longrightarrow }\limits ^{f }}N_{\sigma '} \quad \forall \ \sigma ,\ \sigma '\in \{0,1\}. \end{aligned}$$

Then f has m-symbolic dynamics in $N_0\cup N_1$. In addition, an orbit $x_k$ corresponding, as in Definition 4, to a given sequence $\sigma _0$, $\ldots$, $\sigma _n$, can be chosen so that it is well defined for $i=0$, $\ldots$, $(n+1)m$ and, moreover, $x_{(n+1)m}=x_0$.

5 Application of symbolic dynamics to the studied cases

In this section we apply definitions and theorems provided in Sect. 4. We want to show that the models described in previous sections admit chaotic motions in terms of m-symbolic dynamics. All the following results are numerically proved by an accurate control of propagation errors. Let us present the results in the two following sections.

5.1 Existence of 3-symbolic dynamics of the map ${{\mathcal {P}}}_{{\overline{H}},\Pi ^*}$

Numerical Evidence 1  The map $\mathcal{{P}}_{{\overline{H}},\Pi ^*}$ in (23) has a 3-symbolic dynamics. Moreover, an orbit $\{x_j\}_{j=0,\ldots , 3n}$ corresponding to a given sequence $\sigma _0, \ldots , \sigma _n$, can be chosen to be extendible for $j=0,\ldots , 3(n+1)$ and periodic, with period $N\in \{1,\ldots ,3(n+1)\}$.

Moreover, we provide explicit formulas of sets realizing the 3-symbolic dynamics. Let us consider the map ${{\mathcal {P}}}_{\overline{H},\Pi ^*}$ in (23). The stable and unstable eigenvectors related to $D{{\mathcal {P}}}_{{\overline{H}},\Pi ^*}$ at

$$\begin{aligned} q_*=({G}_*,{r}_*)=( 0.345986, 0.26987) \end{aligned}$$

(25)

have directions, respectively,

$$\begin{aligned} v^s= (0.831003, \,-0.556268 ) , \quad v^u=( 0.0495113, \, -0.998774), \end{aligned}$$

and the angle between them is $\alpha = 0.296467 \, \pi$. We denote as $N_0$ the parallelogram through $q_*$ with edges parallel to $v^s$ and $v^u$, namely:

$$\begin{aligned} N_0 = q_* +A_0 v^s +B_0 v^u \, , \end{aligned}$$

(26)

where $A_0$, $B_0$ are the real intervals

$$\begin{aligned} A_0=[-0.000719075, 0.000719075],\qquad B_0=[-0.0000400491, 0.0000400491]. \end{aligned}$$

We define two analogous parallelograms:

$$\begin{aligned} N_1 = q_1 + A_1 {\widetilde{v}}^s + B_1 v^u,\qquad N_2 = q_2 + A_2 v^s + B_2 v^u \end{aligned}$$

(27)

where

$$\begin{aligned} \left\{ \begin{array}{l} q_1 =({G}_1, {r}_1) =(0.34598,0.269552)\\ q_2 =({G}_2, {r}_2) =(0.343432,0.27124) \end{array} \right. , \end{aligned}$$

with

$$\begin{aligned} A_1= & {} [-0.000028763,0.000208532] ,\qquad B_1 = [-0.000144177,0.00000400491], \\ A_2= & {} [-0.000179769,0.000107861], \qquad B_2 = [-0.00000400491,0.000200246] \end{aligned}$$

and

$$\begin{aligned} {\widetilde{v}}^s=(-0.556143,0.831003).\ \end{aligned}$$

Then, we state the following

Numerical Evidence 2

$$\begin{aligned} N_0 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny {\mathcal {H}},\Pi ^*}}}}N_0 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny {\mathcal {H}},\Pi ^*}}}}N_1 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny {\mathcal {H}},\Pi ^*}}}}N_2 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny {\mathcal {H}},\Pi ^*}}}}N_0 \quad , \quad N_2 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_1. \end{aligned}$$

Splitting such relations as

$$\begin{aligned} \left\{ \begin{array}{lll} N_0 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_1 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_2 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_0\\ \\ N_0 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_1 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_2 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_1\\ \\ N_1 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_2 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_0 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_0\\ \\ N_1 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_2 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_0 {\mathop {\,\Longrightarrow \,}\limits ^{{{\mathcal {P}}}_{\!{\tiny \mathcal H,\Pi ^*}}}}N_1 \end{array} \right. \end{aligned}$$

and in view of Corollary 1, the Numerical Evidence 1 follows, with $N_0$, $N_1$, $N_2$ as in (26), (27).

In Fig. 16 the construction of the covering relations is represented and in Fig. 17, it is possible to see that the sets involved are obtained by analyzing the homoclinic intersections of the stable and unstable manifolds through $q_*$ and exploiting the property of contraction and expansion, respectively, of the stable and unstable manifolds.

Fig. 16

Numerical Evidence 2: 3-symbolic dynamics of map ${{\mathcal {P}}}_{{\overline{H}},\Pi ^*}$ for $N_0$,$N_1$ is represented. Red represents the entry sets and their images and blue the exit sets and their images. The fixed point $(G_*,r_*)$ in (25) is marked in red. The bottom panel represents a zoom of the upper panel (figures already used in paper [9]) (color figure online)

Fig. 17

Details on the construction of the sets (26) and (27). Light blue and orange denote, respectively, the stable and unstable manifolds. The bottom panel represents a wider region (figures already used in paper [9]) (color figure online)

5.2 Existence of a horseshoe of the map ${{\mathcal {P}}}_{{\overline{H}},\Pi }$

The same result in its stronger version is obtained for the map ${{\mathcal {P}}}_{{\overline{H}},\Pi }$ in Eq. (24). In this section we use the same notations for points, intervals and sets as in the previous section but they are related, in this case, to the map ${{\mathcal {P}}}_{{\overline{H}},\Pi }$. We state the following

Numerical Evidence 3 The map $\mathcal{P}_{{\overline{H}},\Pi }$ has a symbolic dynamics.

Also in this case we provide explicitly the sets which form the associated topological horseshoe. Based on a couple of hyperbolic fixed points of ${{\mathcal {P}}}_{{\overline{H}},\Pi }$ whose coordinates read

$$\begin{aligned} \left\{ \begin{aligned}&q_{1}=(g_{1},G_{1}) = (0.203945459,2.06302430), \\&q_{2}=(g_{2},G_{2}) = (0.278077917,2.21418596), \end{aligned} \right. \end{aligned}$$

and whose stable and unstable manifolds and their heteroclinic intersections are shown in Fig. 13, we define two sets $N_{1}, N_{2} \subset {\mathbb {R}}^2$ which are supports of two h-sets as follows:

$$\begin{aligned} \left\{ \begin{aligned}&N_{1} = q_1 + A_1 v_1^s +B_1 v_1^u, \\&N_{2} = q_2 + A_2 v_2^s +B_2 v_2^u, \end{aligned} \right. \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{aligned}&A_{1} = [-0.02,0.08], \quad B_{1} = [-0.025,0.01], \\&A_{2} = [-0.075,0.025], \quad B_{2} = [-0.02,0.01], \end{aligned} \right. \end{aligned}$$

and $v_{1}^s,v_1^u,v_2^s,v_2^u$ are the stable and the unstable eigenvectors related to $q_{1},q_{2}$, respectively. Then:

Numerical Evidence 4 The following covering relations hold

$$\begin{aligned} N_1 {\mathop {\Longrightarrow }\limits ^{{{\mathcal {P}}}_{{\overline{H}},\Pi }}}N_1, \quad N_1 {\mathop {\Longrightarrow }\limits ^{{{\mathcal {P}}}_{{\overline{H}},\Pi }}}N_2, \quad N_2 {\mathop {\Longrightarrow }\limits ^{{{\mathcal {P}}}_{{\overline{H}},\Pi }}}N_1, \quad N_2 {\mathop {\Longrightarrow }\limits ^{{{\mathcal {P}}}_{{\overline{H}},\Pi }}}N_2, \end{aligned}$$

proving the existence of a topological horseshoe for ${{\mathcal {P}}}_{{\overline{H}},\Pi }$.

Namely, we prove, numerically, the existence of symbolic dynamics for ${{\mathcal {P}}}_{{\overline{H}},\Pi }$. The obtained horseshoe associated to $q_{1}$ and $q_{2}$ with the aforementioned parameters is illustrated in Fig. 18. Looking at Fig. 13 it is possible to see how the two sets $N_1,N_2$ are, respectively, contracted and stretched under the map ${{\mathcal {P}}}_{{\overline{H}},\Pi }$ according to the stable and unstable directions.

Fig. 18

Horseshoe connecting the points $q_1$ and $q_2$ proving symbolic dynamics for the map $P={{\mathcal {P}}}_{\overline{H},\Pi }$. Red represents the entry sets and their images and blue the exit sets and their images (figure already used in paper [8]) (color figure online)

6 Conclusions and perspectives

The problem covered in this article arises from the important paper by V.I. Arnold ( [1]), and it has been investigated by many authors in the last decades (see for example [2, 5, 7, 10, 13, 14]). Related to the current paper are [4, 16, 17] where the same problem is faced by an analytical point of view in order to prove stability estimates by using normal form theory.

The idea of the numerical investigation and the application of covering relations and symbolic dynamics to this problem comes from the recent paper [11]. In the current paper, we have summarized the results obtained in previous articles (see [8, 9]) underlining a method to prove numerically the existence of chaos in the full three-body problem. The authors of these papers are carrying on the study by analyzing how the results change when the non-averaged problem given by Eq. (3) is considered. We would like also to extend the results to the spatial case and to prove the obtained results about onset of chaotic motions from an analytically point of view.