Abstract
Models of epidemic dynamics in the form of systems of differential equations of the type SIR and its generalizations, for example SEIR and SIRS, have become widespread in epidemiology. Their coefficients are averages of some epidemic indicators, for example the time when a person is contagious. Statistical data about spreading of the epidemic are known in discrete periods of time, for example twenty-four hours. Therefore, adjustment of the differential equations system under such data comes across cleanly calculable difficulties. They can be avoided, initially to build a model in discrete time as a system of difference equations. Such initial consideration allows, as it shown in the article, to get a general model. On its basis, the models of development of epidemics can be built taking into account their specific. There is another way to obtain a model in discrete time. It consists in discretizing the original model in continuous time. The model obtained in this way is inaccurate, and it is only an approximation to the original one, which makes it possible to simplify calculations and increase the stability of the calculation process. This model is inappropriate, for example, for fitting the model to statistical data. Another argument against the use of systems of differential equations is that the coefficients of such a model may not be the same during a day. For example, the number of contacts of an infected person with susceptible people during a day differs from that at night. However, there is no such difference for daily data. It is possible depending on the day of the week.
Similar content being viewed by others
1 Model of Kermack and McKendrick and their system of differential equations SIR
We will use the set denotations according to that all population of some territory (region, country) in quantity \(N\) is divided by categories: \(S\) (susceptible, receptive are people that were not infected or lost immunity after infecting), \(I\) (infected, infected and being contagious) and \(R\) (recovered). Let \(S(t)\) is a number of susceptible people in the moment of time \(t\), where \(t\) is a continuous value. The values \(I(t)\) and \(R(t)\)—numbers of infected and recovered in the moment of time \(t\)—have analogical sense.
The enumerated values satisfy to balance equation
Assumption 1 A number \(N\) is fixed. Functions of time in (1) are determined.
This assumption will be faithful for an interval of time of epidemic modeling, if it is possible to omit the demographic changes on this interval.
If the epidemic is being modeled for the large interval of time, then \(N\) will be also depend on time to take into account demographic changes.
If assumption 1 is correct, then, from (1), we have
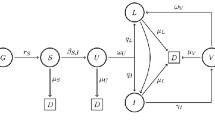
The values in right part of (1) are connected with each other. This connection can be presented as a chain (Figs. 1, 2, 3, 4 and 5).
Hypergeometrical distribution of duration of recovery \(h_{\tau }\) depending on lag \(\tau\) for \(\overline{W}_{R} (s) = {k \mathord{\left/ {\vphantom {k {A(s)}}} \right. \kern-0pt} {A(s)}}\), \(k = \left( {1 - q_{1} } \right)\left( {1 - q_{2} } \right)\), \(A(s) = \left( {1 - q_{1} s} \right)\left( {1 - q_{2} s} \right)\), \(q_{1} = 0,8\), \(q_{2} = 0,61\)
Hypergeometrical distribution of duration of recovery \(h_{\tau }\) depending on lag \(\tau\) for \(\overline{W}_{R} (s) = {k \mathord{\left/ {\vphantom {k {A(s)}}} \right. \kern-0pt} {A(s)}}\), \(k = \left( {1 - q_{1} } \right)\left( {1 - q_{2} } \right)\left( {1 - q_{3} } \right)\), \(A(s) = \left( {1 - q_{1} s} \right)\left( {1 - q_{2} s} \right)\left( {1 - q_{3} s} \right)\), \(q_{1} = 0,8\), \(q_{2} = 0,61\) \(q_{3} = 0,2\)
Susceptible \(S \Rightarrow\) infected \(I \Rightarrow\) recovered \(R\), which is designated as \({\text{SIR}}\).
Exactly this name was got by one of the most popular models of epidemiology. A few its modifications are known now. We will formulate the model SIR using the model of Kermack and McKendrick.
Let \(i(t - \tau )\) be a number of not recovered (active infected, so contagious people) to the moment of time \(t\), infected before on an interval of time \(\tau\), it is decreasing exponentially at process of recovering as \(\tau\) is increasing. Then the whole number of active infected people in the considered population at the moment of time \(t\) is
where \(e^{ - \lambda \tau }\) is a weight coefficient and \(\lambda\) is a coefficient.
The sum of weight coefficients is \(\int\limits_{0}^{\infty } {e^{ - \lambda \tau } {\text{d}}\tau } = \frac{1}{\lambda }\). Dividing both parts of (3) on this number, we will get the average number of active infected on the interval from \(- \infty\) to \(t\)
Here, in an integrand, \(\lambda e^{ - \lambda \tau }\) is the probability density of distribution exponential law with the parameter \(\lambda\) of random value \(\tau\)—the duration of one infected person staying in the state of active infecting, in the flow of that he is being treated, remaining contagious.
We will denote the basic number of reproduction by \(r_{0}\). It means the average number infected by one diseased in times of his active infecting. It is assumed that the infected person is surrounded by unvaccinated individuals in the absence of anti-epidemic measures.
Multiplying both parts (4) on \(\frac{{S(t)r_{0} }}{N}\), we will get
So
This expression is the model of Kermack and McKendrick [3]. In (6), \(\frac{S(t)}{N}\) is the probability of meeting of one infected person and healthy person who is receptive to the infection. Then \(r_{0} \frac{S(t)}{N}\) is the average number of random “successful” (resulting in an infection) contacts of one infected person for the time, when he is contagious. Then, because the integral in right part (4) is the average number of active infected person to the moment of time \(t\), we come to the conclusion that in (6) \(i(t)\) is a number of new infected people in the moment of time \(t\).
We will show out a model SIR. From exponential distribution of duration of active infecting, when a man is contagious, it follows that the expectation of duration of stay in a state of contagiousness is
Taking into account this expression, we get from the first equality in (5)
Because the number of people in population is fixed, then
From (8) and (9), it follows that
From this equation and (2), we have
From the last two equations, considering the speed of recovery \(\frac{{{\text{d}}R(t)}}{{{\text{d}}t}}\) equal to the average of infected people to the moment of time \(t\), defined in (4), we will get the differential equations system of model SIR of Kermack and McKendrick [9] that found the wide use; in particular, it was used for modeling of distribution of COVID–19 [2]:
The brought conclusion (10) is some simpler than the conclusion of this model in [3], where differentiation of certain integral depending on a parameter is used.
It is possible to solve a reverse task: on the second–basic equation in (10) to get the first equality in (5). It ensues from the second equation in (10), relation \(I(t) = \int\limits_{0}^{t} {i(\tau )} {\text{d}}\tau - R(t)\) and (7).
To the known drawbacks of the model (10), it is possible to take that it is based on an exponential distribution law of one person infecting duration. However, the protracted application of model SIR showed that this limitation was not critical. Another drawback of this model takes place from the third equation in (10). It supposes that speed of recovery, i.e., number of recovered people in arbitrary moment of time, relates proportionally to the number of contagious people. Actually, the speed of recovery depends on immunity of a person, other properties of their organism, medications and other factors. Because the recovery of infected people is a process with distributed lag [6, 14], then more difficult expression, than the third equation in (10), can appear its adequate model. In particular, this may lead to the use of higher-order derivatives \(R(t)\). The third drawback (10) is that there are no statistical data for the main variable \(I(t)\). To get them, it is necessary to make calculations on present statistics. Such recount can result in appearance of additional error.
2 Models for discrete time
Values \(S,I,R\) can be certain from statistical data only in discrete periods of time (usually, twenty-four hours). Therefore, if the model (10) is driven in to existent statistics, then the behavior of functions of time into these periods of time is not informing. But the considerable calculable resources are spent on the receipt of just the same information. From said follows expediency of transition from the model (10) where continuous time is used, to the model with discrete time \(t = 0,1,2, \ldots\). So we specify that the values \(S,I,R\) are known in equidistant periods of times. Consequently, we must replace in (10) all differentials by differences so that sense of differences corresponded to sense of right parts of equalizations. Therefore, we will replace \({\text{d}}S(t)\) by the difference \(S(t) - S(t - 1)\), \({\text{d}}I(t)\)—by the difference \(I(t) - I(t - 1)\), \({\text{d}}R(t)\)—by the difference \(R(t) - R(t - 1)\). Also we will replace \({\text{d}}t\) by the difference \(t - \left( {t - 1} \right) = 1\). To underline that values \(S,I,R\) are the functions of discrete time, we will specify their argument \(t\) in an index further, for example \(S_{t}\). Taking into account said, from (10), we have
Here \({{r_{0} } \mathord{\left/ {\vphantom {{r_{0} } {T_{I} }}} \right. \kern-0pt} {T_{I} }}\) means the number of contacts of infected person with susceptible ones for one period of time, chosen in the model as the unit of counting (twenty-four hours, week, etc.). We will notice that in (10) the same value does not have such clear sense.
The SIR models for discrete time described in the literature coincide with (11). Thus, the deterministic SIR model, studied in [1], is identical to (11) if the demographic process is excluded from it. The same can be said about the SIR model for discrete time in [22] if the variable, the number of unrecovered (dead) people, is excluded from it.
A model (11) has the same drawbacks as (10), discussed above, plus one more drawback: (11) is an approximation of (10), more about it later, after Statement 1.
To remove them, we will generalize expression (6). We will replace in it the density of exponential distribution on an arbitrary not increasing on a nonnegative numerical axis nonnegative function \(q(\tau )\) such that \(\mathop {\lim }\limits_{\tau \to \infty } q(\tau ) = 0\), \(\int\limits_{0}^{\infty } {q(\tau ){\text{d}}\tau } = 1\), what gives:
Let us put
where \(Q(\tau ) \ge 0\) is an arbitrary non-increasing nonnegative function defined on \([0,\infty )\), and \(\mathop {\lim }\limits_{\tau \to \infty } Q(\tau ) = 0\). This function characterizes the infectivity of the infected person.
Then
Let now \(t \ge 0\), integer. Then from (14), we have \(i_{t} = \frac{{r_{0} }}{{NQ_{\Sigma } }}S_{t - 1}^{{}} \sum\limits_{\tau = 0}^{\infty } {Q_{\tau } i_{t - 1 - \tau }^{{}} }\). Let us add one more to this equation: \(S_{t} = S_{t - 1} - i_{t}\), \(S_{t} \ge 0\). Then we obtain a system of equations for discrete time, in which the fourth equation describes the recovery process in the form of the distributed lag model:
where \(Q_{\Sigma } = \sum\limits_{\tau = 0}^{\infty } {Q_{\tau } }\).
In (15), \(i_{t}\) is a number of infected people in the period of time \(t\); \(I_{t}\) is a number of active infected people before the period of time \(t\)—an analogue of (3) for discrete time; \(\tau\) is the time shift backward (integer number of periods of time); \(U_{t}\) is a quantity of recovering or not recovering (the dead) people in the period of time \(t\); and \(h_{\tau } \ge 0\) is a lag coefficient.
It follows from the definition of \(U_{t}\) and non-negativity of \(h_{\tau }\) that
According to the terminology [6, 14], we will name the sequence of coefficients of lag in (15)
by the lag structure of treatment. It is infinite in this case, because consists of infinite number of coefficients of lag. According to (16), since \(h_{\tau } \ge 0\)
The lag structure, satisfying (16), (18), is named normalized. Here \(h_{0}\) is a part of number of infected (diseased) people that were ill 1 period of time, \(h_{1}\) is a part of being ill 2 periods of time, \(h_{2}\) is a stake of being ill 3 periods of time,…, \(h_{\tau }\) is a part of being ill \(\tau\) periods of time. Thus, in (15) \(h_{\tau } i_{t - 1 - \tau }^{{}}\) is part of the people infected in the period of time \(t - 1 - \tau\) that recovered or died to the period of time \(t - 1\).
According to (16) and (18), it is possible to examine \(h_{\tau }\) as probability of event that the infected person will be ill \(\tau\) periods of time. Such interpretation of \(h_{\tau }\) results in a conclusion that, in (15), \(U_{t}\) is the average number of recovered and not recovered (the dead) persons in the period of time \(t\).
If the lag structure is finite: \(h_{\tau }\), \(\tau = 1,2, \ldots ,\tau_{R}\); \(Q_{\tau }\), \(\tau = 1,2, \ldots ,\tau_{I}\), \(\tau_{I} \le \tau_{R}\), than (15) has a view:
As it applies to the model (19) it is simpler to understand the meaning of basic number of reproduction of \(r_{0}\). We will present that, in a population, only one infected person appeared in the period of time \(t - 1\). Then, for large \(N\), it is possible to consider \(S_{t - 1}^{{}} = S_{t}^{{}} = S_{t + 1}^{{}} = \cdots = S_{{t + \tau_{I} }}^{{}} = N\). According to (19) in the period of time \(t\), one man will infect \({{r_{0} Q_{0} S_{t - 1}^{{}} } \mathord{\left/ {\vphantom {{r_{0} Q_{0} S_{t - 1}^{{}} } {NQ_{\Sigma } }}} \right. \kern-0pt} {NQ_{\Sigma } }}\) people on the average, after 1 period—\({{r_{0} Q_{1} S_{t}^{{}} } \mathord{\left/ {\vphantom {{r_{0} Q_{1} S_{t}^{{}} } {NQ_{\Sigma } }}} \right. \kern-0pt} {NQ_{\Sigma } }}\) people, after 2 periods of time—\({{r_{0} Q_{2} S_{t + 1}^{{}} } \mathord{\left/ {\vphantom {{r_{0} Q_{2} S_{t + 1}^{{}} } {NQ_{\Sigma } }}} \right. \kern-0pt} {NQ_{\Sigma } }}\) people, etc. to \({{r_{0} Q_{{\tau_{I} }} S_{{t + \tau_{I} - 1}}^{{}} } \mathord{\left/ {\vphantom {{r_{0} Q_{{\tau_{I} }} S_{{t + \tau_{I} - 1}}^{{}} } {NQ_{\Sigma } }}} \right. \kern-0pt} {NQ_{\Sigma } }}\). As a result, for all the time, while a person is the carrier of infection, he will infect \({{\left( {r_{0} Q_{0} + r_{0} Q_{1} + r_{0} Q_{2} + \cdots + r_{0} Q_{{\tau_{I} }} } \right)} \mathord{\left/ {\vphantom {{\left( {r_{0} Q_{0} + r_{0} Q_{1} + r_{0} Q_{2} + \cdots + r_{0} Q_{{\tau_{I} }} } \right)} {Q_{\Sigma } }}} \right. \kern-0pt} {Q_{\Sigma } }} = r_{0}\) people. Thus, \(r_{0}\) is a number of susceptible people that at the beginning of epidemic can be infected by one infected person for time, when he is contagious. Therefore, the number of reproduction depends on the density of distribution of people in a population and its quantity.
We introduce the function
that, according to (16), (18), is such that
We will define now in (19) values \(Q_{\tau }\), \(\tau = 1,2, \ldots ,\tau_{I}\) that we will call the infection lag coefficients. According to (19) the number \(S_{t}^{{}}\) of susceptible people in the period of time \(t\) cooperate with infected ones in periods of time \(t - 1,\;t - 2,\;t - 3, \ldots ,t - \tau_{I}\), part of them had recovered to the period of time \(t\). We will define the number of remaining contagious (not yet recovered) people in indicated by \(\tau_{I}\) periods of time.
All people, infected in the period of time \(t\), are the carriers of infection. Therefore, \(Q_{0} = 1 - H_{0 - 1} = 1\). In the period of time \(t - 1\), the part of carriers of infection will make \(Q_{1} = 1 - H_{0} = 1 - h_{0}\). Analogously, we get \(Q_{2} = 1 - H_{1} = 1 - \left( {h_{0} + h_{1} } \right)\). In general case by account of (21)
Formula (22) can be applied for the infinite lag structure, when \(\tau_{I} = \infty\). In this case the second equality in (22) is not required.
The systems of Eqs. (15) and (19) can be written more compactly. To do this, we introduce the concept of a shift operator in time backward by one period of time: \(Lf_{t} = f_{t - 1}\), where \(f_{t}\) is an arbitrary function of discrete time \(t\). Then,
where \( W_{R} (L) = \sum\nolimits_{{\tau = 0}}^{{\tau _{R} }} {h_{\tau } L^{\tau } } \) in accordance with [14] we will name the transmission function of the treatment lag. In the formula, \(\tau_{I}\) can be both finite and infinite value for \(W_{R} (L)\). At the same time, \(\sum\limits_{\tau = 0}^{{\tau_{R} }} {h_{\tau } } = 1\); therefore, in (15), (19) \(Q_{\Sigma } = \sum\nolimits_{\tau = 0}^{{\tau_{I} }} {Q_{\tau } }\) will be a finite value, if \(\tau_{I} = \infty\). Not to estimate the infinite number of coefficients of lag in (15) that is impossible, \(W_{R} (L)\) is expedient to describe by a fractional–rational function \(L\) with the not high degree of polynomials of numerator and denominator [14]. The structure of treatment lag of the known fractional–rational function \(W_{R} (L)\) is determined on simple enough formulas [14]. In case of infinite lag structure, its replacement by finite structure consists of determination of such maximal lag \(\tau_{R}\), for that, for example, \(\left| {1 - \sum\nolimits_{\tau = 1}^{{\tau_{R} }} {h_{\tau } } } \right| \le 0,05\), \(\tau_{R} < \infty\).
Analogously we will enter the transmission function of infecting \(w_{I} (L)\):
Then
Taking into account the entered designations, we have from (15) and (19) for the case of vaccination
where \(v_{t}\) is a number of vaccinated people in \(t\)th period of time that are immune to the infection; \(\overline{I}_{t - 1} = {{I_{t - 1} } \mathord{\left/ {\vphantom {{I_{t - 1} } {Q_{\Sigma } }}} \right. \kern-0pt} {Q_{\Sigma } }}\) is the average number of infected people in \(t - 1\)th period of time; \(W_{I} (L) = {{w_{I} (L)} \mathord{\left/ {\vphantom {{w_{I} (L)} {w_{I} (1)}}} \right. \kern-0pt} {w_{I} (1)}} = \sum\nolimits_{\tau = 0}^{{\tau_{I} }} {q_{\tau } L^{\tau } }\); and \(\tau_{I}\) is a finite or infinite value.
Transmission function \(W_{R} (L)\) in (24) can be evaluated on time series \(U_{t}\) and \(i_{t}\), \(t = 1,2, \ldots\) by methods [6, 14]. To find \(W_{I} (L)\), if \(W_{R} (L)\) is a polynomial or fractional–rational function, we will define connection of these transmission functions.
Theorem 1
If durations of recovery and active infecting are random nonnegative integer values, then
Proof
If the lag structure of recovery (17) satisfies to the conditions (16), (18), then it can be considered as the law of distribution of integer random value with some generating function \(W_{R} (s)\). Then \(\frac{{W_{R} (s)}}{1 - s}\) is a generating function of sequence \(H_{t}\), \(t = 0,1,2, \ldots\), given in (20). For a sequence \(H_{t - 1}\), \(t = 1,2, \ldots\), there is a generating function \(\frac{{sW_{R} (s)}}{1 - s}\). From here, using a theorem 1 in [7], chapter XI, we get the generating function of the sequence \(Q_{t}\), \(t = 0,1,2, \ldots\) in (22).
From (26), we get the generating function of duration of infecting
where \(w_{I} (1) = \mathop {\lim }\limits_{s \to 1} w_{I} (s)\), and concordantly (23), \(Q_{\Sigma } = w_{I} (1)\).
Replacing in (27) \(s\) by an operator \(L\), we will get expressions for transmission functions in an operator form (25).◊
It is necessary to use expression (25) if \(W_{R} (s)\) is fractional–rational function. If \(W_{R} (s)\) is a polynomial, then establishing a connection of structures of recovery lag and active infecting lag consists in determination of sequence \(Q_{\tau }\), \(\tau = 0,1,2, \ldots ,\tau_{I}\) on a formula (22) that follows from (26). After that, according to (27), we obtain coefficients \(q_{\tau } = {{Q_{\tau } } \mathord{\left/ {\vphantom {{Q_{\tau } } {Q_{\Sigma } }}} \right. \kern-0pt} {Q_{\Sigma } }}\), \(\tau = 0,1,2, \ldots ,\tau_{I}\), of function \(W_{I} (s)\), \(Q_{\Sigma }\) is set by (23).
Corollary 1
Let (1) duration of recovery be described by the geometrical law of distribution with the generating function \(W_{R} (s) = \frac{{\left( {1 - p} \right)}}{{\left( {1 - ps} \right)}}\), \(0 < p < 1\); and (2) durations of recovery and active infecting coincide. Then duration of the active infecting also submits to this law: \(W_{I} (s) = \frac{{\left( {1 - p} \right)}}{{\left( {1 - ps} \right)}}\).
Proof
From (26), we have \(w_{I} (s) = \frac{1}{{\left( {1 - ps} \right)}}\). From here, \(w_{I} (1) = \frac{1}{{\left( {1 - p} \right)}}\). Then according to (27) \(W_{I} (s) = W_{R} (s) = \frac{{\left( {1 - p} \right)}}{{\left( {1 - ps} \right)}}\). Thus, if recovery lag submits to the geometrical law, then actively infected people lag is described by the same law with the same parameter \(p\).◊
An important special case of (24) should be considered.
Statement
(discrete-time model \({\text{SIR}}\)). From the general system of Eq. (24), the model with variables \(S_{t} ,\;I_{t} ,\;R_{t}\) follows for \(W_{I} (s) = \frac{{\left( {1 - p} \right)}}{{\left( {1 - ps} \right)}}\):
Proof
To prove the statement, it is necessary to write Eq. (24) for \(W_{I} (s) = W_{R} (s)\) (according to Corollary 1) using the variables \(S_{t} ,\;I_{t} ,\;R_{t}\). Therefore, let us turn to (15) which is another form of representation of system (24). For the geometric distribution law of the treatment lag, its coefficients are \(h_{\tau } = \left( {1 - p} \right)p^{\tau }\), \(\tau = 0,1,2, \ldots\). Hence, according to (20) \(H_{\tau - 1} = \left( {1 - p^{\tau } } \right)\), \(\tau = 1,2, \ldots\). According to (22), we obtain \(Q_{\tau } = p^{\tau }\), \(\tau = 0,1,2, \ldots\), which gives \(Q_{\Sigma } = \left( {1 - p} \right)^{ - 1}\) in (15). Then it follows from the second equation in (15) that \(i_{t} = \frac{{r_{0} \left( {1 - p} \right)}}{N}S_{t - 1} I_{t - 1}\). If \(S_{t} \ge 0\), then \(S_{t} - S_{t - 1} = - i_{t}\), which gives.
From the fourth equation in (24) and the conditions of this statement, we have
From here, we get
Considering the initial condition to be zero: \(U_{t} = i_{t} = 0\), \(t < 0\), we have \(\sum\nolimits_{j = 0}^{t} {U_{j} } = R_{t}\), \(\sum\nolimits_{j = 0}^{t} {U_{j - 1} } = \sum\limits_{j = 0}^{t - 1} {U_{j} } = R_{t - 1}\), \(\sum\limits_{j = 0}^{t} {i_{j - 1} } = \sum\limits_{j = 0}^{t - 1} {i_{j} } = R_{t - 1} + I_{t - 1}\). It follows from the last four equalities that
Let us replace the functions of continuous time \(S(t),\;I(t),\;R(t)\) in formula (1) by the functions \(S_{t} ,\;I_{t} ,\;R_{t}\), respectively, which gives for \(N = const\) the relation \(I_{t} - I_{t - 1} = - \left( {S_{t} - S_{t - 1} } \right) - \left( {R_{t} - R_{t - 1} } \right)\). Substituting into it the difference equations obtained above for \(S_{t}\) and \(R_{t}\), we have \(I_{t} - I_{t - 1} = \frac{{r_{0} \left( {1 - p} \right)}}{N}S_{t - 1} I_{t - 1} - \left( {1 - p} \right)I_{t - 1}\). Combining this formula with the mentioned equations for \(S_{t}\) and \(R_{t}\) (taking into account the non-negativity of \(S_{t}\)) gives the desired model.◊
It does not coincide exactly with the system of Eqs. (11), which follows from the model \({\text{SIR}}\) of Kermack and McKendrick by replacing differentials in it by differences. The discrepancy appeared due to different first equations and different coefficients at \(I_{t}\) in all equations, since \(\frac{1}{{T_{I} }} = \frac{{\left( {1 - p} \right)}}{p} \ne 1 - p\) for \(0 < p < 1\). Here \(T_{I} = {p \mathord{\left/ {\vphantom {p {\left( {1 - p} \right)}}} \right. \kern-0pt} {\left( {1 - p} \right)}}\) is the expectation of the duration of infecting, distributed according to the geometric law. The discrepancy is due to the fact that (11) is an approximation of a model \({\text{SIR}}\) with an exponential law of infecting duration distribution, while the model formulated in Statement 1 is based on the description of the durations of all processes by a geometric distribution law.
The graphs \(I_{t}\) for the model (11) and the model \({\text{SIR}}\) for discrete time under the condition that mathematical expectations of duration of infecting, distributed according to exponential and geometric laws, are the same and equal to \(T_{I}\), are shown in Fig. 4. Figure 4 shows that the discrepancy between the two curves is significant. For example, for \(t = 70\) \(I_{70} = 0.678 \cdot 10^{6}\) (discrete-time model \({\text{SIR}}\)), \(I_{70} = 1.953 \cdot 10^{6}\) (model (11)).
The system of equations with variables, obtained in Statement 1, is equivalent to the system of equations with variables \(S_{t}\), \(i_{t}\), \(U_{t}\), which is the particular case of (24):
We note that in the model (29) the population value can be variable over time, while the model in Statement 1 assumes its constancy.
The important feature of the model (29) follows from said—it corresponds to the process of recovery when greater part of people recover for short time. Such situation is met not always. Then the distribution law mode will be not zero. The example of such situation is a structure of treatment lag, corresponding to the law of Pascal distribution. Other example, when this structure is a sum of \(n\) independent random values which have a geometrical law of distribution [19]. In both cases, a generating function of law of distribution (17) is a fractional–rational function \(s\).
In first case (Pascal distribution), lag coefficients in (17) and their generating function:
Calculating the first difference \(\Delta h_{t + 1} = h_{t + 1} - h_{t}\) and equating it to the zero, we will get a formula for the mode of Pascal distribution.
where \([a]\) means rounding off \(a\) to the nearest bigger integer.
The law of distribution and the generating function of the sum of \(n\) independent random values with the geometrical law of distribution are
where constants \(C_{i}\), \(i = 1, \ldots ,n\), are functions of \(p_{i}\), \(i = 1, \ldots ,n\) and \(h_{0}\).
At \(n = 2\) and \(p_{1} = p_{2}\), a generating function in (30) follows from a generating function in (31).
According to (30), (31) for these distributions, \(h_{0} \ne 0\).
If it is impossible to ignore a value \(h_{0}\), and infecting and recovery for the same twenty-four hours do not correspond to the real data, it is possible, in \(W_{R} (s)\), to enter a constant lag \(\tau_{0}\)—minimal interval of time necessary for treatment. Then \(W_{R} (s)\) will have a view
where \(k\) is a constant and\(A(s)\) is a polynomial of \(s\).
It is possible to go by another way, decreasing \(h_{0}\) in distribution (31). Then it is necessary to increase \(n\) as it follows from this formula. However, the mathematical expectation and the mode of distribution (31) will increase here that is not always acceptable. An attempt, increasing \(n\) at preservation of these descriptions of distribution (31), results in small reduction of \(h_{0}\). The said is illustrated in Figs. 1, 2 and 3 for \(\tau_{0} = 0\) in (32).
Thus, (32) remains as the cardinal method of reduction of \(h_{0}\).
In conclusion, we present a connection diagram of the main models described in this paragraph, see Fig. 5@@@@@.
3 Solution analysis of Eqs. ( 24 ) system
The solution of (24) is determined by the first three equations of this system, because a dynamics of \(U_{t}\) is fully set by a change of \(i_{t}\).
From the second and third equations in (24), we have
where
Equation (33) is linear homogeneous difference equation of \(n\)th order with variable coefficients, where \(n\) is an order of polynomial in a denominator \(W_{I} (L)\), if \(W_{I} (L)\) is a fractional–rational function. If \(W_{I} (L)\) is a polynomial, then \(n = \tau_{I}\).
A solution of (33), which is identically not equal to the zero, turns out for nonzero initial conditions, i.e., corresponds to appearance of the infected people in a population. It initiates a change of their number, which is a transition process in a population from one stable state to another.
From (33), because according to explanation to formula (24) \(W_{I} (L) = \sum\limits_{\tau = 0}^{{\tau_{I} }} {q_{\tau } L^{\tau } }\), where \(\tau_{I}\) can be a finite or infinite value, we have
where \(0 \le q_{\tau } \le 1\); \(\tau_{I}\)\(\le \infty\).
We will consider, as \(q_{\tau }\) in (35) is changing, if in (32) \(\tau_{0} \ne 0\). In this case, we have from (26).
The generating function \(w_{I1} (s) = \left( {\frac{1}{1 - s} - \frac{{s^{{\tau_{0} }} }}{1 - s}} \right) =\)\(Q_{0} + Q_{1} s + \cdots + Q_{{\tau_{0} - 1}} s^{{\tau_{0} - 1}}\), where \(Q_{0} = Q_{1} = \cdots = Q_{{\tau_{0} - 1}} = 1\), in the time domain, corresponds to the function
A generating function \(w_{I2} (s) = \left( {1 - s} \right)^{ - 1} \left( {1 - s\overline{W}_{R} (s)} \right)\,s^{{\tau_{0} }}\) is product multiplication of rational (polynomial) or fractional–rational function \(s\) to \(s^{{\tau_{0} }}\). The function \(f_{t2} = 0\), \(0 \le t \le \tau_{0} - 1\), corresponds it. If \(f_{t2}\) is a fractional–rational function, then for \(t \ge \tau_{0}\) it either exponentially decreases to the zero or has one maximum and also converges to the zero, as on a Fig. 3, Fig. 4, Fig. 1. Otherwise a function \(f_{t2}\) has arbitrary values on an interval \(\left[ {\tau_{0} ,\,\tau_{I} } \right]\), \(\tau_{I} < \infty\).
Thus, we get that in general case in (35).
Thus, if there is a constant lag in (32), then at first \(\tau_{0}\) periods of time contagiousness of infected will be identical and maximal. If it is known that ability of transmission of infection decreases, since the period of time, when it was received, then a variable \(\tau_{0}\) needs to be decreased to the necessary value, maybe to the zero, in a transmission function \(W_{R} (s)\) in a formula (26).
Now we will define the character of function \(g_{t}\) changing in (35).
Lemma 1
Let: (1) quantity \(N\) of population in time is constant, \(v_{t} = 0\); 2) \(S_{t - 1}^{{}} > 0\), 3) in a sequence \(\left\{ {i_{t - 1 - \tau }^{{}} } \right\}\), \(\tau = 0, \ldots ,\tau_{I}\), there is at least one member more than zero. Then \(g_{t} > g_{t + 1}\).
Proof
We will suppose opposite that \(g_{t} = g_{t + 1}\) (other alternatives are not present). From here, it follows that \(S_{t - 1}^{{}} = S_{t}^{{}}\). Then from the first equation in (24), we will get \(i_{t} = 0\). But according to (35) and assumption 3) \(\overline{I}_{t - 1} > 0\). Therefore, from the second equation in (24) we get \(S_{t - 1}^{{}} = 0\). We came to contradiction with assumption 2) that completes the proof of the lemma.◊
Thus, for a finite \(t\), limit number of infected people \(i_{t - \tau }\), \(\tau = 1,2, \ldots ,\tau_{\max }\), according to (35) \(i_{t} = 0\) only, if \(g_{t} = 0\) that gives \(S_{t - 1}^{{}} = 0\) and means the end of the transition process in the population.
Let us study the properties of the transient process. We will consider the particular case (33) at first, when duration of recovery is described by the geometrical law of distribution. Then according to Corollary 1\(W_{I} (s) = \frac{{\left( {1 - q} \right)}}{{\left( {1 - qs} \right)}}\). From here and (33), we have difference equation of the first order
where \(a_{t} = q + g_{t} (1 - q)\).
Thus, the only coefficient of Eq. (36) is the linear function \(g_{t}\). Solution of this equation
If in the initial period of time \(t = 0\) we do not have the infected people, \(i_{0} = 0\), then \(i_{t} = 0\) due to the limitation of \(g_{t}\) according to (34), for any \(t > 0\). Let \(i_{0} > 0\), \(g_{{t^{*} }} \le 1\). By virtue of strictly monotonic decrease of \(a_{t}\) that is determined by the same change of \(g_{t}\), \(i_{t} \to 0\) also strictly monotonously as \(t \to \infty\), if \(S_{\infty } = \mathop {\lim }\limits_{t \to \infty } S_{t} \ge 0\). In this case duration of transition process will be infinitely large. If \(S_{t - 2}^{{}} > 0\) and \(S_{t - 1}^{{}} = 0\) for some finite \(t\), than, from equality \(S_{t} = \max \left( {0,S_{t - 1} - i_{t} } \right)\), it follows that \(i_{t} = 0\), \(t > 0\). In this case the duration of a transition process will be finished in the period of time \(t\), i.e., on a finite interval of time. These reasoning prove such result.
Theorem 2
If the process of development of epidemic is described by the model (24) at \(v_{t} = 0\), \(\forall t\), in that the duration of treatment lag is distributed on a geometrical law, then a population will be steady to the infection in an arbitrary period of time \(t = t_{0}\), when \(g_{{t^{*} }} \le 1\). In this case, the number of infected people \(i_{t}\) in the period of time \(t > t_{0}\) will converge asymptotically to the zero with the increase of time at \(\mathop {\lim }\limits_{t \to \infty } S_{t} \ge 0\): \(\mathop {\lim }\limits_{t \to \infty } i_{t} = 0\), \(t > t_{0}\). Other variant of transition process, when for some point \(t = t_{*}\) it will be \(S_{{t_{*} - 2}} > 0\), \(S_{{t_{*} - 1}} = 0\) that draws \(S_{t} = i_{t} = 0\), \(t \ge t_{*}\).
If \(g_{{t^{*} }} > 1\), then a population will be unstable to the infection. In this case \(i_{t}\) will monotonously increase to some \(t = t^{*}\), for that \(g_{{t^{*} }} = 1\). Then according to (37) because of strictly monotonous reduction of \(g_{t}\) the number of infected will decrease to the zero, as well as in case of population which is stable to the infection.◊
This theorem gives a sufficient condition to stability of population to the infection, because it can be that \(g_{t} > 1\) and \(q < a_{t} < 1\).
We will consider a general case now.
Theorem 3
Let the process of development of epidemic be described by a model (24), where \(v_{t} = 0\), \(\forall t\); dependence \(i_{t}\) on an amount of infected people in previous periods of time is determined by formula (35), in that \(\sum\limits_{\tau = 0}^{{\tau_{I} }} {q_{\tau } } = 1\), \(q_{\tau } \ge 0\), \(\tau = 0, \ldots ,\tau_{I}\). A sequence \(\left\{ {i_{t - \tau } } \right\} = i_{t - 1} ,i_{t - 2} ,i_{t - 1} , \ldots\) is given. Then inequality \(g_{{t^{*} }} \le 1\) is the sufficient condition of stability of population to the infection in the period of time \(t\):
\(\mathop {\lim }\limits_{\tau \to \infty } i_{r + \tau } = 0\) or \(i_{t + \tau } = 0\), \(\tau \ge \tau^{*}\), \(\tau^{*}\) is finite, in addition \(i_{r + \tau } \le c\), \(\forall \tau \ge 0\), \(c = \mathop {\max }\limits_{\tau \ge 0} i_{t - 1 - \tau }\).
Proof
Let an initial sequence has identical members, equal to \(c\):
In accordance with (35), coming from (38), we will define a sequence.
\(\left\{ {\overline{i}_{t + \tau } } \right\}\), \(\tau = 0,1,2, \ldots\).
1) Suppose, at first, that \(\tau_{I} = \infty\). We have concordantly (35) and conditions of the theorem \(\overline{i}_{t} \le g_{t} c\sum\limits_{\tau = 0}^{{\tau_{I} }} {q_{\tau } } = g_{t} c\). In accordance with (38)
For the subsequent periods of time, taking into account monotonous decrease of \(g_{t}\), according to Lemma 1, we have
Continuing, for some \(j \ge 1\), we will get
This inequality is turning into strict inequality at \(\tau = 0, \ldots ,j - 2\).
We will show that \(\overline{i}_{t + j} < \overline{i}_{t + j - 1}\), where \(\overline{i}_{t + j - 1}\) is the result of monotonous decrease in the number of infected that corresponds to (40). We have taking into account (38).
Analogously.
According to Lemma 1, \(g_{t}\) is strictly monotonously decreasing function; therefore, from the last two inequalities concordantly (40) we have
From this inequality and (40), it follows
2) Let now \(\tau_{I}\) is a finite value. Then \(c = \mathop {\max }\limits_{{0 \le \tau \le \tau_{I} }} i_{t - 1 - \tau }\). Thinking like in the case 1), we will get inequalities.
from that we have like in the case 1)
To obtain inequality of the form (42) for the large values of \(t\), we will use relations
From here, we have
From this inequality, using (42), for arbitrary \(j \ge 1\) we get
which corresponds to (40).
From (44), because \(\overline{i}_{t + j - 1 - \tau } - \overline{i}_{t + j - 2 - \tau } \le 0\), \(\tau = 0, \ldots ,\tau_{I}\), concordantly (40), it follows that \(\overline{i}_{t + j} < \overline{i}_{t + j - 1}\).
Thus, for a finite and infinite value \(\tau_{I}\), the number of infected \(\overline{i}_{t + \tau }\) is strictly monotonously decrease, at least, since \(\tau = 1\). Therefore, \(\overline{i}_{t + \tau }^{{}} \le c\), \(\forall \tau \ge 0\). By virtue of restriction \(\overline{i}_{t + \tau } \ge 0\) there is a limit \(\mathop {\lim }\limits_{\tau \to \infty } \overline{i}_{r + \tau } = \overline{i}_{\infty } \ge 0\). Function of time \(S_{t}\), also monotonously decreasing, can become equal to 0 for some finite \(t\) according to the first equation in (24) or asymptotically approach the limit \(S_{\infty } \ge 0\).
3) Let \(S_{t} \to S_{\infty } \ge 0\) at \(t \to \infty\). Then from the first equality in (24), it follows that \(i_{\infty } = \mathop {\lim }\limits_{\tau \to \infty } i_{t + \tau } = 0\). Otherwise, when \(S_{t + \tau - 1} > 0,\;\;S_{t + \tau } = 0\) for some finite time \(t + \tau\), we have \(\overline{i}_{t + \tau + l} = 0\), \(l \ge 1\). Consequently, always \(\overline{i}_{\infty } = 0\).
We will compare now sequences \(\left\{ {\overline{i}_{t + \tau } } \right\}\) and \(\left\{ {i_{t + \tau } } \right\}\), \(\tau = 0,1,2, \ldots\) An initial sequence (38) generates the first sequence. The second sequence is generated by a sequence of general view \(\left\{ {i_{t - \tau } } \right\} = i_{t - 1} ,i_{t - 2} ,i_{t - 3} , \cdots\). For some \(\theta \ge 0\) concordantly (35), we have
If \(\overline{i}_{t + \theta - 1 - \tau }^{{}} \ge i_{t + \theta - 1 - \tau }^{{}}\) for \(\forall \tau \ge 0\), then \(\overline{i}_{t + \theta } \ge i_{t + \theta }\). Thinking in the same way, we get sequentially \(\overline{i}_{t + \theta + 1} \ge i_{t + \theta + 1}\), \(\overline{i}_{t + \theta + 2} \ge i_{t + \theta + 2}\),… Because \(i_{t - 1} \le c,\;\,i_{t - 2} \le c,\;\,i_{t - 3} \le c, \cdots\), from the brought reasoning, it follows that \(\overline{i}_{t + \tau }^{{}} \ge i_{t + \tau }^{{}}\), \(\forall \tau \ge 0\). It was shown above that \(c \ge \overline{i}_{t + \tau }^{{}}\), \(\forall \tau \ge 0\). Consequently, \(c \ge \overline{i}_{t + \tau }^{{}} \ge i_{t + \tau }^{{}}\), \(\forall \tau \ge 0\). From this, the rest of the statements of the theorem follow.◊
Corollary 2
Let an epidemic begin in the period of time \(t = 0\): \(i_{0} > 0\), and \(S_{ - 1} = N\), \(i_{ - 1} = 0\). Restrictions on the coefficients of lag in (35) are the same that in Theorem 3. Then \(g_{0} = r_{0} \le 1\) is the sufficient condition of stability of population to the infection in this period of time.
Proof
We have \(S_{0} = N - i_{ - 1}\), consequently, \(g_{1} < 1\). From (35), we get \(i_{1} = g_{1} q_{0} i_{0} < i_{0}\). Thinking further, as well as in 1) and 2) of proof of Theorem 3, we will get \(i_{t} < i_{0}\), \(t \ge 1\). Then like in 3) of this proof, we have \(\mathop {\lim }\limits_{t \to \infty } i_{t} = 0\).◊
Similar result is given by the threshold theorem of mathematical epidemiology for continuous time. The flash of epidemic takes place if and only if when \(r_{0} > 1\). Otherwise, the infection disappears.
According to Theorem 3\(g_{t}\), it is possible to use for the prognosis of time period, when a number of infected will be maximal. For this purpose, it is needed to have a forecast of the susceptible number. The result obtained is the period of time after which the number of infected people is guaranteed to decrease. This clarification is explained by that at a value \(g_{t} > 1\), near by 1, the value of \(i_{t}\) may begin to decrease because condition of Theorem 3 is sufficient.
4 Model in presence of latent period in infection
In this case, there is a time interval of random length, during that a person is infected, but is not contagious. We will denote the number of such people in a time period \(t\) by \(e_{t}\) (\(e_{t}\) is the first letter of word exposed). Generalizing (24), we will get a corresponding model:
where \(W_{E} (L)\) is a latent state transmission function or in the other words \(W_{E} (s)\) is the generating function of the duration of the latent state is a random variable.
Statement 2
(discrete-time model \({\text{SEIR}}\)). From (45) for \(W_{I} (s) = \frac{{\left( {1 - p} \right)}}{{\left( {1 - ps} \right)}}\), \(W_{E} (s) = \frac{{\left( {1 - p_{E} } \right)}}{{\left( {1 - p_{E} s} \right)}}\) It follows a model that is equivalent to the model continuous-time \({\text{SEIR}}\):
where \(T_{E} = {{p_{E} } \mathord{\left/ {\vphantom {{p_{E} } {\left( {1 - p_{E} } \right)}}} \right. \kern-0pt} {\left( {1 - p_{E} } \right)}}\) is the mathematical expectation of the duration of the latent state, distributed according to the geometric law.
Proof
To prove the statement, it is necessary to write Eqs. (45) using the variables \(S_{t} ,\;E_{t} ,I_{t} ,\;R_{t}\), taking into account that according to Corollary 1 we have \(W_{I} (s) = W_{R} (s)\).
Since the last equations in (24) and (45) are the same, the fourth equation in this statement coincides with (28).
For the condition of this statement, the third equation in (45) follows the equality \(\left( {1 - p_{E} L} \right)i_{t} = \left( {1 - p_{E} } \right)e_{t}\); moreover, \(e_{t} = i_{t} = 0\), \(t < 0\). Let us sum both its parts from 0 to \(t\): \(\sum\limits_{j = 0}^{t} {i_{j} } - p\sum\nolimits_{j = 0}^{t} {i_{j - 1} } = \left( {1 - p} \right)\sum\nolimits_{j = 0}^{t} {e_{j - 1} }\). We have \(\sum\nolimits_{j = 0}^{t} {i_{j} } = I_{t} + R_{t}\), \(\sum\nolimits_{j = 0}^{t} {i_{j - 1} } = \sum\nolimits_{j = 0}^{t - 1} {i_{j} } = I_{t - 1} + R_{t - 1}\), \(\sum\nolimits_{j = 0}^{t} {e_{j - 1} } = \sum\nolimits_{j = 0}^{t - 1} {e_{j} } = E_{t - 1} + R_{t - 1} + I_{t - 1}\). After transformations, we obtain from the last four equalities that \(I_{t} = I_{t - 1} + \frac{{\left( {1 - p_{E} } \right)}}{{p_{E} }}E_{t} - \left( {R_{t} - R_{t - 1} } \right)\). Taking into account (28), the third equation in the statement assertion follows from here. The second equation in it is obtained from the equality following from the condition \(N = const\): \(E_{t} - E_{t - 1} = - \left( {S_{t} - S_{t - 1} } \right) - \left( {I_{t} - I_{t - 1} } \right) - \left( {R_{t} - R_{t - 1} } \right)\). According to Statement 1, \(S_{t} - S_{t - 1} = - \frac{{r_{0} \left( {1 - p} \right)}}{N}S_{t - 1} I_{t - 1}\). Let us substitute this difference, as well as the growth increase in the numbers of infected and recovered, which follow from the above formulas for \(I_{t}\), \(R_{t}\), into the right side of the expression for \(E_{t} - E_{t - 1}\). After the transformation, we get the second and first equations in the statement.◊
Let us now transform the model \({\text{SEIR}}\) [3], p. 6.5 to discrete time, replacing differentials by differences, similarly to derivation of (11). We have
This model is an approximation of \({\text{SEIR}}\) for continuous time and is different from the model \({\text{SEIR}}\) for discrete time. This difference is illustrated in Fig. 5. A significant difference in the curves for the number of infected \(I_{t}\) is shown in it. For example, for \(t = 127\) \(I_{127} = 1.410 \cdot 10^{6}\) (discrete-time model \({\text{SEIR}}\)), \(I_{127} = 0.413 \cdot 10^{6}\) (model \({\text{SEIR}}\) approximation for continuous time). Turning to the comparison of models \({\text{SIR}}\), see above, we come to the conclusion that the models discrete-time \({\text{SIR}}\) and \({\text{SEIR}}\), which are special cases of (29) and (45), respectively, differ from the discrete approximations of these models that can lead to a significant difference in the variables of the same name. For discrete time, models of the first type are adequate, since they are based on the geometric law of the distribution of integer durations of the latent period, infecting and other processes. Models of the second type use the exponential law, which is the law of distribution of a continuous random variable, to describe the same processes in discrete time.
Stability of population to the infection, if its distribution is described by (45), is in a next statement.
Theorem 4
Let the process of development of epidemic be described by the model (45) in which all transmission functions of lag are a polynomial from \(L\) or a fractional–rational function of \(L\) and \(W_{I} (1) = W_{E} (1) = 1\). Then the sufficient condition of stability of population to the infection in the time period \(t\) is inequality \(g_{t} \le 1\), \(g_{t} = \frac{{r_{0} }}{N}S_{t - 1}^{{}}\).
Proof
We have from (45).
Behavior of \(e_{t}\), being described by this expression, determines stability of population to the infection. We will find condition for that a sequence \(e_{t} ,e_{t} ,e_{t} , \ldots\) will be not non-increasing for arbitrary \(t\).
According to said above, \(W_{I} (s)\) is generating function of sequence \(\left\{ {q_{\tau } } \right\}\), \(\tau = 0, \ldots ,\tau_{I}\). We will enter a nonnegative sequence \(\left\{ {d_{\tau } } \right\}\), \(\tau = 0, \ldots ,\tau_{E}\), generating function of which is \(W_{E} (s)\). This sequence makes sense as the structure of transition lag from latent to the infected state. Then \(W_{I} (s)W_{E} (s)\) is a generating function of sequence \(\left\{ {\eta_{\tau } } \right\}\), \(\tau = 0, \ldots ,\tau_{\max }\), \(\tau_{\max } = \tau_{I} \tau_{E}\) is convolution of previous two sequences: \(\left\{ {\eta_{\tau } } \right\} = \left\{ {q_{\tau } } \right\}*\left\{ {d_{\tau } } \right\}\) or more detailed
because sequences \(\left\{ {q_{\tau } } \right\}\) and \(\left\{ {d_{\tau } } \right\}\) are nonnegative. On the other hand, \(W_{I} (1)W_{E} (1) = 1\), because \(W_{I} (1) = W_{E} (1) = 1\) on conditions of the theorem. From here and (47), it follows that
From (46), we have
where \(\overline{E}_{t}\) is the average number of people in a latent state in the time period \(t\).
The expression (49) with the accuracy to the designations coincides with formula (35). Therefore, applying to (49) all reasoning at proof of Theorem 3, we will get that for arbitrary \(t\) at implementation of terms of this theorem, \(\mathop {\lim }\nolimits_{\tau \to \infty } e_{r + \tau } = 0\), if \(S_{\infty } > 0\). If \(S_{t + \tau } = 0\) for some finite time \(t + \tau\), we have \(e_{t + \tau + l} = 0\), \(l \ge 1\). Then from (45), we have \(\mathop {\lim }\limits_{\tau \to \infty } i_{r + \tau } = 0\) or \(i_{r + \tau } = 0\) for finite \(t + \tau\), what completes proof of the theorem.
We will consider a situation now, when at presence of latent period the part of the infected people are ill without symptoms (type 1), and other part (type 2) are isolating themselves (easy form of illness) or hospitalized (heavy form of illness). People of type 1 do not pass testing on a presence for them of infection, do not treat them self and do not appear in statistics of diseased and recovered unlike the people of the second type. We will consider that such people pass testing not immediately, as they become contagious, but through an interval of time of random length with a generating function \(W_{c} (s)\).
We will denote: \(\Delta_{j}\) is a number of people of \(j\)th type \(\left( {j = 1,2} \right)\); \(e_{tj}\) and \(i_{tj}\) are number of people of \(j\)th type in \(t\)th period of time, respectively, getting the hidden form of infecting and becoming contagious; \(\overline{I}_{tj}\) is the average number of infected (contagious) \(j\)th type in the period of time \(t\); \(U_{tj}\) is a number of recovered people of \(j\)th type in the time period \(t\) (\(U_{t2}\) includes non-recovered). We will enter the generating functions of durations of treatment and contagiousness of people of \(j\)th type \(W_{Rj} (s)\) and \(W_{Ij} (s)\); \(i_{t}\) is a number of infected of all types for time period \(t\); \(ic_{t}\) is a number of the infected people of the second type, the infecting of which is laboratory confirmed for time period \(t\); and \(e_{t}\) is a number of people of all types getting the hidden form of infecting for time period \(t\).
For the brought values, we have
A value \(ic_{t}\) is needed for its comparison with statistics of the new infected people.
Based on (45) and (50), we obtain a model for the case under consideration.
We will assume that the duration of the time interval when the sick is contagious is the same for both types of people. Then previous expressions are simplified:
Here \(W_{I1} (L)\) is determined according to (26), (27), if to put in these formulas \(W_{R} (s) = W_{R1} (s)\) and \(W_{I} (s) = W_{I1} (s)\) responsibly, \(W_{I1} (L)\). \(W_{I1} (L) = \sum\limits_{\tau = 0}^{{\tau_{I} }} {q_{\tau } L^{\tau } }\), \(W_{I2} (L) = \sum\limits_{\tau = 0}^{{\tau_{I} }} {q_{\tau } \rho_{\tau } L^{\tau } }\), where \(0 < \rho_{\tau } \le 1\) is a multiplier, taking into account the reduction of probability of getting infected of healthy man \(q_{\tau }\) in case of self-isolation and (or) hospitalization of sick of the second type; \(\tau\) is the duration of the time interval, when a sick is contagious.
We will mark that at \(\Delta_{1} = 1\), (45) follows from (51).
We will suppose that, since the time period when the results of testing in the presence of infection become known, sick person of the second type is isolated. Then the time interval during which a sick person is contagious is divided into two non-overlapping intervals: 1) from the period of time, when a sick person became contagious, to the period of time, when his infection was confirmed by laboratory testing; 2) the time interval, when a sick person is isolated and contagious.
Let a sequence (law of distribution) \(\left\{ {c_{\tau } } \right\}\), \(\tau = 0,1,2, \ldots\), corresponds to a generating function \(W_{c} (s)\), \(c_{\tau }\) is unimodal function. We will enter the sets \(\Omega_{1} = \left\{ {\tau :\;\;c_{\tau } \ge c_{\tau - 1} } \right\}\), \(\Omega_{2} = \left\{ {\tau :\;\;c_{\tau } \le c_{\tau - 1} ,\;\;c_{\tau } \ge \varsigma } \right\}\), \(\Omega = \Omega_{1} \cup \Omega_{2} \cup \left\{ 0 \right\}\), where \(\varsigma = 0.05(0.1)\). Then in the formula for \(W_{I2} (L)\) in (51)
where \(m \ge 1\). Thus, it is allowed that in a state of isolation, sick person can be contagious in the period of active infecting, but with less intensity.
Taking into account said, from (51), we have
The relationship between the models described in this paragraph is shown in Fig. 7.
We will define the condition of stability to the infection for a population that is described by a model (52). According to Sect. 2 of this paper, \(r_{0}\) is a number of people that at the beginning of epidemic can be infected by one person for time, when they are contagious. Analogously, for the same situation in the conditions of isolation of a person, a relation \({{r_{0} } \mathord{\left/ {\vphantom {{r_{0} } m}} \right. \kern-0pt} m}\) means the number of people that can be infected from one infected person. Consequently, \({{r_{0} > r_{0} } \mathord{\left/ {\vphantom {{r_{0} > r_{0} } m}} \right. \kern-0pt} m}\) and \(m > 1\). We put \(\frac{{r_{0} }}{m} = n_{1} p_{1} + n_{2} p_{2}\), where \(n_{1}\) and \(n_{2}\) are numbers of people that can be infected by one person under conditions of self-isolation and during hospitalization responsibly; \(d_{1}\) and \(d_{2}\) are proportions of people who are treated in self-isolation and in hospitals, \(d_{1} + d_{2} = 1\).
From the equality for \({{r_{0} } \mathord{\left/ {\vphantom {{r_{0} } m}} \right. \kern-0pt} m}\), it follows that
We will denote: \(\alpha = \beta + \frac{1 - \beta }{m} < 1\), because \(m > 1\), where \(\beta = \sum\limits_{\tau \in \Omega } {c_{\tau } }\) (\(\Omega\) is defined in a formula for \(\rho_{\tau }\), \(\beta\)—the of sum \(c_{\tau }\) without the right tail of this distribution); \(\tilde{W}_{I2} (L) = \alpha^{ - 1} W_{I2} (L)\). Besides, \(\tilde{W}_{I2} (1) = 1\), because \(W_{I2} (1) = \alpha\).
From (52), we have
From here and (51), we get
Poles of generating functions \(W_{I1} (s)\) and \(W_{E} (s)\) are real and lie out of single circle. This their property follows from that the laws of distributions of nonnegative integer random values correspond to these functions. The poles of generating function \(W_{I1,E} (s) = W_{I1} (s)W_{E} (s)\) coincide with the poles \(W_{I1} (s)\) and \(W_{E} (s)\), and consequently, a sequence \({\rm H}_{t1} = \sum\limits_{\tau = 0}^{t} {\eta_{\tau 1} }\), \(t = 0,1,2, \ldots ,\tau_{\max }\), \(\tau_{\max } = \tau_{I1} \tau_{E}\), is strictly monotonously increasing. It is also bounded, and its members are nonnegative and limited above by 1, because \({\rm H}_{01} = \eta_{01} = W_{1,R} (0) = W_{I1} (0)W_{E} (0) \ge 0\) and \({\rm H}_{{\tau_{\max } ,1}} = W_{1,R} (1) = W_{I1} (1)W_{E} (1) = 1\). Here \(\left\{ {\eta_{\tau 1} } \right\},\;\;\tau = 0,1,2, \ldots ,\tau_{\max }\), sequence that generates \(W_{I1,R} (s)\). Thus,
According to (55), we have
With analogous reasoning, we will get from (51) and (54) taking into account the designations entered above
where \(\sum\limits_{\tau = 0}^{{\tau_{\max } }} {\eta_{\tau 2} } = 1\), \(\eta_{\tau 2} \ge 0\).
Moreover, \(\tilde{W}_{I2} (s) = \alpha^{ - 1} W_{I2} (L) = \sum\limits_{\tau = 0}^{{\tau_{\max } }} {\eta_{\tau 2} } s^{\tau }\).
Adding the left and right parts of expressions (57) and (58), taking into account balance equality in (51), we will get
Denoting \(\gamma = \Delta_{1} + \alpha \Delta_{2} \le 1\), we get
where \(g_{t} = \frac{{r_{0} }}{N}\gamma S_{t - 1}^{{}}\).
Equality (59) in the designation given above coincides with difference Eq. (49) that describes a stable to the infection population under the conditions of Theorem 4. Thus, the following result is obtained.
Theorem 5
Let the process of development of epidemic be described by a model (52). Then the sufficient condition of stability of population to the infection in the time period \(t\) is inequality \(g_{t} \le 1\). In it \(g_{t} = \frac{{r_{0} }}{N}\gamma S_{t - 1}^{{}}\); \(\gamma = \Delta_{1} + \alpha \Delta_{2}\); \(\alpha = \beta + {{\left( {1 - \beta } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \beta } \right)} m}} \right. \kern-0pt} m} \le 1\); \(\beta = \sum\limits_{\tau \in \Omega } {c_{\tau } }\).◊
5 Solutions for model with latent period with different processes of treatment. identification task
We will consider a model (52) in which transmission functions (TF) have the next sense. TF \(W_{I1} (L) = \frac{{\left( {1 - p_{1} } \right)}}{{\left( {1 - p_{1} s} \right)}}\) corresponds to geometrical distribution of duration of infecting with the average \(T_{1} = 4\). TF \(W_{c} (L) = \frac{{\left( {1 - p_{c} } \right)}}{{\left( {1 - p_{c} s} \right)}}\) corresponds to geometrical distribution of duration of expectation of laboratory confirmation of infecting of person with the average \(T_{c} = 3\). TF \(W_{E} (L)\) is determined by a formula (30) at substituting \(s\) by \(L\) in it, corresponds distributions of Pascal of duration of latent period with a parameter \(p = p_{E} = 0.4\) and the average \(T_{E} = 1.333\). The all averages are given in days.
Other values in (51): \(r_{0} = 10\), \(N = 400\), \(\Delta_{1} = 0,3\), \(\Delta_{2} = 0,7\), \(n_{1} = 1\), \(n_{2} = 0\) (under conditions of quarantine, one not hospitalized person can infect one person, under conditions of hospitalization, infect 0 people), \(d_{1} = {5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}\), \(d_{2} = {2 \mathord{\left/ {\vphantom {2 7}} \right. \kern-0pt} 7}\).
For the indicated parameters of model (52) on a Fig. 8 charts of some variables are brought for the case, when, in the time period \(t = 0\), 1 person appeared in a latent period. According to the figure, since the finite time period \(t = 13\), functions \(g_{t} = S_{t - 1} = 0\). Let us note that \(g_{t} = 1\) on 1 time period later than point of maximum of \(e_{t}\) and coincides with a maximum of \(ic_{t}\).
Let us now study the problem of identifying the same model, without taking into account vaccination and without expressions describing the treatment:
The exit of model is the function \(ic_{t}\). It must be compared to the actual number of people infected every day \(i_{ta}\). This time series according to [12] has periodic oscillations with a period of 7 days. Further we will understand \(i_{ta}\) as the actual number of infected, smoothed out by moving average with a period 7 [12]. The actual number of the infected people for twenty-four hours during the time interval of large enough length changes in wide ranges. Therefore, for the decision of task of identification we will use heteroscedastic regression
where \(ic_{t}\) is a nonlinear function regression, \(ic_{t} = \varphi_{t} ({\mathbf{a}})\), \(\varepsilon_{t}\) is a sequence of independent random values with the mathematical expectation \(E\left\{ {\xi_{t} } \right\} = 1\) and variance \(E\left\{ {\left( {\xi_{t} - 1} \right)^{2} } \right\} = \sigma^{2}\). A function \(\varphi_{t} ({\mathbf{a}})\) is set by (60) and determined by the multidimensional parameter \({\mathbf{a}}\), components of which are coefficients of formulas in (60).
From (61), we have:
Thus, the deviation of the number of infected people from the function regression has the mathematical expectation equal to null, and its variance depends on \(t\).
Coming from said, we will get the task of evaluation of the least squares method.
where minimum is taking on \({\mathbf{a}}\).
We will solve (61) for daily allowance data about a number infected in the first wave of COVID-19 in Ukraine [20]. The segment of observation begins from \(t = t_{0} = 21\) (2020–09-1) and closes \(t = T = 177\) (2021–02-05). It embraces basic part of the people infected in this wave. After \(t = T\), other wave of diseases is begin.
For determination of necessary prehistory (the number of infected before on the time interval with length \(t_{0}\)) the mean value of duration of the active infecting \(T_{1} = 4.5\) days, defined from statistical data [4], was used. In a formula for TF \(W_{I1} (L)\), \(p_{1} = 0.818\) corresponds to it. Maximal lag of infecting \(\tau_{i} = 20\) was then defined, coming from a fact that the coefficients of geometrical lag \(q_{\tau }\) decrease strictly monotonously and \(q_{20} = \left( {1 - p_{1} } \right)p_{1}^{20} = 0.0033 \approx 0\). Consequently, for calculation of \(e_{t1}\) and \(e_{t1}\) in (60), the information about the number of infected people for 21 days before the beginning of modeling interval is needed. Therefore, a sequence \(ic_{\tau } = i_{\tau a}\), \(t = 0,1,2, \ldots ,20\) \(({2020 - 08 - 11}\;, \ldots ,{2020 - 08 - 31})\) was used as initial data, and besides, \(\nu = {83812}\) is a whole number of infected from the beginning of epidemic to \({2020 - 08 - 10}\) inclusive. All these data are present in the [20].
From the last formula in (60), we have \(i_{t2} = W_{c}^{ - 1} (L)ic_{t} = \frac{{\left( {1 - p_{c} L} \right)}}{{\left( {1 - p_{c} p_{2} } \right)}}ic_{t} = \left( {1 - p_{c} } \right)^{ - 1} \left( {ic_{t} - p_{c} ic_{t - 1} } \right)\). From here, we get an initial sequence quantities of all the infected people, including asymptomatic, \(i_{t} = \Delta_{2}^{ - 1} i_{t2}\), \(t = 0,1,2, \ldots ,20\), necessary for calculation \(e_{t1}\) and \(e_{t2}\). In these calculations, initial values \(p_{2} = 0.4\) and \(\Delta_{2} = 0,7\) of iteration process of solving the problem (62) were used. It could be possible to use these values, got on a previous iteration, instead of \(p_{2}\) and \(\Delta_{2}\) on every iteration of solving (62). However, such complication of task seems ineffective because the length of basic data (21 days) is far less than time interval for the evaluation of model parameters (156 days).
We will define now, whether a maximum of \(i_{at}\) will coincide with a maximum of \(ic_{t}\) for \(N = 43733759\)—a quantity of population of Ukraine [20]. According to Theorem 5 in the neighborhood of the maximum point, to the right of it, for some \(t\) we will have the condition
It follows from (63) that in a maximum point number of susceptible
We will find a low bound of \(r_{0}\), higher than which an epidemic will develop. In its beginning (\(t = 1\)), the difference \(N - S_{0}\) is negligibly small. Then concordantly (62), \(r_{0} = {1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0pt} \gamma }\). For large enough \(\gamma = 0.95\) we have \(r_{0} = 1.053\). Choosing \(r_{0} = 1.2\) that guarantees instability of population to the infection, we will get \(S_{m} = 3836946\) from (63). Consequently, total number of the infected people to time of achievement of a maximum of number of the people infected every day \(I_{m} = N - S_{m} = 5370813\). Assume that the chart \(i_{ta}\) is approximately symmetric, we will get that, to completion of the first wave, more than 10.7 million people will be infected. Actually according to [20], there are a little more than 1.1 million people that have symptoms. We will consider that there are approximately the same amount of asymptomatic infected that gives 2.2 million people of all infected totally that far less than 10.7 million people. Therefore, for maximums \(i_{tf}\) and \(ic_{t}\) to coincide, the number of susceptible in a population at the beginning of epidemic must be approximated in 5 times less than quantity of all population and be not more than 8,746,752. This value will decrease with the increase of \(r_{0}\). The said is easily explained by the fact that the hard quarantine restrictions were operated in a considerate time interval in Ukraine.
Thus, we come to conclusion that \(N\) in (60) must be unknown varied value. Its meaning is the upper bound on the number of infected people during the epidemic. So, we have the next estimated values which are components of \({\mathbf{a}}\) in the task (62):
A value \(p_{1} = 0.818\) was not varied.
We express \(N\) and \(S_{t}\) in scale millions of people so that all values in (65) are approximately on the same scale. Therefore, calculation of \(S_{t}\) will be according to the formula \(S_{t} = S_{t - 1} - 10^{ - 6} e_{t}\). All values in (65) are positive, part of them belong to the interval \((0,1)\). For the account of this factor, it is needed to enter corresponding restrictions for values in (65) that would result in considerable complication of evaluation task [15, 16]. Therefore, we went on the other way—stage-by-stage solving of (62). On the first stage—the minimization on \({\mathbf{a}} = {\mathbf{a}}_{1} = \left[ {\begin{array}{*{20}c} {r_{0} } & N \\ \end{array} } \right]^{\prime }\), where a stroke means transposition. On the second stage—the minimization on \({\mathbf{a}} = \left[ {\begin{array}{*{20}c} {{\mathbf{a^{\prime}}}_{1} } & {{\mathbf{a^{\prime}}}_{2} } \\ \end{array} } \right]^{\prime }\), where \({\mathbf{a^{\prime}}}_{2} = \left[ {\begin{array}{*{20}c} {p_{1} ,} & {p_{2} } & p & {\Delta_{1} } \\ \end{array} } \right]\). On the third stage—the minimization on \({\mathbf{a}} = \left[ {\begin{array}{*{20}c} {{\mathbf{a^{\prime}}}_{1} } & {{\mathbf{a^{\prime}}}_{2} } & {{\mathbf{a^{\prime}}}_{3} } \\ \end{array} } \right]^{\prime }\), where \({\mathbf{a^{\prime}}}_{3} = \left[ {\begin{array}{*{20}c} {n_{1} } & {n_{2} } & {d_{1} } \\ \end{array} } \right]\). The calculations were produced in the environment of MS Excel using of superstructure on solving search. The initial values of the estimated quantities are obtained from [4], the missing quantities were determined by an expert. Results are presented in Table 1. In it, the accuracy of got model was determined by a criterion \(\Phi ({\mathbf{a}}) = \sum\limits_{t = 1}^{{T - t_{0} }} {\left| {1 - \frac{{ic_{t} ({\mathbf{a}})}}{{i_{ta} }}} \right|}\). An evaluation on it considerably becomes complicated due to non-differentiability of \(\Phi ({\mathbf{a}})\), what stipulated an evaluation on (62), in spite of the fact that \(F({\mathbf{a}})\) "underlines" large deviations from 1. An average module of relative errors \({{\Phi ({\mathbf{a}})} \mathord{\left/ {\vphantom {{\Phi ({\mathbf{a}})} {\left( {T - t_{0} } \right)}}} \right. \kern-0pt} {\left( {T - t_{0} } \right)}}\) also was determined.
The value \(N = 6.939\) million people appeared considerably less than quantity of population of \(43733759\) people that can be explained by effective quarantine measures. Not high accuracy of evaluation of number of the infected people is caused by a high level of noise that is left after smoothing out in this value, see a Fig. 9. This consideration is confirmed by comparison of the whole number of infected: actual \(\sum\nolimits_{{t = t_{0} }}^{T} {i_{ta} } = 1140654\) and calculated by the model (60) \(\sum\nolimits_{{t = t_{0} }}^{T} {ic_{t} } = 1056695\). They differ on 7.36% that is far less than error 15.6% in Table 1. Explaining of this phenomenon is possible by the fact that adding up is the smoothed operation.
Model (60) accuracy can be increased, calculating the number of hospitalized people and non-hospitalized ones separately. Other approach is based on assumption that probability of meeting of infected person and susceptible person equals not \({{S_{t - 1} } \mathord{\left/ {\vphantom {{S_{t - 1} } N}} \right. \kern-0pt} N}\), but \(\left( {{{S_{t - 1} } \mathord{\left/ {\vphantom {{S_{t - 1} } N}} \right. \kern-0pt} N}} \right)^{b}\), where \(b > 0\) is unknown value. Then from (60), we will pass to the model
This model will satisfy to Theorem 5 for \(g_{t} = r_{0} \left( {\frac{{S_{t - 1}^{{}} }}{N}} \right)^{b}\), where \(\left( {\frac{{S_{t - 1}^{{}} }}{N}} \right)^{b}\)—probability of infecting of one susceptible person by one infected person. In (66) \(b\), as well as other parameters of this model, can be a constant or function of time. In the last case, in particular, it can be a step function of \(t\). Transition from one step to another will take place in the points named switching points. Then the function regression set by (66) determines nonlinear regression with switching. A few methods of construction of linear switching regressions are presently known. For the evaluation of model (66) parameters, in particular, a method [17] that is offered for linear regression can be used.
Here we will consider a case, when \(b = const\). Initial data, criteria of evaluation and determination of accuracy of a model are the same that used above for the evaluation of model (60) parameters. Model parameters (65) plus \(b\) are estimated. A task (62) was managed to solve in 2 stages: on the first stage minimization on \({\mathbf{a}} = {\mathbf{a}}_{1} = \left[ {\begin{array}{*{20}c} {r_{0} } & N & b \\ \end{array} } \right]^{\prime }\), on the second—on all parameters of model (65). The got results are present in Table 2, graphs \(ic_{t}\), \(i_{ta}\), \(g_{t}\) are on a Fig. 10.
The obtained model is slightly more accurate than the model (60). In addition, parameters of \({\mathbf{a^{\prime}}}_{3} = \left[ {\begin{array}{*{20}c} {n_{1} } & {n_{2} } & {d_{1} } \\ \end{array} } \right]\) considerably changed in relation to their initial values in comparison with Table 1. The value of \(N\) has decreased significantly, since the formula for the probability of infection of one person changed.
Let us now determine the confidence interval for the actual number of infected people per day \(i_{tf}\).
From (61), we have
From the properties of \(\xi_{t}\), see above, it follows that \(E\left\{ {\varepsilon_{t} } \right\} = 0\), \(E\left\{ {\varepsilon_{t}^{2} } \right\} = \sigma^{2} = const\). From here and (67), we obtain a nonlinear homoscedastic regression
where \(\varphi_{t} ({\mathbf{a}}) = \ln ic_{t} = \ln \psi_{t} ({\mathbf{a}})\).
Let us suppose that \(\varepsilon_{t} \sim N\left( {0,\sigma^{2} } \right)\), \(\forall t\). Then the \((1 - p)100\)%th probability interval for \(\ln ic_{t}\):
where \(u_{{{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}}}\) is the \(100{\raise0.7ex\hbox{$p$} \!\mathord{\left/ {\vphantom {p 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\%\)th point of the standard normal distribution.
Let \({\hat{\mathbf{a}}}\) is an estimate \({\mathbf{a}}\), whose components are in the fourth column of Table 2. Then, according to (68), the residuals for the model (66) are \(\hat{\varepsilon }_{t} = \ln i_{ta} - \varphi_{t} ({\hat{\mathbf{a}}})\). Using the criterion of normality based on the coefficients of skewness and kurtosis [18], the hypothesis of normal distribution of residuals was accepted at the 5% level. This confirms our assumption about normality of \(\varepsilon_{t}\). Therefore, approximate probability intervals follow from (68) for \(\ln ic_{t}\) and \(ic_{t}\):
where \(\hat{\sigma }\) is the least squares method estimate of \(\sigma\).
Interval (69) is shown in Fig. 10. From a practical point of view, its upper bound is important, since, by it, one can plan the maximum load of medical institutions, etc.
The parameter \({\mathbf{a}}\) of the regression (68), as mentioned above, is a solution of the task (62). However, its estimate can also be obtained by solving the task
Generally speaking, the solutions of problems (62) and (70) are different. In contrast to solving problem (62), for solving (70), one can apply the well-known methods for estimating the parameters of nonlinear regression and analyzing their accuracy [8, 11, 19, 21], etc.
The solution of (70) using solving search of MS Excel for the same data on infected people and initial parameters values as given in Table 2 is shown below. It was obtained in the same 2 stages as given in Table 2.
According to Tables 1, 2 and 3, the smallest value of the criterion \(\Phi ({\mathbf{a}})\) is obtained as a result of solving the estimation task (70). Therefore, we will consider it in more detail. The values \(r_{0} ,N,b\) are approximately the same as given in Table 2. The average duration \(T_{c} = 1.448\) of the day corresponds to the value \(p_{c}\). Since this value is distributed according to geometric law, the maximum waiting time for the test result, which is approximately equal to \(3T_{c}\), will be about 4.5 days. The duration of the latent period with the distribution parameter \(p_{E} = 0.685\) has the average \(T_{E} = 4.351\) days. This value in [5] for a number of countries is taken equal to 5.1 days. The value \(\Delta_{1}\) turned out to be a little more than its initial value of 0.3, defined in [4]. As for indicators such as \(n_{1} ,n_{2} ,d_{1}\), it is unambiguously difficult to determine them in model (66), because they specify only 1 parameter in it—\(m\), which characterizes the degree of decrease of the main number of reproduction in cases of self-isolation or hospitalization. For the data in Table 3, \(m = 1.48\). It should be said that the estimates of quantities \(n_{1} ,n_{2} ,d_{1} ,d_{2}\) and the relationships between them correspond to meaningful ideas about them. Also worth noting the presence of multicollinearity, which is an approximate linear dependence for the estimated parameters. It is expressed in the fact that in the neighborhood of the minimum of criterion (70) the surface \(F({\mathbf{a}})\) is gently sloping that leads to the fact that for \({\mathbf{a}}^{\left( 1 \right)} \ne {\mathbf{a}}^{\left( 2 \right)}\), it takes place that \(F({\mathbf{a}}^{\left( 1 \right)} ) \approx F({\mathbf{a}}^{\left( 2 \right)} )\). Multicollinearity was also noted for criterion (62). Graphs of \(ic_{t}\) and other variables for the parameters of the model (66) with the values in Table 3 are shown in Fig. 11. It shows that the maximum of \(ic_{t}\) has increased in comparison with Fig. 8 that improved the accuracy of the model.
For the residuals of the model at the 1% level, the hypothesis of their normality was accepted that made it possible to determine the interval (69).
A further increase in the accuracy of models like (62) and (66) can be achieved by determining the type of distributions of processes durations a posteriori, i.e., according to the data, and not a priori, as it was done in the above calculations. Also, models (60), (66) can be detailed.
The given examples of estimation of discrete-time model parameters show possibility of their identification and its importance. Above, in order to estimate \(r_{0}\) and \(N\) it was not necessary to establish a relationship between these quantities. Such task is not simple, arising up at the modeling of dynamics of different biological processes [3], Ch. 6). To solve it is difficult even because the connection of no measurable values \(r_{0}\) with measurable \(N\) is searched.
In general, the task of identification of models offered here, and also other models got on their basis, is a separately standing important task requiring further researches.
6 Conclusions
The model of the dynamics of the epidemic development proposed in the article is found in the fact that the model should be fitted to a time series of indicators, and not to unknown continuous functions of time. This requirement leads to the need to use difference equations instead of differential equations. The use of discrete time, in addition, allows us to clearly comprehend such a concept, for example, as the number of infected per unit of time.
The construction of the model is based on taking into account the delayed influence of some variables on others in the form of distributed lag models. The construction of these models uses the dual nature of integer nonnegative random variables that have the meaning of the duration of any process. Duality consists of that the law of distribution of such value can be interpreted also as an impulse transient function of some dynamic system. Analogical duality is present for continuous nonnegative values [13]. This fact allows us to build a model of the epidemic dynamics in the form of dynamic blocks reproducing a lag and blocks of interaction of variables in the form of their products. The blocks of dynamics are described on the basis of theory of the linear systems, and description of interaction is based on the same idea that, apparently, Kermack and McKendrick offered first in biology, and Cobb and Douglas entered as production functions in economy approximately at the same time—in 1928. These authors suggest describing interaction of different factors by their products.
The construction of the model on the basis of the principles described above allows to get various models and to analyze them not as nonlinear systems by means of phase portraits that befits for the systems of differential equations not higher the second order, but to interpret a model as a linear dynamic system with various in time coefficients. Such approach allows using the methods of the theory of linear systems that simplifies the analysis of model, in particular, its stability. It is simple enough and can be realized on a desktop computer with the use of the known application programs. In the described models, a population size \(N\) is a constant. It can be replaced with a time function \(N_{t}\) that takes into account demographic changes in a population. Models do not change; thus, simple changing applies to only the first equation, while for continuous time, account of demography in the system of differential equations even simplified causes the change of all model of epidemiology, see, for example, [3], p. 6.2, [10].
The example of construction of one type of model from real data presented in the article shows also possibility to its identification.
Based on the proposed approach, quite complicated models of the development of the epidemic can be built under the conditions of vaccination and the existence of different strains of the virus.
Data availability
The authors declare that the data supporting the findings of this study are available within the article. In case of any additional data relevant to these findings, the same are available on request from the corresponding author A.S. Korkhin.
References
Allen L (2000) Comparison of deterministic and stochastic SIS and SIR models in discrete time. Math Biosci 163(1):1–33
Atkeson AG (2020) On using SIR models to model disease scenarios for COVID-19, Federal Reserve Bank of Minneapolis. Quart Rev 41(1):le33
Bratus AS, Novozhilov AS, Platonov AI (2010) Dynamic systems and models in biology. Moscow: PHISMATLIT, p. 436 (in Russian)
Brovchenko I (2020) Creation of mathematical model of distribution of epidemic of COVID–19 in Ukraine//Svitoglyad, 82(2) 2–14. (in Ukrainian)
Buckman SR, Glick R, Lansing KJ, Petrosky-Nadeau N, Seitelman LM (2020) Replicating and projecting the path of COVID-19 with a model-implied reproduction number. Infect Disease Model 5:635–651
Dhrymes P (1981) Distributed lags: problems of estimation and formulation. Elsevier, Newyork, p 480
Feller W (1967) An Introduction to probability theory and its applications, vol 1. Wiley, Newyork, p 419
Ivanov VA (1997) Asymptotic theory of nonlinear regression. Kluwer, Dordrecht
Kermack WO, McKendrick AG (1927) A contribution to the mathematical theory of epidemics. In: proceedings of the royal society of London. Series a containing papers of a mathematical and physical character, vol. 115, No. 772. (Aug. 1, 1927), pp. 700–721
Knopov PS, Atoyev KL, Gorbachuk V et al. (2020) Some approaches to the use of stochastic models of epidemiology to the problem COVID-19. https://www.researchgate.net/
Knopov PS, Korkhin AS (2012) Regression analysis under a priory parameter restrictions. Springer, Newyork, p 234
Knopov PS, Korkhin AS (2020) Statistical analysis of the dynamics of coronavirus cases using stepwise switching regression. Cybern Syst Anal 56(6):943–952
Korkhin AS (1971) One of methods of modeling of dynamics of productive processes, Economy and Mathematical Methods, (2) 17–23. (in Russian)
Korkhin AS (1981). Modeling of economic systems with distributed lag.–Moscow: Finances and Statistics. p. 160 (in Russian)
Korkhin AS (1999) Solution of problems of the nonlinear least-squares method with nonlinear constraints based on the linearization method. J Autom Inf Sci 31(6):110–120
Korkhin AS (2005) Determining sample characteristics and their asymptotic linear-regression properties estimated using inequality constraints. Cybern Syst Anal 41(3):445–456
Korkhin AS (2018) Constructing a switching regression with unknown switching points. Cybern Syst Anal 54(3):443–455
Korkhin AS, Minakova EP (2008) Computer statistics. Part 2. Dnepr: NMU─150 p. (in Russian)
Korkhin AS, Pzhebitsin Z (2022) Bases of probability theory and mathematical statistics (for economists). Dnepr: Lira, 534 p. (in Russian)
Ritchie H, Roser M (2021) Coronavirus source data. https://ourworldindata.org/coronavirus-source-data
Seber GAF, Wild CJ (1989) Nonlinear regression. Wiley, New York
Sekiguchi M, Ishiwata E, Nakata Y (2018) Dynamics of an ultra-discrete SIR epidemic model with time delay. Math Biosci Eng 15(3):653–666. https://doi.org/10.3934/mbe.2018029
Funding
Funding for this study was received from the budget of the National Academy of Sciences of Ukraine.
Author information
Authors and Affiliations
Contributions
PSK contributed 50% and ASK contributed 50%.
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of financial and non-financial interests.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Knopov, P.S., Korkhin, A.S. Dynamic models of epidemiology in discrete time taking into account processes with lag. Int. J. Dynam. Control 11, 2193–2214 (2023). https://doi.org/10.1007/s40435-023-01135-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40435-023-01135-3