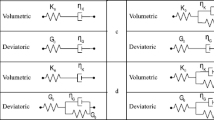1 Introduction

The Prony series is probably the most commonly used generic function of viscoelasticity. From the mechanistic point of view, this function yields from the generalized Maxwell rheological model [10, 13, 29, 37]. The constitutive equations of linear viscoelasticity utilizing the Prony series are implemented in numerous finite element analysis programs, such as Abaqus [17], ADINA [1] or MSC Marc [25]. This is the reason why the evaluation of the viscoelastic constants of this particular model becomes a compelling issue.

In practice, it is common to examine the properties of a viscoelastic solid using the creep tests, e.g., [24]. This approach is justified by the fact that standard creep experiments require relatively simple apparatus compared to other testing techniques. Another reason is that a uniaxial stress state during a creep test results in a simplification of the one-dimensional process equations which yield from the compliance form of tensor constitutive equation, e.g., [37]. However, the widely used engineering software is mainly based on the displacement formulation of the finite element method (FEM). This fact requires the compliance constitutive equation of viscoelasticity to be inverted in order to obtain the parameters of the relaxation function which could be further utilized in the stiffness constitutive equations used by the finite element software.

In the case of material memory functions using more than one exponential term, the inversion of the constitutive equation utilizing an analytical approach is usually troublesome, if possible. Thus, numerous numerical algorithms have been proposed to enable interconverting generic functions which employ multiple exponential terms. Such algorithms are usually based on the relation between creep and relaxation functions which can be expressed in the form of a convolution integral, e.g., [3, 12]. A different approach is to utilize the iterative adjusting of the measured and theoretical complex moduli [2, 21].

Through the years, numerous algorithms for the determination of the Prony series material parameters were proposed. Due to the presence of the exponential terms, the generic functions of viscoelasticity are highly sensitive to the parameter values. Garbarski [14, 15] utilized a systematic search algorithm to determine the constants of double exponential function from multistep rheological test data for various thermoplastic polymers. Chambers [6] and Chen [7] independently employed pattern search algorithms to evaluate the constants of multiple exponential functions from relaxation data including ramp loading. The more rapid, yet less stable gradient methods are occasionally used for the identification of viscoelastic constants, e.g., [3].

Some researchers postulate that better convergence and stability are achieved if the material characteristic times are excluded from the classical optimization. This can be achieved by setting the number of relaxation times and their values a priori, e.g., [6]. On the other hand, Ciambella et al. [9] introduced a method where the relaxation times were estimated using a quasi-genetic algorithm, whereas the viscoelastic coefficients were iteratively optimized using both gradient and pattern search methods. A modification of the aforementioned algorithm was proposed by Suchocki [32]. It appears that currently, due to the increased computational power of modern computers, the relaxation times in both linear and nonlinear viscoelasticity do not require any special treatment and can be determined by means of the least squares method the same way other material constants are evaluated. This fact allows for a reduction in number of the utilized exponential terms.

The material parameter evaluation algorithms discussed in the literature concern in major part one-dimensional rheological models; thus, many problems occurring during the identification of three-dimensional, tensor constitutive models are skipped. It should be emphasized that in the case of relaxation data, the material constants determined for a one-dimensional prototype of a constitutive equation are usually in no way usable for the tensor equations utilized by FEM. This fact is associated with the existence of three-dimensional strain state and a time-dependent Poisson’s ratio which have to be taken into account during the derivation of the process equations. The aforementioned problem was discussed by Qvale and Ravi-Chandar [30] who proposed approximating the measured lateral strain data with a polynomial function of time in order to enable evaluating the hereditary integral and obtaining a closed-form process equation. This relationship describing the stress relaxation could be further used for the purpose of approximating the relaxation data.

An analytical integration of the hereditary integrals usually results in lengthy and complicated process equations which have to be further handled during the determination of material parameters. What is more, the closed-form result of evaluating a hereditary integral can be obtained only for relatively simple deformation histories. Goh et al. [16] demonstrated for a nonlinear viscoelastic model that exact values of the material constants can be identified when a numerical integration of the constitutive equation is used instead of a closed-form process equation. For that purpose, the numerical integration algorithm developed by Taylor et al. [33] was utilized. The same procedure of material parameter evaluation was later successfully applied by Sorvari and Malinen [31] in the case of a one-dimensional linear viscoelastic model.

In this work, a newly developed method for determining the material constants of a three-dimensional linear viscoelastic model is introduced. The material memory function is assumed in the form of a Prony series. The presented identification algorithm utilizes the Taylor’s numerical integration method to calculate the theoretical material response which is further used during the least squares optimization procedure. The algorithm can be used for arbitrary strain histories. The nonconstant Poisson’s ratio which generates the effect of lateral strain evolution during a uniaxial relaxation test can be taken into account easier than it was proposed before [30, 37]. Thus, the parameters of the shear and bulk relaxation functions can be evaluated directly from the data collected in a standard uniaxial stress relaxation experiment. There is no need for performing any other more elaborate rheological test, subsequent identification of the material parameters and further conversion of the determined function of viscoelasticity in order to obtain the parameters of the shear and bulk relaxation functions. The proposed material parameter identification algorithm is applied to evaluate the viscoelastic constants of acrylonitrile butadiene styrene (ABS) on which the uniaxial stress relaxation tests in tension have been performed. The collected measurements include the specimen’s lateral contraction changing over time which results in a time-variable strain deviator and axiator. The significance of the lateral strain’s measurement for the determination of viscoelastic constants is investigated. A number of boundary value problems are analyzed in order to assess the influence of the identified material parameter values on the obtained solutions.

2 Basic notions

The stiffness form of the constitutive equation of isotropic linear viscoelasticity takes the form [10, 13, 37]:

$$\begin{aligned} {\varvec{\sigma }}(t)=\mathbf{s}(t)+p(t)\mathbf{1}, \end{aligned}$$
(1)

where

$$\begin{aligned} \mathbf{s}(t)=\int \limits _{0}^{t}2G(t-\tau )\frac{\partial \mathbf{e}(\tau )}{\partial \tau }\mathrm {d}\tau , \qquad p (t)=\int \limits _{0}^{t}B(t-\tau )\frac{\partial \epsilon (\tau )}{\partial \tau }\mathrm {d}\tau , \end{aligned}$$
(2)

and

$$\begin{aligned} \mathbf{e}(t)={\varvec{\varepsilon }}(t) -\frac{1}{3}\epsilon (t)\mathbf{1}, \quad p(t)=\frac{1}{3}{{\,\mathrm{tr}\,}}{\varvec{\sigma }}(t), \quad \epsilon (t)={{\,\mathrm{tr}\,}}{\varvec{\varepsilon }}(t), \end{aligned}$$
(3)

with \({{\,\mathrm{tr}\,}}(\bullet )\) being the trace operator.

The shear and bulk relaxation functions are assumed in the form of Prony series, i.e.

$$\begin{aligned} G(t)=G_{\infty }+\sum _{j=1}^{N}G_{j}e^{-\frac{t}{\tau _{j}}}, \quad B(t)=B_{\infty }+\sum _{j=1}^{M}B_{j}e^{-\frac{t}{{\tilde{\tau }}_{j}}}, \end{aligned}$$
(4)

where \(G_{\infty }\) is the long-term shear modulus, \(G_{j}\) and \(\tau _{j}\) (\(j=1,2,\dots ,N\)) are the coefficients and relaxation times, respectively, accounting for the nonequilibrium shear response, whereas \(B_{\infty }\) is the long-term bulk modulus, \(B_{j}\) and \({\tilde{\tau }}_{j}\) (\(j=1,2,\dots ,M\)) are the coefficients and relaxation times, respectively, accounting for the nonequilibrium bulk response.

Sometimes it is convenient to rewrite Eq. (2) in an equivalent differential form by utilizing the so-called viscoelastic shear and bulk nonequilibrium stresses. i.e., \(\mathbf{h}_{j}\) (\(j=1,2,\dots ,N\)) and \({\tilde{h}}_{j}\) (\(j=1,2,\dots ,M\)), respectively. Thus:

$$\begin{aligned} \begin{aligned} \mathbf{s}(t)&=2G_{\infty }{} \mathbf{e}(t)+\sum _{j=1}^{N}{} \mathbf{h}_{j}(t), \quad \dot{\mathbf{h}}_{j}(t)+\frac{1}{\tau _{j}}{} \mathbf{h}_{j}(t)=2G_{j}\dot{\mathbf{e}}(t)\\ p(t)&=B_{\infty }\epsilon (t)+\sum _{j=1}^{M}{\tilde{h}}_{j}(t), \quad \dot{{\tilde{h}}}_{j}(t)+\frac{1}{{\tilde{\tau }}_{j}}{{\tilde{h}}}_{j}(t)=B_{j}{\dot{\epsilon }}(t). \end{aligned} \end{aligned}$$
(5)

Equations (5)\(_{2}\) and (5)\(_{4}\) can be derived based on the analysis of mechanistic Maxwell model, e.g., [10, 13, 37], whereas the additivity of nonequilibrium stresses yields from the generalized Maxwell model (Fig. 1) which may be also called the H-nMFootnote 1 model.

Fig. 1
figure 1

Mechanistic rheological model comprising of Hooke’s element and n Maxwell elements (H-nM) combined in parallel

Full size image

By taking advantage of the Laplace transform, i.e.

$$\begin{aligned} {\bar{f}}(s)={\mathcal {L}}[f(t)]=\int \limits _{0}^{\infty } f(t) e^{-st}\mathrm {d}t, \end{aligned}$$
(6)

Eq. (2) can be written in a form which resembles the stress–strain relationships of the linear elasticity:

$$\begin{aligned} \bar{\mathbf{s}}(s)=s2{\bar{G}}(s)\bar{\mathbf{e}}(s), \, \, \, \, \, {\bar{p}}(s)=s{\bar{B}}(s){\bar{\epsilon }}(s). \end{aligned}$$
(7)

The fictitious “elastic constants” \({\bar{G}}'(s)\) and \({\bar{B}}'(s)\) can be introduced in the form of the following functions of the transformation parameter s:

$$\begin{aligned} {\bar{G}}'(s)=s{\bar{G}}(s), \, \, \, \, \, {\bar{B}}'(s)=s{\bar{B}}(s), \end{aligned}$$
(8)

which are called the shear and bulk relaxances, respectively [35], and are related to the so-called stretch relaxance \({\bar{E}}'(s)\) and Poisson’s retardance \({\bar{\nu }}'(s)\) by the following formulas:

$$\begin{aligned} {\bar{G}}'(s)=\frac{{\bar{E}}'(s)}{2(1+{\bar{\nu }}'(s))}, \, \, \, \, \, {\bar{B}}'(s)=\frac{{\bar{E}}'(s)}{3(1-2{\bar{\nu }}'(s))}, \end{aligned}$$
(9)

with

$$\begin{aligned} {\bar{\sigma }}_{a}(s)={\bar{E}}'(s){\bar{\varepsilon }}_{a}(s), \, \, \, \, \, {\bar{\nu }}'(s)=-\frac{{\bar{\varepsilon }}_{l}(s)}{{\bar{\varepsilon }}_{a}(s)}, \end{aligned}$$
(10)

where \({\bar{\sigma }}_{a}(s)\) and \({\bar{\varepsilon }}_{a}(s)\) are the Laplace transforms of the axial stress and axial strain, respectively, whereas \({\bar{\varepsilon }}_{l}(s)\) is the transform of the lateral strain in an infinitesimal cube subjected to uniaxial tension. The time-dependent Young’s modulus and Poisson’s ratio are given by the following equations:

$$\begin{aligned} {\bar{E}}(s)=\frac{1}{s}{\bar{E}}'(s), \, \, \, \, \, {\bar{\nu }}(s)=\frac{1}{s}{\bar{\nu }}'(s), \end{aligned}$$
(11)

which yields

$$\begin{aligned} E(t)=\int \limits _{0}^{t}E'(\tau )\mathrm {d}\tau , \, \, \, \, \, \nu (t)=\int \limits _{0}^{t}\nu '(\tau )\mathrm {d}\tau . \end{aligned}$$
(12)

In the case of a strain excitation defined by the Heaviside’s step function H(t), i.e., \(\varepsilon _{a}(t)=\varepsilon _{0}H(t)\), the time-dependent elastic constants are given as [18, 35]:

$$\begin{aligned} E(t)=\frac{\sigma _{a}(t)}{\varepsilon _{0}}, \, \, \, \, \, \nu (t)=-\frac{\varepsilon _{l}(t)}{\varepsilon _{0}}. \end{aligned}$$
(13)

The relationships given above facilitate the method of solving the boundary value problems called the correspondence principle, e.g.,   [10, 13, 37].   This method assumes that when a solution to a problem of the elasticity theory is known, a solution to a corresponding problem of the viscoelasticity theory can be found by replacing the elastic constants by the proper relaxances and retardances and subsequent inverse Laplace transform. The applicability of this method is limited to the cases when the boundary conditions have the form of a multiplication of independent time and coordinate functions.

3 Model computation algorithm

The numerical algorithm which is utilized for the time integration of Eq. (2) is a modification of the numerical scheme introduced by Taylor et al. [33]. The calculations performed during a single time step are listed in the table below. An assumed strain history is treated as an input for the algorithm. The shear and bulk relaxation functions are taken in the form of Prony series as given in Eq. (4).

The presented algorithm is utilized to compute the theoretical deviatoric and volumetric stresses which are used for the calculation of the total square error during the determination of material parameter values [16, 32].

Numerical integration of linear viscoelastic model

Input: \({\varvec{\varepsilon }}(t_{n+1})\), \(\mathbf{e}(t_{n})\), \(\epsilon (t_{n})\), \(\mathbf{h}_{j}(t_{n})\), \({\tilde{h}}_{k}(t_{n})\)\(n+1\)

1. Calculate strain deviator and dilatation from time step \(n+1\)

\(\begin{aligned} \mathbf{e}(t_{n+1})={\varvec{\varepsilon }}(t_{n+1})-\frac{1}{3}\epsilon (t_{n+1})\mathbf{1}, \quad \epsilon (t_{n+1})={{\,\mathrm{tr}\,}}{\varvec{\varepsilon }}(t_{n+1}) \end{aligned}\)

2. Update nonequilibrium viscoelastic stresses (\(j=1,2,\dots ,N\)), (\(k=1,2,\dots ,M\))

\(\begin{aligned} \mathbf{h}_{j}(t_{n+1})= &\, {} e^{-\frac{\varDelta t}{\tau _{j}}}\mathbf{h}_{j}(t_{n})+2G_{j}\frac{1-e^{-\frac{\varDelta t}{\tau _{j}}}}{\frac{\varDelta t}{\tau _{j}}} \left( \mathbf{e}(t_{n+1})-\mathbf{e}(t_{n})\right) ,\\ {\tilde{h}}_{k}(t_{n+1})= &\, {} e^{-\frac{\varDelta t}{{\tilde{\tau }}_{k}}}{\tilde{h}}_{k}(t_{n})+B_{k}\frac{1-e^{-\frac{\varDelta t}{{\tilde{\tau }}_{k}}}}{\frac{\varDelta t}{{\tilde{\tau }}_{k}}} \left( \epsilon (t_{n+1})-\epsilon (t_{n})\right) \end{aligned}\)

3. Calculate total Cauchy stress in time step \({n+1}\)

\(\begin{aligned} \mathbf{s}(t_{n+1})= &\, {} 2G_{\infty }{} \mathbf{e}(t_{n+1})+\sum _{j=1}^{N}{} \mathbf{h}_{j}(t_{n+1}),\\ p(t_{n+1})= &\, {} B_{\infty }\epsilon (t_{n+1})+\sum _{k=1}^{M}{\tilde{h}}_{k}(t_{n+1}),\\ {\varvec{\sigma }}(t_{n+1})= &\, {} \mathbf{s}(t_{n+1})+p(t_{n+1})\mathbf{1} \end{aligned}\)

4. Store stresses and strains: \(\mathbf{e}(t_{n+1})\), \(\epsilon (t_{n+1})\), \(\mathbf{h}_{j}(t_{n+1})\), \({\tilde{h}}_{k}(t_{n+1})\)

4 Discretized scalar equations for uniaxial stress relaxation

In order to determine the scalar process equations, it is assumed that during the stress relaxation an infinitesimal material cube is subjected to a uniaxial stress state (i.e., \(\sigma _{11}=\sigma _{11}(t)\), \(\sigma _{22}=\sigma _{33}=0\)) and a three-dimensional strain state. The components of the strain tensor in a Cartesian coordinate system \(Ox_{1}x_{2}x_{3}\) can be gathered in a square matrix:

$$\begin{aligned} {\varvec{\varepsilon }}_{3 \times 3}= \left[ \begin{array}{ccc} \varepsilon _{a}(t) &{} 0 &{} 0 \\ 0 &{} \varepsilon _{l}(t) &{} 0 \\ 0 &{} 0 &{} \varepsilon _{l}(t) \end{array}\right] , \end{aligned}$$
(14)

where \(\varepsilon _{11}=\varepsilon _{a}(t)\) and \(\varepsilon _{22}=\varepsilon _{33}=\varepsilon _{l}(t)\) are the time-variable axial and lateral strains, respectively. The application of Eqs. (3)\(_{1}\) and (3)\(_{3}\) yields

$$\begin{aligned} \mathbf{e}_{3 \times 3}= \left[ \begin{array}{ccc} \frac{2}{3}\left( \varepsilon _{a}(t)-\varepsilon _{l}(t)\right) &{} 0 &{} 0 \\ 0 &{} \frac{1}{3}\left( \varepsilon _{l}(t)-\varepsilon _{a}(t)\right) &{} 0 \\ 0 &{} 0 &{} \frac{1}{3}\left( \varepsilon _{l}(t)-\varepsilon _{a}(t)\right) \end{array}\right] , \end{aligned}$$
(15)

and dilatation

$$\begin{aligned} \epsilon (t)= \varepsilon _{a}(t) + 2 \varepsilon _{l}(t). \end{aligned}$$
(16)

Assuming that the axial strain component is given by the Heaviside step function, i.e., \(\varepsilon _{a}(t)=\varepsilon _{0}H(t)\), the substitution of Eq. (15) into Eq. (2)\(_{1}\) and Eq. (16) into Eq. (2)\(_{2}\) leads to the following expressions for the stress components (cf [37]):

$$\begin{aligned} \begin{aligned}&s_{11}(t)=\frac{4}{3}\int \limits _{0}^{t} G(t-\tau )\frac{\partial }{\partial \tau }\left[ \varepsilon _{0}H(\tau ) - \varepsilon _{l} (\tau ) \right] \mathrm {d}\tau , \quad s_{11}(t)=\frac{2}{3}\sigma _{11}(t), \\&\quad p(t)=\int \limits _{0}^{t} B(t-\tau )\frac{\partial }{\partial \tau }\left[ \varepsilon _{0}H(\tau ) + 2 \varepsilon _{l} (\tau ) \right] \mathrm {d}\tau , \quad p(t)=\frac{1}{3}\sigma _{11}(t), \end{aligned} \end{aligned}$$
(17)

which have to be solved in order to determine the theoretical stress components \(\sigma _{11}(t)\) and \(s_{11}(t)\) along with the volumetric stress p(t). It should be emphasized that while \(\varepsilon _{0}\) is an imposed kinematic excitation, the lateral strain \(\varepsilon _{l} (t)\) is an unknown time function which has to determined experimentally. Qvale and Ravi-Chandar [30] used a polynomial function to approximate the lateral strain measurements. By this way, an analytical function \(\varepsilon _{l} (t)\) was obtained which, after inserting into Eqs. (17)\(_{1}\) and (17)\(_{3},\) allowed to solve the hereditary integrals.

In common practice, a simplification based on the assumption of a constant Poisson’s ratio \(\nu ={{\,\mathrm{const}\,}}\) is utilized, i.e.

$$\begin{aligned} \varepsilon _{l}(t)=-\nu \varepsilon _{a}(t)=-\nu \varepsilon _{0}H(t). \end{aligned}$$
(18)

Substitution of Eq. (18) into Eqs. (15) and (16) yields:

$$\begin{aligned} e_{11}(t)= \frac{2}{3}(1+\nu )\varepsilon _{0}H(t), \, \, \, \, \, \epsilon (t)=(1-2\nu )\varepsilon _{0}H(t), \end{aligned}$$
(19)

Upon inserting Eq. (19) into the hereditary integrals, the following relationships are found:

$$\begin{aligned} s_{11}(t)= \frac{4}{3}G(t)(1+\nu )\varepsilon _{0}, \, \, \, \, \, p(t)=B(t) (1-2\nu )\varepsilon _{0}. \end{aligned}$$
(20)

It follows from Eqs. (17)2, (17)4 and (20), that in the case of constant Poisson’s ratio, the shear and bulk relaxation functions differ by a constant factor only, i.e., \(B(t)=\frac{2(1+\nu )}{3(1-2\nu )}G(t)\). However, postulating \(\nu ={{\,\mathrm{const}\,}}\) a priori without any experimental justification can lead to a loss of precision or even serious errors, as it will be demonstrated in the sections to follow.

The problems of solving the hereditary integrals (17)1 and (17)3 can be skipped when the constitutive equation of linear viscoelasticity is integrated numerically by utilizing the algorithm presented in the previous paragraph. For the input time histories of axial and lateral strains, the axial component of deviatoric strain and the dilatation at the time step \(t_{n+1}\) are given as:

$$\begin{aligned} e_{11}(t_{n+1})=\frac{2}{3}\left( \varepsilon _{a}(t_{n+1})-\varepsilon _{l}(t_{n+1}) \right) , \, \, \, \, \, \epsilon (t_{n+1})=\varepsilon _{a}(t_{n+1})+2\varepsilon _{l}(t_{n+1}), \end{aligned}$$
(21)

while the deviatoric viscoelastic overstress component is defined by the following recurrence-update formula:

$$\begin{aligned} {h}_{j \, 11}(t_{n+1})=e^{-\frac{\varDelta t}{\tau _{j}}}{h}_{j \, 11}(t_{n})+2G_{j}\frac{1-e^{-\frac{\varDelta t}{\tau _{j}}}}{\frac{\varDelta t}{\tau _{j}}} \left( e_{11}(t_{n+1})-e_{11}(t_{n})\right) , \end{aligned}$$
(22)

whereas the volumetric overstress

$$\begin{aligned} {\tilde{h}}_{k}(t_{n+1})=e^{-\frac{\varDelta t}{{\tilde{\tau }}_{k}}}{\tilde{h}}_{k}(t_{n})+B_{k}\frac{1-e^{-\frac{\varDelta t}{{\tilde{\tau }}_{k}}}}{\frac{\varDelta t}{{\tilde{\tau }}_{k}}} \left( \epsilon (t_{n+1})-\epsilon (t_{n})\right) . \end{aligned}$$
(23)

The total axial component of the stress deviator at time step \(t_{n+1}\) is given as:

$$\begin{aligned} s_{11}(t_{n+1})=2 G_{\infty }e_{11}(t_{n+1})+\sum _{j=1}^{N} h_{j \, 11}(t_{n+1}), \end{aligned}$$
(24)

while the volumetric stress

$$\begin{aligned} p(t_{n+1})=B_{\infty }\epsilon (t_{n+1})+\sum _{k=1}^{M} {\tilde{h}}_{k}(t_{n+1}). \end{aligned}$$
(25)

Equations (21–25) are utilized within the material parameter determination algorithm to compute the theoretical stress response for the experimentally measured histories of \(e_{11}(t)\) and \(\epsilon (t)\). The experimental strain histories have been obtained by performing the uniaxial stress relaxation tests on acrylonitrile butadiene styrene (ABS).

5 Experimental setup

For all the conducted mechanical tests of ABS, the material testing machine Zwick/Roell Z005 was used with the maximum load capacity of 5 kN. The samples were gripped into the pressure jaws with constant pressure of about 4 MPa (Fig. 2). For the purpose of assessing the real elongation of polyamide specimens, the long-range extensometer with the total measurement range of about 1.2 m was employed.

Fig. 2
figure 2

Sample gripped into pressure jaws of Zwick/Roell Z005

Full size image
Fig. 3
figure 3

Uniaxial stress relaxation tests: a scheme of experimental arrangement, b randomly spotted specimen with noncontact extensometer based on DIC method, c speckle pattern

Full size image

In order to simultaneously measure both the specimen’s elongation and its lateral contraction, an optical method based on the digital images correlation (DIC) was utilized. The method was invented in the 1980s [4, 8, 28] and has a wide range of applications in the mechanical testing of materials [5, 22, 23]. The DIC method allows to obtain the maps of displacements and macroscopic deformations measured on a surface of a tested specimen. A DIC stand consists of a monochromatic digital camera with a suitable lens and a PC with software (Fig. 3a). The images of the specimen’s surface were collected by the DIC system at the frequency of 1 Hz. A commercial program Vic2D [36] was later used for the postprocessing of images. Before the test, random spots with high contrast must be applied to the surface of the specimen (Fig. 3b, c). After selecting the field for analysis, it is divided into smaller subareas characterized by a unique distribution of shades of gray. The computer algorithm compares digital photographs of a nondeformed sample with the photographs taken after the deformation and finds the new positions of analyzed subareas by the method of best fit. As a result, a map of displacements or macroscopic deformations can be obtained for the entire analyzed area. The accuracy of displacement measurements depends on the camera’s resolution and reaches 0.01 pixels.

The dogbone specimens with a rectangular cross section (\(4\times 10\) mm) and the reduced section length of 60 mm were used for the experiments. The samples were designed according to the guidelines of PN-EN ISO 527-2:2012 “Plastics - Determination of tensile properties - Part 2: Test conditions for molding and extrusion plastics”. The high-heat MAGNUMTM 3416 SC ABS produced by Trinseo LLC was used to manufacture the specimens by injection molding. Each of the conducted mechanical tests was performed on a different dogbone specimen at the room temperature of 20 °C.

The initial phase of the research is comprised of several introductory relaxation tests which were conducted in order to check the performance of the DIC method and verify that the results obtained for the same rheological experiments are repeatable. Additionally, uniaxial ramp tension experiment was performed for the purpose of measuring the basic mechanical characteristics of the examined material. A yield stress \(\sigma _{y}=40.36\) MPa was registered for the axial strain \(\varepsilon _{a}=2.51\%\). The specimen’s failure was observed for the stress \(\sigma _{f}=45.82\) MPa and the axial strain \(\varepsilon _\mathrm{max}=43.74\%\). These measurements are in a good agreement with the specification provided by the producer [34]. The strain field at the gauge length of the specimen remained homogenous until failure and no necking were observed.

The data collected during the uniaxial ramp test were utilized to specify the parameters of the main relaxation experiment. For the purpose of mimicking the case of a Heaviside step excitation, a preloading was performed at the strain rate set to \({\dot{\varepsilon }}=0.01\,\hbox {s}^{-1}\) with the target value of the axial strain set to \(2\%\). After the maximum axial strain of \(2.56\%\) was reached, the testing machine’s automatic control system corrected the strain value. Subsequently, the axial strain of \(2\%\) was held constant for 3600 s allowing the axial stress to relax. The straining period lasted 4.5 s which is short compared to the total stress relaxation time. This fact justifies the assumption that the measured material response can be viewed as a response to a Heaviside step loading. In order to eliminate any initial transient effects which might have been introduced during preloading, the data from the initial 8 s of the experiment were discarded from the analysis.

6 Determination of material parameters

The experimental measurements collected during the stress relaxation test are presented in Fig. 4, i.e., the axial strain \(\varepsilon _{11}(t)=\varepsilon _{a}(t)\), the lateral strain \(\varepsilon _{22}(t)=\varepsilon _{l}(t)\) and the axial stress \(\sigma _{11}(t)\). Equations (21) were utilized to calculate the time history of the axial strain deviator component \(e_{11}(t)\) and the dilatation \(\epsilon (t)\) which are shown in Fig. 5. The collected data were used for the determination of viscoelastic constants of ABS.

The material parameters were evaluated by utilizing the least squares method. For that purpose, the “fminsearch” function available in Scilab software was utilized. The following total square error function was defined for the minimization:

$$\begin{aligned} {{\mathcal {F}}}(\mathbf{p})=\sum _{k=1}^{K}\left[ (s_{11}(\mathbf{p}))_{k}-({\widetilde{s}}_{11})_{k} \right] ^{2}+ \sum _{k=1}^{K}\left[ (p(\mathbf{p}))_{k}-({\widetilde{p}})_{k} \right] ^{2}, \end{aligned}$$
(26)

where \(\mathbf{p}=[\tau _{1},\dots ,\tau _{N},G_{1},\dots ,G_{N},{\tilde{\tau }}_{1},\dots ,{\tilde{\tau }}_{M},B_{1},\dots ,B_{M}]^{{{\,\mathrm{T}\,}}}\) is the column matrix of the searched parameters and \(s_{11}(\mathbf{p})\) and \({\widetilde{s}}_{11}\) are the theoretical and experimental axial deviatoric stress, respectively, whereas \(p(\mathbf{p})\) and \({\widetilde{p}}\) are the theoretical and experimental volumetric stress, respectively, at the time instants k (\(k=1,2,\dots ,K\)). The collocation points were chosen to be distributed uniformly in the logarithmic time. The long-term elastic moduli \(G_{\infty }\) and \(B_{\infty }\) were calculated from the following relations:

$$\begin{aligned} G_{\infty }=\frac{\sigma _{11}(\infty )}{2\left( \varepsilon _{0}-\varepsilon _{l} (\infty )\right) }, \, \, \, \, \, B_{\infty }=\frac{\sigma _{11}(\infty )}{9\left( \varepsilon _{0}+2\varepsilon _{l}(\infty ) \right) }, \end{aligned}$$
(27)

with the approximations \(\sigma _{11}(\infty )\approx \sigma _{11}(t_\mathrm{max})\) and \(\varepsilon _{l}(\infty )\approx \varepsilon _{l}(t_\mathrm{max})\).

Two different approaches were employed for the identification of viscoelastic constants. In the first approach, the experimental time histories of the axial strain deviator component and the dilatation, measured during the relaxation test (Fig. 5), were used as an input for Eqs. (22–25) to compute the theoretical values of stresses in Eq. (26). In this case, the time-dependent Poisson’s ratio was taken into account. Two versions of the viscoelastic model were considered, i.e., the simplified version (\(N=1\) and \(M=0\) in Eq. (4) which leads to the standard solid model in shear) and the extended version (\(N=2\) and \(M=2\)).

The comparison of the experimental results and the simplified model predictions (\(N=1\), \(M=0\)) can be seen in Fig. 6 while the parameter values are gathered in Table 1 (model 1).

Table 1 Material parameters of simplified viscoelastic model (elastic volumetric response and viscoelastic deviatoric response modeled by standard solid) determined from ABS stress relaxation data assuming time-dependent (model 1) and constant (model 2) Poisson’s ratio
Full size table
Fig. 4
figure 4

Experimental measurements for ABS: a axial strain versus time, b lateral strain versus time, c axial stress versus time

Full size image
Fig. 5
figure 5

Deformation history: a axial strain deviator component versus time, b dilatation versus time

Full size image
Fig. 6
figure 6

Comparison of linear viscoelastic model predictions (elastic volumetric response and deviatoric response modeled by standard solid) and stress relaxation data obtained for ABS (time-dependent Poisson’s ratio): a axial stress deviator component versus time, b volumetric stress versus time, total \(\hbox {RSS}=682.15984\)

Full size image
Fig. 7
figure 7

Comparison of linear viscoelastic model predictions (volumetric and deviatoric response modeled independently by two Prony terms) and stress relaxation data obtained for ABS (time-dependent Poisson’s ratio): a axial stress deviator component versus time, b volumetric stress versus time, total \(\hbox {RSS}=0.1626020\)

Full size image
Fig. 8
figure 8

Comparison of linear viscoelastic model predictions (elastic volumetric response and viscoelastic deviatoric response modeled by standard solid) and stress relaxation data obtained for ABS (constant Poisson’s ratio): a axial stress deviator component versus time, b volumetric stress versus time, total \(\hbox {RSS}=168.9458\)

Full size image
Fig. 9
figure 9

Comparison of linear viscoelastic model predictions (volumetric and deviatoric response modeled independently by two Prony terms) and stress relaxation data obtained for ABS (constant Poisson’s ratio): a axial stress deviator component versus time, b volumetric stress versus time, total \(\hbox {RSS}=0.0763265\)

Full size image

The comparison of the experimental results and the extended model predictions (\(N=2\), \(M=2\)) can be seen in Fig. 7 with the parameter values gathered in Tables 2 and 3 (model 1). Increasing the number of Prony terms in Eq. (4) did not result in improving the quality of the approximation. The value of viscoelastic coefficient of the third Prony term tended to zero during the course of minimizing the total square error. The information about the residual sum of squares (RSS) has been included in the figure captions.

In the second approach, it was assumed that the material parameters of viscoelasticity would be determined based on the measurements of the axial strain and the axial stress, solely (simulated case when the lateral strain data are unavailable because a proper measurement was not performed). Thus, the specimen’s lateral contraction is taken to be a linear function of the axial strain, i.e., \(\varepsilon _{l}(t)=-\nu \varepsilon _{a}(t)\), where \(\varepsilon _{a}(t)=\varepsilon _{0}H(t)\) while \(\nu \) is a constant value. This assumption corresponds to the case of a constant Poisson’s ratio. Based on the information which can be found in the available technical documentation, it is assumed that \(\nu =0.35\) [11, 34] Footnote 2.

The comparison of the experimental results and the theoretical stresses according to the simplified model (\(N=1\), \(M=0\)) is shown in Fig. 8 while the parameter values are listed in Table 1 (model 2). The curve fitting achieved using the extended model (\(N=2\), \(M=2\)) can be viewed in Fig. 9 with the parameter values gathered in Tables 2 and 3 (model 2).

Table 2 Material parameters of extended viscoelastic model (deviatoric response modeled by two Prony terms) determined from ABS stress relaxation data assuming time-dependent (model 1) and constant (model 2) Poisson’s ratio
Full size table
Table 3 Material parameters of extended viscoelastic model (volumetric response modeled by two Prony terms) determined from ABS stress relaxation data assuming time-dependent (model 1) and constant (model 2) Poisson’s ratio
Full size table
Fig. 10
figure 10

Comparison of linear viscoelastic model predictions and experimental data: a time-dependent Young’s modulus, b time-dependent Poisson’s ratio

Full size image

Since the loading is defined by the Heaviside step function, the time-dependent Young’s modulus and Poisson’s ratio can be found using the so-called quasi-elastic approximation [29], i.e.

$$\begin{aligned} E(t)=\frac{9B(t)G(t)}{G(t)+3B(t)}, \, \, \, \, \, \nu (t)=\frac{1}{2} \frac{3B(t)-2G(t)}{G(t)+3B(t)}. \end{aligned}$$
(28)

Equations (28) and (4) were utilized to calculate E(t) and \(\nu (t)\) for the material parameter values gathered in Tables 2 and 3. The constant sets labeled as “Model 1” were used for that purpose. The experimentally measured time-dependent Young’s modulus and Poisson’s ratio were computed using Eq. (13). It can be seen in Fig. 10 that a very good agreement was found between the experimental data and the functions calculated from Eqs. (28) and (4). Both the experimentally measured and the simulated Poisson’s ratios are decreasing with time. The Poisson’s ratio of polymers is generally reported as an increasing function of time, e.g., [27]. The observed decrease is possibly caused by the secondary relaxations which are associated with the motions of side groups or short segments of the main polymer chains.

7 Analysis of selected boundary value problems

In order to investigate the influence of the material parameter identification method on the obtained results, several examples are analyzed including two variations of the Lamé problem. Below both the analytical and the approximate solutions are discussed.

7.1 Thick-walled tube

As an example of a two-dimensional problem, let us consider a thick-walled tube with the external radius of \(a=100\) mm and the internal radius of \(b=50\) mm (Fig. 11). The tube is loaded with the internal pressure \(p=23\) MPa; thus, the boundary conditions in the polar coordinates are [13]:

$$\begin{aligned} r=b \, \, \rightarrow \, \, \sigma _{rr}=-p, \quad r=a \, \, \rightarrow \, \, \sigma _{rr}=0, \end{aligned}$$
(29)

where \(\sigma _{rr}\) is the radial stress component. The elastic solution of the considered problem is given by the following relationships:

$$\begin{aligned} \sigma _{rr}(r)=\frac{pb^{2}}{a^{2}-b^{2}}\left( 1-\frac{a^{2}}{r^{2}} \right) , \, \, \, \, \, \sigma _{tt}(r)=\frac{pb^{2}}{a^{2}-b^{2}}\left( 1+\frac{a^{2}}{r^{2}} \right) , \end{aligned}$$
(30)

and

$$\begin{aligned} u_{r}(r)=\frac{(1+\nu )pb^{2}}{E(a^{2}-b^{2})}\left[ (1-2\nu )r+\frac{a^{2}}{r} \right] , \, \, \, \, \, u_{t}=0, \end{aligned}$$
(31)

with \(\sigma _{tt}\) being the tangential stress component while \(u_{r}\) and \(u_{t}\) are the radial and the tangential displacement components, respectively. It should be noted that according to Eq. (30), the stresses are independent of the assumed material properties.

Fig. 11
figure 11

Thick-walled tube loaded by internal pressure in polar coordinate system

Full size image

In the case of simplified viscoelastic model which assumes a single Prony term for simulating the shear response and an elastic volumetric behavior (\(N=1\), \(M=0\)), an analytical viscoelastic solution can be found by utilizing the correspondence theorem. For that purpose, the stress–strain relations given by Eq. (2) have to be written in the form

$$\begin{aligned} \mathbf{s}+p_{1}'\dot{\mathbf{s}}=q_{0}'{} \mathbf{e}+q_{1}'\dot{\mathbf{e}}, \, \, \, \, \, p=q_{0}''\epsilon , \end{aligned}$$
(32)

with \(p_{1}'\), \(q_{0}'\), \(q_{1}'\) and \(q_{0}''\) being the functions of material parameters. After applying the Laplace transform according to Eq. (6), it is found that:

$$\begin{aligned} {\mathbb {P}}_{1}(s)\bar{\mathbf{s}}(s)={\mathbb {Z}}_{1}(s)\bar{\mathbf{e}}(s), \, \, \, \, \, {\mathbb {P}}_{2}(s){\bar{p}}(s)={\mathbb {Z}}_{2}(s){\bar{\epsilon }}(s), \end{aligned}$$
(33)

where \({\mathbb {P}}_{1}(s)\), \({\mathbb {Z}}_{1}(s)\), \({\mathbb {P}}_{2}(s)\) and \({\mathbb {Z}}_{2}(s)\) are the Laplace transforms of differential operators which take the form of polynomial (in this particular case linear) functions of the transformation parameter s, i.e.

$$\begin{aligned} {\mathbb {P}}_{1}(s)=p_{0}'+p_{1}'s, \, \, \, \, \, {\mathbb {Z}}_{1}(s)=q_{0}'+q_{1}'s, \, \, \, \, \, {\mathbb {P}}_{2}(s)=p_{0}'', \, \, \, \, \, {\mathbb {Z}}_{2}(s)=q_{0}'', \end{aligned}$$
(34)

where

$$\begin{aligned} p_{0}'=1, \, \, \, \, \, p_{1}'=\tau _{1}, \, \, \, \, \, q_{0}'=2G_{\infty }, \, \, \, \, \, q_{1}'=2\tau _{1}\left( G_{\infty }+G_{1} \right) , \, \, \, \, \, q_{0}''=B_{\infty }. \end{aligned}$$
(35)

Substituting Eq. (35) into Eq. (34) yields:

$$\begin{aligned}& {\mathbb {P}}_{1}(s)=1+\tau _{1}s, \, \, \, \, \, {\mathbb {Z}}_{1}(s)=2\left[ G_{\infty }+\tau _{1}\left( G_{\infty }+G_{1} \right) \right] , \, \, \, \, \,\\& {\mathbb {P}}_{2}(s)=1, \, \, \, \, \, {\mathbb {Z}}_{2}(s)=B_{\infty }. \end{aligned}$$
(36)

The shear and bulk relaxances are given by the following relations, respectively:

$$\begin{aligned} {\bar{G}}'(s)=\frac{{\mathbb {Z}}_{1}(s)}{2{\mathbb {P}}_{1}(s)}, \, \, \, \, \, {\bar{B}}'(s)=\frac{{\mathbb {Z}}_{2}(s)}{{\mathbb {P}}_{2}(s)}, \end{aligned}$$
(37)

whereas the stretch relaxance and the Poisson’s retardance are given as

$$\begin{aligned} {\bar{E}}^{\prime}(s)=\frac{9{\bar{B}}^{\prime}(s){\bar{G}}^{\prime}(s)}{{\bar{G}}^{\prime}(s)+3{\bar{B}}^{\prime}(s)}, \, \, \, \, \, {\bar{\nu }}^{\prime}(s)=\frac{3{\bar{B}}^{\prime}(s)-2{\bar{G}}^{\prime}(s)}{2({\bar{G}}^{\prime}(s)+3{\bar{B}}^{\prime}(s))}. \end{aligned}$$
(38)

By inserting Eq. (37) into Eq. (38), the following relationships are found:

$$\begin{aligned}& {\bar{E}}^{\prime}(s)=\frac{9{\mathbb {Z}}_{1}(s){\mathbb {Z}}_{2}(s)}{6{\mathbb {P}}_{1}(s){\mathbb {Z}}_{2}(s)+{\mathbb {Z}}_{1}(s){\mathbb {P}}_{2}(s)}, \, \, \, \, \, \\&{\bar{\nu }}^{\prime}(s)=\frac{3{\mathbb {P}}_{1}(s){\mathbb {Z}}_{2}(s)-{\mathbb {Z}}_{1}(s){\mathbb {P}}_{2}(s)}{6{\mathbb {P}}_{1}(s){\mathbb {Z}}_{2}(s)+{\mathbb {Z}}_{1}(s){\mathbb {P}}_{2}(s)}. \end{aligned}$$
(39)

The viscoelastic solution of the problem can be found when the time functions in Eq. (31)\(_{1}\) are replaced by the functions of the proper Laplace transforms, i.e.

$$\begin{aligned} {\bar{u}}_{r}(r,s)=\frac{(1+{\bar{\nu }}'(s)){\bar{p}}(s)b^{2}}{{\bar{E}}'(s)(a^{2}-b^{2})}\left[ (1-2{\bar{\nu }}'(s))r+\frac{a^{2}}{r} \right] , \, \, \, \, \, {\bar{p}}=\frac{p}{s}. \end{aligned}$$
(40)

Substituting Eqs. (36), (39) and (40)\(_{2}\) into Eq. (40)\(_{1}\) and performing the inverse Laplace transform lead to the following solutionFootnote 3:

$$\begin{aligned} {u}_{r}(r,t)= &\, {} \frac{\left( D^{2}-(A+B)D+AB \right) Fe^{-Dt}}{D(D-C)}\nonumber \\&- \frac{\left( C^{2}-(A+B)C+AB \right) Fe^{-Ct}}{C(D-C)}+\frac{ABF}{CD}, \end{aligned}$$
(41)

where

$$ \begin{aligned}&A=\frac{1}{p_{1}^{\prime}}, \, \, \, \, \, B=\frac{q_{0}^{\prime}(3r^{2}+a^{2})+6B_{\infty }a^{2}}{q_{1}^{\prime}(3r^{2}+a^{2})+6B_{\infty }a^{2}p_{1}^{\prime}}, \, \, \, \, \, C=\frac{q_{0}^{\prime}}{q_{1}^{\prime}}, \, \, \, \, \,\\ &\quad D=\frac{q_{0}^{\prime}+6B_{\infty }}{q_{1}^{\prime}+6B_{\infty }p_{1}^{\prime}}, \\&\quad F=- \frac{pb^{2}p_{1}^{\prime}\left[ q_{1}^{\prime}(3r^{2}+a^{2})+6B_{\infty }a^{2}p_{1}^{\prime} \right] }{(b^{2}-a^{2})rq_{1}^{\prime}(q_{1}^{\prime}+6B_{\infty }a^{2}p_{1}^{\prime})}. \end{aligned} $$
(42)

The change of the radial displacement over time as predicted by the analytical solution given by Eqs. (41) and (42) is plotted in Fig. 12 for the two different material parameter sets (model 1 and model 2) which are gathered in Table 1.

Since the pressure loading is defined by the Heaviside step function, an approximate solution to the analyzed problem can be found. The so-called quasi-elastic approximation [29] is found by replacing elastic constants in Eq. (31)\(_{1}\) by the proper time functions. After substituting Eq. (28) into Eq. (31)\(_{1}\) the following approximate solution is found:

$$\begin{aligned} u_{r}(r,t)=\frac{pb^{2}\left[ G(t)\left( 3r^{2}+a^{2}\right) +3B(t)a^{2}\right] }{2G(t)\left( G(t)+3B(t)\right) \left( a^{2}-b^{2}\right) r}. \end{aligned}$$
(43)

The radial displacement’s time evolution according to the quasi-elastic approximation is plotted in Fig. 12. It can be seen that for both material parameter sets gathered in Table 1, the analytical solution and the quasi-elastic approximation are in a very good agreement.

Fig. 12
figure 12

Comparison of analytical solution and quasi-elastic approximation for simplified viscoelastic model (elastic volumetric response and viscoelastic deviatoric response modeled by standard solid) with two different material parameter sets (model 1 and model 2): a radial displacement versus time for \(r=50\) mm, b radial displacement versus time for \(r=100\) mm

Full size image

In the case of extended viscoelastic model for ABS (\(N=2\) and \(M=2\) in Eq. (4)), obtaining an analytical solution encounters a problem since the inverse Laplace transform of Eq. (40)\(_{1}\) could not be found analytically. The quasi-elastic solutions for both material parameter sets collected in Tables 2 and 3 are plotted in Fig. 13.

Fig. 13
figure 13

Quasi-elastic approximate solution for linear viscoelastic model (volumetric and deviatoric response modeled independently by two Prony terms) and two different material parameter sets (model 1 and model 2): a radial displacement versus time for \(r=50\) mm, b radial displacement versus time for \(r=100\) mm

Full size image

7.2 Pin press fitted into infinite plate

A variant of the Lamé boundary value problem was considered where a rigid pin is press fitted into a hole in infinite linear viscoelastic plate (Fig. 14). The radius of the hole is \(r_{0}=50\) mm while the radius of the pin is greater by the value of \(u_{0}=1.5\) mm. The problem can be solved using polar coordinates. In the case of quasi-elastic approximation, the radial and tangential stresses are given by the following equations [26]:

$$\begin{aligned} \sigma _{rr}(r,t)=-2G(t)u_{0}\frac{r_{0}}{r^{2}}, \, \, \, \, \, \sigma _{tt}(r,t)=2G(t)u_{0}\frac{r_{0}}{r^{2}}, \end{aligned}$$
(44)

whereas the displacement field is given as

$$\begin{aligned} u_{r}(r)=u_{0}\frac{r_{0}}{r}, \, \, \, \, \, u_{t}=0, \end{aligned}$$
(45)

and is independent of the material properties of the plate. The radial and tangent stresses given by Eq. (44) are plotted in Fig. 15. The shear relaxation function utilizing two Prony terms was assumed along with the material parameter values gathered in Table 2.

Fig. 14
figure 14

Rigid pin press fitted into infinite viscoelastic plate

Full size image
Fig. 15
figure 15

Evolution of radial (pink) and tangential stress (red) in infinite viscolelastic plate for different material parameter sets: dashed line—model 1, solid line—model 2 (color figure online)

Full size image

7.3 Cyclic volumetric deformation of cube

In the third of the analyzed problems, a linear viscoelastic cube was considered which is subjected to a cyclic dilatation. The strain measures are given as follows:

$$\begin{aligned} {\varvec{\varepsilon }}_{3 \times 3}= \left[ \begin{array}{ccc} \varepsilon (t) &{} 0 &{} 0 \\ 0 &{} \varepsilon (t) &{} 0 \\ 0 &{} 0 &{} \varepsilon (t) \end{array}\right] , \, \, \, \, \, \epsilon (t)=3\varepsilon (t), \, \, \, \, \, \mathbf{e}_{3 \times 3}=\mathbf{0}_{3 \times 3}. \end{aligned}$$
(46)

The dilatation \(\epsilon (t)\) is defined by a trapezoidal function which is shown in Fig. 16a. Since the components of the strain deviator are constant and equal to zero, the material response is purely volumetric. The theoretical predictions of the cyclic volumetric stress p(t) for the two different material parameter sets (Table 3) are shown in Fig. 16b.

Fig. 16
figure 16

Cyclic volumetric deformation of viscoelastic cube: a dilatation program, b volumetric stress response for model 1 (red dashed line) and model 2 (pink solid line) (color figure online)

Full size image

8 Conclusions

In this work, a method for the determination of material parameters of the three-dimensional linear viscoelasticity has been presented. The method allows to evaluate the viscoelastic constants for an arbitrary deformation history. In the case of a uniaxial stress relaxation test, the proposed methodology enables taking into account the true stress deviator and dilatation histories as depicted in Fig. 5. This in turn results in a more precise values of the identified material parameters than in the case of making a common assumption about the constant Poisson’s ratio.

What is more, it has been observed that a simplification based on assuming the relaxation times a priori, e.g., [6, 7] or applying any special systematic search techniques for the purpose of determining them [9, 32] is unnecessary at least for the case of linear viscoelasticity. The computational power of the modern computers allows to identify the values of the relaxation times along with the other constitutive constants by taking advantage of the available optimization packages such as Scilab or MATLAB, for instance.

The discussed material parameter identification algorithm was applied to determine the viscoelastic constants of ABS thermoplastic polymer. Two different linear viscoelastic models were analyzed. The simplified model assumes a linear elastic bulk behavior and a single Prony term for describing the shear response. The extended model for ABS utilizes two Prony terms for capturing both the shear and the bulk behavior (independently). The simplified version of the constitutive model allows for an acceptable description of the material’s shear response (Figs. 6a and 8a). Some analytical solutions of the boundary value problems can be obtained for this model. The extended constitutive model is able to simulate the material response in both shear and bulk deformations with a very good precision (Figs. 7 and 9). In the case of ABS polymer, adding additional Prony terms to the extended version of the model proved pointless since no improvement in the curve fitting was achieved this way.

Determining the material parameters of linear viscoelasticity with the assumption of a constant Poisson’s ratio does not strongly affect the identified values of the relaxation times, cf Tables 1, 2 and 3. However, the errors in the evaluated values of the bulk relaxation function coefficients are substantial, cf Table 3. This fact significantly affects the solutions of problems involving volumetric deformations (Fig. 16b).

The obtained results lead to a conclusion that utilizing material parameters which were determined assuming a constant Poisson’s ratio does not necessarily have to generate completely incorrect solutions to the boundary value problems, cf Figs. 12, 13 and 15. Nevertheless, this simplification will always cause a certain loss in precision. Generally, the uniaxial stress relaxation data used for the determination of the viscoelastic constants should include the measurements of the specimen’s lateral contraction, if possible. It is particularly important for the correctness of solutions to boundary value problems where a significant volume change takes place.