1 Introduction

Volterra integral equations have been considered as the core of applied mathematics. Recently, it has been noticed that the models presented to express the Corona virus using Volterra equations are better than the existing models presented in the form of differential equations. Since, Volterra integral equations allow to monitor the initial reproduction number, thus determining the incubation period of the virus and then adjusting the preventive measures Fodor et al. (2020) and also due to the tremendous progress made in computer science, and partly due to the complexity of synthetic computational models aided by integration equations in modeling these various complexities. The so-called deep neural network, plays a major role in various applications of artificial intelligence starting with applications of faceprinting, self-driving cars and ending with automatic flight. What we have presented earlier is the importance it has in a particular field, such as medicine and network. As well as, the extent of this importance in other fields such as physics, nuclear energy, as well as dynamics (Tricomi 1985; Wazwaz 2011).

There are different types of Volterra integral equations, like the non-linear weakly singular equation of the second kind which is analyzed in Micula (1862). Also, we mention some of the models that have emerged recently, such as Fredholm and Volterra integro-differential equations, Fredholm integral equations and Volterra–Fredholm equations (Ghiat et al. 2020; Ghiat and Guebbai 2018; Ghiat et al. 2021; Touati et al. 2019). But the important question is how to search for a solution to these equations? In the first place, is there a solution to find it ? Finding a way to get the right solution is difficult and sometimes impossible. Thus, many mathematicians have resorted to the numerical process by innovating, inventing and developing computational methods that allow them to find a solution which converges to the exact solution (Karamov et al. 2021; Deepa et al. 2022; Dehbozorgi and Maleknejad 2021; Fawze et al. 2021; Micula and Cattani 2018; Micula 2015).

In this paper, our objective is to focus on a specific numerical method, called block-by-block, to find an approximate solution of u which is an unknown functions verified the following integral equation:

$$\begin{aligned} \forall x \in [0,X], \; \int _0^x {\mathcal {K}}(x,t,u(t)) \; \textrm{d}t =f(x),\; X < +\infty , \end{aligned}$$
(1)

where f is a given function in the Banach space \(C^1[0,X]\) and the kernel \(K \in C^1([a,b]^2 \times {\mathbb {R}})\). This equation is named the non-linear Volterra equation of the first kind.

In the article Brunner (1997) titled by ’100 years of Volterra equations’, it is noted that the equation (1) first appeared in 1887 Jaëck (2018). It is the result of six papers presented by Volterra and also appears in his book Volterra (2005). Many researchers have followed its path, so we find that in 1959, it entered the world of economics Kantorovich and Gorkov (1959) through Sloan, who developed a capital equation and received the Nobel Prize for it Solow (1969). In 1960, it was used in the modeling of heat transfers between solids and gases Levinson (1960), and in 1996 it was used in the dynamic systems of the economy (Hritonenko and Yatsenko 1996; Muftahov et al. 2017), notably the life span of certain equipment. This is related to the last decade, and recently we find other applications in areas such as: energy (Karamov et al. 2021; Markova et al. 2021), engineering Solodusha and Bulatov (2021), in studies of the evolution of the rapid spread and mutation of Corona virus (Gao et al. 2022; Noeiaghdam et al. 2021; Giorno and Nobile 2022), biology (Brauer 1976; Halpea et al. 2021) and neural network Jafarian et al. (2022).

We note that the analytical study was carried out by Linz in his book Linz (1987), and therefore, we can say that the equation (1) has a unique solution under certain conditions. There are several research papers that are interested in the numerical solution of (1). As Petryshyn’s fixed point theorem Deepa et al. (2022), Taylor collocation method De Bonis et al. (2022), Homotopy perturbation Fawze et al. (2021), direct operational scheme Dehbozorgi and Maleknejad (2021), Hp-version collocation method Nedaiasl et al. (2019), wavelets method Micula and Cattani (2018), iterative method Micula (2015), etc.

In this article, the focus of our attention is on the numerical solution of (1) based on the block-by-block method. In Kasumo and Moyo (2020), the others have constructed a numerical method using this block-by-block method. They built it in two main steps: linearization of the equation (1) and then descritisation by the block-by-block method fourth order. In this manuscript, we start first with the discretization and then the linearization by the Newton method. We pay attention to the comparison between this method and the classical method based on the quadrature scheme described in the book of Linz (1987). Also, we prove that the approximate solution proposed is convergent to the exact solution.

This article is organized as follows: In the first Sect. 2, we reformulate our equation to another equivalent form which is of the second kind. Then, we construct hypotheses to verify the solution’s existence and uniqueness. Afterwards, we move to the second Sect. 3 in which we describe our digital processor and explain how it functioning to obtain a discretization system. We present theorems that show the existence and uniqueness of the solution of the new system and the convergence of the estimate solution. In the end of our manuscript 4, we test our method in a numerical example and compare it with the Nystöm method.

2 Main problem

The direct numerical treatment of the above equation (1) can create a problem of non-regularity. Because, the first kind version of the Volettra equation is an ill-posed problem. For this reason, it cannot be treated in this form. The idea to deal with this form easily is to find an equivalent equation of (1). For this, Linz in Linz (1987) proposed to derive it. So, we assume that the kernel is derivable with respect to x. This allows us to reform our equation to a new form. Hence, our new problem is given as: Search for u the solution of the following Volterra equation of the second kind

$$\begin{aligned} \forall x \in [0,X],\; {\mathcal {K}}(x,x,u(x))=f'(x)-\int _0^x \dfrac{\partial {\mathcal {K}}}{\partial x}(x,t,u(t))\; \textrm{d}t, \quad f(0)=0, \end{aligned}$$
(2)

where \(f',f \in C^0[0,X]\) and \({\mathcal {K}}\), \(\dfrac{\partial {\mathcal {K}}}{\partial x} \in C^0 \bigg ( [0,X]^2 \times {\mathbb {R}}\bigg )\)

So, we assume that the kernel verifies the below hypothesis.

figure a

The condition (1) is called Lipschitz condition and the condition (3) is called lower-Lipschitz condition propose by Linz in the first time to ensure the solution uniqueness of (2) (see Linz 1987).

Before moving to digital framework, we must ensure the existence and uniqueness of the solution (1) in \(C^0[0,X]\). For this reason, we present the next theorem without proof, because it has already been shown in Linz (1987). Therefore, we recall hat \(C^0[0,X]\) is the Banach space equipped with following norm

$$\begin{aligned} \forall v \; \in C^0[0,X], \; \Vert v\Vert _{C^0[0,X]}=\underset{ 0 \le x \le X}{ \max }\ \mid u(x)\mid . \end{aligned}$$

Theorem 1

Under the hypothesis (H), the equation (1) has a unique solution in the Banach space \(C^0[0,X]\).

Now, we can offer the numerical framework comfortably. Therefore, in the following section, we are going to explain all the necessary and basic steps used in the construction of our proposed numerical method.

3 Block-by-block method

One of the most popular ways to solve this non-linear Volterra equation is Nystöm method. But, it has a clear problem. Because, we cannot start and launch our calculation without choosing \(u_0\). Which in most cases is arbitrament choice, i.e., is not the approximate solution of u at the starting point 0. At the beginning, for \(n \ge 1\) we need to define \(\Delta _n\) the uniform subdivision of the interval [0, X] for all \(n \ge 1\) by

$$\begin{aligned} \Delta _n=\bigg \{ 0=x_0< x_1< \dots< x_{n-1}< x_n=X, \; h=x_{j+1}-x_j, \; 0 \le j \le n\bigg \}. \end{aligned}$$

Then, we propose to solve this problem using a new method which depends on the calculation of the solution in the subdivision \([x_i,x_{i+1}]\) for \(0 \le i \le n\) interval by interval at once separately. This method is good as block-by-block. Each subdivision \([x_i,x_{i+1}]\), is divided into three sub-intervals: \([x_i,x_{i1}]\), \([x_{i1},x_{i2}]\) and \([x_{i2}, x_{i+1}]\) such that \(x_{i1}=x_i+\frac{h}{3}\) and \(x_{i2}=x_i+\frac{2h}{3}\). Therefore, our goal is to find the approximate solution in the points \(x_{i1}\), \(x_{i2}\) and \(x_{i+1}\).

The block-by-block method is a generalization of the known implicit Runge–Kutta method for ordinary differential equations. The idea is quite generalized, but it is more easily understood. As we mentioned earlier, the approximate solution is calculated in the points \(x_{1i}\), \(x_{2i}\) and \(x_{i+1}\).

So, for \(x=x_{i1}\), we have

$$\begin{aligned} {\mathcal {K}}(x_{i1},x_{i1}, u(x_{i1}))= & {} f(x_{i1})-\int _0^{x_{1i}} \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1}, t,u(t))\; \textrm{d}t\nonumber \\= & {} f(x_{i1})-\int _{{x_i}}^{x_{i1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1}, t,u(t))\; \textrm{d}t\nonumber \\{} & {} -\overset{i-1}{\underset{j=0}{\sum }} \int _{x_j}^{x_{j+1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1}, t,u(t))\; \textrm{d}t, \end{aligned}$$
(3)

and for \(x=x_{i2}\), we obtain

$$\begin{aligned} {\mathcal {K}}(x_{i2},x_{i2}, u(x_{i2}))= & {} f(x_{i2})-\int _0^{x_{i2}} \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, t,u(t))\; \textrm{d}t \nonumber \\= & {} f(x_{i2})-\int _{{x_i}}^{x_{i2}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, t,u(t))\; \textrm{d}t \nonumber \\{} & {} -\overset{i-1}{\underset{j=0}{\sum }} \int _{x_j}^{x_{j+1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, t,u(t))\; \textrm{d}t, \end{aligned}$$
(4)

finally, for \(x=x_{i+1}\), we get

$$\begin{aligned} {\mathcal {K}}(x_{i+1},x_{i+1}, u(x_{i+1}))= & {} f(x_{i+1})-\int _0^{x_{i+1}} \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, t,u(t))\;\textrm{d}t \nonumber \\= & {} f(x_{i+1}) -\int _{{x_i}}^{x_{i+1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, t,u(t))\; \textrm{d}t\nonumber \\{} & {} -\overset{i-1}{\underset{j=0}{\sum }} \int _{x_j}^{x_{j+1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, t,u(t))\; \textrm{d}t. \end{aligned}$$
(5)

First of all, we recall the Pouzet-type numerical integration scheme given by (9.53)-(9.55) page 154 in Linz (1987)

$$\begin{aligned} \forall g \in C^0[0,X], \quad \int _{x_i}^{x_i+ h \lambda _k} g(x)\; dx \simeq {{\lambda _k}}\dfrac{h}{4}\bigg [ 3g\left( x_i+{{\lambda _k \dfrac{h}{3}}}\right) +g(x_i+{{\lambda _k}} h)\bigg ], \end{aligned}$$
(6)

where

$$\begin{aligned} \lambda _k=\left\{ \begin{array}{c l r } \frac{1}{3}, \quad &{} k=1, \\ \\ \frac{2}{3}, \quad &{} k=2, \\ \\ 1, \quad &{} k=3. \end{array} \right. \end{aligned}$$

Now, we replace the integral in (5) by the integration scheme (6), to obtain for k=3

$$\begin{aligned} \int _{{x_i}}^{x_{i+1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, t,u(t))\; \textrm{d}t\simeq & {} \dfrac{h}{4}\bigg [ 3\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, x_{i1},u(x_{i1}))\nonumber \\{} & {} +\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, x_{i+1},u(x_{i+1}))\bigg ], \end{aligned}$$
(7)

for k=2

$$\begin{aligned} \int _{{x_i}}^{x_{i}+\frac{2h}{3}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, t,u(t))\; \textrm{d}t\simeq & {} \dfrac{h}{6}\bigg [ 3\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, x_{i}+\frac{2h}{9},u(x_{i}+\frac{2h}{9})) \nonumber \\{} & {} +\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, x_{i}+\frac{2h}{3},u(x_{i}+\frac{2h}{3}))\bigg ], \end{aligned}$$
(8)

and for k=1

$$\begin{aligned} \int _{{x_i}}^{x_{i}+\frac{h}{3}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1}, t,u(t))\; \textrm{d}t\simeq & {} \dfrac{h}{12}\bigg [ 3\dfrac{\partial {\mathcal {K}} }{\partial x}\left( x_{i1}, x_{i}+\frac{h}{9},u\left( x_{i}+\frac{h}{9}\right) \right) \nonumber \\{} & {} +\dfrac{\partial {\mathcal {K}} }{\partial x}\left( x_{i1}, x_{i}+\frac{2h}{3},u\left( x_{i}+\frac{h}{3}\right) \right) \bigg ]. \end{aligned}$$
(9)

From the quadrature interpolation, we obtain

$$\begin{aligned} u\left( x_i+\frac{h}{9}\right) =\dfrac{1}{9}\bigg [20u\left( x_i+\frac{h}{3}\right) -16u\left( x_i+\frac{2h}{3}\right) +5u(x_i)\bigg ], \end{aligned}$$
(10)
$$\begin{aligned} u\left( x_i+\frac{2h}{9}\right) =\dfrac{1}{9}\bigg [14u\left( x_i+\frac{h}{3}\right) -7u\left( x_i+\frac{2h}{3}\right) +2u(x_i)\bigg ]. \end{aligned}$$
(11)

Finally, in each subdivision of the interval \([x_i,x_{i+1}]\), we get the following non-linear system of dimension 3:

$$\begin{aligned} \left\{ \begin{array}{c l r} {\mathcal {K}}(x_{i1},x_{i1},u_{i1})&{}=-\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u_{i1}-16u_{i2}+5u_{i+1}]\bigg ) \\ &{}\quad -\dfrac{h}{12}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u_{i1}) -h \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \bigg [ \dfrac{3}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j1},u_{j1}) \\ \\ &{}\quad +\dfrac{1}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j+1},u_{j+1})\bigg ]+f'(x_{i1}),\\ \\ {\mathcal {K}}(x_{i2},x_{i2},u_{i2})&{}=-\dfrac{h}{2}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u_{i1}-7u_{i2}+2u_{i+1}]\bigg ) \\ \\ &{}\quad -\dfrac{h}{6}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u_{i2}) -h \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \bigg [ \dfrac{3}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j1},u_{j1}) \\ \\ &{}\quad +\dfrac{1}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j+1},u_{j+1})\bigg ] +f'(x_{i2}), \\ \\ {\mathcal {K}}(x_{i+1},x_{i+1},u_{i+1})&{}=-\dfrac{3h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1},u_{i1})-\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u_{i+1}) \\ \\ &{}\quad -h \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \bigg [ \dfrac{3}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j1},u_{j1})+\dfrac{1}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j+1},u_{j+1})\bigg ] \\ \\ &{}\quad +f'(x_{i+1}), \end{array} \right. \end{aligned}$$
(12)

where \(u_{i1}\), \(u_{i2}\) and \(u_{i+1}\) are the approximation of \(u(x_{i1}), u(x_{i2})\) and \(u(x_{i+1})\), respectively. We write the last system in another form

$$\begin{aligned} \left\{ \begin{array}{c l r} {\mathcal {K}}(x_{i1},x_{i1},u_{i1})&{}=-\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u_{i1}-16u_{i2}+5u_{i+1}]\bigg ) \\ \\ &{}\quad -\dfrac{h}{12}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u_{i1})+S_{i1}, \\ \\ S_{i1}&{}= -h \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \bigg [ \dfrac{3}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j1},u_{j1})+\dfrac{1}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j+1},u_{j+1})\bigg ]\\ &{}\quad +f'(x_{i1}),\\ \\ {\mathcal {K}}(x_{i2},x_{i2},u_{i2})&{}=-\dfrac{h}{2}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u_{i1}-7u_{i2}+2u_{i+1}]\bigg ) \\ \\ &{}\quad -\dfrac{h}{6}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u_{i2})+S_{i2}, \\ \\ S_{i2}&{}=-h \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \bigg [ \dfrac{3}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j1},u_{j1})+\dfrac{1}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j+1},u_{j+1})\bigg ]\\ &{}\quad +f'(x_{i2}), \\ \\ {\mathcal {K}}(x_{i+1},x_{i+1},u_{i+1})&{}=-\dfrac{3h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1},u_{i1})-\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u_{i+1})+S_{i+1}, \\ \\ S_{i+1}&{}=-h \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \bigg [ \dfrac{3}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j1},u_{j1})+\dfrac{1}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j+1},u_{j+1})\bigg ] \\ \\ &{}\quad +f'(x_{i+1}). \end{array} \right. \end{aligned}$$
(13)

Before starting the convergence study of this new method, we need to verify that the approximate system (13) has a unique solution. Therefore, we introduce the following theorem.

Theorem 2

For \(h < \dfrac{3\theta }{11 L}\) small enough and under the hypothesis (H), the system (13) has a unique solution in \([x_i, x_{i+1}]\) for \( 0 \le i \le n\).

Proof

We fix i and let \(U_i=(u_{i1}, u_{i2},u_{i+1})\) be a vector of \({\mathbb {R}}^3\), supposed \({\mathbb {R}}^3\) equipped with the next norm

$$\begin{aligned} \forall \; V=(v_1,v_2,v_3)\in {\mathbb {R}}^3, \quad \Vert V\Vert _{{\mathbb {R}}^3}=\overset{3}{\underset{i=1}{\sum }} \mid v_i \mid . \end{aligned}$$

Also, we present this vector \(S(i)=(S_{i1}, S_{i2}, S_{i+1})\). We define two non-linear functional \(\psi \) and \(\rho \) by

$$\begin{aligned} \psi :&{\mathbb {R}}^3&\longrightarrow {\mathbb {R}}^3, \nonumber \\&U_i&\longmapsto \psi (U_i)= \begin{pmatrix} {\mathcal {K}}(x_{i1},x_{i1},u_{i1})\\ {\mathcal {K}}(x_{i2},x_{i2},u_{i2}) \\ {\mathcal {K}}(x_{i+1},x_{i+1},u_{i+1}) \end{pmatrix}, \end{aligned}$$
(14)
$$\begin{aligned} \rho :&{\mathbb {R}}^3&\rightarrow {\mathbb {R}}^3, \\&U_i&\longmapsto \rho (U_i)= \begin{pmatrix} -\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u_{i1}-16u_{i2}+5u_{i+1}]\bigg )-\dfrac{h}{12}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u_{i1}) \\ -\dfrac{h}{2}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u_{i1}-7u_{i2}+2u_{i+1}]\bigg )-\dfrac{h}{6}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u_{i2})\\ -\dfrac{3h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1},u_{i1})-\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u_{i+1}) \end{pmatrix}. \end{aligned}$$

So, the system (13) is equivalent to

$$\begin{aligned} \psi (U_i)=\rho (U_i)+S(i). \end{aligned}$$
(15)

For any i fixed and for each subdivision \([x_i, x_{i+1}]\) we define the sequences \(\{U_i^p\}_{ p \in {\mathbb {N}}}\) by

$$\begin{aligned} \left\{ \begin{array}{c l r} \psi (U_i^{0})&{}=\rho (U_i^p)+S(i), \quad p \ge 1,\\ U_i^0&{}=S(i). \end{array} \right. \end{aligned}$$
(16)

Also, we define the sequences \(\{\sigma _{i} ^{p}\}_{p \in {\mathbb {N}}}\) by

$$\begin{aligned} \left\{ \begin{array}{c l r} \sigma _i^{p+1}&{}=U_i^{p+1}-U_i^p, \quad p \ge 1, \\ \sigma _i^{0}&{}=S(i). \end{array} \right. \end{aligned}$$
(17)

It is clear that \(\underset{q=0}{\overset{p}{\sum } }\sigma _{i}^{q}=U_{i}^{p}\). Then, we prove that \(U_{i}^{p}\) converges to \(U_{i}\).

For all \(p \ge 1\), we have

$$\begin{aligned}{} & {} \mid {\mathcal {K}}(x_{i1}, x_{i1},u_{i1}^{k+1})-{\mathcal {K}}(x_{1i}, x_{1i},u_{1i}^{k}\mid \\{} & {} \quad \le \left| \dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u_{i1}^k-16u_{i2}^k+5u_{i+1}^k]\bigg ) +\dfrac{h}{12}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u_{i1}^k) \right. \\{} & {} \left. \qquad -\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u_{i1}^{k-1}-16u_{i2}^{k-1}+5u_{i+1}^{k-1}]\bigg )-\dfrac{h}{12}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u_{i1}^{k-1}) \right| , \\{} & {} \mid {\mathcal {K}}(x_{i2}, x_{i2},u_{i2}^{k+1})-{\mathcal {K}}(x_{i2}, x_{i2},u_{i2}^{k}\mid \\{} & {} \quad \le \left| -\dfrac{h}{2}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u_{i1}^k-7u_{i2}^k+2u_{i+1}^k]\bigg )+\dfrac{h}{6}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u_{i2}^k)\right. \\{} & {} \qquad \left. -\dfrac{h}{2}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u_{i1}^{k-1}-7u_{i2}^{k-1}+2u_{i+1}^{k-1}]\bigg )-\dfrac{h}{6}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u_{i2}^{k-1})\right| ,\\{} & {} \mid {\mathcal {K}}(x_{i+1}, x_{i+1},u_{i+1}^{k+1})-{\mathcal {K}}(x_{i+1}, x_{i+1},u_{i+1}^{k}\mid \\{} & {} \quad \le \left| \dfrac{3h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1},u_{i1}^k)+\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u_{i+1}^k)-\dfrac{3h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1},u_{i1}^{k-1})\right. \\{} & {} \quad \quad \left. -\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u_{i+1}^{k-1})\right| . \end{aligned}$$

According to the hypothesis (H), (5) and (7), we get the following

$$\begin{aligned} \theta \mid u_{i1}^{p+1}-u_{i1}^p \mid\le & {} \dfrac{L h}{36} \bigg [ 20 \mid u_{i1}^p-u_{i1}^{p-1}\mid +16 \mid u_{i2}^p-u_{i2}^{p-1}\mid +5\mid u_{i+1}^p-u_{i+1}^{p-1}\mid \bigg ] \nonumber \\{} & {} +\dfrac{L h}{12}\mid u_{i1}^p-u_{i1}^{p-1}\mid , \end{aligned}$$
(18)
$$\begin{aligned} \theta \mid u_{i2}^{p+1}-u_{i2}^p \mid\le & {} \dfrac{L h}{18} \bigg [ 14 \mid u_{i1}^p-u_{i1}^{p-1}\mid +7\mid u_{i2}^p-u_{i2}^{p-1}\mid +2\mid u_{i+1}^p-u_{i+1}^{p-1}\mid \bigg ]\nonumber \\{} & {} +\dfrac{L h}{6}\mid u_{i2}^p-u_{i2}^{p-1}\mid , \end{aligned}$$
(19)
$$\begin{aligned} \theta \mid u_{i+1}^{p+1}-u_{i+1}^p \mid\le & {} \dfrac{L h}{4} \bigg [ 3 \mid u_{i1}^p-u_{i1}^{p-1}\mid +\mid u_{i+1}^p-u_{i+1}^{p-1}\mid \bigg ]. \end{aligned}$$
(20)

So, we obtain

$$\begin{aligned} \theta \Vert U_i^{p+1}-U_i^p\Vert _{{\mathbb {R}}^3}\le & {} L h \bigg [ \dfrac{13}{6}\mid u_{i1}^p-u_{i1}^{p-1}\mid +\mid u_{i2}^p-u_{i2}^{p-1}\mid \nonumber \\{} & {} +\dfrac{1}{2}\mid u_{i+1}^p-u_{i+1}^{p-1}\mid \bigg ]. \end{aligned}$$
(21)

Consequently,

$$\begin{aligned} \theta \Vert U_i^{p+1}-U_i^p\Vert _{{\mathbb {R}}^3} \le \dfrac{11 L h}{3} \Vert U_i^{p}-U_i^{p-1}\Vert _{{\mathbb {R}}^3}, \end{aligned}$$
(22)

which gives

$$\begin{aligned} \Vert \sigma _i^{p+1}\Vert _{{\mathbb {R}}^3} \le \dfrac{11 L h}{3 \theta } \Vert \sigma _i^p\Vert _{{\mathbb {R}}^3}. \end{aligned}$$
(23)

By recurrence, we obtain

$$\begin{aligned} \Vert \sigma _i^{p+1}\Vert _{{\mathbb {R}}^3} \le \bigg ( \dfrac{11 L h}{3 \theta }\bigg )^{p+1} \Vert \sigma _i^0\Vert _{{\mathbb {R}}^3}. \end{aligned}$$

Assuming that h is small enough such that \(\dfrac{11\,L h}{3 \theta } <1\), then \( \underset{q\ge 1}{\sum }\ \bigg (\dfrac{11\,h W}{3 \theta } \bigg )^{q}\) is convergent. Therefore, \( \sum \nolimits _{q=0}^{p} \sigma _i^{q}\) is convergent. So, \(\underset{ p \rightarrow +\infty }{\lim } U_i^{p}=U_i\).

It remains to be seen whether this limit checks our system.

From the system (16), we have

$$\begin{aligned} \underset{ p \rightarrow +\infty }{\lim }\rho (U_i^{p+1})=\underset{ p \rightarrow +\infty }{\lim }\psi (U_i^p)+S, \end{aligned}$$

since, \({\mathcal {K}}\) and \( \dfrac{\partial {\mathcal {K}}}{\partial x} \) are continuous, so \(\rho \) and \(\phi \) are continuous functional.

$$\begin{aligned} \psi (\underset{ p \rightarrow +\infty }{\lim }U_i^{p+1})=\rho (\underset{ p \rightarrow +\infty }{\lim }U_i^p)+S(i), \end{aligned}$$

which gives that

$$\begin{aligned} \psi (U_i)=\rho (U_i)+S(i). \end{aligned}$$

Now, let us prove that the system has a unique solution.

Let \(\{U_i\}_{0\le i \le n}\) and \(\{V_i\}_{0\le i \le n}\) to solutions of the system (16). For i fixed and according the hypothesis (H), we get

$$\begin{aligned} \Vert \psi (U_i)-\psi (V_i)\Vert _{ {\mathbb {R}}^3} \ge \theta \Vert U_i-V_i\Vert _{{\mathbb {R}}^3}. \end{aligned}$$

From calculations and simplifications, we obtain

$$\begin{aligned} \Vert U_i-V_i\Vert _{ {\mathbb {R}}^3} \le \dfrac{11 L h}{3 \theta } \Vert U_i-V_i\Vert _{ {\mathbb {R}}^3}, \end{aligned}$$

since, \(\dfrac{11 L h}{3 \theta } < 1\), we get the result. \(\square \)

The system (16) is non-linear system of the size 3 in each subdivision \([x_i, x_{i+1}]\) and to solve it, we apply the principle the newton method which it convergence shown in the book of Argyros (2004).

3.1 Convergence of method

In this section, we study the convergence of the approximate solution obtained from the bloc-by-block method. Since, we define the continuity module \(\omega _0(h,.)\) as

$$\begin{aligned} \forall v \in C^0 [a,b], \; \omega _0(h,v)=\underset{\mid x-y\mid \le h}{sup}\ \mid v(x)-v(y)\mid .\end{aligned}$$

and the local consistency error in each \([x_i,x_{i+1}]\) by

$$\begin{aligned} \delta _i(h,x_{i1})= & {} \int _{{x_i}}^{x_{i1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1}, t,u(t))\; \textrm{d}t- \dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u(x_{i1})\nonumber \\{} & {} -16u(x_{i2})+5u(x_{i+1})]\bigg )-\dfrac{h}{12}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u(x_{i1})), \end{aligned}$$
(24)
$$\begin{aligned} \delta _i(h,x_{i2})= & {} \int _{{x_i}}^{x_{i2}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2}, t,u(t))\; \textrm{d}t- \dfrac{h}{2}\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u(x_{i1})\nonumber \\{} & {} -7u(x_{i2})+2u(x_{i+1})]\bigg )-\dfrac{h}{6}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u(x_{i2})), \end{aligned}$$
(25)
$$\begin{aligned} \delta _i(h,x_{i+1})= & {} \int _{{x_i}}^{x_{i+1}}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1}, t,u(t))\; \textrm{d}t- \dfrac{3h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1}, u_{i1})\nonumber \\{} & {} -\dfrac{h}{4}\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u(x_{i+1})). \end{aligned}$$
(26)

Our numerical method is consistent if

$$\begin{aligned} \underset{n \rightarrow +\infty }{ \lim }\ \bigg ( \underset{ 0 \le i \le n}{\max }\ \underset{ 1 \le k \le 3}{\max }\ \mid \delta _i(h,x_{ik})\mid \bigg )=0, \; \text {where} \; x_{ik}=x_i+\frac{k h}{3}, \; \text {for}, \; k=1,2,3. \end{aligned}$$

Let define the following errors for \(0 \le i \le n\),

$$\begin{aligned} \varepsilon _{i1}=u_{i1}-u(x_{i1}), \quad \varepsilon _{i2}=u_{i2}-u(x_{i2}), \quad \varepsilon _{i+1}= u_{i+1}-u(x_{i+1}), \end{aligned}$$

and

$$\begin{aligned} {\bar{\varepsilon }}_i= \dfrac{3}{4}\mid \varepsilon _{i1}\mid +\dfrac{1}{4}\mid \varepsilon _{i+1}\mid . \end{aligned}$$

Theorem 3

Let \( \theta > \dfrac{11 L h}{3}\) and \( {{ {\tilde{L}}}}=\min \bigg ( \dfrac{1}{h(3+4c_1)},\dfrac{1}{h(1+4c_2)}\bigg )\). Then,

$$\begin{aligned} \underset{n \rightarrow +\infty }{\lim }\ \bigg (\underset{ 0 \le i \le n}{\max }\ \mid \bar{\varepsilon _i}\mid \bigg )=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \underset{n \rightarrow +\infty }{ \lim }\ \bigg ( \underset{ 0 \le i \le n}{\max }\ \mid {\varepsilon _{i2}}\mid \bigg )=0. \end{aligned}$$

Proof

For n large enough and \( 0 \le i \le n\), we have

$$\begin{aligned}{} & {} | {\mathcal {K}}(x_{i1},x_{i1},u_{i1})-{\mathcal {K}}(x_{i1},x_{i1},u(x_{i1}))| \\{} & {} \quad \le \dfrac{h}{12} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u_{i1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{i1},u(x_{i1}))\right| \\{} & {} \qquad + \dfrac{h}{4} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u_{i1}-16u_{i2}+5u_{i+1}]\bigg ) \right. \\{} & {} \left. \qquad -\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i1},x_i+\dfrac{h}{9}, \dfrac{1}{9}[20u(x_{i1})-16u(x_{i2})+5u(x_{i+1})]\bigg )\right| \\{} & {} \qquad + \dfrac{3h}{4} \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j1},u_{j1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j1},u(x_{j1}))\right| \\{} & {} \qquad +\dfrac{h}{4} \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j+1},u_{j+1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i1},x_{j+1},u(x_{j+1}))\right| + \mid \delta _i(h,x_{i1})\mid . \end{aligned}$$

The hypothesis (H) implies that

$$\begin{aligned} \theta \mid \varepsilon _{i1}\mid\le & {} L h \bigg [\dfrac{23}{36} \mid \varepsilon _{i1}\mid + 4 \mid \varepsilon _{i2}\mid +\dfrac{5}{4} \mid \varepsilon _{i+1}\mid +\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left[ \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \right] \bigg ]\nonumber \\{} & {} +\mid \delta _i(h,x_{i1})\mid . \end{aligned}$$
(27)

From the second equation of the system (13)

$$\begin{aligned}{} & {} | {\mathcal {K}}(x_{i2},x_{i2},u_{i2})-{\mathcal {K}}(x_{i2},x_{i2},u(x_{i2}))| \\{} & {} \quad \le \dfrac{h}{6} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u_{i2})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{i2},u(x_{i2}))\right| \\{} & {} \quad \quad + \dfrac{h}{4} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u_{i1}-7u_{i2}+2u_{i+1}]\bigg ) \right. \\{} & {} \left. \quad \quad -\dfrac{\partial {\mathcal {K}} }{\partial x}\bigg (x_{i2},x_i+\dfrac{2h}{9}, \dfrac{1}{9}[14u(x_{i1})-7u(x_{i2})+2u(x_{i+1})]\bigg )\right| \\{} & {} \quad \quad + \dfrac{3h}{4} \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j1},u_{j1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j1},u(x_{j1}))\right| \\{} & {} \quad \quad +\dfrac{h}{4} \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j+1},u_{j+1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i2},x_{j+1},u(x_{j+1}))\right| + \mid \delta _i(h,x_{i2})\mid . \end{aligned}$$

From hypothesis ( H), we get

$$\begin{aligned} \theta \mid \varepsilon _{i2}\mid\le & {} L h \bigg [\dfrac{14}{18} \mid \varepsilon _{i1}\mid + \dfrac{5}{9} \mid \varepsilon _{i2}\mid +\dfrac{1}{9} \mid \varepsilon _{i+1}\mid +\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left[ \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \right] \bigg ]\nonumber \\{} & {} + \mid \delta _i(h,x_{i2})\mid . \end{aligned}$$
(28)

Using the fact \(\dfrac{11 L h}{3} < \theta \), which implies that \( \dfrac{5\,L h}{9} < \theta \), we obtain

$$\begin{aligned} \mid \varepsilon _{i2}\mid\le & {} \dfrac{9 L h}{9 \theta -5 L h }\bigg [\dfrac{14}{18} \mid \varepsilon _{i1}\mid +\dfrac{1}{9} \mid \varepsilon _{i+1}\mid +\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left[ \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \right] \bigg ]\nonumber \\{} & {} + \mid \delta _i(h,x_{i2})\mid . \end{aligned}$$
(29)

Substituting (29) in (27), we get

$$\begin{aligned} \mid \varepsilon _{i1}\mid\le & {} L h \bigg [c_1 \mid \varepsilon _{i1}\mid +c_2 \mid \varepsilon _{i+1}\mid +c_3\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \bigg ] \nonumber \\{} & {} + \mid \delta _i(h,x_{i1})\mid +\dfrac{9 L h }{9 \theta -5 L h }\mid \delta _i(h,x_{i2})\mid , \end{aligned}$$
(30)

where \(c_2=\dfrac{5}{4}+\dfrac{36 L h}{91 \theta -45L h }\), \(c_1=\dfrac{23}{8}+\dfrac{56 L h}{18 \theta -L h 10}\) and \(c_3=1+\dfrac{9 L h}{9 \theta -5L h }\).

From the third equation of the system (13)

$$\begin{aligned}{} & {} | {\mathcal {K}}(x_{i+1},x_{i+1},u_{i+1})-{\mathcal {K}}(x_{i+1},x_{i+1},u(x_{i+1}))| \\{} & {} \quad \le \dfrac{h}{4} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u_{i+1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i+1},u(x_{i+1}))\right| \\{} & {} \quad \quad + \dfrac{3h}{4} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1}, u_{i1}) -\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{i1},u(x_{i1})\right| \\{} & {} \quad \quad + \dfrac{3h}{4} \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j1},u_{j1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j1},u(x_{j1}))\right| \\{} & {} \quad \quad +\dfrac{h}{4} \overset{i-1}{\underset{j=0}{\displaystyle \sum }} \left| \dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j+1},u_{j+1})-\dfrac{\partial {\mathcal {K}} }{\partial x}(x_{i+1},x_{j+1},u(x_{j+1}))\right| + \mid \delta _i(h,x_{i+1})\mid , \end{aligned}$$

then,

$$\begin{aligned} \theta \mid \varepsilon _{i+1}\mid \le L h \bigg [\dfrac{3}{4} \mid \varepsilon _{i1}\mid +\dfrac{1}{4} \mid \varepsilon _{i+1}\mid +\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \bigg ]+ \mid \delta _i(h,x_{i+1})\mid . \qquad \end{aligned}$$
(31)

By summation (30) and (31)

$$\begin{aligned} \theta \bigg [\mid \varepsilon _{i1}\mid +\mid \varepsilon _{i+1}\mid \bigg ]\le & {} L h \bigg [ (\dfrac{3}{4}+c_1)\mid \varepsilon _{i1}\mid +(\dfrac{1}{4}+c_2)\mid \varepsilon _{i+1}\mid \nonumber \\{} & {} +(c_3+1)\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \bigg ] +\mid \delta _i(h,x_{i1})\mid \nonumber \\{} & {} + \dfrac{9 L h}{9 \theta -5 L h }\mid \delta _i(h,x_{i2})\mid + \mid \delta _i(h,x_{i+1})\mid . \end{aligned}$$
(32)

So, we get

$$\begin{aligned}{} & {} \theta \bigg [ \bigg (1-L h(\dfrac{3}{4}+c_1)\bigg )\mid \varepsilon _{i1}\mid +\bigg (1-L h(\dfrac{1}{4}+c_2)\bigg )\mid \varepsilon _{i+1}\mid \bigg ], \end{aligned}$$
(33)
$$\begin{aligned}{} & {} \quad \le (c_3+1)\overset{i-1}{\underset{j=0}{\displaystyle \sum }} \dfrac{3}{4} \mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \nonumber \\{} & {} \quad \quad + \mid \delta _i(h,x_{i1})\mid +\dfrac{9 L h}{9 \theta -5 L h }\mid \delta _i(h,x_{i2})\mid + \mid \delta _i(h,x_{i+1})\mid . \end{aligned}$$
(34)

We have \( {{ {\tilde{L}}}}=\min \bigg ( \dfrac{1}{h(3+4c_1)},\dfrac{1}{h(1+4c_2)}\bigg )\). We get \({{ {\tilde{L}}}} \le \dfrac{1}{h(3+4c_1)} \) which gives \(1-{{ {\tilde{L}}}}h (\dfrac{3}{4}+c_1) \ge \dfrac{3}{4}\). Also, \({{ {\tilde{L}}}} \le \dfrac{1}{h(1+4c_2)} \) which gives \(1-{{ {\tilde{L}}}}h (c_2+\dfrac{1}{4}) \ge \dfrac{1}{4}\). So, we get

$$\begin{aligned} \bigg [\dfrac{3}{4}\mid \varepsilon _{i1}\mid +\dfrac{1}{4}\mid \varepsilon _{i+1}\mid \bigg ]\le & {} \dfrac{(c_3+1)}{\theta }\overset{i-1}{\underset{j=0}{\displaystyle \sum }}\bigg [ \dfrac{3}{4}\mid \varepsilon _{j1}\mid +\dfrac{1}{4}\mid \varepsilon _{j+1}\mid \bigg ] \nonumber \\{} & {} + \dfrac{1}{\theta } \mid \delta _i(h,x_{i1})\mid +\dfrac{9 L h}{ 9 \theta ^2 -5 L h }\mid \delta _i(h,x_{i2})\mid \nonumber \\{} & {} + \mid \delta _i(h,x_{i+1})\mid . \end{aligned}$$
(35)

Applying Gronwel’s lemma Linz (1987), we get

$$\begin{aligned} {\bar{\varepsilon }}_i\le & {} \bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i-1} \bigg [\dfrac{1}{\theta } \mid \delta _i(h,x_{i1})\mid +\dfrac{9 L h}{ 9 \theta ^2 -5 L h }\mid \delta _i(h,x_{i2})\mid \nonumber \\{} & {} + \mid \delta _i(h,x_{i+1})\mid +\dfrac{c_3+1}{\theta }\bar{\varepsilon _0}\bigg ], \end{aligned}$$
(36)

and we have for \(0 \le i \le n\),

$$\begin{aligned} \bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{n-1} < + \infty . \end{aligned}$$

So,

$$\begin{aligned} \underset{n \rightarrow +\infty }{ \lim }\ \bigg ( \underset{ 0 \le i \le n}{\max }\ {\bar{\varepsilon }}_i \bigg )=0. \end{aligned}$$

As a result,

$$\begin{aligned}{} & {} \underset{n \rightarrow +\infty }{ \lim }\ \bigg ( \underset{ 0 \le i \le n}{\max }\ \mid {\varepsilon _{i1}}\mid \bigg )=0, \end{aligned}$$
(37)
$$\begin{aligned}{} & {} \underset{n \rightarrow +\infty }{ \lim }\ \bigg ( \underset{ 0 \le i \le n}{\max }\ \mid {\varepsilon _{i+1}}\mid \bigg )=0. \end{aligned}$$
(38)

Substituting (37) and (38) in (29), we get

$$\begin{aligned} \underset{n \rightarrow \infty }{ \lim }\ \bigg ( \underset{ 0 \le i \le n}{\max }\ \mid {\varepsilon _{i2}}\mid \bigg )=0. \end{aligned}$$

\(\square \)

Now, we give the theorem which prove the order of convergence of our numerical technique

Theorem 4

 

  1. 1.

    If \( \dfrac{\partial K}{\partial x} \in C^0([0,X]^2 \times {\mathbb {R}}, {\mathbb {R}})\) and \(u \in C^1[0,X]\), we have

    $$\begin{aligned} {\bar{\varepsilon }}_i \le \dfrac{h}{4} \; \rho \bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i}, \quad 0 \le i \le n. \end{aligned}$$
  2. 2.

    If \( \dfrac{\partial K}{\partial x} \in C^2([0,X]^2 \times {\mathbb {R}}, {\mathbb {R}})\) and \(u \in C^3[0,X]\), we obtain

    $$\begin{aligned} {\bar{\varepsilon }}_i \le \dfrac{h^3}{3}\; {\bar{\rho }}\bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i}, \quad 0 \le i \le n, \end{aligned}$$

where \(\rho \) and \({\bar{\rho }}\) are positive constants.

Proof

For \(n\ge 1\), we define \(\pi _{n,1}\) and \(\pi _{n,2}\) two piecewise linear interpolation of orders 1 and 2, respectively. So, for all \(x \in [ x_i+\lambda _k \dfrac{h}{3}, x_i+\lambda _k {h}]\)

$$\begin{aligned} \pi _{n,1}(g(x))=\dfrac{3}{2\;\lambda _k h} \bigg [(x_i+\lambda _k h-x)g\left( x_i+\lambda _k \dfrac{h}{3}\right) +\left( x-x_i-\lambda _k \dfrac{h}{3}\right) g(x_i+\lambda _k h)\bigg ], \end{aligned}$$

and for all \(x \in [ x_i, x_{i+1}]\)

$$\begin{aligned} \pi _{n,2}(g(t))= & {} \dfrac{9}{2h^2}\left( x-x_i-\dfrac{h}{3}\right) \left( x-x_i-\dfrac{2h}{3}\right) g(x_i) \\{} & {} +\dfrac{9}{h^2}(x-x_i)\left( x-x_i-\dfrac{2h}{3}\right) g\left( x_i+\dfrac{h}{3}\right) \\{} & {} +\dfrac{9}{2h^2}(x-x_i)\left( x-x_i-\dfrac{h}{3}\right) g\left( x_i+\dfrac{2h}{3}\right) . \end{aligned}$$

Therefore, the consistence errors (24)-(26) are equivalent

$$\begin{aligned} \delta _i(h,x_i+\lambda _k h)= & {} \int _{x_i}^{x_i+\lambda _k h} \dfrac{\partial K}{\partial x}(x_i+\lambda _k h,t,u(t))-\pi _{n,1}\left( \dfrac{\partial K}{\partial x}(x_i+\lambda _k h,t,u(t)\right) \; \textrm{d}t \nonumber \\{} & {} +\dfrac{h}{4}\bigg [ \dfrac{\partial K}{\partial x}\left( x_i+\lambda _k h,x_i+\lambda _k\dfrac{h}{3},u\left( x_i+\lambda _k\dfrac{h}{3}\right) \right) \nonumber \\{} & {} -\dfrac{\partial K}{\partial x}\left( x_i+\lambda _k h,x_i+\lambda _k\dfrac{h}{3}, \pi _{n,2}\left( u\left( x_i+\lambda _k\dfrac{h}{3}\right) \right) \right) \bigg ]. \end{aligned}$$
(39)

Then,

  1. 1.

    If \( \dfrac{\partial K}{\partial x} \in C^0([0,X]^2 \times {\mathbb {R}}, {\mathbb {R}})\) and \(u \in C^1[0,X]\) the consistence error (39) have this markup

    $$\begin{aligned} \mid \delta _i(h,x_i+\lambda _k h)\mid\le & {} \dfrac{h}{4} {\bar{\upsilon }}_k, \end{aligned}$$
    (40)

    where

    $$\begin{aligned} {\bar{\upsilon }}_k=\lambda _k \; \omega _0\bigg ( \dfrac{\partial K}{\partial x}(x_i+\lambda _k h,.,u)\bigg )+ L \omega _0(u,h).\end{aligned}$$

    So, using (40), the estimation (36) is given as

    $$\begin{aligned} {\bar{\varepsilon }}_i \le \bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i-1} \bigg [\dfrac{h}{4}\varrho +\dfrac{c_3+1}{\theta }\bar{\varepsilon _0}\bigg ], \end{aligned}$$

    where \(\varrho =\dfrac{1}{\theta }{\bar{\upsilon }}_1 +\dfrac{9\,L h}{ 9 \theta ^2 -5\,L h }{\bar{\upsilon }}_2+ {\bar{\upsilon }}_3.\) Furthermore, by applying (40) and the definitions of error consistence (24)-(26)

    $$\begin{aligned} \bar{\varepsilon _0} \le \dfrac{h}{4}\rho . \end{aligned}$$

    We obtain

    $$\begin{aligned} {\bar{\varepsilon }}_i \le \dfrac{h}{4}\; \rho \bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i}. \end{aligned}$$
  2. 2.

    If \( \dfrac{\partial K}{\partial x} \in C^2([0,X]^2 \times {\mathbb {R}}, {\mathbb {R}})\) and \(u \in C^3[0,X]\) by the error interpolation theorem (see Endre and David 2003, page 287) the consistence error (39) have the following markup

    $$\begin{aligned}{} & {} \underset{ 1 \le k \le 3}{\max }\ \mid \delta _i(h,x_i+\lambda _k h)\mid \nonumber \\{} & {} \quad \le \Theta \lambda _k^3 \;\dfrac{h^3}{3} + \dfrac{L h}{4 } \left| u\left( x_i+\lambda _k \dfrac{h}{3}\right) -\pi _{n,2}\left( u\left( x_i+\lambda _k +\dfrac{h}{3}\right) \right) \right| \nonumber \\{} & {} \quad \le \dfrac{h^3}{3} {\upsilon }_k, \end{aligned}$$
    (41)

    where

    $$\begin{aligned} \Theta =\underset{ 0 \le x,t \le X}{\max }\ \left| \dfrac{\partial ^3 K}{\partial ^2 t \partial x}(x,t,u(t))\right| , \end{aligned}$$

    and

    $$\begin{aligned} {\upsilon }_k=\Theta \lambda _k^3 + \dfrac{L \lambda _k (1-\lambda _k)(2-\lambda _k) h}{12}\left| u^{(3)} \left( x_i+\lambda _k \dfrac{h}{3}\right) \right| . \end{aligned}$$

    Then, (36) has the following estimation

    $$\begin{aligned} {\bar{\varepsilon }}_i \le \bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i-1} \bigg [\dfrac{h^3}{3}{\bar{\varrho }}+\dfrac{c_3+1}{\theta }\bar{\varepsilon _0}\bigg ], \end{aligned}$$

    where \({\bar{\varrho }}=\dfrac{1}{\theta }{\upsilon }_1 +\dfrac{9\,L h}{ 9 \theta ^2 -5\,L h }{\upsilon }_2+{\upsilon }_3.\) Also, we have

    $$\begin{aligned} \bar{\varepsilon _0} \le \dfrac{h^3}{3} {\bar{\rho }}. \end{aligned}$$

    In addition,

    $$\begin{aligned} {\bar{\varepsilon }}_i \le \dfrac{h^3}{3}{\bar{\rho }}\bigg (1+\dfrac{c_3+1}{\theta }\bigg )^{i}. \end{aligned}$$

\(\square \)

4 Numerical examples

We give two numerical examples to prove the efficiency and accuracy of the method presented. In the following examples, we calculate \(u_i\) according the scheme (16). First, we define the discrete error as

$$\begin{aligned} err_n=\underset{0 \le i \le n}{\max }\mid u(x_i)-u_i^{\nu }\mid , \end{aligned}$$

where \(u_i^{\nu }\) is a solution of the system (16) by Newton method. In the both examples, we choose the initial point of the Newton method \(u_0^{0}=f(0)\).

Let give the next equation

$$\begin{aligned} \forall x \in [0,1], \; \int _0^x \dfrac{1}{x+t+9+\exp (u(t))}\; dx=\dfrac{1}{2}\log \bigg (\dfrac{3x+10}{x+10}\bigg ), \end{aligned}$$
(42)

where the exact solution is \(u(x)=\log (x+1)\).

In addition, we have the lower-Lipschitz coefficient \(\theta =\dfrac{1}{11+\log (2)}\) and the Lipschitz coefficient \(L=\dfrac{1}{9}\). So, the condition of convergence \(\theta > \dfrac{11\,L h}{3}\) is verified.

We give another equation

$$\begin{aligned} \forall x \in [0,3], \; \int _0^x \dfrac{\exp (x) t^2+1}{\cos (t)^2+1+u(t)^2}\; \textrm{d}t=\dfrac{x}{2}+\dfrac{x^3\exp (x)}{6}, \end{aligned}$$
(43)

and the exact solution \(u(x)=\sin (x)\). In addition, we have the lower-Lipschitz coefficient \(\theta =\dfrac{1}{3}\) and the Lipschitz coefficient \(L=1+9e^1+1\). So, the condition of convergence \(\theta > \dfrac{11L h}{3}\) is verified.

Let introduce tables, which explain the error between the numerical and exact solutions in all points \(x_i\). In these following tables, we will calculate the error between the numerical solution and the correct solution using the MATLAB program, where we will apply the method proposed in this article and compare the results obtained with Nystöm method.

In each row of the table, we will choose n, which is the number of divisions of the interval [a, b]. Then, we will choose in each column a number of iterations \({\nu }\), where we notice that the more we increase n and \({\nu }\), the error using the block-by-block method gets closer to zero faster than Nystöm method. Therefore, this table is the best proof that shows the efficiency of the method proposed in this paper.

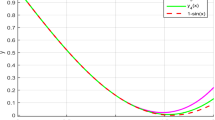
Table 1 Table 01 is the error approximation of equation (42) and table 02 is the error approximate of the equation (43)
Full size table

To further clarify the difference between the error using the two mentioned methods, we have drawn the error statement, where the first statement refers to the equation (42) and the second refers to the equation (43). We, can see from the two statements the great difference between the two methods. We see that the error of the block-by-block method applies to zero.

Fig. 1
figure 1

Block-by-block and Nyström error of Eq. (42) with \(n=10\)

Full size image
Fig. 2
figure 2

Block-by-block and Nyström error of Eq. (43) with \(n=10\)

Full size image

In both graphs, the x-axis is the discretization nodes. The error graph of the block-by-block method is colored in blue. It applies completely to the x-axis. Indicating that, the error of our method compared by the Nyström error is very close or equal to zero.

5 Conclusion

In this paper, we have concentrated and focused on finding a numerical solution to the non-linear Volterra integral equation of the first kind. We did not focus on the analytical study because it has already been verified in the Linz book Linz (1987).

First, we define a condition on the kernel, so that we can convert the first kind equation to a second-kind equation, because dealing directly with the first equation can lead us to the next problem: A small change in the input leads to a huge change in the results, and this is what we call ill-posed problems. We also built some assumptions which then allowed us to be consistent in the numerical and analytical study.

As for the numerical solution, we apply the block-by-block method, which is the opposite of what is done to solve this type of equation. One of the advantages of this method is that it is not necessary to know the value of the solution at the initial point i.e we can choose the initial point only in iteration \(i=0\) by \(u_0^{0}=f(0)\). Then, in every iteration i we put \(u_{i0}^{\nu +1}=u_{(i-1)0}^{\nu }\),   \(u_{i1}^{\nu +1}=u_{(i-1)1}^{\nu }\) and \(u_{i}^{\nu +1}=u_{(i-1)}^{\nu }\). Moreover, the performance of this method depends on transforming the equation of each division \([x_i,x_{i+1}]\) into a non-linear system of dimension three, and thus finding the solution at three different points \(x_{i1}\), \(x_{i2}\) and \(x_{i+1}\)in each division \([x_i,x_{i+1}]\). To solve this system, we apply the Newton’s method Wazwaz (2011). Because, in the literature of the numerical processes of the non-linear Volterra equations there are two essential steps: linearization and discretization. The numerical treatment that starts with the discretization of the equation its consequence is a non-linear algebraic system. It is necessary to solve this system by Newton’s method and the best choice of initial point is \(u_0=f(0)\) (see Ghiat et al. 2021; Ghiat and Guebbai 2018; Ghiat et al. 2020; Touati et al. 2019; Deepa et al. 2022; Linz 1987).

We have presented some theorems that explain the convergence of the numerical solution to the exact solution. We could see that this method is considered as the best one compared to the established method, which is the quadrature method as the numerical examples well illustrate it.