Bernstein Multiscaling polynomials and application by solving Volterra integral equations

Abstract

In this paper, we present a direct computational method to solve Volterra integral equations. The proposed method is a direct method based on approximate functions with the Bernstein Multiscaling polynomials. In this method, using operational matrices, the integral equation turns into a system of equations. Our approach can solve nonlinear integral equations of the first kind and the second kind with piecewise solution. The computed operational matrices in this article are exact and new. The comparison of obtained solutions with the exact solutions shows that this method is acceptable. We also compared our approach with two direct and expansion–iterative methods based on the block-pulse functions. Our method produces a system, which is more economical, and the solutions are more accurate. Moreover, the stability of the proposed method is studied and analyzed by examining the noise effect on the data function. The appropriateness of noisy solutions with the amount of noise approves that the method is stable.

Introduction

Most of integral equations of the first kind are ill-posed problems. Many authors paid attention to solve these equations and presented some methods [1–8]. These problems have application in mathematics, physics, and engineering. Recently, using polynomials have been common to solve these equations, see [9–27].

BMSPs are more general forms of BPs. One of the advantages of BMSPs compared to BPs is that they can approximate piecewise functions. In addition, using BMSP basis, we will have two degrees of freedom which increase accuracy of the method. One of these parameters is m, the degree of polynomials, and the other one k, which corresponds to the number of partitions in the interval $[a,b)$.

In this paper, we review BP properties and preliminary theorems in Subsect. 1 of Sect. “Review of Bernstein polynomials”. In Subsects. “Tranformation matrices” and “Operational matrices”, transformation matrices and operational matrices for BPs are computed. In Sect. “Bernstein Multiscaling polynomials”, BMSPs are defined. Transformational matrices and operational matrices for BMSPs are obtained in Sects. “Transformation matrices” and “BMSPs operational matrices”, respectively. In Sect. “Solution of Volterra integral equation”, by applying obtained matrices and functions approximation, the integral equations are turned into a system of equations. We present some numerical examples to illustrate the accuracy and ability of this method in Sect. “Numerical examples”. In next section, we compare our approach with two direct and expansion–iterative methods based on block-pulse functions. In Sect. “Stability of method”, stability is shown and we end this paper with a short conclusion in Sect. “Conclusion”.

Review of Bernstein polynomials

Preliminaries

Definition 1. Suppose m is a positive integer number, BPs of degree m on the interval $[a, b]$ are defined as

$$ B_{i,m} (x) = \left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right)\frac{{(x - a)^{i} (b - x)^{m - i} }}{{(b - a)^{m} }}, \quad i = 0, \ldots ,m. $$

In addition, $B_{i,m} (x) = 0$ if $i < 0$ or $i > m$.

For convenience, we consider $\left[ {a, b} \right] = \left[ {0, 1} \right]$, namely

$$ B_{i,m} (x) = \left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right)x^{i} (1 - x)^{m - i} , \quad i = 0, \ldots ,m. $$

We denote $\Phi_{m}$, an $m + 1 - {\text{column}}\,{\text{vector}}$, as follows: $\Phi_{m} (x) = [\phi_{0} (x), \ldots, \phi_{m} (x)]^{T}$, where $\phi_{i} (x) = B_{i,m} (x), i = 0, \ldots ,m$.

The BPs have many interesting properties [24–30]. However, here, some of them that are useful in our work are stated:

$$ (\varvec{p1}) \quad \varvec{ }B_{i,m} (x)B_{j,m} (x) = \frac{{\left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {i + j} \\ \end{array} } \right)}}B_{i + j,2m} (x), \quad i,j = 0, \ldots ,m. $$

$$ (\varvec{p2}) \quad B_{i,m} (x) = \mathop \sum \limits_{j = 0}^{k} \frac{{\left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {m + k} \\ {i + j} \\ \end{array} } \right)}}B_{i + j,m + k} (x), \quad j,k = 0, \ldots ,m. $$

$$ (\varvec{p3}) \quad \frac{{B_{i,m} (x)}}{{\left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right)}} = \frac{{B_{i,m + 1} (x)}}{{\left( {\begin{array}{*{20}c} {m + 1} \\ i \\ \end{array} } \right)}} + \frac{{B_{i + 1,m + 1} (x)}}{{\left( {\begin{array}{*{20}c} {m + 1} \\ {i + 1} \\ \end{array} } \right)}}, \quad i = 0, \ldots ,m. $$

The following theorems are a fundamental tool that justifies the use of polynomials.

Theorem A [31] Suppose $H = l^{2} ([a,b])$ is a Hilbert space with the inner product defined by ${\left\langle {f, g } \right\rangle } = \mathop \int \nolimits_{a}^{b} f(t)g(t){\text{d}}t$ , and in addition, $Y = {\text{Span}}\{ B_{0,m} (x),B_{1,m} (x), \ldots ,B_{m,m} (x)\}$ is the span space by Bernstein’s polynomials of degree m. Let f be an arbitrary element in H. Since Y is a finite dimensional and closed subspace, it is a complete subset of H. Therefore, f has the unique best approximation out of Y, such that $y_{0}$

$$ \exists y_{0} \in Y; \forall y \in Y: \left\| {f - y_{0} } \right\|_{2} \le \left\| {f - y} \right\|_{2} . $$

Therefore, there are the unique coefficients $\alpha_{j} , j = 0,1, \ldots ,m$ , such that

$$ f(t) \approx y_{0} (t) = \mathop \sum \limits_{j = 0}^{m} \alpha_{j} B_{j,m} (t) = \alpha^{T} \Phi_{m} , $$

where $\alpha = [\alpha_{0} \;\alpha_{0} \ldots \alpha_{m} ]^{T}$ can be obtained by

$$ \alpha = \frac{\langle{f(t),\Phi_{m} (t)}\rangle}{\langle{\Phi_{m} (t),\Phi_{m} (t)}\rangle} , $$

such that ${\left\langle {f(t),\Phi_{m} (t)} \right\rangle } = \int \limits_{a}^{b} f(t) \Phi_{m} (t)\;{\text{d}}t$.

In above theorem, we denote $Q = \langle\Phi_{m} (t),\Phi_{m} (t)\rangle$ as dual matrix. Furthermore, it is easy to see

$$ Q_{i,j} = \frac{{\left( {\begin{array}{*{20}c} m \\ {i - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ {j - 1} \\ \end{array} } \right)}}{{(2m + 1)\left( {\begin{array}{*{20}c} {2m} \\ {i + j - 2} \\ \end{array} } \right)}}, \quad i,j = 1, \ldots ,m + 1. $$

Next theorem indicates that dual matrix is symmetric and invertible.

Theorem B [31] Elements $y_{1} ,y_{2} , \ldots ,y_{n}$ of a Hilbert space $H$ constitute a linearly independent set in $H$ if and only if $G(y_{1} ,y_{2} , \ldots ,y_{n} ) \ne 0.$

where $G(y_{1} ,y_{2} , \ldots ,y_{n} )$ is the Gram determinant of $y_{1} ,y_{2} , \ldots ,y_{n}$ defined by

$$ G(y_{1} ,y_{2} , \ldots ,y_{n} ) = \left| {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left\langle {y_{1} ,y_{1} } \right\rangle } & {\left\langle {y_{1} ,y_{2} } \right\rangle } \\ {\left\langle {y_{2} ,y_{1} } \right\rangle } & {\left\langle {y_{2} ,y_{2} } \right\rangle } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\left\langle {y_{1} ,y_{n} } \right\rangle } \\ \cdots & {\left\langle {y_{2} ,y_{n} } \right\rangle } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {\left\langle {y_{n} ,y_{1} } \right\rangle } & {\left\langle {y_{1} ,y_{1} } \right\rangle } \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \vdots \\ \cdots & {\left\langle {y_{n} ,y_{n} } \right\rangle } \\ \end{array} } \\ \end{array} } \right|. $$

For a two-dimensional function $k(x,t) \in l^{2} ([0,1] \times [0,1])$ , it can be similarly expanded with respect to BPs, such as

$$ k(x,t) \simeq \Phi_{m}^{T} (x)K\Phi_{m} (t), $$

and $K$ is the $(m + 1) \times (m + 1)$ BP coefficient matrix with

$$ K_{i,j} \simeq Q^{ - 1} \left( {\mathop \int \limits_{0}^{1} (Q^{ - 1} \mathop \int \limits_{0}^{1} k(x,t)\phi_{i} (t)\;{\text{d}}t)\phi_{j} (x)\;{\text{d}}x} \right), \quad i,j = 0, \ldots ,m. $$

Transformation matrices

Transformation matrix is used to change the dimension of the problem. In other words, this matrix can convert $\Phi_{m}$ to $\Phi_{n}$ and vice versa.

Suppose m is less than n, $T_{m}^{n}$ is an $(m + 1) \times (n + 1)$ matrix, called increasing transformation matrix, that converts $\Phi_{m}$ to $\Phi_{n}$. In other words, $\Phi_{m} = T_{m}^{n} .\Phi_{n} .$

The increasing transformation matrix can be computed as follows:

$$ \left[ {T_{m}^{n} } \right]_{i,j} = \left\{ {\begin{array}{*{20}c} {0, {\text{if }}\,i < j\,{\text{or}}\,j > i + k,} \\ {\frac{{\left( {\begin{array}{*{20}c} m \\ {i - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} k \\ {j - 1} \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {m + k} \\ {i + j - 2} \\ \end{array} } \right)}} , {\text{otherwise}}. } \\ \end{array} } \right. $$

It is sufficient to use $p3$, k times, where $k = n - m$.

In addition, decreasing transformation matrix is an $(n + 1) \times (m + 1)$ matrix, which is shown by $T_{n}^{m}$, and converts $\Phi_{n}$ to $\Phi_{m}$, where n is greater than m. In other words, $\Phi_{n} = T_{n}^{m} \Phi_{m} .$

The ith row of decreasing transformation matrix can be calculated as follows:

$$ \left[ {T_{n}^{m} } \right]_{i + 1} = \frac{1}{m + n + 1}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{1}{{\left( {\begin{array}{*{20}c} {m + n} \\ i \\ \end{array} } \right)}}} & {\frac{1}{{\left( {\begin{array}{*{20}c} {m + n} \\ {i + 1} \\ \end{array} } \right)}}} \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\frac{1}{{\left( {\begin{array}{*{20}c} {m + n} \\ {i + m} \\ \end{array} } \right)}}} \\ \end{array} } \\ \end{array} } \right]^{T} Q^{ - 1} , \quad i = 0, \ldots ,n. $$

Operational matrices

Operational matrix is a matrix that works on basis, such as an operator; in other words, if $\varLambda$ is an operator, an operational matrix is a matrix, such as P, such that $\varLambda (\Phi )\simeq P \Phi$.

Operational matrix of integration

Lemma 3 Suppose $\Phi_{m} (x) = [\phi_{0} (x), \ldots ,\phi_{m} (x)]^{T} ,$ , then

$$ \mathop \int \limits_{0}^{x} \Phi_{m} (x){\text{d}}x = M\Phi_{m} (x). $$

(1)

where M is called operational matrix of integration.

Proof With a simple calculation can be seen

$$ B_{i,m} (x) = \mathop \int \limits_{0}^{x} m\left( {B_{i - 1,m - 1} (t) - B_{i,m - 1} (t)} \right){\text{d}}t. $$

Assume $0 \le k \le m,$

$$ \mathop \sum \limits_{i = k}^{m} B_{i,m} (x) = \mathop \sum \limits_{i = k}^{m} \mathop \int \limits_{0}^{x} m\left( {B_{i - 1,m - 1} (t) - B_{i,m - 1} (t)} \right){\text{d}}t = m\mathop \int \limits_{0}^{x} B_{k - 1,m - 1} (t){\text{d}}t. $$

Therefore,

$$ \mathop \int \limits_{0}^{x} B_{k,m} (t){\text{d}}t = \frac{1}{m + 1}\mathop \sum \limits_{i = k + 1}^{m + 1} B_{i,m + 1} (x) = M_{k}^{T} \Phi_{m + 1} , $$

where

$$ M_{k} = \frac{1}{m + 1}\left[ {\overbrace {0 \cdots 0}^{k + 1}\quad \overbrace {0 \cdots 1}^{m + 1 - k}} \right]^{T} , \quad k = 0, \ldots ,m. $$

It is obvious, $im = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {M_{0}^{T} } \\ {M_{1}^{T} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {M_{m}^{T} } \\ \end{array} } \\ \end{array} } \right]$ is an $(m + 2) \times (m + 1)$ matrix. Accordingly, $M = im\,T_{m + 1}^{m}$.

Operational matrix of product

Lemma 4 Let $C$ be an $(m + 1) \times m + 1$ matrix, then

$$ \Phi_{m}^{T} (x) C \Phi_{m} (x) = \hat{C}^{T} \Phi_{2m} (x) , $$

(2)

where

$$ \hat{{C_{k} }} = \mathop \sum \limits_{j = 0}^{k} \frac{{\left( {\begin{array}{*{20}c} m \\ {k - j} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ k \\ \end{array} } \right)}}C_{k - j,j} , \quad k = 0,1, \ldots ,2m. $$

Proof. Let $\phi_{i}^{*} (x) = B_{i,2m} (x), {\text{for}} \quad i = 0, \ldots ,2m$.

$$ \Phi_{m}^{T} (x)C \Phi_{m} (x) = \mathop \sum \limits_{i = 0}^{m} \mathop \sum \limits_{j = 0}^{m} c_{ij} \phi_{i} \phi_{j} . $$

Using $p1$ gives:

$$ \Phi_{m}^{T} (x)C \Phi_{m} (x) = \sum \limits_{i = 0}^{m} \sum \limits_{j = 0}^{m} c_{ij} \frac{{\left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {i + j} \\ \end{array} } \right)}}\phi_{i + j}^{*} = \left[ {\begin{array}{*{20}c} {\frac{{\left( {\begin{array}{*{20}c} m \\ 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ 0 \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ 0 \\ \end{array} } \right)}}c_{00} } & {\sum \limits_{j = 0}^{1} \frac{{\left( {\begin{array}{*{20}c} m \\ {1 - j} \\ \end{array} } \right).\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ 1 \\ \end{array} } \right)}}.c_{1 - j,j} } & {\begin{array}{*{20}c} \ldots & {\sum \limits_{j = 0}^{k} \frac{{\left( {\begin{array}{*{20}c} m \\ {k - j} \\ \end{array} } \right).\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ k \\ \end{array} } \right)}}.C_{k - j,j} } \\ \end{array} \begin{array}{*{20}c} \cdots & {\frac{{\left( {\begin{array}{*{20}c} m \\ m \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ m \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {2m} \\ \end{array} } \right)}}c_{mm} } \\ \end{array} } \\ \end{array} } \right]\Phi_{2m} = \hat{C}^{T} \Phi_{2m} (x). $$

Lemma 5 Let $u$ be an arbitrary $(m + 1)$ vector, then

$$ \Phi_{m} (x)\Phi_{m}^{T} (x)u = \tilde{u}\Phi_{2m} (x). $$

(3)

where $\tilde{u}$ is an $(m + 1) \times (2m + 1)$ matrix with elements

$$ \tilde{u}_{{i + 1,j + 1}} = \left\{ \begin{array}{ll} 0,&\quad if \, j\left\langle {i\, or\,j} \right\rangle m + i, \\ \frac{{\left( \begin{array}{*{20}c} m \\ i \\ \end{array} \right).\left( \begin{array}{*{20}c} m \\ j \\ \end{array} \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {i + j} \\ \end{array} } \right)}}u_{j} ,& \quad otherwise, \\ \end{array} \right.\quad i=0,\ldots , m,\; j=0,\ldots, 2m. $$

Proof. Property $p1$ implies

$$ \Phi_{m} (x)\Phi_{m}^{T} (x)u = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\mathop \sum \limits_{j = 0}^{m} \frac{{\left( {\begin{array}{*{20}c} m \\ 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ j \\ \end{array} } \right)}}u_{j} \phi_{j}^{*} } & {\mathop \sum \limits_{j = 0}^{m} \frac{{\left( {\begin{array}{*{20}c} m \\ 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {j + 1} \\ \end{array} } \right)}}u_{j} \phi_{j + 1}^{*} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\mathop \sum \limits_{j = 0}^{m} \frac{{\left( {\begin{array}{*{20}c} m \\ m \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {j + m} \\ \end{array} } \right)}}u_{j} \phi_{j + m}^{*} } \\ \end{array} } \\ \end{array} } \right]^{T} . $$

Now, the ith entry of the above matrix can be rewritten as follows:

$$ \mathop \sum \limits_{j = 0}^{m} \frac{{\left( {\begin{array}{*{20}c} m \\ {i - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {j + i - 1} \\ \end{array} } \right)}}u_{j} \phi_{j + i - 1}^{*} = \left[ {\begin{array}{*{20}c} {\underbrace {0 \ldots 0}_{i - 1}} & {\begin{array}{*{20}c} {\frac{{\left( {\begin{array}{*{20}c} m \\ {i - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ 0 \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {i - 1} \\ \end{array} } \right)}}u_{0} } & \cdots & {\frac{{\left( {\begin{array}{*{20}c} m \\ {i - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ m \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {m + i - 1} \\ \end{array} } \right)}}u_{m} } \\ \end{array} } & {\underbrace {0 \ldots 0}_{m - i + 1}} \\ \end{array} } \right]\Phi_{2m} . $$

Bernstein Multiscaling polynomials

Definition 3. Suppose $B_{i,m} (x)$ is the ith BPs of degree m on interval $[0, 1],$ Bernstein Multiscaling polynomials on $[0, 1)$ define as follows:

$$ \psi_{i,j} (t) = \left\{ \begin{array}{ll} B_{i,m} (kt - j), &\quad \frac{j}{k} \le t < \frac{j + 1}{k}, \\ 0, &\quad {\text{other wise,}} \end{array} \right. $$

(4)

where $k \ge 1$ is the number of partitions on $[0,1]$ and $i = 0, \ldots ,m$, and in addition, $j = 0, \ldots ,k - 1.$

Now, every function $f \in {\mathcal{L}}^{2} (\left[ {0,1} \right))$ has the unique best approximation with respect to span space by BMSPs as follows:

$$ f(x) = \mathop \sum \limits_{j = 0}^{k - 1} \mathop \sum \limits_{i = 0}^{m} c_{i,j} \psi_{i,j} = C^{T} .\Psi, $$

where $C^{T} = \left[ {c_{0,0} ,c_{1,0} , \ldots ,c_{m - 1,0} ,c_{m,0} , \ldots ,c_{0,k - 1} ,c_{1,k - 1} , \ldots ,c_{m - 1,k - 1} ,c_{m,k - 1} } \right].$

We denote

$$ \Psi = [\Psi_{0} \cdots \Psi_{k - 2} \quad \Psi_{k - 1} ]^{T}\,{\text{where}}\quad \Psi_{i} = [\psi_{0i} \quad \psi_{1i} \cdots \psi_{mi} ]^{T} ,\quad i = 0, \ldots ,k - 1. $$

Equation (4) implies that $\psi_{i}^{'}{\rm s}$ are disjoint. In other words when

$$ i \ne j:\psi_{i}^{T} \psi_{j} = 0. $$

(5)

In addition, Eq. (4) and $p3$ imply

$$ \psi_{i,j(x)} \psi_{p,q(x)} = \left\{ \begin{array}{ll} 0,&\quad j \ne q, \\ \frac{{\left( {\begin{array}{*{20}c} m \\ i \\ \end{array} } \right).\left( {\begin{array}{*{20}c} m \\ j \\ \end{array} } \right)}}{{\left( {\begin{array}{*{20}c} {2m} \\ {i + j} \\ \end{array} } \right)}}\psi^{*}_{i + p,j(x) ,} &\quad j = q, \\ \end{array} \right.,{\text{where}}\,\psi_{i + p,j}^{*} (x)\,{\text{is a elemet of}}\;\Psi_{2m} . $$

(6)

Lemma 6. Suppose $\bar{Q}$ is the dual operational matrix of BMSPs, then

$$ \overline{Q} = \frac{1}{k}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} Q & {\overline{0} } \\ {\overline{0} } & Q \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\overline{0} } \\ \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \ddots \\ {\overline{0} } & \cdots \\ \end{array} } & {\begin{array}{*{20}c} \ddots & {\overline{0} } \\ {\overline{0} } & Q \\ \end{array} } \\ \end{array} } \right], $$

where $\bar{0}$ is an $(m + 1) \times (m + 1)$ zero matrix, and $Q$ is the dual operational matrix of BPs.

Proof. With respect to (5) and (6), it is obvious.For any arbitrary function $f\left( x \right) \in {\mathcal{L} }^{2} \left( {\left[ {0,1} \right)} \right) ,$ there is an expansion with respect to BMSPs, such that

$$ f(x) \simeq \mathop \sum \limits_{j = 0}^{k - 1} \mathop \sum \limits_{i = 0}^{m} f_{i,j} \psi_{i,j} = F^{T} \Psi = \Psi^{T} F , $$

(7)

where F is a $k(m + 1) - {\text{vector}}$

Theorem A indicates

$$ F \simeq \overline{Q}^{ - 1} \mathop \int \limits_{0}^{1} f(x)\Psi (x){\text{d}}x. $$

Let $k(x,t) \in {\mathcal{L}}^{2} (\left[ {0,1} \right) \times \left[ {0,1} \right))$ be a two-dimensional function. With respect to BMSPs, $k$ has the following expansion:

$$ k(x,t) \simeq \Psi^{T} (t)K\Psi (x), $$

(8)

where

$$ K_{i + 1,j + 1} = \overline{Q}^{ - 1} \left(\int \limits_{0}^{1} \left(\overline{Q}^{ - 1} \int \limits_{0}^{1} k(x,t)\phi_{i} (t){\text{d}}t\right)\phi_{j} (x){\text{d}}x\right), i,j = 0, \ldots ,k(m + 1). $$

Transformation matrices

Let $\Psi_{m}$ and $\Psi_{n}$ be two different BMSPs and $m \le n$. There are two matrices, $\tau_{m }^{n}\,{\text{and }}\tau_{n }^{m},$ such that $\Psi_{m} = \tau_{m}^{n} .\Psi_{n }\; {\text{and}}\; \Psi_{n} = \tau_{n}^{m} .\Psi_{m }$. These transformation matrices have dimensions $k (m + 1) \times k (n + 1)$ and $k (n + 1) \times k (m + 1)$, respectively:

$$ \tau_{m}^{n} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {T_{m}^{n} } & {\overline{0} } \\ {\overline{0} } & { T_{m}^{n} } \\ \end{array} } & {\begin{array}{*{20}c} { \cdots } & {\overline{0} } \\ \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \ddots \\ {\overline{0} } & \ldots \\ \end{array} } & {\begin{array}{*{20}c} \ddots & {\overline{0} } \\ {\overline{0} } & {T_{m}^{n} } \\ \end{array} } \\ \end{array} } \right] {\text{and }}\tau_{n}^{m} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {T_{n}^{m} } & {\overline{0} } \\ {\overline{0} } & { T_{n}^{m} } \\ \end{array} } & {\begin{array}{*{20}c} { \cdots } & {\overline{0} } \\ \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \ddots \\ {\overline{0} } & \ldots \\ \end{array} } & {\begin{array}{*{20}c} \ddots & {\overline{0} } \\ {\overline{0} } & {T_{n}^{m} } \\ \end{array} } \\ \end{array} } \right], $$

where $T_{m}^{n}$ and $T_{n}^{m}$ are increasing transformation matrix and decreasing transformation matrix, respectively.

BMSP operational matrices

Operational matrices for BMSPs are obtained by BPs operational matrices and results are similar.

Operational matrices of product

Lemma 7. Assume $A$ is a $k (m + 1) \times k (m + 1)$ matrix, then

$$ \Psi^{T} A\Psi = \hat{A}^{T} \Psi^{*} , $$

(9)

where $\hat{A}$ is a $k(2m + 1) - {\text{vector}}.$

Proof. Let $C$ is a $(m + 1) \times (m + 1)$ matrix, Eq. (5) implies

$$ \Psi_{i}^{T} C\Psi_{j} = 0 , $$

(10)

where $i \ne j.$

Furthermore, Lemma 4 gives:

$$ \Psi_{i}^{T} C\Psi_{i} = \hat{C}^{T} \Psi_{i}^{*} , $$

(11)

where $\hat{C}$ is a $(2m + 1) - {\text{vector}}.$

Now, consider $A$ as follows:

$$ A = \left[ {\begin{array}{*{20}c} {A_{0,0} } & \cdots & {A_{0,k - 1} } \\ \vdots & \ddots & \vdots \\ {A_{k - 1,0} } & \cdots & {A_{k - 1,k - 1} } \\ \end{array} } \right], $$

where $A_{i,j} (i,j = 0, \ldots ,k - 1)$ is an $(m + 1) \times (m + 1)$ matrix.

Equation (10) implies:

$$ \Psi^{T} A\Psi = \mathop \sum \limits_{i = 0}^{k - 1} \Psi_{i}^{T} A_{ii} \Psi_{i} . $$

Equation (11) gives

$$ \Psi^{T} A\Psi = \mathop \sum \limits_{i = 0}^{k - 1} \hat{A}_{ii}^{T} .\Psi_{i}^{*} . $$

Therefore,

$$ \Psi^{T} A\Psi = [\hat{A}_{0,0} \ldots \hat{A}_{k - 1,k - 1} ]\Psi^{*} = \hat{A}^{T} \Psi^{*} , $$

where $\hat{A}_{i,i}$ is a $2m + 1$ vector.

$$ \mathop \sum \limits_{i = 0}^{k - 1} \hat{A}_{ii}^{T} \Psi_{i}^{*} = [\hat{A}_{0,0} \ldots \hat{A}_{k - 1,k - 1} ]\Psi^{*} = \hat{A}^{T} \Psi^{*} . $$

Lemma 8. Suppose $C$ is an arbitrary $k(m + 1)$ vector, then,

$$ \Psi \Psi^{T} C = \tilde{C}\Psi^{*} , $$

(12)

where $\tilde{C}$ is a $k(m + 1) \times k(2m + 1)$ matrix.

Proof. Suppose

$$ C^{T} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {C_{0} } & {C_{1} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {C_{k - 1} } \\ \end{array} } \\ \end{array} } \right] , $$

where $C_{i} (i = 0, \ldots ,k - 1)$ is an $m + 1 - {\text{vector}}.$

Equation (3) implies:

$$ \Psi_{i} \Psi_{i}^{T} C_{i} = \tilde{{C_{i} }}\Psi_{i}^{*} , i = 0, \ldots ,k - 1, $$

(13)

where $\tilde{C}_{i}$ is an $(m + 1) \times (2m + 1)$ matrix.

Now

$$ \Psi .\Psi^{T} .C = \left[ {\begin{array}{*{20}c} {\Psi_{0} } \\ \vdots \\ {\Psi_{k - 1} } \\ \end{array} } \right].\left[ {\begin{array}{*{20}c} {\Psi_{0}^{T} } & \cdots & {\Psi_{k - 1}^{T} } \\ \end{array} } \right].\left[ {\begin{array}{*{20}c} {C_{0} } \\ \vdots \\ {C_{k - 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \Psi_{0} .\Psi_{0}^{T} .C_{0} } & 0 \\ {0 } & { \Psi_{1} .\Psi_{1}^{T} .C_{1} } \\ \end{array} } & {\begin{array}{*{20}c} {0 \cdots } & 0 \\ { \ddots } & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & { \ddots } \\ 0 & { \cdots } \\ \end{array} } & {\begin{array}{*{20}c} \ddots & { 0} \\ 0 & {\Psi_{k - 1} .\Psi_{k - 1}^{T} .C_{i} } \\ \end{array} } \\ \end{array} } \right]. $$

Equation (12) gives:

$$ \Psi \Psi^{T} C = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{C}_{0} .\Psi_{0}^{*} } & 0 \\ 0 & \ddots \\ \end{array} } & {\begin{array}{*{20}c} \cdots & 0 \\ \cdots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \ddots \\ 0 & \cdots \\ \end{array} } & {\begin{array}{*{20}c} \ddots & 0 \\ 0 & {\tilde{C}_{k - 1} .\Psi_{k - 1}^{*} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{C}_{0} } & 0 \\ 0 & {\tilde{{C_{0} }}} \\ \end{array} } & {\begin{array}{*{20}c} \cdots & 0 \\ \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \ddots \\ 0 & \cdots \\ \end{array} } & {\begin{array}{*{20}c} \ddots & 0 \\ 0 & {\tilde{C}_{k - 1} } \\ \end{array} } \\ \end{array} } \right]\Psi^{*} = \tilde{C}\Psi^{*} . $$

Operational matrix of integration

Lemma 7. Assume ${\mathcal{M} }$ be the operational matrix of integration, then

$$ \mathop \int \limits_{0}^{x} \Psi (t){\text{d}}t = {\mathcal{M}}\Psi (x). $$

Proof Lemma 1 implies:

$$ \mathop \int \limits_{0}^{x} \Psi_{0} (t){\text{d}}t = \left\{ \begin{array}{ll} \frac{1}{k}M\Psi_{0} (t), &\quad 0 \le x < \frac{1}{k}, \\ \frac{1}{k(m + 1)}, & \quad x \ge \frac{1}{k}. \end{array} \right. $$

For $i = 1, \ldots ,k - 2$, Eq. (1) gives:

$$ \mathop \int \limits_{0}^{x} \Psi_{i} (t){\text{d}}t = \left\{ \begin{array}{ll} 0, & \quad 0 \le x < \frac{i}{k}, \\ \frac{1}{k}M\Psi_{i} (t), & \quad \frac{i}{k} \le x < \frac{i + 1}{k}, \\ \frac{1}{k(m + 1)}, & \quad x \ge \frac{i + 1}{k}, \end{array} \right. . $$

and

$$ \mathop \int \limits_{0}^{x} \Psi_{k - 1} (t){\text{d}}t = \left\{ \begin{array}{ll} 0 , &\quad 0 \le x < \frac{k - 1}{k}, \\ \frac{1}{k}M\Psi_{k - 1} (t) ,&\quad \frac{k - 1}{k} \le x < 1. \end{array} \right. $$

Consequently,

$$ {\mathcal{M}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{1}{k}M} & {\frac{1}{k(m + 1)}\overline{1} } \\ 0 & {\frac{1}{k}M} \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\frac{1}{k(m + 1)}\overline{1} } \\ \ddots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & { \ddots } \\ 0 & { \cdots } \\ \end{array} } & {\begin{array}{*{20}c} \ddots & {\frac{1}{k(m + 1)}\overline{1} } \\ 0 & {\frac{1}{k}M} \\ \end{array} } \\ \end{array} } \right], . $$

where $\bar{1}$ is an $(m + 1) \times (m + 1)$ matrix that all entries are one.

Solution of Volterra integral equation

In this section, we are going to convert an integral equation to a system.

Linear Volterra integral equation of the first kind

Consider the following Volterra integral equation of the first kind:

$$ f(x) = \mathop \int \limits_{0}^{x} k(x,t)u(t){\text{d}}t. $$

(14)

where f and k are known, but $u$ is not. Moreover, $k(x, t) \in l^{2} ([0, 1) \times [0, 1))$ and $f (t) \in l^{2} ([0, 1)).$

Approximating functions $f, \,u,$ and k with respect to BMSPs gives:

$$ f(x) = F^{T} \Psi (x) = \Psi^{T} (x)F, $$

$$ u(t) = U^{T} \Psi (t) = \Psi^{T} (t)U, $$

$$ k(x,t) \simeq \Psi^{T} (x)K\Psi (t), $$

(15)

where the vectors $F, U$, and matrix K are BMSP coefficients of $f (x), u(t),$ and $k(x, t)$, respectively.

Now, replacing (15) into (14) gives:

$$ F^{T} .\Psi_{m} (x) = \mathop \int \limits_{0}^{x} \Psi_{m}^{T} (x)K\Psi_{m} (t)\Psi_{m}^{T} (t)U{\text{d}}t = \Psi_{m}^{T} (x)K\mathop \int \limits_{0}^{x} \Psi_{m} (t)\Psi_{m}^{T} (t)U{\text{d}}t. $$

Using (12) follows:

$$ F^{T} \Psi_{m} (x) = \Psi_{m}^{T} (x)K\mathop \int \limits_{0}^{x} \tilde{U}\Psi_{2m} (t){\text{d}}t = \Psi_{m}^{T} (x)K\tilde{U}\mathop \int \limits_{0}^{x} \Psi_{2m} (t){\text{d}}t. $$

(16)

Using operational matrix of integration ${ \mathcal{M}} ,$ in Eq. (16) gives

$$ F^{T} \Psi_{m} (x) = \Psi_{m}^{T} (x)K\tilde{U}M\Psi_{2m} (x). $$

(17)

Let $U^{*} = K\tilde{U}M\tau_{2m}^{m},$ where $U^{*}$ is a $k(m + 1) \times k(m + 1).$

Equation (17) changes to:

$$ F^{T} \Psi_{m} (x) = \Psi_{m}^{T} (x)U^{*} \Psi_{m} (x) $$

(18)

Using Eq. (11) in (18) gives:

$$ F^{T} \Phi_{m} (x) = \Phi_{m}^{T} U^{*} \Phi_{m} = \hat{{U^{*} }}^{T} \Phi_{2m} (x). $$

Using decreasing transformation matrix $\tau_{2m}^{m}$, gives the final system:

$$ \overline{U} = F, $$

(19)

where $\overline{U}^{T} = \hat{{U^{*} }}^{T} \tau_{2m}^{m} .$

Nonlinear Volterra integral equation of the first kind

Consider the following nonlinear Volterra integral equation:

$$ f(x) = \mathop \int \limits_{0}^{x} k(x,t)g(u(t)){\text{d}}t, $$

(20)

$$ {\text{Put}}\,w(x) = g(u(x))\,{\text{and subsequently}}\, w(x) = W^{T} \Psi_{m} (x). $$

(21)

where W is an unknown $k(m + 1)$ vector. Following the same procedure, the final system is as follows:

$$ \overline{W} = F, $$

Finally, $u(x) = g^{ - 1} (w(x))$ is the desire solution.

One advantage of this method is solving linear or nonlinear Volterra integral equation of the second kind with piecewise functions. In these equations, solution, kernel, or data function can be piecewise. It is essential k, the number of partitions, be chosen, such that discontinuity points lie on boundary point of partitions.

Linear Volterra integral equation of the second kind

Consider linear Volterra integral equations as the following form:

$$ u(x) = f(x) + \mathop \int \limits_{0}^{x} k(x,t)u(t){\text{d}}t. $$

(22)

Substituting (15) into (22) and a process similar to the previous state final linear system is

$$ U - \overline{U} = F. $$

Nonlinear Volterra integral equation of the second kind

Consider the following nonlinear Volterra equation of the second kind:

$$ u(x) = f(x) + \mathop \int \limits_{0}^{x} k(x,t)g(u(t)){\text{d}}t $$

(23)

where g(x) is one to one on $[0,1]$.

Let $w(t) = g(u(t))$, substituting (23) gives

$$ w(x) = g\left( {f(x) + \mathop \int \limits_{0}^{x} k(x,t)u(t){\text{d}}t} \right). $$

(24)

Now, substituting (15) and (20) into (24) implies:

$$ W^{T} \Psi = g\left( {F^{T} \Psi + \Psi_{m}^{T} (x)K\mathop \int \limits_{0}^{x} \Psi (t)\Psi^{T} (t)W{\text{d}}t} \right). $$

Equations (16)–(19) give:

$$ W = g(F + \bar{W}). $$

Numerical examples

Now, we test our method on some numerical examples; in every example, we use a table to show approximations, exact solution, and absolute errors in some points.

Example 1

Suppose $u(x) = e^{ - x}$ be the exact solution of the following Volterra integral equation of the first kind:

$$ xe^{x} = \mathop \int \limits_{0}^{x} e^{x + t} u(t){\text{d}}t. $$

Table 1 shows results of Example 1.

Table 1 Results of Example 1

Example 2

Consider the following integral equation:

$$ x{ \sin }x = \mathop \int \limits_{0}^{x} \cos (x - t)u(t){\text{d}}t $$

with the exact solution $u(x) = 2{ \sin }x$.

Table 2 shows approximated solutions, absolute errors, and exact solution in some points.

Table 2 Results of Example 2

Example 3

$x = \mathop \int \limits_{0}^{x} (x - t + 1)e^{ - u(t)} {\text{d}}t$

Table 3 shows results of Example 3.

Table 3 Results of Example 3

Example 4

Consider the following linear integral equation $u(x) = f(x) + \mathop \int \limits_{0}^{x} (t - x)u(t){\text{d}}t,$ with exact solution:

$$ u(x) = \left\{ {\begin{array}{*{20}c} {x,} & {0 < x < 0.5,} \\ {x^{2} ,} & {0.5 < x < 1,} \\ \end{array} } \right. $$

and the nonsmooth data function:

$$ f(x) = \left\{ \begin{array}{ll} x + \frac{1}{6} x^{3} ,& \quad 0 < x < 0.5, \\ \frac{ - 5}{192} + \frac{1}{12}x + x^{2} + \frac{1}{12}x^{4}, & \quad 0.5 < x < 1. \end{array} \right. $$

Results of Example 4 are presented in Table 4.

Table 4 Results of Example 4

Example 5

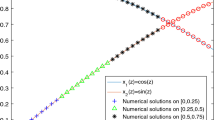
Assume $u(x) = \left\{ \begin{array}{ll} 1 - x,&\quad 0 < x < 0.5, \\ \sqrt {x}, &\quad 0.5 < x < 1, \end{array} \right.$ be the exact solution of the following nonlinear Volterra integral equation of the second kind:

$$ u(x) = f(x) + \mathop \int \limits_{0}^{x} xtu^{2} (t){\text{d}}t, $$

where

$$ f(x) = \left\{ \begin{array}{lll} 0, &\quad x < 0, \\ 1 - x - \frac{{x^{3} }}{2} - \frac{2}{3}x^{4} - \frac{{x^{5} }}{4}, & \quad 0 < x \le 0.5, \\ \sqrt x - 0.01x - \frac{1}{3}x^{4} , &\quad 0.5 \le x < 1, \\ - 0.35x, & \quad x > 1.\ \end{array} \right. $$

Table 5 shows results of Example 5.

Table 5 Results of Example 5

Comparison

Block-pulse functions are a special case of BMSPs. However, our method is different from the methods, as presented in [32] and [33]. Consider Example 1, in Table 6, the expansion–iterative method and direct method are compared with our method. In Table 6, we presented mean-absolute errors for the expansion–iterative method and direct method and absolute error of BMSPs for two different values of m and k. With respect to dimensions of the final system, our method is more accurate than the expansion–iterative method and direct method.

Table 6 Results of comparison in Example 1

Consider Example 2, Table 7 shows a comparison between BMSPs method and the expansion–iterative method and direct method with block-pulse functions. Mean-absolute errors for methods are presented in Table 7.

Table 7 Results of comparison in Example 2

Stability of method

To demonstrate the stability of the method, we review effect of noise on data function. In other words, we replace $f(x)$ by $\left( {1 + \varepsilon p} \right)f(x)$ into integral equation. Where p is a real random number between −1 and 1, and $\varepsilon$ is percent of noise. Now, we want to show that our method is stable and noise is proportional to the variations of solutions.

Example 6

Consider the following Volterra integral equation of first kind:

$$ \frac{7}{12}x^{4} = \mathop \int \limits_{0}^{x} (x + t)u(t){\text{d}}t $$

with exact solution $u(x) = x^{2} .$

Table 8 shows approximated solution, noisy solutions, and exact solution.

Table 8 Results of Example 6

Conclusion

BMSPs that we use to solve Volterra integral equations have acceptable accuracy. Operational matrices, which we have computed, are exact. These exact matrices lead to fewer errors in our computations. In addition, BMSPs can solve piecewise Volterra integral equations of the second kind. Effect of noise on data function shows that our method is reliable and ill-posedness does not occur. This method with respect to complexity of computations and desirable accuracy is recommended. Furthermore, this method can be used to solve optimal control equations, differential equations, and systems of integral or differential equations.