Modeling and simulation of weld solidification cracking part I

Abstract

Several advanced alloy systems are susceptible to weld solidification cracking. One example is nickel-based superalloys, which are commonly used in critical applications such as aerospace engines and nuclear power plants. Weld solidification cracking is often expensive to repair and, if not repaired, can lead to catastrophic failure. This study, presented in three papers, presents an approach for simulating weld solidification cracking applicable to large-scale components. The results from finite element simulation of welding are post-processed and combined with models of metallurgy, as well as the behavior of the liquid film between the grain boundaries, in order to estimate the risk of crack initiation. The first paper in this study describes the crack criterion for crack initiation in a grain boundary liquid film. The second paper describes the model for computing the pressure and the thickness of the grain boundary liquid film, which are required to evaluate the crack criterion in paper 1. The third and final paper describes the application of the model to Varestraint tests of alloy 718. The derived model can fairly well predict crack locations, crack orientations, and crack widths for the Varestraint tests. The importance of liquid permeability and strain localization for the predicted crack susceptibility in Varestraint tests is shown.

1 Introduction

Several alloy systems are susceptible to weld solidification cracking (WSC), which can act as sites for initiation of fatigue and stress corrosion cracking. The crack is normally intergranular and forms in the fusion zone during the terminal stage of the solidification [1]. At this stage of the solidification, the liquid permeability may be low, which renders liquid feeding difficult. Therefore, tensile deformations of a grain boundary liquid film (GBLF) that occurs in the later stage of the solidification can result in a large liquid pressure drop in the film. This can lead to rupture of the GBLF, which then forms WSC. The deformation originates from the contracting weld metal, which is externally and internally restrained. External restraints may be fixturing, while internal restraints can be the fully solid material that surrounds the solidifying weld metal.

The susceptibility of WSC is determined by a complicated interplay among metallurgical, thermal, and mechanical factors. Metallurgical factors such as solidification temperature range, solidification shrinkage, thermal expansion coefficient, distribution and amount of liquid at the end of the solidification, primary solidification phase, surface tension of the grain boundary liquid, and grain structure affect the cracking [1]. Important thermal factors include solidification velocity and cooling rate, which influence the microsegregation, which in turn affects many of the abovementioned metallurgical factors [1]. Mechanical factors such as tensile stresses and strains across the GBLFs are the driving forces behind the formation of cracking. The tensile stresses are responsible for causing the rupture, while tensile strains widen the GBLFs, which makes them more vulnerable to cracking. These mechanical factors are, in turn, dependent on several other factors such as strength of the solidifying weld metal and the solid metal that restrains the solidifying weld metal, size and thickness of the workpiece, joint design, size and shape of the weld bead, and the mechanical fixturing [2].

Numerical simulation of WSC can be a powerful tool for assisting in the design of a welding process such that the risk for WSC can be reduced. To model the cracking, a crack criterion is required. Several crack criteria have been developed during the last sixty years [3], which were often first developed for casting, where solidification cracking is commonly referred to as hot tearing, and then applied to welding [4]. These criteria are often based on critical stress, critical strain, or critical strain rate. However, the major drawback for almost all of them is that they fail to address how the GBLF fractures [4].

It is not fully understood how WSC forms. The book by Campbell [5] describes various nucleation theories of hot tearing. Campbell argued that it is unlikely that the crack can form from homogenous or heterogeneous pore nucleation without impurities. This is because a liquid can withstand very high hydrodynamic tensions. Impurities such as sulfur and oxygen lower the interfacial energy, which reduces the pressure drop for pore nucleation, but still a very large pressure drop in the liquid is required for pore nucleation to occur. However, it is much easier to nucleate a pore if the liquid contains some gas [5]. Then, both the internal pore pressure and the external liquid underpressure can balance the surface tension of the pore. Absorption of gases in the liquid occurs readily in the weld pool due to interaction with the arc atmosphere [6]. When the liquid solidifies, it may become supersaturated with gas due to low solubility in the solid phase and the decrease in temperature and pressure, which may lead to nucleation of a pore. Campbell [5] also pointed out that there may be a microbubble spectrum in the liquid, which can act as initiation sites for hot tearing.

Several in situ experiments have indicated that hot cracks are formed from pores. Hunt and Durrans [7] conducted experiments on a transparent analog of a metal, decribed in [5]. The solidifying material was stretched around a sharp corner, and it was found that when a small inclusion or bubble arrived at the corner, a crack was immediately formed. However, when no nucleus was present at the corner, no crack formed, irrespective of how large strains that were applied. Farup et al. [8] conducted similar experiments in situ on the transparent alloy succinonitrile-acetone and found that crack nucleation is always associated with pores. Terzi et al. [9] performed in situ X-ray tomography on semi-solid aluminum and found that cracks formed from micropores. Puncreobutret et al. [10, 11] performed hot tensile testing on a Al-15 wt Cu alloy. With fast synchrotron X-ray microtomography, they found that the cracking initiated from pre-existing voids and internally nucleated voids. Recently, Aucott et al. [12] studied Varestraint testing in situ with high-energy synchrotron X-ray microtomography of steel. They could also see, in agreement with Puncreobutr, that the cracking started from internal voids.

This paper proposes a criterion for estimating the risk of WSC initiation, which is based on the recent findings that WSC seems to initiate and grow from internal pores [10,11,12]. A pre-existing pore, located in a GBLF, was assumed to be able to grow into a crack as a gas capillary bridge. By solving the Young-Laplace equation for the capillary bridge, a fracture pressure p_f for the given film thickness was determined as the critical liquid pressure for crack initiation. A permanent crack was assumed to form when the GBLF pressure is lower than p_f at the location of the solidus. The crack was then assumed to be permanently frozen into the solid phase and could not be closed by capillarity forces, which may be possible at higher temperatures if the pressure drop decreases.

2 Pore growth model

Recent in situ experiments have indicated that WSC is formed from voids that grow into cracks, as was mentioned in the Introduction. In this work, we assume that the cracking initiates from a small pore that extends across a GBLF. The nucleation of the pore is not considered, instead, the conditions for how such a pre-existing pore can grow into a WSC are studied.

2.1 Geometrical assumptions

Consider a pore located in a GBLF bounded by columnar dendrites, as shown in Fig. 1a. To simplify the study of how the pore grows in the GBLF, we assume that the interfaces of the GBLF are smooth and parallel, as shown in Fig. 1b. It is also assumed that the pore can grow without limits in all directions, except in the thickness direction.

Fig. 1

a Schematic representation of a pore in a GBLF bounded by columnar dendrites and b a simplified pore in a GBLF with smooth parallel interfaces

The pore is assumed to grow as a gas capillary bridge that is rotationally symmetric about the z-axis and symmetric about the z = 0 plane, as shown in Fig. 2. The upper part of the pore (z > 0) can then be represented by

$$ \mathbf{x}(z,\alpha) = [r(z)\cos(\alpha),\ r(z)\sin(\alpha),\ z], \quad 0 \leq z \leq h, 0 \leq \alpha<2\pi $$

(1)

where x is the parametric representation of the pore surface and α is the azimuthal angle about the z-axis. h is the half thickness of the GBLF and r(z) is the perpendicular distance from the z-axis to the surface of the pore. r(z) must satisfy the boundary conditions

$$ \frac{dr(z=0)}{dz} =0,\quad \frac{dr(z=h)}{dz}=-\frac{1}{\tan(\theta)} $$

(2)

The first boundary condition corresponds to the symmetry about the z = 0 plane, while the second condition accounts for the contact angle 𝜃 at the solid-liquid interface.

Fig. 2

Schematic representation of a pore as a capillary bridge in a GBLF

2.2 Pore shape

The shape of the pore profile depends on interfacial energies as well as the pressure difference across its boundary. A force balance of the interfacial energies (see Fig. 3) relates them to 𝜃 by

$$ \cos(\theta)=\frac{\gamma_{gs} - \gamma_{ls}}{\gamma_{gl}} $$

(3)

where γ_gl, γ_gs, and γ_ls are the gas-liquid, gas-solid, and liquid-solid interface energies, respectively.

Fig. 3

Schematic representation of the interface energies of the pore and the associated contact angle

The difference between the pressure inside the pore, p_i, and the external surrounding liquid pressure outside the pore, p_e, is given by the Young-Laplace equation

$$ \begin{array}{@{}rcl@{}} p_{i} - p_{e} &=& 2\gamma_{gl}H\\ &=& \gamma_{gl}\left( \frac{1}{R_{\pi}} + \frac{1}{R_{\mu}}\right) \end{array} $$

(4)

where H is the mean curvature and R_π and R_μ are the principal radii of curvatures of the pore. The effect of gravity on the pore shape is assumed to be negligible. For the rotational symmetric pore given by Eq. (1), the Young-Laplace equation can be written as [13]

$$ \frac{d(r\sin(\varphi))}{rdr} = \frac{p_{i} - p_{e}}{\gamma_{gl}} $$

(5)

where φ is the running slope angle of the pore profile, as shown in Fig. 2. By substituting the dimensionless capillary pressure

$$ p = \frac{(p_{i} - p_{e})R}{2\gamma_{gl}} $$

(6)

into Eq. (5) and using the first boundary condition in Eq. (2), Eq. (5) can be integrated to

$$ \sin(\varphi) = \frac{pr}{R} + \frac{(1 - p)R}{r} $$

(7)

Here, R is defined as the radius of the equator of the pore. φ can be expressed as

$$ \frac{dz}{dr} = \tan(\varphi) = \pm \frac{\sin(\varphi)}{\sqrt{1 - \sin^{2}(\varphi)}} $$

(8)

By substituting Eq. (7) into Eq. (8) and using the non-dimensional variable

$$ x = \frac{r}{R} $$

(9)

Equation (8) can be integrated to

$$ \begin{array}{@{}rcl@{}} z(x) &=& {{\int}_{1}^{x}} R \frac{dz}{dr}(u) du \\&=& \pm R{{\int}_{1}^{x}} \frac{p(u^{2} - 1) + 1}{\sqrt{(1 - u^{2})(p(u - 1) + 1)(p(u + 1) - 1)}} du \end{array} $$

(10)

where u is an integration variable for x. The condition z(x = 1) = 0 was used in the above integration. The integrand is singular at x = 1. This singularity can be removed by the variable substitution

$$ x = \sin(\phi) $$

(11)

which gives

$$ z(\phi) = \pm R{\int}_{\pi/2}^{\phi} \frac{1 - p\cos^{2}(v)}{\sqrt{(p(\sin(v) - 1) + 1)(p(\sin(v) + 1) - 1)}} dv $$

(12)

where v is an integration variable for ϕ. At the solid-liquid interface, we have φ = π − 𝜃. By inserting this into Eq. (7), p can be expressed as

$$ p = \frac{\sin(\phi_{c})\sin(\theta) - 1}{\sin^{2}(\phi_{c}) - 1} $$

(13)

where ϕ_c is the value of ϕ at the solid-liquid interface.

From the condition z(ϕ_c) = h, ϕ_c can be solved for from Eq. (12) for fixed values of R and 𝜃, and with p evaluated from Eq. (13). The root can be found with a numerical root finder such as MATLAB’s fzero function. Once ϕ_c is computed, Eq. (12) can be used to determine the profile curve r(z) of the pore.

The mean curvature of a general surface of revolution is given by Opera [14]. Applying this to the surface of the rotational symmetric gas capillary bridge, given by Eq. (1), gives

$$ H = \frac{-r\frac{d^{2}r}{dz^{2}} + 1 + \left( \frac{dr}{dz} \right)^{2}}{2r\left( 1 + \left( \frac{dr}{dz} \right)^{2} \right)^{3/2}} $$

(14)

Equation (14) can be used to verify that the above computed profile curve r(z) corresponds to a constant mean curvature surface. When doing so, the derivatives of r(z) in Eq. (14) can be evaluated with, for example, central differences.

3 External pore pressure

When the value of ϕ_c has been computed from R, 𝜃, h, and γ_gl, the pressure difference across the pore interface can be determined by combining Eqs. (13) and (6), which gives

$$ p_{i} - p_{e} = \frac{2\gamma_{gl}}{R}\left( \frac{\sin(\phi_{c})\sin(\theta) - 1}{\sin^{2}(\phi_{c}) - 1}\right) $$

(15)

Thus, the external pressure that is required to keep the pore stable at a radius R can be computed from Eq. (15) once the internal pressure is known.

The internal pore pressure depends on the amount of gas and the volume of the pore. The gas can be a diatomic gas that was originally dissolved in the liquid. For example, hydrogen plays an important role in the formation of pores in aluminum alloys, while both hydrogen and nitrogen affect pore formation in nickel-based superalloys. In steels, hydrogen, nitrogen, and oxygen can form porosity [15]. In this study, we assume that diatomic gases are dissolved in the liquid that the pore grows in. These gases can diffuse across the interface of the pore. Inside the pore, we assume that the gases behave as an ideal gas. In order simplify the computation of the gas diffusion to the pore, the pore is assumed to grow in a grain boundary liquid film where the gas concentration only varies in the radial direction from the axis of the pore. The gas flux at the pore interface can then be computed from a one-dimensional diffusion equation in cylindrical coordinates, as will be shown later. Note that this concentration field is not realistic for pores that are located deep in the mushy zone, close to the roots of the dendrites. In this case, the diffusion across the interface will not be uniform around the pore and our approach will probably overestimate the amount of gas that diffuses to the pore. In this work, we do not consider reactions between gases and alloying elements.

In order to compute the internal pore pressure, we consider a diatomic gas I (e.g., hydrogen or nitrogen). Let n_I be the number of moles of the gas inside the pore and let C_I be the mass concentration of the gas element dissolved in the liquid phase. Furthermore, let J_I be the molar flux of the dissolved gas element in the liquid due to diffusion:

$$ \mathbf{J}_{I} = -A_{I}D_{lI} \nabla C_{I} $$

(16)

where D_lI is the diffusion coefficient of the gas element in the liquid. A_I is a conversion factor from mass concentration to molar concentration, given by

$$ A_{I} = \frac{\rho_{l}}{M_{I}} $$

(17)

where M_I is the molar mass of the gas element and ρ_l is the density of the liquid, which is assumed to be constant in this work (i.e., not vary with temperature).

The molar rate of change of the gas I inside the pore can be written as

$$ \frac{dn_{I}}{dt} = -\frac{1}{2} A_{I}D_{lI} {\int}_{S} \mathbf{J}^{*}_{I} \cdot \mathbf{n} dS $$

(18)

where $\mathbf {J}^{*}_{I}$ is the molar flux of I at the pore interface and S is the surface of the gas-liquid interface. n is the outward normal to S. The gas diffusion through the gas-solid interface of the pore is neglected. By using the previous assumption that C_I only depends on the radial distance from the axis of the pore, and that its variation over the pore surface S is negligible, Eq. (18) reduces to

$$ \frac{dn_{I}}{dt} = 2\pi A_{I}D_{lI} \frac{\partial C^{*}_{I}}{ \partial \rho} {{\int}_{0}^{h}} r(z) dz $$

(19)

where r(z) is the profile curve of the pore and $C^{*}_{I}$ is the concentration at the pore interface (i.e., at ρ = R). For a diatomic gas, $C^{*}_{I}$ can be estimated from the partial internal pore pressure via Sievert’s law [16]

$$ C^{*}_{I} = \frac{K_{I}}{f_{I}} \sqrt{p_{iI}} $$

(20)

where K_I is the equilibrium constant and f_I is the activity coefficient for the gas I. p_iI is the partial pressure of the gas I inside the pore. We assume that I behaves as an ideal gas inside the pore. Thus, p_iI can then be related to n_I by the ideal gas law

$$ p_{iI} = \frac{n_{I}\overline{R}T}{V} $$

(21)

where V is the volume of the pore, which is computed by numerical integration of the pore profile curve via:

$$ V = 2{{\int}_{0}^{h}} \pi r^{2} dz $$

(22)

By substituting Eq. (21) into Eq. (20), $C^{*}_{I}$ can be rewritten as a function of n_I, V, and T:

$$ C^{*}_{I} = \frac{K_{I}}{f_{I}} \sqrt{\frac{n_{I}\overline{R}T}{V}} $$

(23)

The concentration gradient $\partial C^{*}_{I}/ \partial \rho$ at the pore interface in Eq. (19) can now be computed as follows. Consider a cylindrical coordinate system where ρ is the radial distance from the axis of the pore. The concentration field was previously assumed to be axisymmetric and therefore will only vary with ρ. By performing a concentration balance on a volume element of thickness Δρ, height 2h, and circumference 2πρ, and letting Δρ go to zero gives

$$ \rho\frac{\partial (hC_{I})}{\partial t} - \frac{\partial}{\partial \rho} \left( D_{lI} h \rho \frac{\partial C_{I}}{\partial \rho} \right) + \frac{\partial}{\partial \rho} \left( \overline{v}_{\rho} h \rho C_{I} \right) = 0, \quad R \leq \rho \leq R_{e} $$

(24)

At the outer boundary, ρ = R_e, the concentration is assumed be fixed at C_I = C_I0. This is a rough approximation that is assumed to account to some degree for the dissolved gas that can enter the domain from the liquid that surrounds it. The surrounding liquid may in turn be feed by gas from, for example, the weld pool. This gives the outer boundary condition to Eq. (24), while the inner is given by Eq. (23). They are summarized as

$$ C_{I}(\rho = R) = C^{*}_{I}, \quad C_{I}(\rho = R_{e}) = C_{I0} $$

(25)

The advection term in Eq. (24) has been added to account for the advection of gas solute due to liquid flow. Note that liquid will flow into or out of the domain R ≤ ρ ≤ R_e when the pore grows or when the liquid film is deformed. By performing a mass balance on the previous volume element that was used to derive Eq. (24), the average liquid velocity across the liquid film, $\overline {v}_{\rho }$, in Eq. (24) can be written as

$$ \overline{v}_{\rho} = -\frac{\rho}{2h} \frac{dh}{dt} + \left( \frac{dR}{dt} + \frac{R}{2h} \frac{dh}{dt} \right) \frac{R}{\rho} $$

(26)

where dR/dt is the velocity of the pore interface and 2dh/dt is the rate of change of the thickness of the film. $\partial C^{*}_{I}/ \partial \rho$ can be determined by solving Eq. (24) numerically with a finite difference method (FDM). Note that the domain is compressed by the rate dR/dt due to the pore growth. Thus, in order to perform the the FDM on a fix grid, the following Landau transformation [15] is used

$$ \xi = \frac{\rho - R}{R_{e} - R} $$

(27)

Substituting ρ by ξ in Eqs. (24), (25), (26) gives

$$ \begin{array}{@{}rcl@{}} && \rho(\xi) \frac{\partial (hC_{I})}{\partial t} + \rho(\xi) \frac{\partial \xi}{\partial t} \frac{\partial (hC_{I})}{\partial \xi} - \frac{\partial \xi}{\partial \rho} \frac{\partial}{\partial \xi} \left( D_{lI} h \rho(\xi) \frac{\partial \xi}{\partial \rho} \frac{\partial C_{I}}{\partial \xi} \right)\\ && + \frac{\partial \xi}{\partial \rho} \frac{\partial}{\partial \xi}\left( \overline{v}_{\rho} h \rho(\xi) C_{I} \right) = 0, \quad 0\leq \xi \leq 1,\\ &&C_{I}(\xi = 0) = C^{*}_{I}, C_{I}(\xi = 1) = C_{I0} \end{array} $$

(28)

where ρ(ξ), ∂ξ/∂t, and ∂ξ/∂ρ can be computed from Eq. (27). Equation (28) can now be solved with the implicit backward time, centered space method (BTCS) on a fixed grid. Once Eq. (28) is solved for a given time increment, $\partial C^{*}_{I}/ \partial \rho$ for the corresponding time can be computed by

$$ \frac{\partial C^{*}_{I}}{\partial \rho} = \frac{\partial \xi}{\partial \rho} \frac{\partial C^{*}_{I}}{\partial \xi} = \frac{1}{R_{e} - R} \frac{\partial C^{*}_{I}}{\partial \xi} $$

(29)

We can now compute the internal pore pressure when dR/dt and 2dh/dt are prescribed as follows. Let the values of 𝜃 and T be fixed. Let ^kR and ^k2h denoted the pore radius and the film thickness at the k th time increment. Let the corresponding profile curve of the pore be denoted by ^kr(z), which is computed from ^kR, ^kh, and 𝜃 as was described in the previous chapter. Once ^kr(z) is known, the pore volume ^kV can be computed from Eq. (22). Now, we approximate dn_I/dt by the backward difference This can be done with:

$$ {~}\!^{^{^{k}}}\!\!\left( \frac{dn_{I}}{dt} \right) = \frac{{{~}^{k} n_{I}} - {{~}^{k-1}n_{I}}}{{\Delta} t} $$

(30)

Substituting Eq. (30) into Eq. (23) gives

$$ {\!{~}^{k}C^{*}_{I}} = \frac{K_{I}}{f_{I}} \sqrt{\left( \!{~}^{^{^{^{k}}}}{\kern-3.5pt}{\left( \frac{dn_{I}}{dt} \right)} {\Delta} t + {\!{~}^{k-1}n_{I}} \right) \frac{\overline{R}T}{{\!{~}^{k}V}}} $$

(31)

By substituting Eq. (31) into the boundary condition for the pore interface in Eq. (28), ${~}\!^{k}(\partial C^{*}_{I} / \partial \xi )$ becomes a function of ^k(dn_I/dt). Thus, Eq. (19) can be written as a single function of ^k(dn_I/dt):

$$ {~}\!^{^{^{k}}}\!\!\left( \frac{dn_{I}}{dt} \right) - \frac{2\pi A_{I}D_{lI}{~}}{R_{e} - {{~}^{k}\! R}}^{k}{}\left( \frac{\partial C^{*}_{I}}{ \partial \rho} \right) {{\int}_{0}^{h}} {{~}^{k}r(z)} dz = 0 $$

(32)

Now, ^k(dn_I/dt) can be solved for from Eq. (32) with a numerical root finder such as MATLAB’s fzero function. When ^k(dn_I/dt) is known, ^kn_I can be determined from Eq. (30), which in turn can be used to determined (together with ^kV) ^kp_iI from Eq. (21). The total internal pore pressure p_i is determined from Dalton’s law, which states that the total pressure for non-reacting gases is equal to the sum of the partial pressures of the individual gases, i.e.,

$$ {~}\!^{k} p_{i} = \sum\limits_{I} {\!{~}^{k} p_{iI}} $$

(33)

Finally, when ^kp_i has been computed, ^kp_e can be computed from Eq. (15).

The above solution procedure for p_e requires an initial condition. In this work, we assume that the initial gas concentration is C_I = C_I0 in the whole domain R_s ≤ ρ ≤ R_e. The initial partial pressure in the pore can then be determined from Eq. (20) by setting $C_{I}^{*} = C_{I0}$. By giving the initial pore radius R_s and film thickness 2h_s, the initial volume of the pore can be computed. Once the partial pressure and the pore volume are known, the initial number of moles of gas I in the pore can be determined from the ideal gas law Eq. (21). When the initial number of moles of gas inside the pore is known, we can use the above procedure for computing the time evolution of the external pore pressure.

4 Pore growth characteristics predicted by the pore model

The previously derived pore growth model can be used to study the relation between the external pore pressure and the pore radius for different gas concentrations, film thicknesses, growth velocities, etc. In this section, this is done for the nickel-based superalloy alloy 718. The results will be used to construct a pore-based crack criterion in the next chapter. Remember that the pore model is limited to pore shapes, concentration fields, and external pressure fields that are axisymmetric. Also remember that the pore was assumed to grow in a liquid film bounded by parallel planes. Thus, the pore interaction with, e.g., dendrite arms and intermetallics, cannot be accounted for with this simple model.

4.1 Material parameters

Felicelli et al. [16] have simulated gas redistribustion and porosity in plate casting of alloy 718. Alloy 718 can dissolve both hydrogen and nitrogen. Typical concentrations in castings are around 2 ppm of hydrogen and 40 ppm of nitrogen dissolved in the melt before solidification [17]. At these concentrations, hydrogen has a much larger effect on the porosity than nitrogen, as was shown by Sung et al. [17]. Thus, in this work we are only going to consider the effect of the hydrogen concentration on the pore growth. This will be done with material data from [16], which is given in Table 1.

Table 1 Thermodynamic and transport properties of alloy 718, from [16]

For hydrogen dissolved in liquid alloy 718, Felicelli et al. [16] used the following equilibrium constant in Sievert’s law (Eq. (20))

$$ \ln \left( K_{H} \right) = -4.154 - \frac{2613}{T} $$

(34)

and the following activity coefficient in Sievert’s law

$$ \ln \left( f_{H} \right) = a_{0} \beta + a_{1} \beta^{2} + a_{2} \frac{\beta}{T} + a_{3} \frac{\beta^{2}}{T} $$

(35)

where

$$ \beta = \sum\limits_{j=1}^{N} {b^{j}_{H}} X^{j} $$

(36)

and a_i and ${b^{j}_{H}}$ are constants given in Table 1, and X^j is the atom fraction of solute j in the liquid phase. In this work, the X^js were determined from the nominal solute mass fractions and the equilibrium partition coefficients, which are all given in Table 1, to represent the liquid composition at the terminal solidification.

Table 1 also contains the diffusion coefficient for hydrogen in liquid and the density of the liquid that were used in this work, given by [16]. The contact angle 𝜃 and the gas-liquid interface energy γ_gl, required by the pore model, were not used by Felicelli et al. in their work. We assume that there are no foreign particles or phases where the pore interface intersects with the solid phase. Therefore, because most metals are very well wetted by their own melt, we assume that the contact angle is small. In this work it was set to 𝜃 = 10^∘. γ_gl has been measured for alloy 718 by the oscillating drop method by Brooks et al. [18]. A value of approximately γ_gl = 1.9 J/m² was found at the liquidus temperature, which was used in this study.

4.2 Model parameters

In order to study the pore growth, the following base model parameters were used. The interface velocity of the pore was set to dR/dt = v_R = 25 μm s^− 1. An initial small pore will then grow to a diameter of 100 μm in approximately 2 s. This is assumed to be the maximum growth time for pore located deep in the mushy zone of a weld before it is frozen into the solid phase. The initial thickness of the liquid film is set to 2h_s = 1 μm and the initial radius of the pore is set to R_s = 2h_s. The outer boundary of the domain is set to R_e = 500 μm. The simulation is stopped when the pore radius reaches R_m = 50 μm. At that moment, the liquid film thickness has increased linearly from 2h_s = 1 μm to 2h_e = 10 μm. This is to simulate thermal strains that can localize in the liquid film during the terminal solidification. The initial concentration of hydrogen is set to C_H0 = 10 ppm and the temperature is set to T = 1150 ^∘C, which is 50 ^∘C above the terminal solidification temperature for alloy 718 predicted by a multicomponent Scheil-Guliver model in Thermo-Calc.

4.3 Effect of model parameters

With the above material data and model parameters, the external pore pressure can be computed with the method described in the previous chapter. By varying the model parameters, their effect on the p_e-R relation can be studied. This can provide valuable insight on the susceptibility for a micropore to grow into an unacceptable defect. In the subsequent subsections the effects of several model parameters on the p_e-R relation are shown.

4.3.1 Hydrogen concentration

Figure 4 shows how p_e varies with R for the pore model at different initial hydrogen concentrations. The above base model parameters have been used (but with variations in C_H0). At the initial growth stage, when R = R_s and h = h_s, p_e must have a negative pressure of more than 50 bars in order to expand the pore at a rate of 25 μm s^− 1 when C_H0 is less than 10 ppm. However, when R has increased to R_m and h to h_e, p_e must just have a negative pressure of approximately 3 bars to expand the pore at the same rate. From the figure, it can also be seen that p_e is relatively insensitive to C_H0 when C_H0< 15 ppm. However, for larger initial hydrogen concentrations, the pore can become stable at the atmospheric pressure after it has reached a certain size. After this point, p_e must increase in order to expand the pore at the rate 25 μm s^− 1. Otherwise, the expansion will be faster because of the gas diffusion to the pore. Note also that the gas concentration plays an important role at the early stage of the pore growth. The external pressure required to expand a pore in its initial stage of growth is strongly dependent on the gas concentration.

Fig. 4

p_e vs R for different initial hydrogen concentrations

4.3.2 Film thickness

The thickness of the GBLF that the pore growths in has a great influence on the external pore pressure that is required to keep the pore stable. Figure 5 shows how p_e varies with R for different values of h_e. Remember that h goes from h_s to h_e when R goes from R_s to R_m. The p_e-R relations shown in the figure may arise from the following situation. Consider a location deep in the mushy zone where the liquid film is almost fully solidified. Assume that a pore has nucleated at this location, and that it extended across the thickness of the film. Furthermore, assume that the liquid film is located between large grain clusters. Thermal tensile strains can then strongly localize in the film. This will induce a liquid flow in the film in order to account for the deformation. Because the film is thin, the liquid permeability is low, and the liquid pressure drop at the location of the pore will therefore be large. However, when the deformation progress, the film will widen and the permeability will increase, which result in a decrease of the liquid pressure drop.

Fig. 5

p_e vs R for different values of h_e

The liquid pressure required to expend a micropore into a macropore depends strongly on the thickness of the film, as can be seen from the figure. It requires almost − 35 bar to expand the pore at a rate of 25 μm s^− 1 when R = R_m and the thickness of the film is 1 μm. However, when the film thickness is 20 μm, it requires only − 1 bar.

4.3.3 Initial pore size

The initial pore size has a great impact on the minimum external pore pressure required to expand the pore into a macropore. If R_s = 0.5 μm, p_e must have a minimum value of − 70 bar. However, if R_s = 5 μm, that value increases to − 38 bar, as can be seen in Fig. 6, where p_e vs R has been plotted for different values of R_s. Thus, the risk for a micropore to growth into a macropore does not only depend on the external pore pressure. It also depends on the nucleation process. For example, if we assume that a pore has heterogeneously nucleated on an oxide inclusion, the size of the inclusion will affect the initial size of the micropore and therefore also it susceptibility to grow into a macropore.

Fig. 6

p_e vs R for different values of R_s

It is also interesting to study variations in h_s, which has an even larger impact on the initial value of p_e than R_s. Figure 7 shows variations of h_s for two different gas concentrations.

Fig. 7

p_e vs R for different values of h_s

Figures 6 and 7 also show that p_e is independent of R_s and h_s when R = R_m. This is true as long as the initial gas concentration is not very high and that the growth velocity is not very low. If that is not valid, the pore growth will be effected by the gas diffusion to the pore.

4.3.4 Growth velocity

A pore growth velocity of 25 μm s^− 1 was used for the above plots. As was previously mentioned, this will give the pore time to grow some 10 μm before it is solidified into the solid phase. A slower growth velocity will give more time for gas to diffuse to the pore when it grows to a given size. This will effect the external pore pressure, as can be seen in Fig. 8. From the Figure, it can be seen that the value of p_e at R_m is not largely affected by v_R when the initial gas concentration is below 10 ppm. However, for higher concentrations, it is highly affected by v_R.

Fig. 8

p_e vs R for different values of v_R

4.3.5 Domain size

The domain size will affect the gas concentration profile in the liquid that surrounds the pore. Because the concentration is prescribed on the outer boundary of the domain, a small domain will give a steeper concentration gradient and more gas element will therefore diffuse to the pore compared to a large domain. From Fig. 9, it can be seen that the p_e-R relation is independent of R_e when C_H0 = 10 ppm. However, for 20 ppm, the dependency is stronger.

Fig. 9

p_e vs R for different values of R_e

4.3.6 Nitrogen

Felicelli et al. [16] also provided data for dissolved nitrogen in alloy 718, similar to the one in Table 1 for hydrogen dissolved in alloy 718. That data were used, in the same way as the previously used data for hydrogen, in the pore growth model to study the effect on the pore growth. It was found that several orders higher concentrations than the 40 ppm nitrogen, typical occurring in the melt [17], were required in order to have the same effect as 5–10 ppm of hydrogen. This is because the activity coefficient of nitrogen in alloy 718 is very low. Thus, the effect of nitrogen on porosity in alloy 718 was neglected.

5 Crack criterion

The pore growth model can be used to construct a pore-based crack criterion for WSC. In this work, we assume that cracking occurs when the pore radius goes above 50 μm. From that assumption, and with the results from the previous chapter, a crack criterion can be constructed as follows.

5.1 Crack initiation index

Consider a point in a GBLF. Let 2h and C_H be the thickness of the GBLF and the hydrogen concentration at that point, respectively, and let p be the liquid pressure at the point without the presence of a pore. Furthermore, let p_f be the external pore pressure of a pore with radius 50 μm, computed with the base model parameters in Section 4.2, but with h_e = h and C_H0 = C_H. We assume that there is a risk for cracking when p < p_f, and we define a crack initiation index (CII) as

$$ \text{CII} = \frac{p_{f} - p}{p_{atm}} $$

(37)

where p_atm is the atmospheric pressure. Thus, a CII value larger than 0 is assumed to result in crack initiation. In the previous chapter, it could be seen that p_f is strongly dependent on the model parameters h_e and C_H0, but not particularly dependent on the rest of the parameters when the initial gas concentration is below 20 ppm. For example, from Figs. 6 and 7, it can be seen that p_f is independent on the initial pore size (h_s and R_s). The dependency of p_f on h_e and C_H0, with the values from Section 4.2 for the rest of the model parameters, has been plotted in Fig. 10. This Figure can be used to evaluate p_f at a given location in a GBLF when h and C_H are known at that location.

Fig. 10

p_f as function of C_H and h

If we consider the pore to nucleate as micropore, the crack criterion in Eq. (37) is conservative because a much larger pressure drop than p_f is required to expand a micropore. However, deep in the mushy zone, parts of the GBLF may be isolated or partially isolated. Very large pressure drops may then build up in these cambers if thermal tensile strains act on them, because it is very difficult for liquid feeding to compensate the deformation. A pore may then grow in such a chamber. When the nucleation chamber has been deformed for some time, it may open, and the pore can continue to grow out in the main GBLF if the negative pressure p in the film is large enough.

A major difficulty when evaluating the CII value for a given location in a GBLF is that the pressure and thickness of the GBLF must be known at that location. How these quantities can be estimated for a columnar microstructure of a TIG weld is presented in the second part of this study [19].

5.2 Crack initiation length

A CII value larger than 0 does not guarantee the formation of a permanent crack. For example, if the liquid pressure drop decreases, the surface tension of the pore can contract and close the pore. Figure 11 shows the final radii of pores that have been expanded to R_m = 50 μm, and after that the external pore pressure has been released to 1 atm. The base model parameters in Section 4.2, with different values of h_s and C_H0, were used to construct the plots in the figure. From the figure, it can be seen that h_s must be larger than 3 μm when C_H0 = 15 ppm for the pore to not implode when the pressure drop is released.

Fig. 11

Final pore sizes after pressure release for different values of h_s and C_H0

Figure 12 shows the more extreme situation when the pressure drop is released for a large pore with R_m = 500 μm, h_e = 10 μm, v_R = 250 μm s^− 1, and R_e = 1000 μm. In the figure, it can be seen that even a large pore will implode when the pressure drop is released, unless it is initial size (h_s) or that the hydrogen concentration C_H0 is large.

Fig. 12

Final pore sizes after pressure release for different values of h_s and C_H0, and with h_e = 10 μm, v_R = 250 μm s^− 1, R_m = 500 μm, R_e = 1000 μm

Based on the previous discussion, we assume that an existing pore will implode if the CII value goes below 0 at the location of the pore. Thus, the initial size of the pore or the hydrogen concentration cannot be too large for this assumption to be valid. Neither, for example, can the pore get entangled in the dendrite microstructure nor break the surface of the weld for this assumption to yield. Moreover, we assume that all liquid that remains when the temperature reaches the eutectic temperature during solidification will instantly solidify, and can therefore not flow into colder regions. From these two assumptions, we assume that a permanent crack occurs when the CII value is larger than 0 at the location of the (nonequilibrium) solidus isotherm. The condition that CII is larger than 0 at solidus states that we have the risk for a pore to be frozen into the solid phase, and the condition of instantaneous solidification at liquidus assures that the pore cannot be healed by liquid flow.

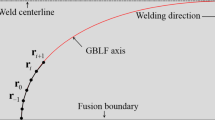
A crack initiation length (CIL) along a GBLF can now be defined as

$$ \text{CIL} = {\int}_{s_{ci}} ds $$

(38)

where s is a coordinate along the GBLF axis, which, for example, can be along the columnar grain growth direction in a TIG weld [19]. The integration path, s_ci, is the part of the GBLF axis where the CII value has been larger than 0 at the intersection with the solidus isotherm, as shown schematically in Fig. 13.

Fig. 13

Schematic representation of the CIL value of a GBLF. The welding direction is from left to right. The shown GBLF axis is located between columnar grains that extend from the fusion boundary and align with the weld centerline. The GBLF axis also extends in the normal direction to the page

A CIL larger than zero indicates risk for cracking. Observe that the CIL value is not associated with a length of a crack. Instead we consider the CIL to be the part of the GBLF where a macroscopic pore can freeze into the solid phase and form a permanent defect. Remember that we have neglected the nucleation, and assumed that a CII value larger than 0 always will leads to crack initiation, which is not true. Thus, if the pore cannot nucleate and grow into a macropore within the part of the GBLF with a CIL value larger than 0, cracking will not occur even if our criterion predicts that.

6 Evaluation

The derived crack criterion was evaluated on Varestraint tests of alloy 718. The test specimens were 3.2-mm-thick plates. Autogenous TIG welding was used in the tests. An augmented strain was applied to a test specimen by bending it over a die block when the welding distance reached 40 mm. The welding speed was 1 mm/s, the stroke rate was 10 mm/s, and the welding was active until 5 s after the start of the bending. The amount of augmented strain was controlled by the radius of the die block. More details about the Varestraint test can be found in part III of this study [20].

Below, the computed CII and CIL are presented, which were evaluated on GBLF axes, located at the weld surfaces. The x and y coordinates in the plots represent the distances from the weld start and weld centerline, respectively. The welding direction is from left to right. The blue lines in the plots represent the computed GBLF axes (their computation is described in part II of this study [19]). They are separated by approximately 1 mm at the fusion line such that they together cover the region where the crack susceptibility is the largest. This region is located 31–35 mm from the weld start. The apex of the die block is located 40 mm from the weld start [20]. Only GBLFs with a solidus temperature inside the fusion zone are considered, while GBLFs that extend into a partially melted zone will be considered in the future. The time in the plots represents the elapsed time from the initiation of the bending. The liquid pressure and film thickness, required to evaluate the CII value, were computed from the models in part II of this study [19]. The p_f value in Eq. (37), required to compute the CII value, was evaluated for a fixed hydrogen concentration of 3.4 ppm. It was computed from the typical concentration of 2 ppm in the melt before solidification [17], divided by the equilibrium partition ratio k_H = 0.589 in Table 1. The temperature field and macroscopic strain field, required to evaluate the pressure and the thickness of the GBLF, originate from the FE model described in part III of this study [20]. They were evaluated on sample points on the GBLF axis.

6.1 CII evaluation

Figure 14 shows the evolution of the CII for a Varestraint test with 1.1% augmented strain. The whole bending took 3.6 s to complete. Only the left part of the symmetric weld is shown. The GBLFs that are aligned perpendicularly to the bending direction have the highest CII values because more deformation will localize in them. During the bending, the maximum CII value increases until 1.5 s into the bending, and then decreases. From part II of this work it was shown that the pressure drop peaks at approximately 0.3 s, while the GBLF thickness peaks at approximately 3 s into the bending. Because the CII is a function of both the GBLF pressure and the thickness, it’s peak value does not have to coincide with a peak value of the pressure drop or the thickness. The reason why the CII starts to decrease after 1.5 s can be explained by the increase in GBLF permeability that occurs when strain is localized in the GBLF. The increase in permeability eases the liquid feeding, which reduces the pressure drop (see part II of this study). How the CII evolves during the bending of Varestraint tests with 0.4% and 0.8% augmented strains can be seen in the appended animations.

Fig. 14

Evolution of GBLF CII at the weld surface of a Varestraint test with 1.1% augmented strain. Only the region with the largest crack susceptibility and the left part of the symmetric weld are shown. The time in the plots represents the elapsed bend time. The abscissa and ordinate represent the distance from the weld start and weld centerline, respectively

6.2 CIL evaluation

Figure 15 shows the computed CIL for a Varestraint test with 0.8% augmented strain, together with the experimental crack locations from four tests with the same augmented strain. The computed CIL for the shown GBLF tracks covers all cracks found in the experiments. Most of the cracks are located 0.5–2 mm from the weld centerline. Interestingly, it is also this region that has the GBLFs with the highest CIL values. Note also that the cracks align fairly well with the GBLF axes, computed with the model in part II of this study.

Fig. 15

Computed CIL at the weld surface of a Varestraint test with 0.8% augmented strain, together with the experimental crack locations from four tests. The abscissa and ordinate represent the distance from the weld start and the weld centerline, respectively

Figure 16 shows the computed CIL for the 1.1% test, together with the experimental crack locations from two test specimens with the same strain. The computed CIL for the shown GBLF axes almost covers all cracks found in the experiments. As for the 0.8% test, most cracks are located 0.5–2 mm from the weld centerline. Again, it is this region in which the model predicts the highest CILs. As for the 0.8% test, the crack orientations and the computed GBLF axes are in fairly good agreement. How the CIL evolves with time for the 0.8% and 1.1% tests can be seen in the appended animations.

Fig. 16

Computed CIL at the weld surface of a Varestraint test with 1.1% augmented strain, together with the experimental crack locations from two tests. The abscissa and ordinate represent the distance from the weld start and weld centerline, respectively

A value of 0.4% augmented strain was considered as the threshold strain for crack initiation of alloy 718 (see part III [20]). The GBLF pressure model has two calibration parameters (see part II), one of them was adjusted such that the computed CIL for the 0.4% test was approximately 300 μm, as shown in Fig. 17.

Fig. 17

Computed CIL at the weld surface of a Varestraint test with 0.4% augmented strain

7 Conclusions

In this study, a solidification cracking criterion, based on observations from recent in situ experiments, was introduced. These experiments have indicated that cracking initiates from voids in GBLFs. To model how such a void can grow into a crack, the void was considered as a rotational symmetric gas capillarity bridge (pore) situated in a GBLF with smooth and parallel solid-liquid interfaces. The relation between the pore radius and external pore pressure could then be studied by applying the Young-Laplace equation to the capillarity bridge. The importance of GBLF thickness and hydrogen concentration on the relation between pore radius and external pore pressure was shown. A fracture pressure, p_f, was derived as a function of the GBLF thickness and the hydrogen concentration. It was assumed that cracking can never occur if the GBLF pressure never goes below this critical pressure. The crack criterion was developed as a CIL, which represents the part of the GBLF where the liquid pressure is below the fracture pressure at the intersection with the solidus isotherm. The criterion was evaluated on Varestraint tests of alloy 718. The computed location of the crack susceptible region was found to be in fairly good agreement with the region where the cracks were located in the experiments.