Introduction

Data envelopment analysis (DEA) was initiated by Charnes et al. (1978) as a method to assess relative efficiency of homogeneous decision making units with multiple inputs and multiple outputs. Then, Banker et al. (1984) extended basic DEA models under returns to scale. As regards, the most models of DEA are introduced the more than one efficient DMU in evaluating the relative efficiency DMUs, thus the investigating rank of efficient DMUs is an interesting research topic. A DMU is called extremely efficient if it cannot be represented as a linear combination (with nonnegative coefficients) of the remaining DMUs (Cooper et al. 2007). In data envelopment analysis, there are several methods for ranking of the extreme efficient DMUs, e.g. AP (Andersen and Petersen 1993) method, MAJ (Mehrabian et al. 1999) method. Andersen and Petersen proposed a new procedure to rank efficient DMUs. The AP method exhibits the rank of a given DMU by removing it from the reference set and by computing its super efficiency score. However, the AP model may be infeasible in some cases. It is proved that super efficient DEA models are infeasible (see Thrall 1996, Cooper et al. 2007, Seiford and Zhu 1999, Charnes et al. 1989). Mehrabian et al. (Charnes et al. 1978) suggested as MAJ model for complete ranking efficient DMUs, but their approach lacks infeasibility in some cases, too. To overcome the drawbacks of the AP (Andersen and Petersen 1993) and MAJ (Mehrabian et al. 1999) models, Jahanshahloo et al. (2004a) presented a method to rank the extremely efficient DMUs in DEA models with constant and variable returns to scale using L 1-norm. The proposed model is a nonlinear programming form which has the computational complexity in solving. A complex treatment was applied in Jahanshahloo et al. (2004a) to convert the nonlinear model into a linear one which provides an approximately optimal solution. Wu and Yan (2010) have also used an effective transformation to convert the nonlinear model in Jahanshahloo et al. (2004a) into a linear model. Also Jahanshahloo et al. (2004b) have applied gradient line for ranking efficient units. Rezai Balf et al. (2012) applied Tchebycheff norm (L 1-norm) introduced in (Briec 1998; Tavares et al. 2001) for complete ranking efficient units. Amirteimoori et al. (2005) introduced a method for ranking of extreme efficient DMUs, based on distance. Hashimoto (1999) proposed a super efficiency DEA model with assurance region in order to rank the DMUs completely. Torgesen et al. (1996) suggested a method for ranking efficient units, by their importance as benchmarks for the inefficient units. Sexton et al. (1986) investigated a ranking method for DMUs based on a cross-efficiency ratio matrix. The cross-efficiency ranking method computes the efficiency score of each DMU that determines a set of optimal weights using linear programs corresponding to each DMU. Then by taking the average of scores of given DMU is obtained the rank of that DMU. Liu and Peng (2008) determined one common set of weights for ranking efficient DMUs, that DMUs are ranked according to the efficiency score weighted by the common set of weights. Bal et al. (2008) suggested a DEA model for ranking of DMUs based on defining the coefficient of variation for input–output weights. Khodabakhshi and Aryavash (2012) proposed a method to rank the efficient DMUs. According to their method, first the minimum and maximum efficiency values of each DMU are computed under the assumption that the sum of efficiency values of all DMUs is equal to unity. Then, the rank of each DMU is determined in proportion to a combination of its minimum and maximum efficiency values. Shetty and Pakkala (2010) suggested a method for ranking efficient units, which is created the average of the corresponding inputs and outputs of all DMUs. Early, Jahanshahloo and Firoozi Shahmirzadi (2013) modified the model which was proposed by Bal et al. (2008). They introduced two new models for ranking efficient DMUs based on L 1-norm and using mean of input–output weights. For our new method it does not need any additional constraints.

In this paper, we suggest a new method for ranking extreme efficient DMUs. The rest of the paper is organized as follows. In “DEA models and ranking models review”, we review the concept of DEA framework. We review some ranking methods in “The proposed ranking model for efficient DMUs”, “Extension to variable returns to scale” proposes the new model for ranking efficient units. “Illustrated examples” includes some numerical examples. The last section concludes the study.

DEA model and ranking model review

DEA model review

DEA is a methodology for assessing the relative efficiency of decision making units (DMUs) where each DMU has multiple inputs used to secure multiple outputs.

It is assumed in DEA that there are \(n\) DMUs and for each DMU j \((j = 1, \ldots ,n)\) is considered a column vector of inputs \((X_{j} )\) to produce a column vector of outputs \((Y_{j} )\), where \(X_{j} = (x_{1j} ,x_{2j} , \ldots ,x_{mj} )^{T}\) and \(Y_{j} = (y_{1j} ,y_{2j} , \ldots ,y_{sj} )^{T}\). Here, the superscript \((T)\) indicates a vector transpose. It is also assumed that \(X_{j} \ge 0, Y_{j} \ge 0, X_{j} \ne 0,\) and \(Y_{j} \ne 0\) for every \(j = 1, \ldots ,n\).

The following input-oriented CCR model [see (Cooper et al. 2007)] in the envelopment form with constant Returns to Scale measures the level of DEA efficiency \((\theta )\) of the \(k\)th DMU \((X_{k} ,Y_{k} )\):

$${\begin{aligned} &{\theta^{*} } { = { {\rm min} }\,\, \theta } \\ & { {\text{s.}} {\text{t.}} { }\sum\limits_{j = 1}^{n} \lambda_{j} x_{ij} \le \theta x_{ik}, \quad i = 1, \ldots ,m} \\ & {\sum\limits_{j = 1}^{n} \lambda_{j} y_{rj} \ge y_{rk} ,\quad r = 1, \ldots ,s} \\ & {\lambda_{j} \ge 0,\quad j = 1, \ldots ,n} \end{aligned} }$$
(1)

Here, \(\lambda = (\lambda_{1} , \ldots ,\lambda_{n} )^{T}\) is a column vector of unknown variables used for components of the input and output vectors by a combination. \(\theta^{*}\) represents the efficiency score of DMU k in (1), where the superscript (*) indicates optimality.

DMU k is relatively efficient if and only if on optimality, the objective of (1) equals to one and all the slacks are zero.

Similarly, the output-oriented CCR model, corresponding to (1), is formulated as follows:

$$\begin{aligned} {\phi^{*} } &= { \text{max} }\;\phi \\ &\quad \begin{array}{ll} {\text{s}} . {\text{t}} . \sum\limits_{j = 1}^{n} \lambda_{j} x_{ij} \le x_{ik} , & i = 1, \ldots ,m \\ \sum\limits_{j = 1}^{n} \lambda_{j} y_{rj} \ge \phi y_{rk} , & r = 1, \ldots ,s \\ \lambda_{j} \ge 0, & j = 1, \ldots ,n \end{array} \end{aligned}$$
(2)

Here, \(1/\phi^{*}\) intends the DEA efficiency score in the output-oriented model.

Also, the following input-oriented BCC model [see Banker et al. (1984)] in the envelopment form with variable Returns to Scale measures the level of DEA efficiency \((\theta )\) of the \(k\)th DMU \((X_{k} ,Y_{k} )\):

$$\begin{aligned} {\theta^{*} } & = { \text {min} }\;\theta \\ &\quad \begin{array}{ll}{\text{s.}} {\text{t.}}\sum\limits_{j = 1}^{n} \lambda_{j} x_{ij} \le \theta x_{ik} ,& i = 1, \ldots ,m \\ \sum\limits_{j = 1}^{n} \lambda_{j} y_{rj} \ge y_{rk} ,& r = 1, \ldots ,s \\ \sum\limits_{j = 1}^{n} \lambda_{j} = 1,\\ \lambda_{j} \ge 0, & j = 1, \ldots ,n \end{array} \end{aligned}$$
(3)

DMU k is relative efficient if and only if on optimality, the objective of (3) equals to one and all the slacks are zero.

Similarly, the output-oriented BCC model, corresponding to (3) which obtains from (2) by adding constraint,

$$\sum\limits_{j = 1}^{n} \lambda_{j} = 1.$$

Moreover, the following additive model is based on input and output slacks which accounts the possible input decreases as well as output increases simultaneously.

$$\begin{aligned} &{ \text {max} } \sum\limits_{j = 1}^{n} s_{i}^{ - } + \sum\limits_{j = 1}^{n} s_{r}^{ + } \\ & \quad \begin{array}{ll}{\text{ s}} . {\text{t}} . \sum\limits_{j = 1}^{n} \lambda_{j} x_{ij} + s_{i}^{ - } \le x_{ik} , & i = 1, \ldots ,m \\ \sum\limits_{j = 1}^{n} \lambda_{j} y_{rj} - s_{r}^{ + } \ge \phi y_{rk} ,& r = 1, \ldots ,s \\ \lambda_{j} ,s_{i}^{ - } ,s_{r}^{ + } , \ge 0, \end{array} \end{aligned}$$
(4)

DMU k is relative efficient if and only if on optimality, the objective of (4) equals to zero.

Ranking models

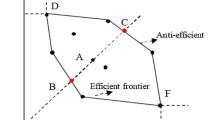
In this subsection we review the some ranking models in data envelopment analysis. The first ranking model proposed by Anderson and Peterson (1993) which is the supper efficiency model. In the AP model DMU under evaluation is excluded from reference set and by using other units, the rank of given DMU is obtained.

The AP model using the CRS super-efficiency model is as follows:

$$\begin{aligned} {\text{AP:}} & { \text{min} } \;\theta\\&\quad \begin{array}{ll} {\text{s}} . {\text{t}} . \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} x_{ij} \le \theta x_{ik} ,& i = 1, \ldots ,m \\ \sum\limits_ {j = 1j \ne k}^{n} \lambda_{j} y_{rj} \ge y_{rk} ,& r = 1, \ldots ,s \\ \quad \lambda_{j} \ge 0, & j = 1, \ldots ,n, j \ne k \end{array} \end{aligned}$$
(5)

The main drawbacks of this model are infeasibility and instability for some DMUs. It is said that a model is stable if a DMU under evaluation is efficient, it is remains efficient after perturbation on data.

The second ranking model under investigation proposed by Mehrabian et al. (1999) to solve infeasibility of AP models in some cases. The following model is MAJ model:

$$\begin{aligned}{\text{MAJ: }} & { \text{min} } \, 1 + w \\ &\quad \begin{array}{ll} \text{s.t} \sum\limits_{{j =1j \ne k }}^{n} \lambda_{j} x_{ij} \le x_{ik} + w, & i = 1, \ldots ,m \\ \sum\limits_{{j = 1j \ne k }}^{n} \lambda_{j} y_{rj} \ge y_{rk} , & r = 1, \ldots ,s \\ \lambda_{j} \ge 0, & j = 1, \ldots ,n, j \ne k \end{array} \end{aligned}$$
(6)

The third ranking model proposed by Jahanshahloo et al. (2004a), that their proposed method to rank the extremely efficient DMUs in DEA models with constant and variable Returns to Scale using the omitted DMU under evaluation from production possibility set and applying L 1-norm. It is shown that the proposed method is able to overcome the existing difficulties in the AP (Andersen and Petersen 1993) and MAJ (Mehrabian et al. 1999) models. On the other hand, the proposed model is the form of nonlinear programming which is difficult to be solved. The model of Jahanshahloo et al. (2004a) is presented as follows:

$$\begin{aligned} {L_{1} - {\text{norm:}} } & {{ \text{min} } \sum\limits_{i = 1}^{m} \left| {x_{i} - x_{ik} } \right| + \sum\limits_{r = 1}^{s} \left| {y_{r} - y_{rk} } \right|} \\ &\quad \begin{array}{ll} {\text{s}} . {\text{t}} .\sum\limits_{j = 1j \ne k}^{n} \lambda_{j} x_{ij} \le x_{i} , &i = 1, \ldots ,m \\ \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} y_{rj} \ge y_{r} ,& \,r = 1, \ldots ,s \\ x_{i} \ge 0, y_{r} \ge 0 & i = 1, \ldots ,m, r = 1, \ldots ,s \\ \lambda_{j} \ge 0,& j = 1, \ldots ,n, j \ne k \end{array} \end{aligned}$$
(7)

The fourth ranking model proposed by Rezai Balf et al. (2012) which applies for ranking extreme efficient units using the leave-one-out idea and \(L_{\infty }\)-norm. The proposed model is always feasible and so, it is able to remove the existing difficulties in some methods, such as Andersen and Petersen (1993). The model of Rezai Balf et al. (2012) is formulated as follows:

$$\begin{aligned} {L_{\infty } - {\text{norm}}: } & { \text{min}\; \nu_{k} } \\ &\quad\begin{array}{ll} {\text{ s}} . {\text{t}} . \nu_{k} \ge \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} x_{ij} - x_{ik} ,& i = 1, \ldots ,m \\ \nu_{k} \ge y_{rk} - \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} y_{rj} ,& r = 1, \ldots ,s \\ \lambda_{j} \ge 0, & j = 1, \ldots ,n, j \ne k \\ \nu_{k} \ge 0 \end{array}\end{aligned}$$
(8)

The proposed ranking model for efficient DMUs

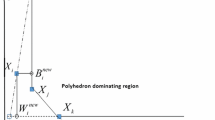
In this section, we suppose that the DMUk is extreme efficient. By excluding the DMUk from the CCR production possibly set, it is obtained a new efficiency frontier. In order to gain the ranking score of DMUk by exploiting the new efficiency frontier, we suggest a new model by by using the leave-one out idea and minimizing distance between DMU under evaluation and virtual DMU. The proposed model is as follows:

$$\begin{array}{ll}{ \text{min} } \sum\limits_{i = 1}^{m} \alpha_{i} + \sum\limits_{r = 1}^{s} \beta_{r} \\ &\\{\text{s}} . {\text{t}} . \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} x_{ij} \le x_{ik} - \alpha_{i} , &i = 1, \ldots ,m \\ \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} y_{rj} \ge y_{rk} + \beta_{r} , & r = 1, \ldots ,s \\ \lambda_{j} \ge 0, & j = 1, \ldots ,n, j \ne k, \\ \alpha_{i} \ge 0, \quad \beta_{r} \ge 0 & i = 1, \ldots ,m \quad r = 1, \ldots ,s,\end{array}$$
(9)

where \(\alpha = (\alpha_{1} , \ldots ,\alpha_{m} )\), \(\beta = (\beta_{1} , \ldots ,\beta_{s} )\) and \(\lambda = (\lambda_{1} , \ldots ,\lambda_{k - 1} ,\lambda_{k + 1} , \ldots ,\lambda_{n} )\) are the variables of the model (9).

Theorem 1

The model (9) is feasible and bounded.

Proof

For \(p \ne k\) we set \(\lambda_{p} = 1, \lambda_{j} = 0, j = 1, \ldots ,n, j \ne k,p; \alpha_{i} = \text{min} \{ x_{ik} - xip\} , i = 1, \ldots ,m; \beta_{r} = min\{ y_{rp} - y_{rk} \} , r = 1, \ldots ,s.\)

Obviously, it can be seen that \((\lambda ,\alpha ,\beta )\) according to above selection is a feasible solution of the model (9). Moreover, the objective function of model (9) is bounded below zero, because the variables of model are nonnegative. Also, the target function is zero when \(\alpha_{i} = 0\) and \(\beta_{r} = 0\) for all \(i, r\) \(\square\).

Extension to variable returns to scale

In this section, the proposed model in previous section is extended to variable Returns to Scale model. For this purpose, the model (9) is reformulated by adjoining the following convexity constraint to the model:

$$\mathop{\sum_{j = 1}}\limits_{j \ne k }^{n} \lambda_{j} = 1, \quad \lambda_{j} \ge 0.$$

So, in order to get the ranking score under variable returns to Scale assumption is solved the following model:

$$\begin{array}{ll} { \text{min} } \sum\limits_{i = 1}^{m} \alpha_{i} + \sum\limits_{r = 1}^{s} \beta_{r} &\\ {\text{s}} . {\text{t}} . \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} x_{ij} \le x_{ik} - \alpha_{i} , &i = 1, \ldots ,m \\ \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} y_{rj} \ge y_{rk} + \beta_{r} , &r = 1, \ldots ,s \\ \sum\limits_{j = 1j \ne k}^{n} \lambda_{j} = 1,&\\ \lambda_{j} \ge 0, &j = 1, \ldots ,n,\quad j \ne k, \\ \alpha_{i} \ge 0,\quad \beta_{r} \ge 0 &i = 1, \ldots ,m,\quad r = 1, \ldots ,s,\end{array}$$
(10)

Theorem 2

The model (10) is feasible and bounded.

Proof

The proof of this theorem is similar to the proof of Theorem 1.

Illustrated examples

In this section, we employ the above DEA model (6) and (7) on the two data sets which they are introduced here, with the assumption of constant returns to scale.

Example 1

As can be seen from Table 1, the data set consists of 19 DMUs with 2 inputs and 2 outputs. The data originally are used by Rezai Balf et al. (2012). Table 2 reports the results of ranking for 6 extremely efficient DMUs \((D_{1} ,D_{2} ,D_{5} ,D_{9} ,D_{15} ,D_{19} )\) in model (7) with constant Returns to Scale and the proposed method is compared with Ap, MAJ, \(L_{1}\) and \(L_{\infty }\). The results imply that the model proposed in this paper provides a easy tool for ranking extremely efficient DMUs. The value of inputs and outputs.

Table 1 Input and output data for Example 1
Full size table
Table 2 Results of ranking by different models
Full size table

Example 2

(Empirical example). We employ DEA model (10) on the empirical example used in Zhu (1998), with the assumption of variable Returns to Scale. The data set in Table 3 provides 13 open coastal Chinese cities and five Chinese special economic zones in 1989. Two inputs and three outputs were chosen to characterize the technology of those cities/zones. Two inputs include Investment in fixed assets by state-owned enterprises, Foreign funds actually used. Three outputs include Total industrial output value, Total value of retail sales and Handling capacity of coastal ports. Table 4 reports the results of ranking for 10 extremely efficient DMUs \((D_{1} ,D_{2} ,D_{5} ,D_{6} ,D_{7} ,D_{9} ,D_{10} ,D_{11} ,D_{13} ,D_{16} )\) in model (10) with variable returns to scale and the proposed method are compared with other methods.

Table 3 The value of inputs and outputs
Full size table
Table 4 Results for several models ranking
Full size table

Conclusion

Many DEA researches are proposed on ranking of efficient decision making units, but they have a problem, e.g. the AP model may be infeasible in some cases. In the present paper, we proposed a model for ranking extreme efficient DMUs in DEA by exploiting the leave-one out and minimizing distance between DMU under evaluation and virtual DMU. The proposed model is linear form and always feasible and bounded. Therefore, it is able to rank all extreme efficient DMUs in the DEA methods with constraint and variable Returns to Scale and so, eliminate the existing difficulties in some methods. In addition, it can be easily used when the number of inputs and outputs is much larger than the number of DMUs. Illustrative examples are included to show good ranking results by the proposed method.