1 Introduction

In the last decades, the theory of integrodifferential equations has been extensively investigated by many researchers, and it has become a very active research area. The study of this class of equations ranges from the theoretical aspects of solvability and well-posedness to the analytic and numerical methods for obtaining solutions. A strong motivation for studying integrodifferential equations of PDEs type comes from the fact that they could serve as mathematical models for many problems in physics, mechanics, biology and other fields of sciences.

In this work, we are concerned with the numerical solution of the following parabolic integrodifferential equation:

$$\begin{aligned} \partial _t u(x,t) - \partial _x^2u(x,t) = \int _0^ta(t-s)u(x,s)\mathrm {d}s + f(x,t), \quad x \in \Lambda , t \in J. \end{aligned}$$
(1.1)

with the initial condition

$$\begin{aligned} u(x,0) = u_0(x), \quad x \in \Lambda . \end{aligned}$$
(1.2)

subject to integral boundary conditions

$$\begin{aligned} \begin{aligned}&\partial _x u(-1,t) = \int _{-1}^{1}u(x,t)K_1(x) \mathrm {d}x,\\&\partial _x u(1,t) = \int _{-1}^{1}u(x,t)K_2(x)\mathrm {d}x. \end{aligned} \end{aligned}$$
(1.3)

where \(\Lambda \) and J stand for the space domain \((-1,1)\) and time interval \([0,T]\) with \(T>0\), respectively. The functions \(a,f,u_0,K_1\) and \(K_2\) are well-defined functions. Assume that the kernel a in the integral part of Eq. (1.1) is bounded, namely

$$\begin{aligned} \vert a(t-s) \vert \le a_0, \quad t,s \in J. \end{aligned}$$
(1.4)

Integrodifferential equations of the form (1.1), and other similar variants, arise in the mathematical modelling of many physical phenomena and practical engineering problems, such as nonlocal reactive flows in porous media [8, 9], heat transfer in materials with memory [13, 17], phenomena of visco-elasticity [7, 19], gas diffusion problems [18], spatio-temporal development of epidemics [21], and so on.

Considerable work has been made on the area of nonlocal boundary values problems in the numerical and theoretical aspects. Indeed theoretical studies devoted to these classes of problems are usually connected with some difficulties due to the presence of an integral terms in the boundary conditions, this promoted researchers to perform some modifications and improvements on the classical methods to overcome this issue (see, e.g., [2, 3, 12, 16]).

On the other hand, integrodifferential equations are usually too complicate to be solved analytically; this made the use of numerical methods is required to obtain approximate solutions. Many efforts have been undertaken to design and develop efficient numerical approaches for solving differential and integrodifferential equations with nonlocal boundary conditions. In [15], Merad and Martín-Vaquero presented a computational study for two-dimensional hyperbolic integrodifferential equations with purely integral conditions, in which, they demonstrated the existence and uniqueness of the solution and proposed a numerical approach based on Galerkin method. Authors in [11], utilized reproducing kernels approach to solve parabolic and hyperbolic integrodifferential equations subject to integral and weighted integral conditions. More recently, Bencheikh et al. [1] implemented numerical method, based on operational matrices of orthonormal Bernstein polynomials, to approximate the solution of an integrodifferential parabolic equation with purely nonlocal integral conditions. The problem under consideration in this paper has been well studied in [10], where the authors proved the existence and uniqueness of the solution using energy inequalities method, and for the numerical resolution, a numerical algorithm based on superposition principle is presented, where the original nonlocal problem was replaced by three auxiliary standard boundary value problems that solved using finite difference method.

As for the numerical methods, Spectral and pseudo-spectral methods [4, 20] have gained increasing popularity in the numerical resolution of many types of problems. In the context of spectral methods, Legendre approximation has been used widely, and this Legendre–Galerkin spectral method has been shown to be computationally efficient and highly accurate with exponential rate of convergence. While plenty of papers have devoted to discussing the use of spectral methods for solving problems with classical boundary conditions. Surprisingly, a limited number of authors touched upon the implementation and analysis of the spectral methods for problems with nonlocal boundary conditions [6].

The primary aim in this paper is to present a suitable way to analysis and implement Legendre–Chebyshev pseudo-spectral method for the numerical resolution of a class of parabolic integrodifferential equations subject to non-local boundary conditions. The proposed approach is based on Galerkin formulation and used Legendre polynomials as a basis for the spatial discretization, followed by, temporal discretization using the trapezoidal method. Both efficiency and accuracy are achieved using the presented method, and the numerical experiments showed that (LC–PSM) can realize better accuracy compared to other existing methods and with less computational time.

This paper is organized as follows. In the next section, we briefly describe the way to implement Legendre–Chebyshev pseudo-spectral method for discretizing the parabolic integrodifferential equation (1.1). In Sect. 3, we first recall some lemmas and results related to spectral methods, and then, the stability and convergence of the method are established in \(L^2\)-norms. In Sect. 4, we provide some numerical tests to confirm the effectiveness and robustness of (LC–PSM) presented in this paper. Finally, in Sect. 5, we summarize some remarks on the main features of our method and cite some possible extensions.

2 Legendre–Galerkin spectral method

In the next subsections, we shall briefly describe the way to implement Legendre–Chebyshev pseudo-spectral method to approximate the solution of the nonlocal boundary value problem considered in this paper. As a starting point, we formulate the nonlocal problem (1.1)–(1.3) in weak formulation: find \(u : J \rightarrow H^1(\Lambda )\) such that for any \(v \in H^1(\Lambda )\)

$$\begin{aligned} \left\{ \begin{aligned}&(\partial _t u,v) + (\partial _xu,\partial _xv) - {\mathcal {K}}(u,v) = \int _{0}^{t}a(t-s)(u(s),v)\mathrm {d}s + (f,v),\quad t \in J, \\&u(0) = u_0. \end{aligned} \right. \end{aligned}$$
(2.1)

where the functional \({\mathcal {K}}(\cdot ,\cdot )\) is defined as follows:

$$\begin{aligned} {\mathcal {K}}(z,v) = v(1)\left( \int _{\Lambda }K_2(x)z(x)\mathrm {d}x\right) - v(-1)\left( \int _{\Lambda }K_1(x)z(x)\mathrm {d}x\right) , \quad v,z \in H^1(\Lambda ). \end{aligned}$$
(2.2)

Here and in what follows, we use the notation \((\cdot ,\cdot )\) to denote the \(L^2\)-inner product and \(\Vert \cdot \Vert \) for the induced norm on the space \(L^2(\Lambda )\). Denote by \(H^m(\Lambda )\) the standard Sobolev space with norm and semi-norm denoted by \(\Vert \cdot \Vert _m\) and \(\vert \cdot \vert _m\), respectively. Solvability of the above variational problem is addressed in the following theorem [10].

Theorem 2.1

Assume that \(a_0\) satisfies rm (1.4), then the variational problem (2.1) admits a unique weak solution in \(L^2(J;H^1(\Lambda ))\).

2.1 Space discretization: LC–PSM

Let \({\mathbb {P}}_N(\Lambda )\) be the space consisting of all algebraic polynomials of degree at most N and denote by \(I_N^C: L^2(\Lambda ) \rightarrow {\mathbb {P}}_N(\Lambda )\) the operator of interpolation at Chebyshev–Gauss–Lobatto points \(\xi _i = cos\left( \frac{i\pi }{N} \right) ,0\le i \le N\) defined as

$$\begin{aligned} I_N^C v(\xi _i) = v(\xi _i), \quad 0\le i \le N, \quad v \in H^1(\Lambda ). \end{aligned}$$

Based on the above weak formulation, we pose the semi-discrete Legendre–Chebyshev Galerkin schema as: find \(u_N : J \rightarrow {\mathbb {P}}_N(\Lambda )\) such that for any \(v \in {\mathbb {P}}_N(\Lambda )\)

$$\begin{aligned} \left\{ \begin{aligned}&(\partial _t u_N,v) + (\partial _x u_N,\partial _xv) - {\mathcal {K}}(u_N,v) = \int _{0}^{t}a(t-s)(u_N(s),v)\mathrm {d}s + (I_N^Cf,v), \\&u_N(0) = I_N^C u_0. \end{aligned} \right. \end{aligned}$$
(2.3)

Let \(L_k\) be the kth degree Legendre polynomial defined by the following three-term recurrence formula:

$$\begin{aligned} L_0(x) = 1, \quad L_1(x) = x, \quad L_{k+1}(x) = \frac{2k+1}{k+1}xL_k(x) + \frac{k}{k+1}L_{k-1}(x), k \ge 1. \end{aligned}$$

We recall that the set of Legendre polynomials is mutually orthogonal in \(L^2(\Lambda )\), namely

$$\begin{aligned} (L_k,L_j) = \int _{\Lambda }L_k(x)L_j(x)\mathrm {d}x = \frac{2}{2k+1}\delta _{j,k}. \end{aligned}$$

Let N be a positive integer, we define [5]

$$\begin{aligned} \begin{aligned}&\varphi _k(x) = \frac{1}{\sqrt{4k+6}} \left( L_k(x) - L_{k+2}(x)\right) , \quad 0\le k \le N-2, \\&\varphi _{N-1}(x) = \frac{1}{2}\left( L_0(x) + L_1(x) \right) , \\&\varphi _{N}(x) = \frac{1}{2}\left( L_0(x) - L_1(x) \right) . \end{aligned} \end{aligned}$$
(2.4)

The following lemma is the key technique in our algorithm.

Lemma 2.2

[22] For two integer \(j,k \in {\mathbb {N}}\), let us denote,

$$\begin{aligned} \begin{aligned}&m_{j,k} = m_{k,j} = (\varphi _j , \varphi _k ) = \int _{-1}^{1}\varphi _j (x)\varphi _k (x) \mathrm {d}x, \\&p_{j,k} = p_{k,j} = (\varphi _j' , \varphi _k ') = \int _{-1}^{1}\varphi '_j (x)\varphi '_k (x) \mathrm {d}x. \end{aligned} \end{aligned}$$

Then, for \(0 \le j,k \le N-2\)

$$\begin{aligned} m_{j,k} = m_{k,j} = {\left\{ \begin{array}{ll} \dfrac{1}{4k+6} \left( \dfrac{2}{2k+1} + \dfrac{2}{2k+5} \right) , &{} j=k, \\ -\dfrac{1}{\sqrt{4k+6}}\cdot \dfrac{1}{\sqrt{4(k+2)+6}}\cdot \dfrac{2}{2k+5}, &{} j = k \pm 2, \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} p_{j,k} = p_{k,j} = \delta _{jk} = {\left\{ \begin{array}{ll} 1, &{} j=k, \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Thanks to linear algebra arguments on can easily prove that

$$\begin{aligned} {\mathbb {P}}_N(\Lambda ) = span\left\{ \varphi _k, 0\le k \le N \right\} , \end{aligned}$$

Consequently, the numerical solution \(u_N\) of (2.3) can be expanded in terms of \(\left( \varphi _k \right) _{k=0}^N\) with time-dependent coefficients, namely

$$\begin{aligned} u_N(x,t) = \sum _{k=0}^{N}\alpha _k(t)\varphi _k(x), \quad (x,t) \in \Lambda \times J. \end{aligned}$$
(2.5)

Inserting (2.5) into (2.3) and taking \(v=\varphi _j, 0\le j \le N\), we obtain the following system of ODEs

$$\begin{aligned} \sum _{k=0}^{N} m_{jk}\alpha _k'(t) + \sum _{k=0}^{N} (p_{jk} - q_{jk})\alpha _k(t) = \sum _{k=0}^{N} m_{jk}A_k(t) + (I_N^Cf,\varphi _j), \quad 0 \le j \le N. \end{aligned}$$
(2.6)

where

$$\begin{aligned} m_{jk} = (\varphi _k,\varphi _j), \quad p_{jk} = (\varphi _k',\varphi _j'), \quad q_{jk} = {\mathcal {K}}(\varphi _k,\varphi _j), \quad A_k(t) = \int _{0}^t a(t-s)\alpha _k(s)\mathrm {d}s. \end{aligned}$$

with initial conditions

$$\begin{aligned} \sum _{k=0}^N p_{jk}\alpha _k(0) = (I_N^C u_0,\varphi _j), \quad 0 \le j \le N. \end{aligned}$$
(2.7)

Denote

$$\begin{aligned} \begin{aligned}&\mathbf{A }(t)=(A_0(t),A_1(t), \ldots , A_N(t))^t, \\&\mathbf{U }(t)=(\alpha _0(t),\alpha _1(t), \ldots , \alpha _N(t))^t, \\&\mathbf{U }_0 =(u_0^0,u_1^0, \ldots , u_N^0)^t , \quad u_j^0 = \int _{\Lambda } I_N^Cu_0(x)\phi _j(x)\mathrm {d}x, \\&{\mathbf {F}}(t) = (f_0(t),f_1(t),\ldots ,f_N(t))^t, \quad f_j(t) = \int _{\Lambda } I_N^Cf(x,t)\phi _j(x)\mathrm {d}x \\&{\mathbf {M}} = [m_{jk}]_{0\le j,k\le N}, \quad {\mathbf {P}} = [p_{jk}]_{0\le j,k\le N}, \quad {\mathbf {Q}} = [q_{jk}]_{0\le j,k\le N}. \end{aligned} \end{aligned}$$

Then, the initial value problem (2.6) and (2.7) can be written in matrix formulation as follows:

$$\begin{aligned} \begin{aligned}&{\mathbf {M}}{\mathbf {U}}'(t) + ( {\mathbf {P}} - {\mathbf {Q}}){\mathbf {U}}(t) = {\mathbf {M}}{\mathbf {A}}(t) + {\mathbf {F}}(t),\\&{\mathbf {U}}(0) = \mathbf{U }_0. \end{aligned} \end{aligned}$$
(2.8)

The coefficients \(m_{jk}\) and \(p_{jk}\) are already determined in Lemma (2.2). For the matrix \({\mathbf {Q}}\), one can uses the values of \(\phi _j(\pm 1)\) to determinate its entries. In fact, since \(\phi _j(\pm 1) = 0\) for \(0\le j \le N-2\), hence \({\mathbf {Q}}\) is almost-null matrix except the two last rows whose entries

$$\begin{aligned} q_{N-1,k} = \int _{\Lambda }K_2(x)\varphi _k(x)\mathrm {d}x, \quad q_{N,k} = \int _{\Lambda }K_1(x)\varphi _k(x)\mathrm {d}x, \quad 0 \le k \le N. \end{aligned}$$

2.2 Fully-discretization schema

For time advancing, we use the second-order Crank–Nicolson scheme to discretize the differential system (2.8). For a given positive integer M, we define the step time \(\Delta t = \frac{T}{M}\). Let \(t_i = i\Delta t,(i=0\cdots ,M)\), we denote by \(\alpha _k^i\) and \(A_k^i\) the approximations of \(\alpha _k(t_i)\) and \(A_k(t_i)\), respectively.

The fully discretization LC–PSM/CN for (1.1)–(1.3) leads to the following recurrent algebraic system

$$\begin{aligned} \begin{aligned}&\left( {\mathbf {M}} + \Delta t({\mathbf {P}} - {\mathbf {Q}}) \right) {\mathbf {U}}^{i+1} = \left( {\mathbf {M}} - \Delta t({\mathbf {P}} + {\mathbf {Q}}) \right) {\mathbf {U}}^{i} + \Delta t ({\mathbf {F}}^{i+1} + {\mathbf {F}}^{i}) + \Delta t{\mathbf {M}}(\mathbf {A^{i}})\quad , i \ge 1 \\&{\mathbf {M}}{\mathbf {U}}^0 = {\mathbf {U}}(0) \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\mathbf {U}}^i = (\alpha _0^i,\alpha _1^i, \ldots , \alpha _N^i)^t, \; {\mathbf {F}}^i = (f_0(t_i),f_1(t_i), \ldots , f_N(t_i)^t, \; {\mathbf {A}}^i = (A_0^i,A_1^i, \ldots , A_N^i)^t. \end{aligned}$$

The above algebraic system can be solved easily using either direct or iterative methods. As a choice, on can use QR factorization method, given its accurate results and ease of implementation.

3 Error analysis

In this section, we derive \(L^2\)-error estimate for the error \(e_N(t) = u_N(t)- u(t)\). For this purpose, we first, in the next subsection, recall a sequence of lemmas that will be needed to perform the error analysis.

3.1 Preliminaries

Now, we introduce two projection operators and their approximation properties. First, let \(P_N : L^2(\Lambda ) \rightarrow {\mathbb {P}}_N(\Lambda )\) be the \(L^2\)-orthogonal projection, namely

$$\begin{aligned} (P_Nv,\varphi ) = (v,\varphi ), \quad \forall \varphi \in {\mathbb {P}}_N(\Lambda ). \end{aligned}$$

We also define the operator \(P^1_N : H^1(\Lambda ) \rightarrow {\mathbb {P}}_N(\Lambda )\) such that

$$\begin{aligned} P_N^1v(x) = v(-1) + \int _{-1}^{x} P_{N-1}\partial _y v(y) \mathrm {d}y. \end{aligned}$$

From the definition of \(P_N^1\), one can obtain

$$\begin{aligned} (\partial _x P_N^1v - \partial _x v,\partial _x \varphi ) = 0, \quad \forall \varphi \in {\mathbb {P}}_N(\Lambda ). \end{aligned}$$
(3.1)

Next, we give the approximation property of the projection operator \(P_N^{1}\) and the interpolation operator \(I_N^C\).

Lemma 3.1

[14] If \( v \in H^r(\Lambda )\) with \(r \ge 1\), then the following estimate holds

$$\begin{aligned} \Vert v - P_N^1v \Vert _l \le CN^{l-r}\Vert v \Vert _r, \quad 0 \le l \le 1. \end{aligned}$$
(3.2)

where \(C>0\) is a positive constant independent on N.

Lemma 3.2

[14] Let \( v \in H^1(\Lambda )\), there exists a positive constant C independent on N such that

$$\begin{aligned} N \Vert I_N^Cv-v \Vert + \vert I_N^Cv \vert _1 \le C\Vert v \Vert _1. \end{aligned}$$
(3.3)

Moreover, if \(v \in H^r(\Lambda )\) for \(r \le 1\), then the following estimate holds

$$\begin{aligned} \Vert v - I_N^Cv \Vert _r \le CN^{r-s}\Vert v \Vert _s, \quad 0 \le r \le 1. \end{aligned}$$
(3.4)

where \(C>0\) is a positive constant independent on N.

Remark 3.3

Under the same assumptions of Lemma (3.2), we can obtain using approximation property (3.3) the following inequality

$$\begin{aligned} \Vert I_N^C v \Vert \le C\Vert v \Vert _1. \end{aligned}$$
(3.5)

Now, we derive a basic estimate that will be used later in our proofs.

Lemma 3.4

[5] Let \({\mathcal {K}}(\cdot ,\cdot )\) defined by (2.2). Assume that \(K_1,K_2 \in L^2(\Lambda )\). Then, for any \(w,v \in H^1(\Lambda )\), the following estimate holds

$$\begin{aligned} \vert {\mathcal {K}}(w,v) \vert \le C_{\varepsilon } \big ( \Vert w \Vert ^2 + \Vert v \Vert ^2 \big ) + \varepsilon \vert v \vert _1^2. \end{aligned}$$
(3.6)

3.2 Error estimates

In this subsection, we consider the stability and convergence of the semi-discrete approximation (2.3). We first state a Gronwall-type inequality that will be used in the proof of our main results.

Lemma 3.5

Let E(t) and H(t) be two non-negative integrable functions on \([0,T]\) satisfying

$$\begin{aligned} E(t) \le H(t) + C_1\int _{0}^tE(s)\mathrm {d}s + C_2\int _{0}^t\int _0^s E(r)\mathrm {d}r\mathrm {d}t, \quad t \in [0,T], \end{aligned}$$
(3.7)

where \(C_1,C_2 \in {\mathbb {R}}^+\), then there exist \(C>0\) such that

$$\begin{aligned} E(t) \le e^{Ct}H(t), \quad t \in [0,T]. \end{aligned}$$
(3.8)

Proof

For a non-negative function E(t), we perform a permutation of variables to obtain:

$$\begin{aligned} \int _{0}^t\int _0^s E(r)\mathrm {d}r\mathrm {d}s = \int _0^t (t-v)E(v)\mathrm {d}v \le C\int _0^t E(s) \mathrm {d}s. \end{aligned}$$

Hence, inequality (3.7) of Lemma (3.5) becomes

$$\begin{aligned} E(t) \le H(t) + C\int _{0}^tE(s)\mathrm {d}s, \quad t \in [0,T]. \end{aligned}$$

Now, applying the standard Gronwall inequality yields the desired estimate (3.8). \(\square \)

Theorem 3.6

Let \( u_0 \in H^1(\Lambda )\) and \(f \in C^1\left( 0,T;H^1(\Lambda )\right) \), then the solution \(u_N(t)\) of (2.3) satisfies

$$\begin{aligned} \Vert u_N(t) \Vert ^2 + \int _{0}^{t} \vert u_N(s) \vert _1^2\mathrm {d}s \le C \left( \int _{0}^{t} \Vert f(s) \Vert _1^2\mathrm {d}s + \Vert u_0 \Vert _1^2 \right) , \quad t \in J. \end{aligned}$$
(3.9)

Proof

Let \(t\in J\), setting \(u_N(t) = v\) in

$$\begin{aligned} \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d} t} \Vert u_N(t) \Vert ^2 + \vert u_N(t) \vert _1^2= & {} \int _{0}^ta(t-s)(u_N(s),u_N(t))\mathrm {d}s + ( I_N^C f(t), u_N(t)) \nonumber \\&+ {\mathcal {K}}(u_N(t),u_N(t)) =: I_1 + I_2 + I_3, \quad t \in J. \end{aligned}$$
(3.10)

We have to estimate the terms on the right-hand side of (3.10). For the first term \(I_1\), we use the hypothesis (1.4) and then apply Cauchy and Young inequalities.

$$\begin{aligned} \begin{aligned} \vert I_1 \vert&\le \int _{0}^{t}\vert a(t-s)(u_N(s),u_N(t)) \mathrm {d}s \\&\le a_0\int _{0}^{t}\vert (u_N(s),u_N(t)) \mathrm {d}s \\&\le \frac{a_0}{2}\left( \Vert u_N(t) \Vert ^2 + \int _{0}^{t}\Vert u_N(s)\Vert ^2 \mathrm {d}s \right) . \\ \end{aligned} \end{aligned}$$
(3.11)

Next, combining Cauchy and Young inequalities with approximation property (3.5) to estimate \(I_2\).

$$\begin{aligned} \begin{aligned} \vert I_2 \vert&\le \vert (I_N^C f(t),u_N(t)) \vert \\&\le \frac{1}{2}\Vert I_N^C f(t)\Vert ^2 + \frac{1}{2}\Vert u_N(t) \Vert ^2 \\&\le C_1\Vert f(t)\Vert _1^2 + \frac{1}{2}\Vert u_N(t) \Vert ^2. \end{aligned} \end{aligned}$$
(3.12)

The estimate of \(I_3\) is an immediate consequence of Lemma (3.6), namely

$$\begin{aligned} \vert {\mathcal {K}}(u_N(t),u_N(t)) \vert \le C_{\varepsilon }\Vert u_N(t) \Vert ^2 + \varepsilon \vert u_N(t)\vert _1. \end{aligned}$$
(3.13)

Putting things together and choosing \(0<\varepsilon <1\) yields

$$\begin{aligned} \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d} t} \Vert u_N(t) \Vert ^2 + \vert u_N(t) \vert _1^2 \le C_2\Vert u_N(t) \Vert ^2 + C_3\Vert f(t) \Vert _1^2 + C_4\int _{0}^t\Vert u_N(s) \Vert ^2\mathrm {d}s. \end{aligned}$$
(3.14)

Integrating both sides of (3.14) form 0 to t, we obtain

$$\begin{aligned} E(t) \le C_5\int _{0}^{t}E(s)\mathrm {d}s + C_6\int _{0}^{t}\int _{0}^{s}E(r)\mathrm {d}r\mathrm {d}s + H(t), \quad t \in J, \end{aligned}$$
(3.15)

where

$$\begin{aligned} \begin{aligned}&E(t) = \Vert u_N(t) \Vert ^2 + \int _{0}^t \vert u_N(s) \vert _1^2\mathrm {d}s, \\&H(t) = \int _{0}^t \Vert f(s) \Vert _1^2\mathrm {d}s + \Vert u_N(0) \Vert ^2. \end{aligned} \end{aligned}$$

Thanks to the Gronwall-type inequality (3.5), we get

$$\begin{aligned} E(t) \le H(t)e^{Ct}, \quad t \in J. \end{aligned}$$

Because of \(u_N(0) = I_N^C u_0 = (I_N^C u_0 - u_0) + u_0\), we use approximation properties (3.3) and (3.5) to obtain \( \Vert u_N(0) \Vert \le C\Vert u_0 \Vert _1^2 \). Then it is easy to show the desired result. \(\square \)

Let u(t) and \(u_N(t)\) be the solutions to (2.1) and (2.3), respectively. Denoting

$$\begin{aligned} \theta _N(t) = u_N(t) - P_N^1u(t), \text { and } \rho _N(t) = P_N^1u(t) - u(t), \quad \forall t\in J \end{aligned}$$

Then, we have the following estimate.

Lemma 3.7

Assume that \(u \in C^1\left( 0,T;H^r(\Lambda )\right) ,r \ge 2\), then the following estimate holds

$$\begin{aligned} \Vert \theta _N(t) \Vert \le CN^{-r}, \quad t \in J. \end{aligned}$$
(3.16)

where \(C>0\) is a positive constant independent on N.

Proof

From (2.1), (2.3) and (3.1) we know that for a fixed \(t\in J\) the \(\theta _N(t)\) satisfies for all \(v\in {\mathbb {P}}_N(\Lambda )\) the following error equation:

$$\begin{aligned}&\left( \partial _t \theta _N(t), v \right) + \left( \partial _x \theta _N(t), \partial _x v \right) = \int _{0}^ta(t-s)(\theta _N(s),v)\mathrm {d}s \; + \nonumber \\&\quad \int _{0}^ta(t-s)(\rho _N(s),v)\mathrm {d}s + \left( I_N^C f(t) - f(t) , v \right) - \left( \partial _t \rho _N(t), v \right) + {\mathcal {K}}(\theta _N(t) + \rho _N(t),v). \end{aligned}$$
(3.17)

Setting \(v = \theta _N(t)\) in (3.17), we obtain

$$\begin{aligned} \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d}t}\Vert \theta _N(t) \Vert ^2 + \vert \theta _N(t)\vert _1^2 \le I_1 + I_2 + I_3 + I_4 + I_5. \end{aligned}$$
(3.18)

where

$$\begin{aligned} \begin{aligned}&I_1 = \int _{0}^t\vert a(t-s)(\theta _N(s),\theta _N(t))\vert \mathrm {d}s, \quad I_2 = \int _{0}^t\vert a(t-s)(\rho _N(s),\theta _N(t))\vert \mathrm {d}s, \\&I_3 = \vert \left( I_N^Cf - f,\theta _N(t) \right) \vert , \quad I_4 = \vert \left( \partial _t \rho _N(t), \theta _N(t) \right) \vert , \quad I_5 = \vert {\mathcal {K}}(\theta _N(t) + \rho _N(t),\theta _N(t))\vert \end{aligned} \end{aligned}$$

Now, we estimate the terms on the right hand-side of inequality (3.17) using a standard procedure. For the term \(I_1\), we apply Cauchy and Young inequalities and take into account (1.4),

$$\begin{aligned} \begin{aligned} I_1&= \int _0^t\vert a(t-s)(\theta _N(s),\theta _N(t))\vert \mathrm {d}s \\&\le a_0\int _0^t\Vert \theta _N(t)\Vert \cdot \Vert \theta _N(s)\Vert \mathrm {d}s \\&\le C_1\left( \Vert \theta _N(t)\Vert ^2 + \int _0^t\Vert \theta _N(s)\Vert ^2\mathrm {d}s\right) \end{aligned} \end{aligned}$$
(3.19)

In a similar manner, we can obtain for \(I_2\)

$$\begin{aligned} I_2 \le C\left( \Vert \rho _N(t)\Vert ^2 + \int _0^t\Vert \theta _N(s)\Vert ^2\mathrm {d}s\right) \end{aligned}$$

By virtue of approximation property (3.2), we bound \(I_2\) as follows

$$\begin{aligned} I_2 \le C_2N^{-2r}\Vert u(t)\Vert _r^2 + C_3\int _0^t\Vert \theta _N(s)\Vert ^2\mathrm {d}s \end{aligned}$$
(3.20)

For the term \(I_3\)

$$\begin{aligned} \begin{aligned} I_3&= \vert (I_N^C f(t) - f(t),\theta _N(t)) \vert \\&\le \Vert I_N^C f(t) - f(t) \Vert \cdot \Vert \theta _N(t)\Vert \\&\le C_4N^{-2r}\Vert f(t) \Vert _r^2 + \Vert \theta _N(t)\Vert ^2. \end{aligned} \end{aligned}$$
(3.21)

Similarly,

$$\begin{aligned} I_4 \le C_5N^{-2r}\Vert \partial _t u(t) \Vert _r^2 + \Vert \theta _N(t)\Vert ^2. \end{aligned}$$
(3.22)

To estimate of the term \(I_5\) we use Lemma (3.4). Setting \(w = \theta _N(t) + \rho _N(t) \) and \( v = \theta _N(t)\) in (3.6) yields

$$\begin{aligned} \vert I_5 \vert&= \vert {\mathcal {K}}(\theta _N(t) + \rho _N(t), \theta _N(t)) \vert \nonumber \\&\le C_{\varepsilon } \big ( \Vert \theta _N(t) + \rho _N(t) \Vert ^2 + \Vert \theta _N(t) \Vert ^2 \big ) + \varepsilon \vert \theta _N(t) \vert _1^2 \end{aligned}$$
(3.23)

using the triangular inequality

$$\begin{aligned} \vert I_5 \vert \le C_{\varepsilon } \big ( \Vert \rho _N(t) \Vert ^2 + \Vert \theta _N(t) \Vert ^2 \big ) + \varepsilon \vert \theta _N(t) \vert _1^2 \end{aligned}$$
(3.24)

hence, due to Lemma (3.1), on can obtain,

$$\begin{aligned} \vert I_5 \vert \le C_{\varepsilon }\Vert \theta _N(t)\Vert ^2 + \varepsilon \vert \theta _N(t)\vert ^2 + C_5N^{-2r}\Vert u \Vert _r^2 \end{aligned}$$
(3.25)

In virtue of above estimates , then inequality (3.18) becomes

$$\begin{aligned} \frac{1}{2}\frac{\mathrm {d}}{\mathrm {d}t}\Vert \theta _N(t) \Vert ^2 + \vert \theta _N(t)\vert _1^2 \le C_4N^{-2r} \Big ( \Vert f \Vert _r^2 + \Vert \partial _t u \Vert _r^2 + \Vert u \Vert _r^2 \Big ) + C_{\varepsilon }\Vert \theta _N(t) \Vert _r^2 + \varepsilon \vert \theta _N(t) \vert _1^2 \end{aligned}$$
(3.26)

By taking \(\varepsilon \) sufficiently small and integrating (3.26) over (0, t), we obtain

$$\begin{aligned} E(t) \le H(t) + C\int _{0}^{t}E(s)\mathrm {d}s + C'\int _{0}^{t}\int _{0}^{s}E(r)\mathrm {d}r\mathrm {d}s, \quad t \in J \end{aligned}$$
(3.27)

where

$$\begin{aligned} \begin{aligned} E(t)&= \Vert \theta _N(t) \Vert ^2 + \int _{0}^{t}\vert \theta _N(s)\vert _1^2\mathrm {d}s \\ H(t)&= CN^{-2r} \int _0^t \left( \Vert f(s) \Vert _r^2 + \Vert \partial _t u(s) \Vert _r^2 + \Vert u(s) \Vert _r^2 \right) \mathrm {d}s + \Vert \theta _N(0) \Vert ^2 \end{aligned} \end{aligned}$$
(3.28)

Gronwall-type inequality (3.5) implies

$$\begin{aligned} E(t) \le H(t)e^{Ct}, \quad t \in J. \end{aligned}$$
(3.29)

Take into account,

$$\begin{aligned} \theta _N(0) = P_N^1u_0 - I_N^Cu_0 = \left( P_N^1u_0 - u_0 \right) + \left( u_0 - I_N^Cu_0 \right) \end{aligned}$$

and approximation results (3.2) and (3.4), we obtain

$$\begin{aligned} \Vert \theta _N(0) \Vert ^2 \le CN^{-2r}\Vert u_0 \Vert _r^2 \end{aligned}$$
(3.30)

Inserting (3.30) into (3.27) yields

$$\begin{aligned} \Vert \theta _N(t) \Vert ^2 + \int _{0}^t\vert \theta _N(s) \vert ^2\mathrm {d}x \le C\left( \int _{0}^t \left( \Vert f(s)\Vert ^2_r + \Vert \partial _t u(s) \Vert _r^2 + \Vert u(s) \Vert ^2_r \right) \mathrm {d}s + \Vert u_0 \Vert ^2_r \right) \end{aligned}$$

for all \(0 < t \le T\), which is the desired result. \(\square \)

Now, we are in position to state our main result concerning the convergence of the semi-discrete approximation (2.3).

Theorem 3.8

Let u(t) and \(u_N(t)\) be the solution of (2.1) and (2.3), respectively. If \(u \in C^1\left( 0,T;H^r(\Lambda )\right) \) with \(r \ge 1\), then the following error estimate holds,

$$\begin{aligned} \Vert u(t) - u_N(t) \Vert \le CN^{-r} , \quad t \in J. \end{aligned}$$
(3.31)

where \(C>0\) is a positive constant independent on N.

Proof

Using triangular inequality, we have

$$\begin{aligned} \Vert u(t) - u_N(t) \Vert \le \Vert u_N(t) - P_N^1u(t)\Vert + \Vert P_N^1u(t) - u(t) \Vert = \Vert \theta _N(t) \Vert + \Vert \rho _N(t) \Vert \end{aligned}$$

By the aid Lemmas (3.2) and (3.7), for all \(t\in J\) we obtain

$$\begin{aligned} \Vert u(t) - u_N(t) \Vert \le CN^{-r} + C'N^{-r} \end{aligned}$$
(3.32)

This completes the proof. \(\square \)

Fig. 1
figure 1

Profiles of exact and approximate solutions, and the absolute error for step time \(\tau =10^{-3}\)

Full size image

4 Numerical experiments

In this section, we carry out several numerical experiments to verify the efficiency and accuracy of the proposed (LC–PSM), and we will compare our results against results obtained using other methods.

Table 1 \(\hbox {L}_{\infty }\)-errors with different discretization parameters for Example (4.1)
Full size table
Table 2 Absolute errors of some numerical solutions at \(t=0.5\) for Example (4.1)
Full size table
Table 3 Spatial convergence rates at \(t=1\) for Example 4.2
Full size table

Example 4.1

In this first test problem, the following parabolic integrodifferential equation is considered

$$\begin{aligned} \begin{aligned}&\partial _t u(x,t) - \partial _x^2 u(x,t) = 2\int _0^te^{t-s}u(x,t)\mathrm {d}s + f(x,t), \\&\partial _x u(0,t) = \frac{-6}{13}\int _{-1}^{1}u(x,t)\mathrm {d}x, \\&\partial _x u(1,t) = \frac{6}{13}\int _{-1}^{1}u(x,t)\mathrm {d}x. \\ \end{aligned} \end{aligned}$$

where \(f(x,t) = -(x^2-x-2)(-3e^{-t}-4t+2t^2+4)-2e^{-t}\) and \(u_0(x) = x^2 -x -2\).

The exact solution to the above integrodifferential problem is given as

$$\begin{aligned} u^*(x,t) = (x^2 -x -2)e^{-t}. \end{aligned}$$

Figure 1 presents the computational results obtained by applying (LC–PSM) to the above test problem, where the profiles of exact and approximate solutions as well as the absolute error are plotted.

From the numerical results illustrated in Fig. 1, one can observe that the approximate solution shows a great agreement with the exact solution, which confirms that (LG–PSM) yields a very accurate an efficient numerical method for the numerical resolution of nonlocal boundary value problems of integrodifferential parabolic type.

For comparison purposes, in Tables 1 and 2 we compared our computational results with the results obtained in [10]. Obviously, the proposed (LC–PSM) in this paper gives more accurate solutions with less CPU time than the finite difference schema used in mentioned reference.

Fig. 2
figure 2

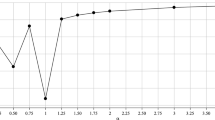
A \(L^2\)-norm versus N. B Pointwise absolute errors with \(N = 20, \Delta t = 10^{-2}\) for Example (4.2) at \(t = 1\)

Full size image

Example 4.2

To examine the spatial discretization, we take in this example a test problem that has an analytic solution with limited regularity. Let us consider the following problem:

$$\begin{aligned} \begin{aligned}&\partial _tu(x,t) - \partial _x^2u(x,t) = \int _{0}^te^{-(t-s)}u(x,t)\mathrm {d}s + f(x,t),\\&\partial _x u(-1,t) = \int _{-1}^{1}x(x+1)^{1/2}(1-x) u(x,t) \mathrm {d}x, \\&\partial _x u(-1,t) = \int _{-1}^{1} \sqrt{1-x}(x^3-x)u(x,t) \mathrm {d}1x. \end{aligned} \end{aligned}$$

The exact solution is given as the following:

$$\begin{aligned} u^*(x,t) = e^t(x+1)^{\frac{5}{2}}(x-1)^2. \end{aligned}$$

We first choose a step time small enough so that the error of the temporal discretization can be eliminated, and make the polynomial degree N varies. Table 3 shows the error in \(L^2\) and \(L^{\infty }\)-norms at a selected point \(t=1\) and by going through each line one can observe an increasing accuracy until the error of the temporal discretization becomes dominant.

To examine the theoretical result, we plot in Fig. 2 the decay rates of error in \(L^2\)-norm versus N in a log-scale and the lines of decay rates \(N^{-2}\) and \(N^{-4}\). As expected, \(L^2\)-error of (LC-PSM) for the solved problem in this example has a rate of convergence between \(N^{-3}\) and \(N^{-4}\) , which supports the results established in Theorem (3.8) since \(u \in H^3(\Lambda )\) and \(u \notin H^4(\Lambda )\)

5 Conclusions

In this paper, we are concerned in the implement and analysis of the spectral method to solve a class of integrodifferential parabolic equations subject to nonlocal boundary conditions of Neumann-type. We combined the Legendre spectral method based on Galerkin formulation to discretize the problem in the spatial direction and the second-order Crank–Nicolson finite difference schema for the temporal discretization. Rigorous error analysis has been carried out in \(L^2\)-norm for the proposed method, and the computational results of numerical examples have supported the theoretical results. Moreover, a comparison with fully finite-difference schema clearly shows that the presented method is computationally superior with less required CPU time. It should be noted that other high-order methods can be used for time integration to improve the accuracy of the fully discretization. Convergence and stability of such combinations are still undiscussed.

In future works, we plan to investigate how to implement space–time spectral method for the resolution of this class and other challenging models, such as nonlocal boundary value problems in the two-dimensional case and fractional integrodifferential problems.