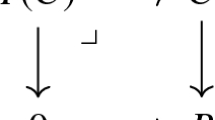The mod 2 Hopf ring for connective Morava K-theory

Abstract

This paper examines the mod 2 homology of the spaces in the Omega-spectrum for connective Morava K-theory, i.e., the mod 2 Hopf ring for connective Morava K-theory. A natural set of generators for this Hopf ring arising from the homology and homotopy of the connective Morava K-theory spectrum is calculated and the non-trivial circle product relations among the generators arising from homology and homotopy are determined. This Hopf ring calculation is accomplished using Dieudonné ring theory and Adams spectral sequences for the connective Morava K-theory of Brown–Gitler spectra.

1 Introduction

Suppose E is a ring spectrum, and let $\underline{E}_{\, k} = \Omega ^\infty \Sigma ^k E$ denote the kth space in its $\Omega$-spectrum. The mod p homology $H_{*}(\underline{E}_{*})$ is a Hopf ring, which is a ring object in the category of coalgebras over $\mathbb {F}_p$. Every Hopf ring $H_{*}(\underline{E}_{*})$ has a unique suspension class $e \in H_1(\underline{E}_1)$ with the property that

$$\begin{aligned} e \circ (-) : \, H_d(\underline{E}_{\, k}) \rightarrow H_{d+1}(\underline{E}_{\, k+1}) \end{aligned}$$

(1.1)

is the homology suspension homomorphism. The homology stabilization (or infinitely iterated homology suspension) homomorphism

$$\begin{aligned} e^{\infty } (-) : \, H_{d+k}(\underline{E}_{\, k}) \rightarrow H_d(E) \end{aligned}$$

(1.2)

is the colimit of

$$\begin{aligned} \cdots \mathop {\longrightarrow }^{e \circ (-)} H_{d+k}(\underline{E}_{\, k}) \mathop {\longrightarrow }^{e \circ (-)} H_{d+k+1}(\underline{E}_{k+1}) \mathop {\longrightarrow }^{e \circ (-)} \cdots . \end{aligned}$$

(1.3)

An element in a Hopf ring is unstable if it is in the kernel of the stabilization homomorphism, and stable if it is not. There is also a destabilization function

$$\begin{aligned} e^{-\infty }(-) : H_d(E) \rightarrow H_{d+k}(\underline{E}_{\, k}) \end{aligned}$$

(1.4)

which is a right-inverse for the stabilization and maps a stable homology class back to its space of origin in a canonical way. Specifically, for each $x \in H_d(E)$ the homology class $e^{-\infty }(x) \in H_{d+k}(\underline{E}_{\, k})$ has the following properties: (1) $e^{\infty }(e^{-\infty }(x)) = x$, (2) the value for k is the smallest value for which $e^{-\infty }(x)$ exists and is nonzero in $H_{d+k}( \underline{E}_{\, k})$, and (3) an algebraic expression for $e^{-\infty }(x)$ is canonically determined from an algebraic expression for x.

The category of Hopf rings over $\mathbb {F}_p$ is equivalent to the category of Dieudonné rings over the p-adic integers $\hat{\mathbb {Z}}_p$ [9]. Thus, every Hopf ring $H_{*}(\underline{E}_{*})$ is equivalent to a Diedonné ring $D_{*}(H_{*}(\underline{E}_{*}))$. In [8], a surjective homomorphism from the E-homology of Brown–Gitler spectra $E_{*}(B(*))$ to the Dieudonné ring $D_{*}(H_{*}(\underline{E}_{*}))$ was constructed that is an isomorphism in certain degrees. In particular, $E_{n-k}(B(n)) \twoheadrightarrow D_n(H_{*}(\underline{E}_k))$ is an isomorphism at $p=2$ when n is even, and at odd primes p when $n \not \equiv \pm 1 \mod 2p$ [9, Proposition 11.3]. Thus, it is often possible to calculate the Hopf ring $H_{*}(\underline{E}_{*})$ using the Adams spectral sequence for $E_{*}(B(*))$ via the composition

$$\begin{aligned} \mathrm {Ext}_A^{*,*}(\mathbb {F}_p,H_{*}(E \wedge B(*))) \Rightarrow E_{*}(B(*)) \twoheadrightarrow D_{*}^{}(H_{*}^{}(\underline{E}_{*})) \mathop {\rightarrow }^{\cong } H_{*}^{}(\underline{E}_{*}). \end{aligned}$$

(1.5)

The fact that it is possible to calculate the Hopf ring $H_{*}(\underline{E}_{*})$ using Adams spectral sequences for $E_{*}(B(n))$, $n \ge 0$, is remarkable for several reasons. First, unlike the bar spectral sequence which computes $H_{*}(\underline{E}_{\, k})$ inductively on k (i.e., one space at a time), this method computes $H_n(\underline{E}_{*})$ inductively on n (i.e., across all spaces at once) and therefore identifies natural generators for the Hopf ring coming from the homotopy and homology of the spectrum E very well. Second, this method for calculating the homology of the spaces $\underline{E}_{*}$ is done using only the (co)homology of the spectrum E and the Brown–Gitler spectra $B(*)$ as input to the Adams spectral sequence. Third, the stable classes in $H_{*}(\underline{E}_{*})$ can be determined from the $s = 0$ line of the Adams spectral sequences for $E_{*}(B(n))$ with $n \ge 0$, while the unstable classes can be determined from $s \ge 1$ lines of these Adams spectral sequences. Finally, this approach can be used even when the spaces $\underline{E}_{*}$ have not been identified in terms of already known spaces.

Now, let $H_{*}(-)$ denote mod 2 homology, $\mathrm {H}\mathbb {F}$ the mod 2 Eilenberg-Mac Lane spectrum, and k(r) the rth connective Morava K-theory spectrum at $p=2$. Recall from [18] that

$$\begin{aligned} H_{*}(k(r)) = P(\zeta _1^{}, \zeta _2^{}, \ldots , \zeta _r^{}, \zeta _{r+1}^{2}, \zeta _{r+2}^{}, \ldots ) \end{aligned}$$

(1.6)

as comodule-algebras over the dual Steenrod algebra, and

$$\begin{aligned} \pi _{*}(k(r)) = k(r)_{*} = P(v_r), \end{aligned}$$

(1.7)

where $\zeta _i = \chi (\xi _i)$ is the conjugate of the Milnor generator $\xi _i$ in the dual of the Steenrod algebra, $deg(\zeta _i) = 2^i-1$, $deg(v_r) = 2^{r+1}-2$, and $P(x,y,\ldots )$ denotes a polynomial algebra over $\mathbb {F}_2$.

Our first main result describes the stable classes in the Hopf ring $H_{*}(\underline{k(r)}_{*})$ as generators of a sub Hopf ring of $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$, which is described in detail in Sect. 4. This result is a consequence of Lemma 7.10, which calculates the $s=0$ line of the Adams spectral sequence for $k(r)_{*}(B(2n))$, $n \ge 0$, where B(2n) denotes a Brown–Gitler spectrum at $p = 2$. The following theorem, which relies upon Lemma 7.10, is given as Theorem 8.1.

Theorem 1.1

The destabilization function $e^{-\infty }: H_{*}(k(r)) \rightarrow H_{*}(\underline{k(r)}_{*})$ is a restriction of the destabilization function $e^{-\infty } : H_{*}(\mathrm {H}\mathbb {F}) \rightarrow H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$ given in Definition 4.7 in that diagram (1.8) is commutative.

(1.8)

Consequently, every stable class in the Hopf ring $H_{*}(\underline{k(r)}_{*})$ is either the destabilization of a class in $H_{*}(k(r))$ or an iterated homology suspension of a destabilized class, and all of the $\circ$-product relations among stable classes in $H_{*}(\underline{k(r)}_{*})$ are known because they have already been determined in $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$.

Our second main result identifies the unstable classes in $H_{*}(\underline{k(r)}_{*})$. More precisely, we show that the stable classes in $H_{*}(\underline{k(r)}_{*})$ that support non-trivial $\circ$-multiplication by powers of the unstable class $v_r$ correspond to elements in the $Q_r$ Margolis homology of $H_{*}(B(2n))$. These Margolis homology calculations are made in Sect. 6, where we also show that the $Q_r$ Margolis homology of $H_{*}(k(r))$ is filtered by the $Q_r$ Margolis homology of $H_{*}(B(2n))$. The following theorem, which relies upon Lemma 7.11, is given as Theorem 8.2.

Theorem 1.2

For $n \ge 0$, there is a one-to-one correspondence of $\mathbb {F}_2$-modules between the stable classes in $H_{2n}(\underline{k(r)}_{*})$ that support non-trivial $\circ$-multiplication by powers of $v_r$ and nonzero classes in the Margolis homology module $H \left( H_{*}(B(2n)), Q_r \right)$.

Our third main result states that the most natural set of Hopf ring generators for $H_{*}(\underline{k(r)}_{*})$ arises from the homology and homotopy of the spectrum k(r). This theorem, which is given as Theorem 8.4, is a consequence of the complete calculation of the Adams spectral sequence for $k(r)_{*}(B(2n))$, $n \ge 0$, which is given in Theorem 7.14.

Theorem 1.3

The Hopf ring $H_{*}(\underline{k(r)}_{*})$ is generated by

• 1. stable generators $e^{-\infty }(H_{*}(k(r)))$, and

• 2. the homotopy generator $[v_r ]\in H_0(\underline{k(r)}_{\, 2-2^{r+1}})$.

Computations of $H_{*}(\underline{k(r)}_{*})$ for primes $p \ge 3$ have been made by Hara [10] and Wilson [23] using the bar spectral sequence. The results in this paper are novel because the Hopf ring $H_{*}(\underline{k(r)}_{*})$ is calculated without the bar spectral sequence and is also carried out at $p=2$. It should be straightforward to use the techniques introduced in this paper to independently verify the results by Hara and Wilson for primes $p \ge 3$ [10, 23]. As noted by Hara [10], one drawback of the bar spectral sequence approach is the difficulty in finding legitimate names for new generators constructed in the process of calculating $H_{*}(\underline{k(r)}_{\, k})$ by induction on k. Our approach, which calculates $H_{2n}(\underline{k(r)}_{*})$ by calculating $k(r)_{*}(B(2n))$ and then uses Dieudonné ring theory to transfer results on $k(r)_{*}(B(2n))$ to $H_{2n}(\underline{k(r)}_{*})$, identifies the most natural possible generators—those coming from the homology and homotopy of k(r). However, one drawback of our approach is that the map $k(r)_{*}(B(2n+1)) \rightarrow H_{2n+1}(\underline{k(r)}_{*})$, given later in Eq. (5.3), is a surjection but not an isomorphism. As a result, $H_{2n+1}(\underline{k(r)}_{*})$ cannot be completely determined from $k(r)_{*}(B(2n+1))$ alone. Consequently, this paper focuses on identifying the stable and unstable generators of this Hopf ring, which do happen to lie in even dimensional homology, rather than trying to determine all of the relations in this Hopf ring or the structure of each individual Hopf algebra $H_{*}(\underline{k(r)}_{\, k})$.

The organization of this paper is as follows. In Sect. 2 we define categories of Hopf rings and Dieudonné rings and establish their equivalence. In Sect. 3 we recall the Lambda algebra, and the Adams spectral sequence. In Sect. 4 we recall the dual of the Steenrod algebra and the Hopf ring for the mod 2 Eilenberg–Mac Lane spectrum. In Sect. 5 we give the connection between Brown–Gitler spectra and Dieudonné rings. In Sect. 6 we calculate the Margolis homology of Brown–Gitler modules and of the mod 2 homology of k(r). In Sect. 7, we calculate the Adams spectral sequence for $k(r)_{*}(B(*))$. Finally, in Sect. 8 we calculate the Hopf ring for k(r) using Dieudonné ring theory and the calculation of $k(r)_{*}(B(*))$.

2 Hopf rings and Dieudonné rings

Fix a prime $p>0$. Let $\mathbb {F}_p$ be the finite field of p elements, and let $\mathcal {C}$ be the category of graded connected cocommutative coalgebras with counit over $\mathbb {F}_p$. Graded group and ring objects in $\mathcal {C}$ comprise the categories of Hopf algebras $\mathcal {HA}$ and Hopf rings $\mathcal {HR}$ over $\mathbb {F}_p$, respectively. A Hopf algebra (or coalgebraic group) is an algebra with addition $+$, multiplication $*$, conjugation $\chi$, and coproduct $\psi$. Its multiplication $*$ is a categorical addition with inverse $\chi$ and zero element $[0]=1$. A Hopf ring (or coalgebraic ring) has an additional product $\circ$ which is a categorical multiplication with unit element [1]. For detailed information about Hopf rings and coalgebraic algebra, please see [11, 20, 22, 24].

Example 2.1

Let E be a ring spectrum and let $\underline{E}_{\, k} = \Omega ^\infty \Sigma ^k E$ be the kth space in its $\Omega$-spectrum. Write $H_{n,k}$ for $H_n(\underline{E}_{\,k})$. Then $H_{*,k}$ is a Hopf algebra over $\mathbb {F}_p$ for each k, and $H_{*,*}$ is a Hopf ring over $\mathbb {F}_p$. Three sub Hopf rings of $H_{*,*}$ are $H_{0,*}$, $H_{*,0}$, and $\{H_{n,k} \}_{(n,k) \in \mathbb {N} \times \mathbb {N}}$.

Every Hopf algebra $H = H_{*,k}$ over $\mathbb {F}_p$ has Frobenius and Verschiebung maps. Let $H^\vee = \mathrm {Hom}_{\mathbb {F}_p-mod}(H,\mathbb {F}_p)$ denote the $\mathbb {F}_p$-linear dual of H.

Definition 2.2

Fix $k \in \mathbb {Z}$. The Frobenius $F: H_{n,k} \rightarrow H_{pn,k}$ is defined by $F(x) = x^{*p}$. The Verschiebung $V: H_{n,k} \rightarrow H_{n/p,k}$ is the $\mathbb {F}_p$-linear dual of the pth power map $f:H^\vee \rightarrow H^\vee$, $f: x\mapsto x^p$, and V is zero when $p \not \mid n$. If H is of finite type, it is equivalent to define the Verschiebung by $V(x) = ax'$ if the iterated coproduct is

$$\begin{aligned} \psi ^{(p-1)}(x) = a \underbrace{x' \otimes x' \otimes \cdots \otimes x'}_{{p \mathrm{factors}}} + \text{(other } \text{ terms), } \end{aligned}$$

where each of the other terms have at least one tensor factor different from the others.

The Verschiebung is a homomorphism of Hopf rings (2.1), but the Frobenius is not. Instead, these maps satisfy the Frobenius reciprocity relations (2.2) and (2.3).

$$\begin{aligned} V(x \circ y)&= V(x) \circ V(y) \end{aligned}$$

(2.1)

$$\begin{aligned} F(x \circ V(y))&= F(x) \circ y \end{aligned}$$

(2.2)

$$\begin{aligned} F(V(x) \circ y)&= x \circ F(y) \end{aligned}$$

(2.3)

The following Hopf algebras are used to define the Dieudonné functor.

Example 2.3

Let $CW(0) = \hat{\mathbb {Z}}_p[\mathbb {Z}]$ be the Hopf algebra over $\hat{\mathbb {Z}}_p$ concentrated in degree 0 with coproduct $\psi ([r]) = [r] \otimes [r]$. For $n>0$, write $n=p^a b$ where $\mathrm {gcd}(p,b)=1$, and let $CW(n) = \hat{\mathbb {Z}}_p[x_0,\ldots ,x_a]$. For $0 \le i \le a$, give CW(n) the grading $|x_i| = p^i b$ and the unique coproduct such that the Witt polynomials

$$\begin{aligned} w_i^{} = x_0^{*p^i} + p x_1^{*p^{i-1}} + p^2 x_2^{*p^{i-2}} + \cdots + p^i x_i^{} \end{aligned}$$

are primitive.

Let H(n) be the Hopf algebra over $\mathbb {F}_p$ which is the mod p reduction of CW(n). Let $v: H(n) \rightarrow H(pn)$ be the identity map if $n=0$ and the inclusion $v: x_i \mapsto x_i$ if $n>0$. Let $f: H(pn) \rightarrow H(n)$ be the multiplication by p map if $n=0$ and the map $f: x_i \mapsto (x_{i-1})^p$ if $n>0$, where $x_{-1}=0$.

We now define the categories $\mathcal {DM}$ and $\mathcal {DR}$ of graded Dieudonné modules and rings over $\hat{\mathbb {Z}}_p$, respectively. Then, we show that the Dieudonné functor D establishes an equivalence between the categories of Hopf rings over $\mathbb {F}_p$ and Dieudonné rings over $\hat{\mathbb {Z}}_p$. For more details on Dieudonné rings please see [6, 9].

Definition 2.4

Fix $k \in \mathbb {Z}$. A graded Dieudonné module $M = M_{*,k}$ over $\hat{\mathbb {Z}}_p$ is a non-negatively graded abelian group with a Frobenius map $F:M_{n,k} \rightarrow M_{pn,k}$ and a Verschiebung map $V:M_{n,k} \rightarrow M_{n/p,k}$, which is zero when $p \not \mid n$, such that $F(V(x)) = V(F(x)) = px$, V is the identity on $M_{0,k}$, and $p^{a+1} M_{p^a b,k} = 0$ if $\mathrm {gcd}(p,b)=1$.

Example 2.5

Fix $k \in \mathbb {Z}$. Let $H = H_{*,k}$ be a Hopf algebra over $\mathbb {F}_p$. The Dieudonné module $D_{*}(H)$ is the graded abelian group $\{ D_n(H_{*,k}) \}_{n \in \mathbb {N}}$ with

$$\begin{aligned} D_n(H_{*,k}) = \mathrm {Hom}_{\mathcal {HA}}(H(n),H_{*,k}). \end{aligned}$$

The Frobenius and Verschiebung

$$\begin{aligned} F&= f^* : D_n(H_{*,k}) \rightarrow D_{pn}(H_{*,k}), \\ V&= v^* : D_{pn}(H_{*,k}) \rightarrow D_n(H_{*,k}) \end{aligned}$$

are induced by the maps f and v of Example 2.3.

Theorem 2.6

(Schoeller’s theorem [9, Theorem 4.7], [21]) The Dieudonné functor D has a right adjoint U, and the pair (D, U) is an equivalence between the category $\mathcal {HA}$ of Hopf algebras and $\mathcal {DM}$ of Dieudonné modules.

We now define the category $\mathcal {DR}$ of Dieudonné rings.

Definition 2.7

A graded commutative Dieudonné ring over $\hat{\mathbb {Z}}_p$ is a collection of Dieudonné modules $\{ M_{*,k} \}_{k \in \mathbb {Z}}$ together with bilinear maps

$$\begin{aligned} \circ : M_{m,j} \mathop {\otimes }_{\hat{\mathbb {Z}}_p} M_{n,k} \rightarrow M_{m+n,j+k} \end{aligned}$$

such that Eqs. (2.1)–(2.3) are satisfied. Graded commutativity is expressed by $x \circ y = (-1)^{mn+jk} y \circ x$ for $x \in M_{m,j}$ and $y \in M_{n,k}$.

In [9], Goerss constructed a symmetric monoidal products $\boxtimes _{\mathcal {HA}}$ and $\boxtimes _{\mathcal {DM}}$ for the categories of Hopf algebras and Dieudonné modules. He showed that the Dieudonné functor was symmetric monoidal, and thus established an equivalence between the category of Hopf rings over $\mathbb {F}_p$ that are group rings in degree zero and Dieudonné rings over $\hat{\mathbb {Z}}_p$.

Theorem 2.8

(Goerss’s Theorem [9, Theorem 7.7]) For any $H, K \in \mathcal {HA}$ such that $H_{0,k}$ and $K_{0,k}$ are group rings for every integer k, there is a natural isomorphism of Dieudonné modules

$$\begin{aligned} D_{*}(H) \mathop {\boxtimes }_{\mathcal {DM}} D_{*}(K) \rightarrow D_{*}(H \mathop {\boxtimes }_{\mathcal {HA}} K). \end{aligned}$$

Example 2.9

Let E be a ring spectrum. Then $H_0(\underline{E}_{\, k}) = \mathbb {F}_p[\pi _0(\underline{E}_{\, k})] = \mathbb {F}_p[\pi _{-k}(E)]$ is a group ring for each k. By Theorem 2.8, the Hopf ring $H_{*}(\underline{E}_{*})$ over $\mathbb {F}_p$ is equivalent to the Dieudonné ring $D_{*}(H_{*}(\underline{E}_{*}))$ over $\hat{\mathbb {Z}}_p$, and under this equivalence $H_n(\underline{E}_{\, k})$ corresponds to $D_n(H_{*}(\underline{E}_{\, k}))$.

3 The Lambda algebra and the Adams spectral sequence

We review the Lambda algebra and the Adams spectral sequence at the prime $p=2$.

Definition 3.1

(Lambda algebra [2]) The Lambda algebra $\Lambda$ is the associative bigraded differential algebra over $\mathbb {F}_2$ with generators $\lambda _a$, $a\ge -1$, of bidegree $(1,a+1) = (s,t)$ modulo the two-sided ideal generated by the relations

$$\begin{aligned} \lambda _a \lambda _b = \sum _{\lceil (b-2a)/2 \rceil \le c < b-2a} { c-1 \atopwithdelims ()2c-b+2a }\, \lambda _{a+c} \lambda _{b-c}, \quad \text{ if } 0 \le 2a < b \end{aligned}$$

(3.1)

and the left ideal generated by $\lambda _{-1}$. Its differential $d_1(\lambda _b) = \lambda _{-1} \lambda _b$ is a derivation.

If $I = (i_1,\ldots ,i_s)$ is an s-tuple of nonnegative integers, set $\lambda _I = \lambda _{i_1}\cdots \lambda _{i_s}$ and $\lambda _{(~)}=1$. We say that $\lambda _I$ is admissible if $2i_j \ge i_{j+1}$ for $1 \le j < s$. The admissible monomials form a basis for $\Lambda$.

The Lambda algebra provides an $E_1$ term for the Adams spectral sequence [2]. Let A denote the mod 2 Steenrod algebra.

Theorem 3.2

(Adams spectral sequence [1, 2]) Let X be a complex or spectrum of finite type, and let E be a spectrum. The $E_1$-term of the E-based Adams spectral sequence is the differential right $(\Lambda ,d_1)$ module

$$\begin{aligned} E_1^{*,*}(A,E \wedge X) = H_{*}(E \wedge X) \mathop {\otimes }_{\mathbb {F}_2} \Lambda \end{aligned}$$

(3.2)

with differential $d_1(z \otimes \lambda _I) = \sum _{i \ge 0} z \cdot \mathrm {Sq}^i \otimes \lambda _{i-1}(\lambda _I)$. Its $E_2$-term is

$$\begin{aligned} E_2^{s,t}(A, E \wedge X) = \mathrm {Ext}_A^{s,t}(\mathbb {F}_2,H_{*}(E\wedge X)) \Longrightarrow \pi _{t-s}(E \wedge X) = E_{t-s}(X). \end{aligned}$$

(3.3)

If $H^*(E)$ is a Hopf algebra quotient of the Steenrod algebra, the Adams spectral sequence for calculating $E_{*}(X)$ can be simplified by a change of rings theorem.

Theorem 3.3

(Change of rings [1]) If E is a ring spectrum such that $H^*(E) = A // C = A \mathop {\otimes }_C \mathbb {F}_2$ for some sub Hopf algebra $C \subset A$, then there is an isomorphism, natural in X,

$$\begin{aligned} \mathrm {Ext}_C^{s,t}(\mathbb {F}_2, H_{*}(X)) \cong \mathrm {Ext}_A^{s,t}(\mathbb {F}_2, H_{*}(E \wedge X)). \end{aligned}$$

4 The Hopf ring $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$ and the dual of the Steenrod algebra

In this section we recall the structure of the Hopf ring $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$, define its conjugate generators $z_i$, define its destabilization function, and determine how the Steenrod algebra acts on it.

Recall that $H_{*}(\underline{\mathrm {H}\mathbb {F}}_1) = H_{*}(\mathbb {R}\mathrm {P}^\infty ) = \mathbb {F}_2 \{ b_i \mid i \ge 0 \}$, where $|b_i|=i$ and $b_0=1$. The product is $b_i * b_j = {i+j \atopwithdelims ()i} \, b_{i+j}$, the Frobenius is $F(b_i) = b_i^{*2} = 0$, and the indecomposables are the module $*\text{-Ind }(H_{*}(\underline{\mathrm {H}\mathbb {F}}_1)) = \mathbb {F}_2 \{ x_i \mid i \ge 0 \}$ where $x_i = b_{2^i}$. The coproduct is $\psi (b_n) = \sum _{0 \le i \le n} b_{n-i} \otimes b_i$, the Verschiebung is $V(b_{2i}) = b_i$ and $V(b_{2i+1}) = 0$, and the primitives are given by Newton polynomials, which are defined recursively by $N_i = N_i(b_1,\ldots ,b_i) = i b_i + \sum _{j=1}^{i-1} b_j * N_{i-j}(b_1,\ldots ,b_{i-j})$ for $i \ge 1$ [see ([1], pp. 93–94; [12], Sect. 3) for more details]. The suspension class in the Hopf ring $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$ is $e = x_0 = b_1$.

The dual of the Steenrod algebra is the stabilization of the Hopf ring $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$. That is, $H_n(\mathrm {H}\mathbb {F}) = \displaystyle \lim \nolimits _{k \rightarrow \infty } H_{n+k}(\underline{\mathrm {H}\mathbb {F}}_{\, k})$, where the limit is taken by iterating the homology suspension $e \circ (-)$. Recall from [16] that the dual of the mod 2 Steenrod algebra is $A^\vee = H_{*}(\mathrm {H}\mathbb {F}) = P(\xi _i \mid i \ge 0)/(\xi _0=1)$. The stabilization homomorphism is given by $e^{\infty }(x_i) = \xi _i$, and satisfies $e^{\infty }(x_i * x_j) = 0$ and $e^{\infty }( x_i \circ x_j) = \xi _i \xi _j$.

Theorem 4.1

[15, 24] As Hopf algebras over $\mathbb {F}_2$ with addition $+$ and multiplication $*$,

$$\begin{aligned} H_{*}(\underline{\mathrm {H}\mathbb {F}}_{\, k}) = {\left\{ \begin{array}{ll} \mathbb {F}_2[\mathbb {F}_2], &{} \quad \text{ if } k = 0, \\ E( x_{i_1} \circ \cdots \circ x_{i_k} \mid 0 \le i_1 \le \cdots \le i_k), &{}\quad \text{ if } k \ge 1. \end{array}\right. } \end{aligned}$$

Further, $*\text{-Ind }(H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})) = \mathrm {Sym}( x_i \mid i \ge 0 )$, the bigraded symmetric algebra over $\mathbb {F}_2$ with addition $+$, multiplication $\circ$, and generators $x_i \in H_{2^i}(\underline{\mathrm {H}\mathbb {F}}_1)$.

The generators $x_n \in H_{2^n}(\underline{\mathrm {H}\mathbb {F}}_1)$ are the destabilizations of the generators $\xi _n \in H_{2^n-1}(\mathrm {H}\mathbb {F})$ in that $e^{\infty }(x_n) = \xi _n$ and $x_n$ is not the suspension of a class in $H_{*}(\underline{\mathrm {H}\mathbb {F}}_0)$. We now define elements $z_n$ that are the destabilization of the conjugate $\zeta _n = \chi (\xi _n)$ in the dual of the Steenrod algebra [16].

Definition 4.2

An ordered partition of the integer n of length $\ell$ is a sequence $(\alpha _1,\alpha _2,\ldots ,\alpha _\ell )$ of positive integers whose sum is n. Let $\mathrm {Part}(n)$ denote the set of all $2^{n-1}$ ordered partitions of n. Given an ordered partition $(\alpha _1,\ldots ,\alpha _\ell ) \in \mathrm {Part}(n)$, let

$$\begin{aligned} \sigma (i) = {\left\{ \begin{array}{ll} \alpha _1 + \alpha _2 + \cdots + \alpha _{i-1}, &{} \quad \text{ if } 1 \le i \le \ell , \\ 2^n-1-(2^{\sigma (1)} + \cdots + 2^{\sigma (\ell )}), &{}\quad \text{ if } i=0. \end{array}\right. } \end{aligned}$$

Let $e = x_0 = z_0 \in H_1(\underline{\mathrm {H}\mathbb {F}}_1)$, and for $n \ge 1$ define $z_n \in H_{2^{n+1}-2}(\underline{\mathrm {H}\mathbb {F}}_{2^n-1})$ by

$$\begin{aligned} z_n = \sum _{(\alpha _1,\ldots ,\alpha _\ell ) \in \mathrm {Part}(n)} x_0^{\circ \sigma (0)} \circ x_{\alpha _1}^{\circ 2^{\sigma (1)}} \circ x_{\alpha _2}^{\circ 2^{\sigma (2)}} \circ \cdots \circ x_{\alpha _\ell }^{\circ 2^{\sigma (\ell )}}. \end{aligned}$$

(4.1)

Remark 4.3

Every term of the sum (4.1) has $2^n - 1 = deg(\zeta _n)$ factors because for each $(\alpha _1, \ldots , \alpha _\ell ) \in \mathrm {Part}(n)$ the sum of the exponents in the term $x_0^{\circ \sigma (0)} \circ x_{\alpha _1}^{\circ 2^{\sigma (1)}} \circ \cdots \circ x_{\alpha _\ell }^{2^{\sigma (\ell )}}$ is $2^n - 1$ by construction.

We now describe the right action of the Steenrod algebra on its dual and on $H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$. Let $\mathrm {Sq} = \sum _{i \ge 0} \mathrm {Sq}^i$ be the total Steenrod square, which is a ring homomorphism.

Lemma 4.4

[2], [5, Lemma 6.1] The right action of $\mathrm {Sq}$ on $H_{*}(\mathrm {H}\mathbb {F})$ is

$$\begin{aligned} \xi _n^{} \cdot \mathrm {Sq} = \xi _n^{} + \xi _{n-1}^{},&\qquad&\zeta _n^{} \cdot \mathrm {Sq} = \displaystyle \sum _{0 \le i \le n} \zeta _{n-i}^{2^i}, \end{aligned}$$

where $\xi _0 = 1$ and $\xi _{-1}=0$.

We will also need the canonical right action of the Milnor primitives on the conjugate basis for the dual of the Steenrod algebra. The Milnor primitives are defined by setting $Q_0 = \mathrm {Sq}^1$ and inductively defining $Q_{i+1} = [\mathrm {Sq}^{2^{i+1}},Q_i] = \mathrm {Sq}^{2^{i+1}}Q_i + Q_i\mathrm {Sq}^{2^{i+1}}$ for $i \ge 0$. Let $Q = \sum _{i \ge 0} Q_i$ denote the total Milnor primitive, which is a derivation.

Lemma 4.5

The right action of Q on $H_{*}(\mathrm {H}\mathbb {F})$ is

$$\begin{aligned} \zeta _n \cdot Q = \sum _{0 \le i \le n} \zeta _{n-i}^{2^i}. \end{aligned}$$

Proof

We show that $\zeta _n \cdot Q_k = \zeta _{n-(k+1)}^{2^{k+1}}$ by induction on k. Clearly, $\zeta _n \cdot Q_0 = \zeta _{n-1}^2$. Suppose that $\zeta _n \cdot Q_{k-1} = \zeta _{n-k}^{2^k}$ for all n. Since $\zeta _{n-i}^{2^i} \cdot \mathrm {Sq}^{2^i} = \zeta _{n-(i+1)}^{2^{i+1}}$ for $i \ge 0$, we have

$$\begin{aligned} \zeta _n \cdot Q_k = \zeta _n \cdot (\mathrm {Sq}^{2^k} Q_{k-1}^{} + Q_{k-1}^{}\mathrm {Sq}^{2^k} ) = \zeta _n \cdot Q_{k-1} \mathrm {Sq}^{2^k} = \zeta _{n-k}^{2^k} \cdot \mathrm {Sq}^{2^k} = \xi _{n-(k+1)}^{2^{k+1}}. \end{aligned}$$

$\square$

We now define the destabilization function $e^{-\infty } : H_{*}(\mathrm {H}\mathbb {F}) \rightarrow H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$ for Hopf rings such that every element in the image of $e^{-\infty }$ cannot be desuspended any further, and $e^{-\infty }$ is a right inverse for the stabilization homomorphism $e^{\infty }$, i.e., the composite map

$$\begin{aligned} H_{*}(\mathrm {H}\mathbb {F}) \mathop {\rightarrow }^{e^{-\infty }} H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*}) \mathop {\rightarrow }^{e^{\infty }} H_{*}(\mathrm {H}\mathbb {F}). \end{aligned}$$

(4.2)

is the identity on $H_{*}(\mathrm {H}\mathbb {F})$. The destabilization function is given by $e^{-\infty }(\xi ^I) = x^{\circ I}$ on monomials. For a sum of monomials $\sum \xi ^I \in H_d(\mathrm {H}\mathbb {F})$, defining $e^{-\infty }(\sum \xi ^I) \in H_{d+k}(\underline{\mathrm {H}\mathbb {F}}_{\, k})$ is more complicated because k must be minimal and the sum $e^{-\infty }(\sum \xi ^I)$ must have exactly k factors of $x_i$’s in each term.

Definition 4.6

Define the $\xi$ factors function $fact_\xi : H_{*}(\mathrm {H}\mathbb {F}) \rightarrow \mathbb {N}$ on monomials by adding the exponents $fact_\xi (\xi ^I) = \sum _{j=1}^n i_j$, and on sums by $fact_\xi (\sum \xi ^I) = max_I \{ fact_\xi (\xi ^I) \}$. If $\sum \zeta ^J = \sum \xi ^I$ under change of basis, then set $fact_\xi (\sum \zeta ^J)$ equal to $fact_\xi (\sum \xi ^I)$.

Definition 4.7

The destabilization function $e^{-\infty } : H_{*}(\mathrm {H}\mathbb {F}) \rightarrow H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$ is given as follows. Set $e^{-\infty }(1) = [1] \in H_0(\underline{\mathrm {H}\mathbb {F}}_0) = \mathbb {F}_2[\mathbb {F}_2 ]$. Suppose $\sum \xi ^I \in H_d(\mathrm {H}\mathbb {F})$ with $d = deg(\sum \xi ^I) > 0$ and $k = fact_\xi (\sum \xi ^I)$, and that $\sum \xi ^I = \sum \zeta ^J$ under change of basis. Then, in terms of the basis of $x_i$’s,

$$\begin{aligned} \textstyle e^{-\infty }\left( \sum \xi ^I \right) = e^{-\infty }\left( \sum \zeta ^J \right) := \sum x_0^{\circ (k - fact_\xi (\xi ^I))} \circ x^{\circ I} \in H_{d+k}(\underline{\mathrm {H}\mathbb {F}}_{\, k}). \end{aligned}$$

(4.3)

In terms of the basis of $z_i$’s,

$$\begin{aligned} \textstyle e^{-\infty }\left( \sum \xi ^I \right) = e^{-\infty }\left( \sum \zeta ^J \right) := z_0^{\circ -(d-k)} \circ \left( \sum z^{\circ J} \right) \in H_{d+k}(\underline{\mathrm {H}\mathbb {F}}_{\, k}). \end{aligned}$$

(4.4)

Remark 4.8

By construction, every term in the sum (4.3) has exactly k factors of $x_i$’s. In contrast, the sum (4.4) does not necessarily have the same number of factors of $z_i$’s in each term. Since $d \ge k$, there is a desuspension factor $z_0^{\circ -(d-k)}$ in (4.4) that needs explanation. By remark 4.3, under the change of basis $\sum z^{\circ J} = \sum x^{\circ L}$, every term $x^{\circ L}$ has $d = deg(\sum \zeta ^J)$ factors. Since $d-k \ge 0$ and $k - fact_\xi (\xi ^I) \ge 0$ for all terms in $\sum \xi ^I$, it follows that

$$\begin{aligned} \textstyle \sum z^{\circ J}&= \textstyle \sum x^{\circ L} \\&= \textstyle \sum x_0^{\circ (d - fact_\xi (\xi ^I))} \circ x^{\circ I} \\&= \textstyle \sum x_0^{\circ (d - k + k - fact_\xi (\xi ^I))} \circ x^{\circ I} \\&= \textstyle x_0^{\circ (d - k)} \circ \left( \sum x_0^{\circ (k - fact_\xi (\xi ^I))} \circ x^{\circ I} \right) \\&= \textstyle x_0^{\circ (d-k)} \circ e^{-\infty }\left( \sum \xi ^I\right) , \end{aligned}$$

and therefore $\sum z^{\circ J}$ desuspended $(d-k)$ times equals $e^{-\infty }(\zeta ^J) = e^{-\infty }(\sum \xi ^I)$. This desuspension occurs for the following reason. When $\sum z^{\circ J}$ is written in terms of the basis of $x_i$’s there may be cancellation of terms mod 2, and in the sum that remains after cancellation $(\sum x^{\circ L})$, the greatest common factor of $x_0$ is $x_0^{\circ (d-k)}$.

Example 4.9

The destabilization of the element $\xi _3^2 + \xi _1^2 \xi _2^4 = \zeta _3^2 + \zeta _1^8 \zeta _2^2 \in H_{14}(\mathrm {H}\mathbb {F})$ with degree $d = 14$ and $k = fact_\xi \left( \xi _3^2 + \xi _1^2 \xi _2^4 \right) = 6$ is

$$\begin{aligned} e^{-\infty } \left( \xi _3^2 + \xi _1^2 \xi _2^4 \right) = x_0^{\circ 4} \circ x_3^{\circ 2} + x_1^{\circ 2} \circ x_2^{\circ 4} \in H_{20}^{}(\underline{\mathrm {H}\mathbb {F}}_{\, 6}), \end{aligned}$$

which also equals

$$\begin{aligned} e^{-\infty } \left( \zeta _3^2 + \zeta _1^8 \zeta _2^2 \right) = z_0^{\circ (-8)} \circ \left( z_3^{\circ 2} + z_1^{\circ 8} \circ z_2^{\circ 2} \right) \in H_{20}^{}(\underline{\mathrm {H}\mathbb {F}}_{\, 6}). \end{aligned}$$

5 Brown–Gitler spectra and Dieudonné rings

Brown and Gitler constructed a family of spectra at the prime 2 in [3]. Analogues of these spectra at odd primes were later constructed by Cohen [7]. We specialize to the prime 2, although analogues at odd primes are also true [9].

The nth mod 2 Brown–Gitler spectrum, which was denoted B(n) and indexed by $n \in \frac{1}{2}\mathbb {N}$ in the original paper [3], will be denoted B(2n) and indexed by $\mathbb {N}$ in this paper. There is a homotopy equivalence $B(2n) \simeq B(2n+1)$ for all $n \in \mathbb {N}$, and B(0) and B(2) are the 2 complete sphere spectrum and mod 2 Moore spectrum, respectively. The Brown–Gitler spectra realize certain cyclic modules over the Steenrod algebra. They are characterized up to homotopy 2-equivalence by the following theorem.

Theorem 5.1

[3] For each $n \in \mathbb {N}$ there is a 2-complete spectrum B(2n) satisfying

• 1. $H^*(B(2n)) = A/A\{\chi (\mathrm {Sq}^i) \mid i > n\}$ as left A modules, and

• 2. If $\iota : B(2n) \rightarrow \mathrm {H}\mathbb {F}_2$ classifies the element $1 \in H^0(B(2n))$, then the induced map of reduced homology theories $\iota _{*} : B(2n)_i(X) \rightarrow H_i(X)$ is an epimorphism for all complexes X and $0 \le i \le 2n+1$.

Definition 5.2

Define the $\zeta$ weight function $wt_\zeta : A^\vee \rightarrow \mathbb {N}$ on monomials by $wt_\zeta (1) = 0$ and $wt_\zeta (\zeta _1^{i_1} \zeta _2^{i_2} \cdots \zeta _\ell ^{i_\ell }) = \sum _{j=1}^\ell i_j 2^{j-1}$, and on sums by $wt_\zeta (\sum \zeta ^I) = max_I \{ wt_\zeta (\zeta ^I) \}$. If $\sum \xi ^I = \sum \zeta ^J$ under change of basis, then set $wt_\zeta (\sum \xi ^I)$ equal to $wt_\zeta ( \sum \zeta ^J)$.

Definition 5.3

Define the $\xi$ weight function on monomials by $wt_\xi (1) = 0$ and $wt_\xi (\xi _1^{i_1} \xi _2^{i_2} \cdots \xi _\ell ^{i_\ell }) = \sum _{j=1}^\ell i_j 2^{j-1}$, and on sums by $wt_\xi (\sum \xi ^I) = max_I \{ wt_\xi (\xi ^I) \}$. If $\sum \xi ^I = \sum \zeta ^J$ under change of basis, then set $wt_\xi (\sum \zeta ^J)$ equal to $wt_\xi ( \sum \xi ^I)$.

The homology of Brown–Gitler spectra can be described as a right A submodule of $A^\vee$ using the $\zeta$ weight function. This weight function is induced by the May filtration of $\Omega ^2 S^3$ by identifying the Thom spectrum of the canonical bundle on $\Omega ^2 S^3$ with $\mathrm {H}\mathbb {F}_2$ [13].

Lemma 5.4

[13] There is an isomorphism of right A modules

$$\begin{aligned} H_{*}(B(2n)) \cong \mathbb {F}_2 \{ \zeta ^I \in A^\vee \mid wt_\zeta (\zeta ^I) \le n \}. \end{aligned}$$

Remark 5.5

The right A module structure of $A^\vee = H_{*}(\mathrm {H}\mathbb {F})$ is given in Lemma 4.4.

The following Mahowald cofiber sequence is very useful for computations.

Lemma 5.6

[9] For each integer $n \ge 1$, there is a cofiber sequence of spectra

$$\begin{aligned} B(2n-2) \mathop {\rightarrow }^\epsilon B(2n) \mathop {\rightarrow }^v \Sigma ^n B(n) \end{aligned}$$

(5.1)

which induces a short exact sequence of right A modules

$$\begin{aligned} 0 \rightarrow H_{*}(B(2n-2)) \mathop {\rightarrow }^{\epsilon _{*}} H_{*}(B(2n)) \mathop {\rightarrow }^{v_{*}} \Sigma ^n H_{*}(B(n)) \rightarrow 0 \end{aligned}$$

(5.2)

in which $\epsilon _{*}(\zeta ^I) = \zeta ^I$ and $v_{*}(\zeta _1^{i_1} \zeta _2^{i_2} \cdots \zeta _k^{i_k}) = \Sigma ^n \zeta _0^{i_1} \zeta _1^{i_2} \zeta _2^{i_3} \cdots \zeta _{k-1}^{i_k}$, where $\zeta _0 = 1$.

We now show that $E_{*}(B(*))$ is a Dieudonné ring.

Example 5.7

Let $E_{*}(-)$ be a generalized homology theory. There are pairings $B(m) \wedge B(n) \rightarrow B(m+n)$ that make $B(*) = \{ B(n) \}_{n \in \mathbb {N}}$ a graded commutative ring spectrum, and $B(*)_{*}(E)$ a graded commutative ring. Additionally, there are maps $f : \Sigma ^n B(n) \rightarrow B(2n)$ and $v: B(2n) \rightarrow \Sigma ^n B(n)$ so that fv and vf are multiplication by 2. The map v is the map in the Mahowald cofiber sequence of equation (5.1). The maps f and v induce the Frobenius and Verschiebung maps in the Dieudonné ring $E_{*}(B(*))$. See [9] for more details.

The next theorem states that Brown–Gitler spectra are, in a weak sense, the representing objects for the Dieudonné functor.

Theorem 5.8

[9] For any ring spectrum E and all $(n,k) \in \mathbb {N} \times \mathbb {Z}$, the map

$$\begin{aligned} T : E_{n-k}(B(n)) \twoheadrightarrow D_n(H_{*}(\underline{E}_{\, k})) \end{aligned}$$

is a surjective homomorphism of Dieudonné rings that respects the Frobenius and Verschiebung, and is an isomorphism when n is even.

To calculate Dieudonné ring and Hopf ring for a ring spectrum E, we use the composite

$$\begin{aligned} E_2^{*,*}(A,E \wedge B(*)) \Longrightarrow E_{*}(B(*)) \mathop {\twoheadrightarrow }^T D_{*}^{}(H_{*}^{}(\underline{E}_{*})) \mathop {\rightarrow }^U H_{*}^{}(\underline{E}_{*}) \end{aligned}$$

(5.3)

of the Adams spectral sequence, the surjective map T which is an isomorphism half of the time, and the right adjoint U of the Dieudonné functor D.

The double suspension homomorphism $\epsilon$ and stabilization $\epsilon ^\infty$ in the context of Dieudonné rings are the maps of Adams spectral sequences

$$\begin{aligned} \epsilon :&\, \mathrm {Ext}_A^{*,*}(\mathbb {F}_2, H_{*}(E \wedge B(2n))) \rightarrow \mathrm {Ext}_A^{*,*}(\mathbb {F}_2, H_{*}(E \wedge B(2n+2))), \\ \epsilon ^\infty :&\, \mathrm {Ext}_A^{*,*}(\mathbb {F}_2, H_{*}(E \wedge B(2n))) \rightarrow \mathrm {Ext}_A^{*,*}(\mathbb {F}_2, H_{*}(E \wedge \mathrm {H}\mathbb {F})), \end{aligned}$$

induced by the inclusion maps $\epsilon : B(2n) \rightarrow B(2n+2)$ and $\epsilon ^{\infty }: B(2n) \rightarrow B(\infty ) = \mathrm {H}\mathbb {F}$ of Brown–Gitler spectra, respectively.

6 Margolis homology of $H_{*}(B(2n))$ and $H_{*}(k(r))$

In this section, we calculate the $Q_r$ Margolis homology of $H_{*}(B(2n))$ in order to determine which classes on the $s=0$ line of the $E_2$-term Adams spectral sequence

$$\begin{aligned} E_2^{s,t}(A, k(r) \wedge B(2n)) = \mathrm {Ext}_{E(Q_r)}^{s,t}(\mathbb {F}_2,H_{*}(B(2n))) \Longrightarrow k(r)_{t-s}(B(2n)) \end{aligned}$$

(6.1)

will support non-trivial multiplication by $v_r$ in $k(r)_{*}(B(*))$. Classes in $H_{*}(B(2n))$ that are not acted upon freely by $Q_r$ are classes on the $s=0$ line of the Adams spectral sequence that support non-trivial multiplication by $v_r$, and therefore will support nonzero $\circ$-multiplication by $[v_r ]$ in the Hopf ring $H_{*}(\underline{k(r)}_{*})$. Since $H^*(k(r)) = A \otimes _{E(Q_r)} \mathbb {F}_2$, the change of rings theorem (Theorem 3.3) was used to simplify the Adams spectral sequence $E_2$-term in Eq. (6.1). The Adams spectral sequence in Eq. (6.1) will be completely calculated in Sect. 7.

To expedite calculation of the Margolis homology of $H_{*}(B(2n))$, we use that the stable summands of $\Omega ^2 S^3$ are Brown–Gitler spectra. Given a space X, let $\Sigma _{}^\infty X_+$ denote its suspension spectrum with disjoint basepoint.

Lemma 6.1

[4, 9] There is a stable homotopy 2-equivalence

$$\begin{aligned} \Sigma ^{\infty }_{} \Omega _{}^2 S^3_+ \simeq \bigvee _{n \ge 0} \Sigma ^n B(n). \end{aligned}$$

(6.2)

Lemma 6.2

[4] Let $y_1 \in H_1 (\Sigma ^{\infty }_{}\Omega _{}^2 S^3_+)$ be the generator and define $y_i = (Q^1)^{i-1} y_1$, where $(Q^1)^{i-1} = Q^1 \cdots Q^1$ denotes the composition of the first Araki-Kudo (or Dyer-Lashof) operation $i-1$ times. Then

$$\begin{aligned} H_{*}(\Sigma ^{\infty }_{} \Omega _{}^2 S^3_+) = P(y_1^{}, y_2^{}, \ldots ). \end{aligned}$$

(6.3)

where $deg(y_1^{i_1} \cdots y_\ell ^{i_\ell }) = \sum _{j=1}^\ell i_j(2^{j}-1)$ and $wt(y_1^{i_1} \cdots y_\ell ^{i_\ell }) = \sum _{j=1}^\ell i_j 2^{j-1}$, and the right action of the Steenrod algebra is given by

$$\begin{aligned} (y_n)\cdot \mathrm {Sq} = \sum _{i=0}^{n-1} y_{n-i}^{2^i}. \end{aligned}$$

Remark 6.3

The right action of the Steenrod algebra on a monomial $y^I \in P(y_1, y_2, \ldots )$ is weight preserving, and $(y_1) \mathrm {Sq}^1 = 0$. In contrast, the right action of the Steenrod algebra on $\zeta ^I \in H_{*}^{}(\mathrm {H}\mathbb {F})$ is not weight preserving, and $(\zeta _1) \mathrm {Sq}^1 = 1$.

We now calculate the Margolis homology of $H_{*}^{}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)$. Given any right module M over the Steenrod algebra, its Margolis homology $H(M,Q_r)$ is the homology of M with respect to the differential $(-)Q_r$ given by the Milnor primitive, which satisfies $Q_r Q_r = 0$. Note that $Q_r$ is a derivation (i.e., $(xy)Q_r = (x Q_r)y + x(y Q_r)$), and that $H(M_1 \otimes M_2, Q_r) = H(M_1,Q_r) \otimes H(M_2,Q_r)$. For more details on Margolis homology, please see [14].

Lemma 6.4

For $r \ge 0$, the $Q_r$ Margolis homology of $H_{*}^{}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)$ is

$$\begin{aligned} H \left( P(y_1, y_2, y_3, \ldots ), \ Q_r \right) = T_{r+1}^{}(y_1^{}, y_2^{}, \ldots , y_{r+1}^{}) \otimes T_{r}^{}(y_{r+2}^2, y_{r+3}^2, \ldots ), \end{aligned}$$

where $T_m(x,y,\ldots ) = P(x,y,\ldots )/(x^{2^m},y^{2^m},\ldots )$ denotes a truncated polynomial algebra over $\mathbb {F}_2$.

Proof

For $Q_r$ Margolis homology with $r \ge 1$, write $P(y_1, y_2, \ldots )$ as a tensor product of subcomplexes

$$\begin{aligned} \left( \bigotimes _{1 \le i \le r+1} P(y_i^{}) \otimes E(y_{i+r+1}^{}) \right) \otimes \left( \bigotimes _{i \ge r+2} P(y_i^2) \otimes E(y_{i+r+1}^{}) \right) . \end{aligned}$$

For $1 \le i \le r+1$, the $Q_r$ homology of $P(y_i^{}) \otimes E(y_{i+r+1}^{})$ is $T_{2^{r+1}}(y_i)$ because $(y_i^j y_{i+r+1}^{})Q_r^{} = y_i^{j+2^{r+1}}$ and $(y_i^j)Q_r^{} = 0$ for all $j \ge 0$. For $i \ge r+2$, the $Q_r$ homology of $P(y_i^2) \otimes E(y_{i+r+1}^{})$ is $T_{2^r}(y_i^2)$ because $(y_i^{2j} y_{i+r+1}^{})Q_r^{} = y_i^{2j+2^{r+1}}$ and $(y_i^{2j})Q_r^{} = 0$ for all $j \ge 0$. $\square$

The topological splitting (6.2) induces an isomorphism between $H_{*}(B(n))$ and the weight n elements of $H_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)$. To avoid duplication issues arising from $B(2n) \simeq B(2n+1)$, we only describe this isomorphism between $H_{*}(B(2n))$ and the weight 2n elements of $H_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)$.

Lemma 6.5

The topological splitting (6.2) induces a graded isomorphism of right A modules between $\Sigma ^{2n} H_{*}(B(2n))$ and the weight 2n elements in $H_{*}(\Sigma ^{\infty }_{} \Omega _{}^2 S^3_+)$ given by

$$\begin{aligned} f_{2n} : \Sigma ^{2n} \zeta _1^{i_1} \zeta _2^{i_2} \cdots \zeta _\ell ^{i_\ell } \mapsto y_1^{2n-2w} y_2^{i_1} y_3^{i_2} \cdots y_{\ell +1}^{i_\ell } \end{aligned}$$

where $w = wt_\zeta (\zeta ^I)$. Given a weight 2n monomial $y_1^{j_1} y_2^{j_2} \cdots y_m^{j_m}$, the inverse is defined by

$$\begin{aligned} f_{2n}^{-1} : y_1^{j_1} y_2^{j_2} \cdots y_m^{j_m} \mapsto \Sigma ^{2n}_{} \zeta _0^{j_1} \zeta _1^{j_2} \zeta _2^{j_3} \cdots \zeta _{m-1}^{j_m}, \end{aligned}$$

where $\zeta _0 = 1$.

We can now determine the Margolis homology of $H_{*}(B(2n))$ from the Margolis homology of $H_{*}(\Sigma ^{\infty } \Omega _{}^2 S^3_+)$ given in Lemma 6.4.

Lemma 6.6

The $Q_0$ Margolis homology of a Brown–Gitler module is

$$\begin{aligned} H\left( H_{*}(B(2n)), Q_0 \right) = \left\{ \begin{array}{lll} \mathbb {F}_2\lbrace 1 \rbrace &{}&{} \text{ if } \; n=0, \\ 0 &{}&{} \text{ if } \; n \ge 1, \end{array} \right. . \end{aligned}$$

For $r \ge 1$, the $Q_r$ Margolis homology of a Brown–Gitler module is

$$\begin{aligned}&H \left( H_{*}(B(2n)), Q_r \right) \\&\quad = \mathbb {F}_2 \left\{ \zeta ^I \in T_{r+1}^{}(\zeta _1^{}, \zeta _2^{}, \ldots , \zeta _r^{}) \otimes T_{r}^{}(\zeta _{r+1}^2, \zeta _{r+2}^2, \ldots ) \ | \ n - 2^r < wt_\zeta (\zeta ^I) \le n \right\} . \end{aligned}$$

Proof

Suppose $r=0$. Clearly, $H( H_{*}(B(0)), Q_0) = \mathbb {F}_2\lbrace 1 \rbrace$. Since $H_{*}(B(2))$ is a free right $E(Q_0)$ module, a straightforward induction using the Mahowald cofiber sequence (5.2) gives that $H_{*}(B(2n))$, $n \ge 1$, is also a free right $E(Q_0)$ module, and thus $H( H_{*}(B(2n)), Q_0) = 0$ for $n \ge 1$.

Suppose $r \ge 1$ and $y_1^{i_1} y_2^{i_2} \cdots y_\ell ^{i_\ell }$ is a weight 2n monomial in $H( P(y_1,y_2,\ldots ), Q_r)$, so that

$$\begin{aligned} 2n = \sum _{j=1}^\ell i_j 2^{j-1}. \end{aligned}$$

Then the $\zeta$ weight of $f_{2n}^{-1}(y_1^{i_1} y_2^{i_2} \cdots y_\ell ^{i_\ell }) = \Sigma ^{2n} \zeta _0^{i_1} \zeta _1^{i_2} \zeta _2^{i_3} \cdots \zeta _{\ell -1}^{i_\ell } \in \Sigma ^{2n} H_{*}(B(2n))$ is

$$\begin{aligned} w = wt_\zeta (\zeta _0^{i_1} \zeta _1^{i_2} \zeta _2^{i_3} \cdots \zeta _{\ell -1}^{i_\ell }) = \sum _{j=2}^\ell i_j 2^{j-2}, \end{aligned}$$

and thus $i_1 = 2n - 2w$. Since $y_1^{i_1} y_2^{i_2} \cdots y_\ell ^{i_\ell }$ is in $H( P(y_1^{}, y_2^{}, \ldots ), Q_r)$, the exponent on $y_1$ must be less than $2^{r+1}$. Thus, $i_1 = 2n-2w < 2^{r+1}$ and hence $n - 2^r < w$. Since $\zeta _1^{i_2} \zeta _2^{i_3} \cdots \zeta _{\ell -1}^{i_\ell }$ is in $H_{*}(B(2n))$, $w \le n$. $\square$

Next, we calculate the $Q_r$ Margolis homology of $H_{*}(k(r))$ and observe that it is filtered by the $Q_r$ Margolis homology of $H_{*}(B(2n))$.

Lemma 6.7

The $Q_0$ Margolis homology of $H_{*}(k(0))$ is

$$\begin{aligned} H \left( P(\zeta _1^2, \zeta _2^{}, \zeta _3^{}, \ldots ), Q_0^{} \right) = \mathbb {F}_2 \lbrace 1 \rbrace , \end{aligned}$$

while for $r \ge 1$ the $Q_r$ Margolis homology of $H_{*}(k(r))$ is

$$\begin{aligned} H \left( P(\zeta _1^{}, \ldots , \zeta _r^{}, \zeta _{r+1}^2, \zeta _{r+2}^{}, \ldots ), Q_r^{} \right) \!=\! T_{r+1}^{}(\zeta _1^{}, \zeta _2^{}, \ldots , \zeta _r^{}) \otimes T_{r}^{}(\zeta _{r+1}^2, \zeta _{r+2}^2, \ldots ). \end{aligned}$$

Proof

For $Q_0$ Margolis homology, write $P(\zeta _1^2, \zeta _2^{}, \ldots )$ as a tensor product of subcomplexes

$$\begin{aligned} \bigotimes _{i \ge 1} P(\zeta _i^2) \otimes E(\zeta _{i+1}^{}). \end{aligned}$$

Then the $Q_0$ homology is $\mathbb {F}_2$ because for each $i \ge 1$, $(\zeta _i^{2j} \zeta _{i+1}^{}) Q_0^{} = \zeta _i^{2j+2}$ and $(\zeta _i^{2j})Q_r^{} = 0$ for all $j \ge 0$.

For $Q_r$ Margolis homology, write $P(\zeta _1^{}, \zeta _2^{}, \ldots , \zeta _r^{}, \zeta _{r+1}^2, \zeta _{r+2}^{}, \ldots )$ as a tensor product of subcomplexes

$$\begin{aligned} \left( \bigotimes _{1 \le i \le r} P(\zeta _i^{}) \otimes E(\zeta _{i+r+1}^{}) \right) \otimes \left( \bigotimes _{i \ge r+1} P(\zeta _i^2) \otimes E(\zeta _{i+r+1}). \right) \end{aligned}$$

For $1 \le i \le r$, the $Q_r$ homology is $T_{r+1}^{}(\zeta _i)$ because $(\zeta _i^j \zeta _{i+r+1}^{})Q_r^{} = \zeta _i^{j+2^{r+1}}$ and $(\zeta _i^j)Q_r^{} = 0$ for all $j \ge 0$. For $i \ge r+1$, the $Q_r$ homology is $T_{r}^{}(\zeta _i^2)$ because $(\zeta _i^{2j} \zeta _{i+r+1})Q_r^{} = \zeta _i^{2j+2^{r+1}}$ and $(\zeta _i^{2j})Q_r^{} = 0$ for all $j \ge 0$. $\square$

7 The Dieudonné ring $k(r)_{*}(B(*))$

In this section, we calculate the Adams spectral sequence

$$\begin{aligned} E_1^{*,*}(A, k(r) \wedge B(2n)) = H_{*}(k(r)) \otimes H_{*}(B(2n)) \otimes \Lambda \Longrightarrow k(r)_{*}(B(2n)) \end{aligned}$$

(7.1)

for all $r \ge 0$ and $n \ge 0$.

We begin by defining the destabilization function $\epsilon ^{-\infty }$ for Dieudonné rings that is equivalent to the destabilization function $e^{-\infty }$ for Hopf rings. Suppose E is a ring spectrum such that $H_{*}(E) \subseteq H_{*}(\mathrm {H}\mathbb {F})$. Under the Dieudonné equivalence, every stable class in $H_{d+k}(\underline{E}_{\, k})$ corresponds to a nonzero element in $D_{d+k}(H_{*}(\underline{E}_{\, k}))$ that comes from a permanent cycle in the $s=0$ line of the Adams spectral sequence

$$\begin{aligned} H^{0,d}(H_{*}(E) \otimes H_{*}(B(d+k)) \otimes \Lambda , d_1). \end{aligned}$$

We now define the function that induces the Dieudonné ring destabilization function $H_{*}(E) \rightarrow D_{*}(H_{*}(\underline{E}_{*}))$.

Definition 7.1

Let $E = \mathrm {H}\mathbb {F}$. Define a function

$$\begin{aligned} \epsilon ^{-\infty }: H_{*}(E) \rightarrow H_{*}(E) \otimes H_{*}(B(\infty )) \otimes \Lambda \end{aligned}$$

(7.2)

by $\epsilon ^{-\infty }(y) = \tau ( \chi \otimes 1 ( \psi (y))) \otimes 1$, where $\psi$ is the coproduct, $\chi$ is the antiautomorphism, and $\tau (x \otimes y) = y \otimes x$ is the graded twist map, which has no sign mod 2.

Lemma 7.2

([17, Lemma 7.2]) The destabilization function $\epsilon ^{-\infty }$ in Eq. (7.2) is a ring homomorphism.

Example 7.3

On basis elements, the destabilization $\epsilon ^{-\infty }$ is

$$\begin{aligned} \epsilon ^{-\infty }(\xi _n)&= \sum _{i=0}^n \xi _i^{} \otimes \zeta _{n-i}^{2^i} \otimes 1 \in H_{*}(\mathrm {H}\mathbb {F}) \otimes H_{*}(B(2^n)) \otimes \Lambda , \end{aligned}$$

(7.3)

$$\begin{aligned} \epsilon ^{-\infty }(\zeta _n)&= \sum _{i=0}^n \zeta _{n-i}^{2^i} \otimes \xi _i^{} \otimes 1 \in H_{*}(\mathrm {H}\mathbb {F}) \otimes H_{*}(B(2^{n+1}-2)) \otimes \Lambda , \end{aligned}$$

(7.4)

where $\epsilon ^{-\infty }(\xi _n)$ and $\epsilon ^{-\infty }(\zeta _n)$ both have bidegree $(s,t) = (0,2^{n}-1)$.

Lemma 7.4

For the spectrum $E = \mathrm {H}\mathbb {F}$, every element in the image of the destabilization $\epsilon ^{-\infty }$ is a permanent cycle.

Proof

We begin by showing that $\epsilon ^{-\infty }(\xi _n)$ is a cycle for all $n \ge 0$. By the Cartan formula $(x \otimes y) \cdot \mathrm {Sq} = (x \cdot \mathrm {Sq}) \otimes (y \cdot \mathrm {Sq})$, we have

$$\begin{aligned} \left( \sum _{0 \le i \le n} \xi _i^{} \otimes \zeta _{n-i}^{2^i} \right) \cdot \mathrm {Sq}= & {} \sum _{0 \le i \le n} \left( \sum _{i \le j \le n} \left( \xi _j^{} \otimes \zeta _{n-j}^{2^j} + \xi _{j-1}^{} \otimes \zeta _{n-j}^{2^j} \right) \right) \\= & {} \sum _{0 \le i \le n} \xi _i^{} \otimes \zeta _{n-i}^{2^i}, \end{aligned}$$

because all terms cancel except when $i=j$, and thus $\mathrm {Sq}^0$ is nonzero but $\mathrm {Sq}^k$ is zero for $k \ge 1$. Since $\lambda _{-1} \cdot 1 = 0$ and $\left( \sum _{i = 0}^n \xi _i^{} \otimes \zeta _{n-i}^{2^i} \right) \cdot \mathrm {Sq}^k = 0$ for $k \ge 1$, it follows that

$$\begin{aligned} d_1(\epsilon ^{-\infty }(\xi _n)) = \sum _{k \ge 0} \left( \left( \sum _{0 \le i \le n} \xi _i^{} \otimes \zeta _{n-i}^{2^i} \right) \cdot \mathrm {Sq}^k \right) \otimes \lambda _{k-1} \cdot 1 = 0. \end{aligned}$$

Next, we show that $\epsilon ^{-\infty }(\sum \xi ^I)$ is a cycle for any $\sum \xi ^I \in H_{*}(\mathrm {H}\mathbb {F})$. Since the coproduct $\psi$ and total Steenrod square $\mathrm {Sq}$ are ring homomorphisms, and $d_1$ is an $\mathbb {F}_2$-module homomorphism, it follows that $d_1( \epsilon ^{-\infty }(\sum \xi ^I) ) = 0$ for all $\sum \xi ^I \in H_{*}(\mathrm {H}\mathbb {F})$.

Finally, we show that $\epsilon ^{-\infty }(\sum \xi ^I)$ must be a permanent cycle. By change of rings (Theorem 3.3),

$$\begin{aligned} \mathrm {Ext}_A^{*,*}(\mathbb {F}_2, H_{*}(\mathrm {H}\mathbb {F}) \otimes H_{*}(B(\infty ))) \cong \mathrm {Ext}_{\mathbb {F}_2}^{*,*}(\mathbb {F}_2, H_{*}(B(\infty ))). \end{aligned}$$

Thus, the spectral sequence is concentrated on the $s=0$ line and collapses. $\square$

Lemma 7.5

Given $\sum \xi ^I \in H_d(\mathrm {H}\mathbb {F})$, the degree $d = deg(\sum \xi ^I)$, the maximum number of factors $k = fact_\xi (\sum \xi ^I)$, and the maximum weight $n = wt_\xi (\sum \xi ^I)$ satisfy $d+k=2n$.

Proof

For every term $\xi ^I$ in the sum $\sum \xi ^I$, we have $d = deg(\xi ^I) = deg(\xi _{1}^{i_1} \xi _{2}^{i_2} \cdots \xi _{\ell }^{i_\ell }) = \sum _{j=1}^{\ell } i_j (2^j-1) = 2(\sum _{j=1}^{\ell } i_j 2^{j - 1}) - \sum _{j=1}^{\ell } i_j = 2 wt_\xi (\xi ^I) - fact_\xi (\xi ^I)$. For any term $\xi ^{I'}$ in the sum $\sum \xi ^I$ which has the maximum number of factors, $d + k = 2 wt_\xi (\xi ^{I'})$. Suppose for the sake of contradiction that $wt_\xi (\xi ^{I'})$ is not the maximum weight of all terms in $\sum \xi ^I$. Then, there exists $\xi ^{I''}$ so that $wt_\xi (\xi ^{I''}) > wt_\xi (\xi ^{I'})$ and $k \ge fact_\xi (\xi ^{I''})$. This implies that $d + fact_\xi (\xi ^{I''}) = 2 wt_\xi (\xi ^{I''}) > 2 wt_\xi (\xi ^{I'}) = d + k$, and thus $fact_\xi (\xi ^{I''}) > k$, a contradiction. Therefore, any term with a maximal number of factors also has maximal weight, and $d + k = 2n$. $\square$

In the next definition and lemma, we show that $\epsilon ^{-\infty }$ preserves degree d, the maximum number of $\xi$ factors k, and the maximum weight n. Note that the antiautomorphism $\chi$ and the twist map $\tau$ in the definition of $\epsilon ^{-\infty }$ have the effect of mapping the $\xi$ weight in $H_{*}(E)$ to the $\zeta$ weight in the second tensor factor of $H_{*}(E) \otimes H_{*}(B(\infty )) \otimes \Lambda$.

Definition 7.6

For each $\sum x_i \otimes y_i \otimes 1 \in H_{*}(E) \otimes H_{*}(B(\infty )) \otimes \Lambda$, let

$$\begin{aligned} \textstyle fact_\xi ^1(\sum x_i \otimes y_i \otimes 1)= & {} max_i \lbrace fact_\xi (x_i) \rbrace , \\ \textstyle wt_{\xi }^2(\sum x_i \otimes y_i \otimes 1)= & {} max_i \lbrace wt_\xi (y_i) \rbrace , \\ \textstyle wt_{\zeta }^2(\sum x_i \otimes y_i \otimes 1)= & {} max_i \lbrace wt_\zeta (y_i) \rbrace . \end{aligned}$$

Lemma 7.7

If $\sum \xi ^I = \sum \zeta ^J \in H_{*}(\mathrm {H}\mathbb {F})$ has $d = deg(\sum \xi ^I)$, $k = fact_\xi (\sum \xi ^I)$ and $n = wt_\xi ( \sum \xi ^I)$, then $fact_\xi ^1( \epsilon ^{-\infty }(\sum \xi ^I) ) = k$ and $\epsilon ^{-\infty }(\sum \xi ^I) \in H^{0,d}( H_{*}(\mathrm {H}\mathbb {F}) \otimes H_{*}(B(2n)) \otimes \Lambda , d_1)$.

Proof

It is clear that $\epsilon ^{-\infty }$ preserves degree and that the lemma is true for $\epsilon ^{-\infty }(1) = 1 \otimes 1 \otimes 1$. Suppose $\sum \xi ^I \ne 1$. First, we show that $\epsilon ^{-\infty }$ preserves k. From Eq. (7.3), it is clear that $fact_\xi ^1( \epsilon ^{-\infty }( \xi _r ) ) = 1$. Since $\epsilon ^{-\infty }$ is a ring homomorphism and $\epsilon ^{-\infty }(\sum \xi ^I) = (\sum \xi ^I) \otimes 1 \otimes 1 + (other)$, it follows that $fact_\xi ^1( \epsilon ^{-\infty }(\sum \xi ^I) ) = k$.

Second, we show that $\epsilon ^{-\infty }$ preserves n. From Eq. (7.4), it is apparent that

$$\begin{aligned} wt_\zeta ^2( \epsilon ^{-\infty }(\xi _n) ) = wt_\zeta ^2( 1 \otimes \zeta _n \otimes 1). \end{aligned}$$

Since $\epsilon ^{-\infty }$ is a ring homomorphism, it follows that

$$\begin{aligned} \textstyle wt_\zeta ^2( \epsilon ^{-\infty }(\sum \xi ^I) )= & {} \textstyle wt_\zeta ^2( 1 \otimes (\sum \zeta ^I) \otimes 1) \\= & {} \textstyle wt_\xi ^2( 1 \otimes (\sum \xi ^I) \otimes 1) \\= & {} n. \end{aligned}$$

Therefore, $\epsilon ^{-\infty }( \sum \xi ^I ) \in H^{0,d}( H_{*}(\mathrm {H}\mathbb {F}) \otimes H_{*}(B(2n)) \otimes \Lambda , d_1)$. $\square$

The following lemma shows that the Diedonné ring destabilization $\epsilon ^{-\infty }$ is, in fact, equivalent to the Hopf ring destabilization $e^{-\infty }$.

Lemma 7.8

Suppose $\sum \xi ^I = \sum \zeta ^J \in H_d(\mathrm {H}\mathbb {F})$ with $d = deg\left( \sum \xi ^I \right)$, $k = fact_\xi \left( \sum \xi ^I \right)$, and $n = wt_\xi \left( \sum \xi ^I \right)$. Then under the Dieudonné equivalence of equation (5.3), the destabilized element

$$\begin{aligned} \textstyle e^{-\infty }\left( \sum \xi ^I\right) = e^{-\infty }\left( \sum \zeta ^J\right) \in H_{d+k}(\underline{\mathrm {H}\mathbb {F}}_{\, k}) \end{aligned}$$

corresponds to

$$\begin{aligned} \textstyle \epsilon ^{-\infty }\left( \sum \xi ^I\right) = \epsilon ^{-\infty }\left( \sum \zeta ^J\right) \in E_2^{0,d}(A, \mathrm {H}\mathbb {F} \wedge B(2n)) \cong D_{2n}(H_{*}(\underline{\mathrm {H}\mathbb {F}}_{\, k})). \end{aligned}$$

Proof

From Lemma 7.5, $d+k=2n$ and thus $H_{d+k}(\underline{\mathrm {H}\mathbb {F}}_{\, k}) = H_{2n}(\underline{\mathrm {H}\mathbb {F}}_{\, k})$ is equivalent to $D_{2n}(H_{*}(\underline{\mathrm {H}\mathbb {F}}_{\, k}))$. From Eq. (5.3), it is clear that for any generator $\xi _n \in H_{2^n-1}(\mathrm {H}\mathbb {F})$,

$$\begin{aligned} U(T(\epsilon ^{-\infty }(\xi _n))) = x_n \end{aligned}$$

in the rank 1 module $H_{2^n}(\underline{\mathrm {H}\mathbb {F}}_1)$. The one-to-one correspondence follows for any $\sum \xi ^I \in H_{*}(\mathrm {H}\mathbb {F})$ since $\epsilon ^{-\infty }$ is a ring homomorphism and the right adjoint U to the Dieudonné functor preserves $+$ and $\circ$. $\square$

Example 7.9

The destabilization of the element $\zeta _1^6 + \zeta _2^2 = \xi _2^2 \in H_6(k(1)) = P(\zeta _1^{}, \zeta _2^2, \zeta _3^{}, \ldots )$, which has degree $d = 6$, maximum number of $\xi$ factors $k = fact_\xi (\xi _2^2) = 2$, and maximum $\xi$ weight $n = wt_\xi (\xi _2^2) = 4$, is

$$\begin{aligned} \epsilon ^{-\infty }(\zeta _1^6 + \zeta _2^2) = \epsilon ^{-\infty }(\xi _2^2)= & {} \xi _2^2 \otimes 1 \otimes 1 + \xi _1^2 \otimes \zeta _1^4 \otimes 1 + 1 \otimes \zeta _2^2 \otimes 1 \\\in & {} H^{0,6}( H_{*}(k(1)) \otimes H_{*}(B(8)) \otimes \Lambda , d_1), \end{aligned}$$

which corresponds to the class

$$\begin{aligned} z_0^{\circ -4} \circ (z_1^{\circ 6} + z_2^{\circ 2}) = x_2^{\circ 2} \in H_8(\underline{k(1)}_2). \end{aligned}$$

Lemma 7.10

There is a bijection of $\mathbb {F}_2$-modules

$$\begin{aligned}&\textstyle \epsilon ^{-\infty } : \left\{ \sum \zeta ^I \in H_{*}(k(r)) \mid wt_\xi (\sum \zeta ^I) \le n \right\} \nonumber \\&\quad \rightarrow H^{0,*}(H_{*}(k(r)) \otimes H_{*}(B(2n)) \otimes \Lambda , d_1). \end{aligned}$$

(7.5)

Proof

First, we show the map $\epsilon ^{-\infty }$ in (7.5) is well-defined. Take $E = k(r)$ in Eq. (7.2).

From Eq. (7.4), it is clear that the elements in the first tensor factor of $\epsilon ^{-\infty }(\zeta _n)$ are in $H_{*}(k(r))$ when $n \ne r+1$, and the same is true for $\epsilon ^{-\infty }(\zeta _{r+1}^2)$. Since $\epsilon ^{-\infty }$ is a ring homomorphism, it follows that if $\sum \zeta ^I \in H_{*}(k(r))$, then the first tensor factor of $\epsilon ^{-\infty }(\sum \zeta ^I)$ is also in $H_{*}(k(r))$.

Now suppose $\sum \zeta ^I \in H_{*}(k(r))$ satisfies $wt_\xi (\sum \zeta ^I) \le n$. From Eq. (7.4), $\epsilon ^{-\infty }(\zeta _n) = 1 \otimes \xi _n \otimes 1 + (other)$ where all of the other terms have second tensor factor of smaller $\zeta$ weight than $wt_\zeta (\xi _n) = 2^n - 1$. Since $\epsilon ^{-\infty }$ is a ring homomorphism, it follows that $\epsilon ^{-\infty }(\sum \zeta ^I) = 1 \otimes (\sum \xi ^I) \otimes 1 + (other)$, where all of the other terms have second tensor factor of smaller $\zeta$-weight than $wt_\zeta (\sum \xi ^I)$, and none of the other terms cancel with $1 \otimes (\sum \xi ^I) \otimes 1$. Since $wt_\zeta (\sum \xi ^I) = wt_\xi (\sum \zeta ^I)$, it follows that $\epsilon ^{-\infty }(\sum \zeta ^I)$ is in $H^{0,*}( H_{*}(k(r)) \otimes H_{*}(B(2n)) \otimes \Lambda , d_1)$.

Second, we show that $\epsilon ^{-\infty }$ in (7.5) is injective. Since $\epsilon ^{-\infty }(\sum \zeta ^I) = (\sum \zeta ^I) \otimes 1 \otimes 1 + (other)$, where none of the other terms cancels with $(\sum \zeta ^I) \otimes 1 \otimes 1$, $\epsilon ^{-\infty }$ is injective.

Third and finally, we show $\epsilon ^{-\infty }$ in (7.5) is surjective. Suppose $z \in H^{0,*}( H_{*}(k(r)) \otimes H_{*}(B(2n)) \otimes \Lambda ,d_1)$. Since $H_{*}(k(r)) \subset H_{*}(\mathrm {H}\mathbb {F})$, it is clear that diagram (7.6) commutes.

(7.6)

From diagram (7.6), z can be included as an element $H^{0,*}( H_{*}(\mathrm {H}\mathbb {F}) \otimes H_{*}(B(2n)) \otimes \Lambda , d_1)$, which determines an element $\sum \zeta ^I \in H_{*}(\mathrm {H}\mathbb {F})$. Thus, $z=\epsilon ^{-\infty }(\sum \zeta ^I) = (\sum \zeta ^I) \otimes 1 \otimes 1 + (other)$ where none of the other terms cancel with $(\sum \zeta ^I) \otimes 1 \otimes 1$, and thus $\sum \zeta ^I \in H_{*}(k(r))$ by the definition of $\epsilon ^{-\infty }$. Since $z \in H^{0,*}( H_{*}(k(r)) \otimes H_{*}(B(2n)) \otimes \Lambda , d_1)$ and $z = \epsilon ^{-\infty }(\sum \zeta ^I) = 1 \otimes (\sum \xi ^I) \otimes 1 + (other)$ where none of the other terms cancel with $1 \otimes (\sum \xi ^I) \otimes 1$, we must have $wt_\zeta (\sum \xi ^I) \le n$. But, $wt_\zeta (\sum \xi ^I) = wt_\xi (\sum \zeta ^I)$, and therefore $\epsilon ^{-\infty }$ in Eq. (7.5) is also surjective. $\square$

Next, we determine which classes on the zero line of the $E_2$ page of the Adams spectral sequence for $k(r)_{*}(B(2n))$ might support non-trivial multiplication by $v_r$ at $E_\infty$. These will be classes in $H_{*}(B(2n))$ that are not acted upon freely by $Q_r$, and will be represented by classes in the $Q_r$ Margolis homology of $H_{*}(B(2n))$, which is given in Lemma 6.6.

Lemma 7.11

Let $\mathrm {Ext}_{E(Q_r)}^{*,*}(\mathbb {F}_2,\mathbb {F}_2) = \mathbb {F}_2[a_r]$, where $a_r$ detects $v_r \in k(r)_{*} = \mathbb {F}_2[v_r]$. There is a one-to-one correspondence of $\mathbb {F}_2$-modules between the classes in $\mathrm {Ext}_{E(Q_r)}^{0,*}(\mathbb {F}_2, H_{*}(B(2n)))$ that support non-trivial multiplication by $\mathbb {F}_2[a_r]$ and classes in the Margolis homology $H(H_{*}(B(2n)),Q_r)$.

Next, we show that the Adams spectral sequence for $k(r)_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)$ collapses ($E_2 \cong E_\infty$), which will require the non-connective Morava K-theory for $\Sigma _{}^\infty \Omega _{}^2 S^3_+$.

Lemma 7.12

[19, Theorem 3.7], [25] Let K(r) denote the rth non-connective Morava K-theory at $p=2$ with $K(r)_{*} = \mathbb {F}_2[v_r^{},v_r^{-1}]$. Then,

$$\begin{aligned} K(r)_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+) = \mathbb {F}_2^{}[v_r^{},v_r^{-1}] \otimes T_{r+1}^{}(y_1^{}, y_2^{}, \ldots , y_{r+1}^{}) \otimes T_{r}^{}(y_{r+2}^{2}, y_{r+3}^{2}, \ldots ). \end{aligned}$$

(7.7)

Lemma 7.13

The Adams spectral sequence

$$\begin{aligned} E_2 = \mathrm {Ext}_{E(Q_r)}^{*,*}(\mathbb {F}_2, H_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)) \Longrightarrow k(r)_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+) \end{aligned}$$

collapses, i.e., $E_2 \cong E_\infty$.

Proof

Let $\mathrm {Ext}_{E(Q_r)}^{*,*}(\mathbb {F}_2,\mathbb {F}_2) = \mathbb {F}_2[a_r]$, where $a_r$ detects $v_r \in k(r)_{*} = \mathbb {F}_2[v_r]$. From Lemma 6.4, the $a_r$-torsion free quotient of $E_2^{*,*} = \mathrm {Ext}_{E(Q_r)}^{*,*}(\mathbb {F}_2,H_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+))$ is

$$\begin{aligned} \mathbb {F}_2^{}[a_r^{}] \otimes T_{r+1}^{}(y_1^{}, y_2^{}, \ldots , y_{r+1}^{}) \otimes T_{r}^{}(y_{r+2}^2, y_{r+3}^2, \ldots ). \end{aligned}$$

Since the $a_r$-torsion in $E_2^{*,*}$ arises from free $E(Q_r)$ summands of $H_{*}(\Sigma _{}^\infty \Omega _{}^2 S^3_+)$, this $a_r$-torsion is concentrated in $E_2^{0,*}$. Thus, the only possibility for nonzero differentials occurs in the $a_r$-torsion free quotient; however, a nonzero differential in the $a_r$-torsion free quotient would contradict the results of Lemma 7.12. $\square$

To be useful for the computation of $H_{*}(\underline{k(r)}_{*})$, we must express the result of Lemma 7.13 in terms of Brown–Gitler spectra using the topological splitting in Eq. (6.2). As a consequence of Lemmas 7.10, 7.11 and 7.13, we have now completely calculated the Adams spectral sequence for $k(r)_{*}(B(2n))$.

Theorem 7.14

The Adams spectral sequence

$$\begin{aligned} \mathrm {Ext}_{E(Q_r)}^{s,t}(\mathbb {F}_2, H_{*}(B(2n))) \Longrightarrow k(r)_{t-s}(B(2n)) \end{aligned}$$

has $s=0$ line consisting of elements $\sum \zeta ^I \in H_{*}(k(r))$ such that $wt_\xi (\sum \zeta ^I) \le n$. There is a bijection of $\mathbb {F}_2$-modules between the elements on the $s=0$ line that support non-trivial multiplication by all positive powers of $a_r$, which represents $v_r$ in homotopy, and classes in the Margolis homology module $H(H_{*}(B(2n)),Q_r)$. Further, this spectral sequence collapses.

8 The Hopf ring $H_{*}(\underline{k(r)}_{*})$

We now take the results of Sect. 7 on the Dieudonné ring $k(r)_{*}(B(*))$ and translate them into results for the Hopf ring $H_{*}(\underline{k(r)}_{*})$.

Theorem 8.1

The destabilization $e^{-\infty }: H_{*}(k(r)) \rightarrow H_{*}(\underline{k(r)}_{*})$ is a restriction of the destabilization $e^{-\infty } : H_{*}(\mathrm {H}\mathbb {F}) \rightarrow H_{*}(\underline{\mathrm {H}\mathbb {F}}_{*})$, i.e., diagram (8.1) is commutative.

(8.1)

Proof

Lemma 7.10 implies that diagram (8.2) commutes for all $n \ge 0$.

(8.2)

The spectral sequences in diagram (8.2) collapse by Lemma 7.13. It follows that diagram (8.1) commutes by translating diagram (8.2) from Dieudonné rings to Hopf rings using Eq. (5.3). $\square$

Theorem 8.2

For $n \ge 0$, there is a one-to-one correspondence of $\mathbb {F}_2$-modules between the stable classes in $H_{2n}(\underline{k(r)}_{*})$ that support non-trivial $\circ$-multiplication by powers of $v_r$ and nonzero classes in the Margolis homology module $H \left( H_{*}(B(2n)), Q_r \right)$.

Proof

Since the Dieudonné functor preserves addition and scalar multiplication and the Adams spectral sequence for $k(r)_{*}(B(2n))$ collapses, the Dieudonné correspondence in Eq. (5.3) defines an $\mathbb {F}_2$-module isomorphism between classes in $\mathrm {Ext}_{E(Q_r)}^{0,*}(\mathbb {F}_2, H_{*}(B(2n)))$ that support non-trivial multiplication by $P(a_r) = \mathrm {Ext}_{E(Q_r)}^{*,*}(\mathbb {F}_2,\mathbb {F}_2)$ and stable classes in $H_{2n}(\underline{k(r)}_{*})$ that support non-trivial $\circ$-multiplication by powers of $v_r$. By Lemma 7.11, there is an $\mathbb {F}_2$-module isomorphism between classes in $\mathrm {Ext}_{E(Q_r)}^{0,*}(\mathbb {F}_2, H_{*}(B(2n)))$ that support non-trivial multiplication by $P(a_r) = \mathrm {Ext}_{E(Q_r)}^{*,*}(\mathbb {F}_2,\mathbb {F}_2)$ and classes in the Margolis homology $H(H_{*}(B(2n)), Q_r)$ . $\square$

The elements in the Hopf ring $H_{*}(\underline{k(r)}_{*})$ that support non-trivial $\circ$-multiplication by $v_r$ are the destabilized elements of the Margolis homology $H( H_{*}(k(r)), Q_r)$. The next example shows that the filtration

$$\begin{aligned} H( H_{*}(B(2n)), Q_r) \subset H( H_{*}(k(r)), Q_r) \end{aligned}$$

has an important role in determining which representative of a Margolis homology class should be chosen as input to the destabilization function.

Example 8.3

Consider the homology class $\zeta _2^2$ in

$$\begin{aligned} H\left( H_{*}(B(8)), Q_1\right) = \mathbb {F}_2 \lbrace \zeta _1^3, \zeta _2^2 \rbrace \subset H\left( H_{*}(k(1)), Q_1\right) . \end{aligned}$$

The destabilization of the degree 6 class represented by $\zeta _2^2 \in H(H_{*}(B(8)),Q_1)$ will be in $H_8(\underline{k(1)}_{\, 8-6})= H_8(\underline{k(1)}_{\, 2})$. Note that $e^{-\infty }(\zeta _2^2) = x_0^{\circ 4} \circ x_2^{\circ 2} + x_1^{\circ 6} \in H_{12}(\underline{k(1)}_{\, 6})$, which cannot be desuspended further, so $\zeta _2^2$ is not the right choice of representative for this Margolis homology class. However, $\zeta _2^2$ is homologous to $\zeta _2^2 + \zeta _1^6 = \xi _2^2$ in $H(H_{*}(B(8)),Q_1)$ because $\zeta _1^4 = (\zeta _3^{})Q_1$, and $e^{-\infty }(\xi _2^2) = x_2^{\circ 2}$ in $H_8(\underline{k(1)}_{\, 2})$ has the correct bidegree. Thus, $[v_1 ]^{\circ j} \circ x_2^{\circ 2}$ is non-trivial in $H_8(\underline{k(1)}_{\, 2-2j})$ for all $j \ge 0$.

Finally, we identify the generators of the Hopf ring $H_{*}(\underline{k(r)}_{*})$.

Theorem 8.4

The Hopf ring $H_{*}(\underline{k(r)}_{*})$ is generated by

• 1. stable generators $e^{-\infty }(H_{*}(k(r)))$, and

• 2. the homotopy generator $[v_r ]\in H_0(\underline{k(r)}_{\, 2-2^{r+1}})$.

Proof

This result follows from Theorem 7.14 by translating from Hopf rings to Dieudonné rings using Eq. (5.3). $\square$