Skip to main content
SpringerLink
Log in

A Novel Low-Conservative Constrained H∞ Model Predictive Control for Linear Switched Systems

  • ORIGINAL CONTRIBUTION
  • Published:
Journal of The Institution of Engineers (India): Series B Aims and scope Submit manuscript

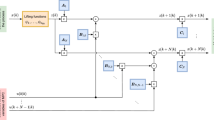
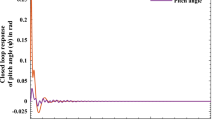
Abstract

The problem of unacceptable conservatism and the lack of disturbance consideration are important research gaps for model predictive control (MPC) schemes in linear switched systems (LSSs). To solve these challenges, this study develops, for the first time, an organized strategy of MPC and persistent dwell time (PDT) structure for LSSs through multiple Lyapunov functions (MLFs) to dramatically reduce conservatism. Additionally, exogenous perturbations are considered in the system dynamics, and the H∞ performance is ensured to reduce the effects of the perturbations. Assuming the input constraints as well as the aforementioned assumptions, the proposed scheme is designed through MLFs, and asymptotic stability is proved. Finally, the effectiveness of the suggested strategy for the target systems is investigated through the numerical simulation of two examples. The simulation results suggest the stated strategy for real systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

\(a_{s}\) :

Variation rate of Lyapunov function

\(b\) :

Limiting factor of Lyapunov function at switching moments

\(\varepsilon_{k}\) :

Maximum limit of cost function

\(n\) :

Persistent dwell time

\(m\) :

Persistent duration

\(C\) :

Total number of switching in \(m\)-sub-interval

r :

Switching rate in \(m\)-sub-interval

\(\gamma_{h}\) :

Disturbance rejection level

\(q_{\max }\) :

Maximum limit of disturbance energy

\(u_{eu,\max }\) :

Maximum limit of eu-th component of input

\(s_{es,\max }\) :

Maximum limit of the eu-th component within the state

\(\Pi_{\sigma (k)}\) :

Control gain

\(h\) :

Predictive horizon

\(J_{\sigma (k)}\) :

Cost function

\(f_{\sigma (k)}\) :

Lyapunov function

\(\Theta_{\sigma (k)}\) :

Matrix describing Lyapunov function

\(\Sigma_{\sigma (k)}\), \(\Delta_{\sigma (k)}\), \({\rm T}_{\sigma (k)}\), and \(\Omega_{\sigma (k)}\) :

Variables in optimization problem

\(\sigma (k)\) :

Switching signal

\(G_{\sigma \left( k \right)} ,H_{\sigma \left( k \right)} ,V_{\sigma \left( k \right)}\), \(W_{\sigma \left( k \right)}\) and \(N_{\sigma \left( k \right)}\) :

State space matrices

\(s(k)\) :

State

\(u(k)\) :

Input

\(q(k)\) :

Disturbance

\(d(k)\) :

Controlled output

References

  1. Z. Sun, S.S. Ge, Analysis and synthesis of switched linear control systems. Automatica 41(2), 181–195 (2005)

    Article  MathSciNet  Google Scholar 

  2. H. Yang, B. Jiang, V. Cocquempot, A survey of results and perspectives on stabilization of switched nonlinear systems with unstable modes. Nonlinear Anal. Hybrid. Syst. 13, 45–60 (2014)

    Article  MathSciNet  Google Scholar 

  3. S. Saki, H. Bolandi, Optimal direct adaptive soft switching multi-model predictive control using the gap metric for spacecraft attitude control in a wide range of operating points. Aerosp. Sci. Technol. 77, 235–243 (2018)

    Article  Google Scholar 

  4. I. Nodozi, M. Rahmani, LMI-based model predictive control for switched nonlinear systems. J. Process. Control 59, 49–58 (2017)

    Article  Google Scholar 

  5. H. Lin, P.J. Antsaklis, Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans. Automat. Control 54(2), 308–322 (2009)

    Article  MathSciNet  Google Scholar 

  6. Z. Sun, S. S. Ge, Stability Theory of Switched Dynamical Systems (2011)

  7. H. Zhang, D. Xie, H. Zhang, G. Wang, Stability analysis for discrete-time switched systems with unstable subsystems by a mode-dependent average dwell time approach. ISA Trans. 53(4), 1081–1086 (2014)

    Article  Google Scholar 

  8. T. Liu, C. Wang, Quasi-time-dependent asynchronous H∞ control of discrete-time switched systems with mode-dependent persistent dwell-time. Eur. J. Control. 48, 66–73 (2019)

    Article  MathSciNet  Google Scholar 

  9. S. Shi, Z. Shi, Z. Fei, Asynchronous control for switched systems by using persistent dwell time modeling. Syst. Control Lett. 133, 104523 (2019)

    Article  MathSciNet  Google Scholar 

  10. Y. Fan, M. Wang, G. Sun, W. Yi, G. Liu, Quasi-time-dependent robust H∞ static output feedback control for uncertain discrete-time switched systems with mode-dependent persistent dwell-time. J. Frankl. Inst. 357(15), 10329–10352 (2020)

    Article  MathSciNet  Google Scholar 

  11. Y. Qi, P. Zeng, W. Bao, Event-triggered and self-triggered $ H_\infty$ control of uncertain switched linear systems. IEEE Trans. Syst. Man Cybern. Syst. 50(4), 1442–1454 (2018)

    Article  Google Scholar 

  12. H. Zheng, G. Sun, Y. Ren, C. Tian, Quasi-time-dependent controller for discrete-time switched linear systems with mode-dependent average dwell-time. Asian J. Control 20(1), 263–275 (2018)

    Article  MathSciNet  Google Scholar 

  13. J. Huang, X. Hao, X. Pan, Asynchronous switching control of discrete-time linear system based on mode-dependent average dwell time. Int. J. Control. Autom. Syst. 18, 1705–1714 (2020)

    Article  Google Scholar 

  14. A.A. Ladel, A. Benzaouia, R. Outbib, M. Ouladsine, Robust fault tolerant control of continuous-time switched systems: an LMI approach. Nonlinear Anal. Hybrid Syst. 39, 100950 (2021)

    Article  MathSciNet  Google Scholar 

  15. Y. Hou, S. Tong, Adaptive fuzzy output-feedback control for a class of nonlinear switched systems with unmodeled dynamics. Neurocomputing 168, 200–209 (2015)

    Article  Google Scholar 

  16. Z. Lyu, Z. Liu, K. Xie, C.L.P. Chen, Y. Zhang, Adaptive fuzzy output-feedback control for switched nonlinear systems with stable and unstable unmodeled dynamics. IEEE Trans. Fuzzy Syst. 28(8), 1825–1839 (2019)

    Article  Google Scholar 

  17. W. Wu, S. Tong, Y. Li, Fuzzy adaptive tracking control for switched nonlinear systems with full time-varying state constraints. Neurocomputing 352, 1–11 (2019)

    Article  Google Scholar 

  18. D. Zhai, A.-Y. Lu, J. Dong, Q. Zhang, Adaptive tracking control for a class of switched nonlinear systems under asynchronous switching. IEEE Trans. Fuzzy Syst. 26(3), 1245–1256 (2017)

    Article  Google Scholar 

  19. M.A. Müller, P. Martius, F. Allgöwer, Model predictive control of switched nonlinear systems under average dwell-time. J. Process Control 22(9), 1702–1710 (2012)

    Article  Google Scholar 

  20. M. Benallouch, G. Schutz, D. Fiorelli, M. Boutayeb, H∞ model predictive control for discrete-time switched linear systems with application to drinking water supply network. J. Process Control 24(6), 924–938 (2014)

    Article  Google Scholar 

  21. C. Yuan, Y. Gu, W. Zeng, P. in 2020 American Control Conference (ACC) (IEEE, 2020), pp. 2888–2893

  22. Y. Qi, W. Yu, J. Huang, Y. Yu, Model predictive control for switched systems with a novel mixed time/event-triggering mechanism. Nonlinear Anal. Hybrid Syst. 42, 101081 (2022)

    Article  MathSciNet  Google Scholar 

  23. Y. Ma, X. Hui, Design of a new model predictive control for Lipschitz non-linear delayed switched systems with application to water pollution system. Multiscale Multidiscip. Model. Exp. Des. 1–10 (2023)

  24. H. Zhao, H. Yang, Z. Wang, H. Li, Nonlinear switched model predictive control with multiple Lyapunov functions for trajectory tracking and obstacle avoidance of nonholonomic systems. Int. J. Robust Nonlinear Control 33, 6171–6187 (2023)

    Article  MathSciNet  Google Scholar 

Download references

Funding

No funding.

Author information

Authors and Affiliations

  1. College of Mechanical and Electrical Engineering, Guangzhou Institute of Technology, Guangzhou, 510075, Guangdong, China

    Yuancheng Xie

Authors
  1. Yuancheng Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuancheng Xie.

Ethics declarations

Competing interests

The authors declare no competing of interests.

Research Involving Human Participants and/or Animals

The observational study conducted on medical staff needs no ethical code. Therefore, the above study was not required to acquire ethical code.

Informed Consent

This option is not neccessary due to that the data were collected from the references.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xie, Y. A Novel Low-Conservative Constrained H∞ Model Predictive Control for Linear Switched Systems. J. Inst. Eng. India Ser. B (2024). https://doi.org/10.1007/s40031-024-01068-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40031-024-01068-1

Keywords

Search

Navigation