1 Introduction

Although the five-card trick by Den Boer [1] is believed to be the first card-based cryptographic protocol, other authors used playing cards to showcase cryptographic concepts long before; for instance, Shamir, Rivest, and Adleman [2] (the authors of RSA) created a game named Mental Poker using playing cards to illustrate secure multi-party computation without trusted third-party a decade before the five-card trick. Nevertheless, the five-card trick was one of the first to introduce the idea of using physical cards as cryptographic primitives.

The five-card trick showed one way of performing two-party zero-knowledge computation. The idea was illustrated with a matchmaking scenario of two people (i.e., players) where the “trick” would show a specific pattern only if both players gave a positive “secret” response without disclosing to the other party if one, or both, replied negatively.

The beauty of the five-card trick was its simplicity, as its operation demands the minimum requirements from players, namely: (i) Arranging their cards in the desired ordering and (ii) alternating to “cut the cards,” where the former was used as binary encoding, while the latter as the simplest way to hide the original arrangement using cyclic permutations.

Generally speaking, card-based cryptographic protocols require the following:

  1. (a)

    A set number of cards from a common alphabet representing (binary) bits.

  2. (b)

    Encoding such bits with the cards that represent each player’s message.

  3. (c)

    A set of (shuffling) operations to securely compute the functions with cards.

Card-based protocols can be used as educational tools to visually illustrate relatively complex cryptographic concepts (e.g., Secure Multiparty Computation) to cryptography practitioners and, most importantly, non-experts such as high school students [3] using the above elements. However, most card-based cryptographic protocols exploit only points (a) and (c), namely: Cards’ Alphabet [4,5,6,7,8,9,10], the number of cards [6, 11,12,13,14,15,16] and Shuffling Operations [11, 12, 17,18,19,20,21]. Therefore, the encoding aspect (b) has been assumed, for the most part, to be the same (known) fixed pattern for all players, constraining the other elements and the construction of new protocols as the requirements have become more strict and, in some cases, even impractical to be performed by the intended target audience.

This study’s main contribution is providing players with a framework to negotiate the operations of card-based protocols when the encodings are variable and also a method to assess the time and space complexity. The specific advances herein are as follows:

  • The asymmetric five-card trick; a protocol that computes the logical AND function of two input bits and generalizes the five-card trick. After analyzing the different versions of the five-card trick, we show that it is possible to choose the players’ positions, the position of the auxiliary card, and their encodings flexibly, obtaining the same result.

  • We show the importance of the initial negotiation and training of protocols. Unfortunately, most existing work in the field neglects these aspects and only presents protocols at the execution phase, which is sometimes not as straightforward as authors think.

  • We present a thorough analysis to assess the protocol’s time and space complexity using a practical method.

The points above can lead to more flexible protocol designs, which in turn help to understand cryptographic principles or information security concepts.

The remainder of this paper is organized as follows. Section 2 presents a brief summary of preliminary concepts related to card-based protocols and the issues addressed in this study. Then, Section 3 introduces the formal notation used throughout the manuscript. The asymmetric five-card trick is introduced in Section 4, including the idea behind it and a thorough analysis of its complexity. This section also describes the protocol handshake and the overall framework for implementing card-based cryptographic protocols with variable encoding, the details of which are discussed and contrasted with related work in Section 5. Finally, Section 6 concludes this paper with final thoughts and future work.

2 Preliminaries

This section begins with a detailed review of the five-card trick to show the importance of having variable encodings and how to agree upon them in card-based protocols.

2.1 Den boer five-card trick

The original version of the five-card trick was presented by den Boer [1], which was illustrated with a matchmaking example. Let us introduce Alex and Bjorn–we give Alice and Bob a break in this paper–who would like to know whether they have mutual romantic interest without disclosing it to others as they might be embarrassed that other people around know who rejected whom. Den Boer made this scenario possible using five playing cards with the following properties:

  • All cards must have the same back-side (e.g., )

  • Two of the five cards must be identical on the face side (e.g., two-of-hearts )

  • The remaining three cards must be identical but other than the former (e.g., two-of-spades ).

Both players would be co-located at the same table and perform the following steps, as detailed in [1]:

  • Step 1: Alex and Bjorn are given two of each card type, that is, one , and one card. The remaining card () would be left facing down on the table.

  • Step 2: Then, they individually select the secret ordering of their cards to represent the positive answer and the reverse ordering to represent the negative answer. Bjorn, for instance, might arrange his cards as follows: heart on top and spade at the bottom () to reply “yes,” and the inverse order (i.e., ) to reply “no” to the matchmaking question. On the other hand, Alex might arrange her cards differently; for instance, she could “mirror” Bjorn’s ordering and choose spades on top and heart at the bottom () to reply positively and the inverse otherwise.

  • Step 3: Then, Bjorn places his cards on top of the independent card, and Alex places hers at the bottom (both with either a positive or negative reply). In card-based protocols, this step is called a commitment. For instance, if they both would answer positively, the initial state would be as shown in Figure 1. We call this setup the “working example,” as it works only for this particular instance (card arrangements and position).

  • Step 4: Afterwards, Alex and Bjorn take turns cutting the cards until they are satisfied with the secrecy of their initial selection.

  • Step 5: Finally, the cards are placed on top of the table and turned back to show the face side, and voilá, since they both answered yes in the working example, they are “magically” organized in a consecutive pattern of two hearts () as shown in Figure 2.

Fig. 1
figure 1

Initial state of the “working example” as seen from below the table. Alex (two cards on the right), Bjorn (two on the left) expressing “yes”, and the independent card in the middle

Full size image
Fig. 2
figure 2

One of the possible resulting states in the “working example” seen by everyone on the table. Note the consecutive pattern of cards

Full size image

The “trick” part is that, regardless of the number of cuts, only when both answers are positive does the resulting state shows two consecutive heart suits cards.

This seminal application of cards is not much of a trick, but mathematical concepts illustrated with cards. Cards represent bits, in the particular working example = 1 and = 0. The ordering represents their bits’ encoding, while the cut operations are cyclic permutations.

However, the five-card trick had certain hidden requirements for it to work, namely:

  1. 1.

    In Step 2, the encoding seems to be non-fixed for Alex (A) and Bjorn (B), but in fact, Bjorn’s must be exactly the opposite of Alex (\(B= \overline{A}\)) and only works if the encoding is the same as in the working example, i.e.:

  2. 2.

    In Step 3. Alex and Bjorn must place their cards precisely in the same positions: Bjorn’s cards on top of the independent card and Alex’s on the bottom, i.e.:

  3. 3.

    In Step 4, the random cuts must be valid cyclic permutations. That means some cards must be taken from the top and placed at the bottom.

  4. 4.

    Finally, Alex and Bjorn must be honest players. So, they will not change their reply once the protocol has started.

If players fail to fulfill one of the above requirements, the whole trick fails, meaning that the resulting permutation will not show the pattern of consecutive cards (or any of its cyclic variants) when both players answer positively.

An essential aspect of the five-card trick (and this paper’s conception) is that Alex and Bjorn could arrange (encode) their cards differently. However, as stated in the hidden requirements above, this must be done using the same encoding in a specific layout. This fact was cleared later on by Crépeau and Kilian [4], which we briefly describe next.

2.2 Crépeau and Kilian’s variation of the five-card trick

Crépeau and Kilian [4] presented a modified version of den Boer’s five-card trick. The cards’ requirements are the same: five cards with identical backs , two with identical faces and three identical-faced but different from the former. For simplicity, they used only the symbols and instead of the playing cards. However, and most importantly for this study, the secret ordering was pre-defined for both players:

figure w

As a result, although the commitment is still secret, the encoding is fixed, uniform, and disclosed to all players.

Moreover, as a consequence of the fixed encoding, they needed two extra modifications:

  • An extra step that shifts the commitment of one of the players (i.e., negates the commitment) is required.

  • The position of the independent card () was moved from the center to the far most right position.

These modifications allowed them to perform the trick. That is, obtaining side-by-side heart suits cards, in case both players have positive answers.

2.3 Issues with existing work

From Crépeau and Kilian’s [4] variant onwards, most, if not all, versions of the five-card trick use a fixed encoding. However, they do not follow the same rules and operations.

For instance, Mizuki in [21] describes the five-card-trick using three clubs, two hearts cards, no additional position switching, and fixed encoding = 0, = 1 (i.e., the inverse of [1, 4]). Later, the same author in [6] describes it using three hearts, two club cards (reverse of [21]), with no change in the operations or encodings. In another instance, Takashima et al. [22] add extra steps to the process by moving the auxiliary card from the initial far most right to the central position and negating Alex’s commitment instead of Bjorn’s. Toyoda et al. [23], move the auxiliary card to the far most left; even if the authors claim the change was made for explanation’s sake, it is nonetheless another version.

The above are but a subset of versions available for this simple protocol.

Now, imagine a Junior High School Mathematics Teacher or a College Professor who would like to explain the concept of Secure Multiparty Computations to 12-year-old students. After explaining any of the five-card-trick versions above, it would be more fruitful to let students develop their version based on their understanding of the underlying concepts instead of asking them to memorize the constrained protocol.

On the other hand, imagine the Teacher would like to explain the concept of Public and Private Keys with the same didactic cards. Since, to the best of our knowledge, most existing literature only uses fixed symmetric encoding, expressing these concepts in the current state of card-based crypto has yet to be addressed.

Hence, this paper proposes a framework that allows players to explicitly negotiate and agree on the protocol before it is executed. In particular, we focus on breaking the (self-imposed) limitation of only using fixed encoding, as using variable encoding could help card-based protocols express other cryptographic concepts (e.g., Public-key cryptography).

3 Definitions and notation

Prior to presenting the main part of this study, this section introduces various formal definitions and notations related to card-based protocols used throughout the paper. We partially extend the nomenclature of Mizuki and Shizuya [24].

Initially, we start by defining a protocol \({\mathscr {P}}\) as a quintuple \(\mathscr {P} = (\mathscr {D},\mathscr {U},\mathscr {Q},\mathscr {A},\mathscr {E})\) that computes a function \(f:\{0,\,1\}^*\rightarrow \{0,\,1\}\) where \({\mathscr {D}}\) is a deck of cards comprised by a sequence of individual cards within an alphabet \(\varSigma \) (e.g., \(\varSigma : \{\heartsuit , \,\clubsuit \}^*\)) for the face-side and a standard (identical) back-side (e.g., ). Each card constitutes an atom c that can be either face-up, denoted by \(\frac{c}{?}\) or simply c, or face-down denoted by \(\frac{?}{c}\) or ?. Cards can be arranged in a sequence \(\varGamma \in {\mathscr {U}}\), which is the set of possible (valid) input sequences into the protocol, e.g., \((\frac{?}{\clubsuit },\frac{?}{\heartsuit },\frac{\clubsuit }{?},\frac{?}{\clubsuit },\frac{?}{\heartsuit })\) or \((?,?,\clubsuit ,?,?)\) are equivalent. The input sequence can transition from one state \(q_i \in {\mathscr {Q}}: \{q_0, q_1, ... , q_{n-1}, q_n\}\) to another using a set of actions in \({\mathscr {A}}\); being \(q_0\) the initial and \(q_n\) the final state (also denoted by \(q_f\)). We extend the model by adding a set \({\mathscr {E}}\), which encloses the possible encoding rules \(\lambda \in {\mathscr {E}}\).

Each player uses a sequence of atoms (c) to encode a commitment (\(C: \{c\}^*\)) using its encoding \(\lambda ^c\); for instance, in den Boer’s [1] five-card trick, A encodes two bits (a, a) using cards with the following encoding rule \(\lambda ^a: \{\spadesuit \heartsuit =1, \, \heartsuit \spadesuit =0\}\).

Note that most existing work in card-based cryptography assumes the same rule to encode bits for all players; thus, it is decided in advance. However, in our case, each player can select its own encoding from a valid set.

Finally, the set of actions \({\mathscr {A}}\) is as follows:

  • Place a card (\(\textsf{place},\,\{i\}\)): Adds a card into the sequence. This operation was originally to add a card facing up so that players could confirm the value. We generalize it to add a card, either face up (i.e., {c}) or face down (i.e., {?}). Players can also place their commitments C, where the number of \(\textsf{place}\) operations is multiplied by the number of cards encoding C.

  • Turn a card over (\(\textsf{turn},\,i)\): Turning from the face down of the card to the face up or vice-versa (i.e., \(c \rightleftharpoons \,?\)).

  • Permutation (\(\textsf{perm},\,\pi \)): Rearrangement or permutation of type \(\pi \) in the sequence. The operation is performed in a symmetric group, that is, the resulting state \(\varGamma ^\pi \in {\mathscr {Q}}\). This operation can involve specific rearrangements of card positions or the entire sequence. For instance, the permutation \(\pi : \overline{C}\) negates the player’s commitment.

  • Shuffling cards (\(\textsf{shuffle},\,\varPi \)): The shuffling operation, involves a permutations \(\pi \in \varPi \). We assume the operation will be performed in a closed group that is uniformly distributed; thus, we omit the distribution in the original model. Moreover, \(\pi \) must specify the type of shuffling; for instance, a random cut shuffle is denoted as \(\pi _{RC}: \langle \sigma \rangle \) where \(\sigma \) is the sequence.

  • Result (\(\textsf{result}, \,\{\varphi \})\): Returns the result of the computation (i.e., at \(q_f\)), and therefore the protocol ends. This comprises the \(\textsf{turn}\) operation of \(\varphi \), which might contain specific cards’ positions or the whole sequence.

  • Encode (\(\textsf{encode}, C, \,\lambda )\): Encodes players’ commitment C according to the encoding rule \(\lambda ^c \in {\mathscr {E}}\). This action was not included in [24] or other models.

Based on the notation above, a protocol \({\mathscr {P}}\) performs a set of actions \({\mathscr {A}}\) from the initial state \(q_0\) and terminates when it reaches the final state \(q_n/q_f \in {\mathscr {Q}}\); during this process, the sequence \(\varGamma \in {\mathscr {U}}\) goes through changes within the same group and returns either a positive (i.e, one or “yes” or “true”) or negative (i.e., zero or “no” or “false”) value.

4 Proposed framework–working with variable encodings in card-based protocols

Before delving into the proposed framework, this section presents the overall idea through an example we call the Asymmetric Five-Card Trick.

4.1 The asymmetric five-card trick

4.1.1 The trick behind the trick

Den Boer’s five-card trick [1] showcased an interesting use of bits’ encoding, the properties of Commutative Groups, Galois Fields, and cyclic permutations. However, the main idea was working with “blobs” instead of individual bits to compute Zero-knowledge Boolean functions [25].

A blob is the primitive for minimum disclosure of players’ commitments which must be computed to either 0 or 1 [26]. Moreover, a blob should contain some extra data to allow the separation of the given bits [1]. For instance, in the working example of Section 2.1, Alex and Bjorn’s blobs are separated by an extra zero (0) bit; therefore, the initial blob in vector representation would be: \(i_{A,B}=(b,b,0,a,a)\). After the random cuts, the sequence will turn into a different state \(r_{A,B}\); however, \(r_{A,B}\) there could only be in one of the following resulting patterns \(R^1_{A,B}\) (state 1) if the blob is computed as true/positive/1 or \(R^0_{A,B}\) (state 2) otherwise.

$$\begin{aligned} \begin{array}{cc} R^1_{A,B}= &{} \{(1,1,0,0,0), (0,1,1,0,0), (0,0,1,1,0),\\ &{}(0,0,0,1,1), (1,0,0,0,1)\} \end{array} \end{aligned}$$
(1)
$$\begin{aligned} \begin{array}{cc} R^0_{A,B}= &{} \{(0,1,0,1,0), (0,0,1,0,1), (1,0,0,1,0),\\ &{}(0,1,0,0,1), (1,0,1,0,0)\} \end{array} \end{aligned}$$
(2)

Given that the random cuts are cyclic permutations, the five-card trick can only be “true” when the initial input \(i_{A,B}\) is already in \(R^1_{A,B}\). We call this condition a “True Blob Commitment” (TBC), which we use to construct the following proposition for the five-card trick:

Proposition 1

If players achieve the TBC in the initial state, the encoding need not be fixed, uniform, or even disclosed to others.

To prove the above proposition, consider the original five-card trick [1] or Crépeau and Kilian [4] variation, whose encodings and operations are different; nevertheless, the initial TBCs:

figure af

respectively, are elements of \(R^1_{A,B}\) (state 1). Or, in [23], the position for the auxiliary card, the encodings, and the swapping operations are different than in previous cases; yet, the initial TBC (0, 0, 1, 1, 0) = is also an element of \(R^1_{A,B}\) (state 1).

Now, assume for the sake of contradiction that the resulting state \(r_{A,B} \in R^0_{A,B}\) even if the initial state \(i_{A,B} \in R^1_{A,B}\) on a TBC, since the random cuts will simply perform circular permutation in a closed group, this could not be possible, unless the random cut operation has been violated, by one or both players (intentionally or unintentionally).

Therefore, the initial true state will remain, regardless of the players’ encodings, the auxiliary card’s position between the commitments, or the number of (valid) random cuts.

The trick behind the trick is achieving the TBC in the initial state. To do so, the protocol must adapt based on the encoding using a process we call Protocol Handshake.

4.1.2 Protocol handshake

To illustrate how the protocol handshake works, consider the following scenario. Assume Alex and Bjorn want to decide on a topic without revealing it to others who say “no” (false). Mister Carl (their Math Teacher), who was nearby, heard the issue and thought they could use the five-card-trick to solve their problem. However, he does not remember the exact operations nor how to arrange the cards. The only information he remembers is that they must use five cards with two different colors so that each one will receive one of each, an auxiliary card with one of the colors, and the result would be a sequential pattern of the cards if they replied positively. He explains that to the students and gives them five cards he held in his pocket.

For illustration’s sake, the available cards are as follows: two types of cards as the face-side and as the backside, so the Deck is as follows \({\mathscr {D}}:(\clubsuit ,\clubsuit ,\clubsuit ,\heartsuit ,\heartsuit )\).

Since Alex and Bjorn do not trust each other or Mr. Carl yet, they do not want to share the arrangement (encoding); and prefer to select them individually and in private. Therefore, their selected encoding rules (\(\lambda \)) might be the same, or each uses a different one; however, since the alphabet is limited, it will be one of the instances in Table 1.

Table 1 Encoding schemes (\({\mathscr {E}}\)) for Alex and Bjorn
Full size table

Mr. Carl explains to students that, since the input sequence will be indistinguishable to all of them (\(\varGamma : \{\heartsuit , \,\clubsuit \}^5\)) once they place their cards, before using their real commitments, they must perform a pre-process, as test runs to agree on how to adapt the protocol based on their encodings.

  • Step 1: Alex and Bjorn are given one of each card, that is, one and one .

  • Step 2: Then, they must decide their secret encoding for the true/yes/1 value, knowing that the reverse order will be the opposite false/no/0. We assume both are honest and will not change it afterward. For instance, let us assume they independently select an encoding that matches case 3 in Table 1. Thus, Alex encodes her bits as for \(A=1\) while Bjorn (independently of Alex’s) decided for \(B=1\).

  • Step 3: One of them, Alex or Bjorn, places their cards face down with a True Commitment on the table. For example, let us assume this time Alex will start. Therefore, her cards will be: Note that these cards are facing down, so players only see the backside of the card .

  • Step 4: The other player, in this example Bjorn since Alex performed Step 3, places his cards face down with a True Commitment (i.e., \(B=1\)) on the table. He can choose to place them on the left or right of Alex’s cards:

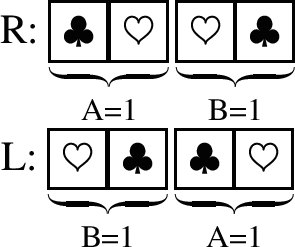
    figure cb

    For example, let us assume he places them at the right (R) viewed from above. Therefore, in this example, the initial player’s placement is: Note that they must remember their position.

  • Step 5: Then, the other player, in this example Alex, decides where to place the extra (auxiliary) card facing up in any of the following positions: leftmost (L), middle (M), or rightmost (R) from their commitments:

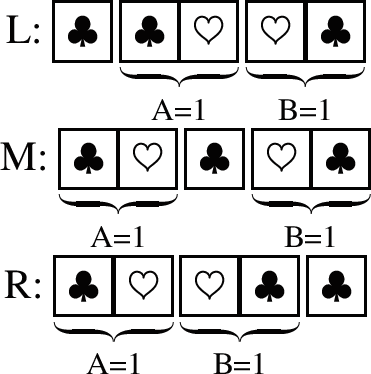
    figure cd

    For instance, let’s assume he/she decides to place it in the middle (M). Therefore, in this example, the initial full card placement would look as follows: Note that, for convenience, the auxiliary card would be initially placed facing up, so players do not mix it up with their commitments. However, in a later step, this will be turned face down.

  • Step 6: The other player, Bjorn in this example, then performs (if he/she wants) an operation on their commitments. For simplicity, these operations might be shifting the placement of players (i.e., \((A) \rightleftharpoons (B)\)) or negating any of the commitments by switching the positions of the cards (i.e., \(\overline{A}\) or \(\overline{B}\)). However, he/she could also leave the cards as they are. In this example, for the sake of brevity, let us assume that Bjorn would like to switch the placements from Alex and his (\(\alpha : (A) \rightleftharpoons (B)\)). Therefore, the setup would look as follows after the operation:

  • Step 7: The other player (Alex) has one last optional operation in the commitments, as in the previous step, or he/she could also skip the operation. For this example, let us assume he/she decides to skip any extra operation and move to the next step directly. This is the initial state of the protocol (\(q_0\)) denoted by the variable \(i_{A,B}\).

    figure ce

  • Step 8: Any of the players flips the auxiliary card down so that all cards are on their backs.

    figure cg

  • Step 9: Then, players take turns performing Random Cuts until they are satisfied with the secrecy of the True commitment, which will constitute the final state (\(q_f\)) denoted by the variable \(r_{A,B}\).

  • Step 10: Finally, the cards are revealed to all players.

Based on the configuration in the steps above (i.e., encoding and operations), \(r_{A,B}\) can be either:

  1. (i)

    including its cyclic permutations, or

  2. (ii)

    including its cyclic permutations

If the resulting state is (i), the pre-processing was successful, so they achieved a TBC state. Therefore, players can use their “real commitments” (not necessarily positive) using the same selected encoding and operations as in the pre-processing. Of course, they can try the same steps until they are convinced the procedure is correct. Moreover, Mr. Carl can leave the room at this point, as it is no longer needed.

Pseudocode 1
figure cr

The Asymmetric Five-Card Trick Protocol Handshake. Player A bits encoded in {a, a} according to selected encoding \(\lambda ^a\), Player B bits encoded in {b, b} according to selected encoding \(\lambda ^b\). Terminates when \(r_{A,B} \in R^1_{A,B}.\)

Full size image

On the contrary, if the result shows the pattern in (ii), the conditions were not met for the TBC; therefore, the pre-process must restart from Step 1.

We call this pre-process the protocol handshake, as the steps are negotiated by the players.

A more compact description of the above handshake is shown in Pseudocode 1, which uses the notation described in Section 3. The loop can take one to multiple tries until the players agree on the set of placements and operations to achieve the True Blob State. However, once the handshake has finished, the protocol has a straightforward execution. For instance, Pseudocode 2 shows the resulting five-card trick built with the process above.

Readers may verify the resulting state will be in \(R^1_{A,B}\) (i) in the example above. However, it is worth mentioning that multiple versions could have made the protocol achieve a TBC depending on the players’ encoding and placement, the position of the auxiliary card, and the operations performed by each player. Therefore, the possibilities for building and adapting a protocol increase considerably and are no longer constrained by the same encoding or operations.

Pseudocode 2
figure cs

The Asymmetric Five-Card Trick Sample Protocol from the steps in Section 4.1.2. Player A bits encoded in {a, a} as \(\lambda ^a:\{\clubsuit \heartsuit =1,\heartsuit \clubsuit =0\}\), Player B bits encoded in {b, b} as \(\lambda ^b:\{\heartsuit \clubsuit =1, \clubsuit \heartsuit =0\}\). Permutation \(\alpha : (A) \rightleftharpoons (B)\). Computes to 1 if \(r_{A,B} \in R^1_{A,B}\), and 0 otherwise.

Full size image
Pseudocode 3
figure ct

Original den Boer’s Five-Card Trick. Player A bits encoded in {a, a} as \(\lambda ^a:\{\clubsuit \heartsuit =1,\heartsuit \clubsuit =0\}\), Player B bits encoded in {b, b} as \(\lambda ^b:\{\heartsuit \clubsuit =1, \clubsuit \heartsuit =0\}\). No Permutations. Computes to 1 if \(r_{A,B} \in R^1_{A,B}\), and 0 otherwise.

Full size image
Pseudocode 4
figure cu

Crépeau and Kilian’s Five-Card Trick. Player A bits encoded in {a, a} and Player B bits encoded in {b, b} as \(\lambda ^a=\lambda ^b:\{\clubsuit \heartsuit =1, \heartsuit \clubsuit =0\}\). Permutation \(\alpha : \overline{B}\). Computes to 1 if \(r_{A,B} \in R^1_{A,B}\), and 0 otherwise.

Full size image

Although the protocol (in this case, the five-card trick) would use the same procedure after a handshake, the handshake itself does not follow a symmetrical pattern. Moreover, the protocol built by two players might not be the same as others. Hence the name: the asymmetric five-card trick.

The resulting protocols include all possible variations, which makes the asymmetric five-card trick a generalization of the five-card trick. For instance, Pseudocodes 3 and 4 were constructed using different handshakes, achieving the original den Boer [1] and Crépeau and Kilian [4] variation, described in Sections 2.1 and 2.2, respectively.

4.2 Proof of correctness and security

Since the asymmetric five-card trick is an augmented (generalized) version of the original five-card trick, we rely upon the correctness and security from the correctness and security of the original five-card trick itself in [1]. For completeness, we also gave a thorough description and proved the correctness of Proposition 1 in 4.1.1.

Moreover, the protocol handshake might generate a degree of unintentional information leakage if repeated several times. However, in principle, the only public information is that players use their true commitment and the operations. Nevertheless, the secrecy of the response when executing the actual protocol is as secure as the original five-card trick.

4.3 Complexity of the protocol

This section describes the overall protocol’s time and space complexity analysis. The intuition behind the complexity is to approximate the resources required to perform the asymmetric five-card trick, not in the traditional computer science sense but in a practical manner

4.3.1 Space complexity

The space complexity is defined as the number of cards required to execute the protocol. As with the original five-card trick, we require two cards for encoding bits per player plus an auxiliary card, thus: \(2n+1\), where n is the number of players, in this case, only two players. Therefore, the space complexity of the asymmetric five-card trick is five.

4.3.2 Time complexity

The time complexity is the time required to perform the protocol. To calculate this metric, we use the average time per action, i.e., \(\mathsf {\textrm{place}}\), \(\mathsf {\textrm{perm}}\), \(\mathsf {\textrm{shuffle}}\), and \(\mathsf {\textrm{encode}}\) denoted as \(t_{\textrm{place}}\), \(t_{\textrm{turn}}\), \(t_{\textrm{perm}}\), \(t_{\textrm{shuf}}\), and \(t_{\textrm{encode}}\) respectively (as in [27]).

However, we separate the protocol’s execution from the production, a notion not considered in existent work.

  • Execution time: This phase measures the protocol execution of a single run, starting after players receive their cards until the protocol halts its operation when reaching the final state. We define the total execution time (XT) of a protocol \({\mathscr {P}}\) as the summation of individual operations:

    $$\begin{aligned} \textrm{XT}_{{\mathscr {P}}}=\Bigl (t_\mathrm{{encode}} + t_\mathrm{{place}} + t_\mathrm{{turn}} + t_\mathrm{{perm}} + t_\mathrm{{shuf}}\Bigr ) \end{aligned}$$
    (3)

    Note that each component denotes the occurrence of the action throughout the protocol.

  • Production time: This phase calculates the preparation time before the actual execution, including training players on how to perform the protocol or, if necessary, convincing them the protocol works (i.e., testing). All materials (i.e., cards and other possible auxiliary items) are assumed to be already available. We separate this phase from the actual execution time since it might take non-negligible time to memorize the protocol, especially when it involves complicated shuffling operations or specific permutations. In particular, the proposed protocol handshake is also part of this phase, whose time (HT) is defined as:

    $$\begin{aligned} \textrm{HT}_{{\mathscr {P}}}=\sum _{i=1}^{m}\Bigl ( t_\mathrm{{encode}} + t_\mathrm{{place}} + t_\mathrm{{turn}} + t_\mathrm{{perm}} + t_\mathrm{{shuf}}\Bigr ) \end{aligned}$$
    (4)

    This step might be the most time-consuming production phase since the protocol handshake can take from one to multiple times to reach the TBC state. Moreover, we assume that the protocol testing would involve at least two runs (i.e., a positive and a negative sample) to showcase the operation. Therefore, the testing time (TT) of a protocol \({\mathscr {P}}\) is defined as:

    $$\begin{aligned} \textrm{TT}_{{\mathscr {P}}} = \sum _{j=2}^{n} \textrm{XT}_{{\mathscr {P}}} \end{aligned}$$
    (5)

    Therefore, the Production Time of a protocol (PT) of a protocol \({\mathscr {P}}\) is defined as:

    $$\begin{aligned} \textrm{PT}_{{\mathscr {P}}} = \textrm{HT}_{{\mathscr {P}}} + \textrm{TT}_{{\mathscr {P}}} \end{aligned}$$
    (6)

    Note that in the existing protocols, the production time will be equivalent to the testing time \(\textrm{PT}_{{\mathscr {P}}} = \textrm{TT}_{{\mathscr {P}}}\) since they directly execute the protocol.

Based on the above framework, we can analyze the time complexity of the asymmetric five-card trick as follows.

Let us start with the Execution Time of the resulting asymmetric five-card trick in Pseudocode 2.

Since the encoding is decided, both need only to consider whether to encode their answer once every execution (i.e., \(1 t_\mathrm{{encode}}\)). However, we assume the time needed to decide on an encoding is equivalent. Then, players must place their commitments plus the auxiliary card (i.e., \(5 t_\mathrm{{place}}\)). The auxiliary card is then turned face-down during the execution, and all five cards are turned face-up to show the result (i.e., \(6 t_\mathrm{{turn}}\)). Finally, since the protocol only uses Random Cuts as shuffling operations, players will need to perform at least two random cuts with no upper limit, as they might perform as many as they deem necessary to hide the initial commitment. Thus the protocol would need \(\sum _{s=2}^{\infty } t_\mathrm{{shuf}}\) (i.e., at least \(2 t_\mathrm{{shuf}}\)) to shuffle. In summary, if we replace the values in (3), the Execution Time is at least:

$$\begin{aligned} \textrm{XT}_{{\mathscr {P}}_2}=\Bigl (t_\mathrm{{encode}} + 5 t_\mathrm{{place}} + 6 t_\mathrm{{turn}} + t_\mathrm{{perm}} + 2 t_\mathrm{{shuf}}\Bigr ) \end{aligned}$$
(7)

Now, in terms of Production Time, since testing the protocol would need at least two runs, the testing time is \(\textrm{TT}_{{\mathscr {P}}_2} = 2 \textrm{XT}_{{\mathscr {P}}_2}\), as defined in (5). Regarding the Handshake Time in (4), except for the number of permutations (i.e., from 0 to 2), it would be equivalent to an Execution Time. However, recall that in the best-case-scenario players would need at least one try to achieve the handshake; thus, \(\textrm{HT}_{{\mathscr {P}}_2} = \textrm{XT}_{{\mathscr {P}}_2}\). Therefore, replacing the values in (6), the total Production Time of the asymmetric five-card trick in Pseudocode 2 would be at least:

$$\begin{aligned} \textrm{PT}_{{\mathscr {P}}_2}= 3 \textrm{XT}_{{\mathscr {P}}_2} \end{aligned}$$
(8)

For instance, let us set the same values as in [27]: \(t_\mathrm{{place}}=t_\mathrm{{turn}}=0.8 s; t_\mathrm{{perm}}=7t_\mathrm{{turn}}; t_\mathrm{{shuf}} \ge t_\mathrm{{perm}}\). Moreover, we additionally set the encoding time as \(t_\mathrm{{encode}}= 5s\), and since the random cut operation is pretty straightforward, that \(t_\mathrm{{shuf}} = t_\mathrm{{perm}}\). Therefore, replacing these values in (7) and (8) the time complexity lower bounds (\(\varOmega \)) for the asymmetric five-card trick (in Pseudocode 2) are as follows:

$$\begin{aligned} \varOmega (\textrm{XT}_{{\mathscr {P}}_2})&= 30.6 s \end{aligned}$$
(9)
$$\begin{aligned} \varOmega (\textrm{PT}_{{\mathscr {P}}_2})&= 91.8 s \end{aligned}$$
(10)

Regarding the upper bounds (O), the handshake might take several rounds to finish (at the production phase), and since the asymmetric five-card trick is a Las Vegas protocol that uses Random Cut operations, it has no finite runtime but expected finite states. Therefore, it is difficult to determine a close upper bound.

4.4 General framework

This section describes the proposed general framework for using variable encoding in card-based cryptographic protocols. Note that this process could be applied to existing protocols or the design of new ones. In the latter case, when developing new protocols, authors could start by setting up fixed and uniform encodings and then apply a handshake to adapt the operation in the execution phase.

Figure 3 depicts the overall process, as observed, in the production phase (on top), players have to choose their encodings individually. Then, based on those encodings, they need to negotiate how the original protocol will be adapted, which is tested until they have reached an agreement on the operations and are convinced of the correctness. Subsequently, the execution phase (at the bottom) is the actual protocol runtime, using the players’ actual commitment.

Note that most, if not all, existing protocols only show the execution phase; however, as described in Section 4.3.2, players would need at least a test run for the true commitments as well as for the opposite, for training and showcasing the possible results. Therefore, these phases should be present even when using fixed and uniform encodings so that players can execute protocols without incurring mistakes that can lead to distrust.

Fig. 3
figure 3

Overall Framework for variable encoded card-based protocols. Above the Production phase and below the Execution phase

Full size image

5 Discussion and related work

Although protocols for computing logical Boolean functions have been extensively explored in the past few years, as described in Section 1, most of the effort has been devoted to using different alphabets, using fewer cards, or protocol operations. However, very few works address the use variable encoding in card-based cryptography.

In particular, protocols that use non-conventional alphabets for cards (e.g., [6,7,8,9,10]) present interesting encodings. For instance, in [6], the authors propose rotationally asymmetric encoding such that and with interesting operations. However, they still use the same uniform encoding for all players.

Other authors, e.g., Niemi and Renvall [5], use a non-fixed encoding with off-the-shelf deck of cards as a numbered set to represent the players’ encodings; the encoding rule is as follows, two distinguishable cards with sequential values i and j where \(i \ne j \, \Vert \, i,j \in \{1,2,3,..,52\}\) represent one bit, which corresponds to 0 if the value of the card on the left is less than the one on the right and 1 otherwise:

$$\begin{aligned} i \, j \mathrel {\hat{=}} {\left\{ \begin{array}{ll} 0,&{}{} \text{ if } i < j,\\ 1,&{}{} \text{ if } i > j.\\ \end{array}\right. } \end{aligned}$$
(11)

Using the above-mentioned encoding, the authors construct protocols for computing Boolean functions (i.e., AND, NOT, COPY, OR, XOR). These protocols were then improved by Mizuki [28], who used Random Bisection Cuts to decrease the number of shuffling operations. Moreover, a process to change the base of a commitment (i.e., the pair {i, j}) even when these commitments are hidden or opaque (as the author called it) was also introduced.

Koch, Schrempp, and Kirsten [29] thoroughly analyzed and formally defined the impact of encoding in card-based protocols (as a complement to the work above). They proved that under certain conditions, it is possible to freely choose the encoding for adapting protocols by adding shuffles and turns (card reveals). Similarly to [28], the premise is to perform a basis transformation with a process called relabeling, that consists of cyclic permutations on the input until the initial state matches the intended card sequence. One such condition is that cards must be distinguishable from each other and follow the same encoding as in (11). Therefore, although the contribution of the above work is remarkable, they were still working under a uniform and openly disclosed encoding rule.

Finally, Miyahara et al. [30] propose card-based protocols to deal with Yao’s millionaire problem, some of which use non-uniform encodings. Since their protocols compare integer values, the resulting commitment will be (naturally) non-uniform. However, the encoding rules are still fixed for each player. Moreover, given the sensitive data to compare, players would require more than a few tries to determine how (and if) the protocol works. Therefore, having a negotiation phase would still help these types of protocols.

Complementing the above work, this paper showed that it is possible to build protocols using variable encodings using a pre-process we called handshake, where players adapt and agree on the protocol’s operation before the actual execution.

Of course, implementing the handshake over the five-card trick was relatively straightforward as it is a very simple protocol that uses only Random Cuts as the shuffling operation. Moreover, the five-card trick has a unique TBC state, namely when the initial state is in the appropriate position (\(i_{A,B}= (r_{A,B})^\pi \in R^1_{A,B}\)).

However, let us consider, for instance, the AND Protocol in [21], which does not have a single but two true states, and the operations are (for lack of a better word) hard-coded to the fixed uniform encoding for all players (i.e., ). The transformation might not be as straightforward (or possible) for protocols with these characteristics. Consequently, entirely new protocols might need to be reconstructed.

Another discussion point might be related to the necessity/utility of the non-disclosed (i.e., secret) encoding while building protocols. A public and fixed encoding and operations will facilitate the protocol, even if players do not follow the mainstream ones. However, a private/secret encoding and the liberty to build their own operations in a systematic manner without altering the underlying principles would provide more credibility and trust in these types of protocols.

Finally, as mentioned in Section 2.3, using variable encoding could help express cryptographic concepts to non-cryptography practitioners. For instance, consider the asymmetric five-card trick to explain the basic notion of Public-key cryptography. In this scenario, each player’s encoding would act as their private key to encrypt their messages (in this case, a simple “yes” or “no”); the resulting pattern might act as the public key, and the Random Cuts might act as the encryption algorithm. On the other hand, the Protocol Handshake could be used to explain how communication protocols (e.g., TLS) can negotiate a secure connection between the client and server by using handshaking. Of course, limitations exist on what can be expressed with such limited resources, but it could serve as a visual aid to describe the basic notion.

6 Conclusions and future work

Card-based protocols have proven to be a powerful tool for educational purposes, even for non-cryptography practitioners. These protocols rely on the alphabet, the number of cards, the encoding, and the shuffling operations to build and explain relatively complex concepts such as secure multiparty computations. However, for the most part, the encoding aspect has been relegated, leading to the over-dependence on the operations, which are becoming more and more difficult to perform. Consequently, these protocols are losing their simplicity and moving away from their core rationale.

In this paper, we presented the asymmetric five-card trick, a generalized version of the five-card trick, as an example of how protocols can integrate variable encodings so that it becomes part of the elements used to illustrate security and cryptographic concepts visually. Moreover, we also presented a general framework for constructing card-based protocols (or adapting existing ones) and a method for benchmarking them in terms of their required time and space complexity. This framework comprises the production and execution phases, where the former is usually overlooked and treated in a lightweight manner, leading to mistakes and mistakes during execution.

Finally, we also presented a practical method for assessing time and space complexity (or at least the lower bounds) since these factors would determine whether a protocol is worth implementing or executing. For instance, if the protocol takes an unreasonably long time to execute, or needs a large number of cards, or specially crafted objects, then players would be reluctant to use it when digital tools are available; surprisingly, this point is barely discussed in existing work.

As future directions of this research, we plan to study the effects of variable encoding in different types of protocols than the five-card trick. These include but are not limited to, committed protocols, multi-party protocols, non-binary-entry protocols, protocols with asymmetric inputs, and protocols with nonstandard alphabets.