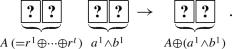Actively revealing card attack on card-based protocols

Abstract

In 1989, den Boer presented the first card-based protocol, called the “five-card trick,” that securely computes the AND function using a deck of physical cards via a series of actions such as shuffling and turning over cards. This protocol enables a couple to confirm their mutual love without revealing their individual feelings. During such a secure computation protocol, it is important to keep any information about the inputs secret. Almost all existing card-based protocols are secure under the assumption that all players participating in a protocol are semi-honest or covert, i.e., they do not deviate from the protocol if there is a chance that they will be caught when cheating. In this paper, we consider a more malicious attack in which a player as an active adversary can reveal cards illegally without any hesitation. Against such an actively revealing card attack, we define the t-secureness, meaning that no information about the inputs leaks even if at most t cards are revealed illegally. We then actually design t-secure AND protocols. Thus, our contribution is the construction of the first formal framework to handle actively revealing card attacks as well as their countermeasures.

1 Introduction

In 1989, den Boer presented the first card-based protocol, called the five-card trick, that securely computes the AND function using a deck of physical cards (den Boer 1990). Assuming that Alice has a private bit $a\in \{0,1\}$ and Bob has a private bit $b\in \{0,1\}$, the five-card trick, which uses five cards , proceeds as follows.

• 1. According to the encoding rule:

  

  (1)

  Alice commits her private bit a to two face-down cards of different colors $(\clubsuit ,\heartsuit )$ without anyone else seeing the order of the two cards:

  

  Such a pair of face-down cards is called a commitment to a. Similarly, Bob places a commitment to b on the table. Therefore, together with the remaining red card , the initial sequence of the five cards is

  

• 2. Move the rightmost red card to the center and turn it over:

  

• 3. Swap the first and second cards (from the left), namely the two cards constituting the commitment to a; owing to the encoding (1), this action performs the NOT operation such that a commitment to the negation $\overline{a}$ of a is obtained:

  

  It is noteworthy that only when $a=b=1$, the three cards in the middle will be .

• 4. Apply a random cut, denoted by $\langle \cdot \rangle$; it is a shuffle action to cyclically shift the sequence of cards at random:

  

  Note that the shift offset is uniformly distributed on $\{0,1,2,3,4\}$ and nobody knows the offset¹.

• 5. Open all the five cards.

  • If three consecutive red cards (apart from cyclic rotation) appear, we have $a\wedge b=1$.

  • If do not appear, we have $a\wedge b=0$.

This is the five-card trick, which securely computes the AND function, i.e., it reveals only the value of $a\wedge b$. As an application, for instance, this card-based protocol enables Alice and Bob to confirm their mutual love without revealing their individual feelings.

During such a secure computation protocol, it is important to keep any information about the inputs secret. As seen above, the five-card trick preserves the secrecy of the inputs a, b by virtue of the face-down cards, and the shuffle action eliminates the individual values of the inputs aside from the exact value of $a\wedge b$. In other words, the five-card trick is secure provided that all players obey the protocol. Similar to the five-card trick, almost all existing card-based protocols (e.g., Mizuki and Sone 2009; Koch et al. 2015; Niemi and Renvall 1998; Mizuki et al. 2012; Ishikawa et al. 2015) are secure under the assumption that all players are semi-honest or covert, i.e., they do not deviate from the protocol if there is a chance that they will be caught when cheating. In most cases, a card-based protocol is executed completely publicly with all eyes fixed on how the cards are manipulated, and hence, any illegal actions by the players (or others) will be noticed (Mizuki and Shizuya 2014b); thus, any semi-honest or covert player always follows the protocol.

By contrast, this paper considers a more malicious attack: We assume that one player (e.g., Alice) is an active adversary who may possibly reveal face-down cards illegally without any hesitation. For example, if Alice suddenly reveals the commitment to b at Step 3 during the execution of the five-card trick, Bob’s private input will be leaked immediately. We call such a malicious attack the actively revealing card attack. (It should be noted that active attacks on card-based protocols have been comprehensively discussed in Koch and Walzer (2020).)

To the best of our knowledge, this actively revealing card attack has not been studied so far except for using envelopes considered by Koch and Walzer (2020). In their work, we may place each card into an envelope to prevent face-down cards from being revealed illegally. However, using envelopes is not convenient; hence, we solicit another solution that does not rely on any additional tools such as envelopes. Thus, we have to devise a method to keep individual players’ inputs secret even if some of the face-down cards are revealed maliciously. To this end, we borrow an idea from secret sharing schemes (Shamir 1979) such that each input commitment will be split into several “share” commitments. Specifically, as the “revealing-card tolerance,” we introduce the concept of “t-secureness” in which any information regarding the inputs will be preserved even if at most t cards are revealed maliciously. Subsequently, we design a 1-secure AND protocol as well as a general t-secure AND protocol. Thus, our main contribution is to construct the first formal framework to handle actively revealing card attacks and their countermeasures.

This paper focuses on non-committed format protocols that specify the output value by revealing some face-down cards, as shown in the five-card trick (or in others, e.g., Mizuki et al. 2012). By contrast, there are committed format protocols that produce commitments (consisting of face-down cards) as the output (e.g., Mizuki and Sone 2009; Stiglic 2001; Niemi and Renvall 1998; Crépeau and Kilian 1994): Because the output is hidden owing to the face-down cards, during such a committed format protocol, information regarding the input as well as output will not be leaked. Meanwhile, committed format protocols have been formalized well; no formal treatment of non-committed format protocols has been reported (note that because a committed format protocol does not leak any information, it suffices to consider perfect secrecy; meanwhile, a non-committed format protocol needs to leak some information regarding the input to reveal the output value, and hence, a more careful treatment is required). Herein, we first formalize a non-committed format protocol. This formalization is one of our major results.

It is noteworthy that Mizuki and Shizuya (2014b) previously adopted a similar idea to deal with the situation where some of the cards may be flawed, i.e., the cards may have scuff marks on their backs (undoubtedly, the problem of flawed cards is different from that of the actively revealing card attack, but they may share some common features). Because this previous work (Mizuki and Shizuya 2014b) considered only committed format protocols, it is interesting future work to apply the technique proposed herein to design “scuff-proof” non-committed format protocols.

The remainder of this paper is organized as follows. In Sect. 2, we briefly introduce a formal approach for describing a card-based protocol. In Sect. 3, we formally define a non-committed format protocol. In Sect. 4, we define the t-secureness against the actively revealing card attack. In Sect. 5, we construct a 1-secure AND protocol and confirm its security. In Sect. 6, we construct a t-secure AND protocol and confirm its security. Finally, the paper is concluded in Sect. 7.

An earlier version of this paper was presented and appeared as a conference paper (Takashima et al. 2019). The main difference is twofold. First, we have expended Sect. 5 to elaborate on our 1-secure AND protocol; especially, Figs 2, 3 and 4 are new materials. Second, we have added Sect. 6 to extend our 1-secure AND protocol to a general t-secure one so that t-secureness can be achieved. In addition, we have enhanced the definitions of security in a more rigorous way in Sect. 4.

2 Preliminaries

In this section, we present the way to formally describe a card-based protocol.

The computational model of card-based protocols has been formalized via abstract machine (Mizuki and Shizuya 2014a, 2017; Koch et al. 2015). Roughly speaking, a protocol consists of a series of three actions: $\mathsf {turn}$, $\mathsf {perm}$, and $\mathsf {shuf}$ actions, along with a sequence of cards.

Consider a sequence of d cards. A $\mathsf {turn}$ action is specified by a set $T\subseteq \{1,2,\ldots ,d\}$ of positions of cards; the action $(\mathsf {turn}$ $, T)$ turns over every card whose position is in T. A $\mathsf {perm}$ action is specified by a permutation $\pi \in S_d$, where $S_d$ denotes the symmetric group of degree d; the action $(\mathsf {perm}$ $, \pi )$ rearranges the positions of d cards according to $\pi$. A $\mathsf {shuf}$ action is specified by a set $\Pi \subseteq S_d$ of permutations; the action $(\mathsf {shuf}$ $, \Pi )$ probabilistically rearranges the positions of d cards according to a permutation $\pi$ uniformly drawn from $\Pi$. We call a protocol using exactly d cards a d-card protocol.

To illustrate, recall the execution of the five-card trick (den Boer 1990) presented in the previous section. It uses two types of cards, and , whose backs are . All cards of the same type are indistinguishable. The five-card trick, which is a 5-card protocol, starts with a sequence of five cards:

(2)

Step 2 of the five-card trick is formally captured by $(\mathsf {perm}, (3\;4\;5))$ along with $(\mathsf {turn}, \{3\})$. Step 3 is captured by $(\mathsf {perm}, (1\;2))$. In Step 4, we apply a random cut that can be written as $(\mathsf {shuf}, \mathsf {RC}_{\mathsf {5}})$, where $\mathsf {RC}_{\mathsf {5}}=\{(1\;2\;3\;4\;5)^i\mid 1\le i\le 5\}$. Step 5 is $(\mathsf {turn}, \{1,2,3,4,5\})$.

To discuss the correctness and security of protocols, we use the concept of statuses of a protocol. For example, the initial status of the five-card trick (as in Eq. (2)) is described as follows:

$$\begin{aligned}&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \; \; (p_{00},0,0,0)\; \\&\clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \; \; (0,p_{01},0,0)\; \\&\heartsuit \clubsuit \clubsuit \heartsuit \heartsuit \; \; (0,0,p_{10},0)\; \\&\heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \; \; (0,0,0,p_{11}), \end{aligned}$$

where $p_{ij}$ denotes the probability that input (a, b) is equal to (i, j) for every $(i,j)\in \{0,1\}^2$; in other words, ($p_{00}, p_{01}, p_{10}, p_{11}$) denotes a probability distribution on the input set $\{0,1\}^2$. The status above consists of four entries, each of which is a pair of a symbol sequence (such as $\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit$) and a probability trace (such as ($p_{00}$, 0, 0, 0); the first entry means that the symbol sequence $\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit$ and the event $(a,b)=(0,0)$ occur with a probability of $p_{00}$ (and $\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit$ with $(a,b)\ne (0,0)$ never occurs), the second entry means that $\clubsuit \heartsuit \heartsuit \clubsuit \heartsuit$ and $(a,b)=(0,1)$ occur with a probability of $p_{01}$, and so on. The initial status (and succeeding statuses) are transformed into another status by an action as shown in Fig. 1. In particular, the $\mathsf {turn}$ action results in ten “leaf” statuses.

The expression of protocols illustrated in Fig. 1 was established by Koch et al. (2015) where a tree structure specifies a protocol. We modify it slightly using the probability traces introduced by Mizuki and Komano (2018). We call such a tree the (modified) KWH-tree of a protocol. Borrowing a terminology in graph theory, we call the bottom statuses in a KWH-tree the leaf statuses.

Fig. 1

The (modified) KWH-tree of the five-card trick

Note that in each of the first three statuses (namely, “non-leaf” statuses) depicted in Fig. 1, the (coordinate-wise) sum of all probability traces is equal to $(p_{00}$, $p_{01}$, $p_{10}$, $p_{11})$; this guarantees that no information about the input (a, b) will be leaked. Regarding the ten leaf statuses, each of them has only one probability trace, which is either

$$\begin{aligned} \left( \textstyle \frac{p_{00}}{p_{00}+p_{01}+p_{10}} ,\frac{p_{01}}{p_{00}+p_{01}+p_{10}},\frac{p_{10}}{p_{00}+p_{01}+p_{10}},0\right) \text { or } (0,0,0,1); \end{aligned}$$

this implies that any information other than the value of $a\wedge b$ will not be leaked.

During a protocol execution, the “status” captures the joint distribution of (I, S) conditioned on P, where I is the input, S is the current card sequence, and P is the publicly available information. The two distribution above are the distribution of I conditioned on $f(I)=0$ and the distribution of I conditioned on $f(I)=1$, respectively.

To the best of our knowledge, Fig. 1 is the first attempt to depict the KWH-tree of the five-card trick. Because a formal treatment for non-committed format protocols does not exist, we will create such a formal framework, as will be explained in the next section.

3 Formalizing non-committed format protocols

In this section, we formally define a non-committed format protocol for a Boolean function, based on the encoding (1).

First, we define an “n-input protocol,” where the first 2n cards on the table are n input commitments.

Definition 1

Let $d\ge 2n$ for an integer $n\ge 2$, and let $\mathcal P$ be a d-card protocol. We say that $\mathcal P$ is an n-input protocol if its initial status consists of the following $2^n$ entries:

where $\alpha$ is a symbol sequence of length $d-2n$. Here, $p_i,~0\le i\le 2^n-1$, is the probability that the n-bit input is equal to the binary expression of i. Furthermore, we call the tuple $(p_0,\ldots ,p_{2^n-1})$ an input distribution.

As shown in Definition 1, we implicitly assume a one-to-one mapping between $\{0,1\}^n$ and $\{0,1,\ldots ,2^n-1\}$. Thus, throughout this paper, if we write $q_b$ for $b\in \{0,1\}^n$ and a tuple $(q_0,\ldots ,q_{2^n-1})$, we regard the subscription b as the corresponding decimal number.

Next, we define some properties regarding the statuses.

Definition 2

Let $\mathcal P$ be an n-input protocol with an input distribution $(p_0,\ldots ,p_{2^n-1})$, and consider a Boolean function $f:\{0,1\}^n \rightarrow \{0,1\}$.

• A status S of $\mathcal P$ is called an opaque status (in regard to f) if there exists two constants $c_0$ and $c_1$, $0\le c_0,c_1\le 1$, with $c_0{\sum _{i\in f^{-1}(0)}^{}p_i} + c_1{\sum _{i\in f^{-1}(1)}^{}p_i}=1$ such that the (coordinate-wise) sum of its probability traces $(q_0,\ldots ,q_{2^n-1})$ satisfies

  $$\begin{aligned} {\left\{ \begin{array}{ll} q_b=c_0\cdot p_b &{} \mathrm {if}\;f(b)=0\\ q_b=c_1\cdot p_b &{} \mathrm {if}\;f(b)=1 \end{array}\right. } \end{aligned}$$

  for every $b\in \{0,1\}^n$, where $f^{-1}(0)$ and $f^{-1}(1)$ are the preimages of 0 and 1 under f, respectively.

• We say that a status S is an output-0 status if the above constants satisfy $c_0=1$ and $c_1=0$, i.e., the sum of its probability traces $(q_0,\ldots ,q_{2^n-1})$ satisfies

  $$\begin{aligned} {\left\{ \begin{array}{ll} q_b=\frac{p_b}{\sum _{i\in f^{-1}(0)}^{}p_i} &{} \mathrm {if}\;f(b)=0\\ q_b=0 &{} \mathrm {if}\;f(b)=1 \end{array}\right. } \end{aligned}$$

  for every $b\in \{0,1\}^n$.

• We say that a status S is an output-1 status if the above constants satisfy $c_0=0$ and $c_1=1$, i.e., the sum of its probability traces $(q_0,\ldots ,q_{2^n-1})$ satisfies

  $$\begin{aligned} {\left\{ \begin{array}{ll} q_b=0 &{} \mathrm {if}\;f(b)=0\\ q_b=\frac{p_b}{\sum _{i\in f^{-1}(1)}^{}p_i} &{} \mathrm {if}\;f(b)=1 \end{array}\right. } \end{aligned}$$

  for every $b\in \{0,1\}^n$.

For example, see the leaf statuses in Fig. 1; the five left leaves are output-0 statuses, and the five right leaves are output-1 statuses. Note that $f(a,b)=a\wedge b$ satisfies $f^{-1}(0)=\{0,1,2\}$ and $f^{-1}(1)=\{3\}$.

We are now ready to formally define a non-committed format protocol.

Definition 3

Let $\mathcal P$ be an n-input protocol, and let $f:\{0,1\}^n \rightarrow \{0,1\}$ be a Boolean function. We say that $\mathcal P$ works for f in a non-committed format if the following holds:

• every leaf status is either an output-0 status or an output-1 status, and all other statuses are opaque;

• $\mathcal {P}$ terminates almost surely in a number of actions that is finite in expectation.

One can easily verify that the five-card trick satisfies the conditions in Definition 3.

As seen in Definition 3, this paper focuses on one-bit output functions.

4 Defining revealing-card tolerance

As mentioned before, this paper considers the active attack where an adversary can reveal some cards without obeying a protocol. Because the execution of a protocol is conducted publicly, it is difficult for an adversary to illegally reveal many cards simultaneously. Thus, we assume that, for a threshold $t\ge 1$, such a malicious adversary can reveal at most t cards at most once during an execution of the protocol.

Note that any n-input protocol (defined in Definition 1) cannot be “secure” against the actively revealing card attack because the adversary is able to reveal some cards that constitute the input commitments to obtain the secret values immediately after the protocol starts. Therefore, the input commitments must be masked. To achieve this, we borrow an idea from secret sharing schemes. Hence, instead of directly placing commitments to their private bits, Alice places two commitments to $a^1,a^2\in \{0,1\}$ where $a=a^1\oplus a^2$, i.e., her private bit a is split into $a^1$ and $a^2$ randomly, and Bob places two commitments similarly:

(3)

For such an input sequence, even if at most one card is revealed illegally, the values of a and b will not be leaked. The status of the above input sequence can be written as:

$$\begin{aligned}&\clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \quad \left( \frac{p_{00}}{4},0,0,0\right)&\\&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \clubsuit \quad \left( \frac{p_{00}}{4},0,0,0\right)&\\&\heartsuit \clubsuit \heartsuit \clubsuit \clubsuit \heartsuit \clubsuit \heartsuit \quad \left( \frac{p_{00}}{4},0,0,0\right)&\\&\heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \quad \left( \frac{p_{00}}{4},0,0,0\right)&\\&\clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \quad \left( 0,\frac{p_{01}}{4},0,0\right)&\\&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \clubsuit \heartsuit \quad \left( 0,\frac{p_{01}}{4},0,0\right)&\\&\heartsuit \clubsuit \heartsuit \clubsuit \clubsuit \heartsuit \heartsuit \clubsuit \quad \left( 0,\frac{p_{01}}{4},0,0\right)&\\&\heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \clubsuit \heartsuit \quad \left( 0,\frac{p_{01}}{4},0,0\right)&\\&\clubsuit \heartsuit \heartsuit \clubsuit \clubsuit \heartsuit \clubsuit \heartsuit \quad \left( 0,0,\frac{p_{10}}{4},0\right)&\\&\clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \quad \left( 0,0,\frac{p_{10}}{4},0\right)&\\&\heartsuit \clubsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \quad \left( 0,0,\frac{p_{10}}{4},0\right)&\\&\heartsuit \clubsuit \clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \clubsuit \quad \left( 0,0,\frac{p_{10}}{4},0\right)&\\&\clubsuit \heartsuit \heartsuit \clubsuit \clubsuit \heartsuit \heartsuit \clubsuit \quad \left( 0,0,0,\frac{p_{11}}{4}\right)&\\&\clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \clubsuit \clubsuit \heartsuit \quad \left( 0,0,0,\frac{p_{11}}{4}\right)&\\&\heartsuit \clubsuit \clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \quad \left( 0,0,0,\frac{p_{11}}{4}\right)&\\&\heartsuit \clubsuit \clubsuit \heartsuit \heartsuit \clubsuit \clubsuit \heartsuit \quad \left( 0,0,0,\frac{p_{11}}{4}\right)&. \end{aligned}$$

By further extending this, we have an $(n,t+1)$-input protocol, as in the following Definition 4. Hereinafter, for $b\in \{0,1\}^n$, b[i] denotes the i-th bit (of the n-bit sequence b).

Definition 4

Let $d\ge 2n(t+1)$ for integers $n\ge 2$ and $t\ge 1$, and let $\mathcal P$ be a d-card protocol. We say that $\mathcal P$ is an $(n,t+1)$-input protocol if its initial status consists of all entries in $\bigcup _{b\in \{0,1\}^n}^{}\mathcal {E}_b$ such that

for every $b\in \{0,1\}^n$, where $x^j_i\in \{0,1\}$ is interpreted as a pair of symbols based on the encoding: $0=\clubsuit \heartsuit$ and $1=\heartsuit \clubsuit$, and $\alpha$ is a symbol sequence of length $d-2n(t+1)$.

When implementing an $(n,t+1)$-input protocol, each player $P_i$ generates t random bits to prepare $t+1$ commitments to $\varvec{x}_i=(x_i^1, x_i^2, \ldots , x_i^{t+1})\in \{0,1\}^{t+1}$:

In this case, player $P_i$ knows the values of $x_i^1$ through $x_i^{t+1}$; for example, for the input (3) above, Alice knows the values of $a^1$ and $a^2$ and Bob knows the value of $b^1$ and $b^2$. Taking this into account, we consider KWH-trees “conditioned on player’s view,” as follows. Let us start with a small example. For the input (3) above, assume that Alice knows that $\varvec{a}=(a^1,a^2)=(0,0)$, i.e., the first four cards are $\clubsuit \heartsuit \clubsuit \heartsuit$; then, the “conditioned” status becomes:

$$\begin{aligned}&\clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \quad \left( {\textstyle \frac{p_{00}}{2(p_{00}+p_{01})},0,0,0}\right) \nonumber \\&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \clubsuit \quad \left( {\textstyle \frac{p_{00}}{2(p_{00}+p_{01})},0,0,0}\right) \nonumber \\&\clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \quad \left( 0,{\textstyle \frac{p_{01}}{2(p_{00}+p_{01})},0,0}\right) \nonumber \\&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \clubsuit \heartsuit \quad \left( 0,{\textstyle \frac{p_{01}}{2(p_{00}+p_{01})},0,0}\right) . \end{aligned}$$

(4)

Following this initial status, we can easily create its KWH-tree; we call it the player-view $\text {KWH-tree}^{\mid \varvec{a}}$${=(0,0)}$. To extend this idea, generally, we can have the player-view $\text {KWH-tree}^{\mid \varvec{x}_i=s}$ for i, $1\le i\le n$, and $s\in \{0,1\}^{t+1}$. (Thus, this paper considers only the case where each player has a one-bit input.)

We are now ready to define the “t-secureness” as in the following Definition 7 along with Definitions 5 and 6.

First, Definition 5 is a natural extension of Definitions 2 and 3.

Definition 5

Let $\mathcal P$ be an $(n,t+1)$-input protocol, and let $f:\{0,1\}^n \rightarrow \{0,1\}$ be a Boolean function. We define opaque, output-0, and output-1 statuses similarly as in Definition 2. In addition, we define “working for f” similarly to Definition 3.

Next, we have to consider “opaque” statuses in a player-view KWH-tree. The reason is as follows. Assume that $a=a^1\oplus a^2$ and $b=b^1\oplus b^2$, and that we happen to have a commitment to $(a^1\wedge b^1)\oplus (a^1\wedge b^2)$. If Alice knows $a^1=1$, for instance, revealing this commitment immediately gives Alice the value of $b^1\oplus b^2=b$; by contract, just knowing the value of $(a^1\wedge b^1)\oplus (a^1\wedge b^2)$ (without any knowledge about $a^1$, $b^1$, and $b^2$) does not provide the exact value of b. Therefore, we need the following Definition 6.

Definition 6

Let $\mathcal P$ be an $(n,t+1)$-input protocol. Consider the player-view $\text {KWH-tree}^{\mid \varvec{x}_i=s}$ for any i, $1\le i\le n$, and $s\in \{0,1\}^{t+1}$. A status S is said to be opaque under player’s view $\varvec{x}_i=s$ if the (coordinate-wise) sum of its probability traces $(q_0,\ldots ,q_{2^n-1})$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} q_b=0 &{} \mathrm {if } b\notin \mathcal {G},\\ q_b={\textstyle \frac{p_b}{\sum _{j\in \mathcal {G}}p_j}} &{} \mathrm {if } b\in \mathcal {G}, \end{array}\right. } \end{aligned}$$

for every $b\in \{0,1\}^n$, where

Finally, it suffices to consider any attacks of revealing at most t cards and opaqueness against them under any player’s view.

Definition 7

Let $\mathcal P$ be an $(n,t+1)$-input protocol working for a Boolean function f in a non-committed format. We say that $\mathcal P$ is t-secure if any resulting status from applying any action $(\mathsf {turn}$ $, T)$ with $|T|\le t$ to every status of $\mathcal P$ satisfies one of the followings:

• it is an opaque status under $x_i=s$ in any player-view $\text {KWH-tree}^{\mid \varvec{x}_i=s}$ for every i, $1\le i\le n$, and $s\in \{0,1\}^{t+1}$;

• it is an output-0 status;

• it is an output-1 status.

5 Our 1-secure AND protocol

In this section, we describe the construction of a 1-secure AND protocol. In Sect. 5.1, we present its outline; our protocol consists of the setup, first, second, and third phases. In Sects. 5.2, 5.3, and 5.4, we provide the details of the first, second, and third phases, respectively.

5.1 Outline of our protocol

Because we wish to design a 1-secure AND computation of two variables (namely, $n=2$ and $t=1$), we should use a (2, 2)-input protocol. Therefore, Alice and Bob create commitments to $a^1,a^2\in \{0,1\}$ and $b^1,b^2\in \{0,1\}$ such that $a=a^1\oplus a^2$ and $b=b^1\oplus b^2$, respectively. Given such input commitments, to obtain the AND value, it suffices to compute $(a^1\wedge b^1)\oplus (a^1\wedge b^2)\oplus (a^2\wedge b^1)\oplus (a^2\wedge b^2)=a\wedge b$. To this end, our protocol proceeds as follows.

Setup phase.:

Satisfying Definition 4, Alice places two commitments to $a^1$ and $a^2$, and Bob places two commitments to $b^1$ and $b^2$:

(5)

First phase.:

Make two copied commitments to each of $b^1$ and $b^2$ using the existing COPY protocol (Mizuki and Sone 2009):

Second phase.:

From three commitments to $a^1$, $b^1$, and $b^2$, make two commitments to $a^1\wedge b^1$ and $a^1\wedge b^2$ using the existing AND protocol (Mizuki and Shizuya 2014b); similarly, from three commitments to $a^2$, $b^1$, and $b^2$, make two commitments to $a^2\wedge b^1$ and $a^2\wedge b^2$:

Third phase.:

Compute $(a^1\wedge b^1)\oplus (a^1\wedge b^2)\oplus (a^2\wedge b^1)\oplus (a^2\wedge b^2)$.

Here, we analyze the security of the setup phase. There are 16 possibilities for $(a^1,a^2,b^1,b^2)\in \{0,1\}^4$, and as seen in Sect. 4, the initial status can be written as the first four columns and the last column in Table 1. From this, one can obtain any player-view $\text {KWH-tree}^{\mid \varvec{x}_i=s}$ for every i, $1\le i\le 2$, and $s\in \{0,1\}^{2}$, such as the status (4) above. For example, if Alice knowing $a^1=a^2=0$ is malicious and reveals the fifth card illegally, the resulting status becomes either

$$\begin{aligned}&\clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \quad \left( {\textstyle \frac{p_{00}}{(p_{00}+p_{01})},0,0,0}\right) \\&\clubsuit \heartsuit \clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \quad \left( 0,{\textstyle \frac{p_{01}}{(p_{00}+p_{01})},0,0}\right) \end{aligned}$$

or

$$\begin{aligned}&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \heartsuit \clubsuit \quad \left( {\textstyle \frac{p_{00}}{(p_{00}+p_{01})},0,0,0}\right) \\&\clubsuit \heartsuit \clubsuit \heartsuit \heartsuit \clubsuit \clubsuit \heartsuit \quad \left( 0,{\textstyle \frac{p_{01}}{(p_{00}+p_{01})},0,0}\right) , \end{aligned}$$

and one can confirm that both of them are opaque under $\varvec{x}_1=(0,0)$. In this way, one can easily confirm that an action $(\mathsf {turn}, \{j\})$ for any j results in an opaque status under $\varvec{x}_i=s$ (in any player-view KWH-tree). Note that $(\mathsf {turn}, \{j\})$ reveals (at most) one bit among $a^1,a^2,b^1,b^2$.

5.2 First phase

In this phase, we duplicate the commitments to $b^1$ and $b^2$. To this end, we use the existing COPY protocol (Mizuki and Sone 2009) whose KWH-tree is shown in Fig. 2; it performs the following:

By executing the COPY protocol twice, we have

Fig. 2

The KWH-tree of the existing COPY protocol (Mizuki and Sone 2009)

Fig. 3

The KWH tree of the existing AND protocol (Mizuki and Shizuya 2014b)

Table 1 Essential truth table for deriving statuses of our protocol

During this first phase, an action $(\mathsf {turn}, \{j\})$ for any j reveals at most one bit among $b^1$ and $b^2$; hence, similar to the setup phase, any resulting status from an illegal revealment will be opaque under every player’s view.

5.3 Second phase

In this phase, we use the existing AND protocol (Mizuki and Shizuya 2014b):

Figure 3 is the KWH-tree of this AND protocol. We destroy the commitments to $\overline{x}\wedge y$ and $\overline{x}\wedge z$ by shuffling each of them.

By executing the AND protocol twice, we have

During this second phase, an action $(\mathsf {turn}, \{j\})$ for any j reveals at most one bit among $a^1,a^2,b^1,b^2$, $a^1\wedge b^1,a^1\wedge b^2,a^2\wedge b^1,a^2\wedge b^2$, $\overline{a^1}\wedge b^1,\overline{a^1}\wedge b^2,\overline{a^2}\wedge b^1,\overline{a^2}\wedge b^2$; Table 1 implies that any illegal resulting status will be opaque under every player’s view. For example, suppose that Alice knows $a^1=a^2=1$ and she reveals the value of $a^1\wedge b^1=0$; then, there are two entries for $(a^1,a^2,a^1\wedge b^1)=(1,1,0)$ in Table 1 (namely, the fourth and eighth rows), from which we can calculate that the sum of the probability traces of the current status is $(\tfrac{p_{00}}{p_{00}+p_{01}}, \tfrac{p_{01}}{p_{00}+p_{01}}, 0, 0)$.

5.4 Third phase

In this phase, we compute $(a^1\wedge b^1)\oplus (a^1\wedge b^2)\oplus (a^2\wedge b^1)\oplus (a^2\wedge b^2)$ from the commitments to $a^1\wedge b^1$, $a^1\wedge b^2$, $a^2\wedge b^1$, and $a^2\wedge b^2$:

Note that the number of commitments to 1 among the four commitments can be 0, 1, 2, or 4 (as known from Table 1) and that the number is 1 if and only if $a\wedge b=1$.

In the current status, for instance, $(a^1\wedge b^1,a^1\wedge b^2,a^2\wedge b^1,a^2\wedge b^2)=(0,0,0,0)$ occurs with a probability trace $(\frac{3}{4}p_{00},\frac{1}{2}p_{01},\frac{1}{2}p_{10},0)$ as known from Table 1; thus, the current status is the topmost box in Fig 4. Our “specialized 4-bit XOR subprotocol” proceeds as follows.

• 1. Negate the commitment to $a^1\wedge b^1$ by $(\mathsf {perm}, (1\;2))$:

  

  Note that the number of commitments to 1 among the four commitments can be 0, 1, 2, or 3 and that the number is 0 or 2 if and only if $a\wedge b=1$.

• 2. By this step along with the next two steps, we add a common random bit to the four commitments. Rearrange the sequence of the eight cards by $(\mathsf {perm}$, $(2\;5\;3)(4\;6\;7))$:

  

• 3. Apply a random bisection cut (Mizuki and Sone 2009), denoted by $\left[ \, \cdot \, | \, \cdot \, \right]$, which is the shuffle action $(\mathsf {shuf},{\{\mathsf {id}, (1\,5)(2\,6)(3\,7)(4\,8)\}})$:

  

• 4. Apply $(\mathsf {perm},{(2\,3\,5)(4\,7\,6)})$, which is the inverse permutation of Step 2:

  

• 5. Apply $(\mathsf {shuf},{\{(1\,2\,3\,4\,5\,6\,7\,8)^{2i}\mid 1\le i\le 4\}})$, which is a pile-shifting scramble (Nishimura et al. 2018) denoted by:

  

• 6. Reveal all the cards by $(\mathsf {turn},{\{1,2,3,4,5,6,7,8\}})$. Then, count the commitments :

  • If the number of commitments to 1 is odd, $a\wedge b=0$.

  • If the number of commitments to 1 is even, $a\wedge b=1$.

The KWH-tree of our XOR subprotocol, which implies the correctness and secrecy, is shown in Fig. 4.

Fig. 4

The KWH-tree of our specialized 4-bit XOR subprotocol

During this third phase, an action $(\mathsf {turn}, \{j\})$ for any j reveals at most one bit among $a^1\wedge b^1$, $a^1\wedge b^2$, $a^2\wedge b^1$, and $a^2\wedge b^2$; Table 1 implies that any illegal resulting status from the statuses except for the leaf statuses will be opaque (under any player’s view) and any illegal resulting status from the leaf statuses will be an output-0 status or an output-1 status.

To summarize, our 1-secure AND protocol satisfies Definition 7; hence, it is proved to be 1-secure.

6 Our t-secure AND protocol

We extend our 1-secure AND protocol presented in Sect. 5 to a general one so that we have a t-secure AND protocol in this section.

6.1 Idea

To construct a t-secure AND protocol, let us first consider how to construct a 2-secure AND protocol. As our 1-secure AND protocol (shown in Sect. 5) does, we make Alice’s private bit a be split into $a^1$, $a^2$, and $a^3$ randomly, and make Bob’s private bit b be split similarly. Then, one should consider the following formula (by virtue of the distributivity in the field $\{\{0,1\},\oplus ,\wedge \}$):

$$\begin{aligned} a\wedge b&= (a^1\oplus a^2\oplus a^3)\wedge (b^1\oplus b^2\oplus b^3),\nonumber \\&=(a^1\wedge b^1)\oplus (a^1\wedge b^2)\oplus (a^1\wedge b^3)\nonumber \\&\oplus (a^2\wedge b^1)\oplus (a^2\wedge b^2)\oplus (a^2\wedge b^3)\nonumber \\&\oplus (a^3\wedge b^1)\oplus (a^3\wedge b^2)\oplus (a^3\wedge b^3). \end{aligned}$$

(6)

Remember that in our 1-secure AND protocol, we directly compute $(a^1\wedge b^1)\oplus (a^1\wedge b^2)\oplus (a^2\wedge b^1)\oplus (a^2\wedge b^2)$ by using our specialized 4-bit XOR subprotocol. Because it seems somewhat difficult to construct such a specialized 9-bit XOR subprotocol, we consider the use of the existing XOR protocol (Mizuki and Sone 2009), by which we can obtain a commitment to $x\oplus y$ from two given commitments to x and y.

To compute $a\wedge b$ according to Eq. (6), it is natural to first make a commitment to $(a^1\wedge b^1)\oplus (a^1\wedge b^2)$. However, note that this commitment has information about $b^1$ and $b^2$; if Alice knows $a^1=1$ for example, the value of this commitment implies $b^1\oplus b^2$ and the value of a commitment to $a^1\wedge b^3$ implies $b^3$. Therefore, Alice can learn the value of $b^1\oplus b^2\oplus b^3=b$ by revealing the corresponding two cards maliciously as soon as such commitments are produced. That is, 2-secureness cannot be realized by just using the existing XOR protocol, based on Eq. (6). To overcome this, it suffices to add two random bits $r^1$ and $r^2$. That is, we can consider the following formula:

$$\begin{aligned} a\wedge b&= (r^1\oplus r^2)\oplus (a^1\wedge b^1)\oplus (a^1\wedge b^2)\oplus (a^1\wedge b^3)\nonumber \\&\quad \oplus (a^2\wedge b^1)\oplus (a^2\wedge b^2)\oplus (a^2\wedge b^3)\nonumber \\&\quad \oplus (a^3\wedge b^1)\oplus (a^3\wedge b^2)\oplus (a^3\wedge b^3) \oplus r^1 \oplus r^2. \end{aligned}$$

(7)

Based on the above idea, the construction of our 2-secure AND protocol is as follows.

• 1. Make two pairs of random commitments:

  

  where $r^1$ and $r^2$ are uniformly distributed random bits. Make a single commitment to $r^1\oplus r^2$ using the existing XOR protocol (Mizuki and Sone 2009):

  

  We call this commitment the accumulator A, which will be updated by adding $a^i\wedge b^j$ as in Eq. (7).

• 2. Make two copied commitments to each of $b^1$, $b^2$, and $b^3$ using the existing COPY protocol (Mizuki and Sone 2009).

• 3. Make three commitments to $(a^1\wedge b^1)$, $(a^1\wedge b^2)$, and $(a^1\wedge b^3)$ using the existing AND protocol (Mizuki and Shizuya 2014b).

• 4. Make a commitment to $A\oplus (a^1\wedge b^1)$ using the existing XOR protocol (Mizuki and Sone 2009):

  

  We regard the obtained commitment as the accumulator $A{:}{=} A\oplus (a^1\wedge b^1)$. Similarly, we add $a^1\wedge b^2$ and $a^1\wedge b^3$ to A one by one.

• 5. In a similar manner, add everything from $a^2\wedge b^1$ to $a^3\wedge b^3$ to the accumulator A.

• 6. Reveal the accumulator A and the commitments to $r^1$ and $r^2$. The parity of all the revealed values is equal to $a\wedge b$.

Intuitively, this protocol is 2-secure because to learn the values added to the accumulator A, one has to reveal the values of the three commitments, namely the accumulator A and commitments to $r^1$ and $r^2$. We will show the t-secureness in Sect. 6.4; roughly speaking, revealing two values among available commitments does not recover the value of b.

Finally, let us extend the above idea to realize t-secureness. First, we make an input private bit a be split into $t+1$ bits $a^1,a^2,\ldots ,a^{t+1}$. Similarly, we make b be split into $t+1$ bits. Then, to compute $a\wedge b$, we consider the following formula:

$$\begin{aligned} a\wedge b = (r^1\oplus \cdots \oplus r^t)\oplus \left( \bigoplus _{i=1}^{t+1}\bigoplus _{j=1}^{t+1} (a^i \wedge b^j)\right) \oplus r^1\oplus \cdots \oplus r^t. \end{aligned}$$

To compute this, we make $t+1$ commitments, namely the accumulator $A=r^1\oplus \cdots \oplus r^t$ and commitments to $r^i$, $1\le i\le t$. Then, we add everything from $a^1\wedge b^1$ to $a^{t+1}\wedge b^{t+1}$ to the accumulator A.

6.2 Procedure of our t-secure AND protocol

Based on the idea explained in Sect. 6.1, our t-secure AND protocol proceeds as follows.

• 1. Satisfying Definition 4, Alice places $t+1$ commitments to $a^1,a^2,\ldots ,a^{t+1}$, and Bob places $t+1$ commitments to $b^1,b^2,\ldots ,b^{t+1}$:

  

• 2. Make t pairs of random commitments:

  

  where $r^i$, $1\le i\le t$, is a uniformly distributed random bit. Make a single commitment to the accumulator $A=r^1\oplus \cdots \oplus r^t$ using the existing XOR protocol (Mizuki and Sone 2009) $t-1$ times:

  

• 3. Make two copied commitments to each of $b^j$, $1\le j\le t+1$, using the existing COPY protocol (Mizuki and Sone 2009).

• 4. Make commitments to $a^1\wedge b^j$, $1\le j\le t+1$, using the existing AND protocol (Mizuki and Shizuya 2014b).

• 5. Make a commitment to $A\oplus (a^1\wedge b^1)$ using the existing XOR protocol (Mizuki and Sone 2009):

  

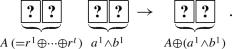
  We regard the obtained commitment as the accumulator $A{:}{=} A\oplus (a^1\wedge b^1)$. Similarly, we add $a^1\wedge b^k$, $2\le k\le t+1$, to A one by one.

• 6. In a similar manner, add everything from $a^2\wedge b^1$ to $a^{t+1}\wedge b^{t+1}$ to the accumulator A. (For $a^{t+1}$, making two copied commitments to each of $b^j$ is not needed.)

• 7. Reveal the accumulator A and the commitments to $r^i$, $1\le i\le t$. The parity of all the revealed values is equal to $a\wedge b$.

6.3 Evaluation

Let us count the number of required cards for our t-secure AND protocol presented in Sect. 6.2. In Step 1, $4(t+1)$ cards are needed. In Step 2, 4t cards are needed. Note that $2(t-1)$ revealed cards which arise during the existing XOR protocol (Mizuki and Sone 2009) can be reused for the next step. In Step 3, we need four additional cards to make two copied commitments to $b^1$ by using the existing COPY protocol (Mizuki and Sone 2009). In this protocol, two cards should be revealed, and we can reuse them to make two copied commitments to $b^2$ and so on. That is, $4+2t$ cards are needed. Since $2(t-1)$ cards are left in the previous step, we need six more cards in this step. In Step 4, since the existing AND protocol (Mizuki and Shizuya 2014b) requires four additional cards, we need two more cards along with two cards revealed in the previous step. In this step, six cards are revealed and can be reused. In Step 5, since the existing XOR protocol (Mizuki and Sone 2009) is used $t+1$ times, $2(t+1)$ cards (along with the six cards revealed in the previous step) can be reused for the next step. In Step 6, for $a^i$, $2\le i \le t$, to make two copied commitments to each of $b^j$, $1\le j\le t+1$, we need $4+2t$ cards as mentioned before. Since $2(t+1)+6$ cards are left, no more card is needed. In total, $4(t+1)+4t+6+2=8t+12$ cards are needed.

Let us count the number of required shuffles. In our protocol, we use the existing AND, XOR, and COPY protocols (Mizuki and Sone 2009; Mizuki and Shizuya 2014b). Each of them needs one shuffle to execute. In Step 2, we apply a random cut t times and execute the existing XOR protocol $t-1$ times. In Step 3, we execute the existing COPY protocol $t+1$ times. In Step 4, we execute the existing AND protocol and destroy the unnecessary two commitments by shuffling all of them. In Step 5, we execute the existing XOR protocol $t+1$ times. In Step 6, for $a^i$, $2\le i \le t+1$, we execute the existing COPY protocol $t+1$ times (except for the case of $i=t+1$), the existing AND protocol (along with destroying commitments), and the existing XOR protocol $t+1$ times. In total, $t+t-1+t(t+1+2+t+1)+2+t+1=2t^2+7t+2$ shuffles are needed.

Our 1-secure AND protocol uses 16 cards and 8 shuffles, and our t-secure AND protocol (when $t=1$) uses 20 cards and 11 shuffles. The difference is that, while the former (1-secure) one uses our specialized 4-bit XOR subprotocol (where a shuffle is applied twice), the later (t-secure) one creates two pairs of t random commitments (where a shuffle is applied once) and adds the value of $a^i\wedge b^j$ for all i and j, $1\le i,j\le t+1$, to the accumulator one by one (where a shuffle is applied four times).

6.4 Security of our protocol

In this subsection, we show that our protocol presented in Sect. 6.2 is t-secure (recall Definition 7).

Without loss of generality, suppose that Alice will reveal t cards illegally. During our protocol, commitments to $a^i\wedge b^j$, $1\le i,j\le t+1$, will appear; if $a_i=0$, those commitments always have the value of 0. Therefore, we assume for now that Alice knows $a^i=1$ for all i. That is, we consider the $\text {KWH-tree}^{\mid \varvec{x}_1=(1,1,\ldots ,1)}$. Then, during the protocol, possibly available commitments (to be revealed by Alice) are “shares” $b^1,\ldots ,b^{t+1}$, the accumulator A, and random bits $r^1,\ldots ,r^{t}$. If Alice reveals t values from $b^1,\ldots ,b^{t+1}$ and $r^1,\ldots ,r^{t}$ (without A), then the resulting status is still opaque obviously. Therefore, we may assume that Alice reveals the accumulator A.

Now, Alice can reveal $t-1$ more commitments. There are two cases to consider.

• Case 1: A contains all $b^1,\ldots ,b^{t+1}$.

  Without loss of generality, assume that Alice reveals neither $b^1$ nor $r^1$. Aside from these two values $b^1$ and $r^1$, let us reveal all values of $b^2,\ldots , b^{t+1}$ and $r^2,\ldots , r^t$ (this may be more than t cards revealed, but we can still show that the status will be opaque). Without loss of generality, all revealed values are assumed to be 0, i.e., $b^2=\cdots =b^{t+1}=r^2=\cdots =r^t=0$ and $A=b^1\oplus \cdots \oplus b^{t+1}\oplus r^1\oplus \cdots \oplus r^{t+1}=0$. Then, we have $b=b^1=r^1$, and hence, we have no knowledge about whether $b=0$ or $b=1$ (because $b^1$ and $r^1$ are unknown random bits). All the current face-up cards are commitments to b:

  

  in the current status, we have entries

  $$\begin{aligned}&\left( \cdots \clubsuit \heartsuit \clubsuit \heartsuit \cdots , \left( 0,0,\tfrac{p_{10}}{p_{10}+p_{11}},0\right) \right) \\&\left( \cdots \heartsuit \clubsuit \heartsuit \clubsuit \cdots , \left( 0,0,0,\tfrac{p_{11}}{p_{10}+p_{11}}\right) \right) , \end{aligned}$$

  implying that it is opaque under player’s view $\varvec{x}_1=(1,\ldots ,1)$. A similar discussion works for other player’s views $\varvec{x}_1=s$.

• Case 2: A does not contain some of $b^1,\ldots ,b^{t+1}$.

  Without loss of generality, assume that A does not contain $b^1$. Then, reveal all cards except for $b^1$ and $r^1$. In a similar way to Case 1, we can show that the resulting status is opaque.

7 Conclusion

In this paper, we first described the KWH-tree of the five-card trick and formally defined non-committed protocols. Against the actively revealing card attack, we defined the t-secureness and presented a 1-secure AND protocol and a general t-secure AND protocol.

We assume in this paper that players’ inputs are one-bit and they want to securely compute a one-bit output function. Thus, extending the results to the case of multiple bits is an intriguing direction for future research. Furthermore, considering actively revealing attacks on other problems or models (e.g., Ono and Manabe 2020; Ruangwises and Itoh 2020; Shinagawa and Nuida 2021; Sasaki et al. 2020; Miyahara et al. 2020; Takashima et al. 2020; Koch et al. 2019; Ibaraki and Manabe 2016; Ono and Manabe 2019, 2018) will be future work in the research area of card-based cryptography.