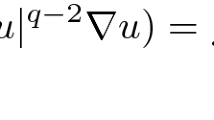Bounded weak solutions to superlinear Dirichlet double phase problems

Abstract

In this paper we study a Dirichlet double phase problem with a parametric superlinear right-hand side that has subcritical growth. Under very general assumptions on the data, we prove the existence of at least two nontrivial bounded weak solutions to such problem by using variational methods and critical point theory. In contrast to other works we do not need to suppose the Ambrosetti–Rabinowitz condition.

1 Introduction

In this paper we consider the following Dirichlet double phase problem

$$\begin{aligned} \begin{aligned} -{\text {div}} \big (|\nabla u|^{p-2}\nabla u +\mu (x)|\nabla u|^{q-2}\nabla u \big )&= \lambda f(x,u)\quad{} & {} \text {in } \Omega ,\\ u&= 0{} & {} \text {on } \partial \Omega , \end{aligned} \end{aligned}$$

(1.1)

where $\Omega \subseteq \mathbb {R}^N$, $N\ge 2$, is a bounded domain with Lipschitz boundary $\partial \Omega$, $1<p<N$, $p<q<p^*$ and $0\le \mu (\cdot )\in L^\infty (\Omega )$ with $p^*=\frac{Np}{N-p}$, $\lambda >0$ is a parameter and $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function that satisfies subcritical growth and a certain behavior at $\pm \infty$.

The operator involved is the so-called double phase operator defined by

$$\begin{aligned} {\text {div}} \big (|\nabla u|^{p-2}\nabla u +\mu (x)|\nabla u|^{q-2}\nabla u \big )\quad \text {for }u\in W^{1, \mathcal {H}}_0(\Omega )\end{aligned}$$

(1.2)

with $W^{1, \mathcal {H}}_0(\Omega )$ being an appropriate Musielak-Orlicz Sobolev space, see its Definition in Sect. 2. It is clear that (1.2) reduces to the p-Laplacian if $\mu \equiv 0$ and to the (q, p)-Laplacian if $\inf _\Omega \mu \ge \mu _0>0$. Moreover, the double phase operator is related to the two-phase integral functional $J:W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}$ given by

$$\begin{aligned} J(u)=\int _{\Omega }\left(|\nabla u|^p+\mu (x)|\nabla u|^q\right)\,\textrm{d}x. \end{aligned}$$

(1.3)

Zhikov [24] was the first who introduced and studied functionals of type (1.3) whose integrands change their ellipticity according to a point in order to provide models for strongly anisotropic materials. It is clear that the integrand of (1.3) has unbalanced growth. The main characteristic of (1.3) is the change of ellipticity on the set where the weight function is zero, that is, on the set $\{x\in \Omega :\, \mu (x)=0\}$. In other words, the energy density of (1.3) exhibits ellipticity in the gradient of order q on the points x where $\mu (x)$ is positive and of order p on the points x where $\mu (x)$ vanishes. We also refer to the book of Zhikov-Kozlov-Oleĭnik [25]. Functionals of the form (1.3) have been studied by several authors with respect to regularity of local minimizers, see, for example, the works of Baroni-Colombo-Mingione [1,2,3], Colombo-Mingione [9, 10] and for nonautonomous integrals, the recent work of De Filippis-Mingione [12].

The main objective of our work is to apply an abstract critical point theorem to problem (1.1) in order to get two nontrivial bounded weak solutions with different energy sign. In addition, we give a precise interval to which the solutions belong. Our paper can be seen as an extension of a work of the first two authors recently published in [22]. The differences to [22] are twofold: First, in [22] the operator is the well-known (q, p)-Laplacian and so the function space is a usual Sobolev space. Second, we are able to weaken the assumptions on f in our paper. Indeed, in contrast to [22] and lots of other works in this direction we do not need to assume that f fulfills the usual Ambrosetti–Rabinowitz condition, which says, that there exist $\tilde{\mu }>q$ and $M>0$ such that

for a. a. $x\in \Omega$ and for all $|s|\ge M$. Instead of (AR) we suppose that the primitive of f is q-superlinear at $\pm \infty$ (see (H2)(ii)) and we have another behavior near $\pm \infty$, see (H2)(iii). Both conditions are weaker than (AR) and they also imply that f is $(q-1)$-superlinear at $\pm \infty$. Note that we do not need any behavior of f or its primitive near the origin, see Theorem 3.4.

The abstract critical point theorem we used is due to Bonanno-D’Aguì  [4, see Theorem 2.1 and Remark 2.2] and was applied in the same paper to the p-Laplace problem

$$\begin{aligned} \begin{aligned} -\Delta _pu&= \lambda f(x,u)\quad{} & {} \text {in } \Omega ,\\ u&= 0{} & {} \text {on } \partial \Omega , \end{aligned} \end{aligned}$$

(1.4)

in order to get two nontrivial solutions of (1.4).

Finally we would like to mention related works dealing with multiplicity results for (p, q)-Laplacians or double phase problems via different methods, like truncation techniques, comparison principles, critical point theory, Nehari manifold treatment and so on. We refer to the papers of Bonanno-D’Aguì-Livrea [5] (general nonhomogeneous operators), Bonanno-D’Aguì-Winkert [6] (nondifferentiable functions), Chinnì-Sciammetta-Tornatore [7] (anisotropic (p, q)-equations), Colasuonno-Squassina [8] (double phase eigenvalue problems), Gasiński-Winkert [14, 15] (convection and superlinear problems), Liu-Dai [17] (Nehari manifold treatment), Papageorgiou-Winkert [20] (subdiffusive and equidiffusive (p, q)-equations), Perera-Squassina [21] (Morse theory for double phase problems), see also the references therein.

The paper is organized as follows. In Sect. 2 we recall some facts about Musielak-Orlicz Sobolev spaces and state the abstract critical point theorem mentioned above, see Theorem 2.4. Then, in Sect. 3 we formulate our hypotheses, state and prove our main result, see Theorem 3.4 and we consider some consequences for special cases of (1.1), see Corollaries 3.5 and 3.6, especially when f is nonnegative and independent of x.

2 Preliminaries

In this section we recall some preliminary facts and tools which are needed in the sequel. To this end, let $\Omega \subseteq \mathbb {R}^N$, $N\ge 2$ be a bounded domain with Lipschitz boundary $\partial \Omega$. For $1\le r\le \infty$ we denote by $L^{r}(\Omega )$ and $L^r(\Omega ;\mathbb {R}^N)$ the usual Lebesgue spaces equipped with the norm $\Vert \cdot \Vert _r$ and for $1\le r<\infty$, $W^{1,r}(\Omega )$ and $W^{1,r}_0(\Omega )$ stand for the Sobolev spaces endowed with the norms $\Vert \cdot \Vert _{1,r}$ and $\Vert \cdot \Vert _{1,r,0}=\Vert \nabla \cdot \Vert _r$, respectively.

Let $1<p<\infty$. From the Sobolev embedding theorem we know that for any $\ell \in [1,p^*]$ we have the continuous embedding $W^{1,p}_0(\Omega )\rightarrow L^{\ell }(\Omega )$ with best constant $c_{\ell }>0$, that is,

$$\begin{aligned} \Vert u\Vert _{\ell } \le c_{\ell } \Vert \nabla u\Vert _{p} \quad \text {for all }u\in W^{1,p}_0(\Omega ). \end{aligned}$$

(2.1)

It is clear that the embedding in (2.1) is compact if $\ell <p^*$. Suppose that $\ell <p^*$. Then, from Hölder’s inequality and (2.1), we obtain

$$\begin{aligned} c_\ell \le c_{p^*}|\Omega |^{\frac{p^*-\ell }{p^*\ell }} \end{aligned}$$

(2.2)

with $|\Omega |$ being the Lebesgue measure of $\Omega$ in $\mathbb {R}^N$.

Let

$$\begin{aligned} R:=\sup _{x\in \Omega } {\text {dist}}(x,\partial \Omega ). \end{aligned}$$

(2.3)

Then we can find an element $x_0 \in \Omega$ such that the ball with center $x_0$ and radius $R>0$ belongs to $\Omega$, that is,

$$\begin{aligned} B(x_0,R)\subseteq \Omega . \end{aligned}$$

(2.4)

We set

$$\begin{aligned} \omega _{R}:=|B(x_0,R)|=\frac{\pi ^{\frac{N}{2}}}{\Gamma (1+\frac{N}{2})}R^N \end{aligned}$$

(2.5)

and

$$\begin{aligned} K:= \frac{c_{p^*}^p\omega _R\left( 2^{N}-1\right) }{\left( 2^{N-q}\right) |\Omega |^{\frac{p}{p^*}}}\max \left\{ \dfrac{1}{R^p},\dfrac{\Vert \mu \Vert _\infty }{R^q}\right\} . \end{aligned}$$

(2.6)

In the following we use the subsequent assumptions:

• (H1) $1<p<N$, $p<q<p^*$ and $0\le \mu (\cdot )\in L^\infty (\Omega )$, where $p^*$ is the critical Sobolev exponent to p given by $p^*=\frac{Np}{N-p}$.

Let $M(\Omega )$ be the space of all measurable functions $u:\Omega \rightarrow \mathbb {R}$ and let $\mathcal {H}:\Omega \times [0,\infty )\rightarrow [0,\infty )$ be the nonlinear function defined by

$$\begin{aligned} \mathcal H(x,t)= t^p+\mu (x)t^q. \end{aligned}$$

Then, the Musielak-Orlicz space $L^\mathcal {H}(\Omega )$ is defined by

$$\begin{aligned} L^\mathcal {H}(\Omega )=\left\{ u\in M(\Omega )\,:\, \rho _{\mathcal {H}}(u)<+\infty \right\} \end{aligned}$$

equipped with the Luxemburg norm

$$\begin{aligned} \Vert u\Vert _{\mathcal {H}} = \inf \left\{ \tau >0 \,:\, \rho _{\mathcal {H}}\left( \frac{u}{\tau }\right) \le 1 \right\} , \end{aligned}$$

where the modular function $\rho _{\mathcal {H}}$ is given by

$$\begin{aligned} \rho _{\mathcal {H}}(u):=\int _{\Omega }\mathcal {H}(x,|u|)\,\textrm{d} x=\int _{\Omega }\big (|u|^{p}+\mu (x)|u|^q\big )\,\textrm{d} x. \end{aligned}$$

(2.7)

Furthermore, we define the seminormed space

$$\begin{aligned} L^q_\mu (\Omega )=\left\{ u\in M(\Omega )\,:\,\int _{\Omega }\mu (x) |u|^q \,\textrm{d} x< +\infty \right\} , \end{aligned}$$

which is endowed with the seminorm

$$\begin{aligned} \Vert u\Vert _{q,\mu } = \left( \int _{\Omega }\mu (x) |u|^q \,\textrm{d} x \right) ^{\frac{1}{q}}. \end{aligned}$$

The Musielak-Orlicz Sobolev space $W^{1,\mathcal {H}}(\Omega )$ is defined by

$$\begin{aligned} W^{1,\mathcal {H}}(\Omega )= \left\{ u \in L^\mathcal {H}(\Omega ) \,:\, |\nabla u| \in L^{\mathcal {H}}(\Omega ) \right\} \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert _{1,\mathcal {H}}= \Vert \nabla u \Vert _{\mathcal {H}}+\Vert u\Vert _{\mathcal {H}}, \end{aligned}$$

where $\Vert \nabla u\Vert _\mathcal {H}=\Vert \,|\nabla u|\,\Vert _{\mathcal {H}}$. The completion of $C^\infty _0(\Omega )$ in $W^{1,\mathcal {H}}(\Omega )$ is denoted by $W^{1,\mathcal {H}}_0(\Omega )$. We know that $L^{\mathcal {H}}(\Omega )$, $W^{1,\mathcal {H}}(\Omega )$ and $W^{1,\mathcal {H}}_0(\Omega )$ are reflexive Banach spaces and we can equip the space $W^{1,\mathcal {H}}_0(\Omega )$ with the equivalent norm

$$\begin{aligned} \Vert u\Vert =\Vert \nabla u\Vert _{\mathcal {H}}, \end{aligned}$$

see Proposition 2.18(ii) of Crespo-Blanco-Gasiński-Harjulehto-Winkert [11].

The norm $\Vert \cdot \Vert _{\mathcal {H}}$ and the modular function $\rho _\mathcal {H}$ are related as follows, see Liu-Dai [17, Proposition 2.1].

Proposition 2.1

Let (H1) be satisfied, let $y\in L^{\mathcal {H}}(\Omega )$ and let $\rho _{\mathcal {H}}$ be defined by (2.7). Then the following hold:

• (i) If $y\ne 0$, then $\Vert y\Vert _{\mathcal {H}}=\lambda$ if and only if $\rho _{\mathcal {H}}(\frac{y}{\lambda })=1$;

• (ii) $\Vert y\Vert _{\mathcal {H}}<1$ (resp. $>1$, $=1$) if and only if $\rho _{\mathcal {H}}(y)<1$ (resp. $>1$, $=1$);

• (iii) If $\Vert y\Vert _{\mathcal {H}}<1$, then $\Vert y\Vert _{\mathcal {H}}^q\le \rho _{\mathcal {H}}(y)\le \Vert y\Vert _{\mathcal {H}}^p$;

• (iv) If $\Vert y\Vert _{\mathcal {H}}>1$, then $\Vert y\Vert _{\mathcal {H}}^p\le \rho _{\mathcal {H}}(y)\le \Vert y\Vert _{\mathcal {H}}^q$;

• (v) $\Vert y\Vert _{\mathcal {H}}\rightarrow 0$ if and only if $\rho _{\mathcal {H}}(y)\rightarrow 0$;

• (vi) $\Vert y\Vert _{\mathcal {H}}\rightarrow +\infty$ if and only if $\rho _{\mathcal {H}}(y)\rightarrow +\infty$.

We have the following embedding results for the spaces $L^{\mathcal {H}}(\Omega )$ and $W^{1,\mathcal {H}}_0(\Omega )$, see [11, Proposition 2.16].

Proposition 2.2

Let (H1) be satisfied. Then the following embeddings hold:

• (i) $L^{\mathcal {H}}(\Omega ) \hookrightarrow L^{r}(\Omega )$ and $W^{1, \mathcal {H}}_0(\Omega )\hookrightarrow W^{1,r}_0(\Omega )$ are continuous for all $r\in [1,p]$;

• (ii) $W^{1, \mathcal {H}}_0(\Omega )\hookrightarrow L^{r}(\Omega )$ is continuous for all $r \in [1,p^*]$;

• (iii) $W^{1, \mathcal {H}}_0(\Omega )\hookrightarrow L^{r}(\Omega )$ is compact for all $r \in [1,p^*)$;

• (iv) $L^{\mathcal {H}}(\Omega ) \hookrightarrow L^q_\mu (\Omega )$ is continuous;

• (v) $L^{q}(\Omega ) \hookrightarrow L^{\mathcal {H}}(\Omega )$ is continuous.

Let $A:W^{1, \mathcal {H}}_0(\Omega )\rightarrow W^{1, \mathcal {H}}_0(\Omega )^*$ be the nonlinear map defined by

$$\begin{aligned} \langle A(u),\varphi \rangle :=\int _{\Omega }\big (|\nabla u|^{p-2}\nabla u+\mu (x)|\nabla u|^{q-2}\nabla u \big )\cdot \nabla \varphi \,\textrm{d} x \end{aligned}$$

(2.8)

for all $u,\varphi \in W^{1, \mathcal {H}}_0(\Omega )$, where $\langle \,\cdot ,\,\cdot \,\rangle$ is the duality pairing between $W^{1, \mathcal {H}}_0(\Omega )$ and its dual space $W^{1, \mathcal {H}}_0(\Omega )^*$. The operator $A:W^{1, \mathcal {H}}_0(\Omega )\rightarrow W^{1, \mathcal {H}}_0(\Omega )^*$ has the following properties, see Liu-Dai [17].

Proposition 2.3

Let hypotheses (H1) be satisfied. Then, the operator A defined in (2.8) is bounded, continuous, strictly monotone and of type $({{\,\textrm{S}\,}}_+)$, that is,

$$\begin{aligned} u_n\rightharpoonup u \quad \text {in }W^{1, \mathcal {H}}_0(\Omega )\quad \text {and}\quad \limsup _{n\rightarrow \infty }\,\langle Au_n,u_n-u\rangle \le 0, \end{aligned}$$

imply $u_n\rightarrow u$ in $W^{1, \mathcal {H}}_0(\Omega )$.

We refer to the books of Harjulehto-Hästö [16], Musielak [18] and the papers of Colasuonno-Squassina [8], Crespo-Blanco-Gasiński-Harjulehto-Winkert [11] and Liu-Dai [17] for more information about Musielak-Orlicz Sobolev spaces and double phase operators.

Let X be a Banach space and $X^*$ its topological dual space. Given $\varphi \in C^1(X)$ we say that $\varphi$ satisfies the Cerami-condition (C-condition for short), if every sequence $\{x_n\}_{n\in \mathbb {N}}\subseteq X$ such that $\{\varphi (u_n)\}_{n\ge 1} \subseteq \mathbb {R}$ is bounded and

$$\begin{aligned} \left(1+\Vert x_n\Vert _X\right)\varphi '(x_n)\rightarrow 0 \quad \text { in }X^* \text { as }n\rightarrow \infty , \end{aligned}$$

admits a strongly convergent subsequence.

The following theorem is used in our proofs and can be found in the paper of Bonanno-D’Aguì  [4, see Theorem 2.1 and Remark 2.2].

Theorem 2.4

Let X be a real Banach space and let $\Phi$, $\Psi :X \rightarrow \mathbb {R}$ be two functionals of class $C^1$ such that $\displaystyle \inf _X \Phi (u) = \Phi (0) = \Psi (0) = 0$. Assume that there are $r \in \mathbb {R}$ and $\tilde{u} \in X$, with $0< \Phi (\tilde{u}) < r$, such that

$$\begin{aligned} \frac{\mathop {{\mathop {\sup }\nolimits _{u \in \Phi ^{-1} \big (\left]- \infty ,r\right]\big )}}}\limits \Psi (u)}{r} < \frac{\Psi (\tilde{u})}{\Phi (\tilde{u})}, \end{aligned}$$

(2.9)

and, for each

$$\begin{aligned} \lambda \in \tilde{\Lambda } = \Bigg ] \frac{\Phi (\tilde{u})}{\Psi (\tilde{u})}, \frac{r}{\displaystyle \mathop {{\mathop {\sup }\nolimits _{u \in \Phi ^{-1}(]- \infty ,r])}}}\limits \Psi (u)}\Bigg [, \end{aligned}$$

the functional $I_{\lambda } = \Phi - \lambda \Psi$ satisfies the C-condition and it is unbounded from below. Moreover, $\Phi$ is supposed to be coercive.

Then, for each $\lambda \in \tilde{\Lambda }$, the functional $I_{\lambda }$ admits at least two nontrivial critical points $u_{\lambda ,1}$, $u_{\lambda ,2}\in X$ such that $I_\lambda (u_{\lambda ,1})< 0 < I_\lambda (u_{\lambda ,2})$.

3 Main result

In this section we formulate and prove our main results concerning the existence of nontrivial bounded weak solutions to problem (1.1). First, we state the hypotheses on the nonlinearity $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$. We suppose the following conditions:

• (H2) $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function satisfying the following conditions:

  • (i) There exist $\ell \in (q,p^*)$ and constants $\kappa _1, \kappa _2>0$ such that

    $$\begin{aligned} |f(x,s)| \le \kappa _1+\kappa _2|s|^{\ell -1} \end{aligned}$$

    for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$;

  • (ii) If $F(x,s)=\int _0^sf(x,t)\,\textrm{d}t$, then

    $$\begin{aligned} \lim _{s\rightarrow \pm \infty } \frac{F(x,s)}{|s|^q}=+\infty \end{aligned}$$

    uniformly for a. a. $x\in \Omega$;

  • (iii) There exists

    $$\begin{aligned} \zeta \in \left((\ell -p)\frac{N}{p},p^*\right) \end{aligned}$$

    such that

    $$\begin{aligned} 0<\zeta _0 \le \liminf _{s\rightarrow \pm \infty }\, \frac{f(x,s)s-qF(x,s)}{|s|^ \zeta } \end{aligned}$$

    uniformly for a. a. $x\in \Omega$.

Remark 3.1

Note that (H2)(ii) and (H2)(iii) imply that

$$\begin{aligned} \lim _{s\rightarrow \pm \infty }\frac{f(x,s)}{|s|^{q-2}s}=+\infty \end{aligned}$$

uniformly for a. a. $x\in \Omega$.

Remark 3.2

Due to Remark 3.1 we know that $f(x,\cdot )$ is $(q-1)$-superlinear at $\pm \infty$. Our conditions are weaker than the Ambrosetti–Rabinowitz condition (AR-condition for short). Indeed, instead of the AR-condition, we suppose hypotheses (H2)(ii) and (H2)(iii) which are less restrictive. Consider the function

$$\begin{aligned} f(s)= {\left\{ \begin{array}{ll} |s|^{\beta _1-2}s&{}\text {if }|s|\le 1,\\ |s|^{q-2}s\ln (|s|)+|s|^{\beta _2-2}s&{}\text {if } 1<|s|, \end{array}\right. } \end{aligned}$$

where $1<\beta _1<p$ and $1<\beta _2<q$, then we see that f satisfies (H2) but fails to satisfy the AR-condition.

The energy functional $I_\lambda :W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}$ of (1.1) is given by

$$\begin{aligned} I_\lambda (u)=\frac{1}{p}\Vert \nabla u\Vert _{p}^{p}+\frac{1}{q}\Vert \nabla u\Vert _{q,\mu }^{q}-\lambda \int _{\Omega } F(x,u)\,\textrm{d}x \end{aligned}$$

for all $u\in W^{1, \mathcal {H}}_0(\Omega )$. It is clear that $I_\lambda \in C^1$ and the critical points of $I_\lambda$ are the weak solutions of (1.1). Next, we introduce the functionals $\Phi ,\,\Psi :W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \Phi (u)=\frac{1}{p}\Vert \nabla u\Vert _{p}^{p}+\frac{1}{q}\Vert \nabla u\Vert _{q,\mu }^{q} \quad \text {and}\quad \Psi (u)= \int _{\Omega } F(x,u)\,\textrm{d}x \end{aligned}$$

(3.1)

for all $u\in W^{1, \mathcal {H}}_0(\Omega )$. We have that $I_\lambda = \Phi (u)-\lambda \Psi (u)$ and all these functionals are of class $C^1$, where their derivatives are given by

$$\begin{aligned} \left\langle I_\lambda '(u),v \right\rangle&=\int _{\Omega }\left(|\nabla u|^{p-2}\nabla u+\mu (x)|\nabla u|^{q-2}\nabla u\right)\cdot \nabla v\,\textrm{d}x-\lambda \int _{\Omega }f(x,u)v\,\textrm{d}x,\\ \left\langle \Phi ' (u),v \right\rangle&=\int _{\Omega }\left(|\nabla u|^{p-2}\nabla u+\mu (x)|\nabla u|^{q-2}\nabla u\right)\cdot \nabla v\,\textrm{d}x,\\ \left\langle \Psi '(u),v \right\rangle&=\int _{\Omega }f(x,u)v\,\textrm{d}x \end{aligned}$$

for all $u,v\in W^{1, \mathcal {H}}_0(\Omega )$.

First, we obtain the following proposition.

Proposition 3.3

Let hypotheses (H1) and (H2) be satisfied. Then the functional $I_{\lambda }:W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}$ satisfies the C-condition.

Proof

Let $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1, \mathcal {H}}_0(\Omega )$ be a sequence such that

$$\begin{aligned}&\left|I_\lambda (u_n)\right| \le c_1 \quad \text {for some }c_1>0 \text { and for all }n\in \mathbb {N}, \end{aligned}$$

(3.2)

$$\begin{aligned}&\left(1+\Vert u_n\Vert \right)I_\lambda '(u_n)\rightarrow 0 \quad \text {in }W^{1, \mathcal {H}}_0(\Omega )^* \text { as }n\rightarrow \infty . \end{aligned}$$

(3.3)

From (3.3) we get

$$\begin{aligned} \begin{aligned}&\left|\left\langle A(u_n),h\right\rangle -\lambda \int _{\Omega }f\left(x,u_n\right)h\,\textrm{d}x\right| \le \frac{\varepsilon _n\Vert h\Vert }{1+\Vert u_n\Vert } \end{aligned} \end{aligned}$$

(3.4)

for all $h\in W^{1, \mathcal {H}}_0(\Omega )$ with $\varepsilon _n\rightarrow 0^+$. Choosing $h=u_n\in W^{1, \mathcal {H}}_0(\Omega )$ in (3.4) gives

$$\begin{aligned} -\Vert \nabla u_n\Vert _p^p-\Vert \nabla u_n\Vert _{q,\mu }^q+\lambda \int _{\Omega }f(x,u_n)u_n\,\textrm{d}x \le \varepsilon _n \end{aligned}$$

(3.5)

for all $n\in \mathbb {N}$. From (3.2) we have

$$\begin{aligned} \frac{q}{p}\Vert \nabla u_n\Vert _p^p+\Vert \nabla u_n\Vert _{q,\mu }^q-\lambda \int _{\Omega }qF(x,u_n)\,\textrm{d}x \le qc_1. \end{aligned}$$

(3.6)

Adding (3.5) and (3.6) and recalling that $p<q$, we derive

$$\begin{aligned} \lambda \int _{\Omega }\left(f\left(x,u_n\right)u_n-qF\left(x,u_n\right)\right)\,\textrm{d}x\le c_2 \end{aligned}$$

(3.7)

for some $c_2>0$ and for all $n\in \mathbb {N}$.

Hypotheses (H2)(i) and (H2)(iii) imply that we can find $c_3 \in (0,\zeta _0)$ and $c_{4}>0$ such that

$$\begin{aligned} c_3|s|^\zeta -c_{4} \le f(x,s)s-qF(x,s) \end{aligned}$$

(3.8)

for a. a. $x\in \Omega$ and for all $s\in \mathbb {R}$. Using (3.8) in (3.7) leads to

Hence

(3.9)

Note that $p < N$. From hypothesis (H2)(iii) it is clear that we may assume that $\zeta<\ell <p^*$. Then we can find $t\in (0,1)$ such that

$$\begin{aligned} \frac{1}{\ell }=\frac{1-t}{\zeta }+\frac{t}{p^ *}. \end{aligned}$$

(3.10)

Using the interpolation inequality (see Papageorgiou-Winkert [19, p. 116]), we have

This combined with (3.9) and Proposition 2.2(ii) results in

(3.11)

with some $c_{6}>0$. Testing (3.4) with $h=u_n\in W^{1, \mathcal {H}}_0(\Omega )$ we obtain

$$\begin{aligned} \left\Vert\nabla u_n\right\Vert_p^p+\Vert \nabla u_n\Vert _{q,\mu }^q-\lambda \int _{\Omega }f(x,u_n)u_n\,\textrm{d}x \le \varepsilon _n \quad \text {for all } n\in \mathbb {N}. \end{aligned}$$

From Proposition 2.1(iii), (iv) and (H2)(i) as well as (3.11) we arrive at

$$\begin{aligned} \min \left\rbrace \Vert u_n\Vert ^p, \Vert u_n\Vert ^q\right\lbrace \le \lambda \int _{\Omega }f(x,u_n)u_n\,\textrm{d}x +\varepsilon _n \le \lambda c_7\left[1+\Vert u_n\Vert ^{t\ell }\right]+\varepsilon _n \end{aligned}$$

(3.12)

for some $c_7>0$ and for all $n\in \mathbb {N}$.

From (3.10) and (H2)(iii) it follows

$$\begin{aligned} t\ell =\frac{p^*(\ell -\zeta )}{p^*-\zeta }=\frac{Np(\ell -\zeta )}{Np-N\zeta +\zeta p}<\frac{Np(\ell -\zeta )}{Np-N\zeta +(\ell -p)\frac{N}{p} p}=p<q.\nonumber \\ \end{aligned}$$

(3.13)

Then, from (3.12) and (3.13) we obtain that

$$\begin{aligned} \{u_n\}_{n\in \mathbb {N}}\subseteq W^{1, \mathcal {H}}_0(\Omega )\text { is bounded.} \end{aligned}$$

Hence there exists a subsequence, not relabeled, such that

$$\begin{aligned} u_n\rightharpoonup u \quad \text {in }W^{1, \mathcal {H}}_0(\Omega )\quad \text {and}\quad u_n\rightarrow u \quad \text {in }L^{\ell }(\Omega ). \end{aligned}$$

(3.14)

If we use $h=u_n-u\in W^{1, \mathcal {H}}_0(\Omega )$ in (3.4), pass to the limit as $n\rightarrow \infty$ and use (3.14), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } \left\langle A(u_n),u_n-u \right\rangle =0. \end{aligned}$$

The $({{\,\textrm{S}\,}}_+)$-property of A (see Proposition 2.3) implies that $u_n\rightarrow u$ in $W^{1, \mathcal {H}}_0(\Omega )$. This shows that $I_\lambda$ satisfies the C-condition. $\square$

Now we are ready to formulate our main existence result.

Theorem 3.4

Let hypotheses (H1), (H2) be satisfied and let $\xi , \eta >0$ be two constants with $\xi >\eta$ such that

$$\begin{aligned} F(x,s)&\ge 0 \quad \text {for a. a.}x\in \Omega \text { and for all }s\in [0,\eta ],\end{aligned}$$

(3.15)

$$\begin{aligned} \kappa _1\xi ^{1-p}+\frac{\kappa _2}{\ell } \xi ^{\ell -p}&<\frac{1}{K|\Omega |} \cdot \frac{\displaystyle \int _{B\left(x_0,\frac{R}{2}\right)}F(x,\eta )\,\textrm{d}x}{\eta ^p+\eta ^q}, \end{aligned}$$

(3.16)

where $\kappa _1, \kappa _2$, $\ell$, R and K are given in (H2)(i), (2.3) and (2.6), respectively. Then, for each

$$\begin{aligned} \lambda \in \Lambda := \left]\dfrac{K|\Omega |^{\frac{p}{p^*}}}{pc_{p^*}^p}\cdot \dfrac{\eta ^p+\eta ^q}{\displaystyle \int _{B\left( x_0,\frac{R}{2}\right) } F(x,\eta )\,\textrm{d}x}\,,\,\frac{1}{pc_{p^*}^p|\Omega |^{\frac{p}{N}}}\cdot \dfrac{1}{ \kappa _1\xi ^{1-p}+\dfrac{\kappa _2}{\ell }\xi ^{\ell -p}}\right[, \end{aligned}$$

problem (1.1) has at least two nontrivial bounded weak solutions $u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )$ such that $I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )$.

Proof

Let $\Phi$ and $\Psi$ be as given in (3.1). First we see that $\Psi$ and $\Phi$ fulfill all the required regularity properties in Theorem 2.4. Indeed, $\Phi$ is coercive due to Proposition 2.1(iv) and the functional $I_\lambda$ is unbounded from below because of (H2)(ii). Also we see that

$$\begin{aligned} \inf _{u\in W^{1, \mathcal {H}}_0(\Omega )}\Psi (u)=\Psi (0)=\Phi (0). \end{aligned}$$

It is clear that the interval $\Lambda$ is nonempty due to assumption (3.16). Hence, we can fix $\lambda \in \Lambda$ and we set

$$\begin{aligned} r=\frac{1}{p} \frac{|\Omega |^{\frac{p}{p^*}}}{c^p_{p^*}}\xi ^p, \end{aligned}$$

(3.17)

where $c_{p^*}$ is the best constant of the embedding $W^{1,p}_0(\Omega )\hookrightarrow L^{p^*}(\Omega )$. Next, we define the function

$$\begin{aligned} \tilde{u}(x)= {\left\{ \begin{array}{ll} 0 &{}\text {if }x\in \Omega \setminus B\left(x_0,R\right),\\ \dfrac{ 2\eta }{R} \left(R-|x-x_0|\right) &{}\text {if } B\left(x_0,R\right)\setminus B\left(x_0,\frac{R}{2}\right),\\ \eta &{}\text {if } x\in B\left(x_0,\frac{R}{2}\right), \end{array}\right. } \end{aligned}$$

(3.18)

where $x_0\in \Omega$ is such that $B(x_0,R)\subseteq \Omega$, see (2.4). It is easy to see that $\tilde{u}\in W^{1, \mathcal {H}}_0(\Omega )$.

Step 1 $0<\Phi (\tilde{u})<r$

Using the representations of $\omega _R$ in (2.5) and R in (2.6) we obtain

$$\begin{aligned} \begin{aligned}&\Phi \left(\tilde{u}\right)\\&=\frac{1}{p}\left\Vert\nabla \tilde{u}\right\Vert_{p}^{p}+\frac{1}{q}\left\Vert\nabla \tilde{u}\right\Vert_{q,\mu }^{q}\\&=\frac{1}{p}\int _{B\left(x_0,R\right)\setminus B\left(x_0,\frac{R}{2}\right)}\left(\frac{2\eta }{R}\right)^p\,\textrm{d}x +\frac{1}{q}\int _{B\left(x_0,R\right)\setminus B\left(x_0,\frac{R}{2}\right)}\mu (x)\left(\frac{2\eta }{R}\right)^q\,\textrm{d}x\\&\le \left[\frac{1}{p}\left(\frac{2\eta }{R}\right)^p+\frac{\Vert \mu \Vert _\infty }{q}\left(\frac{2\eta }{R}\right)^q\right]\cdot \left[\frac{\pi ^{\frac{N}{2}}R^N}{\Gamma \left(1+\frac{N}{2}\right)}-\frac{\pi ^{\frac{N}{2}}}{\Gamma \left(1+\frac{N}{2}\right)}\left(\frac{R}{2}\right)^N\right]\\&\le \frac{1}{p}\left(\eta ^p+\eta ^q\right)\omega _R \frac{2^N-1}{2^{N-q}}\max \left\rbrace \frac{1}{R^p},\frac{\Vert \mu \Vert _\infty }{R^q}\right\lbrace \\&\le \frac{K|\Omega |^{\frac{p}{p^*}}}{pc_{p^*}^p}\left(\eta ^p+\eta ^q\right). \end{aligned}\nonumber \\ \end{aligned}$$

(3.19)

From the definition of r and (3.19) we see that we have to show that

$$\begin{aligned} K\left(\eta ^p+\eta ^q\right)<\xi ^p. \end{aligned}$$

(3.20)

Assume (3.20) is not true, so let us suppose that

$$\begin{aligned} K\left(\eta ^p+\eta ^q\right)\ge \xi ^p. \end{aligned}$$

(3.21)

From the growth condition of f in (H2)(i) we derive that

$$\begin{aligned} \int _{B\left(x_0,\frac{R}{2}\right)}F(x,\eta )\,\textrm{d}x \le \int _{B\left(x_0,\frac{R}{2}\right)} \left(\kappa _1\eta +\frac{\kappa _2}{\ell }\eta ^{\ell }\right)\,\textrm{d}x \le \left(\kappa _1\eta +\frac{\kappa _2}{\ell }\eta ^{\ell }\right)|\Omega |. \end{aligned}$$

(3.22)

Using (3.21) and (3.22) along with $\xi >\eta$ we have that

$$\begin{aligned} \kappa _1\xi ^{1-p}+\frac{\kappa _2}{\ell }\xi ^{\ell -p}&=\frac{\kappa _1\xi +\frac{\kappa _2}{\ell }\xi ^\ell }{\xi ^p} \ge \frac{\kappa _1\xi +\frac{\kappa _2}{\ell }\xi ^\ell }{K\left(\eta ^p+\eta ^q\right)} \ge \frac{|\Omega | \left(\kappa _1\eta +\frac{\kappa _2}{\ell }\eta ^{\ell }\right)}{K|\Omega |\left(\eta ^p+\eta ^q\right)}\\&\ge \frac{\displaystyle \int _{B\left(x_0,\frac{R}{2}\right)}F(x,\eta )\,\textrm{d}x}{K|\Omega |\left(\eta ^p+\eta ^q\right)}. \end{aligned}$$

This is a contradiction to (3.16). Therefore, (3.20) holds, so we have shown that $0<\Phi (\tilde{u})<r$.

Step 2 We need to verify the validity of condition (2.9) for r and $\tilde{u}$ defined in (3.17) and (3.18), respectively.

The representation of r in (3.17) gives

$$\begin{aligned} \xi =\left(\frac{c_{p^*}^ppr}{|\Omega |^{\frac{p}{p^*}}}\right)^{\frac{1}{p}}. \end{aligned}$$

(3.23)

From the growth condition in (H2)(i), (2.2) and (3.23) we derive that

$$\begin{aligned}{} & {} \frac{\mathop {{\mathop {\sup }\nolimits _{u \in \Phi ^{-1} (]- \infty ,r])}}}\limits \Psi (u)}{r} \nonumber \\{} & {} \quad \le \frac{\mathop {{\mathop {\sup }\nolimits _{u \in \Phi ^{-1}(]- \infty ,r])}}}\limits \left(\kappa _1\Vert u\Vert _1+\frac{\kappa _2}{\ell }\Vert u\Vert _{\ell }^\ell \right)}{r}\nonumber \\{} & {} \quad \le \frac{\mathop {{\mathop {\sup }\nolimits _{u \in \Phi ^{-1}(]- \infty ,r])}}}\limits \left(\kappa _1c_{p^*}|\Omega |^{\frac{p^*-1}{p^*}}\Vert \nabla u\Vert _{p}+\frac{\kappa _2}{\ell }c_{p^*}^\ell |\Omega |^{\frac{p^*-\ell }{p^*}}\Vert \nabla u\Vert _{p}^\ell \right)}{r}\nonumber \\{} & {} \quad \le \dfrac{\kappa _1c_{p^*}|\Omega |^{\frac{p^*-1}{p^*}}(pr)^\frac{1}{p}+\frac{\kappa _2}{\ell }c_{p^*}^\ell |\Omega |^{\frac{p^*-\ell }{p^*}}(pr)^{\frac{\ell }{p}}}{r}\nonumber \\{} & {} \quad =pc_{p^*}^p|\Omega |^{\frac{p^*-p}{p^*}} \left[\kappa _1 \left(\frac{c_{p^*}^ppr}{|\Omega |^{\frac{p}{p^*}}}\right)^{\frac{1-p}{p}}+\frac{\kappa _2}{\ell }\left(\frac{c_{p^*}^ppr}{|\Omega |^{\frac{p}{p^*}}}\right)^{\frac{\ell -p}{p}}\right]\nonumber \\{} & {} \quad =pc_{p^*}^p|\Omega |^{\frac{p}{N}} \left[\kappa _1\xi ^{1-p}+\frac{\kappa _2}{\ell }\xi ^{\ell -p}\right]. \end{aligned}$$

(3.24)

On the other hand, using (3.15), we get that

$$\begin{aligned} \begin{aligned} \Psi \left(\tilde{u}\right)&=\int _{\Omega }F\left(x,\tilde{u}\right)\,\textrm{d}x\\&=\int _{B\left(x_0,R\right)\setminus B\left(x_0,\frac{R}{2}\right)} F\left(x,\dfrac{ 2\eta }{R} \left(R-|x-x_0|\right)\right)\,\textrm{d}x\\&\quad +\int _{B\left(x_0,\frac{R}{2}\right)} F(x,\eta )\,\textrm{d}x\\&\ge \int _{B\left(x_0,\frac{R}{2}\right)} F(x,\eta )\,\textrm{d}x. \end{aligned}\nonumber \\ \end{aligned}$$

(3.25)

Combining (3.24), (3.16), (3.19) and (3.25) gives

$$\begin{aligned} \begin{aligned} \frac{\mathop {{\mathop {\sup }\nolimits _{u \in \Phi ^{-1}(]- \infty ,r])}}}\limits \Psi (u)}{r}&\le pc_{p^*}^p|\Omega |^{\frac{p}{N}} \left[\kappa _1\xi ^{1-p}+\frac{\kappa _2}{\ell }\xi ^{\ell -p}\right]\\&<pc_{p^*}^p|\Omega |^{\frac{p}{N}} \left[\frac{1}{K|\Omega |} \cdot \frac{\displaystyle \int _{B\left(x_0,\frac{R}{2}\right)}F(x,\eta )\,\textrm{d}x}{\eta ^p+\eta ^q}\right]\\&=\dfrac{\displaystyle \int _{B\left(x_0,\frac{R}{2}\right)}F(x,\eta )\,\textrm{d}x}{\frac{K|\Omega |^{\frac{p}{p^*}}}{pc_{p^*}^p}\left(\eta ^p+\eta ^q\right)}\\&\le \dfrac{\Psi \left(\tilde{u}\right)}{\Phi \left(\tilde{u}\right)}. \end{aligned} \end{aligned}$$

This proves Step 2.

From Steps 1 and 2 and Proposition 3.3 we see that all the conditions in Theorem 2.4 are satisfied and so we conclude that problem (1.1) has at least two nontrivial weak solutions $u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )$ such that $I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )$. From Gasiński-Winkert [13, Theorem 3.1] we know that $u_\lambda , v_\lambda \in L^{\infty }(\Omega )$. $\square$

Let us now consider the special case when f is nonnegative and independent of x. We suppose the following conditions:

• (H3) $f:\mathbb {R}\rightarrow \mathbb {R}$ is a continuous function with $f(s)\ge 0$ for all $s\in \mathbb {R}$ satisfying the following conditions:

  • (i) There exist $\ell \in (q,p^*)$ and constants $\kappa _1, \kappa _2>0$ such that

    $$\begin{aligned} f(s) \le \kappa _1+\kappa _2|s|^{\ell -1} \end{aligned}$$

    for all $s\in \mathbb {R}$;

  • (ii) If $F(s)=\int _0^sf(t)\,\textrm{d}t$, then

    $$\begin{aligned} \lim _{s\rightarrow \infty } \frac{F(s)}{s^q}=+\infty ; \end{aligned}$$

  • (iii) There exists

    $$\begin{aligned} \zeta \in \left((\ell -p)\frac{N}{p},p^*\right) \end{aligned}$$

    such that

    $$\begin{aligned} 0<\zeta _0 \le \liminf _{s\rightarrow \infty }\, \frac{f(s)s-qF(s)}{s^ \zeta }. \end{aligned}$$

The next result is a consequence of Theorem 3.4.

Corollary 3.5

Let hypotheses (H1), (H3) be satisfied and let $\xi , \eta >0$ be two constants with $\xi >\eta$ such that

$$\begin{aligned} \kappa _1\xi ^{1-p}+\frac{\kappa _2}{\ell } \xi ^{\ell -p}&<\frac{\omega _R}{2^NK|\Omega |} \cdot \frac{F(\eta )}{\eta ^p+\eta ^q}, \end{aligned}$$

(3.26)

where $\kappa _1, \kappa _2$, $\ell$, R and K are given in (H3)(i), (2.3) and (2.6), respectively. Then, for each

$$\begin{aligned} \lambda \in \Lambda _1:= \left]\dfrac{2^NK|\Omega |^{\frac{p}{p^*}}}{\omega _R pc_{p^*}^p}\cdot \dfrac{\eta ^p+\eta ^q}{\displaystyle F(\eta )}\,,\,\frac{1}{pc_{p^*}^p|\Omega |^{\frac{p}{N}}}\cdot \dfrac{1}{ \kappa _1\xi ^{1-p}+\dfrac{\kappa _2}{\ell }\xi ^{\ell -p}}\right[, \end{aligned}$$

problem (1.1) has at least two nontrivial bounded weak solutions $u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )$ such that $I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )$ and $u_\lambda , v_\lambda \ge 0$.

Proof

We are going to apply Theorem 3.4. First, we point out that, since f is nonnegative, we have $F(t)\ge 0$ for all $t\in \mathbb {R}$. So (3.15) is satisfied. In addition, we know that

$$\begin{aligned} \int _{B\left( x_0,\frac{R}{2}\right) } F(\eta )\,\textrm{d}x=\frac{\pi ^{\frac{N}{2}}}{\Gamma \left(1+\frac{N}{2}\right)}\frac{R^N}{2^N}F(\eta )=\frac{\omega _R}{2^N}F(\eta ), \end{aligned}$$

(3.27)

see (2.5). From (3.27) and (3.26) we see that (3.16) is fulfilled as well. Then, applying Theorem 3.4, for each

$$\begin{aligned} \lambda \in \Lambda _1= \left]\dfrac{2^NK|\Omega |^{\frac{p}{p^*}}}{\omega _R pc_{p^*}^p}\cdot \dfrac{\eta ^p+\eta ^q}{\displaystyle F(\eta )}\,,\,\frac{1}{pc_{p^*}^p|\Omega |^{\frac{p}{N}}}\cdot \dfrac{1}{ \kappa _1\xi ^{1-p}+\dfrac{\kappa _2}{\ell }\xi ^{\ell -p}}\right[, \end{aligned}$$

problem (1.1) has at least two nontrivial bounded weak solutions $u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )$ such that $I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )$. Testing the corresponding weak formulation with $-u_\lambda ^-\in W^{1, \mathcal {H}}_0(\Omega )$ and $-v_\lambda ^-\in W^{1, \mathcal {H}}_0(\Omega )$, respectively, shows that both are nonnegative, so $u_\lambda , v_\lambda \ge 0$. $\square$

We get another result for nonnegative functions $f:\mathbb {R}\rightarrow \mathbb {R}$.

Corollary 3.6

Let hypotheses (H1), (H3) be satisfied and suppose that

$$\begin{aligned} \limsup _{t\rightarrow 0^+} \frac{F(t)}{t^p}=+\infty . \end{aligned}$$

(3.28)

Then, for each

$$\begin{aligned} \lambda \in \Lambda _2=\left]0, \frac{1}{pc_{p^*}^p|\Omega |^{\frac{p}{N}}}\cdot \mathop {{\mathop {\sup }\nolimits _{\xi >0}}}\limits \dfrac{1}{ \kappa _1\xi ^{1-p}+\dfrac{\kappa _2}{\ell }\xi ^{\ell -p}}\right[, \end{aligned}$$

problem (1.1) has at least two nonnegative, nontrivial bounded weak solutions $u_\lambda , v_\lambda$ $\in W^{1, \mathcal {H}}_0(\Omega )$ such that $I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )$.

Proof

Let $\lambda \in \Lambda _2$ be fixed. Then we can find $\xi >0$ such that

$$\begin{aligned} \lambda < \frac{1}{pc_{p^*}^p|\Omega |^{\frac{p}{N}}}\cdot \dfrac{1}{ \kappa _1\xi ^{1-p}+\dfrac{\kappa _2}{\ell }\xi ^{\ell -p}}. \end{aligned}$$

On the other hand condition (3.28) implies that

$$\begin{aligned} \limsup _{t\rightarrow 0^+} \frac{F(t)}{t^p+t^q}=+\infty . \end{aligned}$$

Hence, we can find a number $\eta \in (0,\xi )$ such that

$$\begin{aligned} \frac{1}{\lambda }< \dfrac{\omega _R pc_{p^*}^p}{2^NK|\Omega |^{\frac{p}{p^*}}}\cdot \dfrac{\displaystyle F(\eta )}{\eta ^p+\eta ^q}. \end{aligned}$$

Then the assertion of the theorem follows from Corollary 3.5. $\square$

Finally, we want to give a concrete example for a function which fits in our setting.

Example 3.7

Let $p=3$, $N=4$ and $q=4$, then $1<p<N$ and $p<q<p^*=12$. Let $\Omega =B\left( 0,3^{\frac{1}{8}}\right) \subset \mathbb {R}^4$. Then $\left| B\left( 0,3^{\frac{1}{8}}\right) \right| =\dfrac{3^{\frac{1}{2}}}{2} \pi ^2$. We consider the function

$$\begin{aligned} f(t)=\left( 1+t\right) ^3\left[ 4 \ln (1+t)+1\right] \quad \text {for } t\ge 0. \end{aligned}$$

Then we have

$$\begin{aligned} F(s)= \int _0^{s} f(t) \,\textrm{d}t =\int _0^{s} \left( 1+t\right) ^3\left[ 4 \ln (1+t)+1\right] \,\textrm{d}t = \left( 1+s\right) ^4 \ln (1+s). \end{aligned}$$

For each

$$\begin{aligned} \lambda \in \left] 0, \dfrac{2 \cdot 5^{\frac{1}{4}}\cdot \pi ^{\frac{3}{4}}}{3^6 } \right[, \end{aligned}$$

the problem

$$\begin{aligned} \begin{aligned} -{\text {div}} \bigg (|\nabla u|^{p-2}\nabla u +\sqrt{x^2+y^2+z^2+w^2}|\nabla u|^{q-2}\nabla u \bigg )&= \lambda f(u)\quad{} & {} \text {in } \Omega ,\\ u&= 0{} & {} \text {on } \partial \Omega , \end{aligned} \end{aligned}$$

admits at least two nonnegative, nontrivial bounded weak solutions.

Indeed, if we put $\kappa _1=15$, $\kappa _2=20$, $\ell =5$ and $\xi =\left( \frac{15}{4}\right) ^{\frac{1}{4}}$ we observe that (H3) and (3.28) are satisfied. Moreover, due to Talenti [23], one has that

$$\begin{aligned} c_{p^*}\le \pi ^{-\frac{1}{2}}4^{-\frac{1}{3}} 2^{\frac{2}{3}} \left( \frac{\Gamma (3)\Gamma (4)}{\Gamma \left( \frac{4}{3}\right) \Gamma \left( \frac{11}{3}\right) }\right) ^{\frac{1}{4}}= \left( \dfrac{3^{\frac{11}{2}}}{2^{3}\cdot 5 \cdot \pi ^3}\right) ^{\frac{1}{4}}, \end{aligned}$$

This gives

$$\begin{aligned} \dfrac{1}{pc^p_{p^*}\left| \Omega \right| ^{\frac{p}{N}} }\displaystyle \sup _{\xi > 0}\dfrac{1}{ k_1\xi ^{1-p}+\dfrac{k_2}{l}\xi ^{l-p}}= \dfrac{2 \cdot 5^{\frac{1}{4}}\cdot \pi ^{\frac{3}{4}}}{3^6 }. \end{aligned}$$

Then, the assertion follows from Corollary 3.6.