1 Introduction

Let \({\mathbb {D}}_r=\{z\in {\mathbb {C}}:|z|<r\}\) be the open disc of the radius r of the complex plane, \({\mathbb {T}}_r=\{z\in {\mathbb {C}}:|z|=r\}\) and let \({\mathbb {D}}_1 ={\mathbb {D}}\) be the unit disk. Also, we denote by \({\mathcal {A}}\) the class of analytic functions on \({\mathbb {D}}\) with standard normalization \(f(0)=f'(0)-1=0\).

A harmonic mapping f of the simply connected region \(\Omega \) is a complex-valued function of the form

$$\begin{aligned} f = h + {\overline{g}}, \end{aligned}$$
(1.1)

where h and g are analytic in \(\Omega \), with \(g(z_0)=0\) for some prescribed point \(z_0 \in \Omega \). We call h and g analytic and co-analytic parts of f, respectively. If f is (locally) injective, then f is called (locally) univalent. The Jacobian and the second complex dilatation of f are given by \(J_f(z) = |f_z|^2-|f_{{\bar{z}}}|^2 =|h'(z)|^2-|g'(z)|^2\) and \(\omega (z) = g'(z)/h'(z)\ (z\in \Omega )\), respectively. A result of Lewy [5] states that f is locally univalent if and only if its Jacobian is never zero, and is sense-preserving if the Jacobian is positive. By \({\mathcal {H}}={\mathcal {H}}({\mathbb {D}})\) we denote the class of complex valued, sense-preserving harmonic mappings in \({\mathbb {D}}\). We note that each f of the form (1.1) is uniquely determined by coefficients of the power series expansions [3]

$$\begin{aligned} h(z) = a_0+\sum _{n=1}^{\infty } a_n z^n, \quad g(z) = b_0+\sum _{n=1}^{\infty } b_n z^n \quad (z\in {\mathbb {D}}), \end{aligned}$$
(1.2)

where \(a_n \in {\mathbb {C}}\), \(n=0,1,2,...\) and \(b_n \in {\mathbb {C}}\), \(n=1,2,3,...\). By \({\mathcal {H}}_0\) a subclass of \({\mathcal {H}}\) with the normalization \(h(0) = g(0) = 0, h'(0)=1\). Following Clunie and Sheil-Small notation [3], we denote by \({\mathcal {S}}_{\mathcal {H}}\) the subclass of \({\mathcal {H}}_0\), consisting of all sense-preserving univalent harmonic mappings of \({\mathbb {D}}\). Several fundamental information about harmonic mappings in the plane can also be found in [4].

2 Differential operators

For \(f\in C^1({\mathbb {D}})\), let the differential operators D and \({\mathfrak {D}}\) be defined as follows

$$\begin{aligned} Df=z\ \dfrac{\partial f}{\partial z}-{\overline{z}}\ \dfrac{\partial f}{\partial {\overline{z}}}= zh'(z)-\overline{zg'(z)},\end{aligned}$$
(2.1)

and

$$\begin{aligned} {\mathfrak {D}}f=z\ \dfrac{\partial f}{\partial z}+{\overline{z}}\ \dfrac{\partial f}{\partial {\overline{z}}}=zh'(z)+\overline{zg'(z)},\end{aligned}$$
(2.2)

where \(\partial f/\partial z\) and \(\partial f/\partial {\overline{z}}\) are the formal derivatives of the function f

$$\begin{aligned} \dfrac{\partial f}{\partial z}=\dfrac{1}{2}\left( \dfrac{\partial f}{\partial x}-i\dfrac{\partial f}{\partial y}\right) \quad \text{ and }\quad \dfrac{\partial f}{\partial {\overline{z}}}=\dfrac{1}{2}\left( \dfrac{\partial f}{\partial x}+i\dfrac{\partial f}{\partial y}\right) . \end{aligned}$$

Moreover, we define n-th order differential operator by the recurrence relation

$$\begin{aligned} \begin{array}{c} D^2f=D(Df)=zh'-\overline{z g'}+z^2h''-\overline{z^2g''}\\ \qquad \qquad = Df+z^2h''-\overline{z^2g''},\quad D^nf= D(D^{n-1}f),\\ {\mathfrak {D}}^2 f={\mathfrak {D}}({\mathfrak {D}}f)= zh'+\overline{zg'}+z^2h''+\overline{z^2g''}\\ \qquad \qquad ={\mathfrak {D}}f+z^2h''+\overline{z^2g''}, \quad {\mathfrak {D}}^nf={\mathfrak {D}}({\mathfrak {D}}^{n-1}f).\end{array} \end{aligned}$$

We note that in the case when f is an analytic function (i.e. \(g(z)=0\)), then both D and \({\mathfrak {D}}\) reduce to the Alexander differential operator \(zf'\).

Now, we present several properties of the differential operators Df and \({\mathfrak {D}}f\). Most of them follow from the usual rules of differential calculus therefore the proofs will be omitted.

Proposition 2.1

Let \(\varphi , \psi \in C^1({\mathbb {D}})\) and let the linear differential operators D and \({\mathfrak {D}}\) be defined by (2.1) and (2.2). Then:

$$\begin{aligned} \begin{array}{lll} (i)&{}D(\varphi \psi )=\varphi D\psi +\psi D\varphi , &{} {\mathfrak {D}}(\varphi \psi )=\varphi {\mathfrak {D}}\psi +\psi {\mathfrak {D}}\varphi ,\\ (ii)&{}D\left( \dfrac{\varphi }{\psi }\right) =\dfrac{\psi D\varphi -\varphi D\psi }{\psi ^2}, &{} {\mathfrak {D}}\left( \dfrac{\varphi }{\psi }\right) =\dfrac{\psi {\mathfrak {D}}\varphi -\varphi {\mathfrak {D}}\psi }{\psi ^2},\\ (iii)&{}D(\varphi \circ \psi )=\dfrac{\partial \varphi }{\partial \psi }D\psi +\dfrac{\partial \varphi }{\partial \overline{\psi }}D\overline{\psi }, &{} {\mathfrak {D}}(\varphi \circ \psi )=\dfrac{\partial \varphi }{\partial \psi }{\mathfrak {D}}\psi +\dfrac{\partial \varphi }{\partial \overline{\psi }}{\mathfrak {D}}\overline{\psi }.\end{array} \end{aligned}$$

Proposition 2.2

Let \(f\in C^1({\mathbb {D}})\) and let D and \({\mathfrak {D}}\) be defined by (2.1) and (2.2). Then

Proposition 2.3

Let \(f\in C^1({\mathbb {D}})\), and let D, \({\mathfrak {D}}\) be defined by (2.1) and (2.2). Also, let \(z=re^{i\theta }\). Then

$$\begin{aligned}&\dfrac{\partial f}{\partial \theta }=iDf, \qquad r\dfrac{\partial f}{\partial r}= {\mathfrak {D}}f, \qquad \ r\dfrac{\partial }{\partial r}Df=D^2f, \end{aligned}$$
(2.3)
$$\begin{aligned}&\quad \dfrac{\partial |f|}{\partial \theta }=-|f|\mathrm{Im \, }\dfrac{Df}{f},\quad \dfrac{\partial |f|}{\partial r}=\dfrac{|f|}{r}\mathrm{Re \, }\dfrac{{\mathfrak {D}}f}{f}\quad (f(z)\ne 0), \end{aligned}$$
(2.4)
$$\begin{aligned}&\quad \dfrac{\partial }{\partial \theta }\arg f=\mathrm{Re \, }\dfrac{Df}{f}= \mathrm{Re \, }\frac{zh'(z)-\overline{zg'(z)}}{h(z)+\overline{g(z)}}\quad (f(z)\ne 0), \end{aligned}$$
(2.5)
$$\begin{aligned}&\quad \dfrac{\partial }{\partial \theta }\arg f=\dfrac{1}{r}\mathrm{Im \, }\dfrac{{\mathfrak {D}}f}{f}= \frac{1}{r}\mathrm{Im \, }\frac{zh'(z)+\overline{zg'(z)}}{h(z)+\overline{g(z)}}\quad (f(z)\ne 0). \end{aligned}$$
(2.6)

Remark 2.4

If \(G\in {\mathcal {H}}\), then \(DG(z{\overline{z}})=0\) and \({\mathfrak {D}}G(\arg z)=0\). Therefore the constant functions for the operators D and \({\mathfrak {D}}\) are the functions of the form \(G(|z|^2)\) and \(G(\arg z)\), respectively.

Remark 2.5

We note also that, if \(f(z) = \alpha z +\beta {\overline{z}}\ \alpha , \beta \in {\mathbb {C}}\), then \({\mathfrak {D}}f(z) =\alpha z +\beta {\overline{z}} = f(z).\)

3 Starlikeness and spirallikenes of analytic functions

A domain \(D\subset {\mathbb {C}}\) is said to be starlike w.r.t. origin if each point \(w\in D\) may be connected with origin by a segment that lies entirely in D. Geometrically, this means that the linear segment joining the origin to every other point w lies entirely in D. An analytic function f that maps the unit disk \({\mathbb {D}}\) onto starlike domain is called starlike function [9]. Every starlike function in \({\mathcal {A}}\) is necessarily univalent. An analytic necessary and sufficient condition for starlikeness of univalent functions is:

$$\begin{aligned} \Re \dfrac{zf'(z)}{f(z)} > 0\quad (z\in {\mathbb {D}}). \end{aligned}$$

Modifying the starlikeness condition by inserting a factor \(e^{i\gamma }\ (|\gamma |<\pi /2)\) we obtain

$$\begin{aligned} \Re \left( e^{i\gamma }\dfrac{zf'(z)}{f(z)}\right) > 0\quad (z\in {\mathbb {D}}), \end{aligned}$$
(3.1)

that is the condition of \(\gamma \)-spirallikeness of analytic functions f in \({\mathbb {D}}\). The notion of \(\gamma \)-spirallikeness of \(f({\mathbb {D}})\) geometrically means that the arc of the logarithmic spiral \((\sigma _t)=te^{i\gamma }\ (t \in [0,\infty ))\) joining the origin to every other point w lies entirely in \(f({\mathbb {D}})\). It was shown by Spa\({\check{c}}\)ek [8] that spirallike functions are univalent. Gamma spirallike functions gained recognition of many researchers, their generalizations were introduced and many properties were studied (see, for example [2, 6, 10]).

In 1981 Al-Amiri and Mocanu [1] proved a sufficient condition for a function \(f\in C^1({\mathbb {D}})\) to be univalent and to map \({\mathbb {D}}\) onto a spirallike domain.

Theorem 3.1

([1])Suppose that a function \(f\in C^1({\mathbb {D}})\) that vanishes only at the origin, and let \(\gamma \) be a given real number such that \(|\gamma |<\pi /2\). If \(J_f > 0\) on \({\mathbb {D}}\), and

$$\begin{aligned} \Re \left\{ e^{i\gamma }\frac{Df(z)}{f(z)}\right\} > 0\qquad (z\in {\mathbb {D}}\setminus \{0\}) \end{aligned}$$
(3.2)

then f is univalent in \({\mathbb {D}}\) and \(f({\mathbb {D}})\) is \(\gamma \)- spirallike domain.

It is noteworthy that (3.2) reduces then to (3.1) in the case of \(f\in {\mathcal {A}}\). The properties of harmonic starlike and spirallike functions were considered in [7].

4 Harmonic Archimedean and hyperbolic spirallikeness

Al-Amiri and Mocanu in their paper [1] stated that the same method of proof for \(\gamma \)-spirallikeness can be used to show a sufficient conditions for Archimedean and hyperbolic starlikeness.

Definition 4.1

Let \((\sigma _\phi )\) be the parametric family of Archimedean spiral arcs defined by \(\sigma _\phi : w = w_\phi (t) = te^{i(t+\phi )},\ t \in (0,\infty ),\ \phi \in [0,2\pi )\). It is clear that through each point \(w\in {\mathbb {C}}\setminus \{0\}\) passes only one spiral of the family \((\sigma _\phi )\). We say that D is an Archimedean spirallike domain if for each \(w\in D,\ w \ne 0\), the part of the spiral arc \(\sigma _\phi \) joining the origin to the point w lies entirely in D.

Definition 4.2

Let the family \((\sigma _\phi )\) of hyperbolic spiral be defined by \(\sigma _\phi : w = w_\phi (t) = e^{i(t+\phi )}/t,\ t\in (0,\infty ),\ \phi \in [0,2\pi )\). We say that D is a hyperbolic spirallike domain if for each point \(w\in D,\ w \ne 0\), the part of the spiral arc \(\sigma _\phi \), joining the origin to the point w, lies entirely in D.

Definition 4.3

Let G be differentiable function in the interval \((0,\infty )\). We say that D is a generalized spiral-shaped domain, if for each point \(w\in D,\ w \ne 0\), the part of the spiral arc \(w_\phi (t) = t e^{i(G(t)+\phi )},\ t\in (0,\infty ),\ \phi \in [0,2\pi )\), joining the origin to the point w, lies entirely in D.

Remark 4.4

We remark that the Definition 4.3 reduces to the definition of:

(i) starlikeness, if \(G= 0\);

(ii) spirallikeness, if \(G(w)=e^{i\gamma },\ |\gamma | <\frac{\pi }{2}\);

(iii) Archimedean spirallikenes, if \(G(w) = w\).

Now, we define harmonic Archimedean, hyperbolic and generalized spirallikeness.

Definition 4.5

A harmonic function \(f\in {\mathcal {H}}_0\) is called Archimedean spirallike function if f is orientation-preserving and univalent on \({\mathbb {D}}\) and if \(f({\mathbb {D}})\) is Archimedean spirallike domain. The class of such functions will be denoted by \({\mathcal {H}}_0^{{\mathcal {A}}_S}\). Similarly, a harmonic function \(f\in {\mathcal {H}}_0\) is called hyperbolic spirallike if it is orientation-preserving and univalent on \({\mathbb {D}}\) and if \(f({\mathbb {D}})\) is a hyperbolic spirallike domain. We denote by \({\mathcal {H}}_0^{{\mathcal {H}}_S}\) the class of such functions. Generally, a harmonic function \(f\in {\mathcal {H}}_0\) will be called generalized spiral-shaped function, if it is orientation-preserving and univalent on \({\mathbb {D}}\) and if \(f({\mathbb {D}})\) is a generalized spiral-shaped domain. This class of functions will be denoted by \({\mathcal {H}}_0^{{\mathcal {G}}_S}\).

Theorem 4.6

Suppose that a function \(f \in {\mathcal {H}}_0\) be such that \(f(z) = 0\) iff \(z =0\), and that \(J_f > 0\) on \({\mathbb {D}}\). Then \(f\in {\mathcal {H}}_0^{{\mathcal {A}}_S}\) if and only if the following inequality

$$\begin{aligned} \Re \left\{ \left( 1-i|f(z)|\right) \frac{Df(z)}{f(z)}\right\} > 0\qquad (z\in {\mathbb {D}}\setminus \{0\}) \end{aligned}$$
(4.1)

is satisfied.

Proof

The proof will be a modification and supplement to that from [1], which concerned the \(\gamma \)-spirallikeness conditions of \(f\in C^1({\mathbb {D}})\), and contained only necessary condition for \(\gamma \)-spirallikeness.

Assume first that (4.1) is satisfied. For \(0< r < 1\) we denote \(C_r = f({\mathbb {T}}_r)\). We note that \(0\not \in C_r\) for \(0<r<1\). We now prove that the function f is univalent in \({\mathbb {D}}\). To do this we will show that \((C_r)\) contains only non-intersecting Jordan curves. Let \((\sigma _\phi )\) be the family of spirals such that \(\sigma _\phi \) has the parametric representation \(\sigma _\phi : w=w_\phi (t),\ t \in {\mathbb {R}}\), and \(w_\phi =t e^{i(t+\phi )}\). It is clear that through each point \(z\in {\mathbb {C}}\setminus \{0\}\) passes only one spiral of the family \((\sigma _\phi )\). Hence, for \(z=re^{i\theta }\) \((0<r< 1, \ 0\le \theta < 2\pi \)), the equation \(f(z)= w_\phi (t)\) determines a unique \(\phi = \phi (r,\theta ) \in [0,2\pi )\). We first prove that \(C_r\) is a Jordan curve for each \(0< r<1\). It can be achieved by showing that

$$\begin{aligned} \frac{\partial \phi }{\partial \theta } > 0\qquad (\theta \in [0,2\pi ))\end{aligned}$$
(4.2)

and that the total variation of \(\phi (r,\theta )\) on a segment \([0,2\pi )\) is equal \(2\pi \). From the representation of \(w_\phi \) we get

$$\begin{aligned} |f(z)| = t,\quad {{\,\mathrm{\mathrm Arg}\,}}f(z) = t+\phi , \end{aligned}$$
(4.3)

and from this

$$\begin{aligned} \phi = {{\,\mathrm{\mathrm Arg}\,}}f(z) -|f(z)|={{\,\mathrm{\mathrm Arg}\,}}f(z) - t.\end{aligned}$$
(4.4)

Differentiating with respect to \(\theta \) and using (2.4) and (2.5) we obtain from (4.4)

$$\begin{aligned} \frac{\partial \phi }{\partial \theta }=\mathrm{Re \, }\frac{Df}{f}+ |f(z)| \mathrm{Im \, }\frac{Df}{f}= \mathrm{Re \, }\left\{ \left( 1-i\,|f(z)|\right) \frac{Df}{f}\right\} .\end{aligned}$$
(4.5)

Hence, by (4.1) the condition (4.2) is satisfied.

Furthermore, condition \(f(z) = 0\) for \(z \in {\mathbb {D}}\setminus \{0\}\) implies that the curves \(C_r, r \in (0,1)\), are homotopic in the domain \({\mathbb {C}}\setminus \{0\}\). Thus they have the same index with respect to the origin, i.e., \(ind_0 C_r = const\) for all \(r\in (0,1)\). By condition \(J_f > 0\) the function f is univalent and preserves the orientation in a neighborhood of the origin. This implies the existence of \(r_0 \in (0,1)\) such that \(ind_0 C_r = 1\) for \(r < r_0\). Hence the total variation of the argument along \(C_r\) is \(2\pi \), that is,

$$\begin{aligned} Var_{0\le \theta <2\pi }{{\,\mathrm{\mathrm Arg}\,}}f(r e^{i\theta })=2\pi \quad (r\in (0,1)).\end{aligned}$$
(4.6)

Now (4.4) and (4.6) yield

$$\begin{aligned} Var_{0\le \theta<2\pi }\phi (r,\theta )=Var_{0\le \theta <2\pi }{{\,\mathrm{\mathrm Arg}\,}}f(r e^{i\theta })=2\pi ,\end{aligned}$$
(4.7)

which gives that for each \(r\in (0,1)\), \(C_r\) is a simple Archimedean spirallike.

To complete the proof of the theorem we need only show that \(C_r\cap C_\rho = \emptyset \), whenever \(r \ne \rho ,\ r, \rho \in (0,1)\). Fix a value \(\phi \in [0, 2\pi )\). The system

$$\begin{aligned} f(z) = w_\phi (t)\qquad (|z|=r,\ 0<r<1) \end{aligned}$$

yields a unique \(z = re^{i\theta },\ \theta = \theta (r)\), and a unique \(t = t(r,\theta ) = t(r)\). It follows that our assertion is equivalent to showing

$$\begin{aligned} \frac{dt}{dr} > 0 \quad {for}\quad r\in (0,1). \end{aligned}$$
(4.8)

Differentiating (4.3) with respect to r, and applying (2.4) and (2.5) we obtain

$$\begin{aligned} \frac{1}{t}\frac{dt}{dr} =\frac{1}{r}\mathrm{Re \, }\frac{{\mathfrak {D}}f}{f}- \frac{d\theta }{dr}\mathrm{Im \, }\frac{Df}{f}, \\ \frac{dt}{dr} =\frac{1}{r}\mathrm{Im \, }\frac{{\mathfrak {D}}f}{f}+ \frac{d\theta }{dr}\mathrm{Re \, }\frac{Df}{f}. \end{aligned}$$

Multiplying the first equality by \(\mathrm{Re \, }\frac{Df}{f}\), and the second by \(\mathrm{Im \, }\frac{Df}{f}\) and summing up we get

$$\begin{aligned} \begin{array}{rcl} \left( \dfrac{1}{ t}\mathrm{Re \, }\dfrac{Df}{f}+\mathrm{Im \, }\frac{Df}{f}\right) \dfrac{dt}{dr}&{}=&{}\dfrac{1}{r}\left( \mathrm{Re \, }\dfrac{Df}{f}\mathrm{Re \, }\dfrac{{\mathfrak {D}}f}{f}+ \mathrm{Im \, }\frac{Df}{f}\mathrm{Im \, }\dfrac{{\mathfrak {D}}f}{f}\right) \\ &{}=&{}\dfrac{1}{r}\mathrm{Re \, }\dfrac{Df\,\overline{{\mathfrak {D}}f}}{f\,{\overline{f}}}\ =\ \dfrac{1}{r}\dfrac{r^2\, J_f(z)}{|f|^2}\\ &{}=&{}\dfrac{r\, J_f(z)}{|f|^2}.\end{array} \end{aligned}$$

Hence

$$\begin{aligned} |f|^2\left( \frac{1}{t}\mathrm{Re \, }\frac{Df}{f}+\mathrm{Im \, }\frac{Df}{f}\right) \frac{dt}{dr}=r\, J_f(z), \end{aligned}$$

that is, applying (4.3)

$$\begin{aligned} |f|\left( \mathrm{Re \, }\frac{Df}{f}+|f|\mathrm{Im \, }\frac{Df}{f}\right) \frac{dt}{dr}=r\, J_f(z),\end{aligned}$$
(4.9)

which is equivalent to

$$\begin{aligned} |f|\mathrm{Re \, }\left\{ \left( 1-i|f|\right) \frac{Df}{f}\right\} \frac{dt}{dr}=r\, J_f(z).\end{aligned}$$
(4.10)

By the assumpion f is orientation preserving, so that \(J_f > 0\) in \({\mathbb {D}}\) and therefore, by (4.10), the condition (4.8) holds, Hence f is univalent in \({\mathbb {D}}\). Moreover \(f({\mathbb {D}}_r)\subset f({\mathbb {D}}_\rho )\) for \(0<r<\rho <1\). Thus \(f({\mathbb {D}}_r)\) and hence \(f({\mathbb {D}})\) are Archimedean spirallike.

Assume now that f is univalent on \({\mathbb {D}}\), orientation preserving and that \(f({\mathbb {D}}_r)\) is Archimedean spirallike. Then the intersection of \(C_r\) with \(w_\phi (t)\) is connected for each \(0<r<1\) and \(\phi \in {\mathbb {R}}\). Hence \(\phi (\theta )\) and \(t=t(r)\), given by (4.3) are nondecreasing in \(\theta \), and \(0<r<1\), respectively. The identities (4.10) and (4.5) yields then (4.1). \(\square \)

Reasoning along the same line, we obtain

Theorem 4.7

Suppose that a function \(f \in {\mathcal {H}}_0\) vanishes only for \(z=0\), and be such that \(J_f > 0\) on \({\mathbb {D}}\). Then \(f\in {\mathcal {H}}_0^{{\mathcal {H}}_S}\) if and only if the following inequality

$$\begin{aligned} \Re \left\{ \left( |f(z)|+i\right) \frac{Df(z)}{f(z)}\right\} > 0\qquad (z\in {\mathbb {D}}\setminus \{0\}) \end{aligned}$$
(4.11)

is satisfied.

Theorem 4.8

Suppose that a function \(f \in {\mathcal {H}}_0\) satisfies the conditions that \(f(z) = 0\) for \(z=0\) and that \(J_f > 0\) on \({\mathbb {D}}\). Moreover, let G be a differentiable function in the interval \((0,\infty )\). Then \(f\in {\mathcal {H}}_0^{{\mathcal {G}}_S}\) if and only if the following inequality

$$\begin{aligned} \Re \left\{ \left( 1-i|f(z)|\, G'(|f(z)|)\right) \frac{Df(z)}{f(z)}\right\} > 0\qquad (z\in {\mathbb {D}}\setminus \{0\}) \end{aligned}$$
(4.12)

is satisfied.

Remark 4.9

We note that the condition (4.12) can be rewritten as

$$\begin{aligned} \Re \left\{ \left( 1-i|f(z)|\right) \frac{zh'(z) - \overline{zg'(z)}}{h(z)+\overline{g(z)}}\right\} > 0\qquad (z\in {\mathbb {D}}\setminus \{0\}). \end{aligned}$$
(4.13)

5 Examples

The introduced function classes are not empty, even though it is not easy to determine the appropriate examples. Below we present some examples of the functions of the considered classes.

Example 5.1

We note that the harmonic Koebe function does not satisfy the condition (4.1), that is the harmonic Koebe function is not Archimedean spirallike. Also, harmonic Koebe function is not hyperbolic spirallike. Indeed, for \(k_{{\mathcal {H}}}(z)=h(z) +\overline{g(z)}\), where

$$\begin{aligned} h(z) =\frac{z-z^2/2+z^3/6}{(1-z)^3}, \qquad g(z) = \frac{z^2/2+z^3/6}{(1-z)^3} \end{aligned}$$

we have

$$\begin{aligned} D\,k_{{\mathcal {H}}}(z) = \frac{z(1+z)}{(1-z)^4} -\overline{\frac{z^2(1+z)}{(1-z)^4}}, \end{aligned}$$

and for Archimedean case we obtain (using Wolfram Mathematica, ver. 8.0)

$$\begin{aligned} \mathrm{Re \, }\left\{ \left( 1-i\,|k_{{\mathcal {H}}}(z_0)|\right) \frac{Dk_{{\mathcal {H}}}(z_0)}{k_{{\mathcal {H}}}(z_0)}\right\} \approx -7.8026\quad {for}\quad z_0=-\frac{1}{2} +\frac{ i}{2}, \end{aligned}$$

and for \(z_0=\frac{1}{2} -\frac{ i}{2}\) in the hyperbolic case we have

$$\begin{aligned} \mathrm{Re \, }\left\{ \left( |k_{{\mathcal {H}}}(z_0)|+i\right) \frac{Dk_{{\mathcal {H}}}(z_0)}{k_{{\mathcal {H}}}(z_0)}\right\} \approx -0.2847. \end{aligned}$$

But for \(G(w) = \log \, w\) and \(z_0=-\frac{1}{2} +\frac{ i}{2}\) we obtain

$$\begin{aligned} \mathrm{Re \, }\left\{ \left( 1-i\,|k_{{\mathcal {H}}}(z_0)|G'(|k_{{\mathcal {H}}}(z_0)|)\right) \frac{Dk_{{\mathcal {H}}}(z_0)}{k_{{\mathcal {H}}}(z_0)}\right\} \approx 0.6655, \end{aligned}$$

which means, that generalized spirallikeness is possible, for some G.

Fig. 1
figure 1

The domain \(f({\mathbb {D}})\) for \(f(z) = \dfrac{4z}{4+z}+\dfrac{2{\overline{z}}}{4+{\overline{z}}}\)

Full size image

Example 5.2

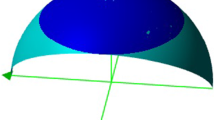
Let \(f(z) = \dfrac{4z}{4+z}+\dfrac{2{\overline{z}}}{4+{\overline{z}}}=h+{\overline{g}}.\) The image of the unit disk is very regular and a disk-like as seen in the attached figure (Fig. 1)

This function satisfy the normalized condition \(f(0) = 0,\ h'(0)=1\). The analytic part of f that is \(h(z) = \dfrac{4z}{4+z}\) is Archimedean spirallike, since

Also

$$\begin{aligned} D\, f(z)= \frac{16z}{(4+z)^2}-\dfrac{8{\overline{z}}}{(4+{\overline{z}})^2}, \end{aligned}$$

hence

$$\begin{aligned} \left| \frac{g'(z)}{h'(z)}\right| =\frac{8}{16}\left| \frac{4+z}{4+{\overline{z}}}\right| ^2\le \frac{1}{2}<1. \end{aligned}$$

Therefore \(J_f(z) > 0\) in \({\mathbb {D}}\) and then f is sense-preserving. However f is not Archimedean spirallike, since

$$\begin{aligned} \mathrm{Re \, }\frac{Df(z)}{f(z)}+|f(z)|\mathrm{Im \, }\frac{Df(z)}{f(z)}\approx -1.1766\ {for}\ z=-\frac{1}{6}-\frac{1}{2}i, \end{aligned}$$

and, for the same z

$$\begin{aligned} \mathrm{Re \, }\left\{ \left( |f(z)|+i\right) \frac{Df(z)}{f(z)}\right\} \approx -8.4093, \end{aligned}$$

which means that f is not hyperbolic spirallike.

Fig. 2
figure 2

The domain \(f({\mathbb {D}})\) for \(f(z) = \dfrac{z}{(1-z/5)(1-{\overline{z}}/5)}\)

Full size image

Example 5.3

Consider now the function mapping the unit disk to a domain similar in shape to the mapping from the previous example (Fig. 2)

$$\begin{aligned} f(z)=\dfrac{z}{(1-z/5)(1-{\overline{z}}/5)}. \end{aligned}$$

Then

$$\begin{aligned} h'(z)=\dfrac{1}{(1-z/5)^2(1-{\overline{z}}/5)},\quad h'(0)=1,\quad g'(z) = \dfrac{z}{(5-z)(1-{\overline{z}}/5)^2}, \end{aligned}$$

hence \(|g'(z)/h'(z)|<1\), so that f is orientation-preserving mapping. Moreover

$$\begin{aligned} \dfrac{Df(z)}{f(z)}=\dfrac{5}{5-z}-\dfrac{{\overline{z}}}{5-{\overline{z}}}\quad \textit{then}\quad \mathrm{Re \, }\dfrac{Df(z)}{f(z)}=1,\quad \mathrm{Im \, }\dfrac{Df}{f}>-\dfrac{5}{12}. \end{aligned}$$

Also \(|f(z)|<25/16\). Hence

$$\begin{aligned} \mathrm{Re \, }\frac{Df(z)}{f(z)}+|f(z)|\mathrm{Im \, }\frac{Df(z)}{f(z)}>1-\frac{5}{12}|f(z)|>1-\frac{125}{192}>0\quad (z\in {\mathbb {D}}), \end{aligned}$$

so that f is Archimedean spirallike in \({\mathbb {D}}\).

Consider now hyperbolic spirallikeness of f. We have

$$\begin{aligned} \mathrm{Re \, }\left\{ \left( |f(z)|+i\right) \frac{Df(z)}{f(z)}\right\} =|f(z)|\mathrm{Re \, }\dfrac{Df(z)}{f(z)}-\mathrm{Im \, }\dfrac{Df(z)}{f(z)}=|f(z)|-\mathrm{Im \, }\dfrac{Df(z)}{f(z)}.\nonumber \\ \end{aligned}$$
(5.1)

Since

$$\begin{aligned} |f(z)|=\dfrac{25|z|}{|5-z|^2},\quad \mathrm{Im \, }\dfrac{Df(z)}{f(z)}=\dfrac{10\,\mathrm{Im \, }z}{|5-z|^2},\quad \mathrm{Re \, }\dfrac{Df(z)}{f(z)}=1, \end{aligned}$$

then (5.1) holds if, and only if \(25|z|-10\,\mathrm{Im \, }z > 0\), which is satisfied for \(z\in {\mathbb {D}}\). Thus f is also hyperbolic spirallike.