Aerodynamic modeling of a delta-wing UAV for model-based navigation

Abstract

This study aims to identify an optimal, as well as practical, parametric structure for a delta-wing UAV aerodynamic model for the purpose of model-based navigation. We present a comprehensive procedure for characterizing the aerodynamics of this platform, utilizing a hybrid approach that combines open-air wind-tunnel experiments with the processing of real flight data using filter error method. The experimental design employs Latin Hypercube Sampling to maximize the observability of aerodynamic coefficients while adhering to time constraints. Candidate aerodynamic models are selected through step-wise regression. Numerical values for model coefficients are determined experimentally and subsequently calibrated through a two-phase procedure using real flight data. We then compare these models by assessing their effectiveness in improving navigation in the absence of GNSS signal in four different test flights, with respect to conventional inertial coasting using the autopilot IMU. The experimental evidence demonstrates that the model-based navigation, utilizing the proposed aerodynamic model structures, significantly reduces positioning errors compared to traditional navigation methods during GNSS outages.

1 Introduction

1.1 Motivation

Successful drone missions depend on accurate pose and velocity determination, typically achieved by fusing IMU¹ and GNSS² measurements. However, positioning drift caused by intermittent GNSS signal, poses a significant challenge for small UAVs, especially those equipped with less accurate IMUs due to weight, size and cost constraints. To address this issue, Vehicle Dynamic Model (VDM)-based navigation has gained traction as a promising method to enhance dead-reckoning without the need for additional navigation-aiding sensors. VDM leverages information about the adopted vehicle by incorporating knowledge of its aerodynamic model, materialized as a structure and the numerical values of its parameters, into the navigation filter. It has thus become an attractive solution for small UAVs experiencing GNSS outages when operating close to the ground or in constrained environments, as it significantly limits the growth of error in the navigation solution as compared to inertial coasting. Nonetheless, these benefits also come with the challenge of correctly identifying a reliable model representative of the platform aerodynamics. Many recent works [1,2,3,4,5,6,7] rely on the aerodynamic model proposed by Ducard [8] for conventional aircraft configurations. Simulations [9] and empirical testing [1, 4] on a small drone of a conventional aircraft with 4 (3-independent) control surfaces have demonstrated significant improvements in localization (an order of magnitude or more) compared to inertial coasting. However, the use of this type of platform is mostly limited to recreational flying or research applications. In the commercial drone market, tailless fixed-wing UAVs have emerged as the preferred platform for multiple purposes. These are found in literature referred as delta-wing UAVs [10,11,12,13] or flying wing UAVs [14,15,16]. Due to the blended wing-body (BWB) design of these platforms, the fuselage actively participates in lift generation. As a result, the lift-to-drag ratio of such platforms is improved with respect to traditional aircraft configurations, giving delta-wing UAVs the edge in missions requiring increased flight autonomy. A greater proportion of wing area in relation to the overall surface area enables flying wing UAVs to achieve slower flight speeds in the range of 10-13 m/s. This characteristic is particularly important to avoid blurring of captured imagery when flying within the EU/US rules which limit flight above ground level (AGL) to 120 m.³ Furthermore, the wing sweep of such vehicles enables a lower aspect ratio, which, in turn, enhances structural rigidity and reduces sensitivity to Reynold number [17]. However, the lack of a horizontal and vertical tail makes delta wing UAVs much less stable and more difficult to maneuver. These platforms are controlled via two control surfaces known as elevons. The elevons can act as elevators or ailerons respectively with symmetrical or asymmetrical deflections, making them underactuated vehicles. The absence of a rudder directly controlling yawing maneuvers of delta-wing UAVs causes an increased coupling of longitudinal and lateral dynamics during flight maneuvers. Consequently, aerodynamic characterization, especially from real flight data, becomes particularly challenging. Compared to UAVs with conventional aircraft configuration, there is a lack of relevant literature addressing the aerodynamic analysis of flying wing UAVs. Here are discussed some of the studies which treat the determination of the aerodynamic model parameters for such platforms and the methodologies employed.

1.2 Common models and approaches

The adaption of a semi-empirical methodology presented in [18] to flying wing UAVs is discussed in [14,15,16]. This methodology is based on the US Data Compendium (DATCOM) often used for preliminary aircraft design due to its ability to provide reasonable estimates of aerodynamic parameters in a timely manner. Given geometric properties and flight conditions of the platform as inputs, DATCOM provides aerodynamic coefficients by relying on interpolation from a vast array of real aircraft flight data. However, accuracy of such estimates is rather low and needs to be corroborated with additional experimental or numerical methodologies. Furthermore, [14] treats the case of a VTOL platform with a propeller in the middle of the body and [15] substitutes the control provided by the rudder with two additional control surfaces placed on the winglets for yaw control, thus differing from the standard configuration discussed in this work.

Experimental methodologies, based on a wind-tunnel, are a classical approach for aerodynamic characterization that are also heavily documented in literature. Wind-tunnel analysis relies on the principle of flow similarity. This principle ensures that the experimental aerodynamic estimates are reliable provided that the wind tunnel testing conditions, in terms of Mach and Reynolds number, are the same as for the free flight case [19]. Low-speed wind tunnels are generally categorized in two types: open-circuit and closed-circuit wind tunnels. In both cases, the test specimen is attached to a fixed sting and surrounded by the tunnel walls. Despite being one of the most reliable and adopted approaches for aerodynamic characterization, traditional wind tunnel testing only provides static estimates of the aerodynamic coefficients. For highly dynamic flight conditions, such as is the case for highly agile tailless UAVs, using coefficients only determined in wind tunnel analysis may not provide the best model predictive capabilities. Furthermore, the measurements are affected by the interference with wall and sting that inevitably bias the estimations.

Numerical approaches based on Computational Fluid Dynamics (CFD) are also widely employed to address the aerodynamic identification problem. The accuracy of a CFD software is dependent on its governing equations. Low fidelity CFD, based on Vortex-Lattice methods, is employed for a flying wing UAV in [14] but exclusively used as a validation method of the semi-empirically derived results. The use of high fidelity CFD using Ansys Fluent, which is based on the Reynolds-averaged Navier–Stokes (RANS) equations, for a delta-wing UAV is discussed in [13]. However, determining the longitudinal and lateral dynamics of a UAV with these methodologies is very time-consuming and requires i) a highly accurate 3D model of the studied platform, ii) the turbulence model and iii) correct selection of boundary conditions. These last requirements often come with the need of high computational resources and experience. Furthermore, numerical computations frequently need to be calibrated with experimental data to ensure reliability. For these reasons, CFD analysis if often not an effective standalone solution for the study of aerodynamics.

System identification from real flight data represents an attractive alternative to the previously introduced methodologies. It does not require access to experimental facilities or accurate modelling of complex flow conditions and provides more realistic mathematical models of the UAV dynamics as many maneuvers are difficult to replicate in traditional wind tunnel testing or in numerical computation with sufficient accuracy [20]. However, optimal observability of aerodynamic behavior would require flight tests to be performed in open loop control and with minimal wind disturbance [20, 21]. Delta-wing UAVs are often prone to stability issues due to the lack of a horizontal and vertical tail [14]. It thus becomes a necessity for this type of platform to fly in closed loop control, which leads to data co-linearity [22, 23]. Furthermore, achieving minimal wind disturbance may not always be feasible, and the process of estimating wind components in conjunction with aerodynamic coefficients can hinder the ability to identify parameters due to potential correlations. As described in [12], system identification methods can be classified as gradient based and non-gradient based. Equation error methods (EEM), output error methods (OEM), or filter error methods belong to the first category, whereas particle swarm optimization (PSO) is an example of the second. In [10,11,12], several of these approaches are analyzed and compared for a cropped delta-wing UAV with a vertical tail and a rudder using lower Cramer–Rao bounds to motivate the accuracy of results.

1.3 Paper scope

The aforementioned methodologies are built upon benchmark models derived from traditional aircraft designs, which were subsequently modified to suit the unique structure of a tailless delta-wing UAV. Notably, most of the literature studying flying wing UAVs refers to the aerodynamic model structure provided for the Zagi FW in [24]. In this work, we focus on analyzing possible alternative model structures, which are capable of correctly capturing the coupled dynamics of flying wings. The benefit of different model structures is evaluated for the scope of VDM-based navigation. For the aerodynamic characterization, we propose a hybrid approach which involves the combination of an experimental analysis methodology (wind-tunnel) and filter error methods based on real flight data.

The remainder of this paper is organized as follows: In Sect. 2, we introduce the theoretical framework of VDM-based navigation including basic propulsion and aerodynamic models. In Sect. 3, we present the experimental set up and the studied platform. Section 4 depicts the collected experimental data. In Sect. 5, we identify the coefficients of the propulsion model, while in Sect. 6, we determine the structure and numerical values of the coefficients for the platform aerodynamic model. The dead-reckoning performance of VDM-based navigation employing the proposed models is also discussed in this section.

2 Theoretical framework

Before introducing the mathematical equations characterizing the platform dynamics, we define the nomenclature used in this work. Figure 1 presents the relation between the two main coordinate frames adopted in this research: the body frame (FRD), denoted by ($x_b$, $y_b$, $z_b$), and the wind frame ($x_w$, $y_w$, $z_w$). The latter has its first axis in the direction of airspeed V and is defined by two angles with respect to the body frame: angle of attack $\alpha$ in the longitudinal plane and angle of side-slip $\beta$ in the lateral plane.

Fig. 1

Wind frame and related flight parameters with respect to the platform body frame

The deflection of two control surfaces, respectively denoted with $\alpha _L$ for the left elevon and $\alpha _R$ for the right elevon, is decomposed in i) symmetrical deflection, or elevator effect $\delta _e$, and in ii) asymmetrical deflection, or aileron effect $\delta _a$. These are mathematically defined as follows:

$$\begin{aligned} \delta _a = \frac{ \alpha _L - \alpha _R}{2},\; \; \delta _e = \frac{ \alpha _L + \alpha _R}{2} \end{aligned}$$

(1)

The UAV dynamics is jointly characterized by the propulsion model, providing the thrust $T^b$ and torque $Q^b$, and the aerodynamic model. Both are introduced in the following:

2.1 Propulsion model

According to [25], and as already reported in [26], the propulsion model dynamics can be generally characterized via the following thrust and torque equations expressed in the body frame:

$$\begin{aligned}&T^b(J,\omega _p) \,\, = \,\, C_{T0} \cdot \rho \cdot D_p^4 \cdot \omega _p^2 \,\, + \,\, C_{T1} \cdot \rho \cdot D_p^4 \cdot J \cdot \omega _p^2 \end{aligned}$$

(2)

$$\begin{aligned}&Q^b(J,\omega _p) \,\, = \,\, C_{Q0} \cdot \rho \cdot D_p^5 \cdot \omega _p^2 \,\, + \,\, C_{Q1} \cdot \rho \cdot D_p^5 \cdot J \cdot \omega _p^2 \end{aligned}$$

(3)

where $\rho$ indicates the air density and $D_p$ the propeller diameter. The non-dimensional quantity $J = V/\omega _p D_p$ is the advance ratio and contains the true airspeed V and propeller rotation speed $\omega _p$. The $C_{Ti}$ and $C_{Qi}$ quantities represent respectively the thrust and torque coefficients, that characterize the unique behavior of the studied propulsion system.

2.2 Aerodynamic model

The aerodynamic model specifies the forces and moments perceived by the platform as a consequence of flight parameters, i.e. angle of attack $\alpha$ and side slip angle $\beta$, control parameters, i.e. control surface deflection, and dynamic parameters, i.e. angular velocities $\omega _x$, $\omega _y$ and $\omega _z$. Its formulation is defined in terms of aerodynamic coefficients, dimensionless quantities independent of the platform size. Each model has three equations to define the aerodynamic forces and three for the aerodynamic moments. The force components in the wind-frame are respectively referred to as drag D, side force Y and lift L whereas the moment components, expressed in the body frame, are roll $M_x$, pitch $M_y$ and yaw $M_z$. When specific details about the model structure tailored for a particular platform are not available, the aerodynamic model’s design is based on a standardized benchmark formulation. This formulation decouples longitudinal and lateral dynamics and incorporates all flight, control and dynamic parameters [27]. The general equations for such a model are presented as follows:

$$\begin{aligned}&C_D= C_{D0}+C_{D\alpha }\alpha +C_{D\alpha 2}\alpha ^2+C_{D\beta }\beta \nonumber \\&\quad + C_{D\delta _e}\delta _e+C_{D\omega _x}\omega _x\nonumber \\&\quad +C_{D\omega _y}\omega _y+C_{D\omega _z}\omega _z \end{aligned}$$

(4)

$$\begin{aligned}&C_Y = C_{Y\beta }\beta +C_{Y\beta 2}\beta ^2 +C_{Y\delta _a}\delta _a\nonumber \\&\quad +C_{Y\omega _x}\omega _x+C_{Y\omega _y}\omega _y+C_{Y\omega _z}\omega _z\end{aligned}$$

(5)

$$\begin{aligned}&C_L = C_{L0}+C_{L\alpha }\alpha +C_{L\alpha 2}\alpha ^2+C_{L\beta }\beta + C_{L\delta _e}\delta _e\nonumber \\&\quad +C_{L\omega _x}\omega _x+ C_{L\omega _y}\omega _y+C_{L\omega _z}\omega _z\end{aligned}$$

(6)

$$\begin{aligned}&C_{Mx} = C_{M_{x\beta }}\beta +C_{M_{x\beta 2}}\beta ^2 +C_{M_{x\delta _a}}\delta _a\nonumber \\&\quad +C_{M_{x\omega _x}}\omega _x+ C_{M_{x\omega _x}}\omega _x+C_{M_{x\omega _z}}\omega _z \end{aligned}$$

(7)

$$\begin{aligned}&C_{My} = C_{My0}+C_{My\alpha }\alpha +C_{My\alpha 2}\alpha ^2+C_{My\beta }\beta + C_{My\delta _e}\delta _e\nonumber \\&\quad +C_{My\omega _x}\omega _x+C_{My\omega _y}\omega _y+C_{My\omega _z}\omega _z \end{aligned}$$

(8)

$$\begin{aligned}&C_{Mz} = C_{M_{z\beta }}\beta +C_{M_{z\beta 2}}\beta ^2 +C_{M_{z\delta _a}}\delta _a\nonumber \\&\quad +C_{M_{z\omega _x}}\omega _x+ C_{M_{z\omega _x}}\omega _x+C_{M_{z\omega _z}}\omega _z \end{aligned}$$

(9)

The specific force acting on the UAV in the body frame (b-frame) due to aerodynamic interactions and the propulsion system is determined according to:

$$\begin{aligned}{} & {} \textbf{f}^b = \frac{1}{m}\left( \begin{bmatrix} T^b\\ 0\\ 0 \end{bmatrix} + (\textbf{R}_b^w)^T\begin{bmatrix} q S C_D\\ q S C_Y\\ q S C_L \end{bmatrix}\right) \nonumber \\{} & {} \quad \text {with}\;\;\textbf{R}_b^w = \begin{bmatrix} \cos {\beta } &{} \sin {\beta } &{} 0\\ -\sin {\beta } &{} \cos {\beta } &{} 0\\ 0 &{} 0 &{} 1 \end{bmatrix}\begin{bmatrix} \cos {\alpha } &{} 0 &{} \sin {\alpha }\\ 0 &{} 1 &{} 0 \\ -\sin {\alpha } &{} 0 &{} \cos {\alpha } \end{bmatrix}\;\; \end{aligned}$$

(10)

with:

• $q = \frac{1}{2}\rho V^2$: dynamic pressure

• $\rho$: air density

• V: airspeed vector magnitude

• S: reference area

The total aerodynamic moment components are determined as follows:

$$\begin{aligned} \textbf{M}^b = \begin{bmatrix} q S bC_{M_x} + Q^b\\ q S \bar{c} C_{M_y}\\ q S b C_{M_z} \end{bmatrix} \end{aligned}$$

(11)

with:

• $\bar{c}$: mean aerodynamic chord (pitch lever arm)

• b: wing span

2.3 Model-based navigation filter architecture

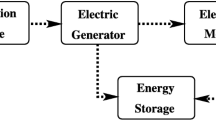
The employed model-based navigation architecture follows that of [9] and is shown in Fig. 2.

Fig. 2

VDM-based navigation filter architecture. After [9]

Here the vehicle dynamic model is implemented using Eq. 10 - 11 as the input to rigid body dynamics. Together with initial conditions, the solution of the rigid body equations defines the platform dynamics. An Extended Kalman Filter (EKF) utilizes VDM as a process model, contrary to the traditional kinematic implementation. Hence, IMU and GNSS data are both treated as observations. The VDM is fed with inputs from the autopilot control U and with a recursive estimation of the navigation states and wind components. The filter provides corrections to the following via state augmentation: navigation states $X_n$, wind $X_w$, IMU error parameters $X_e$ and aerodynamic model coefficients $X_p$.

3 Hardware

3.1 UAV platform

We use a custom-made delta-wing UAV developed at the Swiss Federal Institute of Technology Lausanne (EPFL) (Fig. 1). The wings are sourced from an externally manufactured product (Xeno Electric from Multiplex⁴), whereas the fuselage has been redesigned to accommodate a larger payload, and the power-train system has been upgraded to provide sufficient power for the increased weight. The autopilot employed is a Pixhawk 4 holybro running the open-source software PX4 (firmware version FMU-v5) with custom driver modifications. A precise GNSS receiver (JAVAD TR-2S), an airspeed sensor (single hole pitot tube) and an rpm sensor are connected to the autopilot in addition to the servos and two communication modules (telemetry, radio). Figure 3 presents a schematic of the platform payload with its sensors.

Fig. 3

Schematic of the components connected to the onboard autopilot

3.2 UAV propulsion

The propulsion system consists of a fixed-pitch propeller actuated by a brushless direct current (BLDC) motor (AXI 2814/20 gold line v2), providing a maximum power output of 355W which is sufficient to sustain the UAV take-off weight. The motor, connected to the propeller blade via a custom 3D printed connector, is controlled via an ESC⁵ (MULTIPLEX BL 55 SBEC⁶). The control command to the ESC arrives as a PWM signal issued by the PixHawk autopilot. Fig. 4 illustrates the power-train system components for the studied UAV.

Fig. 4

UAV power-train system

The RPM sensor (Beastx brushless) is connected to two of the three phases of the motor where it measures the produced back-emf voltage. These observations are output as PWM⁷ signal with a frequency proportional to the motor RPMs that is recorded by the autopilot. The Pixhawk ADC port, equipped with a dedicated topic in the internal communication protocol ($\textbf{uORB}$⁸), is utilized to avoid customization of the autopilot firmware. An additional MCU board, the Seeduino XIAO, is therefore employed to convert the PWM signal into an analog signal within the [0.0V; 3.3V] range. Figure 5 depicts the data conversion path that enables the transformation of the initial back-emf signal to an analog input for the Pixhawk autopilot.

Fig. 5

RPM data conversion path

3.3 Open-air wind tunnel experimental set-up

The wind-tunnel experiments were carried out in the facility of the LIS (Laboratory of Intelligent Systems) at EPFL. The set-up, shown in Fig. 6, is characterized by a modular wind generator called Windshaper [28], a 6-degree-of-freedom Staubli robotic arm used for changing the drone attitude with respect to the airstream, a 6-axis load cell to collect force and moment measurements and an optitrack motion capture system to follow the evolution in the UAV’s attitude. Motion capture markers (Fig. 6b) are strategically positioned on the UAV fuselage surface. Placement of markers on the wings was avoided to prevent interference with the airflow. These markers enable the Optitrack software to track the rigid body’s attitude using an array of cameras (Fig. 6c) in the experimental room. The load cell is placed directly below the delta-wing platform and secured to the robotic arm via a 3D printed custom holder (Fig. 6d).

Fig. 6

a Experimental set-up, b motion capture markers, c motion capture camera and d UAV custom holder

4 Experiment methodology

The wind-tunnel experimental analysis aims to isolate the aerodynamic behavior of the Delta-wing UAV in relation to variations in flight, control and dynamic parameters. The robotic arm allows control of flight and dynamic parameters through changes in attitudes at different rates following a designed flight sequence. The control parameters are managed by individually controlling the elevons to generate different combinations of control commands. Measurement of the total force and moments resulting from interaction of the drone with the Windshaper generated airflow are collected with the load cell. These measurements account for three main contributions: (i) aerodynamic interaction, (ii) gravity, (iii) inertial components caused by linear/angular acceleration. To isolate the first component, experiments are repeated twice; the first experiment is conducted without any wind (no-wind experiment), whereas the second experiment involves generating a desired reference airflow (wind experiment). We then employ cross-correlation to align the no-wind experiment and subtract it from the wind experiment. As the gravity and inertial components are the same in both experiments, this operation eliminates their combined effects in addition to any sensor bias, thereby yielding the required aerodynamic forces and moments. Two classes of experiments are performed: static and dynamic. In static experiments, the drone is held at desired attitudes during a predetermined acquisition time whereas in dynamic experiments real flight conditions are replicated by continuously evolving the drone orientation with respect to the upcoming airflow. Figure 7 presents a schematics of the wind tunnel experiment pipeline.

Fig. 7

Experimental pipeline

4.1 Data transformation

The force and moments measured by the load cell are expressed in the load cell frame, also referred to as the measurement frame (m-frame), having its origin situated within the load cell. The desired aerodynamic force and moment are, on the other hand, expressed respectively in the wind and body frame, with their origin in the UAV center of gravity. The difference between the involved frames, once the misalignment has been corrected, can be expressed in the form of a lever arm that indicates the position of the center of gravity in the m-frame $r_{cg}^m = [x_{cg}, y_{cg}, z_{cg}]^T$.

The location of the center of gravity has been experimentally determined in the FRD⁹ oriented m-frame, and resulted to be

$$\begin{aligned} \begin{bmatrix} x^m_{cg} \\ y^m_{cg} \\ z^m_{cg} \end{bmatrix} = \begin{bmatrix} -2.44 \pm 0.02 \;\;\;\; cm \\ \;\;\; 0.01 \pm 0.02 \;\;\;\; cm \\ -5.90 \pm 0.07 \;\;\;\; cm \end{bmatrix} \end{aligned}$$

(12)

which, as expected, situates it in the payload area.

The measured moments are therefore corrected and the expression in the body frame is given by

$$\begin{aligned} {\textbf {M}}^b = {\textbf {M}}^m - {\textbf {r}}^m_{cg} \times {\textbf {F}}^m \end{aligned}$$

(13)

with ${\textbf {M}}^m$ indicating the measured moments in the m-frame and ${\textbf {M}}^b$ their expression in the body frame.

4.2 Data sampling

The data sampling strategy is established to maximize the observability of aerodynamic coefficients while minimizing experimental time and avoiding the injection of systematic biases by the experimenter. The principle of randomization is one of the cornerstones established by the branch of statistics devoted to optimization of experimental design (DOE). This technique ensures that the errors in the experimental procedure will consist of independently distributed random variables [29]. While random sampling of experimental points respects this principle, it does not efficiently explore the multi-dimensional state space defined by the possible attitudes during the wind tunnel experiment. Latin hypercube sampling (LHS) solves this problem by maximizing the variability of the sampled points. Contrary to random sampling this approach accounts for the previously sampled points. It divides each dimension of the N-dimensional state space into M non-overlapping, equal intervals thus creating a subdivision of $M\times N$ hypercubes. Latin hypercube sampling ensures that within each hypercube, random samples are taken in such a way that for each variable, only one sample point is selected from each interval. This approach maintains variability across the experimental points in the entire state space while still meeting the requirement for randomization.

Static experiments: The reference attitudes for the static experiment data are sampled using Latin hypercube sampling, which minimizes the number of data points needed to explore the state space while ensuring that a representative dataset is collected. Figure 8 illustrates the chosen reference attitudes for static acquisition.

Fig. 8

Data sampling for static experiment reference attitudes [26]

Dynamic Experiments: Dynamic experiments analyze the impact of different flight dynamics by sampling data obtained combining Euler angle oscillations with varying angular frequencies in the form of Lissajous curves. The parameters for these curves are iterated based on Latin hypercube sampling allowing for the description of complex harmonic-motion based trajectories. The resulting attitude components are depicted in Fig. 9.

Fig. 9

Reference attitudes for dynamic experiments [26]

4.3 Static experiment data

Static experiments allow for the evaluation of the steady-state response of the UAV platform at different attitudes. The steady-state condition is reached when transient effects settle. This is ensured by holding each attitude for a duration of three seconds, allowing the transient time to elapse and the collection of a buffer of data during the steady-state condition. Given the acquisition frequency of $100 \,Hz$, this allows for the collection of a data buffer of approximately 300 data points. Physical vibration of the platform due to the inherent challenges in generating a perfectly uniform and constant airflow using the Windshaper are then filtered for the buffer of data. Consequently, this type of experiment has the benefit of providing a dataset with reduced noise, enabling a more accurate fitting of the data. Figure 10 depicts the result of the data collection for the longitudinal dynamics in a static experiment with trimmed control surfaces (i.e. held at zero-deflection position by the autopilot control system).

Fig. 10

Longitudinal dynamics for trimmed static experiments

The curves show the low noise during steady-state acquisitions which allow for an accurate estimate of the platform static behavior. Another interesting finding emerging from the data is the positive correlation observed between the angle of attack and the pitching moment which suggests that the UAV being studied is statically unstable. Nonetheless, overall stability is achieved via actuation of the wing control surfaces. The position of the neutral point being ahead of the center of gravity is the cause of the static instability rendering the UAV more susceptible to external conditions such as gusts of wind. However, it also makes the platform highly agile due to the high maneuverability and quick responsiveness to control commands. Figure 11 illustrates the data collected during a static experiment with concurrent excitation of the elevons. Notably, a linear relationship is depicted in the longitudinal dynamic with a symmetrical deflection of the control surfaces (elevator effect). The control surface deflection in Fig. 11 is mapped in a $[-1,1]$ interval with the end of range values respectively denoting maximum negative and positive deflection.

Fig. 11

Longitudinal dynamics for static experiments with elevons control

4.3.1 Reynolds number effect

The Reynolds number is a dimensionless parameter, measuring the relative importance of inertial forces with respect to viscous forces within an airflow. It is defined as:

$$\begin{aligned} Re = \frac{\rho V L_c}{\mu } \end{aligned}$$

(14)

where $L_c$ indicates the characteristic length of the system, V the airspeed magnitude, $\rho$ and $\mu$ respectively the density and viscosity of the medium. For an aircraft, the adopted characteristic length is generally the mean aerodynamic chord $\bar{c}$. The corresponding Reynolds number is thus often referred to as the chord-based Reynolds number ($Re_c= \rho V\bar{c} / \mu$). This parameter impacts the aerodynamic behavior of a flying vehicle as it defines the airflow regime, laminar or turbulent, during flight conditions and when the transition from one to the other occurs. It is particularly relevant for small UAVs since it is often close to its critical value ($1\times 10^5$) [30], due to the typical reference length and flight speed.

Table 1 shows the ranges of Reynolds numbers for the considered delta wing ($\bar{c} = 0.26m$), based on the range of attainable airspeeds, for a variety of air density ($\rho \in [0.9; 1.2] Kg/m^3$) and temperature ($T \in [0^{\circ }; 35^{\circ }] C$) values.

Table 1 Reynolds number values for the range of flight speeds [26]

We examined the impact of Reynolds number on static experiments for a range of values around its critical threshold. Figure 12 illustrates how the drag and lift coefficient curves are affected.

Fig. 12

Impact of different Reynolds numbers on drag and lift coefficient curves

While the drag coefficient curve shows minimal impact across a large span of angles of attack, corroborating the findings in [31], the behaviour of the lift coefficient is influenced. The slope of the curve indicated a relatively higher lift produced at higher Reynolds numbers for the same angle of attack. This is in accordance with the results observed in [32], a study focusing on the aerodynamics of an unpowered fixed-wing MAV (Micro Aerial Vehicle).

4.4 Dynamic experiments data

Static experiments offer a dataset with reduced noise, yet they fail to account for the influence of flight dynamics on the airflow distribution around the UAV. In this context, dynamic experiments offer a more accurate depiction of real-world flight conditions.

Fig. 13 illustrates the results of data collection during dynamic experiments. Multivariate plots, depicting the dependence of three explanatory variables, have been used to show the different dependencies of force and moment coefficients.

Fig. 13

Full dynamics experimental data

Notably, the longitudinal force and moment coefficients (upper row) exhibit a clear relationship with pitching angular velocity. Contrarily, the lateral dynamics (lower row) show a less defined dependence on the angular rate. This is particularly evident in the yaw moment coefficients case, where the absence of dedicated control surface (rudder) results in a scattered data distribution due to the highly coupled lateral dynamics.

5 Propulsion model identification

In this section, we present the experimental process followed to identify the propulsion system model coefficients described in Eq. 8 and 9. These coefficients describe the aerodynamic interaction of the actuated propeller blades with an upcoming airflow. The wind generator (Windshaper) is controlled to output different reference airflow velocities, while the autopilot varies the level of throttle issued. The resulting thrust $T^b$ and torque $Q^b$ are measured by the load cell while the attitude is maintained constant throughout the experiment. Physical vibrations within the raw data were removed via low-pass filtering. Figure 14 depicts the relationship between the input throttle command and the corresponding observed propeller speed at the output, measured using an RPM sensor.

Fig. 14

Measured propeller speeds for experimental input throttle and airspeed ranges. After [26]

The measured propeller speed for lower input throttle commands and higher airflow are non-linear. This phenomenon is referred as windmilling [25]. Its effect progressively diminishes in significance as the throttle input level increases, ultimately ceasing when the propeller accelerates the air mass beyond the reference airspeed. Figure 15 presents the result of fitting the experimental data with the model expressed by equations 8 and 9.

Fig. 15

Thrust and torque models fitted to experimental data. After [26]

A comparison between the acquired data and the model-predicted thrust and torque is depicted in Fig. 16

Fig. 16

Comparison of model prediction on thrust and torque with raw and filtered data. After [26]

In certain situations, the measurements from the load cell can exhibit considerable noise, especially when dealing with torque, as the values are typically quite small, leading to a lower signal-to-noise ratio. In these cases, it may be sufficient to use the simplified model we’ve suggested for navigation purposes. This model relies on relative airspeed and propeller speed information and can provide a reliable solution.

6 Aerodynamic model structure identification

6.1 Methodology

To determine different candidate aerodynamic model structures, we make use of step-wise regression analysis on data from static and dynamic experiments. This technique is an iterative approach that entails the gradual addition (forward selection) or exclusion (backward elimination) of explanatory variables in a regression model based on their statistical significance [21]. We consider the aerodynamic force and moment components (D,Y,L,$M_x$,$M_y$,$M_z$) as the dependent variables, while the flight parameters $\alpha$, $\beta$, the control parameters $\delta _e$, $\delta _a$ and the dynamic parameters $\omega _x$, $\omega _y$, $\omega _z$ are regarded as independent variables (or explanatory variables). Each step of the model building process, candidate explanatory variables are ranked based on the amount of correlation showed with the correspondent dependent variable. This is measured using the coefficient of determination $R^2$ [29]. This coefficient, ranging from 0 to 1, indicates the percentage of the output variable that the constructed model is capable of reproducing, highlighting the statistical significance of its regressors. As more explanatory variables are added in the model, the value of this coefficient increases. We stop adding new explanatory variables in the step-wise regression when an increase of the coefficient of determination is less than $1\%$. However, a more complex model, characterized by a higher $R^2$, does not necessarily translate to better prediction qualities as depicted in Fig. 17 [22].

Fig. 17

Model complexity effect

However, in its classical formulation, the coefficient of determination has a tendency to increase as more predictors are added to the model. Consequently, the adjusted coefficient of determination $R^2_{adj}$ is utilized in this work and is defined as follows:

$$\begin{aligned} R^2_{adj} = (1 - [(1-R^2)\frac{N-1}{N-n_p}])\times 100 \end{aligned}$$

(15)

where N indicates the total number of experimental data points and $n_p$ the number of model predictors (explanatory variables). The adjusted coefficient of determination penalizes over-parametrized models where the number of predictors tend to grow larger. Figures 18 and 19 present the $R^2_{adj}$ plots, incrementally constructed with step-wise regression, for each of the aerodynamic force and moment equations, for both static and dynamic experiments.

Fig. 18

Force-related adjusted coefficient of determination plots for static and dynamic experiments

Fig. 19

Moment-related adjusted coefficient of determination plots for static and dynamic experiments

These plots provide a visual representation of the correlation levels between various explanatory variables and the force and moment components and will be used as reference in the following discussion (Sect. 6.2) for the determination of candidate aerodynamic model structures. The coefficients weighting the influence of the highest correlated explanatory variable within each force and moment equation are known as "main effects". Utilizing this information, we can develop different models with varying levels of complexity. Numerous test models were examined to determine the ideal compromise between the simplicity of the model and its predictive capabilities. Given our aim of using the aerodynamic model for VDM-based navigation using an error (augmented) state filter, an additional objective is to create a model that is more resilient to the development of inter-state correlations. Consequently, significant effort has been dedicated to constructing models that reduce the inter-model correlation among parameters in the various force and moment equations by separating flight and control parameters.

6.2 Candidate aerodynamic model structures

The following presents a subset of the tested models, which provide a representative outlook of the global behavior observed during the model identification phase, along with the corresponding static and dynamic $R^2_{adj}$ tables (Tables 2, 3, 4).

• 1. Model A In this structure, the moments (Eqs. 19–20) are only governed by control derivatives and the resulting change in attitude alters the stability derivatives ($\alpha$, $\beta$) governing the forces (Eqs. 16–18). This results in a decorrelation of force and moment coefficients. The yaw contribution is deemed negligible due to the absence of the rudder (Table 2).

  $$\begin{aligned}&C_D=C_{D0}+C_{D\alpha 2}\alpha ^2 \end{aligned}$$

  (16)
  $$\begin{aligned}&C_Y=C_{Y0}+C_{Y\beta }\beta \end{aligned}$$

  (17)
  $$\begin{aligned}&C_L=C_{L0}+C_{L\alpha }\alpha \end{aligned}$$

  (18)
  $$\begin{aligned}&C_{Mx}=C_{Mx0}+C_{Mx\delta _a}\delta _a\end{aligned}$$

  (19)
  $$\begin{aligned}&C_{My}=C_{My0}+C_{Mx\delta _e}\delta _e \end{aligned}$$

  (20)

Table 2 Summary table of $R^2_{adj}$ statistics for model A

• 1. Model B Model B (Eqs. 21–26) accounts for the main effects among the independent variables described both in static and dynamic experiments. With respect to model A, it introduces a formulation for the yaw coefficient by including the highest ranked explanatory variable that, interestingly, is the result of a combination of elevator and aileron effects.

  $$\begin{aligned}&C_D=C_{D0}+C_{D\alpha }\alpha +C_{D\alpha 2}\alpha ^2 \end{aligned}$$

  (21)
  $$\begin{aligned}&C_Y= C_{Y0} + C_{Y\beta }\beta \end{aligned}$$

  (22)
  $$\begin{aligned}&C_L=C_{L0}+C_{L\alpha }\alpha \end{aligned}$$

  (23)
  $$\begin{aligned}&C_{Mx}=C_{Mx0}+C_{Mx\delta _a}\delta _a\end{aligned}$$

  (24)
  $$\begin{aligned}&C_{My}=C_{My0}+C_{My\alpha }\alpha +C_{Mx\delta _e}\delta _e\end{aligned}$$

  (25)
  $$\begin{aligned}&C_{Mz}=C_{Mz\delta _a\delta _e}\delta _a\delta _e \end{aligned}$$

  (26)

Table 3 Summary table of $R^2_{adj}$ statistics for model B

• 1. Model C This model includes, on top of the main effects, interaction coefficients and dynamic derivatives.

  $$\begin{aligned}&C_D=C_{D0}+C_{D\alpha }\alpha +C_{D\alpha 2}\alpha ^2 +C_{D\delta _e}\delta _e +C_{D\alpha \delta _e}\alpha \delta _e +C_{D\omega _y}\omega _y \end{aligned}$$

  (27)
  $$\begin{aligned}&C_Y= C_{Y0} + C_{Y\beta }\beta + C_{Y\omega _x}\omega _x + C_{Y\alpha }\alpha \end{aligned}$$

  (28)
  $$\begin{aligned}&C_L=C_{L0}+C_{L\alpha }\alpha +C_{L\delta _e}\delta _e+C_{L\omega _y}\omega _y\end{aligned}$$

  (29)
  $$\begin{aligned}&C_{Mx}=C_{Mx0}+C_{Mx\delta _a}\delta _a\end{aligned}$$

  (30)
  $$\begin{aligned}&C_{My}=C_{My0}+C_{My\alpha }\alpha +C_{Mx\delta _e}\delta _e\end{aligned}$$

  (31)
  $$\begin{aligned}&C_{Mz}=C_{Mz0} + C_{Mz\delta _a\delta _e}\delta _a\delta _e + C_{Mz\delta _a}\delta _a + C_{Mz\beta }\beta \end{aligned}$$

  (32)

Table 4 Summary table of $R^2_{adj}$ statistics for model C

6.3 Model coefficients identification

The values of the coefficients determined via the previously described experimental analysis of wind-tunnel data are not definitive due to two reasons:

• 1. Differences between real flight and experimental conditions.

• 2. Possible variation of the payload configuration between flights.

Due to the approaches taken in performing the experiments, secondary aerodynamic effects, such as Reynolds number effect (discussed in Sect. 4.3.1) and propwash effect (discussed in [26]), are not accounted for in the identified aerodynamic coefficients. Furthermore, the presence of a small support system for the UAV during testing, inevitably causes minor interference in the air-flow [33]. On the other hand, the non-repeatability over different flights is related to the modular nature of the considered platform. Small differences in the alignment of the removable payload and of the battery (small variations in position are possible due to the velcro-dry-zipper attachment) or of the external assembly (fuselage cover) affect inertial and aerodynamic properties of the UAV. Furthermore, the small damage to the wings accumulated over the UAV lifespan due to landings and drone manipulations can also impact its aerodynamic behavior. Consequently, the value of aerodynamic coefficients will slightly differ at each flight.

A Bayesian approach is employed for taking into account the variability of model coefficients values. Priors for the aerodynamic derivatives are set as Gaussian distributions centered at the values estimated during the experimental campaign. The navigation EKF is then employed as a Bayesian filter to incorporate flight data and recursively generate a posteriori estimate of the aerodynamic derivatives. Notably the calibration procedure can be separated into two phases:

• Coarse adjustment (or Phase 1 calibration)

• Fine adjustment (or Phase 2 calibration)

Here we use an offline implementation of the filter (VDM-EKF) to replay the pre-recorded flight data for calibration as well as navigation performance evaluation.

Coarse adjustment is driven by the availability of post-processed data, using a Kalman smoother, with a GNSS accuracy in cm-level for position and cm/s for velocity to adapt the experimentally pre-determined coefficients to real flight conditions. An initial uncertainty of $\sim 1\%$ of their initial values is assigned to the aerodynamic derivatives’ initial covariance matrix $P_0$.

Fine adjustment is intended to be performed in-flight to slightly re-tune the $X_p$ coefficients to their optimal value using GNSS in single-point positioning after take-off. Here we employ the data recorded from the onboard autopilot to reproduce the same condition as would be obtained by running the VDM-based navigation filter in real time. A small uncertainty ($\sim 0.1\%$) is assigned to the model aerodynamic parameters as determined in Coarse adjustment. This allows the aerodynamic coefficients to slightly adjust at the beginning of the flight, when the GNSS positioning is still available. The model hence evolves towards a more representative depiction of the current flight condition. At the same time, the small uncertainty prevents a divergence or overfitting of model coefficients in case of limited observability (e.g. a flight with constant direction and velocity). Once the values of aerodynamic coefficients stabilize, usually within the first 2 min of flight, the filter is well conditioned to produce a dead-reckoning navigation solution in the absence of GNSS signal. Figure 20 provides a schematic of the coefficient identification procedure while Figs. 21 and 22 depict the numerical values of the aerodynamic coefficients in the various phases of the identification process for model B.

Fig. 20

Schematics of the coefficient identification phases

Fig. 21

Aerodynamic force coefficients during the three phases of the identification process

Fig. 22

Aerodynamic moment coefficients during the three phases of the identification process

6.4 Model comparison

Inter-model:Here we compare the three model structures proposed in Sect. 6.2. Each model candidate is evaluated offline using four test flights with respect to improvements in dead-reckoning using a VDM-based navigation filter. The objective is to assess the self-localization performance that can be achieved on-board using a minimal set of inertial and barometric sensors such as those available on the PixHawk autopilot. Single-point GNSS positioning is made available at the beginning of the flight for fine-tuning coefficients (phase 2 calibration) before testing the effect of GNSS signal withdrawal. The VDM-based navigation filter relies on a subset of measurements available on the Pixhawk autopilot: IMU, GNSS, barometer and motor rpms.

Three instances of the VDM-EKF are generated, each employing one of the presented candidate solutions as its model structure. Table 5 summarizes the employed flights

Table 5 Summary of the testing reference flights

The flights trace different trajectories and are characterized by different dynamics and wind conditions. The initial part is performed in manual flight mode and presents several turns to ensure proper excitation of the aerodynamic derivatives through different flight maneuvers while preserving stability through the autopilot control loop. This part of the flight is essential as it enables the fine-tuning of the aerodynamic coefficients (phase 2 calibration) and estimation of the wind components within the augmented state vector. The remaining part of the flight is devoted to test the quality of the VDM-based navigation solution for GNSS outages in different flight scenarios.

Figure 23 depicts the performance of each candidate model during 2 min GNSS outages within the 4 flights. The displayed metric is the horizontal error with respect to the reference trajectory obtained via post-processing solution with continuous GNSS data. The positioning error is evaluated only in the horizontal plane as the information from the barometer sensor allows to prevent the vertical drift of the platform during dead-reckoning navigation.

Fig. 23

Horizontal drift comparison of the proposed models for model-based navigation during GNSS outage in different test flights

It can be observed that the proposed models perform comparably throughout the different test flights although model A and B appear to be slightly more robust in flight 2. Figure 24 shows a direct comparison of the VDM-based navigation performance of candidate models with respect to the reference trajectory respectively for flight 1 (manual-stabilized flight mode) and flight 4 (Mission mode) for longer (200-second) outages.

Fig. 24

Horizontal drift comparison of the proposed models for model-based navigation during GNSS outage

Notably the dynamics of the flight is retained in both cases for all considered models. Similar results were obtained for the remaining flights and hence not shown. From the obtained results, it seems that models A and B represent a good compromise between the dead-reckoning quality and simplicity of the model structure. In particular, model A benefits from the decorrelation of moment and force equations due to the separation of dependency between control surfaces and flight parameters. This separation prevents the build-up of correlation between the respective coefficients during the calibration phases (1 and 2) while offering a navigation solution comparable to more complex models. The additional advantage of a minimal model structure is that it results in lower computational load, particularly in terms of covariance matrix propagation, and has thus the potential to be implemented in hardware with low computational resource. This is important to consider for micro-processor implementations such as that which the PX4 autopilot stack is currently running.

Inertial coasting: Here we compare the dead-reckoning performance of VDM-based navigation on a delta wing UAV with respect to inertial coasting. Since the barometer allows for the mitigation of vertical drift, we depict errors exclusively in the horizontal plane. Figure 25 shows the errors of VDM dead-reckoning using model B and that of inertial coasting for the autopilot IMU.

Fig. 25

Evolution of the horizontal error under GNSS outage

The drift of inertial coasting varies among the test flights from $\sim 500$ to $\sim 3000$ m, most likely due to the differences in trajectory shape, flight dynamics and wind conditions. On the other hand, the maximum drift of the VDM-based solution appears to be less dependent on these factors with horizontal error being between one and two orders of magnitude less than those of inertial coasting.

6.5 Conclusion

The contributions of this work can be summarized in the following aspects:

First, we present a model structure identification methodology for small delta-wing UAV in an open-air wind tunnel set-up. The collected experimental data are based on a combination of static and dynamic observations sampled with LHS. The experimental design allows for the observability of explanatory variable to be enhanced, while minimizing the required experimental time. From these data, we identify three possible model structures with approximate values of their coefficients employing step-wise regression. The selection criterion is based on increments of the adjusted coefficient of determination.

Second, we both fine-calibrate and evaluate the presented aerodynamic models in different flights under varying wind and flight dynamics conditions. Differences between experimental and real flight conditions lead to significant discrepancies in aerodynamic coefficient values which must be compensated. One of the possible sources of variation analyzed is the Reynolds number effect showed in this work to be a non-negligible secondary aerodynamic effect due to the platform Reynolds number being near to the critical value. We show that relatively simple models (A and B) are sufficiently representative for navigation purposes; i.e. they depict a one to two order of magnitude improvement with respect to inertial navigation in GNSS denied scenarios.

The size of both identified models remains reasonable for implementations in resource constrained micro-controllers. Model A is further attractive due to the functional independence of its force and moment coefficients.

As a result, this study shows that appropriate selection of a vehicle aerodynamic model structure specific to VDM-based navigation is crucial. The optimal formulation for the model, providing the best dead-reckoning performance, does not necessarily coincide with the best model formulation in the traditional aerodynamic sense.